Active subthreshold dendritic conductances shape the local field potential

Abstract

Key points

• The local field potential (LFP), the low‐frequency part of extracellular potentials recorded in neural tissue, is often used for probing neural circuit activity. Interpreting the LFP signal is difficult, however.

• While the cortical LFP is thought mainly to reflect synaptic inputs onto pyramidal neurons, little is known about the role of the various subthreshold active conductances in shaping the LFP.

• By means of biophysical modelling we obtain a comprehensive qualitative understanding of how the LFP generated by a single pyramidal neuron depends on the type and spatial distribution of active subthreshold currents.

• For pyramidal neurons, the h‐type channels probably play a key role and can cause a distinct resonance in the LFP power spectrum.

• Our results show that the LFP signal can give information about the active properties of neurons and imply that preferred frequencies in the LFP can result from those cellular properties instead of, for example, network dynamics.

Abstract

The main contribution to the local field potential (LFP) is thought to stem from synaptic input to neurons and the ensuing subthreshold dendritic processing. The role of active dendritic conductances in shaping the LFP has received little attention, even though such ion channels are known to affect the subthreshold neuron dynamics. Here we used a modelling approach to investigate the effects of subthreshold dendritic conductances on the LFP. Using a biophysically detailed, experimentally constrained model of a cortical pyramidal neuron, we identified conditions under which subthreshold active conductances are a major factor in shaping the LFP. We found that, in particular, the hyperpolarization‐activated inward current, I _h, can have a sizable effect and cause a resonance in the LFP power spectral density. To get a general, qualitative understanding of how any subthreshold active dendritic conductance and its cellular distribution can affect the LFP, we next performed a systematic study with a simplified model. We found that the effect on the LFP is most pronounced when (1) the synaptic drive to the cell is asymmetrically distributed (i.e. either basal or apical), (2) the active conductances are distributed non‐uniformly with the highest channel densities near the synaptic input and (3) when the LFP is measured at the opposite pole of the cell relative to the synaptic input. In summary, we show that subthreshold active conductances can be strongly reflected in LFP signals, opening up the possibility that the LFP can be used to characterize the properties and cellular distributions of active conductances.

Key points

• The local field potential (LFP), the low‐frequency part of extracellular potentials recorded in neural tissue, is often used for probing neural circuit activity. Interpreting the LFP signal is difficult, however.

• While the cortical LFP is thought mainly to reflect synaptic inputs onto pyramidal neurons, little is known about the role of the various subthreshold active conductances in shaping the LFP.

• By means of biophysical modelling we obtain a comprehensive qualitative understanding of how the LFP generated by a single pyramidal neuron depends on the type and spatial distribution of active subthreshold currents.

• For pyramidal neurons, the h‐type channels probably play a key role and can cause a distinct resonance in the LFP power spectrum.

• Our results show that the LFP signal can give information about the active properties of neurons and imply that preferred frequencies in the LFP can result from those cellular properties instead of, for example, network dynamics.

Abbreviations

LFP

local field potential

PSD

power spectral density

Introduction

The local field potential (LFP), the low‐frequency part ($\genfrac{}{}{0pt}{}{<}{\sim \phantom{{}_x}}$500 Hz) of the extracellular potential recorded in the brain, has experienced rejuvenated interest in the last decade. This is partly due to the development of novel silicon‐based microelectrodes with tens or hundreds of electrode contacts covering large volumes of brain tissue, the realization that the LFP offers a unique window into neural population activity, and the possibilities offered by the signal in steering neuroprosthetic devices (Buzsáki et al. 2012; Einevoll et al. 2013 a). The interpretation of the LFP signal in terms of neural activity is challenging, however, as in general thousands of neurons contribute to the recorded signal (Lindén et al. 2011). Careful mathematical modelling is thus needed to take full advantage of the opportunities that the LFP signal offers (Einevoll et al. 2013 a).

Fortunately, the biophysical origin of LFP signals seems well understood in the context of volume conduction theory (Nunez & Srinivasan, 2006), and a forward‐modelling scheme linking transmembrane neural currents to recorded electrical potentials, including LFPs, has been established (Rall & Shepherd, 1968; Holt & Koch, 1999). The forward‐modelling scheme has been successfully used to study the cortical LFP signal generated by single neurons (Lindén et al. 2010) as well as cell populations (Pettersen et al. 2008; Lindén et al. 2011; Łęski et al. 2013; Reimann et al. 2013; Tomsett et al. 2015). These studies showed, for example, that the lower frequencies of the synaptic input current give the largest contributions to the LFP for two reasons. First, the lowest frequencies give the largest transmembrane current dipole moments due to the filtering properties of dendrites (Lindén et al. 2010). Second, increased correlations in synaptic input to a population of neurons can strongly amplify the LFP signal (Lindén et al. 2011; Einevoll et al. 2013 a,b), and this amplification is strongest for the lowest input frequencies (Łęski et al. 2013). Furthermore, the amplification of the LFP due to synaptic input correlations requires the input to be asymmetrically distributed over the dendrites (Lindén et al. 2011; Łęski et al. 2013).

While many of these studies were carried out using neuron models with passive dendrites (Pettersen et al. 2008; Lindén et al. 2010, 2011; Łęski et al. 2013; Tomsett et al. 2015), recent studies have also been done with neuron models with active dendrites (Schomburg et al. 2012; Reimann et al. 2013; Taxidis et al. 2015; Sinha and Narayanan, 2015). Neurons express a variety of active conductances that are distributed in specific ways across both soma and dendrites (Stuart et al. 2007). For example, the h‐type current is most densely concentrated in the distal apical dendrites (Williams & Stuart, 2000; Magee, 1998), whereas the M‐type slow potassium current is mostly localized close to the soma (Hu et al. 2007). It is well established that such active conductances can affect the subthreshold processing of synaptic input (e.g. Magee, 2000; Stuart et al. 2007; Remme & Rinzel, 2011). This is highly relevant for understanding the LFP signal because, in cortex, the LFP is thought to mainly reflect synaptic currents and their associated return currents (Mitzdorf, 1985; Einevoll et al. 2007, 2013 a).

Here we use a modelling approach to investigate specifically the role of voltage‐dependent conductances in shaping the LFP in the subthreshold regime. We focused on pyramidal cells as they are thought to be the main contributor to the LFP in cortical recordings (Einevoll et al. 2013 a) and used the state‐of‐the‐art cortical layer 5 pyramidal neuron model by Hay et al. (2011) as a starting point for our investigation. With this highly detailed model we established that subthreshold active conductances can indeed have a sizable impact on the LFP signal. Using a simplified neuron model that used generalized descriptions of active conductances, so‐called quasi‐active currents (Koch, 1984; Remme, 2014), we were able to obtain an understanding of how any active conductance can affect the LFP, depending on the characteristics of the current and its distribution across the neuron.

Methods

Pyramidal neuron model

Numerical simulations for Figs 1 and 2 were carried out using a model of a cortical layer 5 pyramidal cell that was published by Hay et al. (2011). We used the cell morphology named ‘cell #1’ with model parameters from table 3 in Hay et al. (2011), available from ModelDB (Hines et al. 2004; accession number 139653). This model has a detailed morphology and includes ten active ionic conductances fitted to experimental data by multi‐objective optimization with an evolutionary algorithm. The model exhibits both the perisomatic firing response to current steps and back‐propagating action potential‐activated Ca²⁺ spike firing. For simulations of a passive model, the active conductances were removed from the model. Simulations with a so‐called ‘frozen’ h‐type conductance were performed by keeping the gating variable of the h‐current constant, yielding an additional passive conductance. The original model showed a voltage gradient from soma to distal apical dendrites. To simplify the interpretation of the simulation results, we adjusted the leak reversal potential of each compartment such that we could set the resting potential uniformly to a specified chosen potential (Carnevale & Hines, 2006). Cell models where the original membrane potential gradient was retained exhibited the same qualitative behaviour as cell models with a uniform resting membrane potential, only the level of the activation of voltage‐gated ion channels was affected.

Figure 1. Active conductances can shape the extracellular signature of synaptic inputs .

A, a single synaptic input is provided to a cortical layer 5 pyramidal cell model. The extracellular response is shown at five positions (cyan circles) for two cases: the active model that includes various voltage‐dependent conductances (red; see Methods), or a passive model from which the active conductances have been removed (black). The position of the input is marked by the yellow star: at the distal apical dendrite (top panels) or at the soma (bottom panels). The cell's resting potential was held uniformly at a hyperpolarized potential of −80 mV (left panels) or at a depolarized potential of –60 mV (right panels). The synaptic peak conductance was 0.001 μS. The plots show the x–z plane of the cell; the soma and the electrodes are positioned at y = 0. B, as in A, but using white‐noise current input (see Methods) instead of synaptic input, and displaying the response as the power spectral density (PSD). The PSD is calculated from 1000 ms simulations. C, apical input (marked by star) to the cell model held at a hyperpolarized potential (–80 mV). The extracellular potential is shown at two positions (cyan circles) for the active (red) and passive (black) model and for two additional versions of the model: the passive model supplemented by I _h (dashed blue), and the passive model supplemented by frozen I _h (dotted grey; see Methods).

Figure 2. Quasi‐active conductances accurately mimic the responses of nonlinear conductances .

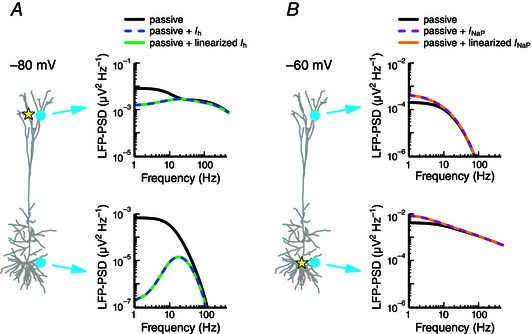
A, apical white‐noise current input (yellow star) is provided to a cortical pyramidal cell model held at a hyperpolarized potential (–80 mV). The LFP‐PSD is shown at two locations (cyan circles) for a passive model (black), a passive model with I _h (dashed blue) and a passive model that includes a linearized or quasi‐active I _h (green; see Methods). B, as in A, but with somatic white‐noise current input and using the following three models: a passive model (black), a passive model with I _NaP (dashed magenta) and a passive model with linearized I _NaP (orange).

The neuron model received either excitatory synaptic input or white‐noise current input. Synaptic inputs were modelled as steps in the synaptic conductance followed by an exponential decay with a time constant of 2 ms and used a reversal potential of 0 mV. The white‐noise current input consisted of a sum of sinusoids with identical amplitudes but random phases for each integer frequency from 1 to 500 Hz (see Lindén et al. 2010). The resulting white‐noise signal was scaled to obtain current fluctuations with a standard deviation of 8 pA. Injection of this input into the distal apical dendrite at a distance of 1094 μm from the soma of the active cell held at −60 mV yielded local membrane potential fluctuations with a standard deviation of 1.5 mV. The exact same white‐noise input was used in all simulations (i.e. so‐called ‘frozen’ noise).

Quasi‐active approximation of voltage‐dependent ion currents

Voltage‐dependent membrane currents often behave in a near‐linear fashion for small perturbations around a holding potential. This can be exploited by making linear approximations, so‐called ‘quasi‐active’ models, of the non‐linear ionic currents (Mauro et al. 1970; Koch, 1984; Hutcheon & Yarom, 2000; Remme, 2014). In this way one can reduce the parameter space while retaining key dynamic features of the system. The results in Figs 2, 3, 4, 5, 6, 7, 8, 9 used quasi‐active currents to simplify the original, non‐linear cortical pyramidal cell model (see above) and to allow for a systematic study of the effects of active conductances on the LFP.

Figure 3. The type of active conductance, its distribution across the cell membrane and the location of the input shape the LFP .

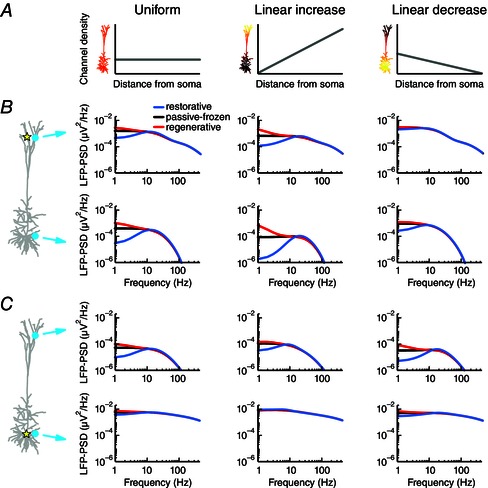
A, a single quasi‐active conductance was distributed across the pyramidal cell model in three ways: uniformly (left), linearly increasing (centre) or linearly decreasing (right) with distance from the soma. The density of the linearly increasing conductance increased 60‐fold from the soma to the most distal apical dendrite, while the linearly decreasing conductance had a sixty‐fold decrease over the same range. B, apical white‐noise current input (yellow star) was provided to the cell model and the LFP‐PSD was determined at two positions (cyan circles). The quasi‐conductance was either regenerative (red), passive‐frozen (black) or restorative (blue). The three cases had the same total resting membrane conductance and the total passive leak conductance was equal to the total quasi‐active conductance. C, as in B, but with white‐noise current input provided to the soma.

Figure 4. Activation time constants of active conductances determine the frequencies for which they affect the LFP .

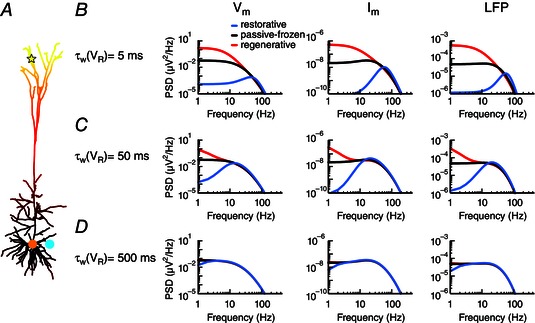
A, apical white‐noise current input (yellow star) to the cortical pyramidal cell model with a single linearly increasing quasi‐active conductance (as in middle column of Fig. 3 B). B, the quasi‐active conductance is either restorative (blue), passive‐frozen (black) or regenerative (red), and the PSD is shown for the somatic membrane potential $V_m$ (left panel), the somatic transmembrane currents $I_m$ (middle panel) and the LFP (right panel) at a position close to the soma (cyan dot). The activation time constant of the quasi‐active conductance is ${\tau }_w\left(V_R\right)=5\mathrm{ms}.$ C, as B, but with ${\tau }_w\left(V_R\right)=50\mathrm{ms}.$ D, as B, but with ${\tau }_w\left(V_R\right)=500\mathrm{ms}.$

Figure 5. Resonance is retained for asymmetric input from distributed synapses .

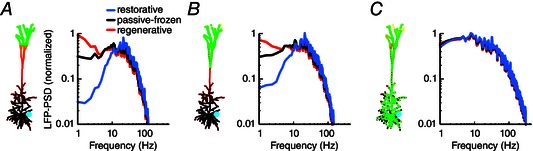
A, the pyramidal cell model expressed a single linearly increasing quasi‐active conductance (see Fig. 4 A) that was either restorative (blue), passive‐frozen (black) or regenerative (red). One thousand excitatory conductance‐based synapses (green circles) with a peak conductance of 0.0001 μS were distributed across the distal apical tuft more than 900 μm from soma. The synapses were activated by independent Poisson processes with a mean rate of 5 spikes s^–1. Simulations were run for 20 s and the LFP‐PSD was calculated using Welch's method. B, as A, but with synapses distributed above the main bifurcation, 600 μm from the soma. C, synapses were distributed uniformly across the entire cell.

Figure 6. Resonance in the LFP resulting from a restorative conductance is a spatially stable feature .

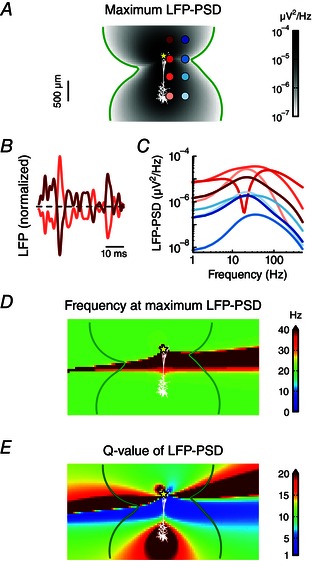
A, apical white‐noise current input (yellow star) is provided to the cortical pyramidal cell model with a single quasi‐active conductance with increasing density with distance from soma. The resulting LFP‐PSD was calculated at a dense 2D grid surrounding the cell. The maximum power of the LFP is denoted in shades of grey. The green contour line shows where the LFP power is 10^–7 μV² Hz^–1. B, excerpts of LFP time traces at two extracellular positions, corresponding to the two electrodes at the opposite side of the zero crossing region of the dipole in A (i.e. the first and third electrode contact in the left column). C, LFP‐PSD computed at the eight electrode positions marked by shades of red and blue in A. D, the frequency for which the LFP‐PSD shows the maximum power (see A). E, the Q‐value of the LFP‐PSD, defined as the maximum power (see A) divided by the power at 1 Hz.

Figure 7. Membrane‐potential and LFP resonance frequencies are closely related .

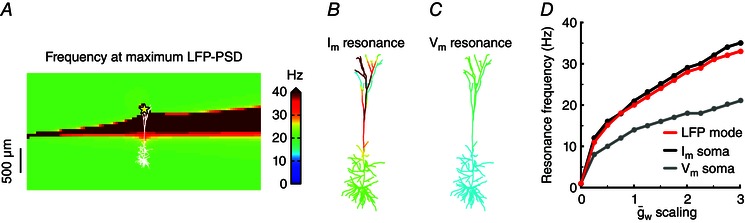
A, the resonance frequency in the LFP surrounding a cell receiving apical white‐noise current input (yellow star) is shown for a cortical pyramidal cell model with a single quasi‐active conductance with increasing density with distance from soma. This panel is identical to Fig. 6 D, but shown again for easy reference. B, the resonance frequency of the transmembrane currents of each cellular compartment is calculated for the same simulation as in A, and superimposed on the cellular morphology, using the colour coding from A. C, same as B but for the membrane potential. D, the resonance frequency of the LFP mode (the most commonly occurring resonance frequency of the LFP in the probed region, red curve), the somatic transmembrane currents (black curve) and the somatic membrane potential (grey curve), as a function of different scalings of the quasi‐active conductance strength, ${\overline{g}}_w$ (see Methods). The overall spatial distribution of the quasi‐active conductance, i.e. a 60‐fold linear increase along the apical dendrite, was retained, and A–C correspond to a ${\overline{g}}_w$scaling of 1.

Figure 8. Membrane potential, transmembrane current and LFP for a pyramidal neuron with a single quasi‐active conductance .

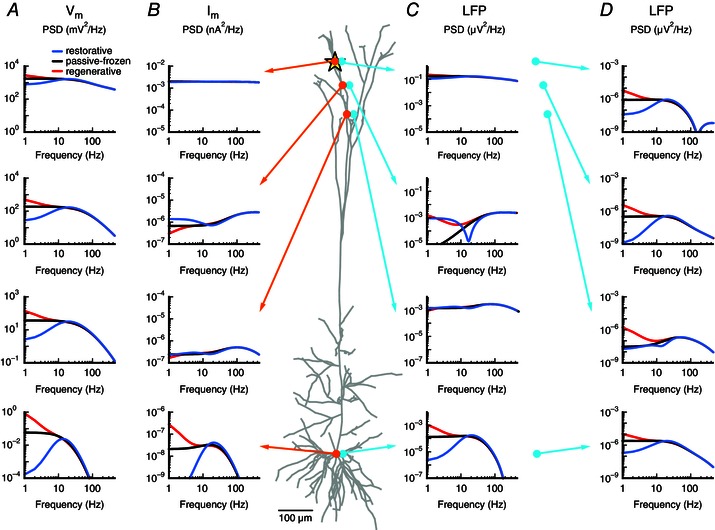
White‐noise current input (yellow star) was applied to a cortical pyramidal cell model with a single quasi‐active conductance with increasing density with distance from soma, corresponding to the case in Figs 6 and 7. The quasi‐active conductance was restorative (blue), passive‐frozen (black) or regenerative (red). A, membrane potential PSD ($V_m$) is shown at the (intracellular) positions marked by the orange circles. B, as in A, but showing the transmembrane current PSD at the positions of the orange circles. C, as in A, but showing the LFP‐PSD for the extracellular positions marked by the cyan circles (20 μm from the corresponding cellular compartment marked in orange). D, as in C, but showing the LFP‐PSD for electrode positions (cyan circles) 600 μm from the corresponding cellular compartment marked in orange.

Figure 9. Membrane potential, transmembrane current and LFP for a semi‐infinite neurite with a quasi‐active conductance .

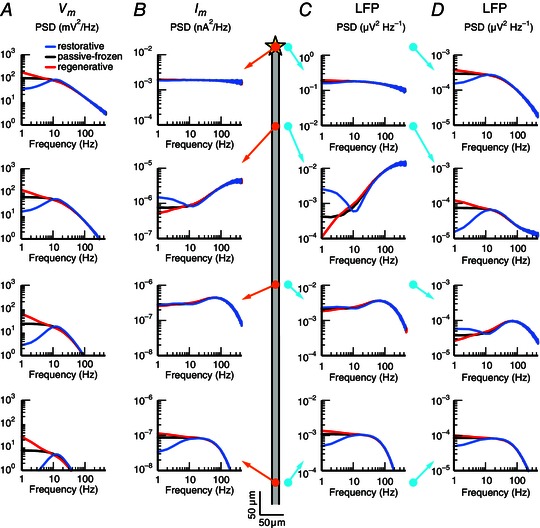
White‐noise current input (yellow star in schematic illustration in the middle) was applied to the end of a semi‐infinite neurite with a single quasi‐active conductance that was either restorative (blue), passive‐frozen (black) or regenerative (red). The simulated neurite had length 2000 μm, diameter 2 μm and intracellular resistivity $R_a=100\Omega$cm, and the passive leak and quasi‐active conductance density were both uniformly set to 50 μS cm^–2. A, membrane potential PSD ($V_m$) is shown at the (intracellular) positions marked by the orange circles in the schematic (at 0, 177, 531 and 973 μm distance from the input). B, as in A, but showing the transmembrane current PSD at the positions of the orange circles. C, as in A, but showing the LFP‐PSD for the (extracellular) positions marked by the cyan circles (20 μm from the neurite). D, as in C, but showing the LFP‐PSD for electrodes 300 μm from the neurite, marked by the cyan circles.

We here briefly describe the derivation of a quasi‐active description of a single cellular compartment. The compartment includes one active current $I_w$ that depends on the membrane potential $V\left(t\right)$ and is described by $I_w\left(t\right)={\overline{g}}_{w}w\left(t\right)\left(V\left(t\right)-{\mathit{E}}_{\mathit{w}}\right)$, with peak conductance ${\overline{g}}_w$, reversal potential E_w and gating variable $w\left(t\right)$. The passive leak current is given by ${\mathit{I}}_{\mathit{L}}\left(t\right)=g_L\left(V\left(t\right)-{\mathit{E}}_{\mathit{L}}\right)$, with conductance g_L and reversal potential E_L. Finally, the axial current, i.e. the net current entering or leaving to neighbouring cellular compartments, is denoted by $I_{\mathrm{axial}}\left(t\right)$. The voltage of the compartment then evolves according to

$$\begin{array}{ccc}\hfill {\mathit{c}}_{\mathit{m}}\frac{\mathrm{d}\mathit{V}\left(t\right)}{\mathrm{d}t}& =& -{\overline{g}}_{w}w\left(t\right)\left(V\left(t\right)-{\mathit{E}}_{\mathit{w}}\right)-g_L\left(V\left(t\right)-{\mathit{E}}_{\mathit{L}}\right)\hfill \\ & & +I_{\mathrm{axial}}\left(t\right),\hfill \end{array}$$ (1)

where the term $c_m\frac{\mathrm{d}V\left(t\right)}{\mathrm{d}t}$ is the capacitive current with membrane capacitance $c_m$. The dynamics of the gating variable $w\left(t\right)$ is given by

$${\tau }_w\left(V\right)\frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}=w_{\infty }\left(V\right)-w\left(t\right),$$ (2)

with voltage‐dependent activation time constant ${\tau }_w\left(V\right)$ and activation function $w_{\infty }\left(V\right)$.

The quasi‐active description is obtained by linearizing V and w around resting‐state values $V_R$ and $w_{\infty }\left(V_R\right)$, respectively, by means of Taylor expansions. Defining the variable $m\left(t\right)\equiv \left(w\left(t\right)-w_{\infty }\left(V_R\right)\right)/\frac{\partial }{\partial V}{w}_{\infty }\left(V_R\right)$, we can write the linearized equation describing the voltage dynamics of a single compartment:

$${\mathit{c}}_{\mathit{m}}\frac{\mathrm{d}\mathit{V}\left(t\right)}{\mathrm{d}t}=-{\mathit{g}}_{\mathit{L}}\left({\gamma }_R\left(\mathit{V}\left(\mathit{t}\right)-{\mathit{V}}_{\mathit{R}}\right)+\mu m\left(t\right)\right)+{\mathit{I}}_{\mathit{axial}}\left(t\right),$$ (3)

where ${\gamma }_R\equiv 1+{\overline{g}}_w{w}_{\infty }\left(V_R\right)/g_L$, i.e. the ratio between the total membrane conductance (at $V_R$) and the leak conductance. The parameter $\mu \equiv \left({\overline{g}}_w/g_L\right)\left(V_R-E_w\right)\frac{\partial }{\partial V}{w}_{\infty }\left(V_R\right)$ determines whether the quasi‐active current functions as a positive feedback (when μ<0; i.e. a regenerative current) amplifying voltage deviations from the holding potential $V_R$, or as a negative feedback (when μ>0; i.e. a restorative current) counteracting changes in the voltage. When μ = 0, the quasi‐active current is frozen and functions as a static passive current (throughout the text we will refer to this as the ‘passive‐frozen’ case). The dynamics of the linear gating variable m is described by

$${\tau }_w\left(V_R\right)\frac{\mathrm{d}m\left(t\right)}{\mathrm{d}t}=V\left(t\right)-V_R-m\left(t\right).$$ (4)

The description of the ionic currents in a single compartment is easily extended to a multi‐compartmental model where each compartment can have its own set of parameters to describe the passive and quasi‐active currents.

For the simulations with a single linearized h‐type current or persistent sodium current (see Fig. 2), we kept the passive parameters, as well as the peak conductance and activation time constant (at the specified holding potential) of the relevant active current, the same as in the original detailed model.

To systematically study the effect of the cellular distribution of a quasi‐active current on the LFP (see Fig. 3), we used three different channel density distributions: (1) linearly increasing with distance from the soma, (2) linearly decreasing with distance from the soma and (3) a uniform distribution. The slopes of the increasing (decreasing) distributions were set such that the most distal tip of the apical dendrite had a 60‐fold larger (smaller) density than that of the soma (in line with experimental estimates for I _h distributions: Lörincz et al. 2002; Kole et al. 2006; Nusser, 2009; Mishra & Narayanan, 2015), and the total membrane conductance of the quasi‐active current (i.e. summed over all compartments) was the same as the total passive leak conductance $g_L$. The passive leak conductance was set uniformly to 50 μS cm^–2 for all cases. For $w_{\infty }\left(V_R\right)=0.5$ the distance‐dependent quasi‐active peak conductance was ${\overline{g}}_w\left(x\right)=5.29+0.242x$ μS cm^–2 for the linear increase, and ${\overline{g}}_w\left(x\right)=143-0.109x$ μS cm^–2 for the linear decrease, where the distance x was measured in micrometres and had a maximum of 1291 μm. Note that the three distributions had the same total quasi‐active membrane conductance summed over the neuronal membrane.

The parameters μ and ${\gamma }_R$ vary along the cell for the non‐uniform channel distributions. We introduced μ*≡ μ(x)$g_L/{\overline{g}}_w\left(x\right)$, such that μ* =$\left(V_R-E_w\right)\frac{\partial }{\partial V}{w}_{\infty }\left(V_R\right)$ is independent of the distribution of the quasi‐active conductance and can be specified as a single constant. We used μ* = −0.5 for the regenerative conductance, μ* = 0 for the passive‐frozen conductance and μ* = 2 for the restorative conductance. For the uniform distribution this gives the same values as those used in Remme & Rinzel (2011), namely μ = −1, 0 and 4 for the regenerative, passive‐frozen and restorative cases, respectively. The activation time constant ${\tau }_w\left(V_R\right)$ of the quasi‐active conductance was set to 50 ms (unless specified otherwise) in order to have dynamics similar to the h‐type conductance. Intracellular resistivity was $R_a=100$ Ω cm, and the specific membrane capacitance $c_m=1$ μF cm^–2.

Calculation of extracellular potentials

Extracellular potentials recorded inside the brain are generated by transmembrane currents from cells in the vicinity of the electrode contact (Nunez & Srinivasan, 2006). The biophysical origin of the recorded signals is well understood in the context of volume conduction theory. Extracellular potentials originating from a simulated multi‐compartmental neuron model can be computed by first obtaining the transmembrane currents $I_n\left(t\right)$ from each compartment n at position $\overrightarrow{r_n}$. Next, the extracellular potential $\phi \left(\vec{r},t\right)$ at position $\vec{r}$ resulting from these transmembrane currents can be calculated (Holt & Koch, 1999; Lindén et al. 2014):

$$\phi \left(\vec{r},t\right)=\frac{1}{4\pi \sigma }\sum _{n=1}^N{I}_n\left(t\right)\int \frac{\mathrm{d}{\vec{r}}_n}{\left|\vec{r}-{\vec{r}}_n\right|},$$ (5)

where σ is the conductivity of the extracellular medium. This corresponds to the so‐called line‐source formula assuming the transmembrane currents to be evenly distributed along the axes of cylindrical neural compartments; see Lindén et al. (2014) for a detailed description.

All simulations and computations of the extracellular potentials were carried out using LFPy (Lindén et al. 2014), an open‐source Python package that provides an interface to NEURON (Carnevale & Hines, 2006). The time step of the neural simulation was 0.0625 ms. For all simulations the first 1000 ms was discarded to avoid initialization effects. All simulation code used to produce the figures in this study is available upon request.

Results

To examine the contribution of subthreshold, active conductances on the extracellular potential we started by considering a previously published, detailed model of a layer 5 cortical pyramidal neuron endowed with a large variety of active conductances (Hay et al. 2011; see Methods).

Note that the term LFP commonly refers to the low‐pass filtered version (below 300–500 Hz) of the extracellular potential (to filter away spikes). As there is no spiking activity in the present use of the model, we simply refer here to the unfiltered version of the extracellular potential as the LFP.

Active subthreshold conductances shape the LFP

We first determined the LFP in response to a single excitatory synaptic input. We compared the LFP signal of the active neuron model with a passive version of the model (i.e. all active conductances removed). The synaptic input was provided either to the distal apical dendrite (Fig. 1 A, top row) or to the soma (Fig. 1 A, bottom row) while the entire cell was hyperpolarized to −80 mV (Fig. 1 A, left column) or depolarized to −60 mV (Fig. 1 A, right column). The LFP was calculated at five different positions outside the neuron (marked by cyan circles). The difference between the LFPs of the active and passive models depended on the holding potential of the cell, the synaptic input position, as well as the extracellular recording position. In particular, we observed for hyperpolarized potentials that the active and passive LFPs were markedly different for apical synaptic input, while being very similar for somatic input.

To more fully characterize the effects of active currents on the LFP we next applied white‐noise current input instead of a single synaptic input, and determined the power spectral density (PSD) of the resulting LFP (i.e. the square of the Fourier amplitude of the signal as a function of frequency). The white‐noise input current had equal signal power at all integer frequencies in the considered frequency range (1–500 Hz; see also Lindén et al. 2010). At most extracellular recording positions, a low‐pass filtering was observed in the LFP of both the active and the passive model. This results from the intrinsic dendritic filtering (e.g. Pettersen & Einevoll, 2008; Lindén et al. 2010; Pettersen et al. 2012) and increases with distance from the synaptic input site (Fig. 1 B). The most striking difference between the active and the passive case was again found for the cell in a hyperpolarized state with apical input (Fig. 1 B, top left), which showed a strong resonance (i.e. band‐pass filter with a peak around 17–22 Hz) for the active model LFP, but not for the passive one. Note that the cell in a depolarized state and apical input shows qualitatively the same effect, although less prominent (Fig. 1 B, top right).

While the main effect of the active conductances in the case of apical input was to reduce the LFP power at the lowest frequencies, the effect from active conductances on somatic input was qualitatively different. For the cell with a depolarized resting potential, white‐noise current resulted in an amplification of the low frequencies (Fig. 1 B, bottom right). Note that increasing the standard deviation of the white‐noise input current above 8 pA (see Methods) led to spiking for the depolarized cell with somatic input, while results from the hyperpolarized cell were essentially unaffected even when the membrane potential showed fluctuations of 10–15 mV. In all situations considered, a difference between the active and passive model was only apparent below about 30–50 Hz. At higher frequencies, capacitive currents dominated the transmembrane return currents in both the active and the passive models (Lindén et al. 2010). The exact cross‐over frequency where the capacitive currents become dominant over the ionic membrane currents depends on neuronal properties (e.g. ion channel densities), as well as the positions of the input and the recording electrode.

Which ionic currents in the model are responsible for the large difference between the active and passive model for hyperpolarized potentials and with apical input? One obvious candidate is the hyperpolarization‐activated inward current I _h. This current operates at subthreshold voltages, is concentrated in the apical dendrites and dampens the lowest frequency components of the membrane potential response to input (Magee, 1998; Hu et al. 2002, 2009; Kole et al. 2006; Almog & Korngreen, 2014). Indeed, we found that when we extended the passive model with only the h‐type conductance, the LFP was indistinguishable from the full active model when the cell was in a hyperpolarized state and received apical input (Fig. 1 C).

Two effects are involved in the reduction of the LFP signal power at low frequencies in the model with I _h. First, with an additional active current comes an increased membrane conductance, which shifts the transmembrane return currents associated with the input current closer to the input position on the neuron. This gives smaller current‐dipole moments and thus generally smaller LFPs (Pettersen & Einevoll, 2008; Lindén et al. 2010; Pettersen et al. 2012). This is still a passive‐membrane effect and can simply be incorporated into a passive model by rescaling the leak conductance corresponding to adding a ‘frozen’ h‐type conductance. The second effect stems from the dynamic properties of an active conductance such as I _h, which actively counteract voltage fluctuations at low frequencies. While the extension of the passive model with a ‘frozen I _h’ was found to strongly dampen the low‐frequency components of the LFP compared to the full active case (Fig. 1 C, grey dotted lines), it failed to reproduce the resonance of the models with the dynamic I _h conductance (blue dashed and red). This demonstrates that the resonance observed in the LFP was an effect caused by the dynamics of the h‐type channels, similar to previously reported I _h‐induced resonances in the membrane potential (Hutcheon & Yarom, 2000; Hu et al. 2009; Zhuchkova et al. 2013).

Linear models capture the effects of active conductances on the LFP in the subthreshold regime

Above, we established that the h‐type conductance is key in shaping the LFP for subthreshold input to the apical dendrites in the model by Hay et al. (2011). In reality there is considerable variation between pyramidal neurons regarding their biophysical properties, depending on, for example, brain region, developmental stage and even the neurons’ post‐synaptic targets (Spruston, 2008; Dembrow et al. 2010). Furthermore, not all relevant subthreshold currents can be expected to be captured by the specific model by Hay et al. (2011). We therefore next set out to perform a systematic study of the effects that any subthreshold active conductance can have on the LFP.

For this we made use of the so‐called ‘quasi‐active’ approximation of voltage‐dependent currents. Active membrane conductances in general exhibit non‐linear behaviour, but for small deviations of the membrane potential around a holding potential, active conductances often behave in a near‐linear fashion. The dynamics of an active conductance can then be approximated by linearizing the current around a holding potential (Mauro et al. 1970; Koch, 1984; Remme & Rinzel, 2011; Remme, 2014; see Methods). This retains the voltage‐dependent current dynamics for potentials not too far away from that potential, while strongly reducing the parameter space of the model and allowing an intuitive understanding of the model behaviour.

Linearized active conductances can be divided into two classes: restorative and regenerative. Restorative conductances act as phenomenological inductances, dampening the lowest frequency components of the membrane potential response to synaptic input, thereby also leading to narrower synaptic voltage responses (Remme & Rinzel, 2011). The intrinsic low‐pass filtering of the cellular membrane (Koch, 1999), in combination with the active dampening of low frequencies (i.e. high‐pass filtering) by restorative conductances, can thus cause a resonance in the membrane potential PSD (Hu et al. 2009; Remme & Rinzel, 2011; Zhuchkova et al. 2013). Examples of restorative currents are the h‐current and the M‐type slow potassium current. In contrast, regenerative conductances act as phenomenological capacitances, amplifying the low‐frequency components of the membrane potential response to synaptic input, making the voltage responses to synaptic input broader in time as they propagate along the dendrites. This will only add to the intrinsic low‐pass filtering of the cellular membrane, and as such, regenerative conductances lack the easily recognizable feature of the restorative conductances. Examples of regenerative conductances are the persistent sodium current I _NaP and the low‐voltage activated calcium current (Remme & Rinzel, 2011).

It is well established that quasi‐active approximations of active currents can accurately capture the subthreshold effects on the membrane potential (Koch, 1984; Remme & Rinzel, 2011). To test whether this conclusion also holds for the LFP, we started with the original cortical pyramidal cell model from Hay et al. (2011), and simplified it to two separate cases with only a single active conductance remaining in each. For the first case, we kept only the restorative I _h conductance, with its increasing conductance along the apical dendrite away from the soma. The resting potential was set uniformly to the hyperpolarized potential of −80 mV and the cell was stimulated with apical white‐noise input. In the second case we kept only the regenerative persistent sodium current, solely present in the soma, set the resting potential uniformly to the depolarized potential of −60 mV and applied somatic white‐noise input. The I _h‐only model yielded the resonance in the LFP that was discussed above (Fig. 2 A, blue dashed lines), while the I _NaP‐only model gave an amplification of the low‐frequency components of the LFP (Fig. 2 B, pink dashed lines). We then simulated the models with linearized versions of the original conductances and found the LFP from the active and linearized conductances to be indistinguishable (Fig. 2, blue vs. green, pink vs. orange). In fact, for all tested combinations of resting potentials, input positions and LFP recording positions, the quasi‐active approximation was found to faithfully reproduce the signature of the active conductance in the membrane potentials, the transmembrane currents, as well as in the LFP. This applied as long as the perturbations of the membrane potential around the resting potential were not too large. For I _h, fluctuations of 10–15 mV are typically within the appropriate range (data not shown, but see, for example, Remme & Rinzel, 2011).

In summary, we have shown that the subthreshold dynamics of the experimentally constrained cortical pyramidal cell model can be excellently represented by a model with a passive membrane supplemented only with the h‐type conductance (Fig. 1 C). Further, this h‐type conductance can be excellently represented by a linearized (quasi‐active) version (Fig. 2 A). We conclude that systematic studies with a single quasi‐active conductance are justified.

Spatially asymmetric distributions of ion channels and inputs enhance the effect of active currents on the LFP

We next turned to a systematic exploration of how active subthreshold currents affect the LFP. For this we used a pyramidal cell model with a single quasi‐active current. The key parameter characterizing the quasi‐active current is μ*, the sign of which determines whether the current is regenerative (μ* < 0) or restorative (μ*>0), while μ* = 0 for a passive‐frozen conductance (i.e. the added conductance has no dynamics and thus simply adds to the passive leak conductance). The quasi‐active current was distributed across the cell either uniformly, linearly increasing with distance from soma or linearly decreasing with distance from soma (Fig. 3 – left, middle and right columns, respectively). In all cases the models had the same total membrane conductance summed over the neuronal membrane. We applied white‐noise current input either to the apical dendrite (Fig. 3 B) or to the soma (Fig. 3 C) and calculated the LFP‐PSD for each case in the apical region and in the somatic region. A large difference between the results from the passive‐frozen model and the restorative or regenerative models would imply that the dynamics of the active conductance in question shapes the LFP. Indeed, we found for most scenarios that the regenerative current caused an amplification of the low‐frequency components of the LFP (Fig. 3, red lines) compared to the passive‐frozen case (black line), while a restorative current dampened the low frequencies, leading to the previously discussed resonance (Fig. 3, blue lines). However, as discussed below, there were exceptions.

We found that the impact of the quasi‐active current was always largest in the LFP recorded on the opposite side of the cell compared to the position of the input, i.e. next to the soma for apical input (Fig. 3 B, bottom row) and next to the apical dendrite for somatic input (Fig. 3 C, top row). This can be understood as the LFP is a distance‐weighted sum of all transmembrane currents, so that transmembrane currents close to the recording electrode will contribute more to the measured LFP signal. For recordings on the opposite side relative to the input, the transmembrane return currents have been strongly affected by the active conductance after propagating along the apical dendrite. The effect was also largest when the quasi‐active current was non‐uniformly distributed and concentrated at the position of the input (Fig. 3 B, middle column; Fig. 3 C, right column), and smallest when the input was to a region of low density (Fig. 3 B, right column; Fig. 3 C, middle column). This also follows from the reasoning above: when the input is to a region with a low density of an active current, the return currents close to the input will be hardly affected by the active current. As the signal propagates along the dendrites to regions with higher densities of the active current, it will be increasingly affected by the active current, although the signal amplitude will also gradually decrease. Therefore, the LFP is less affected by the presence of a non‐uniformly distributed active current when the input is provided to a region with low densities compared to when input is provided to a high‐density region.

Besides the type of an active current (i.e. restorative or regenerative) and how it is distributed across the neuron, also its activation time constant is key for the effects on the LFP. The dynamics of an active current will only express its effect on the membrane potential, transmembrane currents and LFP for frequencies that are sufficiently low relative to the activation time constant ${\tau }_w\left(V_R\right)$. This is seen by considering different activation time constants for the quasi‐active conductance (Fig. 4). Increasing the activation time constant decreased the frequency at which the regenerative/restorative responses became similar to the passive‐frozen case. For the resonance this means that its peak becomes broader and shifts to lower frequencies for larger activation time constants.

Resonance is expressed for asymmetrically distributed synaptic input

In the above simulations we considered a single white‐noise current input to characterize the effect of active currents on the LFP. We next examined whether the observed effects also hold when the cell receives a barrage of synaptic input as is typical for in vivo conditions (Destexhe et al. 2003).

We considered a cell model with a single quasi‐active conductance that increases linearly in density with distance from the soma. The model received input from 1000 conductance‐based excitatory synapses that were distributed across the neuronal membrane and randomly activated according to independent Poisson statistics. Note that using current‐based synapses instead of conductance‐based synapses did not significantly affect the results (results not shown). We considered three synaptic distributions: (1) uniformly distributed across the distal apical tuft dendrites located more than 900 μm from the soma (Fig. 5 A), (2) uniformly distributed across the apical dendrites more than 600 μm from the soma (Fig. 5 B) and (3) uniformly across the entire cell (Fig. 5 C). For each distribution the exact same 1000 synapse positions and input spike trains were used in the simulations for the regenerative, passive‐frozen and restorative conductances. Hence, the only difference between the simulations with a given synapse distribution was the nature of the quasi‐active conductance.

The resonance for the restorative model was clearly retained for LFP signals recorded close to the soma when the synaptic inputs were distributed asymmetrically, being concentrated in the apical dendrites (Fig. 5 A, B). However, for uniformly distributed input (Fig. 5 C) the resonance was practically undetectable. Similarly, for the regenerative model, increases of low frequencies in the LFP‐PSD were only reliably observed for the models with asymmetric synaptic input distributions (Fig. 5 A, B). Note that we obtained the same results when keeping the synapse densities fixed across the three synapse distributions, instead of keeping the total synapse number constant (results not shown). The dependence of the modulation of the LFP on the input distribution can be understood by considering the results in Fig. 3: the case with uniform input approximately corresponds to a linear combination of the LFPs stemming from apical and somatic input (Fig. 3, middle column). In the somatic region the net LFP signal will be strongly dominated by the transmembrane currents resulting from the somatic input, which are hardly affected by the active conductances because these are concentrated in the distal apical dendrites.

Resonance is a spatially stable feature in the LFP

The LFP signals measured in in vivo experiments are generated by many neurons located within a distance from a few hundred micrometres up to a few millimetres away from the recording electrode (Lindén et al. 2011; Łęski et al. 2013). An effect of a quasi‐active conductance on the LFP generated by a single neuron will only carry over to the LFP generated by an entire population if the effect is spatially ‘robust’. For example, the resonance of the single‐neuron LFP will only be observed in the population‐LFP if it is present in a sizable part of the volume surrounding the cell. If it were only recorded at special electrode positions, then it would be expected to average out when considering an entire population. The linearity of the LFP signal generation implies that the summed contributions of many single neuron‐LFP signals with similar shape would result in a population LFP with a similar shape. It is therefore key to study how the LFP varies in the space around the neuron.

We calculated the LFP at a dense grid of positions around a pyramidal cell receiving apical white‐noise input (Fig. 6). The model expressed a restorative quasi‐active conductance that increased in density with distance from the soma. Our previous results (see Fig. 3) demonstrated that such a model can show strong resonances in the LFP. The maximum amplitude of the LFP‐PSD on the position‐grid around the cell had the shape of a dipole (Fig. 6 A), as expected following the requirement of charge conservation (Lindén et al. 2010). This dipolar nature of the LFP pattern was also demonstrated by comparing two normalized LFP time traces at opposite sides of the zero‐crossing region of the dipole and noting that they are almost mirror images (Fig. 6 B; depicted traces correspond to first and third electrode contacts from the top in the first column in Fig. 6 A).

For two columns of electrode positions (marked in Fig. 6 A) we examined the LFP‐PSD in detail (Fig. 6 C). The LFP signals again demonstrated that the resonance was most pronounced on the side of the cell opposite to the input (compare lightest trace to the darker ones). Note that the electrodes positioned in the zero‐crossing region of the dipole exhibited more variable PSD shapes, for example a strong band‐stop at around 20 Hz. This is because different frequency components of the LFP will have slightly different zero‐crossing regions (see also Lindén et al. 2010). We focused on the LFP resonance and determined the frequency of maximum LFP power for the grid of positions around the neuron. The peak frequency was found to be stable at around 20 Hz, except in the zero‐crossing region of the dipole (Fig. 6 D).

The so‐called Q‐value is commonly used to characterize resonances. In the neurophysiological literature it is often defined as the magnitude of a variable (typically the membrane potential) at the resonance frequency divided by its value at the lowest frequency considered (Hutcheon et al. 1996). We found that the LFP Q‐value was stable and large at the soma region of the cell (Fig. 6 E), i.e. on the side opposite to the input, in accordance with observations from Figs 1, 2, 3. Note that the largest LFP Q‐values were in fact observed in the zero‐crossing region. However, in this region it does not reflect a resonance caused by a restorative current, but rather the very variable LFP pattern in this region. The lower signal power in this region (Fig. 6 A), in combination with the fact that the position of the zero‐crossing region will depend on various parameters, such as the exact position of the synaptic input, means that the very large Q‐values seen here will not carry over to the population LFP.

Membrane potential and LFP resonance frequencies are closely related

To investigate the relationship between membrane potential and LFP resonances, we used the same cell model and apical white‐noise input as in the previous section (see Fig. 6) and compared the LFP resonance frequency (Fig. 7 A) with the resonance frequency of both the transmembrane current (Fig. 7 B) and the membrane potential (Fig. 7 C). The resonance frequency of the transmembrane currents was very high close to the input site (≫ 40 Hz; see also next section), but it became more similar to the LFP resonance frequency (∼20 Hz) with increasing distance from the input site (Fig. 7 B). The membrane potential resonance frequency was relatively constant along the entire cell (14‐20 Hz; Fig. 7 C). We then uniformly scaled the quasi‐active peak conductance, ${\overline{g}}_w$ (see Methods), with a scaling factor ranging from 0 to 3, thereby leaving the shape of the spatial distribution intact, i.e. a 60‐fold linear increase along the apical dendrite. For each scaling of ${\overline{g}}_w$ we calculated the mode of the LFP resonance frequency, i.e. the most commonly occurring resonance frequency in the probed region, and compared this with the resonance frequencies of the transmembrane current and the membrane potential in the soma of the cell. The resonance frequencies of the membrane potential, transmembrane current and LFP increased steadily from 0 to ∼20‐30 Hz with increasing ${\overline{g}}_w$ (Fig. 7 D). For all other tested restorative quasi‐active conductance distributions and input positions (as in Fig. 3) that exhibited significant LFP resonances, we found a similar relationship between the intracellularly and extracellularly recorded resonances (results not shown).

An interesting qualitative point, however, is that for the situation considered in Fig. 7, the membrane‐potential resonance occurs for a somewhat lower frequency than the resonance in the LFP. This can be understood from basic considerations of the biophysical properties of the cable equation underlying multicompartmental modelling: the LFP is set up by transmembrane currents that generally exhibit weaker low‐pass filtering than the membrane potential (Lindén et al. 2010), i.e. the low‐pass cut‐off frequency is higher for the transmembrane currents than for the membrane potential. The observed LFP peak can be thought of as being given by the peak in compound spectra found by multiplying a ‘resonance peak’ with a ‘low‐pass filter’ background. Thus, the lower the low‐pass filter cut‐off frequency, the lower the resonance frequency will be.

Spatial profile of the membrane potentials, transmembrane currents and LFP

Above we demonstrated an amplification and a dampening of low‐frequency LFP components caused by regenerative and restorative conductances, respectively. These effects were qualitatively similar to the effects of such active conductances on the membrane potential as reported by, for example, Remme & Rinzel (2011). However, as LFP signals reflect transmembrane currents, it is a fundamentally different measure of neural activity than the membrane potential (Pettersen et al. 2012; Einevoll et al. 2013 a). It can therefore not be expected a priori that quasi‐active conductances always have qualitatively similar effects on the LFP and the membrane potential. We thus next studied the differences in the effects of active currents on the membrane potential, transmembrane currents and LFP, for apical white‐noise current input to the cell model from the previous section, i.e. a cortical pyramidal cell with a single quasi‐active conductance that increases linearly in strength along the apical dendrite.

Focusing first on the membrane potential ($V_m$, Fig. 8 A), we indeed observe that the low‐frequency components are always amplified by regenerative currents (red), whereas they are always dampened by restorative conductances (blue), compared to the passive‐frozen case (black). The effects increase with ‘exposure’ to the quasi‐active current, i.e. how far the input has propagated along the neurite (Remme & Rinzel, 2011). In addition, the membrane potential is increasingly low‐pass filtered with distance, resulting in a stronger membrane‐potential resonance with distance from the input site.

The position dependence of transmembrane currents is more complicated ($I_m$, Fig. 8 B). We first consider the passive‐frozen case: at the input site (Fig. 8 B, top) the transmembrane current is approximately equal for all frequencies, as expected due to the white‐noise current input. From charge conservation it follows that the current that enters the cell must also exit the cell, i.e. that transmembrane currents across the neuron sum to zero (Koch, 1999). As high‐frequency components propagate less than low‐frequency components, they dominate close to the input. Hence, the transmembrane currents show a high‐pass filtered PSD at positions close to the white‐noise input (Fig. 8 B, second row). The reverse is true far away from the input (Fig. 8 B, bottom), where there is a low‐pass effect similar to that for the membrane potential. This results from the stronger propagation of the low frequencies, which therefore dominate over the high frequencies at larger distances (Koch, 1999; Lindén et al. 2010). Note that at intermediate distances, a ‘passive resonance’ (Fig. 8 B, third row) can be observed through the combination of a low‐pass and a high‐pass filter.

A restorative current functions as a negative feedback, counteracting membrane potential changes, such that voltage signals do not spread as far down the cell as in the passive‐frozen case (Fig. 8 A; compare blue and black traces). Therefore, the return currents resulting from the current injections move closer to the input site, leading to an amplification of the transmembrane currents close to the input site, and a decrease far from the input site, relative to the passive‐frozen case (Fig. 8 B).

Regenerative currents amplify membrane potential deviations along the neurite (Fig. 8 A; compare red and black traces) and thus shift the return currents further away from the input compared to the passive‐frozen case. This leads to a decrease in the transmembrane currents close to the input site, and an amplification far from the input site compared to the passive‐frozen case (Fig. 8 B).

Because the LFP signal is a distance‐weighted sum of all transmembrane currents, the described effects in the transmembrane currents are all present in the LFP measured very close to the neurite (Fig. 8 C; 20 μm). For electrodes further away from the cell (Fig. 8 D; 600 μm) the LFP is no longer dominated by transmembrane currents from any single part of the cell. As the restorative currents move the transmembrane return currents closer to the input site, a smaller current dipole moment is generated, thus resulting in a decrease of the LFP power at most recording positions. The opposite is found for the model with a regenerative conductance. As we demonstrated in Fig. 4, these effects hold for the low‐frequency components of the LFP, because the dynamics of the active current only affect the cell response for frequencies that are slow compared to the activation time constant.

The resulting transmembrane currents from a single white‐noise input into a neurite also help to explain why we needed asymmetrical input to retain the effects that an active current has on the LFP‐PSD (see Fig. 5). For a single input location, the effects of an active current on the low‐frequency components of the transmembrane currents close to and far from the white‐noise input were opposite (Fig. 8 B, second vs. fourth row). Hence, for input that is localized to one region of a cell, the contributions from active currents will sum ‘constructively’ and largely retain the characteristic LFP signatures for a single individual synaptic input. For uniform input, however, an active current will give a combination of amplifying and dampening effects which will sum ‘destructively’, decreasing the total effect of the active current on the shape of the LFP.

The relationship between the PSD profiles of the membrane potential, transmembrane current and LFP described in the previous paragraph is quite general in nature, and not limited to a specific morphology. To demonstrate this, we show results for white‐noise current input to an infinite neurite: all the effects described above are found to equally well describe the relationship between membrane potentials, transmembrane currents and LFP in this simplified setting (Fig. 9). Note that the measurement positions in both models were chosen to cover the full range of transmembrane current profiles that the models exhibited. Because the electrotonic properties of the detailed model and the infinite neurite are different, the measurement positions are not the same in the two models.

Discussion

In the present paper we explored the role played by active conductances in shaping the LFP generated by neurons. It thus goes beyond previous principled studies on the LFP generated by synaptically activated passive neurons (Lindén et al. 2010, 2011; Łęski et al. 2013). While the various effects of active conductances in forming the LFP have previously been explored in comprehensive network simulations of thousands of spiking neurons (Reimann et al. 2013), the present work was instead tailored to probe subthreshold effects in detail.

With a morphologically detailed and experimentally constrained cortical pyramidal cell model, we demonstrated that active conductances can strongly shape the LFP stemming from subthreshold input. The precise effects depended on the position of the input, the position of the extracellular electrode and the membrane potential of the cell (Fig. 1). The subthreshold active conductances had distinct effects on the PSD of the LFP, providing either amplification or attenuation of the low frequencies, in the latter case leading to a resonance in the LFP‐PSD. The effects on the LFP were observed for various spatial distributions of the active conductances across the cell, but generally required an asymmetric distribution of synaptic input onto the cell (Fig. 5). We found that the effect of a subthreshold active conductance on the LFP was maximized for (1) an asymmetric distribution of the active conductance, (2) when the input was targeted to regions where the active conductance was most strongly expressed and (3) the LFP was recorded on the opposite side of the cell with respect to the input (Fig. 3).

Peaks in the LFP‐PSD are commonly observed experimentally (see, for example, Nolan et al. 2004; Roberts et al. 2013; Hadjipapas et al. 2015), and such peaks are usually interpreted as the result of network oscillations, i.e. oscillatory firing activity driving the LFP‐generating neurons (Buzsáki & Draguhn, 2004). While this interpretation certainly is appropriate in many situations, importantly our work shows that such peaks may also be due to subthreshold restorative conductances moulding the transmembrane return currents. The LFP resonance phenomenon is thus closely related to the observations of resonances in the membrane potential (Hutcheon et al. 1996; Hu et al. 2009; Remme & Rinzel, 2011), yet expected to occur for a somewhat higher frequency due to the fundamental cable properties of the neuronal dendrites (Fig. 7). In particular, in our simulations with the pyramidal cell model by Hay et al. (2011) we found that the h‐type current had a prominent role in shaping the LFP and could cause a strong resonance in the LFP‐PSD (Figs 1 C and 2 A). The h‐type current is strongly expressed in cortical and hippocampal pyramidal neurons and has a particularly asymmetric distribution across the cell, increasing in density along the apical dendrites and peaking in the distal apical tuft dendrites (Magee, 1998; Williams & Stuart, 2000; Harnett et al. 2015). The h‐type current can be expected to impact the LFP resulting from synaptic input that is predominantly targeting the apical dendritic tuft of populations of cortical or hippocampal pyramidal neurons. Indeed, various input pathways to pyramidal neurons target specific domains of the cell (see, for example, Petreanu et al. 2009). An intriguing consequence of our work is that the LFP can contain information on the spatial distribution of subthreshold active channels, as well as on the location of synaptic input to the LFP‐generating cells. For example, given a known apical concentration of h‐type conductances, a resonance in the LFP due to I _h would suggest that the cells receive asymmetric input. Vice versa, if asymmetrical input is provided, an absence of a resonance in the LFP (measured at multiple locations along the cell axis) suggests that the cell does not strongly express restorative currents.

A direct approach to test our model predictions would be through in vitro cortical slice experiments. The asymmetrical input can be provided by targeting the apical dendrites using, for example, glutamate uncaging. The polarized distribution of I _h that pyramidal neurons typically display should then give rise to a notable resonance in the LFP‐PSD, in particular when measured close to the pyramidal cell soma (Fig. 6). Addition of an I _h blocker (e.g. ZD7288) is expected to remove any resonance caused by I _h.

In most of our simulations we described voltage‐dependent channels with so‐called quasi‐active currents, which are linear approximations of the voltage‐dependent currents (Mauro et al. 1970; Koch, 1984; Hutcheon & Yarom, 2000; Remme, 2014). The quasi‐active description not only permits the use of various analytical techniques for linear systems, but also strongly reduces the number of parameters to describe an active current. Its use includes scenarios where several active currents interact or where active currents both activate and inactivate (e.g. Remme and Rinzel, 2011). The linear descriptions highlight that there are basically two types of active currents: regenerative and restorative, which have opposite effects on the voltage response, amplifying or counteracting voltage deflections, respectively. The quasi‐active description enables the systematic study of the effect of subthreshold input on the voltage response of active, dendritic neurons and allows a thorough understanding of the dynamics of the system (Koch, 1984; Bressloff, 1999; Coombes et al. 2007; Goldberg et al. 2007; Remme et al. 2009, 2010; Remme & Rinzel, 2011). We showed here that the quasi‐active current descriptions can also be used to accurately capture the LFP signal (Fig. 2). Because the h‐type current was dominating the subthreshold effects on the LFP in the model by Hay et al. (2011), a single quasi‐active current was sufficient to approximate the LFP signal of the full, non‐linear model (see Figs 1 and 2). The approach enabled us to establish an overview of the effects of active currents on the LFP signal. We achieved this by using the detailed neuron morphology with a single quasi‐active current, where the current was either restorative or regenerative, had a range of activation time constants (Fig. 4) and was distributed in various ways across the cell (Fig. 3).

In the in vivo situation, the measured LFP will reflect the activity in populations of neurons (Einevoll et al. 2013 a). A natural extension of the present work will be to investigate the effect of active dendritic currents on the LFP in a population of neurons receiving synaptic inputs (Lindén et al. 2011; Łęski et al. 2013; Reimann et al. 2013; Sinha & Narayanan, 2015). For passive dendrites the key factor in determining the magnitude and spread of the population LFP was found to be the amount of correlation between the numerous synaptic inputs to the population (Lindén et al. 2011; Einevoll et al. 2013 a; Łęski et al. 2013). The synaptic correlation level is also expected to be key for determining the population LFP in the case of active dendritic conductances, but insight into its specific influence will require detailed modelling studies. A key simplifying feature of the present study was the observation that linearized quasi‐active conductances accounted very well for the salient effects of active subthreshold conductances on the single‐neuron LFP. This approximation will also be applicable when studying effects of subthreshold active conductances on population LFPs, thus ensuring linearity of the model system and greatly simplifying the analysis as in Lindén et al. (2011) and Łęski et al. (2013).

In the present study we have not considered suprathreshold active conductances, i.e. the active channels underlying spike generation. While the present biophysical modelling scheme is equally applicable to spikes (Holt & Koch, 1999; Gold et al. 2006; Pettersen & Einevoll, 2008), the contributions to the LFP from such spikes may be expected to be negligible for cortical networks in the in vivo situation, at least for the low frequencies of LFP. In Pettersen et al. (2008) the extracellular potential generated by a synaptically activated population of 1040 pyramidal neurons mimicking a layer‐5 population in rat somatosensory (barrel) cortex was modelled by the present biophysical scheme. In order for the model predictions to be in accordance with measured extracellular potentials from the rat barrel cortex, both for the LFP (frequencies $\genfrac{}{}{0pt}{}{<}{\sim \phantom{{}_x}}$500 Hz) and for multi‐unit activity (frequencies ≳500 Hz), only 4% (40 of 1040) of the model neurons were tuned to fire an action potential following the stimulus input. In this situation the modelled LFP signal was observed to be completely dominated by the synaptic input currents and their associated return currents, with negligible contributions from the spikes themselves. However, in situations with strongly correlated firing, for example during sharp‐wave ripples in hippocampus, the spikes have been found to have sizable contributions to the extracellular potentials for frequencies down to 100 Hz (Schomburg et al. 2012; see also Reimann et al. 2013; Taxidis et al. 2015). For further discussion on the biophysical origin of the extracellular potentials in this ‘high‐gamma’ range, see, for example, Ray & Maunsell (2011) and Scheffer‐Teixeira et al. (2013). Note also that as the extracellular potential is given as a linear sum of contributions from the various transmembrane currents surrounding the contact, putative contributions from spikes can be estimated by adding computed spike signatures (Holt & Koch, 1999; Gold et al. 2006; Pettersen and Einevoll, 2008) to the present results for the LFP.

Even though the LFP has been measured for more than half a century, the interpretation of the recorded data has so far largely been qualitative (for a review, see Einevoll et al. 2013 a). We believe that the present investigation on the role of active dendritic conductances in shaping the recorded signal will turn out to be an important contribution towards the goal of making combined modelling and measurement of the LFP signal a practical research tool for detailed probing of neural circuit activity.

Additional information

Competing interests

The authors declare no competing financial interests.

Author contributions

All authors took part in designing the work, interpreting data and writing the manuscript. T.V.N. wrote the simulation code. T.V.N. and M.W.H.R. made the figures. All authors approved the final version of the manuscript and agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

The research leading to these results received funding from the European Union Seventh Framework Program (FP7/2007‐2013) under grant agreement 604102 (Human Brain Project, HBP), the Research Council of Norway (NevroNor, Notur, nn4661k), the Norwegian node of the International Neuroinformatics Coordinating Facility (INCF, NFR 214842/H10) and the Einstein Foundation Berlin.