Density-functional expansion methods: Grand challenges

Abstract

We discuss the source of errors in semiempirical density functional expansion (VE) methods. In particular, we show that VE methods are capable of well-reproducing their standard Kohn-Sham density functional method counterparts, but suffer from large errors upon using one or more of these approximations: the limited size of the atomic orbital basis, the Slater monopole auxiliary basis description of the response density, and the one- and two-body treatment of the core-Hamiltonian matrix elements. In the process of discussing these approximations and highlighting their symptoms, we introduce a new model that supplements the second-order density-functional tight-binding model with a self-consistent charge-dependent chemical potential equalization correction; we review our recently reported method for generalizing the auxiliary basis description of the atomic orbital response density; and we decompose the first-order potential into a summation of additive atomic components and many-body corrections, and from this examination, we provide new insights and preliminary results that motivate and inspire new approximate treatments of the core-Hamiltonian.

1 Introduction

A great deal of effort, spanning several decades, has been devoted to the design, implementation, and parametrization of semiempirical quantum models to make them practical, efficient, and accessible to a wide variety of problems [1–22]. As a consequence of the community’s success, it can be tempting to dismiss the approximations used in these models as being technical curiosities or to simply underestimate their severity; for it is only upon a careful examination of the magnitude of the corrections required to make these methods successful that one gains an appreciation for their ingenuity, and a somewhat worrying sense of amazement that they should even work at all. Although their approximations may be severe, there are only two metrics by which semiempirical models are ultimately judged: they must be fast and accurate. It is rare for the approximations to be criticized for their severity because the efficiency of the models are founded upon them, and the models can yet be persuaded to reproduce good results. It was for these reasons, after all, that the original developers of the semiempirical models rationalized their use, and it is easy to justify their continued use in the newer models if they are but minor modifications of those original works. This is not to say that the semiempirical development community has stagnated in groupthink, we mean only to highlight the realities that drive the direction of model development. The designer of a next-generation semiempirical model will do so under the influence of one of two prejudices: (1) current models are “fine as they are” and need only minor modifications to their parameters or functional forms; or (2) the parameters of the original semiempirical models have now been sufficiently trained [19], and the parametric freedom of the ad hoc functions used to replace the model’s missing physics has now been sufficiently extended [15], that a further significant advance will need to address the fundamental approximations of the method in some inherently new way [23–25]. The former option is attractive because it promises to offer instant gratification and can be more easily demonstrated to be fast and accurate. The latter option is higher risk, and potentially requires the development of new mathematical and technical advances to convince people that it is worthwhile.

The above discussion used the words “semiempirical models” and “approximation” vaguely, so it is useful to continue by discussing the effects of a specific approximation used by a specific model. Consider the self-consistent-charge density-functional tight-binding (SCC-DFTB) model [22]: its “core-Hamiltonian” matrix, i.e., the matrix of electron kinetic energies and the first-order density-response interactions with the neutral-atom reference, is constructed by an approximation whereby the one-center atomic orbital (AO) blocks presume that the system is but a single atom (itself), and the two-center AO blocks are computed without regard to the presence of any third atom, even if that atom lies directly between the two. Although we feel it is fair to claim that this approximation is severe by using no more than common sense, we have recently examined its use within the framework of Kohn-Sham potential energy expansion (VE) models to quantify its effect [26]. We performed second-order VE calculations with the PBE exchange-correlation (xc) functional [27] and an all-electron 6-31G* AO basis, but which was otherwise free of approximations and parameters, and showed that this reproduces standard PBE/6-31G* results almost exactly; however, when we then applied the above discussed approximation, it caused bond lengths to decrease by about 0.45 Å and angles to have errors in excess of 10°. These poor geometries resulted in dipole moment errors in excess of 50%, and the water dimer was found to be overbound by approximately two orders of magnitude. Although this set of approximations has severe consequences if left unchecked, SCC-DFTB mitigates the adverse effects with surprising success primarily by repelling the atoms with a pairwise additive correction to the energy.

Our goal is not to single-out and criticize SCC-DFTB for the above-mentioned approximation, which has been noted many times in the past [22,28–30], and other semiempirical models have used conceptually similar approximations. Modified neglect of differential overlap (MNDO) models [11,13] construct their core-Hamiltonian matrices using a concept similar to the one described above, even though the theoretical foundations for these methods are quite different [28]. MNDO methods compute the two-center core-Hamiltonian AO blocks from scaled overlap integrals instead of looking up their values from precomputed tables, but like SCC-DFTB, explicit contributions from other atoms are neglected. MNDO’s treatment of the one-center core-Hamiltonian AO blocks is also similar to SCC-DFTB in that it considers the other atoms only insofar as it tries to eliminate the influence of neutral atoms in the resulting “Fock” matrix. And like SCC-DFTB, MNDO relies on the use of pairwise repulsive potentials to retain good geometries. Of course, there are important differences between these methods, such as their treatment of electrostatics and AO overlaps, and these differences should lead one to suspect that each method has varying degrees of success at modeling various properties. Indeed, articles that compare SCC-DFTB and MNDO-like methods suggest that this is true [31], but the differences are such that it is difficult to conclude that one is an overall better method than the other. When we read articles that compare these methods [31], and we ponder their similarities and differences [28], we may verily ask: Could it be that MNDO and SCC-DFTB models are of comparable overall accuracy because their core-Hamiltonians employ conceptually similar approximations, and that these approximations are mitigated in both methods by pairwise additive repulsive energy corrections? Is this approximation a glass ceiling that will prevent new models from making significant advances in overall accuracy?

Much of our work has focused on the exploration of new methods and the development of mathematical tools which, together, motivate the design of next-generation VE models [26,32–37]. These techniques are meant to improve current models by reintroducing the physics that are otherwise only implicitly accounted for. In the process of demonstrating that these techniques add missing physics, we isolate and judge the severity of the underlying approximations used within existing models. To this end, we often find it difficult, and sometimes misleading, to judge the severity of specific approximations by interpreting the failures of parametrized models, because multiple approximations can be parametrized to cancel in unpredictable ways. To minimize the obfuscation of our comparisons, we begin with a parameter-free ab initio-like VE model that reproduces density functional theory (DFT) results very well, and then introduce various approximations to identify where and quantify by how much the model breaks down. The insights that are gained from these explorations, in turn, provide the concepts and motivation for new approximations. Using this strategy, we have concluded [26] that a second-order VE method reproduces standard DFT results extremely well if the model is not encumbered by the following approximations: (1) the limited size of the AO basis, (2) the Slater monopole auxiliary basis representation of the response density, and (3) the one- and two-body treatment of the first-order matrix elements (as discussed above). There are other, more benign approximations, but overcoming the most severe approximations with computational efficiency is the grand challenge for Kohn-Sham potential energy expansion models.

Over the years, we have attempted to address these approximations, and we will review and extend some of those works here so as to unify their motivation within the perspective of this grand challenge. The purpose of this work is three-fold: (1) We present a new model which supplements second-order SCC-DFTB (DFTB2) with a self-consistent charge-dependent dipole polarization correction (DFTB2+CPEQ). This model is based on our earlier work [37,36] (post-self consistent field MNDO/d+CPE), but is made self-consistent, and is applied to a new Hamiltonian. In addition, we go beyond the analysis presented in our previous works by making explicit comparison with a charge-independent model (DFTB2+CPE0), to ascertain the benefits of the charge-dependence. (2) We review our recent work that generalizes the auxiliary basis representation of the response density beyond Slater monopoles [32]. (3) We present new insights into the atomic decomposition of the nonadditive VE reference potential energy and its functional derivatives, and discuss how this relates to the modeling of the core-Hamiltonian. Furthermore, we demonstrate how our observations lead to a new mathematical justification for the approximations used within spin-polarized SCC-DFTB models [38].

2 Methods

2.1 Expansion of the Kohn-Sham potential energy

VE models are derived from Kohn-Sham DFT through Taylor series expansion [29] of the potential energy [39] V [ρ, ω] in density response δρ(r) = ρ(r) − ρ_ref(r) and spin-density ω(r) = ρ^α(r) − ρ^β(r) about the reference density composed from the spin-averaged sum of isolated neutral atoms ρ_ref(r) = ∑_a ρ_a(r) and ω_ref(r) = 0. The VE energy E_VE ≡ E_VE[ρ_ref + δρ, ω] is

$$E_{\mathrm{V}\mathrm{E}}=\sum _{ij}{P}_{ij}{T}_{ij}+V^{(0)}[{\rho }_{\text{ref}}]+V^{(1)}[\delta \rho ]+W[\delta \rho ,\omega ],$$ (1)

where P is the AO basis single-particle density matrix; T is the kinetic energy matrix;

$$V^{(0)}[{\rho }_{\text{ref}}]=E_{\mathrm{x}\mathrm{c}}[{\rho }_{\text{ref}},0]+\sum _{b>a}\frac{Z_a{Z}_b}{R_{ab}}+J[{\rho }_{\text{ref}}]-\sum _{ab}\int \frac{Z_a{\rho }_b(\mathbf{r})}{|\mathbf{r}-{\mathbf{R}}_a|}{d}^{3}r$$ (2)

is the reference potential energy; Z_a is a nuclear charge; R_a is its atomic position;

$$J[\rho ]=\frac{1}{2}\int \int \frac{\rho (\mathbf{r})\rho (\mathbf{r}\prime )}{|\mathbf{r}-\mathbf{r}\prime |}{d}^{3}r{d}^{3}r\prime$$ (3)

is the Coulomb functional; E_xc[ρ, ω] is the xc-functional; $V^{(1)}[\delta \rho ]={\sum }_{ij}(P_{ij}-P_{ij}^{(0)})V_{ij}^{(1)}$, where

$$V_{ij}^{(1)}=\int {\frac{\delta V[\rho ,\omega ]}{\delta \rho (\mathbf{r})}|}_0{\chi }_i(\mathbf{r}){\chi }_j(\mathbf{r})d^{3}r,$$ (4)

is the first-order potential energy; P⁽⁰⁾ is the reference density matrix, which reproduces ρ_ref(r) from the AO basis {χ}; the “0” subscript outside functional derivatives indicate its evaluation about the spin-averaged reference; and W[δρ, ω] is a functional that describes all other response interactions. If the Taylor series expansion was carried out to infinite order, then W[δ, ω] would be the second- and all higher-order energy corrections; however, we specifically write W[δ, ω] as a generic functional to allow us the notational freedom to insert other empirical correction terms that depend on the response density in some complicated way. We will explore the use of empirical correction terms in later sections, and continue here by considering the case of a second-order expansion; i.e., W[δρ, ω] → V⁽²⁾[δρ, ω], where

$$V^{(2)}[\delta \rho ,\omega ]=J[\delta \rho ]+\frac{1}{2}\int \int {\frac{{\delta }^2{E}_{\mathrm{x}\mathrm{c}}[\rho ,\omega ]}{\delta \rho (\mathbf{r})\delta \rho (\mathbf{r}\prime )}|}_0\times \delta \rho (\mathbf{r})\delta \rho (\mathbf{r}\prime )d^{3}r{d}^{3}r\prime +\frac{1}{2}\int \int {\frac{{\delta }^2{E}_{\mathrm{x}\mathrm{c}}[\rho ,\omega ]}{\delta \omega (\mathbf{r})\delta \omega (\mathbf{r}\prime )}|}_0\times \omega (\mathbf{r})\omega (\mathbf{r}\prime )d^{3}r{d}^{3}r\prime .$$ (5)

If E_xc[ρ, ω] is a local functional of the density; i.e., if it does not require the calculation of nonlocal integrals, then the last two terms in Eq. (5) simplify [40],

$${\frac{{\delta }^2{E}_{\mathrm{x}\mathrm{c}}[\rho ,\omega ]}{\delta \rho (\mathbf{r})\delta \rho (\mathbf{r}\prime )}|}_0={\delta (\mathbf{r}-\mathbf{r}\prime )\frac{{\delta }^2{E}_{\mathrm{x}\mathrm{c}}[\rho ,\omega ]}{\delta \rho (\mathbf{r})\delta \rho (\mathbf{r})}|}_0;$$ (6)

and the functional derivatives can be be expressed as local functions of space

$$E_{\mathrm{V}\mathrm{E}}=\sum _{ij}{P}_{ij}{T}_{ij}+V^{(0)}[{\rho }_{\text{ref}}]+\int {\upsilon }_{\text{ref}}^{(1)}(\mathbf{r})\delta \rho (\mathbf{r})d^{3}r+J[\delta \rho ]+\frac{1}{2}\int {\upsilon }_{\text{ref}}^{(2)}(\mathbf{r})\delta \rho {(\mathbf{r})}^2{d}^{3}r+\frac{1}{2}\int w_{\text{ref}}^{(2)}(\mathbf{r})\omega {(\mathbf{r})}^2{d}^{3}r;$$ (7)

where

$${\upsilon }_{\text{ref}}^{(1)}(\mathbf{r})=-\sum _a\frac{Z_a}{|\mathbf{r}-{\mathbf{R}}_a|}+\int \frac{{\rho }_{\text{ref}}(\mathbf{r}\prime )}{|\mathbf{r}-\mathbf{r}\prime |}{d}^{3}r\prime +{\frac{\delta E_{\mathrm{P}\mathrm{B}\mathrm{E}}[\rho ,\omega ]}{\delta \rho (\mathbf{r})}|}_0,$$ (8)

and ${\upsilon }_{\text{ref}}^{(2)}(\mathbf{r})$ and $w_{\text{ref}}^{(2)}(\mathbf{r})$ are the second-functional derivatives of the local xc-functional. Various models can be constructed by applying approximations to the above equations, and these models are described in the next sections.

2.2 Second-order SCC-DFTB

The DFTB2 model [22] differs from Eqs. (1)–(7) in the following ways:

$$V_{ij}^{(1)}\approx \{\begin{array}{cc}\int {\upsilon }_a^{(1)}(\mathbf{r}){\chi }_i(\mathbf{r}){\chi }_j(\mathbf{r})d^{3}r,\hfill & \text{if }i,j\in a\hfill \\ \int {\upsilon }_{ab}^{(1)}(\mathbf{r}){\chi }_i(\mathbf{r}){\chi }_j(\mathbf{r})d^{3}r,\hfill & i\in a,j\in b,\hfill \end{array}$$ (9)

where ${\upsilon }_a^{(1)}(\mathbf{r})={\delta V[\delta \rho ,\omega ]/\delta \rho |}_{\rho (\mathbf{r})={\rho }_a(\mathbf{r})}$ is the first-order potential of atom a and ${\upsilon }_{ab}^{(1)}(\mathbf{r})$ is the potential of the ab-dimer; the second-order energy is evaluated using a Slater monopole auxiliary basis

$$\delta \rho (\mathbf{r})=-\sum _a{q}^a{\phi }^a(\mathbf{r}-{\mathbf{R}}_a),$$ (10)

where

$$q^a=-\sum _i\sum _{j\in a}(P_{ij}-P_{ij}^{(0)})\frac{1}{2}{S}_{ij}-\sum _{i\in a}\sum _j(P_{ij}-P_{ij}^{(0)})\frac{1}{2}{S}_{ij}$$ (11)

is the Mulliken-partitioned partial electric charge of atom a, and S is the overlap matrix. The second-order energy V⁽²⁾, is Coulomb-approximated; and the auxiliary basis representation transforms the functional into a function of partial charges and atomic positions V⁽²⁾[δρ, ω] → J(q, R); where

$$J(\mathbf{q},\mathbf{R})=\sum _{ab}{q}^a{q}^b\frac{1}{2}\int \int \frac{{\phi }^a(\mathbf{r}){\phi }^b(\mathbf{r}\prime )}{|\mathbf{r}-\mathbf{r}\prime |}{d}^{3}r{d}^{3}r\prime .$$ (12)

Although this only explicitly models the electrostatics, the second-order xc-energy is implicitly accounted for by choosing the Slater exponents so that the Coulomb self-energies of the atoms reproduce their experimental chemical hardness’ [41,30]. The matrix elements [Eq. (9)] are evaluated using the atomic densities and minimal valence AOs resulting from isolated atom calculations in the presence of a radial confinement potential, and the xc-potentials are evaluated with the PBE functional [27]. To compensate for the above approximations, the reference potential energy is replaced by a sum of pairwise additive corrections

$$V^{(0)}[{\rho }_{\text{ref}}]\to \sum _{b>a}{f}_{ab}(R_{ab}),$$ (13)

which are parametrized to reproduce molecular geometries and bond energies.

The DFTB2 energy is minimized via a standard self consistent field (SCF) procedure, and the expression for the Fock matrix F_ij = δE/δP_ij is

$$F_{ij}=T_{ij}+V_{ij}^{(1)}-\frac{1}{2}{S}_{ij}(\frac{\partial J(\mathbf{q},\mathbf{R})}{\partial q^a}+\frac{\partial J(\mathbf{q},\mathbf{R})}{\partial q^b}),$$ (14)

where i ∈ a and j ∈ b.

2.3 DFTB2 with self-consistent polarization corrections

This section describes a new method that is similar to Refs. [42–44]; in that, it is founded upon our earlier works [37,36]. The difference between the present method and Refs. [42–44] is: our new method is charge-dependent; but unlike Refs. [37,36], the present work is self-consistent and applied to a different Hamiltonian. Our motivation for introducing this method here is to address the first grand challenge: The limited size of the AO basis.

Like all minimal valence basis models, DFTB2 lacks the sufficient AO degrees of freedom to adequately respond to external perturbations, and this manifests itself in its underprediction of dipole polarzabilities [45]. Obviously, one could increase the size of the AO basis in an attempt to alleviate the underlying cause of the problem [46]; however, the benefits of doing so wouldn’t be fully realized if the electrostatics were limited to monopolar interactions. In lieu of developing an entirely new model, the dipole polarizabilities of DFTB2 can be improved by including a chemical potential equalization (CPE) auxiliary response density [47], represented by atom-centered dipole functions, whose response to external perturbations is not constrained by the limited size of the AO basis.

The CPE response density is the namesake of the CPE principle, sometimes referred to as the electronegativity equalization principle [48–51], and is derived from DFT by Taylor expanding the density functional in density response [52,53]. In this context, the DFTB2 AO density ρ_AO(r) is the reference density in the CPE Taylor expansion, and the CPE density δρ̃(r) is the response about this reference; i.e.,

$$E[{\rho }_{\mathrm{A}\mathrm{O}}+\delta \tilde{\rho }]=E_{\mathrm{V}\mathrm{E}}[{\rho }_{\mathrm{A}\mathrm{O}}]+\int {\frac{\delta E[\rho ]}{\delta \rho (\mathbf{r})}|}_{{\rho }_{\mathbf{A}\mathbf{O}}}\delta \tilde{\rho }(\mathbf{r})d^{3}r+\frac{1}{2}\int \int {\frac{{\delta }^{2}E[\rho ]}{\delta \rho (\mathbf{r})\delta \rho (\mathbf{r}\prime )}|}_{{\rho }_{\mathrm{A}\mathrm{O}}}\times \delta \tilde{\rho }(\mathbf{r})\delta \tilde{\rho }(\mathbf{r}\prime )d^{3}r{d}^{3}r\prime ,$$ (15)

and the CPE correction to the VE energy is

$$E_{\mathrm{C}\mathrm{P}\mathrm{E}}[{\rho }_{\mathrm{A}\mathrm{O}},\delta \tilde{\rho }]\equiv E[{\rho }_{\mathrm{A}\mathrm{O}}+\delta \tilde{\rho }]-E_{\mathrm{V}\mathrm{E}}[{\rho }_{\mathrm{A}\mathrm{O}}].$$ (16)

Although they are both Taylor series expansions, Eq. (15) is fundamentally different from Eq. (1); Eq. (15) expands the total density functional, including the electron kinetic energy, as opposed to the Kohn-Sham potential energy functional [39]. This distinction is important because it has serious implications on the ability of the model to describe covalent bonding. Eq. (15) is not a reasonable model for describing covalent bonds, which are difficult to describe outside of the linear combination of atomic orbitals (LCAO) approach, because the kinetic energy is not well-modeled through the density alone [54]. Fortunately, we can rely on DFTB2 for that purpose, and use the CPE correction to account for the missing response due to those interactions that are sufficiently separated that they can be accurately modeled by electrostatics only. This is, in fact, what the polarizabilities ultimately are: measures of response due to distant electrostatic perturbations. In particular, the isotropic dipole polarizability of a molecule is α = (α_xx + α_yy + α_zz)/3, where

$${\alpha }_{xy}=\frac{{\partial }^{2}E}{\partial E_x\partial E_y}=-\frac{\partial q_x^{(1)}}{\partial E_y},$$ (17)

and

$$q_x^{(1)}=\int x[\sum _a\frac{Z_a}{|\mathbf{r}-{\mathbf{R}}_a|}-{\rho }_{\mathrm{A}\mathrm{O}}(\mathbf{r})-\delta \tilde{\rho }(\mathbf{r})]d^{3}r$$ (18)

and E_x are the electric dipole moment and field strength in the x-direction, respectively.

For the reasons discussed above, we approximate E[ρ] ≈ J[ρ], and damp the short-range Coulomb interactions between the CPE density and the DFTB2 AO density, because the short-range interactions of the density are better modeled by the underlying DFTB2 model. Furthermore, being that only the well-separated Coulomb interactions are treated, we ignore the underlying neutral-atom DFTB2 reference; only the DFTB2 partial atomic charges (and any applied electric field) invoke a CPE response ρ_AO(r) ≈ − ∑_a q^aφ^a(r). The CPE response is represented by atom-centered primitive Gaussian-dipole functions {φ̃}

$$\delta \tilde{\rho }(\mathbf{r})=-\sum _a\sum _{\mu }{d}_{\mu }^a{\tilde{\phi }}_{\mu }^a(\mathbf{r}-{\mathbf{R}}_a)=-\sum _a\sum _{\mu =-1}^1{d}_{\mu }^a{C}_{1,\mu }(\nabla a){\left(\frac{{\zeta }_a}{\pi }\right)}^{3/2}{e}^{-{\zeta }_a{|\mathbf{r}-{\mathbf{R}}_a|}^2},$$ (19)

where C_lμ(∇_a) is the spherical tensor gradient operator [55] acting on R_a, and d is the vector of atomic dipole moments. The basis representation of δρ̃(r) allows us to rewrite the CPE correction energy in a simple algebraic form E_CPE[ρ_AO, δρ̃] → E_CPE(q, d, R); i.e.,

$$E_{\mathrm{C}\mathrm{P}\mathrm{E}}(\mathbf{q},\mathbf{d},\mathbf{R})={\mathbf{d}}^T·\mathbf{B}·\mathbf{q}+\frac{1}{2}{\mathbf{d}}^T·\mathbf{A}·\mathbf{d},$$ (20)

where

$$B_{kb}=D(R_{ab})\int \int \frac{{\tilde{\phi }}_k^a(\mathbf{r}){\phi }^b(\mathbf{r}\prime )}{|\mathbf{r}-\mathbf{r}\prime |}{d}^{3}r{d}^{3}r\prime$$ (21)

is a 3N × N matrix of scaled Coulomb interactions between the CPE Gaussian-dipole and DFTB2 AO Slater-monopole auxiliary basis sets;

$$A_{kk\prime }=\int \int \frac{{\tilde{\phi }}_k^a(\mathbf{r}){\tilde{\phi }}_{k\prime }^b(\mathbf{r}\prime )}{|\mathbf{r}-\mathbf{r}\prime |}{d}^{3}r{d}^{3}r\prime$$ (22)

is a 3N × 3N matrix of Gaussian-dipole Coulomb interactions; and D(R_ab) is a switching function that removes the short-range Coulomb interactions. This switching function has the form: D(R_ab) = 1, if R_ab > R_hi; D(R_ab) = 0, if R_ab < R_lo; and

$$D(R_{ab})=1-10x^3+15x^4-6x^5,$$ (23)

otherwise; where x = (R_hi − R_ab)/(R_hi − R_lo); and R_hi = R_hi,a + R_hi,b and R_lo = R_lo,a + R_lo,b are a sum of atom parameters.

The CPE correction energy is minimized by solving $\partial E_{\mathrm{C}\mathrm{P}\mathrm{E}}(\mathbf{q},\mathbf{d},\mathbf{R})/\partial d_k^a=0$, which has an analytic result:

$$\mathbf{d}=-{\mathbf{A}}^{-1}·\mathbf{B}·\mathbf{q}.$$ (24)

In summary, given the short-range damping parameters R_lo,a and R_hi,a, and Gaussian-dipole exponents ζ_a, the matrices A and B are computed [Eqs. (21)–(22)], the response is then determined [Eqs. (24)], and the energy correction is then evaluated [Eq. (20)].

The CPE energy correction is a modification of the W-functional; i.e., W[δρ, ω] → J(q, R) + E_CPE(q, d, R); and depends on the density matrix through q. Therefore, its derivatives with respect to q enter the Fock matrix;

$$F_{ij}=T_{ij}+V_{ij}^{(1)}-\frac{1}{2}{S}_{ij}(\frac{\partial J(\mathbf{q},\mathbf{R})}{\partial q^a}+\frac{\partial E_{\mathrm{C}\mathrm{P}\mathrm{E}}(\mathbf{q},\mathbf{d},\mathbf{R})}{\partial q^a}+\frac{\partial J(\mathbf{q},\mathbf{R})}{\partial q^b}+\frac{\partial E_{\mathrm{C}\mathrm{P}\mathrm{E}}(\mathbf{q},\mathbf{d},\mathbf{R})}{\partial q^b}).$$ (25)

CPE0: The charge-independent model. If the Gaussian-dipole exponents did not depend on charge, then

$$\frac{\partial E_{\mathrm{C}\mathrm{P}\mathrm{E}0}(\mathbf{q},\mathbf{d},\mathbf{R})}{\partial q^a}=\sum _b\sum _{k\in b}{d}_k^b{B}_{ka}.$$ (26)

CPEQ: The charge-dependent model. In this model, the CPE Gaussian-dipole exponent is made a function of the underlying DFTB2 partial charge

$${\zeta }_a(q^a)={\zeta }_a(0)e^{b_a}{q}^a,$$ (27)

where ζ_a(0) and b_a are atom parameters.

The purpose for making the model charge-dependent is to introduce some elementary, missing physics. In particular, anions are known to be more polarizable than neutral atoms, which are more polarizable than cations. The atomic polarizabilities of minimal valence basis models tend to have the opposite behavior because, as the AO degrees of freedom are extinguished, there is less opportunity to respond to external perturbations. Eq. (27) reproduces the expected behavior when b_a > 0: as an atom becomes anionic q^a < 0, ζ_a(q^a) becomes smaller; the Coulomb self-energy A_kk decreases; and therefore the polarizability increases; i.e., the CPE polarizability correction of an isolated atom is inversely proportional to the dipole self-energy, ∆α = 1/A_kk.

Notice that the charge-dependence takes an exponential-, as opposed to linear-form. One can compute the polarizability of atoms and ions using standard ab initio methods to convince themselves of the exponential behavior, but it can also be gleaned intuitively from tables of experimental atomic electron affinities and ionization potentials, which can be used to plot the energy of an atom as a function of charge state. These plots are monotonic and exponential-like, and are interpreted to suggest certain truisms: Excess electrons are less bound to the atom, and are thus sensitive to external perturbations. The opposite is true when there are a deficient number of electrons. Moreover, the inner-shell electrons are successively bound with ever-increasing strength to the nucleus, making their response to external perturbations exponentially irrelevant.

Having now explained the exponential behavior; and appreciating that, by doing so, this behavior now seems obvious; the reader may question why its explanation is even necessary. Our reason for explaining this in detail is because there have been recent works [56,57] that may cause some readers to believe that the justification for including charge-dependence is founded in the expansion of the Taylor series to third-order; because, in this way, the second-order energy can be corrected for linear changes in the charge. This, of course, is a mathematically sound way for introducing charge-dependence; however, it is unfortunate that a reader can easily misconstrue it into suggesting that the problem at hand is a symptom of a premature truncation of the Taylor series expansion. The symptoms, however, result from a poor auxiliary description of the response density and its restricted response in a limited AO basis. Indeed, a VE model with a sufficient AO and auxiliary basis, but in the absence of other severe approximations, reproduces closed-shell standard DFT results very well even when the VE Taylor expansion of the xc-functional is truncated at first-order!

By making the ζ_a’s a function of the DFTB2 partial charges, the A and B matrix elements now have an explicit q-dependence, and this complicates the Fock matrix correction

$$\frac{\partial E_{\mathrm{C}\mathrm{P}\mathrm{E}\mathrm{Q}}(\mathbf{q},\mathbf{d},\mathbf{R})}{\partial q^a}=\sum _b\sum _{k\in b}{d}_k^b{B}_{ka}+\sum _{k\in a}\sum _b{d}_k^a\frac{\partial B_{kb}}{\partial q^a}{q}^b+\sum _{k\in a}\sum _b\sum _{k\prime \in b}{d}_k^a\frac{1}{2}\frac{\partial A_{kk\prime }}{\partial q^a}{d}_{k\prime }^b.$$ (28)

If the only dependence of the matrix elements are through the CPE Gaussian-dipole exponent, as is the case for DFTB2, then their required derivatives can be expressed solely through a chain-rule of those exponents; e.g.,

$${\frac{\partial B_{kb}}{\partial q^a}=\frac{\partial B_{kb}}{\partial {\zeta }_a}|}_{{\zeta }_a={\zeta }_a(q^a)}\frac{\partial {\zeta }_a(q^a)}{\partial q^a},\text{ for }k\in a;$$ (29)

however, if one were to apply the CPE correction to a third-order SCC-DFTB model (DFTB3) [56–58], whose Slater-monopole exponents also have a q-dependence, then an additional derivative of B would be necessary.

2.4 PBE/6-31G*-based VE models

As discussed above, DFTB2 is limited in both the completeness of its AO basis and the electrostatic description of its response density. In the previous sections, we described how one can try to mask these limitations by making a modest change or extension to the model. In this section, we describe a series of models that approach the problem from a different perspective: we start with a base model that reproduces standard PBE/6-31G* very well and then apply approximations that worsen the model. This allows us to better identify and quantify the limitations of the model, motivate and test new corrections, and convincingly demonstrate that those corrections reintroduce missing physics.

To describe these models, it is useful to discuss how they differ from a base model, which we call VE. As the name suggests, it is a direct application of the VE method [Eqs. (1)–(8)], and it is our best attempt at avoiding all other approximations. The VE model is evaluated with the AOs and reference density resulting from standard PBE/6-31G* calculations, uses the PBE xc-functional within the zeroth-order reference energy and first-order potential, and uses the SPW92 xc-functional [59] within the second-order terms; i.e., the second-order potentials, ${\upsilon }_{\text{ref}}^{(2)}(\mathbf{r})$ and $w_{\text{ref}}^{(2)}(\mathbf{r})$, are the second functional derivatives of SPW92. Had we used the PBE xc-functional for the second-functional derivative and carried out the Taylor series expansion to infinite order, we would expect VE to exactly reproduce standard PBE/6-31G*; therefore, we will compare all of our VE models to standard PBE/6-31G*.

The other models that we describe employ various approximations; some of which are more severe than others. The benign approximations are relevant in our examinations insofar as they are commonly used in existing semiempirical models, and yet provide certain computational advantages. Therefore, we will also introduce more severe approximations upon those; and in these cases, we will continue to compute their errors relative to standard PBE/6-31G*, but with the understanding that, even if we remedied the severe approximations with a new technique, we’d still expect the model to suffer from the errors attributed to the more benign approximations.

The remaining, closely related models are summarized below. Some of the approximations used in these models require more explanation than what is described here, and we defer those explanations to the ensuing sections that follow.

VE: The base model described by Eqs. (1)–(8), where the AO basis and reference densities result from 6-31G* atom calculations, and E_xc[ρ, ω] = E_PBE[ρ, ω], except for the second-functional derivatives, which use E_xc[ρ, ω] = E_SPW92[ρ, ω]. This model differs from standard PBE/6-31G* because of our truncation of the Taylor expansion to second-order, and our uniform gas xc-approximation for the second-functional derivatives.

VE0: The VE model, where the reference potential energy is approximated by a cluster expansion; i.e.,

$$V[{\rho }_{\text{ref}},0]\approx \sum _a{V}_a^{(0)}+\sum _{b>a}\Delta V_{ab}^{(0)},$$ (30)

where

$$\Delta V_{ab}^{(0)}=V_{ab}^{(0)}-V_a^{(0)}-V_b^{(0)},$$ (31)

$V_{ab}^{(0)}\equiv V[{\rho }_a+{\rho }_b,0]$, and $V_a^{(0)}\equiv V[{\rho }_a,0]$. If the cluster expansion was exact, then we would expect VE0 reproduce the VE results

VE1: The VE0 model, where the first-order potential energy is evaluated using a one- and two-body approximation [Eq. (9)]. If Eq. (9) was exact, we would expect VE1 to reproduce the VE0 results.

VE1S: The VE0 model, where the first-order potential [Eq. (8)] is approximated by a sum of isolated-atom potentials; i.e., ${\upsilon }_{\text{ref}}^{(1)}(\mathbf{r})\approx {\sum }_a{\upsilon }_a^{(1)}(\mathbf{r})$. If this approximation was exact, we would expect VE1S to reproduce the VE0 results.

VE1W: The VE0 model, where the first-order potential is approximated by a weighted cluster expansion [Eq. (48)], described later in this text. If Eq. (48) was exact, we would expect VE1W to reproduce the VE0 results.

VEJ: The VE model, where the second-order xc-potentials are completely ignored; i.e., ${\upsilon }_{\text{ref}}^{(2)}(\mathbf{r})=w_{\text{ref}}^{(2)}(\mathbf{r})=0$. VEJ cannot describe spin-polarization at all.

VEJ/1S(M): The VEJ model, where the AO products are represented in an auxiliary basis of atom-centered Slater-monopole functions, whose exponents are chosen to reproduce the experimental hardness of the atoms. This auxiliary basis is analogous to that used in DFTB2; like DFTB2, the atomic charges are chosen by Mulliken partitioning. If the auxiliary basis exactly reproduced the AO products, then we’d expect VEJ/1S(M) to reproduce the VEJ results.

VEJ/2P,3D,4F: The VEJ model, where the AO products are represented with an auxiliary basis of Gaussian multipole expansions (GME)

$${\phi }_{lm}^a(\mathbf{r})=\frac{C_{lm}({\nabla }_a)}{(2l-1)!!}\times \sum _{\gamma =1}^3{c}_{\gamma }{\left(\frac{{\zeta }_{\gamma }(\xi )}{\pi }\right)}^{3/2}{e}^{-{\zeta }_{\gamma }(\xi ){|\mathbf{r}-{\mathbf{R}}_a|}^2},$$ (32)

whose primitive contraction coefficients c_γ, and exponents ζ_γ(ξ), have been chosen to mimic a Slater multipole-like expansion with exponent ξ. The notation 2P,3D,4F indicates that period 1 elements use two GMEs of l_max = 1, each corresponding to one of two Slater exponents; period 2 elements use three GMEs of l_max = 2; and period 3 elements use four GMEs of l_max = 3. The relationship between this generalized auxiliary basis and the AO products is discussed in the next section, and described completely in Ref. [32]. If the auxiliary basis exactly reproduced the AO products, then we’d expect it to match VEJ’s results.

2.5 Generalization of the auxiliary basis

This section reviews a method that has only recently been reported in Ref. [32]. Our purpose for reviewing that work here is to unify its motivation with the second grand challenge: The limited auxiliary basis description of the response density.

DFTB2 explicitly treats the electrostatic interactions of the response density, and is therefore a major advance beyond the traditional first-order tight-binding models whence it is based. Not only does the reintroduction of this missing physics improve the description of interatomic interactions, but it makes DFTB2 a more transferable and accurate predictor of atomic charges. The DFTB2 response density is represented in a basis of Slater-monopoles, whose exponents are chosen to reproduce the atom’s chemical hardness [60,61]. The response density is made to interact with itself electrostatically, and thus the DFTB2 response density self-energy is a quadratic function of atomic partial charges.

The electron affinity and ionization potentials of an atom suggest that the energy of an atom is not a pure quadratic function of charge, but is instead asymmetrical. As electrons are removed from the atom, the chemical hardness increases; because the next electron to be removed is closer to the nucleus; its interaction with the nucleus is stronger; and thus requires even greater energy to eject. This asymmetry might motivate one to try and improve DFTB2 by making the Slater exponent a function of charge, so that the Slater self-energies mimic an exponential-like or asymmetrical behavior. Invoking charge-dependence in this way is an ad hoc correction. By this, we mean that the charge-dependence is being used to alleviate a particular symptom without regard to the underlying problem that gives rise to that symptom. As such, there is no limitation on the functional form of the charge-dependence; i.e., one could make the Slater exponents a linear function of charge, or an exponential function of charge, or a sixth-order spline polynomial of charge, etc.

DFTB3 improves upon DFTB2 by making the Slater exponents a linear function of charge, and then justifies this mathematical form by extending the Taylor series expansion of the Kohn-Sham potential energy to third-order [56–58]. When reading those works [56–58], a reader may misconstrue the use of a third-order expansion to mean that the underlying problem giving rise to the quadratic behavior of the hardness is a premature truncation of the Taylor series to second-order. Our previous works suggest that this is not the case [26,32]. The pure-quadratic response self-energy of an isolated atom, as modeled by DFTB2, results only from having limited the auxiliary basis so completely that both the diffuse and tightly-bound electron densities are represented by the same spatial function, and thus contribute equally to the self-energy. One would instead intuitively expect the excess electrons to be more diffuse, and therefore contribute less to the atom’s self-energy than the more tightly-bound electrons.

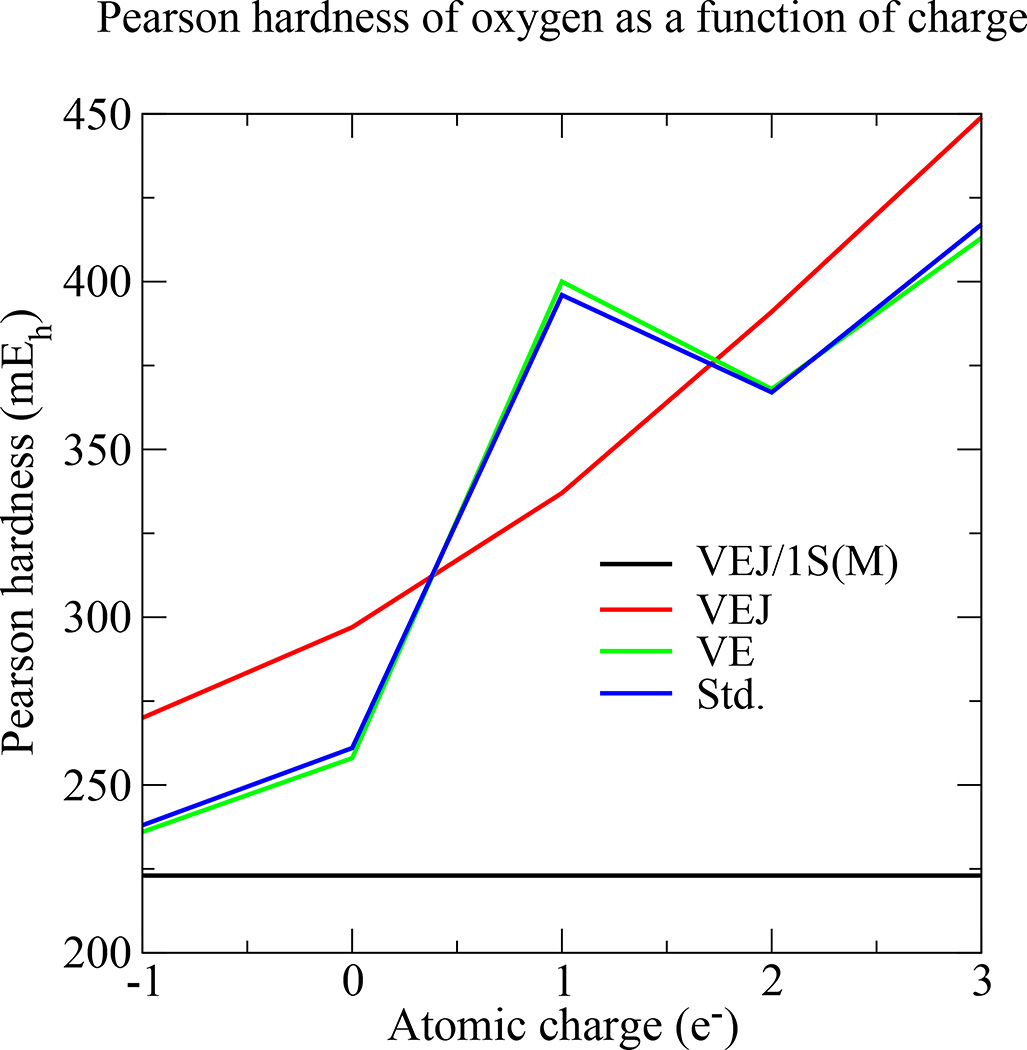
We attribute the source of the error to the incomplete AO and auxiliary basis being used, and not the truncation of the expansion. We’ve come to this conclusion by repeatedly testing the following elementary logic [26,32]: (1) If the source of error was the lack of a third-order term, then the error should continue to manifest itself when all other approximations of the model are removed. (2) If a second-order model is used, and the error ceases to manifest itself when some approximation (other than the expansion order) is removed, then the source of the error is not the second-order truncation. As a simple demonstration, Fig. 1 plots the hardness of oxygen as a function of charge using a variety of approximations. The VE model lacks third- and higher-order expansion terms, but it agrees extremely well with the standard PBE/6-31G* results; therefore, the lack of third- and higher-order expansion terms is not the source of error preventing an asymmetrical charge-dependence.

Fig. 1.

The Pearson hardness of oxygen atom and ions for various models. Let E(q) represent the energy of oxygen with an electric charge of q. We then compute the hardness as [E(q − 1) − E(q + 1)]/2. When the auxiliary basis is limited to a single, charge-independent Slater function [VEJ/1S(M)], the hardness is constant. The hardness becomes variable when more auxiliary functions are used (VEJ is equivilant to having used a complete auxiliary basis). Furthermore, upon including second-order LDA-xc (VE), the second-order model reproduces standard PBE/6-31G* (Std.) extremely well. By having removed the other approximations in the model and showing a strong agreement between the second-order Kohn-Sham expansion with its standard DFT counterpart, we conclude that the a second-order expansion is not a premature truncation of the Kohn-Sham potential energy. If the lack of a third-order expansion term introduced errors of any consequence, then we’d expect those errors to continue to manifest themselves when the other approximations of the model are removed

From the above discussion, it should now be clear that an avenue for improving DFTB2, as an alternative to explicitly modeling a charge-dependence or extending the order of the Taylor series expansion, would be to simply include more Slater functions: those which model the diffuse electrons, and those that model the inner-electrons. Furthermore, one could include higher-order multipoles, as this would: allow for an improved description of dipole polarizabilities, provided that the AO degrees of freedom were available; improve the strength and angular dependence of hydrogen bonds; and improve the nonbonded interactions, in general [62].

Of course, this is all rather easy to say, but how would you actually do it and still have it be practical? Although auxiliary basis sets have been used in traditional ab initio methods, the techniques they use typically require three-center integrals [63–69], whereas the efficiency of SCC-DFTB’s technique is that it requires only two-center integrals, and thus can be precomputed and splined as a function of atom separation. Our approach was chosen to preserve this property, and we call it a generalization of the auxiliary basis because, like SCC-DFTB, we will use the auxiliary basis to directly model the AO products.

Some readers might insist that SCC-DFTB is modeling the atomic response densities, not the individual AO products! So, to convince those readers, and to more clearly demonstrate how our method is a generalization, let us insert Eq. (11) into (10)

$$\delta \rho (\mathbf{r})=\sum _a\sum _{ij\in a}(P_{ij}-P_{ij}^{(0)})[S_{ij}{\phi }^a(\mathbf{r}-{\mathbf{R}}_a)]+\sum _{a\ne b}\sum _{i\in a}\sum _{j\in b}(P_{ij}-P_{ij}^{(0)})\times [\frac{1}{2}{S}_{ij}{\phi }^a(\mathbf{r}-{\mathbf{R}}_a)+\frac{1}{2}{S}_{ij}{\phi }^b(\mathbf{r}-{\mathbf{R}}_b)];$$ (33)

and now, upon comparing this to

$$\delta \rho (\mathbf{r})=\sum _{ij}(P_{ij}-P_{ij}^{(0)}){\chi }_i(\mathbf{r}){\chi }_j(\mathbf{r});$$ (34)

we see that χ_i(r)χ_j(r) ≈ S_ijφ^a(r − R_a), for one-center AO products; and

$${\chi }_i(\mathbf{r}){\chi }_j(\mathbf{r})\approx \frac{1}{2}{S}_{ij}{\phi }^a(\mathbf{r}-{\mathbf{R}}_a)+\frac{1}{2}{S}_{ij}{\phi }^b(\mathbf{r}-{\mathbf{R}}_b),$$ (35)

for two-center AO products. The factors of S_ij and S_ij/2 are the coefficients of a simple partitioning that “map” the AO product onto the atoms’ auxiliary basis.

Our generalization is to simply use more auxiliary functions; i.e.,

$${\chi }_i(\mathbf{r}){\chi }_j(\mathbf{r})\approx \sum _{k\in a}{M}_{ijk}^a{\phi }_k^a(\mathbf{r}-{\mathbf{R}}_a),$$ (36)

for one-center AO products; and

$${\chi }_i(\mathbf{r}){\chi }_j(\mathbf{r})\approx \sum _{k\in a}{M}_{ijk}^a{\phi }_k^a(\mathbf{r}-{\mathbf{R}}_a)+\sum _{k\in b}{M}_{ijk}^b{\phi }_k^b(\mathbf{r}-{\mathbf{R}}_b),$$ (37)

for two-center AO products; where M^a and M^b are matrices of mapping coefficients, which depend on the orientation and separation of the two atoms.

When the two atoms are aligned along the z-axis, and the angular dependence of the AO and auxiliary functions are described by spherical harmonics, many of the mapping coefficients vanish due to symmetry [20]. Therefore, one can spline the nonzero values of these matrices as a function of separation along the z-axis, interpolate their values for a given separation, and then use Wigner-D matrices to rotate those interpolated matrices into the molecular orientation [70].

The values of the nonzero matrix elements in the z-axis orientation are a choice. For example, we’ve described DFTB2 as using a Mulliken partitioning, but some have chosen to use CM3 charge mappings in their post-SCF analysis [71]. We have chosen to use is a constrained electrostatic fitting procedure [63,67,72–76]. The mathematical details of this procedure are fully presented in Ref. [32]; and one may choose differently; so we discuss this only briefly here. An electrostatic fitting procedure chooses the mapping coefficients in an attempt to reproduce the electrostatic potential of the AO product everywhere in space. It is a variational procedure that can be understood as minimizing the vector-norm squared difference between the AO product electric field with its auxiliary basis representation everywhere. By saying that we use a constrained electrostatic fitting procedure, we mean that Lagrange multipliers have been included within the variational solution to preserve the AO product multipole moments.

Just as DFTB2’s Mulliken partitioning yielded partial atomic charges, the generalized auxiliary basis yields vectors of atomic charge moments, m^a: $\delta \rho (\mathbf{r})=-{\sum }_a{\sum }_{k\in a}{m}_k^a{\phi }_k^a(\mathbf{r})$, where

$$m_k^a=-\sum _{ij\in a}(P_{ij}-P_{ij}^{(0)})M_{ijk}^a-\sum _{i\in a}\sum _{j\notin a}(P_{ij}-P_{ij}^{(0)})M_{ijk}^a-\sum _{i\notin a}\sum _{j\in a}(P_{ij}-P_{ij}^{(0)})M_{ijk}^a.$$ (38)

The spin density can be represented in an analogous way: $\omega (\mathbf{r})=-{\sum }_a{\sum }_{k\in a}{s}_k^a{\phi }_k^a(\mathbf{r})$, where the auxiliary spin-charge moment of atom a is

$$s_k^a=-\sum _{ij\in a}(P_{ij}^{\alpha }-P_{ij}^{\beta })M_{ijk}^a-\sum _{i\in a}\sum _{j\notin a}(P_{ij}^{\alpha }-P_{ij}^{\beta })M_{ijk}^a-\sum _{i\notin a}\sum _{j\in a}(P_{ij}^{\alpha }-P_{ij}^{\beta })M_{ijk}^a.$$ (39)

These auxiliary representations of the densities transform the W[δρ, ω] functional into a function of auxiliary charge moments, spin-charge moments, and atomic positions; W[δρ, ω] → W(m, s, R); and the σ-spin Fock matrix generalizes to

$$F_{ij}^{\sigma }=T_{ij}+V_{ij}^{(1)}-\sum _a\sum _{k\in a}{M}_{ijk}^a{\varphi }_k^{a,\sigma },$$ (40)

for one-center products; and

$$F_{ij}^{\sigma }=T_{ij}+V_{ij}^{(1)}-\sum _a\sum _{k\in a}{M}_{ijk}^a{\varphi }_k^{a,\sigma }-\sum _b\sum _{k\in b}{M}_{ijk}^b{\varphi }_k^{b,\sigma },$$ (41)

for two-center products; where

$${\varphi }_k^{a,\sigma }=\frac{\partial W(\mathbf{m},\mathbf{s},\mathbf{R})}{\partial m_k^a}+{(-1)}^{{\delta }_{\sigma ,\beta }}\frac{\partial W(\mathbf{m},\mathbf{s},\mathbf{R})}{\partial s_k^a},$$ (42)

is a spin-resolved auxiliary charge potential.

The VEJ/2P,3D,4F model computes the mapping coefficients as described above; its second-order energy is a Coulomb approximation; and the generalized auxiliary basis transforms Eq. (12) into

$$J(\mathbf{q},\mathbf{R})=\frac{1}{2}\sum _{ab}\sum _{k\in a}\sum _{k\prime \in b}{m}_k^a{m}_{k\prime }^b\times \int \int \frac{{\phi }_k^a(\mathbf{r}){\phi }_{k\prime }^b(\mathbf{r}\prime )}{|\mathbf{r}-\mathbf{r}\prime |}{d}^{3}r{d}^{3}r\prime .$$ (43)

2.6 Decomposition of the nonadditive xc-potentials

This section introduces new, preliminary methods that we’ve been using to gain insight into the decomposition of the xc-potentials. Our purpose for describing them here is to motivate and inspire the development of new approximations that address the third grand challenge: Moving beyond the one- and two-body treatment of the first-order matrix elements.

A topic on which we have yet to publish, and which is a topic that few people have ever attempted to address, are new approximations that go beyond the one- and two-center treatment of V⁽¹⁾, and approximations that consider the many-body character of the second-order VE energy [77]. We believe that this is because it is not immediately apparent how these nonadditive potentials decompose into one-centered functions and two-centered corrections, or whether they can be adequately expressed in that manner at all. This brings us to the purpose of this section: we will determine how the nonadditivity of the first- and second-order potentials decompose into atomic contributions. Our motivation is to gain the insight necessary to propose new VE integral approximations that explicitly consider all the atoms in the system, and to develop the new mathematical techniques that those proposals would require.

What new mathematical techniques potentially need to be developed, and how would that be aided by the present exploration? (1) If the first-order potential was an additive function, or approximated as such, then the contribution of a third-atom requires the potential of only that atom. (2) If one needs to explicitly treat the three-body nonadditivity, then one ultimately requires the potential of atom triplets. (3) If the first-order potential can be expressed as a sum of one-body potentials, or a sum of one-body potentials and two-body corrections, then there is some possibility of reducing the calculation of V⁽¹⁾ to one that requires no more than two-center integrals, even if it requires a loop over third atoms. There are various mathematical tricks that would could try to use for this purpose; for example, using auxiliary basis representations of the AOs and/or first-order potential, or using resolution-of-the-identity techniques [69]. But the problem we are trying to emphasize here is a general lack of insight as to whether it is even possible to avoid many-body corrections [as in case (2)] or not; and if so, how?

Previous descriptions of DFTB2 [30] have attempted to rationalize the use of Eq. (9) by explaining how it differs from a a superposition of atom-centered potentials

$${\upsilon }_{\text{ref}}^{(1)}(\mathbf{r})\approx \sum _a{\upsilon }_a^{(1)}(\mathbf{r}).$$ (44)

Although Eq. (44) ignores the nonadditivity of the xc-potential, it at least recognizes that the system is composed of more than one or two atoms. Being that the only nonadditive component of ${\upsilon }_{\text{ref}}^{(1)}(\mathbf{r})$ is the xc-potential, it begs to question whether or not the error introduced by ignoring nonadditivity in Eq. (44) is acceptable. It is for this reason that we construct the VE1S model, and include it in our comparisons within Table 1.

Table 1.

Bond, angle and dipole moment errors relative to standard PBE/6-31G* results for 52 molecules upon geometry optimization. The statistics under the heading ΔE_rxn are adiabatic SCF energy differences corresponding to the homolytic bond dissociation reactions: C₂H₆ + H₂ → 2CH₄, C₂H₄ + 2H₂ → 2CH₄, C₂H₂ + 3H₂ → 2CH₄, N₂H₄ + H₂ → 2NH₃, Si₂H₆ + H₂ → 2SiH₄, and H₂O₂ + H₂ → 2H₂O. μ_SE and μ_UE are the signed and unsigned errors of the property, respectively, and whose units are shown in the row “Avg.”, which displays the average reference value. “N” is the amount of data included in the statistics. The VE1S statistics exclude any contributions from Si₂H₆, which geometry optimizes into a hopelessly nonsensical configuration where all 6 hydrogens are clustered between the two silicons, at which point we can no longer coax SCF convergence. Thus, we expect the true VE1S errors to be larger than those reported here

	Bond		Angle		Dipole		ΔErxn
N	114		98		52		6
Avg.	1.322 Å		112.546°		0.496 a.u.		158.637 kcal/mol
Model	μSE	μUE	μSE	μUE	μSE	μUE	μSE	μUE
VE	0.002	0.002	−0.006	0.177	−0.007	0.012	0.076	0.221
VE0	−0.013	0.014	−0.629	0.858	−0.005	0.015	−8.408	11.708
VE1	−0.473	0.473	0.785	10.666	0.120	0.373	369.505	511.706
VE1S	−0.128	>0.130	−1.497	>6.070	0.030	>0.185	−79.629	>130.563
VE1W	−0.008	0.011	−0.454	0.827	−0.006	0.013	−0.166	11.621
VEJ	0.012	0.013	−0.198	0.564	−0.045	0.052	−1.161	1.615
VEJ/1S(M)	−0.045	0.046	0.384	1.148	−0.207	0.257	−15.165	15.165
VEJ/2P,3D,4F	0.013	0.014	−0.258	0.577	−0.039	0.053	0.045	1.337

The potential resulting from Eq. (44) is too negative relative to the exact potential; i.e., ${\upsilon }_{\text{ref}}^{(1)}(\mathbf{r})-{\sum }_a{\upsilon }_a^{(1)}(\mathbf{r})>0$; however, a nonadditive multi-center function can be cluster expanded into additive single-center components and many-body corrections; e.g.,

$${\upsilon }_{\text{ref}}^{(1)}(\mathbf{r})=\sum _a{\upsilon }_a^{(1)}(\mathbf{r})+\sum _{b>a}\Delta {\upsilon }_{ab}^{(1)}(\mathbf{r})+\sum _{c>b>a}\Delta {\upsilon }_{abc}^{(1)}(\mathbf{r})+\cdots$$ (45)

where ${\upsilon }_{\text{ref}}^{(1)}(\mathbf{r})-{\sum }_a{\upsilon }_a^{(1)}(\mathbf{r})$ is the nonadditive behavior of ${\upsilon }_{\text{ref}}^{(1)}(\mathbf{r})$, and

$$\Delta {\upsilon }_{ab}^{(1)}(\mathbf{r})={\upsilon }_{ab}^{(1)}(\mathbf{r})-{\upsilon }_a^{(1)}(\mathbf{r})-{\upsilon }_b^{(1)}(\mathbf{r}),$$ (46)

$$\Delta {\upsilon }_{abc}^{(1)}(\mathbf{r})={\upsilon }_{abc}^{(1)}(\mathbf{r})-\Delta {\upsilon }_{ab}^{(1)}(\mathbf{r})-\Delta {\upsilon }_{ac}^{(1)}(\mathbf{r})-\Delta {\upsilon }_{bc}^{(1)}(\mathbf{r})-{\upsilon }_a^{(1)}(\mathbf{r})-{\upsilon }_b^{(1)}(\mathbf{r})-{\upsilon }_c^{(1)}(\mathbf{r}),$$ (47)

are two- and three-body corrections, respectively. The two-body and larger-body corrections owe their existence solely to the nonadditivity of the xc-functional; therefore, in subsequent discussion, we refer to the nonadditivity of the first-order potential or the xc-potential interchangeably, depending on context.

Although the one-body sum [Eq. (44)] is too negative (see e.g., Fig. 2), our experience is that the two-body corrections over-correct it (see e.g., Fig. 3), and the resulting potential is arguably worse than the simple sum; however, we have empirically found that the third- and higher-order many-body corrections act to cancel some of the two-body corrections. Specifically, the many-body corrections cancel those two-body corrections for the pairs of atoms whose contribution to the reference density in the region of their overlap is dwarfed by a larger or intervening third atom. In other words, we have found that one can truncate the cluster expansion and weight the two-body corrections by some factor 0 < W_ab < 1 that accounts for the many-body corrections in an effective way. We call this the weighted cluster expansion

$${\upsilon }_{\text{ref}}^{(1)}(\mathbf{r})\approx \sum _a{\upsilon }_a^{(1)}(\mathbf{r})+\sum _{b>a}{W}_{ab}\Delta {\upsilon }_{ab}^{(1)}(\mathbf{r}),$$ (48)

and this is the primary approximation in the VE1W model.

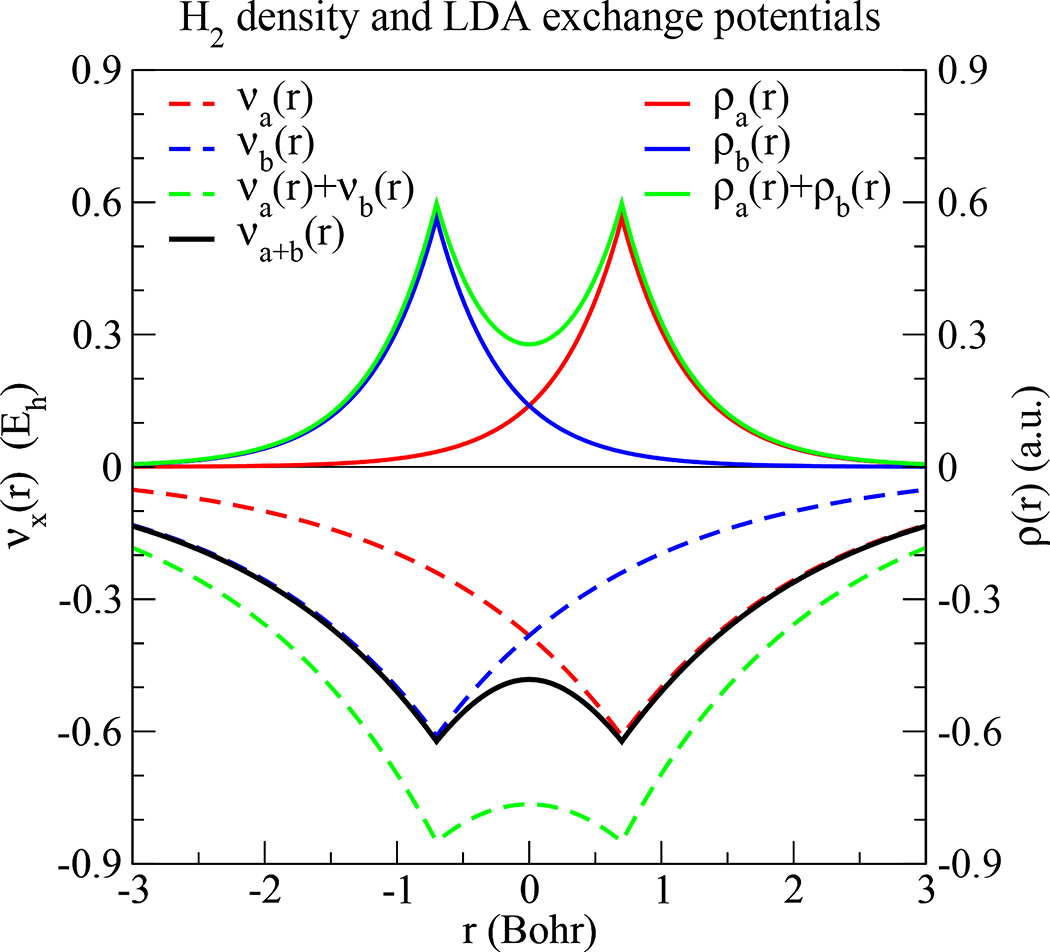
Fig. 2.

Example of exchange-potential nonadditivity using the LDA exchange functional in molecular hydrogen. The hydrogen atom density is the quantum mechanically exact density, and the atoms are separated by 1.4011 Bohr. The x-axis is the position along the internuclear axis. The sum of the isolated atom exchange-potentials (dashed green line) is more negative than the molecular exchange-potential (solid black line). At the bond midpoint (r=0), the ratio of the summed potentials to the molecular potential is exactly 2 : 2^1/3

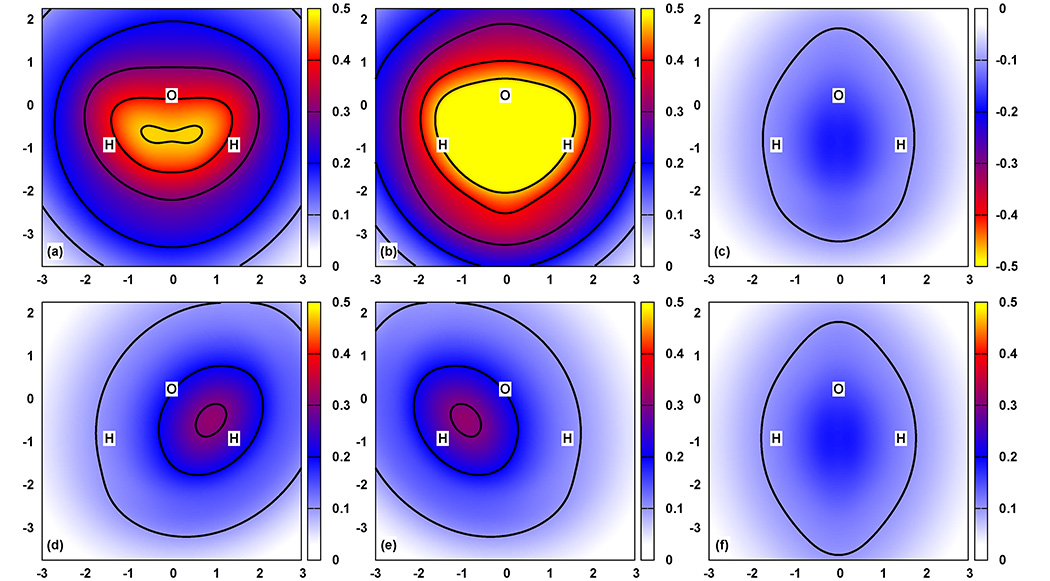
Fig. 3.

Decomposition of water’s PBE first-order potential ${\upsilon }_{\text{ref}}^{(1)}(\mathbf{r})$. The nonadditive potential is depicted in (a), which is the sum of the two- and three-body corrections shown in (b) and (c), respectively. The two-body correction [(b)] is the sum of individual pair-corrections $\Delta {\upsilon }_{ab}^{(2)}(\mathbf{r})$ depicted in (d), (e), and (f). The colors represent the value of the potential along the plane formed by the atoms. The x- and y-axis are expressed in Bohr and the color scale is in E_h. Note that potential in (c) is negative, whereas all other potentials are positive. The color scheme emphasizes that the magnitude of the three-body correction is so similar to the H-H pair-correction, that these potentials cancel. As a result, the nonadditivity shown in (a) is well-reproduced by the sum of (d) and (e). The solid lines are isocontour values of 0.1, 0.2, 0.3, 0.4, and 0.47 E_h

We have explored many forms of W_ab; the simplest of these is W_ab = S_f(X_ab + X_ba), where S_f(x) = x, if x < x₀; S_f(x) = 1, if x > 1;

$$S_f(x)=x_0+(1-x_0)\sum _{i=1}^5{c}_i{\left(\frac{x-x_0}{1-x_0}\right)}^i,$$ (49)

if x₀ < x < 1; x₀ = 19/20; c₁ = 1; c₂ = 0; c₃ = 4; c₄ = −7; c₅ = 3; $X_{ab}=S_{ab}^{\text{ref}}/{\sum }_c{S}_{cb}^{\text{ref}};S_{aa}^{\text{ref}}=0$; and $S_{ab}^{\text{ref}}=\int {\rho }_a(\mathbf{r}){\rho }_b(\mathbf{r})d^{3}r$. We don’t want the reader to become overwhelmed by technical details that are presented for the sole purpose of ensuring the reproducibility of our results. Our discussion can be be understood by interpreting the math as being a model that results in W_ab ≈ 1 for those pairs of atoms that one would intuitively consider to be covalently bonded, and W_ab ≈ 0 for those that are not.

The reader may question why the xc-potential is nonadditive, and why the simple sum of potentials [Eq. (44)] leads to a net potential that is too negative, and why the two-body corrections over-correct the one-body sum. In brief, the xc-functional’s nonadditivity results from a dependence on the density to some fractional order, and the reason why the one-body sum is too negative is because that fractional order is between one and two. Let us clarify through a brief demonstration. Consider the uniform electron gas exchange functional E_x[ρ] = −C_x ∫ ρ(r)^4/3d³r, where $C_x=\frac{3}{4}{(\frac{3}{\pi })}^{1/3}$. The first-order exchange potential is

$${\nu }_x(\mathbf{r})=-\frac{4C_x}{3}\rho {(\mathbf{r})}^{1/3}.$$ (50)

Let us evaluate ν_x(r) with a homonuclear dimer ρ(r) = ρ_a(r − R) + ρ_b(r + R). At the bond midpoint r = 0, it holds that ρ(0) = ρ_a(−R) + ρ_b(R) = 2ρ_a(R) [since ρ_a(r) = ρ_b(r) and each are spherically symmetric], and the exchange potential is

$${\nu }_{x,a+b}(0)=-2^{1/3}\left[\frac{4C_x}{3}{\rho }_a{(\mathbf{R})}^{1/3}\right];$$ (51)

whereas the sum of atom potentials is

$${\nu }_{x,a}(0)+{\nu }_{x,b}(0)=-2\left[\frac{4C_x}{3}{\rho }_a{(\mathbf{R})}^{1/3}\right].$$ (52)

We see that the sum of atom potentials is more negative by a ratio of 2 : 2^1/3. With this insight, it is easy to explain why the two-body corrections [Eq. (46)] over-correct the one-body sum [Eq. (44)]. Just as the sum of one-body potentials [Eq. (44)] results in a net potential that is too negative, the subtraction of one-body potentials in Eq. (46) results in a two-body correction that is too positive.

At this point, we have completed our description of the approximations as they relate to the calculation of the core-Hamiltonian, and to those models discussed in the Results section; however, we have a few comments regarding the second-order potentials. The observations that we describe here are of interest to the community, as they can be used to argue the validity of the approximations employed in spin-polarized SCC-DFTB models [38, 78], and also suggest ways that those approximations can be improved.

Unlike the first-order potential, the second-order potentials, ${\upsilon }_{\text{ref}}^{(2)}(\mathbf{r})$ and $w_{\text{ref}}^{(2)}(\mathbf{r})$, are not well-behaved; they are strictly negative functions that approach −∞ as ρ_ref(r) → 0. Thus, $w_{\text{ref}}^{(2)}(\mathbf{r})$ is poorly modeled by a simple sum of one-body $w_a^{(2)}(\mathbf{r})’\mathrm{s}$. Furthermore, the many-body cluster corrections introduce as many large errors as they remove, and the expansion does not converge until it has been totally exhausted; however, we have found the following approximation to be almost exactly correct:

$$w_{\text{ref}}^{(2)}(\mathbf{r})\approx \sum _a{L}_a(\mathbf{r})w_a^{(2)}(\mathbf{r})+\sum _{b>a}{W}_{ab}\{[L_a(\mathbf{r})+L_b(\mathbf{r})]w_{ab}^{(2)}(\mathbf{r})-L_a(\mathbf{r})w_a^{(2)}(\mathbf{r})-L_b(\mathbf{r})w_b^{(2)}(\mathbf{r})\},$$ (53)

and similarly for ${\upsilon }_{\text{ref}}^{(2)}(\mathbf{r})$, where L_a(r) = ρ_a(r)²/∑_b ρ_b(r)² is a spatial partition function, which one can interpret as being a “fuzzy” Voronoi-like cell. It holds the properties: L_a(r) ≈ 1 in the region of a; L_a(r) ≈ 0 near the region of any other atom; ∑_a L_a(r) = 1 for all r; and as a consequence of all the above, L_a(r)L_b≠a(r) ≈ 0. The sum of partitioned one-body potentials in the partitioned cluster expansion is a much-improved representation of the second-order potentials (see Fig. 4), and the weighted two-body partitioned corrections are relatively small.

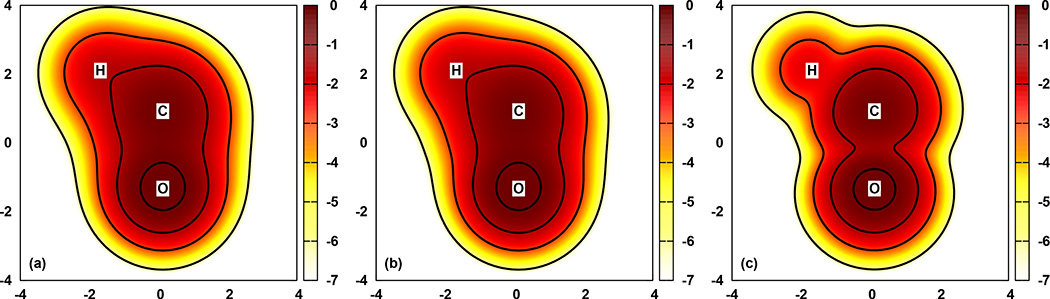
Fig. 4.

Decomposition of the SPW92 second-order spin-polarization potential $w_{\text{ref}}^{(2)}(\mathbf{r})$ for the HCO molecule. The panels depict: (a) the potential, without approximation; (b) the one- and two-body partitioned cluster approximation [Eq. (53)]; and (c) the one-body partitioned cluster approximation; i.e., W_ab = 0 for all pairs. The colors represent the value of these potentials in the plane formed by the atoms. The x- and y-axis are in units of Bohr and the color scale is E_h. The solid lines are isocontour values of −0.7, −1.5, −3, and −6 E_h

If one approximates $w_{\text{ref}}^{(2)}(\mathbf{r})$ by ignoring the two-body corrections, then the potential is described by the isolated-atom potentials within their respective Voronoi cells, and the spin-polarization energy E[ω] becomes

$$E[\omega ]=\frac{1}{2}\int \omega {(\mathbf{r})}^2{w}_{\text{ref}}^{(2)}(\mathbf{r})d^{3}r=\sum _a\frac{1}{2}\int \omega {(\mathbf{r})}^2[L_a(\mathbf{r})w_a^{(2)}(\mathbf{r})]d^{3}r=\sum _a\frac{1}{2}\int \omega (\mathbf{r}){\omega }_a(\mathbf{r})w_a^{(2)}(\mathbf{r})d^{3}r$$ (54)

where ω_a(r) = L_a(r)ω(r) is the atom-partitioned spin-density about a. If ω(r) was represented by an atom-centered auxiliary basis and was chosen to partition the density in a manner analogous to L_a(r), then the spin-polarization energy reduces to one- and two-center overlap-like integrals between auxiliary functions.

A different result is obtained if one employs the exact decomposition ω(r) = ∑_b ω_b(r) = ∑_b L_b(r)ω(r), and then approximates their overlap L_a(r)L_b≠a(r) ≈ 0; i.e.,

$$E[\omega ]=\sum _{ab}\frac{1}{2}\int \omega {(\mathbf{r})}^2{L}_b(\mathbf{r})[L_a(\mathbf{r})w_a^{(2)}(\mathbf{r})]d^{3}r\approx \sum _a\frac{1}{2}\int {\omega }_a{(\mathbf{r})}^2{w}_a^{(2)}(\mathbf{r})d^{3}r\approx \sum _{a}E[{\omega }_a].$$ (55)

If one presumed that the L_a(r)’s are spherical, then Eq. (55) is no different than what is used in spin-polarized SCC-DFTB [38]; however, we feel that we’ve shown that the arguments needed to reach this result are more justified than what one might infer from reading Refs. [38] and [79]; and it also suggests ways that one can try to improve upon their work.

2.7 Computational details

2.7.1 DFTB2 with charge-dependent polarizability corrections

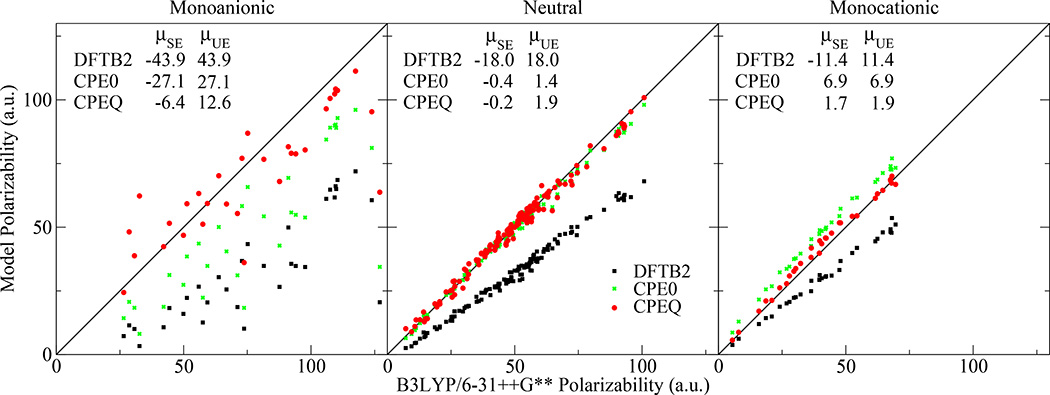
Fig. 5 compares the polarizabilities of DFTB2, DFTB2+CPEQ, and DFTB2+CPE0 to standard B3LYP/6-31++G** results. The comparisons include 33 anionic, 142 neutral, and 35 cationic molecules taken from the QCRNA database [80]. The molecules were selected for having contained some combination of H, C, N, and O, but no other elements.

Fig. 5.

Comparison of DFTB2, DFTB2+CPE0, and DFTB2+CPEQ polarizabilities to standard B3LYP/6-31++G** results. μ_SE and μ_UE are the mean signed and unsigned errors (a.u.), respectively

The H, C, N, and O DFTB2 parameters are described in Ref. [22], and these parameters remain unmodified in our CPE-corrected variations, which we henceforth refer to without the “DFTB2+” prefix. The CPEQ and CPE0 models have four additional atomic parameters: ζ_a(0), b_a, R_lo,a, and R_hi,a. Although, note that the CPE0 model’s b_a parameter is zero for all atoms. These parameters were optimized for each model to B3LYP/6-311++G** dipole moments and B3LYP/6-31++G** isotropic polarizabilities, and the merit function used to judge the goodness of the fit is

$${\chi }^2=\sum _{i=1}^{142}80{|\Delta {\mathbf{q}}^{(1)}|}_i+\sum _{i=1}^{210}{|\Delta \alpha |}_i;$$ (56)

where |∆q⁽¹⁾| is the norm of the difference between the model and reference dipole moment vectors; |∆α| is the absolute difference between the model and reference isotropic polarizabilities; and the summation over dipole moment errors includes only neutral molecules. Both the reference and model calculations are evaluated at the B3LYP/6-31++G** geometry optimized structures.

2.7.2 Generalization of the auxiliary basis

Table 1 compares the geometry optimized bond, angle, dipole moment, and relative energy errors of various PBE/6-31G*-based models to standard PBE/6-31G*. The statistics include results from 52 molecules [81] taken from the G2/97 neutral small molecule test set [82], which were also used in our previous VE studies [26,32]. For the purpose of discussing the generalization of the auxiliary basis, the reader should compare VEJ/1S(M) and VEJ/2P,3D,4F to VEJ, and note how well VEJ compares to VE. The parametrization of the VEJ/2P,3D,4F auxiliary basis Slater exponents is described elsewhere [32].

2.7.3 Decomposition and nonadditivity of the xc-potentials

Table 1 is used to compare the errors of the VE1, VE1S, and VE1W models, all of which are variations of the VE0 model.

Fig. 3 displays the nonadditivity of the PBE first-order potential of water and its decomposition into two- and three-body corrections, and the decomposition of the two-body correction into the individual pair-corrections.

3 Results

3.1 DFTB2 with charge-dependent polarizability corrections

Fig. 5 shows that DFTB2 underpredicts the B3LYP/6-31++G** polarizabilities; the extent to which depends on the ionic character of molecules. The mean unsigned relative percent errors of the anionic, neutral, and cationic molecules are 59%, 38%, and 26%, respectively. In other words, the anionic molecules need a larger polarizability correction than the neutrals, and neutrals need a larger correction than the cations.

To emphasize this further, we examine the results of a charge-independent model, CPE0. It greatly improves the neutral molecule polarizabilities, but the resulting cations are too polarizable, and the anions are still not polarizable enough.

However, the errors are largely corrected with the charge-dependent model, CPEQ. It reduces the neutral and cationic polarizability errors to 5%; and the anionic polarizability errors are two and three times smaller than the CPE0 and DFTB2 errors, respectively.

The DFTB2 mean unsigned dipole moment errors relative to the B3LYP reference is 0.175 a.u.; and the CPE0 and CPEQ models reduce this to 0.167 and 0.166 a.u., respectively. As expected, the CPE0 and CPEQ models do not significantly improve the DFTB2 dipole moments, because the models have been chosen to screen the short-range interactions. The CPE method lacks the proper physics to describe covalent bonds, and thus cannot be relied upon to improve molecular dipole moments. For this purpose, it would be more fruitful to improve the underlying DFTB2 model; for example, by increasing the number of AOs.

We note that there is very little difference between the DFTB2+CPEQ method of the present work and the MNDO/d+CPE method presented in Ref. [37]. The main difference is that we have included Fock matrix corrections [Eq. (28)] in the present work. There are some more trivial differences as well, such as our use of Slater dipole CPE response functions in DFTB2+CPEQ, as opposed to the Gaussian dipole functions used in MNDO/d+CPE. The only other difference is: the reference density about which the DFTB2+CPEQ correction is expanded is a collection of Slater charges, whereas the MNDO/d+CPE correction is expanded about a collection of point charges. The beauty of the CPE correction is that it is expanded about a reference density, and it doesn’t matter what underlying method gave rise to that reference density. However, just as the CPE correction is an ad hoc correction to MNDO/d, so too is it an ad hoc correction to DFTB2.

3.2 Generalization of the auxiliary basis

Table 1 demonstrates that a Taylor series truncation of the xc-functional to first-order (VEJ) has a small effect on geometries and a modest effect on dipole moments. Furthermore, it is capable of closely reproducing closed-shell molecule relative energies. Some new models have extended the Taylor series expansion to third-order as a mechanism for including charge-dependence [56–58], but the VEJ results presented here should clarify that one should take care to not misinterpret those models as having corrected a symptom originating from a premature truncation of the Taylor series expansion.

Approximating the second-order energy with a SCC-DFTB-like Slater monopole auxiliary basis [VEJ/1S(M)] significantly increases the errors, but these errors are alleviated when the auxiliary basis is extended to better reproduce the AO products (VEJ/2P,3D,4F).

Our previous work [32] showed that VEJ/1S(M) underpredicts the hydrogen bond strength of the water dimer by approximately 4 mE_h relative to both VEJ and standard PBE/6-31G*, and that this error was corrected when using a more sophisticated auxiliary basis.

3.3 Decomposition and nonadditivity of the xc-potentials

The introduction to this manuscript emphasized the severity of the VE1 approximation, and we show its results in Table 1. Its severity may seem intuitively obvious because it neglects all atoms in the system other than those coincident with the AO product, and so one may try to improve it by including the potentials caused by the other atoms. The VE1S model attempts to overcome this severe approximation by (incorrectly) assuming that the neutral-atom potentials are additive functions; however, this model is arguably just as bad as VE1. One can try to construe the numerical values in a manner to suggest that VE1S is a minor improvement, but both models optimize the molecular geometries into utterly nonphysical configurations.

The reader may notice that one of the molecules (Si₂H₆) fails to SCF converge once VE1S optimizes it into an unrealistic geometry, but it is best not to over-interpret this. The geometries of VE1 and VE1S are both extremely poor, and the fact that one has SCF converge difficulties when evaluated at a nonsensical configuration, whereas the other does not, does not indicate that its approximations are somehow better. Had we expanded the test set to include even larger molecules, we’d expect the VE1 model to eventually fail as well. We have tried a number of approximations, most of which we do not describe here; and our experience suggests that larger molecules are more likely to optimize into strange configurations and then fail to SCF converge, because the errors introduced by the approximations increase with the system size. It is because of this that we feel our limited test set is sufficient to identify which approximations are severe without reaching that extreme limit of failure.

The VE1S first-order potential is too negative because it incorrectly assumed that the neutral-atom xc-potentials were additive, and as the size of the system increases, the magnitude of this error is compounded. To account for this nonadditivity, one might include two-body corrections. Alas, the resulting potential is then not negative enough, and the magnitude of its error increases with the size of the system. Like VE1S, it readily geometry optimizes to nonsensical configurations.

The prospect of explicitly including three-body or larger-body corrections is sufficiently daunting that it may be tempting to just give up and use VE1 or the VE1-like approximation that most semiempirical models use. To make an advance beyond that, we need to have some way to account for the many-body effects in some new way. To this end, Fig. 3 decomposes the xc-potential of water into its two- and three-body components, and we see that the three-body nonadditivity cancels the two-body correction between the H’s. One can perform similar decompositions for other molecules, and from these, it seems that this is true for all pairs of atoms whose overlap is dwarfed by the densities of the other atoms. This general idea can inspire many different forms of the weighted cluster approximation, and Table 1 displays the statistics for a very simple model (VE1W). This model reduces the errors to those comparable to VE0, the model on which it is based.

4 Conclusion

Kohn-Sham expansion methods can be made to be as accurate and transferable as the density functional methods on which they are based. The primary sources of errors in a second-order VE model are not a consequence of a premature truncation of the Kohn-Sham functional. Instead, the source of errors are much more obvious; in that, just as one would expect standard DFT models to suffer from approximations, so too would one expect the analogous VE models. The most severe VE approximations that we’ve encountered are: the limited size of the AO basis; the poor auxiliary basis representation of the AO products; and the one- and two-body treatment of the first-order interactions.

As a mechanism for discussing these approximations: we’ve introduced a new self-consistent charge-dependent dipole polarization correction model (DFTB2+CPEQ) that improves DFTB2 polarizabilities; we’ve reviewed our recently published work that generalizes the auxiliary basis; and we’re examined the decomposition of the first-order potential into many-body components, and used these observations to gain the insight and motivation for the development of new approximations.

From these discussions, we hope to have communicated the following:

1. The errors introduced from having truncated the Taylor series expansion to second-order are small relative to the other errors that we’ve discussed.

2. The beneficial effects of third-order models arise from introducing charge-dependent corrections, and these corrections mask the limited size of the AO basis.

3. Like all minimal valence AO basis models, DFTB2 underpredicts dipole polarizabilities; however, this underprediction will not be alleviated by increasing the size of the AO basis alone, because it would still lack atomic dipole response. In lieu of generating an entirely new DFTB model, one can improve the polarizabilities with an auxiliary CPE response. If the CPE response is not made charge-dependent, then the anionic and cationic molecular polarizabilities will be under- and over-predicted, respectively; but the polarizability of various charge states can be improved by making the CPE response functions charge-dependent.

4. The VE response density can be modeled more accurately by increasing the radial and angular completeness of the auxiliary basis description of the AO products; and this can be done in a way that requires only two-center integrals, which can be precomputed and splined as a function of internuclear separation.

5. The one- and two-body treatment of the first-order matrix elements is a severe approximation; however, it is not improved by representing the first-order potential as a sum of isolated atom potentials. Nor is it improved by modeling it with a sum of one-body potentials and two-body corrections. We have presented some initial evidence that the many-body nonadditivity of the xc-potential can be modeled by damping some of the two-body corrections.

6. The second-order potentials are not well-described by any truncated cluster approximation, but is well-modeled by a partitioned cluster approximation. By inserting this approximate form into the expression for the spin-polarization energy, one can derive its model form used in spin-polarized DFTB2 methods by making some additional approximations.

It is the hope that the insights provided in this work will be instrumental in directing further research effort toward development of the next-generation of semiempirical quantum models for broad application.