Genome Data Exploration Using Correspondence Analysis

Abstract

Recent developments of sequencing technologies that allow the production of massive amounts of genomic and genotyping data have highlighted the need for synthetic data representation and pattern recognition methods that can mine and help discovering biologically meaningful knowledge included in such large data sets. Correspondence analysis (CA) is an exploratory descriptive method designed to analyze two-way data tables, including some measure of association between rows and columns. It constructs linear combinations of variables, known as factors. CA has been used for decades to study high-dimensional data, and remarkable inferences from large data tables were obtained by reducing the dimensionality to a few orthogonal factors that correspond to the largest amount of variability in the data. Herein, I review CA and highlight its use by considering examples in handling high-dimensional data that can be constructed from genomic and genetic studies. Examples in amino acid compositions of large sets of species (viruses, phages, yeast, and fungi) as well as an example related to pairwise shared orthologs in a set of yeast and fungal species, as obtained from their proteome comparisons, are considered. For the first time, results show striking segregations between yeasts and fungi as well as between viruses and phages. Distributions obtained from shared orthologs show clusters of yeast and fungal species corresponding to their phylogenetic relationships. A direct comparison with the principal component analysis method is discussed using a recently published example of genotyping data related to newly discovered traces of an ancient hominid that was compared to modern human populations in the search for ancestral similarities. CA offers more detailed results highlighting links between modern humans and the ancient hominid and their characterizations. Compared to the popular principal component analysis method, CA allows easier and more effective interpretation of results, particularly by the ability of relating individual patterns with their corresponding characteristic variables.

Introduction

The growing number of completely sequenced organisms¹ offers the opportunity to systematically investigate, as a whole, large amounts of high-dimensional data. Typical examples of such investigations in genome data analysis include studies of predicted ORF products according to their codon² and/or amino acid compositions,³ genes according to multiple experimental conditions in microarray data analysis,⁴ or yet species distribution according to the criteria of different relationships as for example orthology and conservation between species.⁵ A new class of multidimensional data concerns genotyping projects studying healthy populations as well as populations with disease phenotypes.^6,7 Other popular projects concern the observed single-nucleotide polymorphisms (SNPs) in different human populations as obtained from ancient or present-day humans in migration or from disease studies.⁸ Such investigations generally involve large and complex data tables, in which the rows (also called observations) are genes and the columns (also called variables) are conditions. Given the huge amount of available data that can be presented in data table forms (corresponding to genes in the considered species), analysis methods are needed to assist researchers in synthesizing the original data sets and in order to make their understanding easy. Often in these data tables, the amount of independent new information is much smaller than what the number of raw data suggests. The most expected result from such data analyses is a synthetic view of the observations and their characterization by specific variables. Thus, methods that can help extracting subsets of genes associated with subsets of variables are likely to be useful. Such methods aim at clustering objects into discrete groups each possessing similar defined properties. Appropriate methods are multivariate, including factorial and classification methods. Among these, correspondence analysis (CA), developed by Benzecri in the 1970s,^9–12 is a powerful approach to associate specific observations with specific variables. CA is an exploratory and descriptive method that allows reducing high-dimensional data sets into a few independent factors. It reveals principal factorial axes, enabling projection of observations and variables onto a subspace of low dimensionality that accounts for the main variance in the data. The first factor is the combination of columns that accounts for the largest amount of variability in the data set. The second factor corresponds to the next largest amount of variability in the data set, and so on. CA represents observations and variables as vectors in a high-dimensional space. Unlike other multivariate methods, such as principal component analysis (PCA),^13,14 CA enables the joint projection of observations and variables onto the same low-dimensional factorial subspace. CA directly visualizes the associations between observations and variables by allowing their partitions into mutually linked sets, thus revealing which hypotheses can be put forward to help leading to discoveries. Early use of the CA method in sequence analysis involved the prediction of protein regions in nucleic acid sequences.¹⁵ It has also been used in genome data analyses.^{2–5,16–22} However, despite its straightforward application and ease of interpretation of results, CA is still not as familiar to researchers in genomics as are other multivariate statistical analysis methods, particularly PCA.

In this review, I suggest the use of CA in genome data mining.

A short introduction of the method and some examples of its applications are provided in this review in order to demonstrate its performance, effectiveness, and strength in genome data mining.

Method: Correspondence Analysis

CA is an exploratory and descriptive data method designed to analyze two-way and multiway data tables containing measures of association between rows and columns. CA was developed by Benzecri, and his seminal work was published in 1973.⁹ CA dramatically simplifies complex data and provides a detailed description of information they include, yielding a concise, yet exhaustive, analysis. CA has several features that distinguish it from other data projection analysis methods. The multivariate nature of CA can reveal relationships that would not be detected in a series of pairwise comparisons of variables. Another important feature is the graphical display of rows and columns as dots in planar representations, which can help in detecting structural relationships among the variables and/or observations. Finally, CA has highly flexible data requirements, as it can be used for contingency as well as metric tables. The primary and straightforward use of CA applies for contingency data tables where each cell corresponds to the number of occurrences associating the corresponding line and column.

In heterogeneous data sets, a preliminary step of original data coding is needed to consolidate nonuniform data and homogenize them prior to the application of CA. The only strict data requirement for CA is a rectangular data matrix with positive entries, where values on a given row can be meaningfully summed up (see Supplementary File 1A). CA is most effective if the following conditions are satisfied:

• –The data matrix is large enough, so that visual inspection or simple statistical analyses cannot reveal its structure.

• –The variables are homogeneous, so that calculation of statistical distances between rows (summing row values should make sense) or between columns is meaningful.

The primary goal of CA is to transform a table of numerical data into a graphical display, in which each row and each column is depicted as a point. CA yields graphical presentations producing two dual displays whose row and column geometries have similar interpretations, facilitating analysis and detection of relationships, particularly associations between sets of rows and sets of columns. This duality is missing in other multivariate approaches to graphical data representation, as for example in the PCA method, and thus constitutes the most important feature yielded by CA as observed patterns of observations might be explained by patterns of variables to which they are linked.

Basic concepts

A concise description of CA is presented here; more thorough explanations with worked examples can be found in Refs. ⁹ and ¹⁰ (see also Supplementary File 1B for suggested web links). CA is a multivariate method that applies to positive numerical data tables. Rows (denoted I) of such tables are called observations, individuals, or objects; columns are the variables (denoted J). Such a table is generally denoted as K_IJ = {k_ij; i = l, …, n; j = l, …, p}, where n is the number of individuals and p is the number of variables. CA aims at embedding rows and columns of a numerical data table in the same space constructed with the first few (two or three) dimensions that include most of the information and where each row and each column is depicted as a point. CA allows the construction of an orthogonal system of axes (called factors and denoted F₁, F₂, etc.) where observations and variables can be jointly displayed. Each factor is a linear combination of variables that accounts for the variability in the data table. The first corresponds to the largest variability, the second factor to the second largest variability in the data table and that is orthogonal to the first factor, and so on. Thus, each factor is constructed according to the information it represents, independent of the other factors and that are presented in a decreasing order of importance. The origin of this orthogonal system is placed on the barycenter of both the individuals and variables. A maximum of m − 1 such factors can be defined, where m is the lower of the two numbers of observations (n) and variables (p). The factors thus determined constitute an orthogonal system where observations and variables can be displayed. The information included in a subspace of dimension q (q ≤ m − 1) equals the sum of information included in each of the corresponding q factors. The average proportion of the total information represented by one factor is 100/(m − 1). This value serves as a guide in determining the relative importance of a given factor. Practically, only the few first factors that account for the largest amount of variability in the data table are considered for results interpretation. In this system, closeness between observations or between variables provides evidence of similarity, while closeness between observations and variables is interpreted as significant relationships. The ability of displaying observations and variables simultaneously in the same factorial space facilitates the discovery of salient information included in a given data table.

Formally, let k_i = ∑_j k_ij; k_j = ∑_i k_ij and k = ∑_i,j k_ij = ∑_i k_i = ∑_j k_j corresponding, respectively, to the total of line i, column j, and grand total k of the table K_IJ. From the frequency table with elements f_ij = k_ij/k and the corresponding totals f_i = ∑_j f_ij and f_j = ∑_i f_ij, respectively, of lines and columns, a symmetric matrix S is derived with elements s_ij = (f_ij − f_i.f_j).(f_i.f_j)^1/2. S is submitted to singular value decomposition²³ and is decomposed into the product of three matrices: S = UΛV^t where U^tU = V^tV = VV^t = I_dentity. The matrix U is the orthonormalized eigenvectors (denoted F₁, F₂, F₃,., F_α,.) associated with the largest eigenvalues of SS^t. The matrix V consists of the orthonormalized eigenvectors (denoted G₁, G₂, G₃,., G_α,.) of S^tS. Λ is a diagonal matrix of nonnegative square roots of the eigenvalues of S^tS (they are called singular values). The eigenvalues are assumed to be sorted from the largest to the smallest and are denoted λ_α.

Principal and illustrative observations and variables

CA applies to data tables with rows and columns that are, respectively, called principal observations and principal variables. The term active is also sometimes used. For illustrative reasons, supplementary observations and/or variables can be added to the principal data table. The term supplementary is sometimes exchangeable with dummy or illustrative to denote observations or variables that do not contribute to the construction of the factorial axes, but simply plotted on the determined factorial axes based on the transition formulae: $F_{\alpha }(i)={\lambda }_{\alpha }^{-1/2}.\sum \{f_j^i{G}_{\alpha }(j)=1,p\}$ and $G_{\alpha }(i)={\lambda }_{\alpha }^{-1/2}.\sum \{f_j^i{F}_{\alpha }(i);i=1,n\}$ where F_α(i) is the coordinate of i on the α factor in the individuals space, λ_α (eigenvalue) is the total inertia relative to F_α, $f_j^i$ is the frequency of i relative to the total of the jth variable, and G_α(j) is the coordinate of j on the α factor in the variables space.¹⁰ Only the principal observations and variables contribute to the factors determination. The main goal of using supplementary individuals and variables is to show with which active observations and/or variables they are close to. This may also have an explanatory interest, by providing hints for similarity between supplementary and principal individuals or variables.

Furthermore, considering supplementary elements in an analysis might be very important, for example, in typology validation. By plotting new samples, considered as supplementary elements, on a determined typology (following a principal data table), the positions of the new samples on the factorial space are indicative of their possible assignments to closely situated principal individuals.

Data coding to conform to CA: disjunctive coding scheme

CA can be directly performed on data tables where the sum of each row is meaningful; otherwise, a preliminary step of data homogenization is necessary. For example, it makes no sense to sum up columns if the set J includes metric variables expressed in different units (ie, distances cannot be summed with weights). In this case, we need to divide metric variables into ordinal classes and consider presence or absence of individuals in such classes. This procedure is called disjunctive coding scheme and provides a simple way to standardize heterogeneous data tables. With this coding, the original data are recoded to ensure the summing of column values in a given row. This coding consists of considering categories of each of the considered variables instead of the continuous original data. The original values are replaced by a series of 0 and 1 corresponding to the absence or presence in a given category. One may, for instance, consider three categories of distances and three of weights: small, medium, and large classes delimited by suitable interval limits. A medium distance value will be represented by 010 and a large weight value is represented by 001, etc.

Each individual is then represented by a vector of 0 and 1 (absence and presence, respectively) implying the sum of each line to be equal to the number of variables. CA can then be applied to such a transformed data table.

A possible disadvantage of this coding scheme is the loss of information, upon substituting the original continuous values by discrete values of 0 and 1. This is true, but in return there is a significant gain of simplification and ease of interpreting the results, as CA will show possible categories of associations. For example, middle category classes of a subset of variables can be associated with large classes of different sets of variables facilitating their interpretation.²⁴

For this reason, disjunctive coding scheme is systematically performed prior to performing CA on mixed continuous variables describing sets of observations. An example of such a coding scheme can be found in Ref. 25.

Combining CA and clustering methods

One of the objectives of data set processing is the ability to tackle biological questions from accumulated data and interpretation of their analyses. Clustering of observations is one of such objectives that aim at delineating common characteristics and discriminative features to members of groups of observations. As previously indicated, CA may help synthesizing large sets of observations described by a set of variables, by constructing orthogonal factorial axes and projecting observations on factorial spaces. Using coordinates of the observations on such spaces allows calculation of Euclidian distances between pairs of observations, leading to a distance matrix between all the considered observations. It is common use to consider such a matrix in tree-constructing methods in order to cluster observations according to their neighborhood. The main advantage of this procedure is to avoid the noisy data, arising from the possible partial correlation between numerous variables, and reduce fluctuations present in trees directly constructed from the original raw data. Since factorial axes are orthogonal, they constitute independent information that can be considered additively as a whole or partial vision of the analyzed data table.

Applications of this procedure include construction of genome trees.^5,17

Graphical representations

CA results are displayed on graphs that represent the distribution of observations and variables, in projection planes formed by the first principal factorial axes taken two at a time or three at a time in spatial (or 3D) presentations. It is a common use to summarize the row and column coordinates in a single plot. From such presentations, neighborhood (respectively, distance) between observations and variables provides evidence for strong relationships (respectively, weak relationships). From the coordinates of the observations and variables on all constructed factors, it is possible to calculate the Euclidean distances between the observations or between the variables to look for the neighbors of a given point or a set of points. However, it is important to note that calculating distances between observations and variables in such plots is not accurate, whereas it makes sense to interpret the relative positions of one point in one set with respect to all the points in the other set. This is due to the transition formula (see above) that links rows and columns (see Supplementary File 1C for some hints in interpreting factorial representations). This possibility is of fundamental importance for the interpretation of the positions of supplementary elements, where the aim of such plotting is looking for most closely related observations to such supplementary elements.

Examples: Application of CA in Genome and Genotyping Data

In the following sections, we present some examples of different genomic data tables that have been submitted to CA and show how efficient is the method in extracting significant information from the considered data tables.

Species versus amino acid compositions

CA has been used in exploring the relationships between species, genes, and proteins following their corresponding amino acid and codon compositions.^{2,3,16,18–20}

If I denotes the set of predicted ORFs (respectively, their corresponding ORF products) in a given species and J denotes the set of the 20 amino acids, the following tables can be constructed: K_ij represents the number of amino acid j included in the ORF product i. It is generally a good practice to normalize the counts of each amino acid relative to the total number of amino acids in the ORF product i. In this case, K_ij represents a proportion (or frequency) of amino acid j in ORF product i. Observations and variables are defined by their coordinates on the factorial space as obtained by CA. They can then be classified according to their neighborhood (distances), thus allowing the determination of homogeneous clusters or patterns of ORF products and amino acids. A tree can then be constructed to represent the degree of homogeneity between these clusters. Thus, when observations represent ORF products and variables represent the 20 amino acids, it is possible to display ORF products according to their composition and to define patterns of genes with similar amino acid compositions.

Generally, observations and variables are displayed jointly on the same factorial plane defined by the first (F₁) and the second (F₂) factors. By definition, this first factorial plane includes the largest part of the information included in the analyzed data table. But it may be useful to consider and interpret other combinations of factors as they may show relationships not displayed on the first factorial plane.

CA also allows the representation of subsets of variables or observations as illustrative elements, so that they can be placed with regard to all other active variables or observations. For example, charged, polar, and hydrophobic subsets of amino acids can be represented as illustrative variables.¹⁸

Using ORFs, K_ij can also correspond to the transformed data tables as, for example, the relative synonymous codon usage (RSCU) corresponding to the codon j in the ORF i.^16,21

In the following sections, we consider two examples using CA in the study of species versus amino acid compositions.

Yeast and fungal species versus amino acid compositions

A list of 43 yeast and 48 fungal species (see the list in Table 1) is considered. The yeast species were selected mainly following the criteria reported in Refs. ²⁶ and ²⁷.

Table 1.

List of 43 yeast and 48 fungal species considered in the analyses of amino acid composition and in pairwise shared orthologs.

IDENT	#PROTS	SIZE (MB)	GC%	SPECIES (YEAST)
SACE	5769	12.2	38.2	Saccharomyces_cerevisiae
SAAR	5527	11.6195	37.9	Saccharomyces_arboricola
NACA	5592	11.2195	36.7	Naumovozyma_castellii_CBS_4309
KAZA	5378	11.13	36.2	Kazachstania_africana_CBS_2517
CAGL	5204	12.3182	38.6	Candida_glabrata
NADE	5112	10.9691	38.5	Nakaseomyces_delphensis
DECA	6219	11.76	36.7	Debaryomyces_carsonii
PISO	11175	21.4596	41.3	Pichia_sorbitophila
KLLA	5083	10.6891	38.7	Kluyveromyces_Lactis
PIPA	5040	9.2163	41.1	Pichia_pastoris_GS115
PIST	5816	15.4411	41.1	Pichia_Stipidis
CATE	6985	10.75	42.2	Candida_tenuis
CAOR	5677	12.6594	36.9	Candida_orthopsilosis
SPPA	5983	13.1821	37.0	Spathaspora_passalidarum_NRRL_Y-27907
LOEL	5796	15.4	36.7	Lodderomyces_elongisporus
CAPA	5817	12.9984	38.7	Candida_parapsilosis
DEFA	6182	12.00	34.8	Debaryomyces_fabryi
DEHA	6272	12.2	36.3	Debaryomyces_hansenii
DETY	6747	12.40	35.6	Debaryomyces_tyrocola
CATR	6258	14.5798	33.0	Candida_Tropicalis
CAAL	6112	14.4176	33.3	Candida_albicans_WO-1
CADU	5983	14.6184	33.2	Candida_dubliniensis_CD36_uid38659
STAM	5790	unk	unk	Starmera_amethionina
NADA	5772	13.5275	34.0	Naumovozyma_dairenensis_CBS_421
TEPH	5250	12.1	33.5	Tetrapisispora_phaffii_CBS_4417
TEBL	5388	14.0486	31.7	Tetrapisispora_blattae
CAGU	5920	10.61	43.6	Candida_guilliermondii
SCPO	5142	12.6	36.0	Schizosaccharomyces_pombe
DEBR	5255	13.0582	39.1	Dekkera_Bruxellensis_STO5_12_22
ERCY	4434	9.6694	40.3	Eremothecium_cymbalariae_DBVPG_7215
SAKL	5306	11.3458	41.5	Saccharomyces_kluyveri
TODE	4972	9.2207	42.0	Torulaspora_delbrueckii_CBS_1146
ZYRO	4997	9.7646	39.1	Zygosaccharomyces_rouxii
KANA	5321	10.8458	45.8	Kazachstania_naganishii_CBS_8797
CYJA	6038	13.0184	43.6	Cyberlindnera_jadinii
KUCA	6031	11.3712	45.5	Kuraishia_capsulata
OGPA	5325	8.8786	47.8	Ogataea_parapolymorpha_DL-1
KLTH	5103	10.3928	47.2	Kluyveromyces_thermotolerans
CALU	5936	12.1148	44.3	Candida_lusitaniae
SCJA	5167	11.7332	41.5	Schizosaccharomyces_japonicus_yfs275_5
ERGO	4718	9.0957	51.7	Eremothecium_gossypii_(AGOS)
ARAD	6152	11.8046	48.1	Arxula_adeninivorans
YALI	6434	20.5029	49.0	Yarrowia_lipolytica

IDENT	#PROTS	SIZE (MB)	GC%	SPECIES (FUNGI)
CATH	11703	28.1975	42.5	Calcarisporiella_thermophila
BOCI	16389	42.6630	39.1	Botrytis_cinerea
FUGR	13321	36.3130	48.1	Fusarium_graminearum
GIZE	11578	36.2585	47.8	Gibberella_zeae_PH-1_uid243
FUVE	14195	41.1043	48.6	Fusarium_verticillioides
FUOX	17608	57.7206	47.4	Fusarium_oxysporum
ASFL	12587	36.7902	48.2	Aspergillus_flavus
ASOR	12063	37.0886	48.2	Aspergillus_oryzae
PECH	11396	31.3410	48.6	Penicillium_chrysogenum
PERU	12790	32.2237	48.9	Penicillium_rubens
ASTE	10406	29.3312	52.6	Aspergillus_terreus
ASNG	8592	34.0066	50.2	Aspergillus_niger
ASNI	9410	29.7113	50.0	Aspergillus_nidulans
ASFU	9630	29.3849	48.8	Aspergillus_fumigatus
NEFI	10407	32.5517	49.4	Neosartorya_fischeri
ASCL	9120	27.8594	49.1	Aspergillus_clavatus
COIM	9910	28.9479	46.0	Coccidioides_immitis_RS
PABR	8390	29.9525	43.6	Paracoccidioides_brasiliensis
FOME	11338	63.3544	40.8	Fomitiporia_mediterranea_MF3-22
COCI	13544	36.2944	51.6	Coprinus_cinereus
THAU	10450	31.4823	49.0	Thermoascus_aurantiacus
THLA	8133	19.9438	51.0	Thermomyces_lanuginosus
TATH	7920	19.8875	51.7	Talaromyces_thermophilus
POAN	10219	33.7760	51.5	Podospora_anserina_S_mat+
NECR	9822	40.4631	48.4	Neurospora_crassa
CRGA	6565	18.3748	47.8	Cryptococcus_gattii_WM276
CRNE	7302	19.0519	48.5	Cryptococcus_neoformans_var._JEC21
MIVI	7819	26.1389	53.4	Microbotryum_violaceum
USMA	6522	19.6439	53.9	Ustilago_maydis
SPRE	6673	18.4769	58.6	Sporisorium_reilianum
THER	9815	36.9196	54.4	Thielavia_terrestris
THNT	9204	40.6623	51.2	Thielavia_antarctica
CHTH	8280	28.3147	52.5	Chaetomium_thermophilum_ATTC1651
SCTH	10945	29.3248	55.0	Scytalidium_thermophilum
MYTH	9099	38.7442	51.4	Myceliophthora_thermophila_ATCC_42464
CHGL	11124	34.8869	54.6	Chaetomium_globosum
COTH	10644	33.3614	51.0	Corynascus_thermophilus
MYRT	8635	31.6872	52.0	Myriococcum_thermophilum
THST	10387	29.5796	56.9	Thermomyces_stellatus
VEDA	10535	33.9000	54.2	Verticillium_alfalfae
MAOR	12755	41.0278	51.5	Magnaporthe_oryzae
MAGR	11054	41.6955	51.3	Magnaporthe_grisea
FUPG	12447	36.9329	47.7	Fusarium_pseudograminearum_CS3096
PNJI	3520	8.1799	28.3	Pneumocystis_jirovecii
PNCA	6874	6.3	29.8	Pneumocystis_carinii
PNMU	3838	7.4514	26.9	Pneumocystsis_murina
TADE	4663	13.7735	49.0	Taphrina_deformans_JCM_22205
ZYTR	10931	39.6863	52.1	Zymoseptoria_tritici

Note: Each species is characterized by its identification (represented by four-letter code), number of predicted proteins, size in Mbp, and GC content. References relative to the species are shown in Supplementary Table 1.

For each species, the amino acid composition has been calculated and expressed in frequency, ie, percent relative to the total amino acids composition of the species. A table of 91 species versus 20 amino acids has been submitted to CA (see Supplementary Table 1). The main objective of such an analysis is to look for species patterns showing similar amino acid compositions.

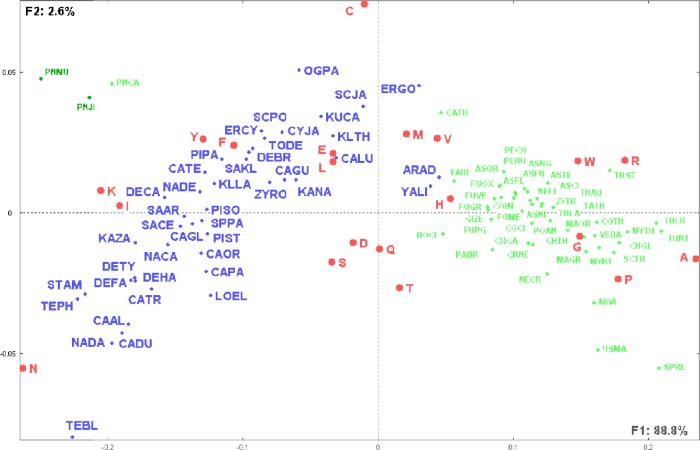
Figure 1 shows amino acids as well as yeast and fungal species displayed on the first factorial plane representing more than 91% of the total information included in the analyzed data table. It is interesting to note the overwhelming importance relative to the first factorial axis (F₁) that corresponds to 88.8% of the total information included in the analyzed data table. Sorting the species following their coordinates on the first factorial axis shows that the species are presented in increasing order of their GC content. This observation is confirmed by the significant Pearson correlation coefficient (r = 0.86, P < 0.0001) between the species GC content and their coordinates on the first factorial axis (Supplementary Table 1). It is interesting to note that apart from the three fungal low GC content Pneumocystis species, yeasts have almost systematically lower GC content than fungal species and that there is almost no overlap between the yeast and fungal groups (Fig. 1). The three fungal low GC content Pneumocystis species constitute a specific group that is segregated from all other fungal and yeast species. The three species have significant higher composition rates in I (Ile) and K (Lys) than all other species (Supplementary Table 1).

Figure 1.

Distribution of yeast and fungal species as well as the 20 amino acids.

Notes: This figure illustrates the first factorial plane as obtained by CA and representing 91% of the total information included in the data table of yeast and fungal species versus their amino acid compositions (see Supplementary Table 1). Species identification follows Table 1. Note the segregation of yeast species (blue dots) from fungal species (green dots). The three fungal Pneumocystis low GC species are clearly separated from yeast and other fungal species.

It is striking to note that the first factorial plane displays the species following a parabolic-like curve. Yeast and fungal species are clearly separated. Yeast species are displayed on a gradient going from the left side (negative F₁) and ending with the small cluster YALI (Yarrowia lipolytica) and ARAD (Arxula adeninivorans) with the first fungi CATH (Calcarisporiella thermophila). The clustering of yeast species follows their phylogenetic relationships. The distribution continues with all the considered fungi and shows small subclusters, including similar fungal species. Amino acids are placed according to their abundance in the species. Amino acids N (Asn), I (Ile), K (Lys), Y (Tyr), and F (Phe) are situated in the yeast species area, whereas A (Ala), R (Arg), W (Trp), G (Gly), and P (Pro) are in the area of the fungi species. C (Cys), V (Val), L (Leu), and E (Glu) are in the frontier between yeast and fungal species. A few amino acids [particularly S (Ser), D (Asp), Q (Gln), and T (Thr)] are placed in the cavity of the parabolic-like curve, reflecting their rather equivalent abundance in all considered species.

This example shows the impressive ability of CA to extract the most informative relationships between the analyzed observations and variables, particularly the overwhelming importance of species GC content, that is not included in the set of variables, represented by the first factorial axis F₁. It is interesting to note that yeast and fungal species can be so clearly segregated by considering their amino acids compositions.

Species clustering can be sharpened by considering their coordinates on all orthogonal factorial axes and by computing Euclidean distances between all pairs of species. The tree obtained by the reciprocal neighborhood clustering method is shown in Supplementary Figure 1. The separation between patterns of yeast and fungal species is clearly emphasized on this tree. The fungal Pneumocystis low GC species form a distinct cluster that is grouped with low GC content yeast species.

Viruses and phages versus amino acid composition

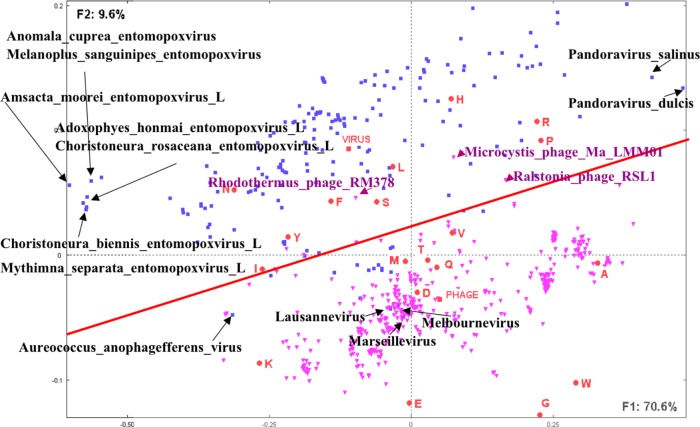
A second example is related to the amino acid compositions of large viruses, ie, viruses with genomes including more than 100 ORF products. A set of 181 viruses and 407 phages have been downloaded from the NCBI (May 2015). Top large viruses include the Pandoravirus (salinus and dulcis) containing, respectively, 2541 and 1487 ORF products²⁸ and the Megavirus (lba and chiliensis) containing, respectively, 1176 and 1120 ORF products. Top large phages include the Bacillus phage G (675 ORF products), Escherichia phage 121Q (611 ORF products), and Cronobacter phage vB CsaM GAP32 (545 ORF products). Calculation of the composition in amino acids of the corresponding proteomes allowed the construction of a data table of 588 species versus 20 amino acids. Figure 2 shows the distribution of the viral species and amino acids on the first factorial plane. The first factorial axis corresponds to 70.6% of the total information included in the analyzed data table, whereas the second axis corresponds to 9.6%, thus totaling more than 80% on the first factorial plan. Viruses are represented in blue squares and phages in purple triangles.

Figure 2.

Distribution of large (ie, including more than 100 predicted proteins) viruses and phages as well as the 20 amino acids.

Notes: This figure illustrates the first factorial plane as obtained by CA and representing 80% of the total information included in the table of viruses (blue point) and phages (purple points) versus their amino acid compositions. Note the segregation between viruses and phages and the positions of the barycenters corresponding to the mean amino acid compositions, respectively, of viruses (VIRUS) and phages (PHAGE). Some viruses are identified on the factorial plane as illustrative examples.

Examination of the species distribution on this factorial plan strikingly reveals a clear segregation between viruses and phages (except for a few species).

The distribution of the species following the first factorial axis shows a significant correlation between GC content and coordinates on the first factorial axis (r = 0.92, P < 0.0001). Viruses and phages are spread all along the first factorial axis. Positions along the second factorial axis (F₂) show a significant segregation between viruses and phages.

A cluster of Entomopoxviruses with low GC content is separated from the rest of the species at the left hand side of F₁. The two Pandoraviruses (salinus and dulcis) with high GC content are situated at the rightmost hand of F₁. The few viruses that overlap with phages include three giant viruses (Marseillevirus, Lausannevirus, and Melbournevirus) and the algae virus Aureococcus anophagefferens that is situated at the left side of the phages area.

Amino acids such as A (Ala), G (Gly), E (Glu), K (Lys), and D (Asp) are situated in the neighborhood of the phages, whereas R (Arg), P (Pro), H (His), L (Leu), N (Asn), F (Phe), and S (Ser) are in the neighborhood of viruses.

Supplementary elements PHAGE and VIRUS representing, respectively, the mean amino acid compositions of the considered sets of phages or viruses are indicative of the barycenter positions of their respective sets.

In this example too, CA shows a striking segregation between viruses and phages, which has not so far been mentioned in the literature, simply by considering their amino acid compositions.

Comparison of yeast and fungal species according to their shared orthologs

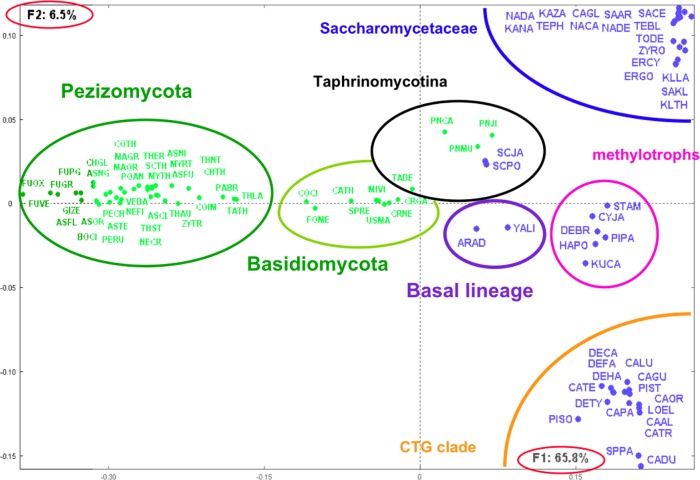
A set of 91 yeast and fungal species presented above for amino acid compositions (Table 1) is considered. Large-scale pairwise comparisons of their corresponding predicted proteomes have been performed following the methodologies developed in Refs. ²⁹ and ³⁰. For each pair of species, reciprocal best-hit proteins were considered to be orthologs.³¹ The square matrix including occurrences of shared orthologs between all pairs of species was transformed into a matrix of similarities between the considered species. The similarity between a pair of species is expressed by the normalized score: k_ij = 100*s_ij/(n_i + n_j), where s_ij is the number of shared orthologs between species i and j; n_i and n_j are, respectively, the total number of proteins in species i and j. This score corresponds to the proportion of core-proteome (s_ij) relative to the pan-proteome (n_i + n_j) in each pair of species. A square symmetrical data table of dimension 91 is then constructed and submitted to CA. Figure 3 shows the obtained distribution of species on the first factorial plan representing more than 72% of the information included in the analyzed data table. The distribution shows a clear segregation between yeast and fungal species. The yeast species show patterns corresponding to clusters of Saccharomycotina members, and fungal species are clustered mainly into two groups: Basidiomycota and Pezizomycotina clearly separated from the yeast species. The obtained clustering corresponds roughly to the known phylogeny of the yeast and fungal species.^26,27,32,33 The Taphrinomycotina cluster includes the Schizosaccharomyces, the Pneumocystis, and Taphrina deformans species in accordance with the classifications shown in recent works.^32–34

Figure 3.

Distribution of yeast and fungal species as obtained from their shared orthologs.

Notes: This figure illustrates the first factorial plan as obtained by CA and representing 72% of the total information included in the matrix of similarity scores between species (see text). Species identification follows Table 1. Yeast (blue points) and fungal (green points) species distributions correspond to the major subdivisions defined from global comparisons. Note the clear-cut segregation between fungal and yeast species.

The corresponding genome tree, based on neighbor joining obtained from Euclidean distances as calculated from the factorial coordinates, is shown in Supplementary Figure 2. Yeast and fungal species are separately clustered. The obtained clusters shown on the tree correspond to known phylogenetic classifications. The only mixed cluster associates A. adeninivorans and its closest sequenced relative Y. lipolytica³⁵ with Taphrinomycotina species with which they share the highest proportion of orthologs among the yeast species.

A similar square data matrix including rates of duplication (intraspecies comparison) and conservation (interspecies comparisons) has been constructed. In this case, k_ii represents the rate of duplication in species i and k_ij represents the rate of conservation of species j in species i. A similar analysis considering a subset of the considered species is shown in Refs. ²⁶ and ²⁷.

In this example, CA highlighted the patterns of species sharing orthologs and evolutionary relationships.

Microarray

DNA microarrays are used extensively for genomewide gene expression measurements. Large-scale transcriptional studies have catalyzed new discoveries and are generating important new insights into the behavior and functioning of cells. Pattern discovery tools have played a key role in this process. Of the various multivariate methods available, clustering of genes has been the most common tool used for the analysis of microarray data.³⁶ PCA³⁷ and CA³⁸ have also been used in such studies.

Before proceeding to clustering, it is often advantageous to visualize the data in order to understand the underlying structure. This initial exploration is useful in revealing patterns and providing clues for further analysis relating subsets of genes and their characteristic properties.

CA defines a factorial space that captures the maximum information present in the initial data table by minimizing the error between the original data set and the reduced dimensional data set.

DNA microarray technology allows for the monitoring of expression levels of thousands of genes under various conditions. A major question in microarray studies is how to select genes associated with specific physiological states or clinical parameters, as for example, genes whose expression in a tumor sample is related to a specific tumor subtype or to patient survival. Such differentially expressed genes are often useful in identifying the clinical markers and may lead to improve diagnosis, treatment, and prediction of clinical outcomes.

Moreover, relating specific groups of genes with specific biological correlates is a critical step toward understanding the underlying molecular mechanisms and identifying novel therapeutic targets.

The most commonly used methods for the identification of differentially expressed genes include qualitative observation (usually following some form of clustering of expression patterns), heuristic rules, and model-based probabilistic analysis.³⁹

As microarray data are often noisy and not normally distributed,⁴⁰ it is challenging to consider a typology structure that allows refined exploration of the data. In this context, CA followed by clustering methods is the step to perform in such studies.

Genotyping data

PCA is the most popular method used in genotyping data.^41–45 In a recent work,⁴⁵ PCA was used to compare the genome sequence of the 45,000-year-old remains of a modern male human from Siberia (denoted Ust’_Ishim) to the genomes of 922 present-day human males belonging to 53 distinct populations. Each human is described by his/her genotyping data, ie, the observed SNPs on each of the 22 chromosomes with the following possibilities: 0, 1, or 2 copies of reference allele. The plot of all considered humans on the two first principal components of the PCA analysis showed the distribution of the 922 humans according to their geographical origins and with respect to the genetic diversity. The main conclusion from this PCA was that Ust’_Ishim individual is more related to present-day Eurasian than to present-day Africans (see Fig. 2⁴⁵). Unfortunately, the genetic diversity that is at the heart of the interpretation of these results is not shown. Also no indication is given about the relationships of the genetic diversity indicated here by the SNPs observed on the chromosomes and the considered individuals.

Considering the same data set used in this work (thanks to Fu et al who shared with us the data set used in the published work⁴⁵), we constructed a contingency data table T that crosses the 922 present-day individuals and Ust’_Ishim with the set of variables defined as follows:

Each variable is defined by nonnull SNP that is preceded by the corresponding chromosome number and ended by its modality (0, 1, or 2 according to the number of copies of reference allele). For example, 5GC2 corresponds to the SNP G/C observed on chromosome 5 with the modality 2 (2 copies of reference allele).

In total, there were 622 such defined SNPs. Note that in the original data, there were only 12 distinct SNPs, not taking into account their corresponding chromosomes and modalities. In the contingency table T, T_ij = the number of positions corresponding to human individual i showing an SNP j (defined by its corresponding chromosome, SNP, and modality), ie, the number of SNPs defined by its chromosome and modality observed for individual i.

Fifty-three supplementary lines were constructed corresponding to the distinct considered present-day populations by summing the corresponding lines in T for each population. These lines were considered as supplementary elements as well as the Ust’_Ishim line.

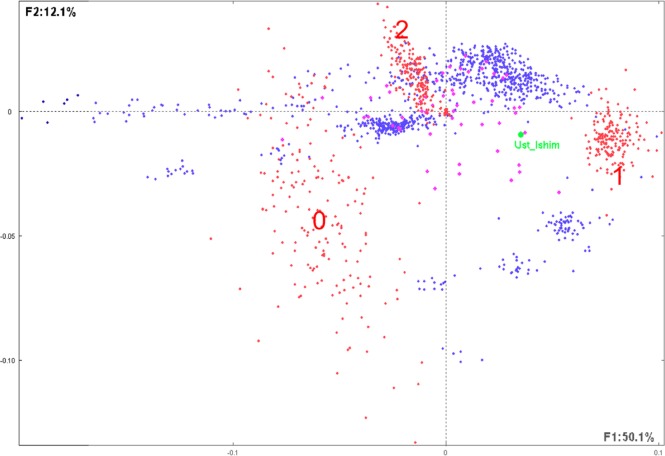
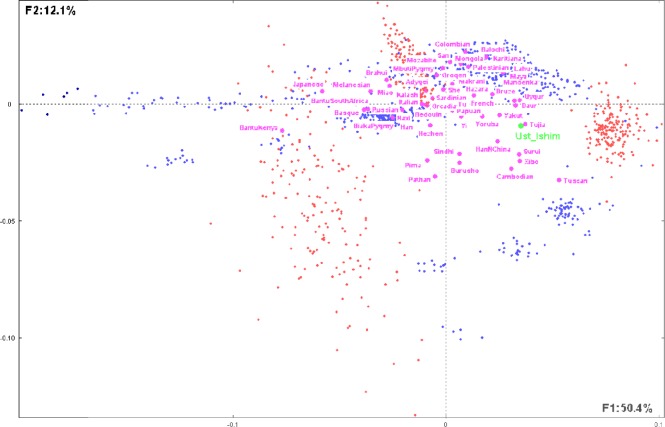
The final table T with 976 (922 + 53 + 1) lines and 622 columns has been submitted to CA. Figure 4 shows the first factorial plan representing more than 62% of the total information included in T (F₁: 50.4%; F₂: 12.1%).

Figure 4.

Distribution of the considered modern humans, populations, and SNPs.

Notes: This figure illustrates the first factorial plan representing the 922 present-day humans (represented by blue dots) observed on 622 SNPs (as defined in text and represented by red dots). Compact clusters of SNPs in the right and the upper parts of the graph correspond, respectively, to modalities 1 (1 copy of reference allele) and 2 (2 copies of reference allele). The dispersed SNPs at the left part correspond to 0 (0 copy of reference allele). The green dot represents the 45,000-year-old modern human from Siberia Ust’_Ishim as supplementary individual and purple dots represent the 53 distinct populations considered in the study.⁴⁵ The first factorial axis F₁ corresponds to 50.1% of the whole information included in the analyzed data table, whereas the second factor F₂ corresponds to 12.1%. SNP patterns corresponding to modalities 1 and 2 (see text) are rather compact, whereas dots corresponding to modality 0 are more dispersed. Note that some of the modern humans (blue dots) are compact, whereas others are scattered.

SNPs (red dots) are displayed in three distinct clusters corresponding, respectively, to 1 (1 copy of reference allele) in the right part of the graph, 2 (2 copies of reference alleles) in the upper part of the graph, and 0 (0 copy of reference allele) in the left part of the graph. Note that dots corresponding to 1 and 2 are rather compact, whereas dots corresponding to 0 are largely dispersed.

Blue dots are grouped into different clusters, and some are scattered along the first axis toward the SNP region 0. A large compact cluster is situated between SNP regions 1 and 2, meaning that these present-day humans are enriched in these SNP modalities. One other group is situated close to the SNP 1 modality meaning that this group is enriched in this SNP type. Four other smaller groups are situated between SNP modalities 2 and 0.

The purple dots represent the 53 supplementary considered populations corresponding to present-day human individuals.

The Ust’_Ishim supplementary individual is clearly situated between two clusters corresponding to SNP modalities 1 and 2 and between present-day human clusters (Fig. 5). The most proximate populations to Ust’_Ishim shown on this graph are Tujia (China), Yakut (Sakha, Russia), and HanNChina and Xibo (China), among others. This is roughly in accordance with the conclusion reached in the work.⁴⁵

Figure 5.

The same first factorial plan as in Figure 4, emphasizing the distribution of the 53 human populations (purple points) considered as supplementary elements as well as the position of the Ust’_Ishim individual.

Note: This figure shows their corresponding positions relatively to each others as well as to the SNPs represented by red points.

More precisely, considering the coordinates of all 53 populations on the first 10 factorial axes (representing 75% of total information), the Euclidean distance of Ust’_ Ishim with each of the 53 populations was calculated and ranked in increased order (Table 2). Inspection of these distances shows that the most proximate population to Ust’_ Ishim are Chinese, and also Surui (Brazil) and Yakut (Sakha, Russia).

Table 2.

Square Euclidean distances of Ust’_Ishim to each of the 53 considered human populations as calculated from the 10 first factorial axes obtained by CA.

PRESENT-DAY HUMANS	SQUARE DISTANCE TO UST’_ISHIM
Tujia (China)	0.0001
Dai (China)	0.0003
Daur (China)	0.0003
Surui (Brazil)	0.0003
Uygur (China)	0.0003
Xibo (China)	0.0003
Yakut (Sakha, Russia)	0.0003
Yoruba (West Africa)	0.0005
Cambodian	0.0006
Druze	0.0006
HanNChina	0.0006
Mandenka (Senegal)	0.0006
Maya	0.0006
Tuscan	0.0006
Hazara (Persian Afghan)	0.0011
Sindhi (Pakistan)	0.0011
Yi (China)	0.0011
Balochi (Baloshistan)	0.0014
French	0.0014
Karitiana (Brazil)	0.0014
Lahu (Vietnam-China)	0.0014
Burusho (Pakistan)	0.0015
Colombian	0.0018
Papuan	0.0018
Mongola	0.0019
Palestinian	0.0019
Makrani (Pakistan)	0.0021
MbutiPygmy	0.0021
Oroqen (Mongolia – China)	0.0021
Pathan (Pashtun)	0.0021
She (Fuji – China)	0.0021
Tu (Mongoe – China)	0.0021
Hezhen (China)	0.0026
Mozabite	0.0026
Bedouin	0.0027
Italian	0.0027
Kalash (Nuristan – Pakistan)	0.0027
Orcadian (Orkney –Scotland)	0.0027
Pima (Indigenous Americans)	0.0027
San (South Africa)	0.0027
Sardinian	0.0027
Adygei (Caucasus)	0.0030
BiakaPygmy	0.0036
Han	0.0037
Naxi (China)	0.0040
Russian	0.0041
Brahui (Pakistan)	0.0053
Miao (China)	0.0054
Basque	0.0066
BantuSouthAfrica	0.0067
Melanesian	0.0070
Japanese	0.0105
BantuKenya	0.0146

Note: The present-day humans are presented in increasing order of their distance to Ust’_Ishim.

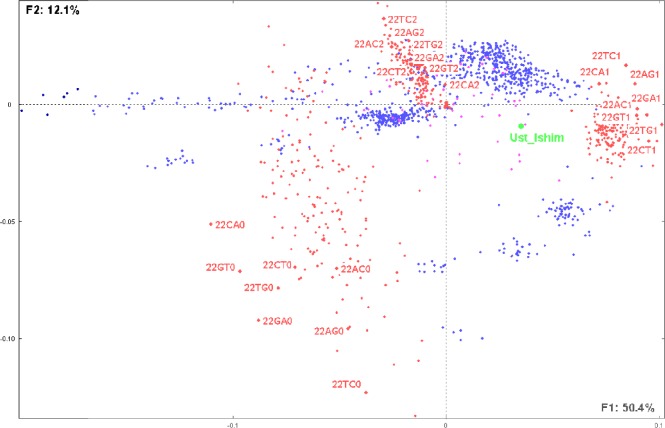
Considering the variables of the analyzed data table, it is interesting to note that the distribution of SNPs shows that not all of them contribute equally to the discriminative positions of the individuals. For example, Figure 6 shows the distribution of all SNPs on chromosome 22. The scattering of the corresponding SNPs and modalities is indicative of their different weights in the considered populations. Human populations situated close to some SNPs are indicative of the abundance of such SNPs in these populations. On the contrary, populations that are distantly situated are indicative of the weak presence of such SNPs.

Figure 6.

The same factorial plan as in Figure 4, illustrating as an example the distribution of the SNPs observed on chromosome 22 and showing their relative distances with the 53 considered populations as well as the Ust’_Ishim individual. Note that, for example, 22TC1 corresponds to SNP T/C on chromosome 22 having modality 1 (ie, 1 copy of reference allele) and 22TC2 corresponds to the same SNP and chromosome with modality 2 (2 copies of reference allele).

This example highlights how CA can provide more detailed information than PCA (see Supplementary File 1D), about human populations’ neighborhood and associated SNPs, thus allowing a finer interpretation of their migration history.

Concluding Notes

CA is a descriptive multivariate data analysis method that allows to synthesize information included in a large data table by constructing an orthogonal system (factors) and by displaying observations and variables on a reduced number of factors that account for a significant part of the whole information included in the original data table. Planar graphical representations of observations and variables allow salient relationships to be easily detected. CA permits to account for general trends in the data, while ignoring minor fluctuations.

In genome data analyses, researchers are facing new challenges related to huge amount of data of multidimensional structures. High-throughput sequencing technologies are producing large amounts of sequences related among others to infectious and cancer diseases observed in natural and experimental conditions. For such genotyping data, huge data tables are constructed generally by crossing genes with SNPs, taking into account their corresponding localizations (chromosomes and positions) as well as possible clinical characters that are associated with the diseases under study.

CA proved to be an efficient method in data reduction of such large data tables. It also proved to be useful in the analysis of ORF products in whole-sequenced species according to their amino acid and codon compositions.

With the expected development of big data sets related to complex systems biology studies, CA might be a helpful method in global analyses by extracting salient trends and patterns embedded in such data.

Application of CA can be extended to data-driven learning and sample classification problems. It facilitates the identification of strong underlying structures in the data. The most important characteristic of CA as compared to PCA is the ability in linking clusters of individuals with subsets of variables to which they are significantly related. This is an important advantage as it facilitates the interpretation of each individual cluster by considering the related characteristic variables.

The application examples discussed above, revealing the interesting underlying data structures, show the effectiveness and straightforward utilization of CA, which might be a helpful tool for researchers in the emerging biology Big Data era.

Supplementary Material

Supplementary Figure 1. Hierarchical clustering tree of yeast (blue colored) and fungal (green colored) species as obtained from Euclidean distances between species calculated using their coordinates on the correspondence analysis factors, resulting from the 91 species versus amino acid compositions. Different clusters are shown with different colors on the tree. Note the fungal Pneumocystis low GC species that are close to yeast species with low GC content.

Supplementary Figure 2. Genome tree of yeast (blue colored) and fungal (green colored) species as obtained from the Euclidean distances between species calculated using coordinates on the correspondence analysis factors, resulting from the 91 species shared orthologs (see text). Clusters correspond to known phylogenetic classifications^27,32,33 indicated on the tree.

Supplementary Table 1. List of yeast and fungal species shown in Table 1 with their respective references, size in Mbp, GC content of the corresponding genome, coordinates on factorial axes F₁ and F₂, and composition in the 20 amino acids.

Supplementary File 1. (A) Examples of data tables that might be submitted to correspondence analysis. (B) Correspondence analysis presentations on the web. (C) Key hints for interpreting the factorial graphs. (D) Examples of what differentiates correspondence analysis from principal component analysis methods.

Abbreviations

CA

correspondence analysis

PCA

principal component analysis

SNP

single-nucleotide polymorphism