Abstract
The dynamic nature of the world requires that our visual representations are continuously updated. These representations are more precise if there is a narrow time window over which information is averaged. We assess the neural processes of visual updating by testing patients with lesions including inferior parietal cortex, control patients and healthy adults on a continuous visual monitoring task. In Experiment 1, observers kept track of the changing spatial period of a luminance grating and identified the final spatial period after the stimulus disappeared. Healthy older adults and neurological controls were able to perform better than simulated guesses, but only 3 of 11 patients with damage including parietal cortex were able to reach performance that differed from simulated guesses. The effects were unrelated to lesion size. Poor performance on this task is consistent with an inability to selectively attend to the final moment at which the stimulus was seen. To investigate the temporal limits of attention, we varied the rate of stimulus change in Experiment 2. Performance remained poor for some patients even with slow 2.5 Hz change rates. The performance of 4 patients with parietal damage displayed poor temporal precision, namely recovery of performance with slower rates of change.
Keywords: neuropsychology, rapid serial visual presentation, temporal order judgment task, temporal resolution, visual perception
Introduction
Much of what we know about spatial attention has come from studies in neuropsychology, with spatial impairments such as hemispatial neglect (Vallar and Perani 1986; Driver and Mattingley 1998) and visual extinction (Karnath et al. 2003; Chechlacz et al. 2013) linked to damage of a number of brain areas but classically involving posterior parietal cortex. More recently, a growing body of evidence suggests that posterior parietal regions, among others, also support aspects of the processing of time and temporal aspects of sensory perception. This is captured in Walsh's (2003) theory of magnitude. In this view, time, space, and quantity are processed by a common mechanism located in inferior, posterior parietal cortex. This theory is in part informed by the growing body of evidence for the importance of these brain regions in temporal processing in a range of tasks which we will briefly review later.
Perhaps the most conceptually simple temporal perception task is that of duration estimation. The posterior parietal cortex has been associated with this in several studies. Alexander et al. (2005) showed that TMS applied over right PPC impaired RT for judgments of auditory durations. Similarly, Rao et al. (2001) used fMRI to demonstrate activation in right inferior parietal lobe among other areas for encoding auditory time intervals. In the visual domain, Danckert et al. (2007) showed that neglect patients with damage including inferior parietal lobe greatly underestimated multisecond time intervals.
Directing attention to points in time also appears to recruit parietal involvement. Coull and Nobre (1998) showed with PET and fMRI that attention to time in a temporal cueing paradigm produced activation in the parietal lobe. The posterior parietal lobe is also implicated in spatio-temporal segmentation of objects, or more simply, keeping track of which objects are near each other in space and time. In a modified visual search task, Olivers and Humphreys (2004) showed that patients with damage to this area showed specific deficits in search where a preview display separated distracters from potential targets on the basis of the spatial and temporal characteristics of the displays.
These studies show that parietal cortex is involved when we make judgments of “when” and “how long” in time, as well as in attending to stimuli at a particular point in time. But what of more complex judgments that involve time, for example when multiple stimuli compete for attention at different times, or when stimuli dynamically change over time?
In temporal order judgment (TOJ) tasks, participants report which of 2 stimuli seemed to occur first. This seemingly simple judgment arguably requires perception of 3 nontrivial factors; the times at which 2 different stimuli occur and the comparison of these 2 temporal representations. Rorden et al. (1997) presented data from 2 patients with right parietal damage and extinction symptoms who were biased to report that ipsilateral stimuli appeared first, despite intact lower-level temporal motion processing. Rorden et al. interpreted this as evidence for “prior entry” of stimuli into awareness on the unaffected side. In a larger scale voxel-based morphological analysis, Roberts et al. (2012) linked deficits in TOJ to lesions to the inferior parietal lobe/temporoparietal region (see also Baylis et al. 2002).
These neuropsychological results have been extended to findings in healthy adults using TMS (Woo et al. 2009). Woo et al. applied TMS to left and right posterior parietal cortex and reported that TMS to right PPC delayed detection of targets in the left visual field by ∼20 ms. In contrast to these results, TMS in left PPC had no effect, indicating a dominant role for right PPC in temporal order coding. Furthermore, right temporal-parietal damage appears to affect TOJ performance even when both stimuli are presented in a vertical arrangement in the same hemifield. Snyder and Chatterjee (2004) presented a case study in which an extinction patient showed apparent prior entry for stimuli presented ipsilaterally. In addition, the patient was more accurate in the TOJ task for vertical arrangements presented in the ipsilateral field than the contralateral field. This is consistent with the results of Roberts et al. (2012) who used varying time intervals between bilaterial stimulus presentation in a TOJ task. They reported that individuals with right temporoparietal and cerebellum damage required unusually long intervals between the presentations of stimuli in order to distinguish between events. These findings implicate a role for temporal-parietal cortex in TOJ tasks over and above preferential attention for stimuli on the unaffected side. Specifically, this area appears to be involved in attention to events at fine timescales, or the temporal resolution of attention. Note that we use the terms “temporal resolution” and “temporal precision” here to mean the limit on the smallest unit of time over which stimuli must be averaged (or equivalently, integrated). We later refer to differences in temporal resolution limits on attention and lower-level perceptual processes.
Further evidence for a role for the parietal lobe in temporal processing comes from the attentional blink (AB) phenomenon observed during the rapid serial visual presentation paradigm. When people are asked to detect 2 successive targets, T1 and T2, presented in a rapid stream of stimuli displayed at a single location, healthy adults show a marked decrement in performance or “attentional blink” if T2 follows T1 by less than ∼400 ms (Raymond et al. 1992). Patients with hemispatial neglect caused by damage in the inferior parietal lobe exhibit AB effects of nearly 4 times the magnitude of healthy adults at ∼1400 ms (Husain et al. 1997). The presence of neglect symptoms does not appear to be necessary for abnormal AB effects to emerge since patients with damage to inferior parietal lobe and superior temporal gyrus, even without neglect, show an exaggerated AB (Shapiro et al. 2002).
Perceiving motion requires processing related to the timing of events. In apparent motion, successive discrete stimuli are associated with one another and interpreted as motion of a single stimulus. Patients with right parietal lesions show deficits in apparent motion perception in both hemifields (Battelli et al. 2001). Battelli et al. also showed slow limits of ∼6 Hz on how fast events could be associated in perceived motion. Parietal areas are also implicated in the continuous wagon wheel illusion (VanRullen et al. 2006, 2008). In this illusion, a smoothly rotating stimulus occasionally appears to rotate in the opposite direction to its veridical motion, and inappropriate matching of successive states (inappropriate apparent motion) has been proposed as the cause. Therefore, abnormal perception of the continuous wagon wheel illusion implies abnormal apparent motion processing, and by implication, abnormal timing perception. Apparent motion requires the association of spatially and temporally separated stimuli. Hence, poor temporal resolution—affecting the units of time over which visual changes can be resolved—could help explain failures to associate these stimuli together and hence to perceive apparent motion.
Low-level vision is known to exhibit varying but generally good temporal precision depending on the task, for example, one can easily detect that a source is flickering at very fast rates (up to ∼50 Hz). In contrast to this, higher-level visual processes appear to exhibit poorer temporal resolution (Holcombe 2009). For example, people are only able to report the simultaneity (pairing in time) of 2 features (1 changing color and 1 changing orientation) presented alongside one another up to ∼3 Hz (Holcombe and Cavanagh 2001). For tracking moving objects, however, the limit appears to be ∼4–8 Hz for the maximum rate of objects passing past a given point in space (Verstraten et al. 2000). For these types of tasks, the “speed limit” for performance is thought to reflect the speed with which attention can individuate stimuli and select them among stimuli appearing at earlier or later points in time. However, the neural locus of these limits on attentional resolution is as yet unresolved. We tested this in the present paper.
We used the continuous monitoring paradigm developed by Howard and Holcombe (2008) to investigate the temporal resolution of attention in patients whose lesions included (and in some cases where confined to) the inferior, posterior parietal lobe, neurological controls with damage at other sites, and healthy older adults. This task requires participants to continuously attend to changing objects and to keep track of their changing features. Here, participants tracked a single luminance grating as it changed continuously in its spatial period. Not only can this task inform us about the temporal characteristics of attention but it more generally can tell us about the extent to which we can update information about the dynamic visual world.
Experiment 1: Smoothly Changing Stimuli
Materials and Methods
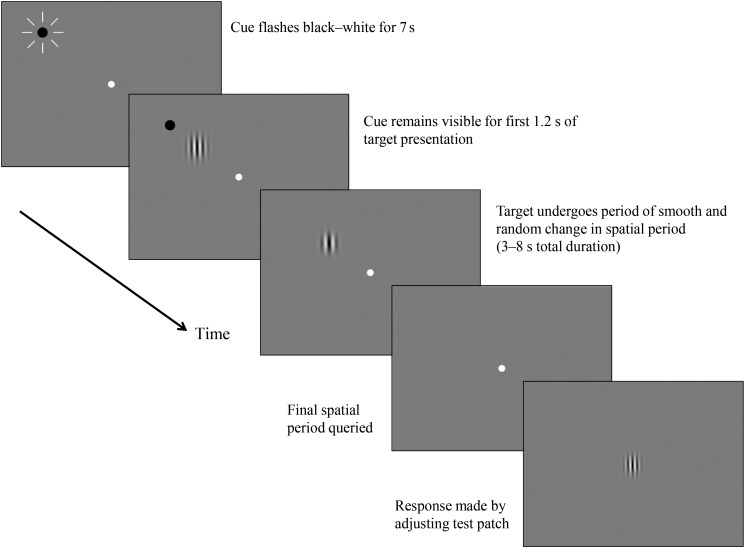
Experiment 1 was based on the continuous monitoring paradigm developed by Howard and Holcombe (2008). In this task, observers must continuously monitor the appearance of a changing stimulus until it disappears after a semi-random interval. At this point, they attempt to report the final appearance of this stimulus. This task is designed to measure the moment-to-moment fidelity of visual representations. Because the observer cannot know when the stimulus is about to disappear, they must continuously update their representation of the changing stimulus. Good temporal resolution means being able to perceive very fine timescales. Conversely, poor temporal resolution means that individuals will only perceive coarser grained “moments” due to integrating visual information over a wider temporal window—and this will lead to an inability to report the most recent moment of a seen stimulus with a high degree of accuracy.
A computer program was written in Python using the VisionEgg library (http://www.visionegg.org) and displayed a single sinusoidal Gabor luminance grating against a mid-gray background on a 16-inch CRT screen refreshing at 85 Hz. Observers viewed the display in a dimly lit room from a distance of 0.4 m. The luminance of Gabors varied from 0.02 (trough) to 120.00 (peak) candelas per square meter. Gabors had a variable spatial period but fixed orientation of 0° (vertical). The Gaussian envelope that windowed the Gabor patches’ amplitudes had a sigma of 1.139° of visual angle.
Phase was such that the centers of Gabors had their maximum luminance defined by the sinusoidal function. The phase of each Gabor was randomized from trial to trial. Phase was randomized to prevent observers using the location of the edge of a “bar” of the Gabors as a cue to their spatial periods. It also minimized formation of afterimages that could have interfered with perception of spatial period near the Gabors' centers.
Observers were given practice trials until they felt comfortable with the experiment (usually <10 trials). At the start of each trial, a black circular pre-cue with a radius of 0.48° of visual angle indicated the position at which the Gabor would appear which was randomly determined on each trial with equal probability at 1 of 5 possible positions. The pre-cue was presented either at fixation, or at 1 of 4 points forming an imaginary square with its center at fixation and corners to the upper left, upper right, lower left, and lower right of fixation. These 4 points were located 11.94° eccentric from the central fixation point and peripheral to the future locations of Gabors.
After 2350 ms, the Gabor appeared in addition to the target pre-cue. On each trial, the Gabor was presented either at fixation or equidistant from a central fixation point at one of the vertices of an imaginary square such that their centers were always 6.79° eccentric from the fixation point.
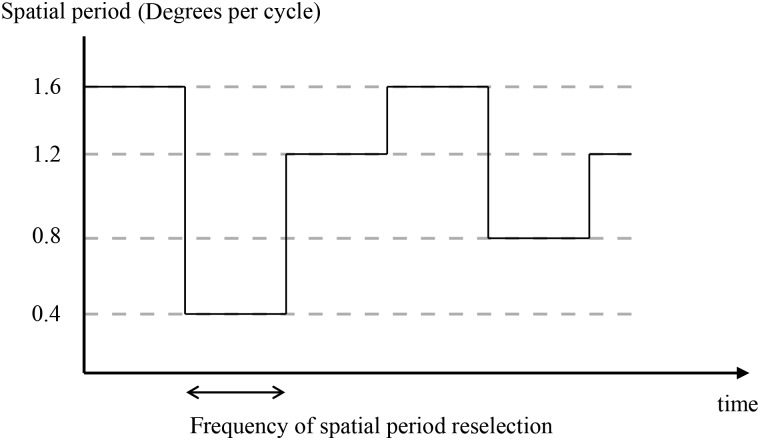
The pre-cue remained on screen for the first 1180 ms of Gabor presentation. Each object stayed at the same spatial location throughout the trial but varied in spatial period (see Fig. 2) according to a semi-random trajectory according to an algorithm described in the “Trajectories” section. At a point randomly varying between 5350 and 10 350 ms after the start of the trial (3000–8000 ms since appearance of the Gabor), the Gabor disappeared.
Figure 2.
Snapshots of spatial period values of a single changing Gabor taken at 400-ms intervals. In the actual stimulus, spatial period changed smoothly and semi-randomly over time.
After the disappearance of the Gabor, the experimenter prompted the observer to report the last spatial period of the Gabor by asking, “was it fairly fat or fairly thin?” At this point, the experimenter started to adjust the spatial period of the sample patch by using a key press to increase or decrease the spatial period of the patch from its starting spatial period of 0.95° per cycle.
As soon as the experimenter started the adjustment using a key press, the sample patch appeared at the center of the screen (i.e., on the first screen refresh after a key press was detected). We delayed the appearance of the sample stimulus until after the first key press to avoid any potential interference of the sample stimulus on the effort of the observer to recall the feature value. Observers then instructed the experimenter to increase/decrease the spatial period of the patch by using the instructions “thinner” and “fatter,” until they felt the sample patch matched the last state of the Gabor. At this point, they instructed the experimenter to hit enter which prompted the appearance of feedback which was presented in the form of a static display containing only the Gabor with its final spatial period and at its previous position on the screen before it disappeared.
The sample patch possessed a randomized phase. It was necessary to present the sample at a location other than that of the queried Gabor to prevent any motion signals being produced which could have allowed observers to access the previous spatial period of the queried Gabor in the absence of attention.
Observers completed 3 or more blocks of 35 trials (for a sample trial timeline, see Fig. 1) or as many as they could manage without becoming excessively tired. Observers completed as many blocks as they could in each 1-h session and returned for further testing sessions on different days over a period of ∼1 month. Due to the demanding nature of the task, only 1 or 2 blocks of trials were completed in several testing sessions before the observer requested a break. For these reasons, testing was conducted in blocks over several different testing sessions for each observer, and some observers withdrew from the study before all speed conditions could be completed. Six observers completed between 80 and 90 trials (BP1, O2, RP5, O3, C9, and C4), 2 completed between 90 and 100 (RP6 and O1), 12 completed between 100 and 110 (RP2, RP3, RP7, LP2, LP1, C8, C6, C7, C1, C2, C5, and SBP1), 2 completed between 110 and 130 (BP2 and C3), and 3 completed between 130 and 160 (FT1, RP1, and RP4). Typically, observers completed these over between 2 and 3 sessions.
Figure 1.
Trial timeline.
Trajectories through Spatial Periods
The spatial period of each Gabor stimulus over time corresponded to a random trajectory generated by the following algorithm (see Fig. 2). Every 20 frames, corresponding to 235 ms, the acceleration of the Gabor through spatial periods would be randomly reassigned to positive or negative. If the Gabor had been changing slowly, the 2 possible accelerations were larger than if the Gabor had been changing quickly. This was to prevent the features of any particular Gabor remaining relatively constant for a prolonged period that could result in an afterimage forming.
The starting spatial period of each Gabor was set independently to a random value between 0.7 and 1.2° per cycle. We parameterized the changes in terms of degrees per cycle (dpc) or “bar” width rather than cycles per degree because it led to the changes appearing more uniform across the range of spatial periods. The velocity through spatial period space, or rate of change of degrees per cycle, was set at the start of each trial randomly and independently for each Gabor between ±0.000425 dpc per ms, ensuring that no Gabor had an absolute velocity of under 8.5 × 10−5 dpc per ms. The starting accelerations were again randomly chosen each to be either ±3.61 × 10−7 dpc per ms2. Every 235 ms, the acceleration of each Gabor was reset to either ±3.61 × 10−7 dpc per ms2. If the velocity was smaller than an absolute value of 0.000425 dpc per ms, the absolute value of the acceleration was increased to 3.61 × 10−6 dpc per ms2.
During the trial, the maximum spatial period was set to 0.4 dpc and the minimum to 1.5 dpc. If the maximum or minimum values were reached, the sign of the velocity was changed such that spatial periods moved back toward the middle of the range of possible values. If the velocity reached a maximum absolute value of 0.00425 dpc per ms, the direction of acceleration would be reversed such that the velocity tended back toward lower values.
Observers
Observers were 9 healthy older adults (aged 57–76), 7 patients with right parietal lobe damage and 2 with left parietal lobe damage (aged 54–73), 3 with occipital damage (aged 57–64), 2 with bilateral parietal lobe damage (aged 63–68), 1 with superior bilateral parietal lobe damage (59) and 1 with frontal and temporal damage (aged 55). For further clinical and demographic observer information, see Table 1 which includes asymmetry scores on the Apple cancelation task (test of attention across the visual field; Bickerton et al. 2011) and sustained auditory attention task scores from the BCoS (Humphreys et al. 2012). The cancelation task involved crossing out all “full apples” on a page and leaving “incomplete apples,” and the asymmetry score reflects the difference between the performance in the 2 hemifields. The sustained auditory attention task involved tapping the table when any of 3 target words are spoken in an auditory stream of spoken words. Posterior parietal patients and neurological controls differed in the magnitude of the Apple cancelation asymmetry scores (t14 = 2.34, P = 0.035) but did not differ in the sustained auditory attention task (t14 = 0.217, P = 0.831).
Table 1.
Clinical and demographic details for the patients
| Patient | Age at test | Gender | Main clinical symptoms | Apple cancelation asymmetry score | Sustained auditory attention score (/54) | Etiology and lesion volume (cm3) |
|---|---|---|---|---|---|---|
| Occipital | ||||||
| O1 | 64 | M | Hemianopia | 0 | 53 | Stroke, 2.12 |
| O2 | 62 | M | Hemianopia | −1 | 54 | Stroke, 10.45 |
| O3a | 57 | F | Hemianopia and alexia | 0 | 54 | Stroke |
| Superior bilateral parietal | ||||||
| SBP1 | 59 | F | Simultanagnosia, left extinction | 0 | 41 | Stroke, 103.10 |
| Frontal-temporal | ||||||
| FT1 | 55 | M | Amnesia, dysexecutive syndrome, object recognition | 0 | 44 | Herpes simplex encephalitis, 154.02 |
| Bilateral parietal | ||||||
| BP1 | 68 | M | Simultanagnosia, verbal STM, naming | 0 | 19 | Stroke, 144.01 |
| BP2 | 63 | M | Naming, pattern construction | 0 | 46 | Dementia, 0.86 |
| Right posterior parietal | ||||||
| RP1 | 64 | M | Left neglect, possible hemianopia | 9 | 52 | Stroke, 282.12 |
| RP2 | 69 | M | Left neglect | 15 | 48 | Stroke, 291.68 |
| RP3 | 72 | F | Left extinction, mild object neglect | 0 | 9 | Stroke, 250.97 |
| RP4 | 66 | M | Left neglect | 20 | 54 | Stroke, 282.48 |
| RP5 | 62 | M | Left neglect | 21 | 54 | Stroke, 332.34 |
| RP6 | 61 | M | Naming, executive | 0 | 53 | Stroke, 185.51 |
| RP7 | 54 | M | Left neglect | 3 | 53 | Stroke, 119.74 |
| Left posterior parietal | ||||||
| LP1 | 73 | M | Right extinction, neglect dyslexia, verbal STM | −3 | 6 | Stroke, 174.66 |
| LP2 | 55 | M | Right extinction, optic ataxia | 0 | 54 | CO poisoning, 5.54 |
Apple cancelation asymmetry scores are the difference in performance between hemifields, and positive scores reflect superior performance in the right hemifield, that is, left neglect. All of those observers who had had strokes were at least 1 year post-stroke at the time of testing.
aCould not be scanned due to metal clips.
Experiment 1 Results
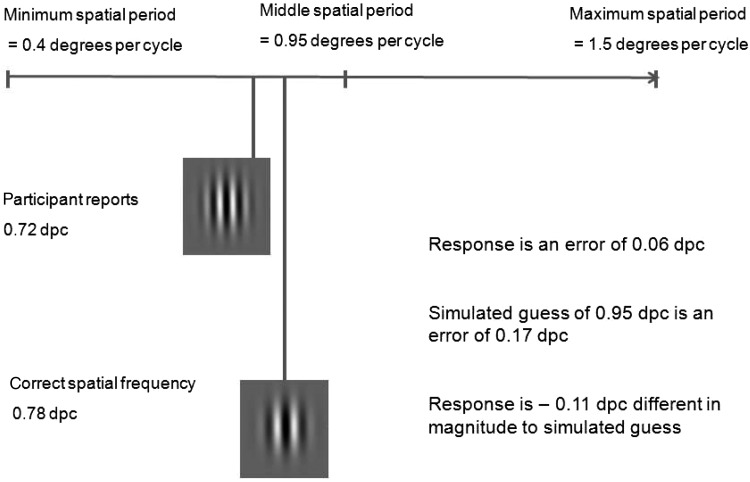
On every trial, observers reported a given spatial period and this differed from the correct spatial period by an error of a given magnitude (see Fig. 3). This results in a minimum possible error magnitude of 0 dpc which would be a perfect response. On every trial, we also simulated a guessing error magnitude using the median spatial period value from the total range of spatial periods the stimulus could possess (0.95 dpc), which was also the starting spatial period of the sample patch using this as the simulated guess value. The simulated guessing error magnitude is then the difference between 0.95 dpc and the correct spatial period.
Figure 3.
Calculation of adjusted error magnitudes.
We calculated how much better each response was than a simulated guess. To do this, we took the difference between the observer's error magnitude and the simulated guessing error magnitude. This yields an adjusted error magnitude on every trial, and these are shown in Table 2. Negative adjusted error magnitudes hence represent performance that is better than simulated guessing. Any responses with positive adjusted error magnitudes are worse than performance would be if the observer had guessed using the central spatial period value on that trial.
Table 2.
Adjusted mean error magnitudes, minimum error magnitudes, perceptual lags, and differences between performance and the simulated guessing model for Experiment 1
| Adjusted mean error magnitude (dpc) | Minimum error magnitude (dpc) | Perceptual lag (ms) | Minimum error better than guessing? | |
|---|---|---|---|---|
| Healthy older adults | ||||
| C1 | −0.152 | −0.158 | 60 | t(104) = 8.13, P < 0.01** |
| C2 | −0.059 | −0.078 | 260 | t(104) = 4.27, P < 0.01** |
| C3 | −0.118 | −0.123 | 130 | t(125) = 6.79, P < 0.01** |
| C4 | −0.076 | −0.076 | 0 | t(88) = 3.40, P < 0.01** |
| C5 | −0.100 | −0.103 | 50 | t(104) = 5.33, P < 0.01** |
| C6 | −0.133 | −0.133 | 0 | t(104) = 5.71, P < 0.01** |
| C7 | −0.103 | −0.120 | 180 | t(104) = 7.59, P < 0.01** |
| C8 | −0.068 | −0.071 | 70 | t(104) = 3.10, P < 0.01** |
| C9 | −0.098 | −0.118 | 150 | t(87) = 6.28, P < 0.01** |
| Occipital lesions | ||||
| O1 (after removing left targets) | −0.048 | −0.063 | 220 | t(61) = 2.40, P = 0.02* |
| O2 | −0.064 | −0.064 | 0 | t(83) = 2.36, P = 0.02* |
| O3 (after removing top right) | −0.064 | −0.068 | 50 | t(67) = 2.56, P = 0.01* |
| Superior bilateral parietal | ||||
| SBP1 | −0.080 | −0.100 | 200 | t(104) = 5.09, P < 0.01** |
| Frontal-temporal | ||||
| FT1 | −0.107 | −0.107 | 0 | t(133) = 6.217, P < 0.01** |
| Bilateral parietal | ||||
| BP1 | 0.119 | — | — | Adjusted mean error magnitude larger than guessing performance |
| BP2 | 0.012 | 0.00 | 280 | t(114) = 0.09, P = 0.93ns |
| Right parietal | ||||
| RP1 | 0.213 | 0.213 | 0 | Minimum error magnitude larger than guessing performance |
| RP2 | 0.037 | 0.017 | 490 | Minimum error magnitude larger than guessing performance |
| RP3 | −0.013 | −0.029 | 130 | t(104) = 1.19, P = 0.24ns |
| RP4 | 0.019 | 0.015 | 80 | Minimum error magnitude larger than guessing performance |
| RP5 | −0.003 | −0.006 | 70 | t(85) = 0.28, P = 0.78ns |
| RP6 | −0.094 | −0.096 | 80 | t(94) = 6.93, P < 0.01** |
| RP7 | −0.049 | −0.057 | 110 | t(104) = 2.67, P < 0.01** |
| Left parietal | ||||
| LP1 | 0.13 | — | — | Adjusted mean error magnitude larger than guessing performance |
| LP2 | −0.067 | −0.091 | 220 | t(104) = 4.73, P < 0.01** |
Missing values for minimum error values and perceptual lag indicate that there was no dip (an inflection point showing a local minimum with a falling and then rising pattern) observed in the lag curve (see below) within the 1000-ms range analyzed.
*P < 0.05, **P < 0.01, and ns indicates non-significance.
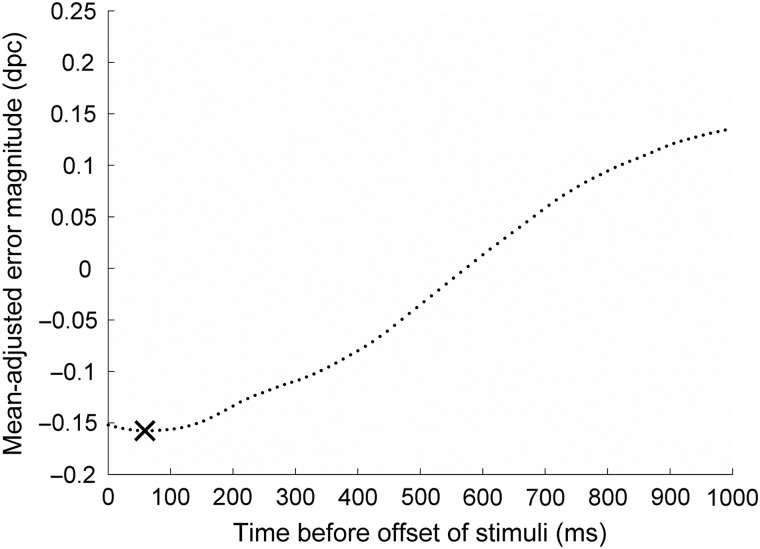
We also calculated perceptual lag curves using the method described by Howard and Holcombe (2008), and a sample curve for 1 healthy control is shown in Figure 4. The leftmost point on the curve where it crosses the ordinate axis is the adjusted mean error magnitude. This indicates how much better performance was than simulated guessing. Just as we can perform this calculation for the final frame of the stimulus displayed by the screen (the “correct” spatial period), we can also perform the same analyses for the frames leading up to the final frame. For example, the second point from the left on the curve represents how much better performance was than guessing had it been the case that the observer was attempting to report the penultimate frame of the stimulus (12 ms before stimulus offset). As reported by Howard and Holcombe (2008), healthy observers display perceptual lag, that is, a tendency for reports to best resemble the state of the stimulus a short period in the past rather than the final state. In this case, the observer's reports best match the stimulus as it was 5 frames (60 ms) before offset. When this perceptual lag is accounted for, performance is slightly better than the adjusted error magnitude—at the minimum point on the curve, the minimum error magnitude is shown and these are included in Table 2 and in Figure 5. Since healthy younger and older participants both tend to display this lag, the minimum error magnitude best reflects performance since it takes this into account.
Figure 4.
Lag analysis for a sample healthy observer, C1. The leftmost point is the mean-adjusted error magnitude for that observer, which is the mean difference between their performance and simulated guessing performance (−0.152 dpc). Negative values indicate that responses are more similar to the actual final spatial period than simulated guesses. Each point moving rightward represents the same calculation, but replacing the final spatial period of the stimulus with states from earlier frames of the stimulus in the moments before it disappeared. For example, the second point shows how much more similar responses were to the penultimate frame of the stimulus than simulated guesses. Responses best match the state of the Gabor a period of 5 frames or 60 ms before its disappearance, and this minimum point on the curve is marked with a cross. Hence, the minimum adjusted error magnitude for this observer is −0.158 dpc.
Figure 5.
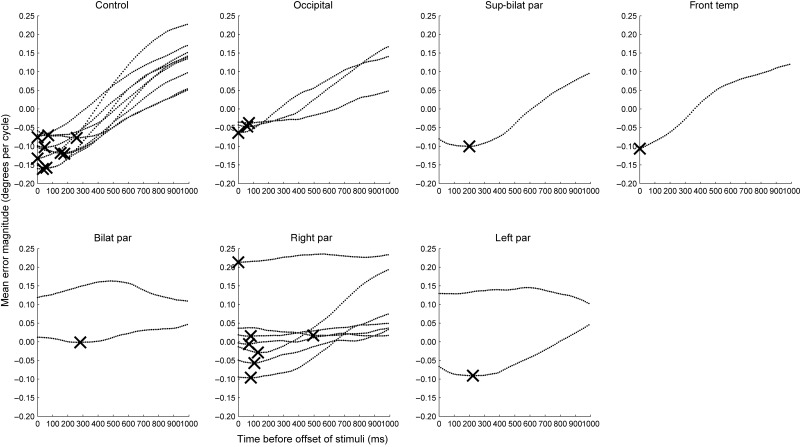
Grouped lag analyses for neurological controls and individuals with damage in occipital cortex, superior bilaterial parietal cortex, frontal-temporal cortex, bilateral parietal cortex, right parietal, and left parietal cortex, respectively. Each line represents the lag analysis for 1 individual, and where a lag is identified, it is marked with a cross.
In Figure 5, one can see that the mean error magnitudes tend to rise toward the right side of the plots, especially for those individuals who achieve large negative error magnitudes toward the left hand side of the plot. This can be understood by considering what we would expect if observers were guessing. Since the plotted values are corrected for simulated guessing performance, observers who were guessing would produce data that would tend toward a flat horizontal line at errors of magnitude zero, that is, performing no better or worse than the guessing model. Since guesses are no more likely to resemble final states of the stimulus (toward the left hand side of the plot) nor older states (toward the right), the line will be flat. Observers who are performing better than guessing will make responses that are closer to the final states of the stimulus than the guessing model. This will be reflected in more negative error magnitudes toward the left of the plot. Since the stimulus is changing over time, this will necessarily make these responses more different on average from past states of the stimulus (toward the right of the plot) than final states. It will also mean that responses are more different from past states of the stimulus (i.e., less negative) than would be produced from guessing.
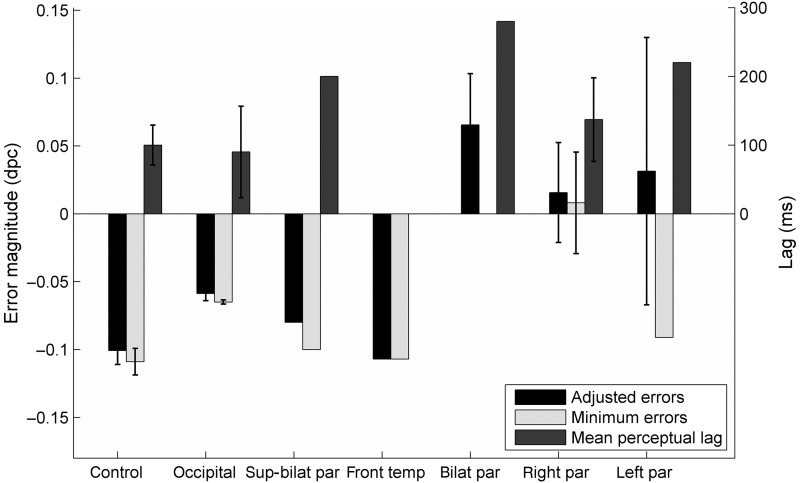
Group performance measures are shown in Figure 6 for different participant types. Mean adjusted error magnitudes are positive for the bilateral parietal, right parietal and left parietal groups, which indicates performance that is worse than simulated guesses. Minimum error magnitudes, which are errors that take account of lags, are negative for the left parietal group but not for the bilateral parietal or right parietal patients. The 11 patients with inferior parietal lobe damage had a mean minimum error magnitude of −0.0038 dpc compared with the mean minimum error magnitudes of −0.0987 dpc for the 14 healthy older adults and neurological controls. This difference was statistically significant (t21 = 3.63, P < 0.01).
Figure 6.
Grouped performance data for Experiment 1 for neurological controls and individuals with damage in occipital cortex, superior bilaterial parietal cortex, frontal-temporal cortex, bilateral parietal cortex, right parietal, and left parietal cortex, respectively. Minimum error magnitude for bilaterial parietal group is 0 and hence not visible. As stated earlier, no lag for the frontal-temporal patient was calculated since there was no dip in the large curve. Error bars represent standard errors where data were available for >1 participant.
For none of the patients with parietal lobe damage did the minimum error magnitudes differ significantly between hemifields (P > 0.05). For this reason, the data are collapsed here across hemifields. Averaged across participants, patients with right parietal lobe damage performed no worse in the contralateral than ipsilateral fields (t473 = 1.60, P = 0.11) and the same held for patients with left parietal lobe damage (t166 = 0.01, P = 0.99). Although between-hemifield differences in performance were not significantly different, they were in the expected direction for patients with right parietal lobe damage: The mean minimum error magnitude was 0.037 dpc for left hemifield stimuli and −0.004 dpc for right hemifield stimuli. Patients with left parietal lobe damage had a mean minimum error magnitude of 0.001 dpc for stimuli on the left and 0.002 dpc on the right.
To address the possibility that lateralization effects may have been affected by performance at or near floor levels, we also repeated these lateralization tests with the criterion that we included only those observers who performed above chance in either one or both hemifields. This was true of only 1 patient with left damage (LP2) for whom no hemifield effects were observed (t83 = 0.59, P = 0.56). Only including 2 observers (RP6 and RP7) in the analysis for those with right damage, there were also no differences observed (t155 = 1.53, P = 0.13) although these analyses were underpowered due to such strict exclusion criteria.
Being able to report the final state of the stimulus with some degree of accuracy is associated with negative minimum error magnitudes, and with perceptual lag curves of the shape shown in Figure 4. To test for whether an individual could perform better than the guessing model, we performed t-tests of the difference between the minimum error magnitude and zero (performance predicted under the guessing model). The results of these tests are included in Table 2.
Overall, 9 healthy older adults, 3 patients with occipital lobe damage, 1 with superior bilateral parietal lobe damage, and 1 with frontal and temporal damage were able to perform this spatial period-monitoring task better than simulated guessing. However, only 2 of the 7 patients with right parietal lobe damage, 1 of the 2 with damage to left parietal lobe, and neither of those with bilateral parietal damage were able to perform better than simulated guessing.
We looked at the relationship between trial duration and minimum error values for all observers. There were no statistically significant correlations except for C1 (r(104) = −0.27, P < 0.01) for whom performance was better for trials of longer duration. For no observers was there a relationship between performance and chronological position of individual trials, that is, no evidence of an increase or decrease in performance over time. There was no correlation between minimum error values and asymmetry score magnitudes for the patients (r(15) = 0.181, P = 0.536) nor between minimum error values and performance on the sustained auditory attention task (r(15) = −0.413, P = 0.143).
We reasoned that there are 2 likely causes for a failure to perform this task better than simulated guessing. First, poor temporal resolution of attention would lead to poor performance since perceptual averaging over too long an interval would produce responses that were very dissimilar to the final appearance of stimuli. Some degree of temporal integration of this kind is seen in healthy younger adults for this task (Howard and Holcombe 2008) and is reflected in perceptual lags of the kind we also observe here. However, wide temporal integration windows lead to flattening of lag curves and make it difficult to accurately estimate lag magnitudes. For this reason, many of the estimates of perceptual lag for individual observers, especially in the patients who completed fewer blocks of trials, are relatively noisy. Wide temporal windows also lead to poor performance, since greater temporal integration leads to responses that tend toward simulated guessing. A second possibility for poor performance is a failure to sustain attention to the stimulus over the several seconds required during the trial. Of course, an additional possibility is that some patients did not fully grasp the task instructions or were unable to respond appropriately for other unknown reasons such as deficits in basic spatial frequency perception. Experiment 2 was designed to address these issues and to investigate the temporal aspects of performance in more detail.
Experiment 2: Discontinuously Changing Stimuli
Materials and Methods
Experiment 2 was designed to test for the possibility of unusually poor temporal resolution of attention. To test for this, we introduced 3 conditions varying in the rate at which the stimulus changed appearance. In 3 conditions, the spatial period of the stimulus was reselected either every 200, 300, or 400 ms, corresponding to rates of change of 5.00, 3.33, or 2.50 Hz. A major difference between Experiments 1 and 2 was that in Experiment 1, the stimulus changed smoothly over time, whereas in Experiment 2, the change was discontinuous (see Fig. 7).
Figure 7.
Discontinuous spatial period change of an example Gabor in Experiment 2.
This experiment was designed to detect the signature of poor temporal resolution, which is an inability to perform at fast rates with an ability to perform at slower rates. If healthy older adults can perform at the fastest rate here (and most likely at even faster rates), patients whose performance recovers as the rate of change decreases from 5.00 to 3.33 Hz, or from 3.33 to 2.5 Hz are exhibiting poor temporal resolution of attention.
Experiment 2 was identical to Experiment 1 but with the following differences. The spatial period of the Gabors was randomly selected from 4 possible spatial periods (0.4, 0.8, 1.2, or 1.6 dpc) at the start of the trial. Then, for the duration of the Gabor presentation, its spatial period was repeatedly and independently re-selected from these 4 possible values at a rate of once either every 200, 300, or 400 ms, depending on the condition. Note that because the trial duration was randomly selected between the minimum and maximum durations described earlier, the duration of presentation of the final spatial period was randomly generated with a range between one frame (12 ms) and either 200, 300, or 400 ms.
In Experiment 2, because no systematic differences were observed between stimulus positions, the number of potential positions was reduced to 3: central presentation, left or right of fixation with the same distances from fixation at in Experiment 1. After the disappearance of the Gabor, the response screen appeared (this was the same on every trial). The response screen consisted of the 4 Gabors arranged vertically in the horizontal center of the screen with the 4 spatial periods. The topmost Gabor was presented 11.46° above the center of the screen and possessed a spatial period of 0.4 dpc. A patch with 0.8 dpc was presented 5.73° above the center of the screen. A patch with 1.2 dpc was presented 5.73° below the center of the screen, and a patch with 1.6 dpc was presented 11.46° below the center of the screen. The observer was given 2 options for responses. They could either point toward the patch they believed was the final one presented, or they could call out “1,” “2,” “3,” or “4” on each trial representing each of the 4 patches. The experimenter entered the response, triggering the next trial.
Each block contained 1 of the 3 duration conditions. Observers completed 3 or more blocks of 35 trials or as many as they could manage without becoming excessively tired. Observers completed as many blocks as they could in each 1-h session and returned for further testing sessions on different days over a period of ∼3 months. The order of presentation of blocks was randomized, although some of the healthy controls completed only the 200-ms condition. For the 5.00-Hz condition, 3 observers completed between 70 and 80 trials (RP5, O2, and BP2), 5 completed between 100 and 140 trials (C4 and RP1, RP2, O3, and C6), 8 completed between 140 and 180 (RP3, RP7, C3, C10, C11, C12, C13, and BP1), and 5 completed between 200 and 320 trials (O1, SBP1, LP1, FT1, and LP2). For the 3.33-Hz condition, 4 observers completed between 30 and 60 trials (RP1, RP4, BP2, and RP6), 3 between 60 and 90 (RP2, C3, and BP1), 4 between 100 and 120 (C8, O2, O1, and SBP1), 5 between 130 and 150 (C6, FT1, O3, RP7, and C1), and 4 between 150 and 280 (RP5, LP1, RP3, and LP2). For the 2.5-Hz condition, 1 observer completed 16 trials (C6), 2 completed 30–50 trials (C14 and C1), 4 completed 100–140 trials (BP2, RP4, RP6, and RP3), 5 completed between 140 and 160 trials (RP1, RP5, RP7, C3, and BP1), 6 completed 160–200 trials (RP2, SBP1, O1, O2, FT1, and O3), and 2 completed 240–280 trials (LP1 and LP2). Typically, observers completed these over 3–6 sessions.
Observers were up to 7 healthy older adults (aged 57–81), up to 7 patients with right parietal lobe damage and 2 with left parietal lobe damage (aged 54–73), 3 with occipital damage (aged 57–64), 2 with bilateral parietal lobe damage (aged 63–68), 1 with superior bilateral parietal lobe damage (aged 59), and 1 with frontal and temporal damage (aged 55).
Results
We calculated adjusted mean error magnitudes, lags, and minimum error magnitudes as for Experiment 1, and these are shown in Tables 2–4. In addition, we also calculated simple percent correct scores. These should be interpreted with caution, however, for 3 reasons. First, the percent correct score is inherently less sensitive than error magnitude measures, since it makes no distinction between trials on which the participant incorrectly chooses a response when it is very far from the correct value compared with trials where the response is wrong but close to correct. Second, it is not possible to perform inferential tests against a 25% guessing score since the percent correct measure gives only 1 score per participant. Third, the percent correct score does not take into account any perceptual lags and therefore will tend to underestimate performance.
Table 3.
Adjusted mean error magnitudes, minimum error magnitudes, perceptual lags, and differences between performance and the simulated guessing model for discontinuous change at 5.00 Hz
| Adjusted mean error magnitude (dpc) | Minimum error magnitude (dpc) | Perceptual lag (ms) | % correct | Minimum error better than guessing? | |
|---|---|---|---|---|---|
| Healthy older adults | |||||
| C3 | −0.063 | −0.086 | 20 | 35.0 | t(139) = 3.46, P < 0.01** |
| C4 | −0.097 | −0.128 | 70 | 46.7 | t(104) = 3.56, P < 0.01** |
| C6 | −0.107 | −0.177 | 40 | 48.8 | t(120) = 5.93, P < 0.01** |
| C10 | −0.083 | −0.100 | 130 | 40.0 | t(139) = 3.76, P < 0.01** |
| C11 | −0.211 | −0.240 | 20 | 59.3 | t(139) = 10.75,P < 0.01** |
| C12 | −0.129 | −0.154 | 50 | 49.3 | t(139) = 5.27, P < 0.01** |
| C13 | −0.129 | −0.177 | 120 | 48.6 | t(139) = 7.11, P < 0.01** |
| Occipital lesions | |||||
| O1 (after removing left targets) | −0.144 | −0.170 | 50 | 45.8 | t(143) = 7.59, P < 0.01** |
| O2 | −0.251 | −0.291 | 50 | 74.3 | t(69) = 9.19, P < 0.01** |
| O3 (after removing top right) | −0.053 | −0.094 | 40 | 36.8 | t(86) = 2.57, P = 0.01* |
| Superior bilateral parietal | |||||
| SBP1 | −0.109 | −0.114 | 100 | 39.5 | t(209) = 5.95, P < 0.01** |
| Frontal-temporal | |||||
| FT1 | −0.090 | −0.116 | 20 | 45.5 | t(243) = 6.16, P < 0.01** |
| Bilateral parietal | |||||
| BP1 | 0.028 | 0.003 | 80 | 29.6 | Minimum error magnitude larger than guessing performance |
| BP2 | 0.057 | −0.029 | 580 | 30.0 | t(69) = 0.71, P = 0.48ns |
| Right parietal | |||||
| RP1 | 0.000 | −0.037 | 80 | 36.4 | t(117) = 1.08, P = 0.28ns |
| RP2 | 0.035 | 0.021 | 220 | 26.5 | Minimum error magnitude larger than guessing performance |
| RP3 | 0.003 | −0.003 | 40 | 30.7 | t(139) = 0.11, P = 0.91ns |
| RP5 | −0.097 | −0.114 | 20 | 30.0 | t(69) = 3.52, P < 0.01** |
| RP7 | 0.003 | −0.020 | 140 | 28.6 | t(139) = 0.85, P = 0.39ns |
| Left parietal | |||||
| LP1 | −0.024 | −0.074 | 120 | 33.2 | t(228) = 3.62, P < 0.01** |
| LP2 | −0.006 | −0.026 | 70 | 30.8 | t(314) = 1.15, P = 0.15ns |
*P < 0.05, **P < 0.01, and ns indicates non-significance.
Table 4.
Adjusted mean error magnitudes, minimum error magnitudes, perceptual lags, and differences between performance and the simulated guessing model for discontinuous change at 3.33 Hz
| Adjusted mean error magnitude (dpc) | Minimum error magnitude (dpc) | Perceptual lag (ms) | % correct | Minimum error better than guessing? | |
|---|---|---|---|---|---|
| Healthy older adults | |||||
| C1 | −0.126 | −0.157 | 70 | 44.3 | t(139) = 7.23, P < 0.01** |
| C3 | −0.112 | −0.162 | 120 | 40.0 | t(104) = 5.70, P < 0.01** |
| C6 | −0.194 | −0.251 | 60 | 54.3 | t(209) = 11.66, P < 0.01** |
| C8 | −0.051 | −0.192 | 220 | 39.1 | t(104) = 6.19, P < 0.01** |
| Occipital lesions | |||||
| O1 (after removing left targets) | −0.140 | −0.147 | 10 | 46.2 | t(105) = 5.48, P < 0.01** |
| O2 | −0.219 | −0.257 | 60 | 63.8 | t(104) = 9.61, P < 0.01** |
| O3(after removing top right) | −0.097 | −0.112 | 20 | 43.4 | t(135) = 4.30, P < 0.01** |
| Superior bilateral parietal | |||||
| SBP1 | −0.080 | −0.088 | 70 | 31.4 | t(174) = 5.03, P < 0.01** |
| Frontal-temporal | |||||
| FT1 | −0.121 | −0.143 | 10 | 46.8 | t(187) = 6.40, P < 0.01** |
| Bilateral parietal | |||||
| BP1 | 0.05 | 0.034 | 660 | 23.9 | Minimum error magnitude larger than guessing performance |
| BP2 | 0.060 | −0.030 | 130 | 18.5 | t(53) = 0.60, P = 0.55ns |
| Right parietal | |||||
| RP1 | 0.064 | −0.008 | 140 | 28.0 | t(49) = 0.16, P = 0.87ns |
| RP2 | 0.024 | −0.024 | 150 | 22.0 | t(81) = 0.80, P = 0.42ns |
| RP3 | −0.004 | −0.044 | 70 | 31.0 | t(225) = 1.96, P = 0.05ns |
| RP4 | 0.00 | −0.032 | 800 | 26.0 | t(49) = 1.32, P = 0.19ns |
| RP5 | −0.071 | −0.079 | 60 | 39.4 | t(154) = 3.30, P < 0.01** |
| RP6 | −0.156 | −0.156 | 0 | 60.0 | t(54) = 4.61, P < 0.01** |
| RP7 | −0.094 | −0.114 | 140 | 32.9 | t(139) = 5.16, P < 0.01** |
| Left parietal | |||||
| LP1 | −0.076 | −0.093 | 110 | 39.7 | t(279) = 5.47, P < 0.01** |
| LP2 | −0.049 | −0.064 | 20 | 37.1 | t(279) = 3.36, P < 0.01** |
*P < 0.05, **P < 0.01, and ns indicates non-significance.
Rate of Stimulus Change of 5.00 Hz
For the 5.00-Hz rate of stimulus change, the healthy adults, the patients with occipital lobe damage, the patient with superior bilateral parietal lobe damage, and the patient with frontal-temporal damage all performed significantly better than simulated guessing performance. One of 5 of those with right parietal lobe damage, 1 of the 2 with left parietal damage, and neither patient with bilateral parietal lobe damage performed better than guessing. It is interesting to note that RP5 and LP1 performed better than chance although they were not able to perform better than simulated guesses in Experiment 1. They may have benefitted from the brief periods during which the stimulus was completely static between spatial period changes. It is also possible that they may have benefitted from the sudden luminance transients caused by the discontinuous stimulus change which may have helped them to sustain attention to the changing stimulus.
For none of the patients with parietal lobe damage did the minimum error magnitudes differ significantly between hemifields (P > 0.05). For this reason, the data are collapsed here across hemifields. Averaged across participants, patients with right parietal lobe damage performed no worse in the contralateral than ipsilateral fields (t207 = 1.59, P = 0.11), nor did patients with left parietal lobe damage (t378 = 0.09, P = 0.93). For those patients with right parietal lobe damage, the mean minimum error magnitude was −0.032 dpc for left hemifield stimuli and −0.008 dpc for right hemifield stimuli. For those patients with left parietal lobe damage, mean minimum error magnitude was −0.042 dpc for left hemifield stimuli and −0.045 dpc for right hemifield stimuli.
To address the possibility that lateralization effects may have been affected by performance at or near floor levels, we also repeated these lateralization tests with the criterion that we included only those observers who performed above chance in either one or both hemifields. This was true of only 1 patient with left damage (LP1) for whom no hemifield effects were observed (t164 = 0.01, P = 0.99). Only including the one observer (RP5) in the analysis for those with right damage, there were also no differences observed (t43 = 0.59, P = 0.59). As in Experiment 1, it is worth noting however that these analyses were underpowered due to such strict exclusion criteria.
We looked at the relationship between trial duration and minimum error values for all observers. There were no statistically significant correlations except for BP1 (r(178) = 0.22, P < 0.01) for whom performance was worse for trials of longer duration. For 1 observer (FT1), there was a relationship between performance and chronological position of individual trials such that there was improvement on the task over time (243) = −0.16, P = 0.01.
Rate of Stimulus Change of 3.33 Hz
For the 3.33-Hz rate of stimulus change, all the healthy adults, the patients with occipital lobe damage, the patient with superior bilateral parietal lobe damage, and the patient with frontal-temporal damage all performed significantly better than simulated guessing performance. More of the patients with parietal lobe damage were able to perform better than guessing here than for the 5-Hz rate of change: 3 of 7 of those with right parietal lobe damage, both of those with left parietal damage but neither of the patients with bilateral parietal lobe damage performed better than guessing.
For none of the patients with parietal lobe damage did minimum error magnitudes differ significantly between hemifields (P > 0.05). For this reason, the data are collapsed here across hemifields. Averaged across participants, patients with right parietal lobe damage performed no worse in the contralateral than ipsilateral fields (t486 = 1.67, P = 0.10), nor did patients with left parietal lobe damage (t379 = 1.13, P = 0.26). Although not significant, hemifield effects were in the expected direction: For patients with right parietal lobe damage, the mean minimum error magnitude was −0.039 dpc for left hemifield stimuli and −0.086 dpc for right hemifield stimuli. Conversely, for patients with left parietal lobe damage, the mean minimum error magnitude was −0.093 dpc for left hemifield stimuli and −0.056 dpc for right hemifield stimuli.
To address the possibility that lateralization effects may have been affected by performance at or near floor levels, we also repeated these lateralization tests with the criterion that we included only those observers who performed above chance in either one or both hemifields. For the 2 observers for whom this was true with left damage (LP2 and LP1), no hemifield effects were observed (t379 = 1.13, P = 0.26). Including the 3 observers (RP5, RP6, and RP7) in the analysis for those with right damage, there were also no differences observed (t224 = 1.81, P = 0.07). The direction of the difference in performance was in the expected direction, with right targets reported with a minimum adjusted error of −0.15 dpc and left targets with an error of −0.08 dpc.
We looked at the relationship between trial duration and minimum error values for all observers. There were no statistically significant correlations except for RP7 (r(139) = −0.19, P = 0.02) for whom performance was better for trials of longer duration.
For 2 observers, there was a relationship between performance and chronological position of individual trials such that performance decreased over time (LP2: r(279) = 0.13, P = 0.04; RP3: r(225) = 0.25, P < 0.01).
Rate of Stimulus Change of 2.50 Hz
For the 2.50-Hz rate of stimulus change, all the healthy adults, the patients with occipital lobe damage, the patient with superior bilateral parietal lobe damage, and the patient with frontal-temporal damage all performed significantly better than simulated guessing performance. Even more of the patients with parietal lobe damage were able to perform better than guessing here than for the 3.33-Hz rate of change: 5 of 7 with right parietal lobe damage, both of those with left parietal damage but neither of the 2 patients with bilateral parietal lobe damage performed better than guessing (Table 5).
Table 5.
Adjusted mean error magnitudes, minimum error magnitudes, perceptual lags, and differences between performance and the simulated guessing model for discontinuous change at 2.50 Hz
| Adjusted mean error magnitude (dpc) | Minimum error magnitude (dpc) | Perceptual lag (ms) | % correct | Minimum error better than guessing? | |
|---|---|---|---|---|---|
| Healthy older adults | |||||
| C1 | −0.209 | −0.243 | 50 | 51.1 | t(46) = 5.95, P < 0.01** |
| C3 | −0.186 | −0.191 | 30 | 57.1 | t(139) = 7.51, P < 0.01** |
| C6 | −0.100 | −0.200 | 50 | 62.3 | t(15) = 2.45, P = 0.03* |
| C14 | −0.143 | −0.166 | 20 | 48.6 | t(34) = 4.00, P < 0.01** |
| Occipital lesions | |||||
| O1 (after removing left targets) | −0.179 | −0.204 | 100 | 47.0 | t(114) = 7.34, P < 0.01** |
| O2 | −0.243 | −0.262 | 20 | 69.7 | t(174) = 12.70, P < 0.01** |
| O3 (after removing top right) | −0.120 | −0.149 | 80 | 42.4 | t(124) = 5.39, P < 0.01** |
| Superior bilateral parietal | |||||
| SBP1 | −0.064 | −0.095 | 150 | 30.4 | t(170) = 5.34, P < 0.01** |
| Frontal-temporal | |||||
| FT1 | −0.129 | −0.144 | 60 | 48.0 | t(191) = 6.25, P < 0.01** |
| Bilateral parietal | |||||
| BP1 | 0.015 | 0.005 | 160 | 27.6 | Minimum error magnitude larger than guessing performance |
| BP2 | 0.073 | −0.018 | 590 | 22.8 | t(100) = 0.52, P = 0.60ns |
| Right parietal | |||||
| RP1 | −0.046 | −0.109 | 100 | 37.1 | t(139) = 3.81, P < 0.01** |
| RP2 | 0.046 | −0.061 | 780 | 24.4 | t(163) = 2.70, P < 0.01** |
| RP3 | 0.000 | −0.009 | 140 | 32.6 | t(131) = 0.52, P = 0.60ns |
| RP4 | 0.013 | −0.036 | 70 | 30.5 | t(104) = 1.14, P = 0.26ns |
| RP5 | −0.060 | −0.091 | 120 | 36.4 | t(139) = 4.35, P < 0.01** |
| RP6 | −0.166 | −0.192 | 50 | 53.3 | t(104) = 7.95, P < 0.01** |
| RP7 | −0.097 | −0.097 | 20 | 32.9 | t(139) = 4.35, P < 0.01** |
| Left parietal | |||||
| LP1 | −0.105 | −0.123 | 120 | 46.6 | t(244) = 6.28, P < 0.01** |
| LP2 | −0.027 | −0.060 | 90 | 31.4 | t(279) = 3.15, P < 0.01** |
*P < 0.05, **P < 0.01, and ns indicates non-significance.
For none of the patients with parietal lobe damage did minimum error magnitudes differ significantly between hemifields (P > 0.05). For this reason, the data are collapsed here across hemifields. Averaged across participants, patients with right parietal lobe damage performed no worse in the contralateral than ipsilateral fields (t609 = 1.20, P = 0.23), nor did patients with left parietal lobe damage (t333 = 0.065, P = 0.95). Although not significant, hemifield effects were in the expected direction: For patients with right parietal lobe damage, the mean minimum error magnitude was −0.037 dpc for left hemifield stimuli and −0.066 dpc for right hemifield stimuli. For patients with left parietal lobe damage, the mean minimum error magnitude was −0.092 dpc for left hemifield stimuli and −0.090 dpc for right hemifield stimuli.
To address the possibility that lateralization effects may have been affected by performance at or near floor levels, we also repeated these lateralization tests with the criterion that we included only those observers who performed above chance in either one or both hemifields. For the 2 observers for whom this was true with left damage (LP2 and LP1), no hemifield effects were observed (t333 = 0.06, P = 0.07)
Including the 4 observers (RP1, RP5, RP6, and RP7) in the analysis for those with right damage, there was a difference between hemifields in the expected direction (t332 = 2.33, P = 0.02) with right targets reported with a minimum adjusted error of −0.15 dpc and left targets with an error of −0.07 dpc.
We looked at the relationship between trial duration and minimum error values for all observers. There were no statistically significant correlations except for O2 (r(174) = −0.16, P = 0.04) for whom performance was better for trials of longer duration. For 1 observer, there was a relationship between performance and chronological position of individual trials such that performance improved over time (O3: r(194) = −0.15, P = 0.04).
Comparison across Speed Conditions
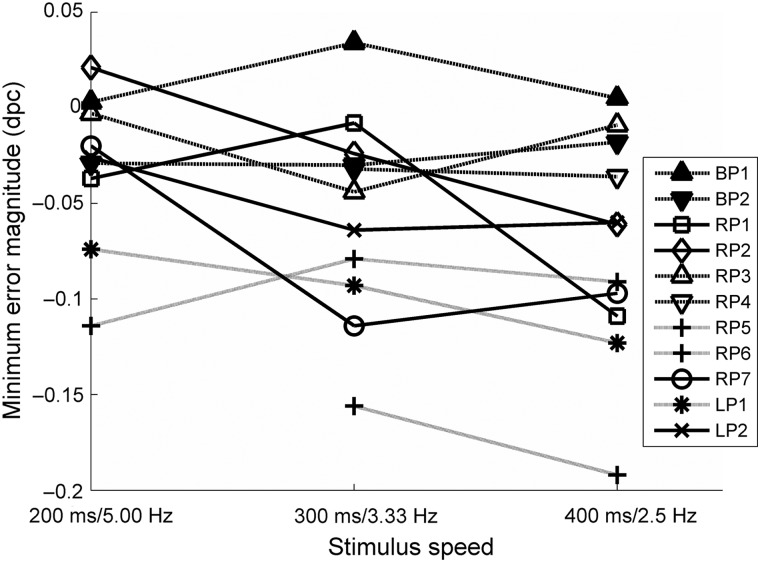
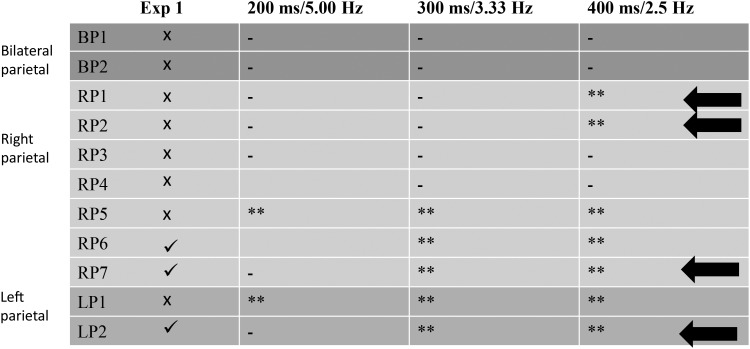
Across the 3 rates of discontinuous change, 3 patients with right parietal lobe damage and 1 with left parietal lobe were able to perform better than simulated guesses at slower rates but not faster rates. For 2 patients (RP1 and RP2), the speed threshold at which they became able to perform the task occurred between 3.33 and 2.5 Hz, and for 2 patients (RP7 and LP2), this threshold was located between 5.00 and 3.33 Hz. For comparison across speeds, minimum errors are plotted for individual patients with parietal lobe damage in Figure 8 and are summarized in Figure 9. Some cells are blank where observers withdrew from the study without completing each speed condition.
Figure 8.
Minimum error magnitudes for patients with parietal lobe damage. Solid lines indicate patients for whom a decrease in stimulus speed enabled them to perform better than chance which they were not able to achieve as faster speeds. Dashed lines indicate patients who could not perform better than chance at any speed. Dotted lines indicate patients who were able to perform better than chance at all speeds.
Figure 9.
Summary of performance for patients with parietal lobe damage. Ticks and crosses in the leftmost column indicate performance that is either better or no better than simulated guessing, respectively, in Experiment 1. Asterisks indicate performance better than simulated guessing performance in Experiment 2 for the 3 rates of stimulus change at P < 0.05; double asterisks indicate significance at P < 0.01; dashes indicate performance no better than simulated guesses. Arrows indicate those 4 observers for whom performance recovers with slower stimulus change in Experiment 2, the signature of poor temporal resolution of attention.
We examined the differences in minimum error magnitudes between 2 groups of observers across the 3 speed settings. The first group consisted of all patients with inferior parietal lobe damage (either right, left, or bilateral), and the second group contained both the healthy older adults and the neurological controls (occipital, frontal-temporal, and superior bilateral parietal damage). We performed a 2 (participant group) × 3 (speed: 5, 3.3, and 2.5 Hz) ANOVA which revealed a main effect of group whereby inferior parietal patients performed significantly worse than healthy adults and neurological controls (F1,54 = 66.76, P < 0.01), but there was no significant effect of speed (F2,54 = 1.85, P = 0.167) and no interaction (F2,54 = 0.05, P = 0.951). There was, however, a trend in the data for both groups to perform better with each decrease in speed (patient group: mean minimum error magnitudes at 5, 3.3, and 2.5 Hz, −0.031, −0.056, and −0.068 dpc, respectively; control group: mean minimum error magnitudes at 5, 3.3, and 2.5 Hz, −0.154, −0.168, and −0.184 dpc respectively).
To evaluate the performance of each patient compared with the control group, we tested for whether their overall behavior differed significantly from the overall mean performance of the control group in terms of minimum error magnitudes. The 3 occipital patients showed somewhat mixed results with 1 patient not differing from controls (O1: P = 0.55), 1 achieving better performance than controls (O2: P = 0.03) and 1 bordering on slightly worse performance (O3: P = 0.05). This mixed pattern of results might be explained by their limited visual capabilities on the one hand and potentially increased attention focus within the functioning field of view. Both the patient with superior bilateral parietal damage (P = 0.13) and the patient with frontal-temporal damage (P = 0.19) performed no differently from controls. Both patients with bilateral parietal damage performed significantly worse than controls (P < 0.01) as did 6 of those with right parietal damage (RP5: P = 0.04, RP1, RP2, RP3, RP4, and RP7: P < 0.01). Patient RP6 was the only right parietal patient not to differ from controls (P = 0.62). Both patients with left parietal damage performed worse than controls (LP1: P < 0.01, LP2: P = 0.046).
Although the experiments here were not designed to test for lower-level perceptual processing, we examined the possible contribution from temporal resolution of lower-level early visual processes. Changes in visual stimulation faster than ∼50 Hz (the flicker fusion limit: note this is 10 times faster than the fastest rate of change in Experiment 2) are not visible. This means that when luminance changes faster than this, it no longer appears to flicker, as the darker and lighter phases are perceptually integrated resulting in a percept that is the sum of the two. This is why the cycling of fluorescent lights and CRT monitors over time is not visible. In the stimulus presented here at any speed, there will be some trials on which the last spatial period change occurred in the final few frames before the stimulus offset, and these changes will not be distinguishable to the observer. Rather the percept will be integrated image of the 2 most recent states of the stimulus, as if one were overlaid transparently on top of the other. When this occurs, the resulting percept will on average be of lower spatial period (higher spatial frequency) than either of the 2 component parts since summation will produce more luminance boundaries. We tested for this by examining the mean signed error (all other reported errors are absolute) and looking for whether these were significantly more negative than zero.
Although this predicted bias appears to be present, there is no clear pattern in terms of whether this is associated with cortical damage or not, parietal or otherwise, and whether the individuals showing the bias are able to perform the task above chance or not. At 5.00 Hz, 11 of 21 observers showed this significant bias (P < 0.05) toward reporting lower spatial periods than the average value, including 4 with parietal damage, 5 healthy older adults, and 2 neurological controls. Three of these patients with parietal lobe damage were unable to perform this task better than chance, but all the other observers with this bias (including one with parietal damage) were able to perform better than chance.
At the medium speed, 12 of 20 observers showed this bias, including 3 healthy older adults, 6 patients with parietal damage, and 3 neurological controls. Of these 6 patients with parietal lobe damage, 4 were and 2 were not able to perform above chance. Even the slowest rate of change, 10 of 20 observers including 6 patients with parietal lobe damage, 1 healthy older adult, and 3 neurological controls showed this significant bias toward reporting low spatial periods. This was the case despite all these observers performing above chance. These biases likely reflect the presence of lower-level temporal resolution limits on vision (flicker fusion limit), which operate over much finer temporal timescales than the limits on temporal resolution of attention. Further, these lower-level perceptual resolution limits bear little relation with neurological damage nor are predictive of overall performance on the task.
Lesion Reconstruction
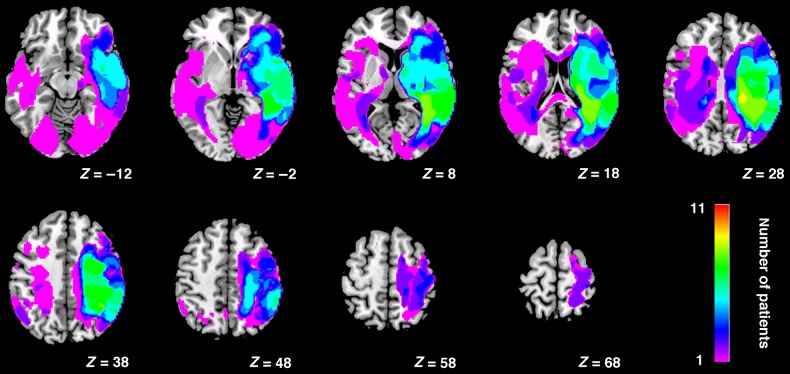
Lesion maps for all 11 patients with inferior parietal lobe damage were reconstructed using an outlier detection algorithm based on fuzzy clustering (for full protocol and method validation, see Seghier et al. 2008; Chechlacz et al. 2013). The results of lesion reconstruction were verified against the patient's T1 scans.
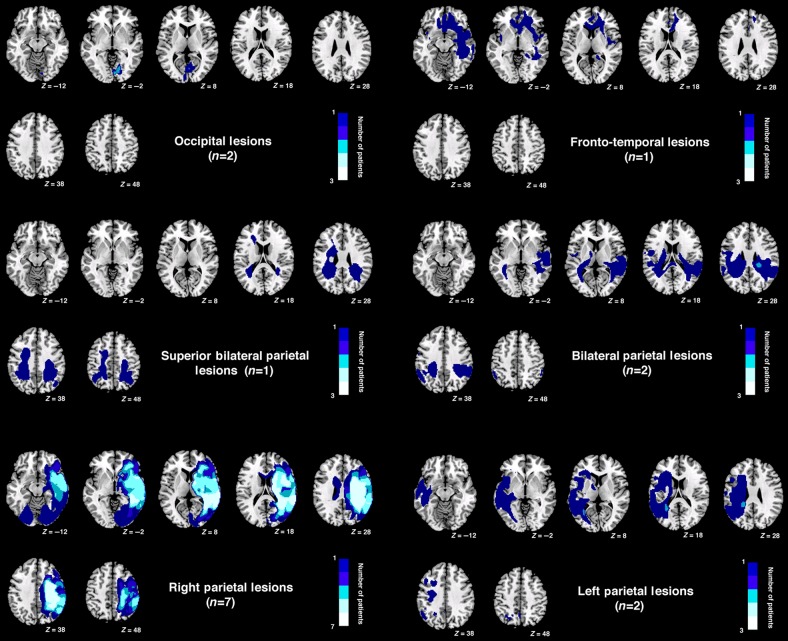
Figure 10 shows the lesion overlap. Maximum overlap (8 patients of 11) is mainly in white matter (9 of 11 SLF, ILF, thalamic radiation, and posterior corona radiata), plus some overlap in the gray matter (8 of 11) within posterior parietal cortex (border angular/sumpramarginal gyri) and extending into superior temporal gyrus within the right hemisphere. Figure 11 shows the lesion overlap by group of lesions.
Figure 10.
Lesion overlap reconstruction for the 11 patients with damage to inferior parietal cortex.
Figure 11.
Lesion overlap by site for groups of patients. Note no scan is available for one of the patients with occipital lobe damage due to metal clips.
We also looked at the relationship between lesion sizes (shown in Table 1) and performance, excluding occipital patients since they were included as neurological controls on the basis of field loss rather than lesion size. In Experiment 1, there was no correlation between lesion volume and minimum error magnitudes r(11) = 0.49, P = 0.12, neither was there any significant correlation in Experiment 2 (5 Hz: r(11) = −0.03, P = 0.93, 3.33 Hz: r(11) = 0.14, P = 0.66, 2.5 Hz: r(11) = −0.10, P = 0.75). It is of note that comparing FT1 and BP1 whose brain lesion volumes differed by only 10.01 cm3, performance differed significantly in Experiment 1 (P < 0.01) and in all 3 conditions of Experiment 2 (P < 0.01), with FT1 achieving significantly more negative error magnitudes than BP1. Thus, it seems that lesion volume was not related to or predictive of performance.
Discussion
We showed in 2 experiments that compared with healthy older adults, patients with damage that included inferior parietal lobe damage showed unusually poor temporal precision of attention in a continuous monitoring task. Observers attempted to monitor a single luminance grating as it changed in its spatial period. In Experiment 1, the grating changed smoothly and randomly in its spatial period and disappeared after a semi-random interval. Observers attempted to report the final spatial period value of the grating before it disappeared. Healthy older adults and neurological controls were able to perform better than simulated guesses, but only 3 of 11 patients with inferior parietal lobe damage were able to reach a performance level that differed significantly from simulated guesses. Poor performance on this task is consistent with an inability to selectively attend to the final moment at which the stimulus was seen. However, it is also consistent with a failure of sustained attention to the task or other unknown factors such as not fully comprehending the task.
To ensure that performance in Experiment 1 reflected temporal precision of attention, we designed Experiment 2 to detect differences in performance for stimulus change requiring differing levels of temporal resolution of attention. By manipulating stimulus speed directly, we were able to assess temporal aspects of performance in an additional manner to estimating perceptual lag curves (lags are difficult to estimate on an individual basis especially for observers who complete relatively few blocks of trials or whose lag curves are flattened due to poor resolution or other performance factors). In Experiment 2, there were 3 rates of discontinuous spatial period change. Four patients with inferior parietal lobe damage were unable to perform better than simulated guesses even at the slowest 2.5-Hz rate of change, and this may be due to very poor temporal precision. It is also consistent with other difficulties such as poor comprehension of the task. However, a recovery of performance when the rate of change is slowed down is a signature of poor temporal precision. Note that concerns about factors such as fully grasping the task instructions or basic spatial frequency perception deficits cannot explain cases where individuals become able to perform the task when the rate of change is slowed down. Four patients with parietal lobe damage showed this pattern. For 2 individuals, the speed threshold at which they became able to perform the task occurred between 3.33 and 2.5 Hz, and for 2 individuals, this threshold was located between 5.00 and 3.33 Hz. All healthy older adults and neurological controls performed better than guessing at the fastest 5.00-Hz rate.
Since the stimulus disappeared after a semi-random time interval, it was on average, visible on the screen for a duration of half of the time period of spatial period reselection. For example, in the slowest 2.5-Hz condition, the spatial period was reselected every 400 ms, meaning that the final spatial period value was visible for between 12 ms (one frame) and 400 ms with a mean of ∼200 ms. Therefore, if an observer is able to perform above chance at this rate, then they are able to process the visual information present in ∼200 ms of the stimulus display to make a reasonable response. If an observer can perform better than chance at 5 Hz, they are able to process the visual information present in ∼100 ms of the stimulus display.
The interaction between observer group and stimulus speed in Experiment 2 was not significant, despite the trend for observers to perform better at slower speeds (difference between fastest and slowest speeds for patient group = −0.037 dpc and for healthy controls = −0.030 dpc). This null interaction is not necessarily unexpected within a temporal resolution account. Temporal resolution limits for any task will produce a non-linear function of performance with changes in stimulus speed. If the stimulus change is faster than can be captured within the temporal integration window, then performance will not differ significantly from guessing. As the rate of stimulus change is slowed down such that the temporal period exceeds the threshold of the temporal integration window, then performance will rise above chance. Therefore, we would not necessarily expect a linear increase in performance with reductions in speed for any single observer. Neither would we necessarily expect the temporal integration window to be of the same duration for different observers. Hence, the effect of stimulus speed will be the sum of the noisy step-like functions of different observers with the threshold occurring between different speeds for different observers, and potentially outside of the range of tested speeds for some observers. Specifically, we suggest that for RP1, RP2, RP7, and LP2, this threshold lies within the range of speeds tested in Experiment 2 since they become able to perform the task above chance as the speed is slowed within this range. This is the signature of poor temporal resolution since even the fastest of these speeds was still slow: Changes only occurred every 200 ms (5 Hz).
Consider now the group of 7 patients with right parietal lobe damage. Figure 11 shows that, as a group, these individuals also had damage in the occipital and temporal cortices, as well as some damage in white matter. It is possible then that functioning in these other areas also supported performance in this task. However, the 2 patients with bilateral parietal damage do not possess such widespread lesions, and yet they were still unable to perform the task better than guessing models in either experiment. The 2 with left parietal damage also had lesions that were centered on parietal areas. Although able to perform the task above chance in some conditions, LP1 could only perform the discontinuous version of the task, and LP2 was unable to perform better than chance for the fastest rate of discontinuous change, becoming able to perform above chance once the rate of change was slowed to 3.33 Hz. RP7, whose damage was centered on right parietal cortex, became able to perform the discontinuous task when it was slowed from 5.00 to 3.33 Hz. Hence, although it is possible that other areas including white matter, temporal, and occipital cortex contributed to performance on this task, the data point toward a necessary role of parietal cortex in temporal updating of vision.
Speed of perceptual processing is the rate at which visual information is accrued over time (e.g., Kent et al. 2012). For a single static visual stimulus presented for a given brief interval, individuals with faster perceptual processing will accrue more visual information than those with slower processing. This will result in those individuals with fast processes performing better on judgments about the stimulus, especially at shorter presentations. The situation is more complex for dynamic stimuli as used here. For these stimuli, if we assume no differences between individuals in temporal resolution (i.e., all observers have good resolution), all observers will make their reports based on information accrued from the last “x” ms of the stimulus where “x” represents the width of the temporal integration window. Note that in Experiment 2, “x” is likely to be ∼100 ms (see paragraph above). This will result in observers with faster processing accruing more visual information in this 100-ms period than slower processors, and therefore, faster processors will outperform slower processors. Critically, with this assumption of equal resolution, faster processors will outperform slower processors at all 3 speeds, since increasing the average duration of the final spatial period of the stimulus beyond the magnitude of the temporal integration window cannot aid performance (note that this is the definition of the temporal integration window). However, if we allow slower processors to also possess wider temporal integration windows, then we would predict a change in performance between the speeds used here. If visual information is accrued more slowly, this may cause individuals to integrate visual input over a longer time window and this will selectively impair performance at faster speeds. Therefore, it is possible that poor temporal resolution may be a result of slowed perceptual processing, but perceptual processing speed cannot explain dependence on speed here without the additional assumption of poor temporal resolution.
Another factor that will have contributed to the difficulty of the task overall is the temporal resolution of lower-level visual processes, that is, the flicker fusion limit. We assessed the extent to which this was occurring in these data by looking for biases toward reporting lower spatial periods (high spatial frequencies) than the average value. Although we find evidence for this bias for many observers in many of the 3 speed conditions, it is not related to cortical damage nor to whether or not individuals are able to perform this task above predicted chance levels. It is therefore likely that the flicker fusion limit detracted from performance generally across all conditions by lowering performance on trials where the stimulus happened to offset just after a spatial period change. However, it did not generate the selective effect in the parietal group. Neither was there a relationship between patients' performance on this task and their performance in a sustained auditory attention task, suggesting that a problem-sustaining attention is not at the root of the difficulty in performing the task here. Note that although it remains a possibility that some failures of sustained attention may have contributed to poor performance seen for some observers in Experiment 1, our analyses for Experiment 2 are immune to concerns about sustained attention. The reason for this is that the strict test of the temporal resolution account (or equivalently, temporal integration or averaging), is an inability to perform the discontinuous task in Experiment 2 at faster speeds and an ability to perform the task at slower speeds. Problems with sustained attention cannot account for differences in performance on trials that differ only in the rate of stimulus change.
Performance here does not seem to be strongly related to spatial neglect since there was no evidence of lateralized effects except for the slowest condition of Experiment 2 nor any straightforward correspondence with asymmetry scores on the Apple cancelation task. For example, although 5 parietal patients did not show high levels of neglect in their asymmetry scores (RP3, RP6, RP7, LP1, and LP2), some of these patients were able to perform above chance in Experiment 1 and some were not. This is consistent with the findings of Shapiro et al. (2002) in a related task who showed that neglect symptoms were not necessary for abnormal AB effects.
The right parietal lobe has previously been suggested to support a “when” pathway for perception (Battelli et al. 2007, 2008), which is involved in a range of temporal judgments such as judgments of duration and ordering of events. The inferior parietal cortex has also been proposed to underlie judgments of magnitude in space, time, and number (Walsh 2003). The data we present here are broadly consistent with these previous arguments. Specifically, we find a likely involvement of both left and right parietal cortex in the temporal resolution of attention, which is a specific example of time-related visual processes.
The fact that we did not find consistent hemifield differences for the patients with parietal lobe damage is perhaps not surprising when we consider 3 things. First, the stimuli were only presented a few degrees from fixation which may mean that the task is not sensitive enough to detect performance impairments in more peripheral vision. Second, the stimuli were high contrast and caused constant fluctuations in luminance for a given point on the retina, and it seems reasonable to assume that this would encourage exogenous attention capture, which may have alleviated traditional spatial neglect associated with parietal lobe damage. Third, while we encouraged observers to fixate the central fixation point, we did not enforce or measure this. Hence, it seems reasonable to assume that on some trials, observers may have moved their eyes toward the stimuli, thus reducing any differences in performance across the 2 hemifields.
We find that patients with damage that included (and in some cases was confined to) parietal cortex show a reduction in temporal resolution of attention. In healthy adults, it seems likely that these areas are recruited during tasks that require attention to time and particularly in tasks that involve judgments requiring fine temporal detail. This is consistent with the evidence that parietal areas are involved in duration estimation (e.g., Rao et al. 2001; Alexander et al. 2005) and attention to temporally cued moments in time (Coull and Nobre 1998).
Our results can help explain findings from TOJ tasks involving the parietal lobe, especially the right parietal lobe (e.g., Rorden et al. 1997; Baylis et al. 2002; Davis et al. 2009; Woo et al. 2009). Poor temporal resolution of attention will make it harder to judge the precise timings of events, since the timings of events would only be represented with a poor level of precision. This ambiguity may increase susceptibility to processes that drive biases to judge certain stimuli as occurring earlier. Our results are consistent with the findings of Snyder and Chatterjee (2004). They presented data from a patient with right temporal-parietal damage with extinction and a bias to perceive ipsilaterally stimuli as appearing earlier. However, this patient also showed better accuracy at a TOJ task with 2 vertically arranged stimuli when both stimuli were presented on the ipsilateral than the contralateral side. Since this would not be predicted from a simple bias to attend to ipsilateral stimuli earlier, they interpreted this as evidence for extended refractory periods in the patient on the contralateral side. However, poor temporal resolution would mimic this pattern of performance. Interestingly, temporal resolution was quite poor even for pairs of ipsilateral stimuli only rising much above chance at ∼200 ms of separation. These temporal separations are consistent with the failures of temporal resolution in the results reported here at speeds of ∼2.5-Hz stimulus change. These findings are consistent too with the findings of Roberts et al. (2012) who measured “just noticeable differences” (JNDs) for patients performing TOJ tasks with bilateral presentation. Compared with patients with no spatial deficit who were able to perform the task with temporal separations of ∼40 ms, those with right temporoparietal and cerebellum damage required ∼250 ms in order to distinguish reliably between events.
That parietal areas may be involved in temporal segmentation is also consistent with the role shown for parietal areas in the AB phenomenon. Damage to this area can result in an extended AB (Husain et al. 1997) and repetitive TMS to right posterior parietal cortex reduces the AB (Cooper et al. 2004). One possibility Cooper and colleagues discuss is that the rTMS facilitated temporal segmentation of stimuli. Fine temporal resolution of attentional processes would be required for this process; hence, damage to areas that support fine temporal resolution would be likely to induce abnormal AB phenomena.
The rate at which events can be precisely individuated and precise judgments of their timing are necessary for high-level motion perception. For this reason, our results are consistent with those that implicate parietal areas in speed thresholds for perceiving apparent motion (Battelli et al. 2001) and for producing illusory apparent motion in the continuous wagon wheel illusion (VanRullen et al. 2006, 2008). Battelli et al. (2003) showed that patients with right parietal damage had a deficit in flicker asynchrony detection. They asked patients to detect a target flickering out of phase with distracters. Although flicker detection itself was unimpaired, patients required abnormally slow alternation rates to detect the object flickering out of phase with the others. They interpreted as an inability to tell apart onsets from offsets at fast rates. Determining whether a transient is an offset or onset may be a specific example of object individuation, that is, determining whether a stimulus is a light or dark object on what background. This suggests that the right parietal lobe is important for making judgments about the relative states (in this case, luminances) of objects at different times. Our results are consistent with these findings as our patients also showed poor temporal resolution of the speed with which stimuli could be individuated by attention.
Parietal cortex has previously been associated with sustained attention, but the methods used have often confounded the role of temporal resolution of attention. For example, Coull et al. (1996) presented rapid streams of digits where participants had to detect short (2–3 items long) sequences in the stream and found parietal activation, suggesting a role in sustained attention to rapid stimuli. Rueckart and Grafman (1998) suggested a role for a fronto-parietal network in the detection of targets embedded in a serial visual presentation. Similarly, Johannsen et al. (1997) reported activation in right middle frontal gyrus and right inferior parietal lobule in healthy older adults attending to the temporal frequency of vibrotactile and visual stimuli oscillating at 110 and 7 Hz, respectively. These sets of results are consistent with a role for parietal cortex in attention to fine timescales.
Our findings add further weight to the growing evidence for parietal involvement in temporally sensitive tasks. Specifically, we present a new task that measures involvement in supporting the temporal resolution of attention. Just as spatial aspects of vision are dissociable into many different perceptual processes, temporal aspects are also multifaceted. Temporal aspects of perception include many sub-processes including duration estimation, order judgments, simultaneity perception, some types of motion, and in this case, attention to fine temporal timescales. We propose a role for parietal cortex in the temporal resolution of attention, analogous to spatial acuity, or the ability to see fine detail. Clearly, this perceptual process contributes heavily to our perception of the changing world around us.
Statement of Ethics
Experiments were undertaken with the permission and written consent of participants, in accordance with the Declaration of Helsinki and with the ethical procedures of University of Birmingham School of Psychology and Nottingham Trent University Division of Psychology.
Funding
This work was supported by grants from the National Institute of Health Research (Oxford Cognitive Health CRF) and the Stroke Association (UK).
Notes
Conflict of Interest: None declared.
References
- Alexander I, Cowey A, Walsh V. 2005. The right parietal cortex and time perception: back to Critchley and the Zeitraffer phenomenon. Cogn Neuropsychol. 22:306–315. [DOI] [PubMed] [Google Scholar]
- Battelli L, Cavanagh P, Intriligator J, Tramo MJ, Hénaff MA, Michèl F, Barton JJ. 2001. Unilateral right parietal damage leads to bilateral deficit for high level motion. Neuron. 32:985–995. [DOI] [PubMed] [Google Scholar]
- Battelli L, Cavanagh P, Martini P, Barton JJ. 2003. Bilateral deficits of transient visual attention in right parietal patients. Brain. 126:2164–2174. [DOI] [PubMed] [Google Scholar]
- Battelli L, Pascual-Leone A, Cavanagh P. 2007. The ‘when’ pathway of the right parietal lobe. Trends Cogn Sci. 11(5):204–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Battelli L, Walsh V, Pascual-Leone A, Cavanagh P. 2008. The ‘when’ parietal pathway explored by lesion studies. Curr Opin Neurobiol. 18:120–126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baylis GC, Simon SL, Baylis LL, Rorden C. 2002. Visual extinction with double simultaneous stimulation: what is simultaneous? Neuropsychologia. 40:1027–1034. [DOI] [PubMed] [Google Scholar]
- Bickerton W-L, Samson D, Humphreys GW. 2011. Separating forms of neglect using the Apples Test: Validation and functional prediction in chronic and acute stroke. Neuropsychology. 25, 567–580. [DOI] [PubMed] [Google Scholar]
- Chechlacz M, Rotshtein P, Hansen PC, Deb S, Riddoch MJ, Humphreys GW. 2013. The central role of temporo-parietal junction and the superior longitudinal fasciculus in supporting multi-item competition: evidence from lesion-symptom mapping of extinction. Cortex. 49(2):487–506. [DOI] [PubMed] [Google Scholar]
- Cooper ACG, Humphreys GW, Hulleman, Praamstr P, Georgeson M. 2004. Transcranial magnetic stimulation to right parietal cortex modifies the attentional blink. Experim Brain Res. 155(1):24–29. [DOI] [PubMed] [Google Scholar]
- Coull JT, Frith CD, Frackowiak RSJ, Grasby PM. 1996. A fronto-parietal network for rapid visual information processing: a PET study of sustained attention and working memory. Neuropsychologia. 34:1085–1095. [DOI] [PubMed] [Google Scholar]
- Coull JT, Nobre AC. 1998. Where and when to pay attention: the neural systems for directing attention to spatial locations and to time intervals as revealed by Both PET and fMRI. J Neurosci. 18:7426–7435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danckert J, Ferber S, Pun C, Broderick C, Striemer C, Rock S, Stewart D. 2007. Neglected time: impaired temporal perception of multisecond intervals in unilateral neglect. J Cogn Neurosci. 19:1706–1720. [DOI] [PubMed] [Google Scholar]
- Davis B, Christie J, Rorden C. 2009. Temporal order judgments activate temporal parietal junction. J Neurosci. 29(10):3182–3188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Driver J, Mattingley JB. 1998. Parietal neglect and visual awareness. Nat Neurosci. 1:17–22. [DOI] [PubMed] [Google Scholar]
- Holcombe AO. 2009. Seeing slow and seeing fast: two limits on perception. Trends Cogn Sci. 13(5):216–221. [DOI] [PubMed] [Google Scholar]
- Holcombe AO, Cavanagh P. 2001. Early binding of feature pairs for visual perception. Nat Neurosci. 4(2):127–128. [DOI] [PubMed] [Google Scholar]
- Howard CJ, Holcombe AO. 2008. Tracking the changing features of multiple objects: Progressively poorer perceptual precision and progressively greater perceptual lag. Vision Res. 48:1164–1180. [DOI] [PubMed] [Google Scholar]
- Humphreys GW, Bickerton W-L, Riddoch MJ, Samson D. 2012. BCoS: cognitive profiling after brain injury. London: Psychology Press. [Google Scholar]
- Husain M, Shapiro K, Martin J, Kennard C. 1997. Abnormal temporal dynamics of visual attention in spatial neglect patients. Nature. 385:154–156. [DOI] [PubMed] [Google Scholar]
- Johannsen P, Jakobsen J, Bruhn P, Hansen SB, Gee A, Stødkilde-Jørgensen H, Gjedde A. 1997. Cortical sites of sustained and divided attention in normal elderly humans. Neuroimage. 6:145–155. [DOI] [PubMed] [Google Scholar]
- Karnath HO, Himmelbach M, Küker W. 2003. The cortical substrate of visual extinction. Neuroreport. 14(3):437–442. [DOI] [PubMed] [Google Scholar]
- Kent C, Howard CJ, Gilchrist ID. 2012. Distractors slow information accumulation in simple feature search. J Vision. 12(1):13. [DOI] [PubMed] [Google Scholar]
- Olivers CNL, Humphreys GW. 2004. Spatiotemporal segregation in visual search: evidence from parietal lesions. J Experim Psychol Hum Percept Perform. 30:667–688. [DOI] [PubMed] [Google Scholar]
- Rao SM, Mayer AR, Harrington DL. 2001. The evolution of brain activation during temporal processing. Nat Neurosci. 4:317–323. [DOI] [PubMed] [Google Scholar]
- Raymond JE, Shapiro KL, Arnell KM. 1992. Temporary suppression of visual processing in an RSVP task: an attentional blink? J Experim Psychol Huma Percept Perform. 18(3):849–860. [DOI] [PubMed] [Google Scholar]
- Roberts KL, Lau JKL, Chechlacz M, Humphreys GW. 2012. Spatial and temporal attention deficits following brain injury: a neuroanatomical decomposition of the temporal order judgement task. Cogn Neuropsychol. 29(4):300–324. [DOI] [PubMed] [Google Scholar]
- Rorden C, Mattingley JB, Karnath H-O, Driver J. 1997. Visual extinction and prior entry: impaired perception of temporal order with intact motion perception after unilateral parietal damage. Neuropsychologia. 35(4):421–433. [DOI] [PubMed] [Google Scholar]
- Rueckart L, Grafman J. 1998. Sustained attention deficits in patients with lesions of posterior cortex. Neuropsychologia. 36:653–660. [DOI] [PubMed] [Google Scholar]
- Seghier ML, Ramlackhansingh A, Crinion J, Leff AP, Price CJ. 2008. Lesion identification using unified segmentation-normalisation models and fuzzy clustering. Neuroimage. 41(4):1253–1266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shapiro K, Hillstrom AP, Husain M. 2002. Control of visuotemporal attention by inferior parietal and superior temporal cortex. Curr Biol. 12:1320–1325. [DOI] [PubMed] [Google Scholar]
- Snyder JJ, Chatterjee A. 2004. Spatial-temporal anisometries following right parietal damage. Neuropsychologia. 42:1703–1708. [DOI] [PubMed] [Google Scholar]
- Vallar G, Perani D. 1986. The anatomy of unilateral neglect after right hemisphere stroke lesions. A clinical/CT-scan correlation study in man. Neuropsychologia. 24:609–622. [DOI] [PubMed] [Google Scholar]
- VanRullen R, Pascual-Leone A, Battelli L. 2008. The continuous wagon wheel illusion and the when pathway of the right parietal lobe: a repetitive transcranial magnetic stimulation study. PLoS ONE. 3(8):e2911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanRullen R, Reddy L, Koch C. 2006. The continuous wagon wheel illusion is associated with changes in electroencephalogram power at approximately 13 Hz. J Neurosci. 26:502–507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verstraten FAJ, Cavanagh P, Labianca AT. 2000. Limits of attentive tracking reveal temporal properties of attention. Vision Res. 40:3651–3664. [DOI] [PubMed] [Google Scholar]
- Walsh V. 2003. A theory of magnitude: common cortical metrics of time, space, and quantity. Trends Cogn Sci. 7:438–488. [DOI] [PubMed] [Google Scholar]
- Woo SH, Kim KH, Lee KM. 2009. The role of the right posterior parietal cortex in temporal order judgment. Brain Cogn. 69:337–343. [DOI] [PubMed] [Google Scholar]