Super-Resolved Traction Force Microscopy (STFM)

Abstract

Measuring small forces is a major challenge in cell biology. Here we improve the spatial resolution and accuracy of force reconstruction of the well-established technique of traction force microscopy (TFM) using STED microscopy. The increased spatial resolution of STED-TFM (STFM) allows a greater than 5-fold higher sampling of the forces generated by the cell than conventional TFM, accessing the nano instead of the micron scale. This improvement is highlighted by computer simulations and an activating RBL cell model system.

It is becoming increasingly clear that mechanical force plays a crucial role in many biological processes, including adhesion, migration, and cell signaling.¹⁻³ Forces act across many length scales, from tissue to the single cell and ultimately down to the molecular level, as is true for cells of the immune system where individual cell–cell and receptor–ligand interactions are crucial.⁴⁻⁶ In order to understand the role of forces within a given biological system, it is important that we have the appropriate tools and techniques that allow quantification of mechanical forces at the relevant length scales. A commonly used technique to measure forces on the micron-scale in cell biological systems is traction force microscopy (TFM) (or simply traction microscopy).

Beginning with the pioneering work of Harris et al., flexible substrates, such as polyacrylamide (PAA) gels, have been used to investigate cellular tractions and forces for over 30 years.⁷ In a typical TFM experiment, a thin (20–30 μm) elastic gel is formed on a glass coverslip onto which proteins facilitating cell adherence can be attached (Figure 1a).⁸ Within the gel, fluorescent beads serve as fiducial markers and imaging of the bead positions over time during the application of cellular tractions allows the displacement of the gel to be quantified. By combining the measured displacement field with knowledge of the mechanical properties of the gel, the tractions responsible for the displacements can be calculated. The optimal theoretical treatment of the traction solution has been the subject of much research.⁹⁻¹¹ Dembo et al. provided a rigorous mathematical framework for the use of elastic materials to measure traction forces,⁹ which was further developed with the introduction of Fourier transform traction cytometry (FTTC) whose treatment of the force reconstruction in Fourier space allowed for greatly decreased computation time.¹⁰ Owing to the inverse nature of the problem, work has shown the need for regularization to control the influence of experimental noise in the measured displacements on the traction solution.¹¹ In addition to FTTC, other methods of traction reconstruction have been developed whereby experimental knowledge of the traction locations is used to aid the traction recovery, for example, traction reconstruction with point forces (TRPF)¹¹ and more recently, model based traction force microscopy (MBTFM).¹² These methods are only applicable in cases where the traction location can be inferred from fluorescent data, as in the case of fluorescently labeled focal adhesions. In the more general case, where no knowledge of the traction location is assumed, FTTC is more suitable and is the methodology used in this work.

Figure 1.

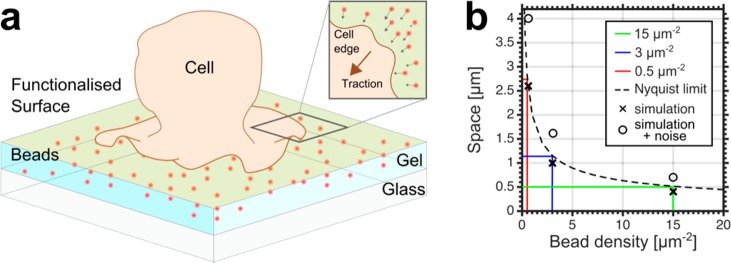
Theoretical characterization of STFM. (a) Schematic representation of a typical TFM setup. An elastic polyacrylamide gel filled with fluorescent marker beads is covalently attached to a glass coverslip and functionalized with proteins that facilitate cell adherence. Traction forces applied by the cell to the top surface of the gel results in lateral displacements of the gel which can be quantified by imaging the displacement of the beads within the gel. (b) Theoretical relationship between the sampling density and the Nyquist limit (dashed line), with three different bead densities highlighted (red, blue, green as labeled), exemplifying that a bead density of 15 μm^–2 would allow the recovery of tractions 500 nm in size. Crosses show the smallest recoverable tractions from simulations performed at the three bead densities shown in Figure 2. Open circles show the smallest recoverable traction from simulations where noise is added and regularization used.

The greatest shortcoming of classical TFM is its limited sensitivity due to the finite density at which the displacement field can be sampled within the gel.¹³ The density of fiducial markers must be high enough to reflect the complexity of the traction field that is applied by the cell. If the bead density is too low, areas of the gel will move without being reported by any bead movement and the traction information is lost. This can be thought of as a sampling problem, where to meet the Nyquist criteria the spatial sampling frequency of the displacement field must be twice that of any details that may be resolved in the displacement field (Figure 1b).¹³ Experimentally, this limit is imposed by the finite size point spread function (PSF) that results from each marker bead. At high densities, the PSF of each individual bead begin to overlap, meaning nearby beads can no longer be resolved individually, obscuring details of their relative displacement. A first attempt to overcome this limitation involved the use of two different colors of marker beads which proved that the recovery of micron sized tractions are feasible.¹³ However, due to its reliance on the spectral separation of the beads, this technique is ultimately limited by the spectral range of the microscope. Because the beads must be imaged at the top surface of the gel, this requires a microscope technique that can operate away from the coverslip, meaning TIRF or near-field microscopy are not suitable. Cellular traction fields are typically on the nanoscale range rather than on the micron-scale. Consequently, there remains a need to improve the spatial resolution of TFM. While improved analysis tools might introduce some advancements in resolving force fields (e.g., using TRPF involving knowledge from additional fluorescence data of the sample, as outlined above), these approaches are experimentally still limited by the finite size of the PSF as given by diffraction for conventional optical microscopes (i.e., they only push the TFM read-out to its ultimate limit as given by diffraction). To overcome these challenges, here we improved the spatial resolution and accuracy of force reconstruction of TFM by using super-resolution optical STED microscopy.¹⁴

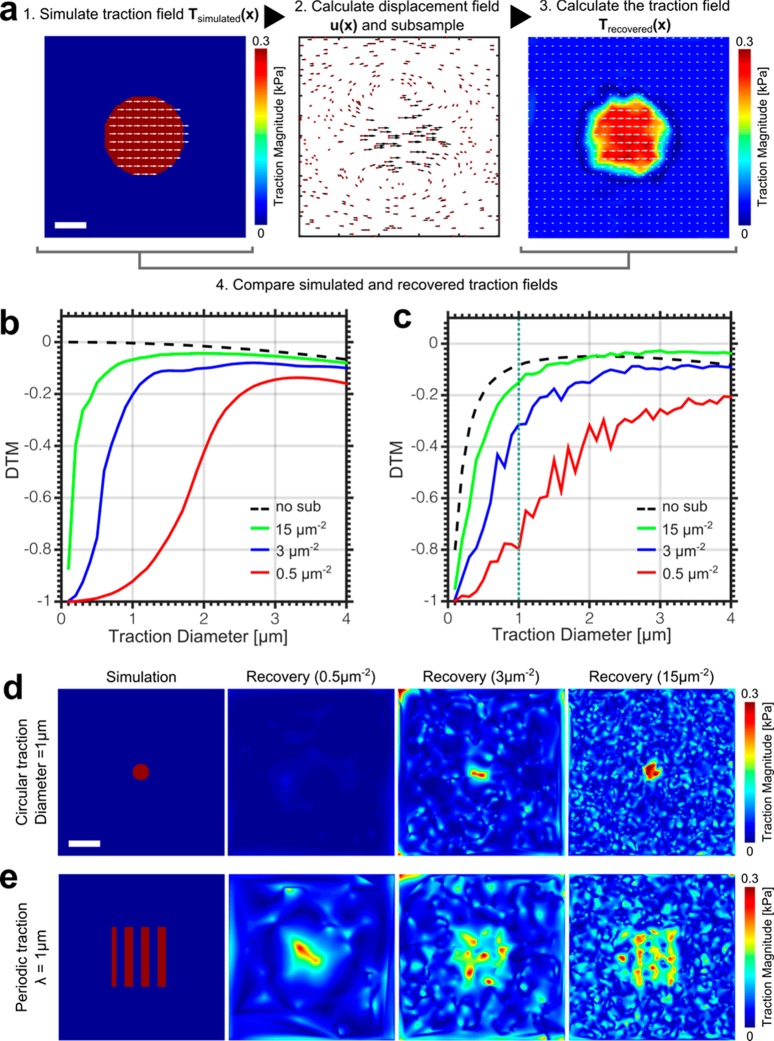
To examine the effects of the sampling density on traction force recovery, we first conducted computer simulations in which a gel of defined stiffness (3 kPa) was exposed to a uniform circular traction field (T) (0.3 kPa) of varying spatial sizes (0.1–4.0 μm). The resulting displacement field was then calculated using the mathematical framework provided by FTTC (Supporting Information, eq S3) (Figure 2a). To simulate the discrete nature of bead sampling, the displacement field was subsampled at random points, with sampling densities corresponding to those attainable by confocal or STED microscopy: 15 beads per μm² for high, theoretically achievable STED resolution (40 nm), 3 beads per μm² for STED resolution achievable in the current experiments (80 nm), and 0.5 beads per μm² for confocal. The subsampled displacement field was then transformed back into a traction field (Supporting Information, eq S5). The recovered and simulated traction field were then compared, and the difference quantified via a metric known as the deviation of traction magnitude (DTM), where a DTM of −1 represents a complete underestimation and 0 represents a perfect recovery of the traction.¹³

Figure 2.

Outline of the simulation process. (a) A uniform circular traction field T_simulated(x) is simulated and the corresponding displacement field u(x) calculated (heat map; high traction magnitude warm colors, low traction magnitudes cold colors, white arrows: traction direction). The displacement field is then subsampled at a confocal and STED density (red dots: bead positions, black arrows: bead displacements), the traction field recovered T_recovered(x) and the simulation and recovery compared by the deviation of traction magnitude (DTM). Scale bar 1 μm. (b) DTM for varying traction diameters at three sampling densities, confocal (red), medium STED (blue), and maximum STED (green). A DTM of 0 represents a perfect traction recovery, whereas a DTM of −1 represents a complete underestimation. Dotted line: DTM for no subsampling. Line deviates from zero at large tractions due to artifacts introduced by the finite size of the simulated gel area. (c) Same as b with the addition of artificial noise and using the regularized solution, showing very similar dependency as b except for the no subsampling case (dotted line), where regularization masks the recovered tractions at length scales matching that of the artificial noise. (d) Simulation and traction recovery for a 1 μm diameter circular traction zone (0.3 kPa). Scale bar 2 μm. (e) Simulation and traction recovery for a 1 μm wavelength periodic traction pattern (0–0.3 kPa). Scale bar 2 μm.

By calculating the DTM for circular traction zones of varying diameters at the three different sampling densities, it is evident that increasing the sampling density allows for the successful recovery of spatially more confined tractions (Figure 2b). By adding artificial Gaussian distributed noise to the displacement field at a level consistent with the experiment (10% of the maximum) and using the regularized solution, it is clear that the relationship between sampling density and traction recovery is maintained (Supporting Information, eq S7) (Figure 2c). For each sampling density, defining a DTM of −0.2 as the minimum required to recover a traction, it is possible to plot the corresponding traction size on Figure 1b, which displayed good agreement between simulation and the Nyquist limit. To further demonstrate this improvement, the simulation and recovery is shown for a circular traction (0.3 kPa) of 1 μm diameter at the three different sampling densities (Figure 2d). We also show the simulation and corresponding recovery of a more complex periodic traction field (0–0.3 kPa) with a wavelength of 1 μm (Figure 2e). In all cases, we find that the higher the sampling density, the more detail is recovered in the traction field.

In addition to the sampling density, another important factor in determining the accuracy of TFM is the method used to recover the displacement of the beads from the fluorescent images. The most common methods of extracting bead displacements are those based on single particle tracking (SPT), where each individual bead must be localized, and those methods based on statistical comparisons of fluorescent images, such as particle image velocimetry (PIV). To this end, the image is divided into a grid, and each grid element is spatially correlated between frames to assess the degree of movement. PIV does not require localization of each bead but is limited spatially by the size of the grid elements required to give accurate correlations. It can be shown that the increased resolution of STED allows for more accurate recovery of the displacement field and hence a more accurate force field in both SPT and PIV (Supporting Information, Figure S3 and Table S1). Note, the magnitude of PIV recovered high bead density based force fields can be close to the simulated values but increased spatial accuracy necessitates STED.

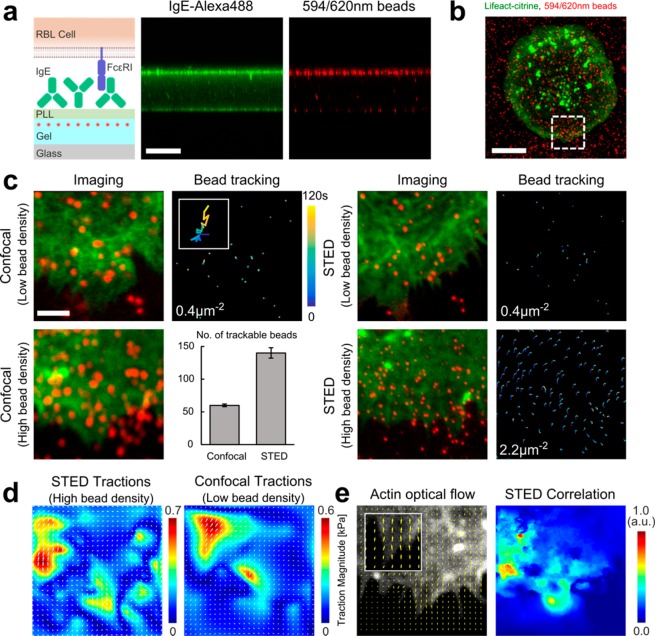
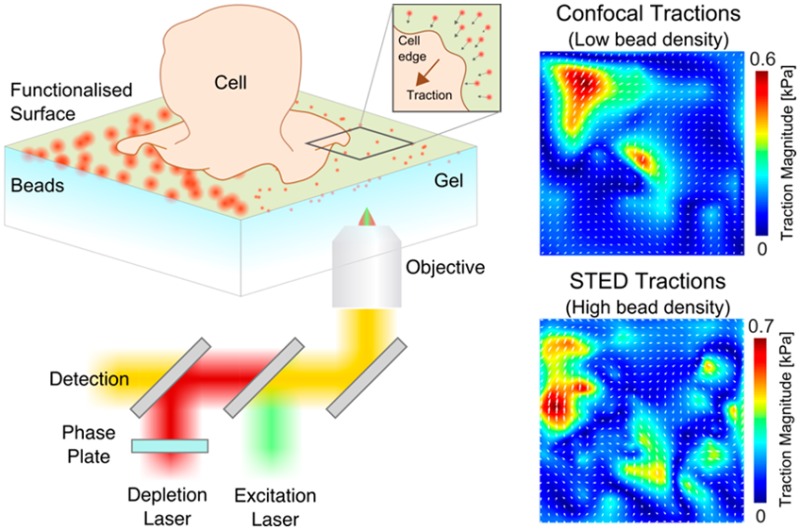
To observe the effect of increased sampling experimentally in the single cell environment, RBL cells, which express high levels of the Fcε receptor-1 (FcεRI), were allowed to interact with a 3 kPa gel loaded with 40 nm red-fluorescent beads and coated with the antibody, IgE (Figure 3a). The Fc portion of IgE binds with high affinity (equilibrium constant K_a = 10¹⁰ M^–1, off-rate k_off = 10^–5 s^–1) to the FcεRI present on the RBL cell surface, which results in cell spreading and activation.^15,16 By fluorescently labeling actin filaments via Lifeact-citrine, we were able to visualize the dynamically spreading cell edge as the cell-gel contact area increased (Figure 3b). On visual inspection (Movie S1), the beads within this area are seen to move elastically in a directed manner toward the direction of cell motion, indicating forces being applied by the cell to the compliant gel beneath via the FcεRI-IgE interaction. By using a water immersion objective, optical aberrations from imaging through the gel layer were low, allowing STED imaging with a spatial resolution of around 80 nm (Figure S1), and we have observed no visible sign of cell degradation (such as cell contraction) during the around 120 s long recordings.

Figure 3.

Experimental demonstration of STFM. (a) Gel functionalization. (Left) Scheme: The roughly 30 μm thick PAA gel layer (light blue) was loaded with 40 nm-large red fluorescent beads (red dots) and surface-coated with poly-l-lysine (light green) followed by attachment of IgE (green). (Middle, right) Confocal z–x profile images of the gel cross-section showing concentration of Alexa488 labeled IgE (green, middle) and red fluorescent beads (red, right) at the top surface of the gel. Scale bar 30 μm. (b) Representative confocal image of fluorescent F-actin (Lifeact-citrine) expressing RBL cell (green) interacting with IgE coated 3 kPa PAA gel loaded with the red fluorescent beads (red). Scale bar 10 μm. (c) Time-lapse imaging of the spreading cell edge results in the displacement of the beads within the gel, monitored for different conditions as labeled. (Left panels) Confocal images of fluorescent F-actin (green) and confocal or STED images of red fluorescent beads (red) at a certain time point together with the temporal displacement tracks of the beads (time color-coded as labeled), for low (0.4 μm^–2) and high (2.2 μm^–2) bead density. Scale bar 2 μm. For confocal at high bead density (lower left) no bead tracks could be resolved; instead a bar chart is shown, quantifying the ability to successfully locate and track beads in the high density confocal case compared to the high density STED case (total number of beads: 140 STED, 60 confocal). (d) Recovered traction field for the high density STED tracking of c (left) and extrapolated low density effective confocal tracking (right) with force color-coded in kPa. (e) Quantification of the F-actin flow from the high density STED recording of c by optical flow (left) and correlation (color coded with 1.0 showing maximum correlation) with the bead displacement (right).

Next, to demonstrate the influence of the bead sampling density, we introduce four different scenarios; low density confocal and STED (0.4 beads μm^–2) (Movies S2 and S3), and high density confocal and STED (2.2 beads μm^–2) (Figure 3c) (Movies S4 and S5). Here we define low density as the maximum trackable density by confocal, and high density as the maximum trackable density of our current STED experiments. Note, bead sampling values in the scenario of high density STED were a moderate and robust choice considering the experimental optical conditions and needs of the biological specimen. However, they were below the computationally predicted possible advances of STFM. Specifically, the bead densities are a function of the microscopes PSF size and could be improved in future work by optimizing the imaging conditions, e.g., minimizing optical aberrations (see discussion).

To assess the displacement of the beads we chose to use SPT as it allows the movements of each individual bead to be captured. PIV is generally best suited to tractions where collective bead movements are expected, for example focal adhesions. For RBL cells, forces may arise from localized receptor–ligand interactions and may be spatially complex. In the low density case, applying a custom written MATLAB SPT algorithm allowed the displacements of all beads within the field of view to be measured in both the confocal and STED image sequences (Supporting Information and Figure S2). In the high density case, confocal imaging resulted in a significant number of overlapping PSFs, preventing reliable bead tracking. However, on applying the STED beam, beads were resolved individually and the tracking was successful (Figure 3c). In all cases, bead tracks were interpolated onto a regular mesh and the corresponding traction field calculated using the appropriate degree of regularization (Figure S4). Obviously, in the high density case only the STED imaging yielded a traction field (Figure 3d). To directly compare the effect of sampling density on the ability to accurately recover the traction field of the same cell, beads in the high density STED case were randomly deleted until the bead density was equal to that attainable by confocal tracking (Figure 3d). It is clear that this reduces the information content present in the displacement field, and hence reduces the fine detail in the traction field.

Finally, to identify the origin of mechanical force generation in RBL cells, we combined fluorescent imaging and STFM. The technique of optical flow enables the spatial change in pixel intensity to be quantified over time and is commonly applied in computer vision to assess the spatial shift between image frames. Here, we apply this technique to extract the retrograde flow vector field of fluorescently labeled filamentous actin (Lifeact-citrine). This vector field was then correlated via a dot product with the displacement field of the beads in the gel, yielding a spatial correlation of actin and bead displacement (Figure 3e).¹⁷ The correlation highlights that areas of the cell showing the most dynamic actin coincide with the areas of greatest bead displacement, highlighting that it was indeed the flow of actin within the cell that was responsible for the observed tractions. As in the case of traction forces, the higher bead density leads to a higher information content in the displacement field and hence a more reliable correlation between the two vector fields.

In summary, the increase in accuracy of STFM is important when considering cellular forces on small length scales, as is the case for receptor-antagonist interactions in immune cells.¹⁸ Using STFM, we are now better able to make links between the forces generated by the cell, and those molecules which are responsible for force generation. This is particularly valuable when force measurements are coupled to fluorescent data, as is shown in Figure 3e.

We have focused on the experimental aspects of TFM. Moreover, recent work has suggested that theoretical aspects may be equally important in optimizing the accuracy of force reconstruction.¹⁹ For example, in the case of sparse focal adhesions, it has been demonstrated that the L1-norm is favorable to the L2-norm used to assess to degree of regularization,^20,21 owing to a greater retention of the high resolution detail in the force maps. We had no prior knowledge of the traction field induced by the RBL cells, therefore we choose L2-norm regularization as the more general case. However, further work should focus on optimizing both experimental and computational aspects of the technique to further increase the accuracy of STFM.

Notably, increasing the location accuracy of STFM is theoretically not limited since it scales with the applied STED power.¹⁴ This needs to be balanced with other optical factors such as maximal bead density within the gel, the ability to track the beads, and fluorescence light sensitivity of the biological specimen. Moreover, the nature of the (S)TFM setup requires all imaging to be done at the top surface of the gel, meaning imaging is subject to aberrations induced by the mismatch in refractive index of the gel and the immersion media. Improvements in aberration correction, for example using adaptive optics would reduce the effect of these aberrations and would result in an improved STED resolution, possibly along all three spatial dimensions,²² allowing even higher bead densities to be used and the accuracy of experiments to approach those shown possible by simulations. This also presents the opportunity of performing 3D-TFM in high resolution. In the same way that 2D-STED can increase the accuracy of the tangential force reconstruction, using 3D-STED would allow for a greater sampling of the forces perpendicular to the gel surface.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.6b00273.

• Materials and methods, a description of the bead tracking software, additional simulations comparing bead tracking algorithms and force recovery, and a description of the fluorescence-force correlation analysis (PDF)

• Representative large field-of-view confocal time-lapse movie of an RBL cell expressing Lifeact-citrine (green) spreading on an IgE coated 3 kPa PAA gel loaded with 40 nm red fluorescent beads (red) at a low density (0.4 μm^–2). The beads are seen to move beneath the cell, indicating that forces are being transferred by the cell to the gel. Scale bar 10 μm. Frame rate 0.2 s^–1. Total acquisition time 200 s (AVI).

• Representative close-up confocal time-lapse movie of a RBL cell expressing Lifeact-citrine (green) spreading on an IgE coated 3 kPa PAA gel loaded with 40 nm red fluorescent beads (red) at a low density (0.4 μm^–2). Again, the beads are seen to move beneath the cell, indicating that forces are being transferred by the cell to the gel. Scale bar 2 μm. Frame rate 0.2 s^–1. Total acquisition time 120 s (AVI).

• Equivalent time-lapse movie to that shown in Supplementary Movie S2, this time imaged with STED microscopy in the case of the beads. Scale bar 2 μm. Frame rate 0.05 s^–1. Total acquisition time 120 s (AVI).

• Representative close-up confocal time-lapse movie of a RBL cell expressing Lifeact-citrine (green) spreading on an IgE coated 3 kPa PAA gel loaded with 40 nm red fluorescent beads (red) at a high bead density (2.2μm^–2). A signicant number of beads are seen to overlap, preventing their reliable tracking. Scale bar 2 μm. Frame rate 0.06 s^–1. Total acquisition time 48 s (AVI).

• Equivalent time-lapse movie to that shown in Supplementary Movie S4, this time imaged with STED microscopy in the case of the beads. The improved spatial resolution made possible using STED now means that all beads in the field of view are trackable. Scale bar 2 μm. Frame rate 0.05 s^–1. Total acquisition time 120 s (AVI).

The authors declare no competing financial interest.