Impact of Pre-adapted HIV Transmission

Abstract

Human Leukocyte Antigen class I (HLA) restricted CD8⁺ T lymphocyte (CTL) responses are critical to HIV-1 control. Although HIV can evade these responses, the longer-term impact of viral escape mutants remains unclear, since these variants can also reduce intrinsic viral fitness. To address this question, we here develop a metric to determine the degree of HIV adaptation to an HLA profile. We demonstrate that transmission of viruses pre-adapted to the HLA molecules expressed in the recipient is associated with impaired immunogenicity, elevated viral load and accelerated CD4 decline. Furthermore, the extent of pre-adaptation among circulating viruses explains much of the variation in outcomes attributed to expression of certain HLA alleles. Thus, viral pre-adaptation exploits “holes” in the immune response. Accounting for these holes may be critical for vaccine strategies seeking to elicit functional responses from viral variants, and to HIV cure strategies requiring broad CTL responses to achieve successful eradication of HIV reservoirs.

Introduction

Immune control of HIV is epidemiologically linked to expression of certain HLA alleles, which mediate control through the presentation of viral peptides to CTL^1,2. The resulting suppression of viral replication induces strong evolutionary pressure that drives selection of CTL escape mutations. These mutations may fully or partially abrogate viral peptide-HLA binding, disrupt peptide processing, or alter peptide-HLA interactions with the T-cell receptor (TCR)³. Within-host selection of escape mutations is thought to increase viral fitness by facilitating immune evasion, which should result in increased plasma viral load (VL) and accelerated CD4 decline. However, at least two factors work against the virus in this context. First, some escape mutations impair the ability of the virus to replicate^4–10. Second, the CTL response itself adapts to the changing virus through the emergence of new TCR variants that either recognize the escaped epitope or shift focus to new epitopes^11–15. Indeed, while case studies report increased VL following escape from highly immunodominant epitopes^11,16–19, the overall impact of within-host escape is unknown.

Once selected, escape mutations are frequently transmitted^7–9 and may be accumulating in some populations^20–22. Transmission of these escape variants to HLA-mismatched hosts has been linked to improved clinical outcomes due to reduced intrinsic viral fitness^7,8,10, but the clinical consequences of transmission of viruses pre-adapted to the recipient’s HLA profile is unknown. Although mutations that abrogate antigen processing and/or HLA binding may confer universal escape consequences in hosts expressing the relevant HLA allele^19,23, TCR escape mutations can retain immunogenicity in subsequent hosts^1,17,24,25 and the loss of some epitopes in the founder virus may simply result in targeting other epitopes¹².

Resolving the role of transmitted escape in HIV progression is central to both vaccine design and epidemiology. A leading hypothesis as to why T-cell vaccines based on whole-protein immunogens have failed to reduce post-infection VL is that they have not adequately accounted for the role of immune escape and viral diversity²⁶. Alternative vaccine strategies have thus emerged. One aims to focus the immune response on relatively conserved HIV regions (“conserved element vaccines”)^27–30, while another aims to stimulate variant-specific responses by incorporating multiple immunogens that reflect circulating viral diversity (“polyvalent vaccines”)³¹. A key assumption of these strategies—the polyvalent approach in particular—is that effective immune responses can be elicited against epitope variants, including those representing HLA-specific escape mutations. This assumption, however, conflicts with concerns that the stable transmission and accumulation of CTL escape mutations at the population level will gradually compromise host immunity and result in increased HIV virulence as the pandemic progresses²⁰. Such concerns assume escape variants are universally non-immunogenic and carry low fitness costs. Furthermore, efforts to quantify the extent to which VL is “heritable” (i.e. determined by the viral sequence) make critical simplifying assumptions, such as assuming viral and host genetics act independently on VL and that escaped epitopes are non-immunogenic^32,33. Thus, fundamental working theories on HIV pathogenesis and vaccine design currently operate on strong—and often opposing—assumptions regarding the impact of transmitted immune escape.

Estimating viral adaptation to HLA

The complexity of escape has prevented in-depth study of the clinical consequences of transmitted and within-host escape. Although escape mutations are remarkably predictable based on HLA subtype, there is a strong stochastic component to both CTL targeting³⁴ and escape selection³. We therefore sought to reduce the complexity of escape to a single metric, which we call “adaptation”. Adaptation to a particular HLA allele h is rooted in a probabilistic model which compares two scenarios: what would an HIV sequence “look like” were it to evolve indefinitely in a host whose immune system either (1) solely targeted epitopes restricted by h, or (2) did not target any HLA-restricted epitopes? We then write the adaptation of a particular sequence s to h as ${\text{Adapt}}_h(s)=g\left(\frac{\mathrm{Pr}(s|h)}{\mathrm{Pr}(s|\varnothing )}\right)$., where $\mathrm{Pr}\left(s|h\right)$ captures scenario (1), $\mathrm{Pr}\left(s|\varnothing \right)$ captures scenario (2), and $g(\cdot )$ scales the ratio to be symmetric on the interval −1 to 1.

We define four types of scores: (1) “autologous adaptation” compares the autologous viral sequence to an individual’s own alleles; (2) “heterologous adaptation” compares a non-autologous virus to an individual’s alleles; (3) “circulating adaptation” is the average heterologous adaptation over all viruses within a cohort with respect to an individual’s alleles; and (4) “transmitted adaptation” is the autologous adaptation of an individual’s founder virus. These scores can be defined with respect to a single HLA allele (“allele-specific adaptation”), or to an individual’s HLA repertoire (the average over the individual’s allele-specific scores). Further, the adaptation-similarity of two alleles (or individuals) is the Pearson correlation coefficient of their respective scores over a panel of heterologous viral sequences. Adaptation can be defined with respect to each viral protein, but it is unclear whether adaptation scores are comparable among proteins (Supplementary Note).

Estimation of adaptation requires estimation of the conditional probability distribution $\mathrm{Pr}(s|h)$. To this end, we extend the phylogenetic logistic regression framework³⁵ to allow estimation of the probability of observing any amino acid, at any site, conditional on any set of HLA alleles (see methods; an implementation is available at https://phylod.research.microsoft.com). We trained two separate models for HIV adaptation, based on the availability of linked HLA and sequence data for chronically infected, untreated individuals. The HIV-1 subtype B (“HIVB”) model was trained on the International HIV adaptation collaborative (IHAC) cohort³⁶, which consists of 1,888 individuals from North America and Australia with sequences from all HIV proteins except gp120. The HIV-1 subtype C (“HIVC”) model was trained on a set of cohorts from southern Africa⁹, which consists of 2,037 individuals with Gag, Pol and Nef sequences. See Supplementary Figure S1 for a synopsis of the datasets used in this manuscript.

As expected, autologous adaptation was substantially higher than heterologous adaptation (Fig. 1a & Supplementary Fig. 2a), and mean autologous adaptation increased during the first two years of infection and beyond (Fig. 1b and Supplementary Fig. 2b,c). These results indicate that adaptation is measuring subject-specific viral variation. Nevertheless, there is substantial overlap between autologous and heterologous adaptation, indicating some individuals will by chance be infected by a virus that is pre-adapted to their HLA alleles.

Figure 1. Adaptation of viral sequence to HLA-I alleles.

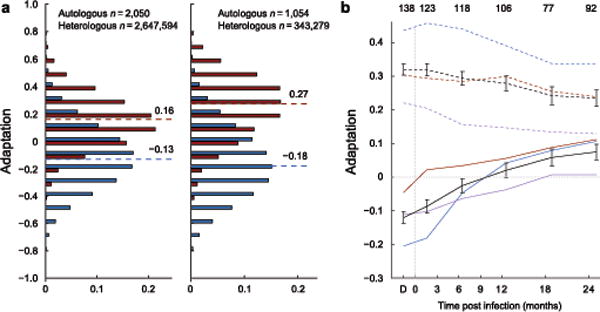
(a) The distribution of adaptation scores computed for all viruses against all HLA profiles in Southern Africa (left) and British Columbia (right). Adaptation of autologous virus to host HLA (autologous adaptation) is shown in red; adaptation of a virus sequence to a different host’s HLA (heterologous adaptation) is shown in blue. Median scores for each distribution are indicated. (b) Autologous adaptation is shown for linked transmission pairs from Zambia. Colors indicate adaptation with respect to recipients’ (solid) or donors’ (dashed) HLA-A (red), -B (blue) and -C (purple) alleles or entire repertoire (black). Error bars, 95% confidence intervals. Number of samples in each time point indicated at top. Adaptation of linked donor sequence (time point ‘D’) is set to −50 d for display.

Within-host adaptation accelerates disease progression

If within-host adaptation in the context of a robust CTL response drives pathogenesis, then our measure of autologous adaptation should correlate with clinical markers of disease progression. Consistent with prior reports³⁷, we observed significantly lower levels of autologous adaptation in HIVB-infected controllers than in non-controllers (Fig. 2a). This pattern held across all HLA loci and proteins as well as among individuals expressing protective alleles (Supplementary Fig. 3a, b). Similarly, among 2,917 chronically infected non-controllers, autologous adaptation was the most important predictor of both VL and CD4 counts (Supplementary Table 1). This result was consistent across HIV subtypes and statistical models, and persisted when host and viral covariates were added to the models.

Figure 2. Autologous adaptation predicts faster disease progression.

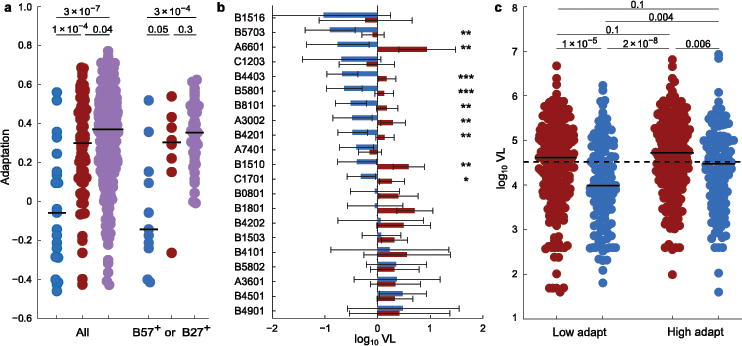
(a) Adaptation in controllers (VL < 50 copies/ml; left blue, n = 21) and non-controllers (middle red, n = 80, Ragon cohort; right purple, n = 383, British Columbia cohort with no missing sequence data). Right, individuals who express B*57 or B*27 (n = 11, 8, and 41, for the three cohorts, respectively). P-values, two-tailed Mann-Whitney U test. (b) Estimated HLA-specific effects on VL in the Southern Africa cohort. Estimated VL (error bars, 95% CI) relative to cohort average for individuals expressing the allele with no (blue) or with complete (red) allele-specific adaptation. Significant adaptation effects are denoted for P < 0.001 (***), P < 0.01 (**), and P < 0.05 (*), estimated from likelihood ratio test. (c) VL for each of n = 691 HIVC-infected subjects from Durban are shown, stratified by Gag-specific adaptation and OLP response breadth (above vs. below population averages). Red, below (blue, above) average OLP responses; solid bars, stratum median; dashed line, cohort median. P-values, two-tailed Mann-Whitney U-test (primary and interaction effects remain significant at P = 0.02 when treated as continuous variables in a mixed model).

Critically, allele-specific autologous adaptation completely abrogated the protection attributable to each HLA allele (Fig. 2b, Supplementary Figs. 3c and 4), including alleles for which multiple escape mutations are known to carry substantial in vitro fitness costs^5,6. This result indicates the benefit the virus receives from evading the CTL responses dominates any reduction in intrinsic fitness, and suggests that the majority of escape mutations either have negligible impact on intrinsic fitness or that any such reduction is typically restored by compensatory mutations. Indeed, there was no clear association between autologous Gag adaptation and in vitro viral gag-protease replicative capacity (vRC) over all alleles (Supplementary Fig. 5a,b), nor among protective alleles (Supplementary Fig. 5c). This is consistent with disappearance of any association between protective alleles and vRC over the course of chronic infection^38,39.

The conserved element vaccine strategy targets epitopes believed to be relatively resistant to escape, under the assumption that robust CTL responses in the absence of escape are critical for control^27–30. To test this hypothesis using our metric for adaptation, we measured Gag-specific CTL responses among 691 HIVC-infected individuals from Durban using 18-mer overlapping peptides (OLPs) based on the subtype C consensus. We then stratified these individuals by both Gag-specific autologous adaptation and response breadth. This stratification demonstrates that the reduction in VL associated with a broad Gag-specific CTL response is observed primarily among individuals whose virus has not adapted to that response (Fig. 2c). Indeed, high levels of adaptation nearly eliminate the benefit of targeting Gag. In the absence of a CTL response, adaptation is not associated with changes in VL (Fig. 2c). This suggests that escape primarily influences VL by reducing effective immune responses, not by reducing intrinsic viral fitness. Critically, the lowest VL was observed among individuals who broadly targeted Gag, yet harbored low levels of autologous adaptation. These individuals appear to be mounting a robust CTL response, associated with a substantial reduction of VL, but with limited selection of escape variants. These observations support protective responses as those that broadly target “difficult-to-escape” epitopes^2,28, which in turn directly supports vaccine strategies that aim to elicit such responses^27–29. We did not observe an interaction between adaptation and the number of OLP-eliciting responses in Pol or Nef; however, Pol adaptation was positively correlated with VL (Supplementary Fig. 6). In contrast with Gag, CTL responses against these proteins have not consistently been linked with viral control⁴⁰.

The ability to define a single metric for adaptation allows us to address the question, “are high levels of autologous adaptation predictive of future disease progression, or simply the result of high virus replication?” To this end, we applied an autoregression model to longitudinal VL and sequence samples from the Zambian transmission pair cohort⁹ to test the ability of autologous adaptation to predict future changes in VL. VL at each time point was modeled as a function of the prior two VL measurements and adaptation at the previous VL measurement, with additional clinical covariates. On average, one standard deviation difference in autologous adaptation predicted an additional 0.13 log increase in VL ( $P<0.001$), whereas VL did not significantly predict subsequent changes in adaptation (Supplementary Fig. 7). Thus, these longitudinal data are consistent with adaptation (on average) driving subsequent changes in VL, not vice versa.

Transmitted adaptation predicts accelerated disease progression

The majority of amino acid variants present in the donor consensus sequence are transmitted to the recipient⁹. Although some of these variants have been linked to lower VL in HLA-mismatched recipients due to presumed reduced intrinsic viral fitness^7,8, if the variants are adapted with respect to the recipient’s HLA alleles, they have the potential to undermine the host immune response⁴¹. We therefore measured the extent to which the donor HIV Gag, Pol, and Nef sequences were by chance pre-adapted to the recipients’ HLA alleles in 129 HIVC-infected, epidemiologically linked Zambian transmission pairs⁹. The extent of transmitted adaptation was associated with an increased rate of CD4 decline (Fig. 3a) and was correlated with recipient VL (Fig. 3b). Overall, transmitted adaptation explained more variation in recipient VL (both early [<12 months post infection] and late) than HLA alleles, vRC, donor VL, age or (for late VL) recipient sex (Supplementary Table 2).

Figure 3. Transmitted adaptation establishes clinical prognosis and largely explains which HLA alleles are protective.

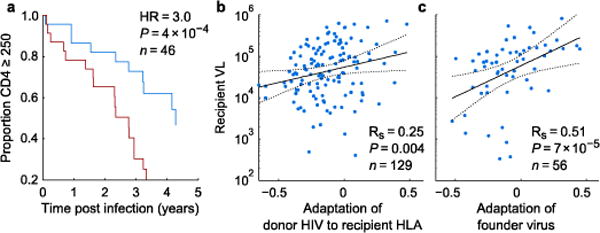
(a, b) Pre-adaptation of donor virus to the recipient HLA alleles among Zambian Transmission Pairs predicts CD4 decline (a) and early setpoint VL (b). (a) For visualization, individuals are stratified into above (red) and below (blue) mean transmitted adaptation; here, adaptation is scaled to define a unit change as the difference of transmitted adaptation means between the two strata. Hazard ratio (HR) and two-tailed P-value from Cox proportional hazard, computed from continuous value. Data for all individuals with longitudinal CD4 counts are shown. (c) Adaptation of founder virus from infected participants of the Step vaccine trial. Data from all individuals in both vaccine and placebo arms with at least two VL measurements prior to initiation of therapy). R_s, P-value, Spearman rank correlation. Best fit and 95% CI lines from unadjusted model. See Supplementary Table 2 for mixed model with additional covariates.

To confirm the role of transmitted adaptation as a predictor of disease progression in newly infected individuals, we evaluated a separate cohort of individuals who were infected during the Step Study HIV vaccine trial⁴². Consistent with our findings in the Zambian cohort, VL was correlated with adaptation of inferred founder viruses to host HLA alleles among seroconverting participants (Fig. 3c and Supplementary Table 2). The larger correlation coefficient in the Step data compared to the Zambian data may be explained by differences among males and females, as the correlation for Zambian males was comparable to that observed in the (all male) Step data (Supplementary Table 2), though this sex difference was not statistically significant within the Zambian cohort.

To determine whether transmitted adaptation affects VL and CD4 counts many years into infection, we used circulating adaptation (over all virus sequences within a cohort) as an estimate for expected transmitted adaptation for each individual in our chronic infection cohorts. Overall, the level of circulating adaptation to an individual’s HLA alleles was an independent predictor of both VL and CD4 counts (Supplementary Table 3), suggesting that transmitted adaptation has long term effects on natural control.

Estimates of host and virus genetic impact on VL are confounded by adaptation

The impact of autologous and transmitted adaptation on markers of disease progression imply a strong interaction between viral and host genetics with respect to these markers. Such interactions suggest that population-level estimates of epidemiologic parameters will depend on the circulating virus and the predominant host alleles in a particular population.

Indeed, allele-specific circulating adaptation explained much of the variation in HLA-specific VL and CD4 effects (Fig. 4a and Supplementary Fig. 8a–c), suggesting that protective alleles are those for which the circulating virus is not well adapted. Moreover, among four alleles with evidence of differential impact on VL among three Southern African cities, the relative differences of city-specific VL effects was largely explained by relative differences in city-specific circulating adaptation (Fig. 4b and Supplementary Fig. 8d). Thus, circulating adaptation may explain many of the differences in allele-specific associations with markers of disease progression among diverse cohorts, and supports the hypothesis that accumulation of escape mutations in a population will undermine natural control^20,22.

Figure 4. Adaptation impacts HLA-VL associations and heritability estimates.

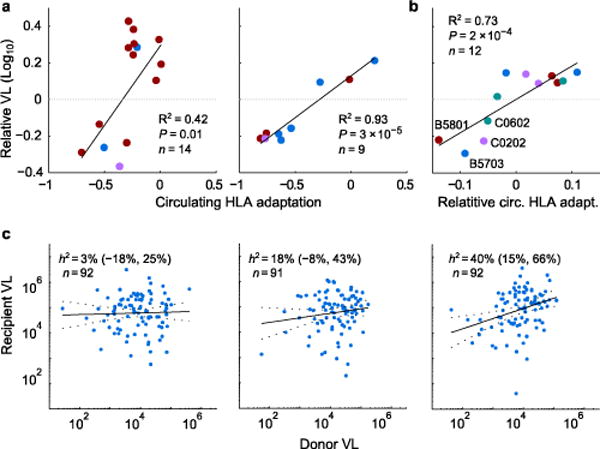
(a) Circulating allele-specific adaptation is compared against allele-specific effects on VL, as estimated from a mixed model fitted to the Southern Africa (left; n = 2,298) or British Columbia (right; n = 1,048) cohorts. Alleles selected in an independent stepwise regression analysis are shown. P-values, pseudo-R², from mixed model with random offsets for each locus. Blue, HLA-A; red, HLA-B, purple, HLA-C. (b) Four alleles showed city-specific VL effects (Durban, Lusaka, Gaborone). Their relative VL and circulating adaptation (mean centered for each allele) is shown. P-value, pseudo-R², from mixed model with random offset for each city. See Supplementary Fig. 8. (c) Heritability (h²) estimates (95% CI) over all 275 Zambian linked transmission pairs with available VL and HLA types, stratified into tertiles by HLA-B adaptation-similarity (from left to right: low, medium, high). Donor and recipient VL adjusted for sex, age, and sample year independently for each stratum.

The role of viral genetics in determining VL can be quantified with population-level estimates of VL heritability³². Published estimates vary from 6% to 59%, with a recent meta-analysis of transmission-pair cohorts estimating broad-sense heritability at 33% (95% CI: 20–46%)³². However, the results presented here predict that the relationship between donor and recipient VL will be substantially higher among pairs with “similar” HLA alleles, as autologous adaptation in these donors (resulting in higher donor VL) will result in increased transmitted adaptation to their recipients (resulting in higher recipient VL).

Indeed, over the set of all 275 HLA-typed Zambian transmission pairs^43,44, heritability was estimated at 18% (95% CI:4–31%). However, when we grouped couples based on HLA-B adaptation similarity (see methods), heritability ranged from 2% (lower tertile) to 41% (upper tertile; $P=0.009$, Fig. 4c and Supplementary Table 4). Thus, heritability estimates vary widely as a function of how similar the recipient’s alleles are to the donor’s, suggesting that discordant heritability estimates in the literature may in part be due to differing levels of HLA heterogeneity in the cohorts.

Dysfunctional responses to pre-adapted transmitted epitopes

The prior results suggest that infection by pre-adapted viruse compromises the initial and long-term efficacy of CTL responses. To confirm this hypothesis, we tested epitope-specific responses to autologous peptides from 11 individuals recently infected with a single HIVB founder virus (median 31d post infection). For each individual, we defined the founder virus sequence and identified all HLA-matched, optimally defined epitopes it encoded⁴⁵. Each founder virus epitope was then classified as non-adapted if it matched the most prevalent circulating HIVB sequence that did not harbor an escape polymorphism; all other epitopes were classified as adapted. Autologous adapted founder virus epitopes were less likely than non-adapted epitopes to elicit an interferon-γ response (Fig. 5a), and the response rate correlated inversely with the proportion of adapted epitopes in the founder virus (Fig. 5b), suggesting that transmitted adapted epitopes are less immunogenic.

Figure 5. CTL responses against pre-adapted transmitted epitopes are dysfunctional.

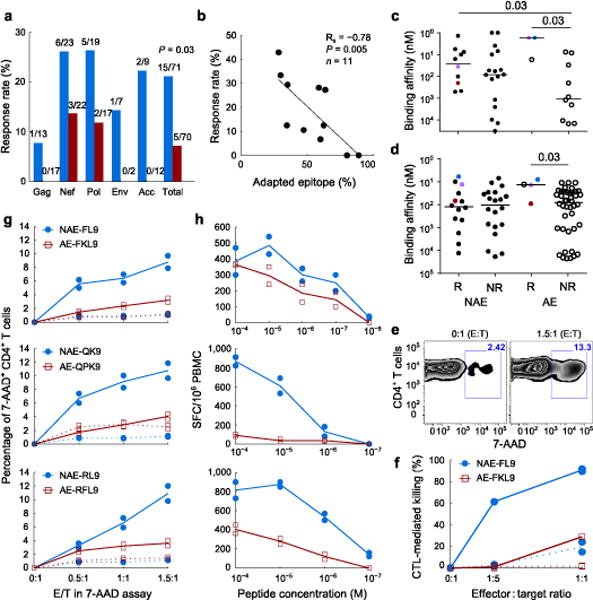
(a, b) Interferon-γ response rates for autologous founder epitopes. (a) Response frequencies for non-adapted (blue) and adapted (red) epitopes. Number of epitopes tested and number of responses for each protein are indicated. P-value, Fisher’s exact test over total. (b) Response rate versus proportion of autologous epitopes that are adapted, on a per-subject level. (c, d) Experimental (c) and predicted (d) HLA-peptide binding affinity for adapted (AE) and non-adapted (NAE) epitopes that elicited response (R) or not (NR). Colored points represent matched immunogenic NAE/AE pairs. Solid bars, median; P-values, Mann-Whitney test. (e–h) Epitope-specific CD8⁺ T-cells (effectors) assessed for cytotoxicity of activated CD4⁺ T-cells (targets). All results from duplicate experiments shown. Lines, mean values; dotted lines, negative controls. (e) Representative flow cytometry plot for 7-AAD⁺ targets in the absence (0:1 E:T) or presence (1.5:1 E:T) of effectors. (f) Relative killing of targets from HLA-matched (solid) and mismatched (dotted) donors, infected with MJ4 virus mutated to contain the NAE or AE FL9 variant and incubated with NAE- or AE-specific effectors. (g, h) Cytoxicity (g) and antigen sensitivity (h) curves are indicated for the three matched NAE/AE epitopes pairs.

In many cases, reduced responses to adapted founder virus epitopes are likely attributable to escape-induced reductions in HLA binding affinity³⁶. However, the HLA-peptide binding affinity of numerous non-immunogenic adapted epitopes was similar to that of immunogenic non-adapted epitopes (Fig. 5c,d), suggesting that some adapted mutations confer escape by exploiting holes in the TCR repertoire. Moreover, for all three epitopes that elicited responses in both adapted and non-adapted variants, the adapted epitopes elicited substantially weaker cytotoxic responses than the non-adapted variant (Fig. 5e–g). These differences could not be explained by HLA-I binding nor T-cell polyfunctionality (Fig. 5c,d and Supplementary Fig. 9a–c), but were consistent with reduced antigen sensitivity and magnitude of interferon-γ response (Fig. 5h and Supplementary Fig. 9d). Together, these in vivo and in vitro data indicate that, when present in the founder virus, adapted epitopes are generally poorly immunogenic and, when recognized, elicit suboptimal primary CTL responses.

Vaccination with adapted epitopes

If acquisition of a pre-adapted founder virus at transmission undermines initial host CTL responses, then the quality of vaccine-induced immune responses will likely depend on the extent to which the vaccine insert is pre-adapted to a recipient’s HLA alleles. The Step Study vaccine trial provides an opportunity to investigate this hypothesis⁴⁶. Among trial participants, there was evidence of a weak inverse correlation between the extent to which the vaccine insert was adapted to an individual’s HLA alleles and pre-infection pooled interferon-γ ELISpot response magnitudes, as measured by two independent laboratories (Supplementary Fig. 10). These observations suggest that different vaccine insert sequences will result in qualitatively different—yet predictable—immune responses in the same individual. Whether simultaneous immunization by polyvalent vaccines will focus the immune response on functional, non-adapted epitopes, or whether such a strategy risks eliciting suboptimal, non-protective responses to adapted epitopes, remains an important open question.

Discussion

Although the importance of the CTL response, and the presence of immune-mediated escape, in the context of HIV infection has been generally recognized for 20 years, the link between transmitted and within-host adaptation and disease progression has been obscured by the complexity of in vivo targeting and escape. By directly measuring adaptation through a probabilistic model, we provide a general framework for estimating host-specific viral adaptation. The results demonstrate the dominant role HLA escape variants play in mediating disease progression, thereby validating some common assumptions while refuting others.

The role of autologous adaptation as a primary correlate of (and predecessor to) key markers of disease progression argues that an effective immune response is one that controls viral replication in the absence of escape (Fig. 2c). This stands in contrast to suggestions that an effective immune response drives selection of escape mutations that substantially reduce intrinsic fitness. Although the cost to intrinsic fitness of potential escape variants is likely critical to delaying time to escape⁴⁷, and thus will serve as a useful correlate of protection in identifying potential vaccine candidates^2,27–29, escape mutations are selected in vivo precisely because they increase overall fitness. In theory, in vivo fitness may not be fully restored by escape, but high levels of adaptation were strongly linked to high VL and loss of allele-specific control, indicating that compensatory mutations typically offset any reduced intrinsic fitness within a clinically relevant time frame. Reducing escape may also be achievable by increasing the breadth of the immune response⁴⁷, though such strategies must take care to account for transmitted adaptation.

Indeed, the impact of transmitted adaptation on host immunity and disease progression is critical. From an epidemiologic perspective, the interaction of host and viral genetic effects undermines efforts to predict individual and population outcomes on the basis of host or viral genetics alone. For example, estimates of VL heritability depends on the degree of similarity between donor and recipient HLA alleles, while allele-specific circulating adaptation explains much of the variation in natural control attributed to individual HLA alleles. Moreover, circulating adaptation defines why some alleles are only protective in certain regions^20,22,48 and predicts clinical outcomes for individuals, suggesting an individual’s prognosis will depend in part on the region in which infection is acquired. These results further provide explanations for epidemiologic observations that may influence transmitted adaptation, including reduced VL associated with rare alleles⁴⁹, and elevated VL associated with multiple-virus infection⁵⁰ or infection by a partner with a shared B allele⁴³. By undermining HLA-mediated control, accumulation of escape variants in different populations will thus lead (all else being equal) to increasing average viral loads as the pandemic progresses, though other factors may mitigate this process²². Measuring transmitted and within-host adaptation will thus be critical for clinical and observational trials in which reduction in VL or rate of CD4 decline is a primary or secondary endpoint.

From an immunologic perspective, the inability of primary immune responses to effectively target adapted epitopes casts doubt on prophylactic and therapeutic vaccine strategies that seek to elicit responses to such variants and argues instead for conserved element approaches that target a restricted set of epitopes with limited circulating variation. Furthermore, the observation that some adapted epitopes may competently bind their cognate HLA and elicit detectable, yet dysfunctional, responses, suggests the virus is exploiting biases in the circulating naïve TCR pool^51,52. Such dysfunctional responses argue for in depth screening for virus-inhibiting responses throughout the vaccine development cycle and raise the disturbing possibility that dysfunctional responses are causally worse than the complete absence of a response⁵³.

By combining the largest, most feature-rich datasets available with a novel statistical method for summarizing the extent of cellular immune adaptation, we have demonstrated the ability of HIV to exploit universal “holes” in the adaptive immune response. These holes explain much of the HLA- and region-specific heterogeneity in clinical outcomes and suggest that vaccine-induced “sieving”⁵⁴ may not simply result from insufficient vaccine coverage, but is in part inherent in the limitations of the naïve immune system. Accounting for these holes will be imperative to ongoing efforts to design strategies that leverage the CTL response to prevent infection^27–31 or clear the latent reservoir⁵⁵.

Online Methods

Datasets

The data used in this study were pooled from multiple, previously published cohorts. Enrollment criteria and available data varied among cohorts. As such, the presented analyses were conducted on different subsets of cohorts. See Supplementary Figure S1 for a synopsis of cohorts and how they are used in this work. For each analysis, we use the most general name possible to describe the datasets used. In this section, we describe each of the cohorts.

For each cohort, we used the same alignments used in previous publications, as obtained from the authors. These alignments were all previously aligned to the HXB2 reference sequence, and were further hand edited to match the alignments used to train the Subtype B and C models. Such hand editing was performed with blinded IDs to ensure the editing did not systematically effect the quality of alignments relative to outcome variables of interest. All individuals (except some in the Ragon non-controller cohort) were therapy naïve. Finally, while the model is described below, we note from the outset that the HIVB model was trained on the IHAC dataset, while the HIVC model was trained on the Southern Africa dataset. Model training was based solely on HLA and sequence information.

Southern Africa Cohort

The Southern Africa cohort consisted of a collection of six chronic-infection cohorts, as previously described⁹, and included gag, pol, and nef sequences paired with high resolution HLA typing data from 2,037 individuals, chronically infected with HIVC. In addition to training the HIVC model on this dataset, we used clinical and functional data from subsets of this cohort, as available. Overall, sequence availability for this cohort was as follows: for Gag-p17/p24 (n = 1,897), Gag-p15 (n = 1,135), Pol-Pr (n = 1,315), Pol-RT (n = 1,364), Pol-Int (n = 698) and Nef (n = 1,336). High-resolution HLA types were missing or ambiguous for at least one allele in 239 of 2,066 (11.5%) of non-Zambian individuals. For estimating HLA allele effect sizes with respect to VL and CD4, we used additional individuals from each of these cohorts (n = 2,298, VL; n = 1,983, CD4). For computing circulating adaptation, only individuals with gag, pol, and nef sequences were used. For VL and CD4 analyses, all individuals with any sequence data were included. Although missing data biases adaptation scores toward zero, the pattern of missing data largely followed cohort divisions, so this bias was largely captured with our cohort covariates. Repeating the analyses only on individuals without missing data resulted in qualitatively similar results. Ethics approval was obtained from the University of Zambia Research Ethics Committee and the Emory University Institutional Review Board (Zambia cohort); the University of KwaZulu-Natal Biomedical Research Ethics Committee and the Massachusetts General Hospital Review Board (Durban cohort); the University of the Free State Ethics Committee (Kimberley and Bloemfontein cohorts); the Office of Human Research Administration, Harvard School of Public Health and the Health Research Development Committee, Botswana Ministry of Health (Gaborone cohort); and the Oxford Research Ethics Committee (Durban, Kimberly, and Thames Valley cohorts). Study subjects from all cohorts gave written informed consent for their participation.

A total of 1,246 individuals from Durban, South Africa, were included in the South African cohort. These individuals were drawn from four maternal cohorts and two mixed-sex HIV clinics. Participant sex was not available for one of the outpatient clinics, so was imputed at 50% based on summary clinic data. The absolute VL and CD4 counts varied significantly among the Durban cohorts (P < 0.001, Kruskal-Wallis test). Thus, in all analyses cohort-specific random effects treated Durban as six distinct cohorts. In all of these cohorts, individuals were enrolled upon first presentation to the clinic and are believed to have been unexposed to therapy. Each of these 6 cohorts enrolled over a 1–3 year time frame. Subject age was unavailable for all of the maternal cohorts, but was assumed to be <40. In vitro viral replicative capacity (vRC) was measured using NL4-3 recombinant viruses encoding gag-protease sequences from 403 of these individuals, as previously described⁵⁶. In vitro HIV-specific CTL responses were determined for 691 subjects from Durban (372 with vRC), as previously described⁵⁷, by means of an IFN-γ ELISpot assay using a set of 410 overlapping 18mer peptides (OLPs) spanning the whole HIV-1 subtype C proteome (2001 consensus sequence). For each individual, the identity of responding OLP, as well as the total number of responding OLP for each protein (“Protein responses”), were used as random effects features in a mixed model (see below).

The Bloemfontein, South Africa, cohort⁵⁸ consisted of a subset of 261 individuals from a cohort enrolling individuals upon first visit to government ARV clinics who self-reported as therapy naive. Gag, Pol and Nef sequences and VL and CD4 counts were available for these individuals.

The Kimberley, South Africa, cohort⁵⁹ consisted of 31 individuals from a maternal cohort. Gag sequences, VL and CD4 counts were available for these women. As in Durban, samples were taken upon first enrollment and the individuals are believed to have been therapy naïve.

The Gaborone, Botswana cohort⁶⁰ consisted of 514 individuals from a maternal cohort, 379 of whom had available sequence data (gag, pol, nef). All individuals are believed to have been therapy naïve at the time of enrollment.

The Thames Valley cohort⁵⁹ derived from individuals presenting at clinics in the Thames Valley area of the United Kingdom (n = 102), other Southern African descent (Botswana, Malawi, South Africa and Zimbabwe) and believed to have been infected in these areas. Gag, Pol and Nef sequences were available for (n = 65) of these individuals.

The Southern Africa combined cohort also included 360 chronically infected partners from the Zambian Transmission Pairs cohort, described below.

International HIV adaptation collaborative (IHAC)

The IHAC cohort consisted of three chronic-infection cohorts, as previously described³⁶, and included sequence data from the entire proteome, excluding gp120, paired with medium-resolution HLA types, for 1,888 individuals, chronically infected with HIVB, from the HOMER cohort of British Columbia, Canada (n = 1,103)^61,62; the Western Australian HIV Cohort Study, (n = 247)^63–65; and the US AIDS Clinical Trials Group (ACTG) protocols 5,142^13,66 and 5,128 (n = 538)⁶⁷. Final HLA/HIV sequence dataset sizes were as follows: Gag (n = 1,548), Pol (n = 1,799) [Pr-RT, n = 1,786, INT, n = 1,566], Nef (n = 1,685), Vif (n = 1,325), Vpr (n = 1,310), Vpu (n = 1,243), gp41 (n = 1,425), Tat (n = 1,734), Rev (n = 1,731). Ethical approval was obtained from the University of British Columbia-Providence Health Care Research Ethics Board (British Columbia cohort), Royal Perth Hospital Ethics Committee (WAHCS), and the NIH’s National Institute of Allergy and Infectious Diseases (NIAID) Clinical Science Review Committee (SRC) (ACTG 5142/5128). Study subjects from all cohorts gave written informed consent for their participation and/or specimens were anonymized by IRB-approved procedures.

Only the British Columbia cohort was used for analysis against VL and CD4 counts. As for the Southern Africa cohort, only individuals with full-proteome data were used for computing circulating adaptation; all individuals with any sequence data were used for VL and CD4 analyses. Notably, the British Columbia cohort consisted largely of individuals with advanced disease, as it primarily enrolled individuals who were initiating therapy in the late-1990s. This enrollment criterion largely limits the association of HLA alleles to CD4 counts, and may explain the relative increase in autologous adaptation relative to the Southern Africa cohort (Fig. 1a). The observation also suggests that HIVB model will estimate larger effect sizes, as more individuals in the training data will have adapted autologous virus. Because both VL assays and therapy guidelines changed during the course of sample collection for this cohort, we treated each sampling year as a separate cohort, specified by indicator variables (reported as the “cohort” random effect in Supplementary Tables S1 and S3). In vitro viral replicative capacity was measured using NL4-3 recombinant viruses encoding gag-protease sequences from 749 of the British Columbia subjects, as previously described³⁸. Time since infection was estimated for a subset (n = 325) of the British Columbia subjects, using either physician-reported estimates of the midpoint between last HIV seronegative and first HIV seropositive samples, as previously described⁶⁸.

Ragon Elite Controller and Non-Controller cohorts (update)

The controller cohort consisted of 21 individuals previously identified as elite controllers (VL < 50 copies/ml for at least one year), for whom full-length genomic HIV sequences and high resolution HLA typing were available^37,69. Autologous adaptation for this group of individuals was compared to the British Columbia cohort, as well as an independent cohort of 80 individuals chronically infected with HIVB who were not used to train the models^70–72. Some of these Ragon non-controllers were on therapy at the time of sequencing. Individuals were included in the analyses only if complete protein sequences were available for all HIV proteins (excluding Env), the sequences were Subtype B, and high resolution HLA types were available.

Zambian Transmission Pairs

The Zambian Transmission Pairs cohort enrolled heterosexual discordant couples in long term stable relationships^73–75. Couples counseling and condoms were provided for all couples. During the timeframe of the samples used in this study, the seropositive partner was offered therapy according to national guidelines (CD4 < 200 cells/mm³). All seropositive partners were chronically infected and believed to be therapy naïve upon enrollment. The individuals used here were all from clinics in Lusaka and were enrolled in one of two protocols, in which the seronegative partner was tested either monthly or quarterly, and samples were collected from both partners upon a positive result.

For 129 individuals, complete gag, pol and nef sequences were available from the donor, longitudinal VL samples (≥ 2) were available for the epidemiologically linked recipients, and VL was available from the donor from the time of sequencing. Samples from both donor and recipient were available a median of 46 days post estimated date of infection (IQR, 43–61; max, 349). The recipient samples were collected on or near the same day as the matched donor samples, allowing us to consider the matched donor HIV sequences as representative of the viral population that was likely present upon exposure⁹. Epidemiological linkage was defined by phylogenetic analyses of gp41 sequences from both partners⁷⁶. Setpoint VL was defined to be the geometric mean VL from 30 d to 365 d post infection. For all studies, only VL measurements taken prior to initiation of therapy were included. Among these subjects, five initiated therapy within two years of infection. At least three VL measurements and complete sequence samples were available for 77 recipients; these individuals were included in the autoregression model. For 46 of the 129 couples, longitudinal CD4 counts were available for the recipients. In vitro gag viral replicative capacity was measured using MJ4 chimera viruses for 113 linked recipients, using the first available blood sample for each individual, as previously described¹⁰. Sequence samples from 360 seropositive individuals, 203 of whom had not yet transmitted to their partners at the time of sample collection, were included in the Southern Africa cohort.

As a separate study, HLA types were previously determined for 275 couples for whom linked transmission was confirmed, longitudinal VL samples were available for the recipients, and donor viral load was available within 12 months of transmission^43,44,77. We used these individuals for the heritability analysis (Fig. 4c).

All subject protocols were approved by both the University of Zambia Research Ethics Committee and the Emory University Institutional Review Board. Before enrollment, individuals received counseling and signed a written informed consent form agreeing to participate.

Step Study dataset

The Step Study (HVTN 502) was a double-blind, phase 2b test-of-concept trial of Merck adenovirus 5 HIV-1 subtype B vaccine⁴². The insert contained gag, pol, and nef sequences, each isolated from a different individual, and thus, expected to carry escape footprints to different HLA alleles. For a subset of individuals, immune responses to the vaccine insert were assessed using Interferon-γ ELISpot assays against overlapping peptides pooled by protein, as previously described⁴⁶. Two pools were assessed for Polymerase. The total magnitude of responses was estimated for each pool and normalized as the number of spot forming cells (SFC) per million cells. ELISpot assays were carried out independently by the HVTN and Merck laboratories. For our analyses, we compared the protein-specific adaptation of the vaccine insert against the log-total magnitude of the pooled response. For polymerase, we used the geometric mean magnitude of the two pools. We limited our analyses to samples collected after the second vaccination and before evidence of HIV infection.

Autologous Gag, Pol, and Nef sequences and HLA types were available for 60 seroconverting males in the modified intent to treat group, of whom 37 were in the vaccine arm⁵⁴. For these individuals, we defined transmitted adaptation as the autologous adaptation of the inferred founder virus. Because sequences were previously derived from samples obtained during acute or early infection using serial dilution, followed by whole- or half- genome amplification and sequencing, we computed for each participant the autologous adaptation of each amplicon separately for each protein. We then computed the mean autologous adaptation over the amplicons for each protein, then combined these protein-specific adaptation scores as described below, yielding the estimated autologous adaptation of each individual’s founder virus (or viruses). As for the Zambian transmission pairs, we compared transmitted adaptation against the participants’ geometric mean VL, taken over all samples that occurred between the first Western blot positive sample and the start of antiretroviral therapy or 365 days post Western blot positive date, whichever was sooner. Four individuals were excluded from this analysis due to missing VL data: three had a single VL measurement; one initiated therapy immediately upon seroconversion.

Functional data for acute infection cohort

Subjects

Thirteen acutely HIVB-infected subjects were recruited from the University of Alabama at Birmingham HIV infection clinic after obtaining written informed consent and approval from the UAB Institutional Review Board for Human Use (IRB) committee. Acute infection was identified by detectable HIV-1 viral RNA in plasma and a lack of HIV-specific antibodies in a Western Blot⁷⁸ at the first screening visit. The founder virus sequences were inferred from the plasma of each subject via a single genome amplification (SGA) method at Fiebig stage III or earlier, performed as previously described⁷⁹. PBMCs for functional analysis were obtained a median of 31 days post estimated date of infection (range 16–51). All subjects were typed for HLA class I alleles. For 2 of 13 subjects, multiple founder viruses were identified. These subjects were excluded from further analysis. No experimental blinding was performed.

Peptide selection and synthesis

For each of the 11 subjects with single founder viruses, we identified all optimally defined epitopes (8–11mer) restricted by the subject’s HLA alleles⁴⁵. For each of those HLA-epitope pairs, we selected the subset for which an HLA-escape association related to the allele in question had been previously identified³⁶. From this subset, the corresponding autologous peptide sequence from the founder virus was identified, resulting in a total of 87 unique peptide variants. These peptides were synthesized from NEP (New England Peptide) in a 96 well array format. Each peptide was reconstituted at 40 mM in 100% DMSO and stored at −70 °C until use. Each epitope was classified as non-adapted (NAE) if it represented the most frequent epitope form found in the circulating HIVB viral population (QuickAlign from Los Alamos Database) that did not contain any HLA-I associated adapted amino acid variants³⁶. All other epitopes were classified as adapted (AE).

In vitro and predicted HLA class I binding affinity

HLA-I binding affinity for peptides tested in the immune assays was determined in vitro according to a previously established protocol involving competition assays that utilize purified HLA molecules and high affinity radiolabeled probe peptides. The competition assays were based on monoclonal antibody capturing of MHC-peptide complexes⁸⁰. In addition, predicted HLA class I binding affinity for these peptides was assessed by using the NetMHC software program^81,82 (version 3.4, http://www.cbs.dtu.dk/services/NetMHC/).

IFN-γ ELISpot assay

ELISpot was performed as previously described^83,84. Experiments were performed in duplicate. Briefly, nitrocellulose plates were coated overnight with anti-IFN-γ antibody. In duplicate experiments, subject-derived PBMCs were added at 10⁵ cells/well and were stimulated with the appropriate autologous peptide at a final concentration of 10 μM for 24 hrs. The cells were then washed, and biotinylated anti-IFN-γ antibody was added for 2 hrs. After this incubation step, streptavidin-alkaline phosphatase was added for 1 hr before using NBT/BCIP substrate for spot detection. The number of spots was counted using an ELISpot plate reader (CTL ImmunoSpot) and was normalized to 10⁶ PBMCs (SFC/10⁶ cells). The mean SFC/10⁶ cells over the two duplicates is reported. A positive response was defined as 55 SFC/10⁶ PBMCs or greater and also at least 4 times the unstimulated media-only controls. PHA (10 μg/mL) was used as a positive control in this assay.

Antigen sensitivity

Four to five 10-fold serial dilutions of peptides were used in an IFN-γ ELISpot assay as described above to assess functional avidity, or antigen sensitivity, of the CD8⁺ T-cell responses. Antigen sensitivity was determined by the peptide concentration that elicited 50% of maximal IFN-γ response (EC50) for any given epitope. Stimulation of PBMCs at each peptide concentration was performed in experimental duplicate, and mean and observed values are reported in the figures.

Intracellular cytokine staining (ICS)

ICS flow cytometry was done as previously described⁸⁵. In brief, 10⁶ PBMCs were pulsed with autologous peptide at 10 μM in the presence of co-stimulatory antibodies (anti-CD28 and anti-CD49D), anti-CD107a-FITC, monensin, and brefeldin A (all from BD Biosciences) for 6 hrs. The cells were then surface stained with LIVE/DEAD cell dye (Invitrogen), anti-CD3-Alexa 780 (eBioscience), and anti-CD8-PE (BD Biosciences). The cells were permeabilized and labeled with anti-IFN-γ-Alexa 700, anti-IL-2-APC, anti-TNFα-PECy7, and anti-Granzyme B-V450 (all from BD Biosciences). CD3 events greater than 100,000 were acquired on an LSR II (BD Immunocytometry Systems), and data were analyzed using FlowJo (version 9.6.4; TreeStar). Polyfunctionality analysis was performed using Boolean gating and SPICE & PESTLE (version 5.1; NIAID)⁸⁶.

In vitro expansion of CD8⁺ T-cell lines

In vitro expansion of epitope-specific CD8⁺ T-cell lines was performed as described previously by our group⁸⁷. Briefly, freshly thawed cryopreserved autologous PBMCs were plated in a 48 well plate at 1.2 × 10⁶ cells/ml in serum free RPMI media. Supernatants containing non-adherent cells were removed after a two-hour incubation at 37°C. Adherent cells, mainly monocytes, were irradiated (3,300 rad, 45 min) and pulsed with the appropriate autologous peptide (10 μM) for 2 hrs. CD8⁺ T cells were isolated from the non-adherent cells using the CD8⁺ untouched isolation kit (MACS Miltenyi Biotec) and were plated onto peptide-pulsed monocytes in the presence of complete media (RPMI+10% Hyclone serum) containing IL-7 (25 ng/ml). The CD8⁺ T-cell culture was maintained by adding IL-2 (50 U/ml) every 2 to 3 days and re-stimulating the CD8⁺ T cells with peptide-pulsed monocytes as described above on day 7. On day 13, T-cell lines were tested for cytokine responses to the cognate HIV peptide in a 6 hr ICS assay as outlined above.

Target killing assay using 7-aminoactinomycin D (7-AAD) staining

7-AAD killing assay was performed according to a modified protocol based on a prior study⁵³. To avoid repeated exposure to autologous peptide stimulation, PBMCs from HLA-I matched HIV-1 seronegative donors were used as target cells. CD4⁺ T cells were isolated from the PBMCs of seronegative donors by depleting their CD8⁺ T cells (Dynabeads® CD8, Invitrogen) and activating them with PHA (5 μg/mL) in the presence of IL-2 (100 U/mL) for 2 days. Activated CD4 targets (5×10⁵ cells) were either pulsed with the relevant HIV peptide at 10μM or the irrelevant CEF peptide pool (containing CMV, EBV, and Flu, synthesized from NIH AIDS Reagents Program) at 2 μg/mL for 1 hr before co-culturing with appropriate epitope-specific CD8⁺ T-cell line for 24 hrs at four effector:target (E/T) ratios (0:1, 0.5:1, 1:1, and 1.5:1). Each E:T co-culture was performed in duplicate. After incubation, the cells were surface stained with anti-CD3-Pac Blue (BD Biosciences) and anti-CD4-Alexa780 (eBioscience) before washing and staining with 0.25 μg of 7-AAD (BD Biosciences) for 20 min at 4 °C. Using flow cytometry, target killing by epitope-specific T-cell lines was determined by comparing the percentage of 7-AAD⁺ CD4⁺ T cells in the presence of effectors (at 0.5:1, 1:1, and 1.5:1 E:T’s) relative to that from the target cells without any effectors (at 0:1 E:T). Mean and observed values over the experimental duplicates are reported.

In vitro killing assay

Two HIV-1 MJ4 viruses (one containing the HLA B*07:02-restricted non-adapted epitope form Nef-FPVRPQVPL, the other one containing the adapted form Nef-FPVKPQVPL) were used to infect targets. While MJ4 is a HIVC virus⁸⁸, the two epitope forms share the same NAE and AE classifications in clades B and C. In vitro killing assay was carried out as previously described by our group⁸³. In brief, to avoid viral outgrowth and competition from a subject’s autologous virus, CD8-depleted PBMCs from HLA B*07:02-matched and mismatched HIV seronegative donors were used as infection targets. Prior to infection, the target cells were activated for 2 days with PHA (5 μg/mL) and IL-2 (100 U/mL). Activated targets were then infected with HIV-1 MJ4 (containing either the NAE or the AE Nef epitope mentioned above) at a multiplicity of infection (MOI) of 0.5 for 2 days, after which cognate peptide-specific CD8⁺ T-cell line (i.e. from Nef-FPVRPQVPL or Nef-FPVKPQVPL) was added to the infected targets (5 × 10⁵ cells) at three E:T ratios (0:1, 1:5, and 1:1) for 24 hrs. Each E:T co-culture was performed in duplicate. Then, the co-cultured cells were surface stained with anti-CD3-Pac Blue and anti-CD4-Percyp Cy5.5 antibodies (both from BD Biosciences), permeabilized, and labeled with the intracellular anti-gag p24-PE antibody (BD Biosciences). Gag p24 reduction from CD4⁺ T cells on flow cytometry was used to assess the % killing of infected targets. The formula used for determining the percentage of CD8⁺ T-cell mediated killing is as follows:

$$[1-\left(\frac{\mathrm{p}24\text{with effector cells}}{\mathrm{p}24\text{without effector cells}}\right)]\times 100$$

This formula was calculated for each experimental duplicate and the mean and observed values are reported.

Statistical methods

For each cohort, viral load (VL) was transformed using log₁₀ and CD4 counts were transformed using the Box-Cox procedure⁸⁹, applied separately to all British Columbia (λ = 0.45) and all Southern Africa (λ = 0.58) data, to make the counts as close to normally distributed as possible. The resulting distributions in the chronic infection cohorts remained modestly right-skewed (CD4) and left-skewed (VL). This effect was most extreme for the British Columbia data, where VL was right censored at 10⁶ copies/ml. This censoring may affect model estimates. As such, we focused cross-sectional analyses on the Southern Africa data and used non-parametric tests where possible (see below). The associations between adaptation and VL and CD4 were highly significant whether estimated with the mixed model (to account for confounders) or Spearman rank correlation (to account for non-normality).

Where HLA alleles were typed to low or medium resolution, we estimated a probability distribution over HLA haplotypes as previously described⁹⁰. The distributions were used in training and applying the adaptation model as described below. When used as independent variables in standard generalized linear fixed and mixed effects models, we imputed the HLA alleles by calculating the marginal probability that the individual expressed each HLA supertype, type, and subtype. The marginal probabilities for each HLA were then treated as a fractional observation of that HLA. HLA alleles were treated as (possibly fractionally observed) binary variables, such that homozygosity was not encoded in the models.

The adaptation model training was based on HLA and viral genetic data alone; clinical parameters were not considered in the model training. Autologous adaptation for the Southern Africa, the British Columbia, and the Zambian transmission pairs cohorts were estimated out of sample using 10-fold cross validation. Individuals lacking both VL and CD4 data were used in the training sets for all 10 folds. For the IHAC cohort, clinical parameters were only available for the British Columbia cohort. Thus, all ACTG and Western Australia individuals were included in all cross validation partitions. All other adaptation scores were computed from models trained on the entire Southern Africa (HIVC) or IHAC (HIVB) datasets.

All reported P-values are from two-sided tests and unadjusted for multiple comparisons. When a large number of comparisons is employed, false discovery rates in the form of q-values are reported^91,92. Wherever possible, analyses were adjusted for subject Age, Sex, cohort of origin and HLA alleles. Age was dichotomized at ≥40⁹³. HLA alleles were treated as random effects (see below). For the British Columbia data, sampling year was treated as a random effect. For the Zambian Transmission Pairs, no significant effect was observed for sampling Year; we therefore used a dichotomous fixed effect (around median sampling year) as a covariate. For the Southern Africa data, sampling dates were not available for a substantial number of samples; however, each cohort (with the exception of Zambia) collected samples within a small time frame. Therefore, any variation due to sampling time will be approximately captured by the cohort indicator variables. For all analyses, missing demographic data (age, sex, sampling year) were imputed using linear imputation; individuals with missing clinical, functional or sequence data were excluded. As noted above, individuals with partially missing sequence data were included in the Southern Africa and British Columbia autologous adaptation results, but excluded in all other analyses.

Stepwise regression

Stepwise regression for generalized linear models was performed using P < 0.05 and P > 0.05 as entry and exit criteria, respectively. For the controller data (Supplementary Fig. 3b) logistic regression was used and all HLA alleles, at both type and subtype resolution, observed in at least 5 individuals were included as potential features. For these analyses, we excluded all HLA supertypes. q-values were estimated from the P-values of all possible features, conditioned on the final model.

Stepwise regression was also applied to the Southern Africa and British Columbia cohorts to identify the dominant alleles that contribute to clinical parameters. For these applications, only HLA-subtypes (4-digit) observed in at least 20 individuals were considered, and age, sex, and cohort indicator variables were included in the model as covariates.

Cox proportional hazards model

The association between transmitted adaptation and CD4 decline was assessed using the 46 Zambian transmission pairs for whom we had longitudinal CD4 counts immediately following transmission. We evaluated the relationship using the Cox proportional hazards model, treating the adaptation of the donor virus to the recipient alleles as a continuous variable, and Sex, Age (≥40), and sample date (>median) as covariates (none were significant). For Figure 3a, we stratified individuals based on the mean transmitted adaptation over those 46 subjects. For this figure only, the adaptation score was scaled so that a one-unit change corresponded to the difference in mean adaptation within the two strata. Thus, the reported hazard ratio (3.0) indicates that an individual with above-average transmitted adaptation progresses to CD4 < 250 cells/mm³ at a three-fold higher rate than an individual with below-average transmitted adaptation.

Our pre-specified endpoint was CD4 < 250 cells/mm³. This end point was based on two factors: 1) national therapy guidelines at the time of sampling were CD4 < 200 cells mm³, and no individuals initiated at CD4 > 250 cells/mm³; and 2) 27 of 46 (59%) of individuals reached CD4 < 250 cells/mm³ within the timeframe of the study. As a post hoc analysis, we repeated the analysis for CD4 count thresholds, incrementing by 50 cells/mm³, and including therapy initiation as an additional endpoint; results were significant (P < 0.05) for all endpoints from 150 to 350 cells/mm³, with hazard ratios ranging from 2.2 to 3.2.

Linear Mixed Models (LMMs)

With the chronic data, our primary goal was to estimate the effect of adaptation on clinical parameters. However, HLA class I alleles are known to represent the primary host genetic factor that influences VL and CD4 counts^94,95. Within the HLA-I loci, a number of different HLA alleles have been reported as significantly associated with VL, with differences observed between HIV subtype, cohort, and disease stage. Furthermore, some HLA alleles appear to have HLA subtype-specific effects on VL and CD4 (most prominently, B*58:01 compared to B*58:02, but others as well), while other alleles act at the type or even supertype level. It is therefore clear that all HLA alleles, at all resolutions, need to be accounted for when assessing the effects of a new independent variable.

To this end, we used linear mixed models (LMMs). In this setup, we conceptually build a linear model with a separate weight for every HLA allele (we provide one at the supertype, type, and subtype levels for each HLA allele). Because such a model is over parameterized, we place a Gaussian prior distribution on the parameter for each HLA and integrate out the HLA effects based on those priors. The parameter-specific Gaussian priors are specified by $\mathcal{N}\left(0,{\sigma }_A\right),\mathcal{N}\left(0,{\sigma }_B\right),\text{and}\mathcal{N}\left(0,{\sigma }_C\right)$ for the HLA A, B, and C alleles, respectively. In this way, we are able to condition on all HLA alleles, while allowing the variance of effect sizes to differ among loci. In addition, we treat the sub-cohorts (Southern Africa) and sampling year (British Columbia) as random effects, drawn from a separate Gaussian distribution with its own variance, and similarly for other random effects noted in the text. When displayed in tables, all features in italics are treated as random effects with their own effect-size variance. We used the LMM implementation from the Matlab statistics toolbox. The model can be expressed as

$$Y=X\beta +{\displaystyle \sum }_{i=1}^R{Z}_i{B}_i+E$$

where Y is the $N\times 1$ response vector, X is the $N\times P$ fixed effects design matrix, $Z_i$ ( $i=1\dots R$) are the $N\times Q_i$ random effects design matrices, β is a $P\times 1$ fixed effects vector; $B_i~N\left(0,{\sigma }_i^{2}I\right)$, and $E~N\left(0,{\sigma }_E^{2}I\right)$; I is the $N\times N$ identity matrix, ${\sigma }_E^2$ is the variance of the elements of E, and ${\sigma }_i^2$ is the variance of the estimates of $B_i$. This model thus groups random effects by categories (e.g., each HLA-B allele is grouped with all HLA-B alleles), then estimates different variance components for each effect category.

Models were fit using both restricted maximum likelihood (REML) and maximum likelihood (ML). Fraction of variation explained (pseudo- $R^2$) was computed according to the likelihood ratio test method⁹⁶, trained using ML. P-values for the fixed effects were derived from the standard error of the estimated effects (trained via REML); P-values for random effects came from the likelihood ratio test (trained via ML), corrected for boundary effects⁹⁷.

Allele specific adaptation

To estimate the effects of allele-specific adaptation, we constructed a series of independent linear models, one for each HLA subtype, h. Each linear model was defined as follows:

$$y_i={\mathrm{\beta }\mathrm{X}}_{\mathrm{i}}+{\beta }_1{h}_i+{\mathrm{\beta }}_2{\text{adapt}}_{s_i}(h_i)+x_i\beta +{\epsilon }_i$$

where $y_i$ is the value of the dependent variable (transformed VL or CD4) for individual i, $h_i$ is a binary variable indicating whether the individual i expresses h, ${\text{adapt}}_{s_i}(h_i)$ is the autologous adaptation to h for each individual i, defined to be 0 if $h_i=0$, $x_i$ is a vector of covariates and β the corresponding vector of weights, and ${\epsilon }_i$ is independently sampled from a Gaussian distribution. In this context, the covariates are indicator variables for cohort of origin, sex, age (≥40) and HLA subtypes identified via an independent stepwise regression analysis. Since ${\text{adapt}}_{s_i}(h_i)$ ranges from $-1$ to 1, ${\beta }_1-{\beta }_2$ defines the expected relative change in VL attributable to h in the complete absence of allele-specific adaptation, and ${\beta }_1+{\beta }_2$ defines the expected relative change in VL attributable to h in the presence of complete allele-specific adaptation. 95% confidence intervals and P-values are readily obtained from the variance-covariance matrix associated with the parameter estimates. Figure 2b and Supplementary Figure S3c show all alleles for which a likelihood ratio test against a null model with ${\beta }_1={\beta }_2=0$ was significant at $P<0.05$. This threshold corresponded to a 10% false discovery rate for both VL and CD4. In Figure 2b, we also indicate the results of testing the null hypothesis ${\beta }_2=0$, indicating the significance of allele-specific adaptation on VL (and similarly for CD4, Supplementary Fig. 3c).

Longitudinal data analysis

To test whether changes in adaptation predict future changes in viral load, we used longitudinal VL and sequence samples from the Zambian transmission pairs dataset, and analyzed them in a autoregression (AR) mixed model with second-order lag and random intercept varying by subject and HLA alleles. Adapting the above notation for mixed models, for each subject i, we modeled VL at time point t (described below) using

$${\mathrm{VL}}_{i,t}={\beta }_{1}V{\mathrm{L}}_{\mathrm{i},\mathrm{t}-1}+{\beta }_2{\mathrm{VL}}_{i,t-2}+{\beta }_3{\text{Adapt}}_{i,t-1}+x_i\beta +{\displaystyle \sum }_{j=1}^R{z}_{ij}{b}_j+\epsilon$$

As above, $x_i\beta$ captures fixed-effect covariates (see Supplementary Fig. 7) and $z_{ij}$ is a vector of random effects, with $b_j~\mathcal{N}(0,{\sigma }_j)$ the random effect weights. Here, we used HLA alleles (as above) and subject identifiers as random effects to account for subject- and HLA-specific effects on the change of VL over time. The model thus assumes that VL at any time point can be predicted based on the prior to VL measurements, the absolute level of adaptation at the prior time point, and a set of covariates. We chose a lag of two based on exploratory analysis in the absence of Adaptation that showed a 3^rd order lag did not significantly improve model fit.

Our primary endpoint was to determine if autologous adaptation at the prior time point predicted changes in VL at the next time point. Secondary analyses show estimated effect sizes of alternative definitions of adaptation (allele specific and protein specific; Supplementary Figure S7b). We also explored a model in which Adaptation is the dependent variable and VL is the independent variable, and varied the definition of adaptation.

To specify the time points, we started with available sequence samples, limiting to samples with complete gag, pol, and nef sequencing. These were sampled approximately 0–3, 3–9, 9–15, 15–21, and 21–30 months post infection, though precise sampling times varied among individuals. Each sequence sample was discretized to one of the above time points; if multiple samples discretized to the same time point, the latest sample in the time point was used. VL measurements were discretized to the same time points. If multiple VL measurements mapped to the same time point, we used that which was closest to the sequencing time point. Only VL measurements made within 90 days of the sequencing samples were used. VL and sampling dates were identical for 384 of 422 matched time points.

Circulating adaptation and HLA alleles

Figure 4a,b and Supplementary Figure S8a–c display the correlation between allele-specific circulating adaptation and the relative protection attributable to each allele. For each allele, we computed adaptation between that allele and the HIV sequences isolated from all individuals in the cohort (limiting to sequences without missing data). Allele-specific circulating adaptation was then defined to be the mean adaptation for each allele over these sequences. We computed this mean separately over all British Columbia and all Southern Africa sequences. City-specific circulating adaptation for the Southern Africa cohort was computed for the three cities with the largest samples sizes (see below). Circulating adaptation thus estimates the expected transmitted allele-specific adaptation were an individual with that allele infected randomly by an HIV sequence selected from that cohort (or city).

To estimate the allele-specific effect on VL or CD4 counts, we used LMMs as described above, but using a single variance parameter for HLA-A, -B, and -C to make cross-locus comparison possible. Age, Sex, and cohort were used as covariates. The allele-specific effect on VL or CD4 was taken to be the best linear unbiased (BLU) estimate for each allele, which was then regressed against allele-specific circulating adaptation. R² and P-values were computed as described above for a LMM that uses the BLU estimate as the dependent variable, HLA locus as a random effect, and allele-specific circulating adaptation as the fixed effect of interest. In all analyses, we limited to HLA subtypes that were observed in at least 20 individuals.

We performed three analyses. In the first (Fig. 4a and Supplementary Fig. 8a), we limited the analysis to alleles selected in a stepwise regression procedure, as described above. The second analysis (Supplementary Fig. 8b,c) included all alleles. By including all alleles, the effect size estimated for each allele shrinks, due to information sharing across allele pairs that are in linkage disequilibrium, as well as the increased regularization effect of the LMM.

In the third analysis (Fig. 4c and Supplementary Fig. 8d), we compared city-specific VL effects against city-specific circulating adaptation. To this end, we limited our samples to individuals from the three cities with the most subjects (Durban, South Africa; Gaborone, Botswana; and Lusaka, Zambia), then performed stepwise regression on those individuals to identify alleles that should be used as covariates. We then tested all alleles for significant interaction effects with the set of city indicator variables using a likelihood ratio test, and identified four alleles with some evidence of differential effects by city (P < 0.1). The city-specific effects on VL were then estimated in a mixed model, including as covariates the other alleles and demographic variables; all effects were estimated jointly. The city-specific effects on VL compared to city-specific circulating adaptation are shown in Supplementary Figure S8d, which shows a clear trend in which cities with higher circulating adaptation for a given allele are also associated with higher relative VL for that allele. To form an omnibus statistical test, we mean-centered the city-specific VL effects and the circulating adaptation for each of the four alleles (Fig. 4b). We then estimated pseudo-R² and P-value by modeling mean-centered VL effects in a mixed model with mean-centered circulating adaptation as a fixed effect and city as a random effect.

Adaptation similarity

For the purpose of adaptation, we consider that two HLA alleles $h_1$ and $h_2$ are similar if they drive similar escape mutations. In the context of the adaptation score, this suggests that similarity of $h_1$ and $h_2$ can be defined as the Pearson correlation coefficient, ${\rho }_{h_1,h_2}$, between the two alleles, over the entire population of HIV sequences. In practice, we must estimate this correlation over a set of observed sequences. Here, we use all Southern Africa sequences that are not missing entire protein sequences. We thus estimate the sample Pearson correlation coefficient, $r_{h_1,h_2}$, over these sequences. To account for sequence features such as gaps, missing regions, and AA mixtures, we perform an additional normalizing step. Specifically, we first compute the matrix $X=\left\{x_{ij}\right\}$, where $x_{ij}={\text{Adapt}}_{s_i}(h_j)$ is the adaptation of the ith sequence to the jth allele, then mean-center each row. The sample “Adaptation similarity” of $h_1$ and $h_2$ is then defined to be the Pearson correlation coefficient between columns i and j of the resulting matrix. The resulting HLA-specific similarity largely recreates supertype definitions (see Supplementary Data File). At the subject level, we extend the above definition such that $h_i,h_j$ refer to the sets of alleles (all alleles, or all alleles at one of the loci). Here, we focus on HLA-B adaptation similarity between donor and recipient pairs, as adaptation to HLA-B consistently had the largest effect size on all the previous analyses (Supplementary Tables 1–3).

Adaptation score

When a CTL response is directed against a particular epitope, there is a fitness advantage for viruses containing genetic mutations that reduce or eliminate that response, provided those mutations do not reduce viral protein function such that the loss of fitness from disrupted protein function is greater than the gain in fitness from reducing the efficacy of the immune response. Although such escape mutations may act by disrupting TCR recognition, HLA binding, or epitope processing, the escape mutations are remarkably consistent across individuals with a particular HLA allele. Typically, escape mutations are specific to HLA subtypes^35,98,99, though the same mutation may be selected across HLA types and even supertypes³⁵. These observations allow us to conceive of HLA-specific adaptation roughly in terms of the proportion of known HLA-associated sites that have escaped, as we have previously done^21,22,100. The problem with this definition is that it ignores the apparent hierarchy of escape: although escape is largely consistent, there are large variations across individuals in the timing of escape¹⁰¹. Some of this variation is due to variation in the frequency with which an epitope is targeted (immunodominance), though even when an epitope is targeted, alternative escape routes may be taken, with some typically preferred over others. In addition, variation in population-wide prevalence of escape mutations make observation of some variants more surprising than others in any given individual²⁰. As such, simple counting-based metrics of escape will under emphasize the presence of rare escapes and overemphasize the presence of common escapes (some of which are consensus in the circulating viral populations).

We consider that a probabilistic approach to estimating HLA-specific adaptation will yield a more intuitive metric that implicitly accounts for the frequency of within-host escape, as well as the baseline frequency of escape polymorphisms in the population. Conceptually, our approach is to estimate the probability distribution over all possible HIV sequences, conditional on all possible HLA repertoires. In practice, these distributions are estimated based on observed data, as described below. We then define adaptation of a particular sequence to a particular HLA allele to be a function of the likelihood ratio that compares a model in which the immune system is restricted by that single HLA allele against a hypothetical null model in which there is no immune response. This ratio is transformed to be on the range −1 to 1. The computation of the adaptation score is thus the result of several steps:

1. Training the model

   1. A feature selection step, in which the HLA alleles that drive selection at each site are identified
   2. The estimation of the multinomial probability distribution over all amino acids (AAs) at each site, conditional on all HLAs and the transmitted sequence
2. Defining adaptation of a sequence s with respect to an HLA allele h

   1. Estimating the probabilities of observing a particular HIV sequence in (1) the presence of a specific HLA and in (2) the absence of all immune pressure
   2. A transformation of the likelihood ratio from step 2a

What follows is a detailed description of each of the steps, beginning with a preliminary introduction that defines the notation and outlines the approach, then following with one section for each of these steps.

Parenthetically, we note that the model described in step 1 does not describe the rate of change in the viral population. Rather, it estimates the distribution of AAs among chronically infected individuals. Since adaptation increases during chronic infection (Supplementary Fig. 2c), parameter learning is dependent on the average duration of infection in the training set. As such, models trained on individuals with advanced disease (our HIVB model) will encode different AA distributions than those trained on individuals who are earlier in infection (our HIVC model). Qualitatively, not observing expected escape mutations will thus be less “surprising” in the HIVC model.

Preliminaries

Let $S=\left\{S_i\right\}$ be a random variable whose state space covers all possible HIV sequences over $i=1\dots N$ sites (which may span multiple proteins). Our aim is to estimate the probability distribution over S conditional on an individual’s HLA alleles. An individual’s HLA class I repertoire consists of three to six HLA alleles (two each from the HLA-A, -B, and -C loci, with a possibility of homozygosity at each locus). HLA alleles are specified hierarchically¹⁰². For our purposes, we consider three levels: supertype, type, and subtype. Because supertypes are defined based on binding profiles, some alleles do not fit within a supertype, while others are classified in two supertypes¹⁰³. We represent the space of possible HLA combinations using a binary vector H, with one entry for each HLA supertype, subtype, and type observed in our training datasets. We refer to a binary vector realization of H as $\stackrel{\rightharpoonup }{h}$, but for ease of notation will sometimes write $H=\left\{h_1,\dots ,h_k\right\}$ to represent the binary vector $\stackrel{\rightharpoonup }{h}$ that consists of all zeros except those supertypes, types, and subtypes corresponding with the k specified HLA alleles. For example H = {B*57:01,  B*58:01} corresponds to the binary vector with five entries set to 1: those for B*57:01, B*57, B*58, B*58:01, and the B58 supertype. Our aim is to estimate

$$\mathrm{Pr}(S=s|H=h)$$

for any sequence s and any set of HLA alleles h. Under the assumption of independence among sites, we factor the distribution as

$$\mathrm{Pr}(S=s|H=h)={\displaystyle \prod }_{i=1}^N\mathrm{Pr}(S_i=s_i|H=h)$$

It should be noted that the state of a sequence in chronic infection is strongly dependent on the transmitted sequence, which in turn will be related to other transmitted sequences based on phylogenetic relatedness. Thus, we write the per-site probability distribution using the law of total probability as

$$\mathrm{Pr}(S_i=s_i|H=h)={\displaystyle \sum }_{t_i}\mathrm{Pr}(S_i=s_i|H=h,T_i=t_i)\mathrm{Pr}(T_i=t_i)$$

where $T=\left\{T_i\right\}$ represents the space of possible transmitted HIV sequences over $i=1\dots N$ sites. See¹⁰⁴ for a full motivation and explanation of this factorization that is used to create the phylogenetically corrected distribution. As described below, in the present application, $\mathrm{Pr}(S_i=s_i|H=h,T_i=t_i)$ is defined according to the modified logistic regression model. The prior distribution over the transmitted sequence, $\mathrm{Pr}(T_i=t_i)$, is specified differently for model training and estimation of adaptation.

For simplicity of notation, we will often use the shorthand $\mathrm{Pr}(s|h)$ to mean $\mathrm{Pr}(S=s|H=h)$, and similarly for other random variables (capital letters) and their realizations (lower case letters).

Step 1: Training the model

The model is trained from large cross sectional observational cohorts of chronically infected, therapy-naïve individuals, for whom HIV sequence and linked HLA types are available.

Step 1a: Feature selection

By assuming independence among sites, we are able to estimate independent per-site models. Importantly, any given site is unlikely to be under selection pressure from more than a couple HLA alleles. Indeed, on a recent large scale HLA association study using our subtype B training data, there were an average of 1.3 HLA alleles associated per site that was associated with at least one HLA allele³⁶. Thus, our first step is to identify site-specific HLA alleles, so that estimation of the probability distribution is parameterized only by those alleles for which there is statistical evidence of selection. To this end, we use previously published approaches to identify HLA associations^{35,36,104,105}. Of note, these methods treat each individual amino acid at each site independently, as it simplifies the model and increases statistical power. The result is a list of HLA-amino acid (AA) pairs with a corresponding q-value, which is an estimate of the proportion of associations that are false positives among those associations that are deemed significant at the corresponding threshold⁹². We chose $q<0.2$ as our threshold. The full list of HLA-AA associations is available in the Supplementary Data File.

These methods are based on the phylogenetically corrected logistic regression model, which models $\mathrm{Pr}(s_i|h,t_i)$ using logistic regression, with 0/1 binary features for each HLA allele, and a −1/1 binary feature for the transmitted state $t_i$. Thus, we can specify the model for amino acid a at site i as

$$\begin{array}{c}\mathrm{Pr}(S_{ia}=1|h,t_{ia})=\frac{1}{1+e^{-z}}\\ z=h\beta +{\beta }_0{t}_{ia}\end{array}$$

for the $1\times M$ binary feature vector h encoding the HLA alleles expressed by the individual, the $M\times 1$ parameter vector $\beta ,$ and the scalar offset parameter ${\beta }_0$. Under this model, in the absence of HLA-mediated selection pressure, the log-odds that $S_{ij}=1$ is ${\beta }_0$ if the individual was transmitted amino acid a, and $-{\beta }_0$ if the individual was transmitted any other amino acid. To perform feature selection, we start with the null model of no selection pressure ( $\beta =0$), then systematically test each HLA j using maximum likelihood to optimize ${\beta }_j$ and ${\beta }_0$. The HLA that results in the maximum likelihood is allowed to stay in the model, and the process is repeated until no HLA yields a significant addition at $P<0.05$ by the likelihood ratio test. These P-values are used to estimate false discovery rates, which are estimated over all amino acids at all sites within a single protein. All tests at $q<0.2$ were treated as significant, while the remaining tests had their weights set to ${\beta }_j=0$.

Because the transmitted AA is not observed, we average over all possible states ( $t_{ia}=1$ and $t_{ia}=-1$). The probability distribution $\mathrm{Pr}(T_{ia}=1)$ is estimated from the phylogeny, which is parameterized as a continuous-time Markov process (CTMP) with a reversible substitution rate matrix. To this end, we begin with a phylogeny, whose structure is estimated using PhyML 3.0¹⁰⁶. For each site, we estimate a general time reversible (GTR) substitution rate matrix R (under two states) and a stationary binary AA probability distribution π using the expectation maximization (EM) algorithm^107,108. For each expectation step, we fix the β parameters from the logistic regression portion of the model, as well as phylogenetic parameters, then estimate the marginal and pairwise-marginal distributions of all hidden nodes in the tree, including the hidden nodes that represent the transmitted virus. Using these marginal distributions, the likelihood is then maximized with respect to both the phylogenetic parameters and the logistic regression parameters (β). The process is repeated until convergence. The details of the EM algorithm for phylogenies are given by Holmes and Rubin¹⁰⁸. Maximization of the logistic regression parameters, conditional on $\mathrm{Pr}(T_{ia}=1)$, is achieved by creating fractional observations for each individual, where $\mathrm{Pr}(T_{ia}=1)$, estimated for each individual in the tree, defines the weight for each fractional observation. For binary models, the matrix exponentials required for the CTMP can be computed analytically, leading to a substantial simplification and speedup. Additional steps can be taken to deal with ambiguous HLA data, which involve treating the high resolution HLA variables as missing data, conditional on the low resolution types and estimated haplotype frequencies, as previously described³⁶.

Step 1b: Multinomial logistic regression

The methods described in step 1a have been previously used to great effect in identifying HIV residues that likely serve as adapted or non-adapted residues in the context of HLA-mediated immune escape³. However, because they treat amino acids at the same position as independent, they do not yield consistent estimates of the probability distribution over all amino acids at a site. To this end, we describe here a modification of the phylogenetically-corrected logistic regression algorithm that uses a multinomial GTR substitution model in the phylogeny and multinomial logistic regression model to estimate $\mathrm{Pr}(s_i|h,t_i)$.

For a multinomial logistic regression model with A states and M predictors, we can define the probabilities for each of the A states as

$$\begin{array}{c}\mathrm{Pr}(S_i={\mathrm{AA}}_a|h,t_i)=\frac{1}{Z}{e}^{{\beta }_a\cdot h+{\beta }_0(2\cdot \mathbf{1}(t_i={\mathrm{AA}}_a)-1)}\\ Z={\displaystyle \sum }_{b=1}^A{e}^{{\beta }_a\cdot h+{\beta }_0(2\cdot \mathbf{1}(t_i={\mathrm{AA}}_b)-1)}\end{array}$$

where ${\mathrm{AA}}_a$ denotes the ath amino acid, ${\beta }_a$ is the $M\times 1$ parameter vector for ${\mathrm{AA}}_a$, and $\mathbf{1}(\cdot )$ evaluates to 1 if the contents are true and 0 otherwise. Thus the transmitted amino acid places ${\beta }_0$ weight in favor of the same amino acid and $-{\beta }_0$ weight against all other amino acids.

To set up this model, we begin with all amino acids observed in at least 3 of our training sequences, then add ‘X’ to represent all other amino acids. The space of HLA variables that are allowed to have non-zero weights is taken as the union of all HLA variables that were associated with any amino acid at site i in step 1a. The weights are then chosen to maximize the likelihood, subject to an L1-norm regularization penalty term that subtracts ${\lambda }_i\cdot ({{\displaystyle \sum }}_{a,j}|{\beta }_{a,j}|+|{\beta }_0|)$, $j=1\dots M,a=1\dots A$, with ${\lambda }_i$ chosen independently for each site using 7-fold cross-validation.

As in step 1a, the distribution over the transmitted amino acid, $\mathrm{Pr}(t_i)$, is taken from the marginal distribution for the hidden node that represents the transmitted sequence in the phylogeny, which in turn is affected by the parameters of the multinomial logistic regression model, as well as the observed amino acids at the tips of the tree and the phylogenetic parameters, which consist of the substitution rate matrix R and stationary distribution π. Optimization of these latter parameters is carried out using an EM algorithm, with the M-step including maximization of both phylogenetic and logistic regression parameters, conditional on the inferred marginal and pair-wise marginal distributions on the internal nodes. We parameterize the phylogenetic model as a site-specific GTR model with A states. The model is trained with a modification of the algorithm described by Holmes and Rubin¹⁰⁸, as described in the next section. Of note, the trained parameters $(R,\pi )$ represent HLA-corrected, site-specific estimates of the standard phylogenetic parameters, with π representing the steady state amino acid frequency distribution, and R representing the transition rate matrix, each corrected for the effect of HLA-mediated selection and the phylogenetic structure.

EM algorithm for multistate phylogenies

Holmes and Rubin¹⁰⁸ describe an EM algorithm for maximizing the likelihood of a continuous time Markov process over A states with respect to the substitution rate matrix R and the stationary state probabilities π. Their model is defined for general (non-reversible) R and π, with reversibility heuristically imposed and the constraints that all substitution rates be positive and that π defines a probability distribution imposed by Lagrange multipliers. In practice, we found that these approaches were numerically unstable and frequently resulted in invalid R (being irreversible or containing negative entries) and π (containing negative entries or failing to sum to one). We therefore modified the procedure as follows.

We start by following Holmes and Rubin in calculating the expected complete log likelihood with respect to given parameters $(R,\pi )$ and update parameters $(R^{\prime },{\pi }^{\prime })$ as

$$\mathcal{Q}(R,\pi ,R^{\prime },{\pi }^{\prime })={\displaystyle \sum }_a^A{\widehat{s}}_a\log {\pi }_a^{\prime }+{\displaystyle \sum }_a^A{\widehat{w}}_a{R}_{aa}^{\prime }+{\displaystyle \sum }_a^A{\displaystyle \sum }_{b\ne a}^A{\widehat{u}}_{ab}\log R_{ab}^{\prime }$$

where a, b index into the A possible amino acid states observable at site i, and ${\widehat{s}}_j$, ${\widehat{w}}_j$, and ${\widehat{u}}_{jk}$ are sufficient statistics computed from $(R,\pi )$ and described in Holmes and Rubin¹⁰⁸. These correspond, respectively, to the expected number of substitution paths that start in state a, the expected time spent in state a, and the expected number of $a\to b$ transitions. Whereas Holmes and Rubin introduce Lagrange multipliers to $\mathcal{Q}$ to enforce boundary constraints, then maximize the resulting expression with respect to $(R^{\prime },{\pi }^{\prime })$ and make a heuristic correction to ensure $R\prime$ is reversible, we begin by parameterizing R with respect to its stationary probability distribution π to enforce reversibility. Specifically, we define the substitution rate matrix to be

$${\left[R\right]}_{ab}=\{\begin{array}{cc}{\pi }_b{\lambda }_{ab}& \text{if}a\ne b\\ -{\displaystyle \sum }_{b\ne a}{\left[R\right]}_{ab}& \text{if}a=b\end{array}$$

We then numerically maximize $\mathcal{Q}$ with respect to $(R^{\prime },{\pi }^{\prime })$ by computing the gradient of $\mathcal{Q}$, which yields

$$\begin{array}{l}\frac{\partial \mathcal{Q}}{\partial {\pi }_a^{\prime }}=\frac{{\widehat{s}}_a}{{\pi }_a^{\prime }}-{\displaystyle \sum }_{b\ne a}^A{\widehat{w}}_b{\lambda }_{ab}^{\prime }+\frac{1}{{\pi }_a^{\prime }}{\displaystyle \sum }_{b\ne a}^A{\widehat{u}}_{ba}\\ \frac{\partial \mathcal{Q}}{\partial {\lambda }_{ab}^{\prime }}=-{\widehat{w}}_a{\pi }_b^{\prime }-{\widehat{w}}_b{\pi }_a^{\prime }+\frac{1}{{\lambda }_{ab}^{\prime }}({\widehat{u}}_{ab}+{\widehat{u}}_{ba})\end{array}$$

To further enforce that ${\lambda }_{ab}\ge 0$, $a\ge 0$, and ${{\displaystyle \sum }}_a^A{\pi }_a=1$, we reparameterize ${\pi }_a$ as

$${\pi }_a=\frac{\exp ({\alpha }_a)}{{{\displaystyle \sum }}_{b=1}^A\exp ({\alpha }_b)}$$

and ${\lambda }_{ab}$ as

$${\lambda }_{ab}=\exp ({\beta }_{ab})$$

For $a\ne b$, these functions have gradients

$$\begin{array}{l}\frac{\partial {\pi }_a^{\prime }}{\partial {\alpha }_a}={\pi }_a^{\prime }(1-{\pi }_a^{\prime })\\ \frac{\partial {\pi }_a^{\prime }}{\partial {\alpha }_b}=-{\pi }_a^{\prime }{\pi }_b^{\prime }\\ \frac{\partial {\lambda }_{ab}^{\prime }}{\partial {\beta }_{ab}}={\lambda }_{ab}^{\prime }\end{array}$$

Thus, we maximize $\mathcal{Q}$ with respect to α and β using

$$\frac{\partial \mathcal{Q}}{\partial {\alpha }_a}=\frac{\partial \mathcal{Q}}{\partial {\pi }_a^{\prime }}\frac{\partial {\pi }_a^{\prime }}{\partial {\alpha }_a}=\frac{\partial \mathcal{Q}}{\partial {\pi }_a^{\prime }}{\pi }_a^{\prime }-{\pi }_a^{\prime }{\displaystyle \sum }_b^A\frac{\partial \mathcal{Q}}{\partial {\pi }_b^{\prime }}{\pi }_b^{\prime }$$

and

$$\frac{\partial \mathcal{Q}}{\partial {\beta }_{ab}}=\frac{\partial \mathcal{Q}}{\partial {\lambda }_{ab}^{\prime }}\frac{\partial \lambda {}_{ab}^{\prime }}{\partial {\beta }_{ab}}=-{\lambda }_{ab}^{\prime }({\widehat{w}}_a{\pi }_b^{\prime }+{\widehat{w}}_b{\pi }_a^{\prime })+{\widehat{u}}_{ab}+{\widehat{u}}_{ba}$$

This parameterization allows us to use gradient-based optimizers that expect unbounded parameters, while assuring reversibility of R and appropriate bounds on the rates and probabilities. For our implementation, we use an efficient implementation of L-BFGS quasi-Newton optimization¹⁰⁹.

Step 2: Defining the adaptation of a sequence s with respect to an HLA allele h

Step 2a: Estimating the probability of a sequence in an HLA context

Step 1 yields a model that allows the estimation of the probability of observing any given amino acid at site i in the context of any set of HLA alleles and given any transmitted amino acid. Since our ultimate goal is to measure adaptation, we consider that a useful distribution over the transmitted AA, $\mathrm{Pr}(t_i)$, is our estimate of the ancestral (equivalently, steady state) distribution, provided by π, which represents an HLA-corrected estimate of the “ideal” distribution in the absence of HLA pressure and corrected for the phylogenetic structure of the observed sequences. We therefore estimate

$$\mathrm{Pr}(S_i=s_i|H=h)={\displaystyle \sum }_a\mathrm{Pr}(S_i=s_i|H=h,T_i={\mathrm{AA}}_a){\pi }_a$$

where ${\pi }_a$ is the stationary probability of amino acid a. Assuming independence of sites yields

$$\mathrm{Pr}(S=s|H=h)={\displaystyle \prod }_{\mathrm{i}}\mathrm{Pr}(S_i=s_i|H=h)$$

which is an estimate of the probability of observing any particular sequence in a chronically infected individual who expresses HLA alleles h.

Step 2b: Defining the adaptation score

Step 2a yields a probability distribution over HIV sequences conditional on a set of HLA alleles. In practice, we find it most helpful to consider a single HLA allele at a time. Thus, if $|h|=1$, then $\mathrm{Pr}(S=s|H=h)$ is the probability of observing s in an individual whose CTL are only targeting epitopes presented by h. We then define the adaptation of s to h to be

$$\begin{array}{l}{\text{adapt}}_h(s)\equiv g\left(\frac{\mathrm{Pr}(S=s|H=h)}{\mathrm{Pr}(S=s|H=\varnothing )}\right)\\ g(x)=\frac{2}{\pi }\text{arctan}\left[\ln (x)\right]\end{array}$$

where $H=\varnothing$ is a vector with all HLA variables set to zero, representing an HIV sequence evolving in the absence of immune pressure. The transformation $g(x)$ maps the ratio to a heavy-tailed sigmoidal function on the range $(-1,1)$, with 0, 0.75, 0.85, and 0.90 respectively corresponding to the cases where the HIV sequence is equally, ≈ 10-, ≈ 100-, or ≈ 1,000-fold more likely in the context of the HLA allele than in the absence of any selection pressure. Because we define $\mathrm{Pr}(t)=\pi$, the adaptation score thus has the intuitive interpretation as a measure of the extent to which the deviation of s from the idealized ancestral sequence is due to selection pressure mediated by h. Further, by defining the adaptation score in terms of a null immune response, we naturally normalize for variations in sequence coverage due to incomplete or ambiguous sequencing.

Notably, our independence-of-sites assumption allows the straightforward combination of adaptation scores computed from two different genomic regions. For example, if we’ve computed adaptation of Gag and Nef with respect to an HLA allele h, then we have

$$\begin{array}{c}{\text{adapt}}_h\left(\text{Gag}+\text{Nef}\right)=g\left(g^{-1}\left({\text{adapt}}_h\left(\text{Gag}\right)\right)\times g^{-1}\left({\text{adapt}}_h\left(\text{Pol}\right)\right)\right)\\ \approx {\text{adapt}}_h\left(\text{Gag}\right)+{\text{adapt}}_h\left(\text{Pol}\right)\end{array}$$

The shape of the inverse tangent function is such that the approximation is close to equality when the adaptation scores of the regions are both between $-0.5$ and $+0.5$.

Because the models are trained on high resolution HLA types, ${\text{Adapt}}_s(h)$ must be extended to cover low and medium resolution datasets. If $h_{j\cdot }$ represents a low- or medium-resolution HLA type, with corresponding subtypes $h_{jk}$, $k=1,\dots K$, then the adaptation of s with respect to $h_{j\cdot }$ is defined to be the weighted average of the adaptation of s to the possible subtypes,

$${\text{adapt}}_{h_{j\cdot }}(s;\theta )={\displaystyle \sum }_k{\text{Adapt}}_{h_{jk}}(s)\cdot \mathrm{Pr}(h_{jk}|h_{j\cdot }\theta )$$

with θ parameterizing the ethnicity-specific distribution of HLA subtypes. In our experiments, $\mathrm{Pr}(h_{jk}|h_{j\cdot }\theta )$ was taken from a modification of a published statistical HLA haplotype completion tool⁹⁰. Our modification allowed the averaging over uncertain ethnicities when the ethnicity of individuals was unknown but the distribution over a population could be provided from external sources.

Finally, when h represents a set of alleles (such as $h=\{h_{a_1},h_{a_2},h_{b_1},h_{b_2},h_{c_1},h_{c_2}\}$, representing an individual’s full class I repertoire), then adaptation is defined to be the average adaptation score over the set of alleles:

$${\text{adapt}}_h(s)=\frac{1}{|h|}{\displaystyle \sum }_{h_k\in h}{\text{adapt}}_{h_k}(s)$$

Thus, we compute the adaptation score for each of an individual’s HLA alleles separately, then use those numbers to compute adaptation scores for each locus and for the entire repertoire. Although our model could instead estimate the distribution of s conditional on a set of alleles, we found it more intuitive to think of adaptation of s to a particular allele as being independent of the other alleles expressed by an individual. Moreover, because most sites are not under selection by multiple alleles, and when multiple selection does occur, most individuals don’t express both alleles, the fully conditional adaptation scores were highly correlated ( $R>0.97$) to the definition we used.

In our HIVB cohort, the distribution of autologous sequences to an individual’s HLA alleles is shown in Figure 1. The mean was 0.26 ( $\mathrm{Pr}(S=s|H=h)$, which is approximately 1.5 fold more likely than $\mathrm{Pr}(S=s|H=\varnothing )$, with a minimum of −0.44 (2.3 fold less likely) and a maximum of 0.8 (22 fold more likely). For HIVC these numbers were respectively 0.18 (1.3 fold), −0.49 (−2.6 fold) and 0.99 (10²⁷ fold). By transforming the numbers this way, large differences in fold (say 1,000–10²⁷) yield a small difference in adaptation score (0.9–0.99), and thus a small difference when used as a linear predictor of clinical outcomes. This property increases robustness against (for example) model overfitting or errors in HLA typing and yields an approximately normal distribution of adaptation scores in any given population (Fig. 1 and Supplementary Fig. 2a).

Code availability

Implementation of the adaptation score and adaptation similarity are available as a web service and downloadable software at https://phylod.research.microsoft.com.