Searching for Category-Consistent Features

Abstract

This article introduces a generative model of category representation that uses computer vision methods to extract category-consistent features (CCFs) directly from images of category exemplars. The model was trained on 4,800 images of common objects, and CCFs were obtained for 68 categories spanning subordinate, basic, and superordinate levels in a category hierarchy. When participants searched for these same categories, targets cued at the subordinate level were preferentially fixated, but fixated targets were verified faster when they followed a basic-level cue. The subordinate-level advantage in guidance is explained by the number of target-category CCFs, a measure of category specificity that decreases with movement up the category hierarchy. The basic-level advantage in verification is explained by multiplying the number of CCFs by sibling distance, a measure of category distinctiveness. With this model, the visual representations of real-world object categories, each learned from the vast numbers of image exemplars accumulated throughout everyday experience, can finally be studied.

Our categories make us who we are; they are the skeleton upon which grows the rest of our psychological being. A reflection of their diverse importance is the fact that they have been studied from multiple perspectives: for example, as a lens through which people perceive visual and acoustic objects in the world (Liberman, Harris, Hoffman, & Griffith, 1957; Regier & Kay, 2009) and the similarity relationships between these objects (Goldstone, 1994; Medin & Schaffer, 1978), and as the structure of concepts that organize people’s knowledge and define who they are (Kaplan & Murphy, 2000; Murphy, 2002; Pazzani, 1991). Some approaches are also highly quantitative. The literature on semantic organization uses formal methods from logic theory to explain the division of information into clusters of semantic nodes (Anderson, 1983; A. M. Collins & Quillian, 1969), and the literature on category learning is ripe with models showing how corrective feedback about category membership can shape categorization decisions (Anderson, 1996; Ashby & Maddox, 1993; Kruschke, 1992; Love, Medin, & Gureckis, 2004; Nosofsky, 1986).

All of these approaches, however, have skirted a basic question of category representation: How might the visual features of common object categories be extracted from the many exemplar images of these objects that people encounter in their day-to-day lives?

Growing in parallel with these largely behavioral literatures has been another literature that may help answer this question. The field of computer vision is rich with operators and algorithms developed to detect members of object classes directly from pixels in images (Duda, Hart, & Stork, 2012). Moreover, these tools work with featurally complex real-world categories, and their performance is evaluated using new, or “unseen,” category exemplars not used during model training. In contrast, behavioral work on category learning has placed less emphasis on real-world application and model prediction, focusing instead on how categories defined by a small number of simple features are learned from feedback (see Ashby & Maddox, 2005). Thus, there is a gap in researchers’ fundamental understanding of categories; much is known about how simple features can be learned and used to discriminate one category from another, but little is known about the features composing the categories of common objects that populate everyday experience. By bridging these different approaches, researchers can achieve a new understanding of categories. Our premise is that tools from computer vision can, and should, be exploited to characterize the feature representations of categories as they exist “in the wild,” formed simply from a lifetime of experience seeing category exemplars.

The Generative Modeling of Visual Categories

We adopt a generative-modeling approach. Because generative models are usually unsupervised, they capture the implicit learning from exemplars that people and other animals use to acquire the within-category feature structure of visual object categories. Figure 1 helps to make this point. A generative model learns the features that are common among the objects of a category, much as the human visual system causes the perception of rectangles in this figure by finding common features among category exemplars grouped at the basic level.

Fig. 1.

Most of the 4,800 images used to train our model, grouped into the 16 basic-level categories used in the present study. The images are shown as tiny thumbnails for purposes of illustration, but each measured at least 100 × 100 pixels and depicted a tightly cropped view of an object against a natural background. Common visual features among the 300 image exemplars of each category, and category-specific differences between these features, create the appearance of rectangles in this stimulus space. See the Supplemental Material for similar illustrations of exemplars grouped randomly (Fig. S1a), at the superordinate level (Fig. S1b), and at the subordinate level (Fig. S1c).

Generative models can be contrasted with discriminative models, which use supervised error feedback to learn features that discriminate target from nontarget categories (Ulusoy & Bishop, 2005). The vast majority of category-learning studies have adopted a discriminative-modeling approach (Ashby & Maddox, 1993; Kruschke, 1992; Nosofsky, 1986), which is appropriate given the heavy reliance on the artificial-classification-learning paradigm in this literature. A generative approach, however, is more appropriate for modeling data that do not reflect explicit classification decisions (Kurtz, 2015; Levering & Kurtz, 2014; see also Chin-Parker & Ross, 2004), such as the visual search data in the present study. Our position is that generative models better capture the features of a category used to construct visual working memory representations of search targets, which are similar to the features one might call to mind when forming a mental image of a target category. If one is searching for a Pekin duck, one would probably look for a white, mailbox-sized object with orange at the top and bottom, even though these features would potentially yield poor discrimination of Pekin ducks from poodles and pumpkins.

Hierarchies of Categories

We evaluate our model within the context of a simple conceptual structure, a three-level hierarchy. Objects can be categorized at multiple levels in a conceptual hierarchy. A sea vessel powered by wind can be categorized as a sailboat (subordinate level), as simply a boat (basic level), or more broadly as a vehicle (superordinate level). The acquisition of and access to categorical information seems to be anchored around the basic level. This basic-level superiority effect (BSE) was first reported by Rosch, Mervis, Gray, Johnson, and Boyes-Braem (1976). They used a speeded category-verification task and found that people were faster in judging a picture of an object as a member of a cued category when the cue was at the basic level rather than a more specific or inclusive level. Subsequent work revealed a broader scope of the BSE by showing that the basic level is the preferred level used in speech and that the first nouns generally learned and spoken by children refer to basic-level categories (Mervis & Rosch, 1981; Rosch, 1978).

In explaining the BSE, researchers have appealed to similarity relationships within and between categories. Basic-level categories are thought to maximize within-category similarity while simultaneously minimizing between-category similarity, striking a balance between the two; subordinate or superordinate-level categories do one or the other, but not both (Rosch et al., 1976). Murphy and Brownell (1985) advanced this idea by theorizing that the BSE is a by-product of concurrent specificity and distinctiveness processes pulling categorization in opposing directions. Subordinate-level categories tend to have very specific features; collies are medium-sized dogs with thin snouts, upright ears, and white hair around their shoulders. However, these features overlap with those of other dog categories, so it is sometimes challenging to distinguish collies from German shepherds or shelties. Superordinate-level categories have the opposite strengths and weaknesses. The features of animals overlap minimally with the features of vehicles or musical instruments, which makes the category distinct. However, animal features are also highly variable, so this superordinate category lacks specificity. The basic level strikes a balance between these opposing processes, and this balance is believed to underlie the BSE. Despite their variability in appearance, dogs have many features in common yet are still relatively distinct from ducks and dolphins and dinosaurs. The present work extends this framework by making the processes of specificity and distinctiveness computationally explicit, and applying these principles directly to images of category exemplars.

Categorical Search

We evaluated the visual representation of common object categories using a categorical search task (Maxfield, Stadler, & Zelinsky, 2014; Schmidt & Zelinsky, 2009; Zelinsky, Adeli, Peng, & Samaras, 2013; Zelinsky, Peng, Berg, & Samaras, 2013). Categorical search differs from standard visual search in that targets are designated by a category label (e.g., “dog”) instead of by a picture precue (e.g., an image of a specific dog), a situation that rarely exists outside the laboratory. Moreover, categorical search can be meaningfully divided into two epochs: (a) the time between the onset of a search display and first fixation on a target (longer times indicate weaker target guidance) and (b) the time between first fixation on the target and the correct target-present judgment (longer times indicate more difficult target verification). Categorical search therefore embeds a standard category-verification task within a search task, which makes it a powerful paradigm for studying the relationship between overt attention and categorization.

We introduce a method for quantifying the visual features of common object categories and show that these features serve both to guide overt attention to a target and to categorize the target after it is fixated, producing a BSE during this latter, target-verification epoch. The fact that our model captured these disparate guidance and verification behavioral patterns provides converging evidence, within the context of a single categorical search task, that it can successfully identify the visual features used to represent common object categories. Thus, this work creates a strong theoretical bridge between the attention (target guidance) and recognition (category verification) literatures.

Behavioral Experiment

Method

Participants

Twenty-six Stony Brook University undergraduates participated in a categorical search task. Sample size was determined on the basis of a previous study using a similar method (Maxfield & Zelinsky, 2012). All participants reported that they had normal or corrected-to-normal visual acuity and color vision, and that English was their native language. All also provided informed consent prior to participation, in accordance with Stony Brook University’s Committee on Research Involving Human Subjects.

Stimuli and apparatus

Images of common objects were obtained from ImageNet (http://www.image-net.org) and various Web sources. Each image was closely cropped, using a rectangular marquee, to depict only the object and a minimal amount of background. Because object typicality can affect categorization and search (Maxfield et al., 2014; Murphy & Brownell, 1985), we selected targets that were typical members of their categories at the subordinate, basic, and superordinate levels. We did this by having 45 participants complete a preliminary norming task in which 240 images (5 exemplars from each of 48 subordinate categories) were rated for both typicality and how closely each matched a mental image of the object category (image agreement; Snodgrass & Vanderwart, 1980) at each hierarchical level using a scale from 1 (high typicality/high image agreement) to 7 (low typicality/low image agreement). The 3 most typical exemplars of each category were used as targets in the search task. Their mean ratings for typicality and image agreement were 2.29 and 2.31, respectively. In total, there were 68 categories spanning the three hierarchical levels: 4 superordinate-level categories, each having 4 basic-level categories, which in turn each had 3 subordinate-level categories. Figure 2 lists the category names at all three levels.

Fig. 2.

The names of the 68 object categories used as search targets, grouped by subordinate (48), basic (16), and superordinate (4) hierarchical level.

Eye position during the search task was sampled at 1000 Hz using an Eyelink 1000 eye tracker (SR Research, Mississauga, Ontario, Canada) with default saccade-detection settings. Calibrations were accepted only if the average spatial error was less than 0.5° and the maximum error was less than 1°. Head position and viewing distance were fixed at 65 cm using a chin rest for the duration of the experiment. Stimuli were presented on a flat-screen CRT monitor set to a resolution of 1,024 × 768 pixels and a refresh rate of 100 Hz. Text was drawn in 18-point Tahoma font, and image patches subtended approximately 2.5° of visual angle. Trials were initiated using a button on the top of a game-pad controller, and judgments were reported by pressing the left and right triggers.

Search procedure

On each trial, a category name was displayed for 2,500 ms, followed by a central fixation cross for 500 ms and finally a six-item search display (Fig. 3). Items in the search display were image patches of objects arranged on a circle having a radius of 8°. There were 288 trials, half with the target present and half with the target absent. Target-present trials depicted a target and five distractor objects chosen from random nontarget categories. Each participant saw one of the three selected exemplars for a given target category twice at each hierarchical level, with exemplars counterbalanced across participants. Half of the target-absent trials depicted six distractors from random categories that differed from the target category at the superordinate level; the other half depicted five distractors and one lure, because lures are needed to encourage encoding at the cued level (see Tanaka & Taylor, 1991). The lure was a categorical sibling of the cued target, drawn from target images included within the category one level above in the category hierarchy (e.g., a police car when the cue was “taxi” or a truck when the cue was “car”). Lures on trials in which the target was cued at the superordinate level (e.g., a sugar cookie when the cue was “vehicle”) were indistinguishable from the distractor objects, except for the fact that these lures were objects in the set of target categories (the set of nonlure distractors was disjoint from the set of target categories).

Fig. 3.

Procedure for the categorical search task. A target was designated by its category name at one of three hierarchical levels. Next, following a delay, a six-item search display was presented. The arrow and circle (not shown to participants) illustrate, respectively, the movement of gaze to the target (the target-guidance epoch) and its subsequent verification as a member of the cued category (the target-verification epoch).

Results

Error rates differed between hierarchy conditions, F(5, 21) = 15.19, p < .001, η² = .378. Post hoc tests (least significant difference corrected) showed that accuracy on target-present trials was lower at the superordinate level (M = 84.9%, 95% confidence interval, or CI = [81.1, 88.7]) than at the basic level (M = 91.6%, 95% CI = [89.5, 93.7]) and the subordinate level (M = 92.3%, 95% CI = [90, 94.6]), ps < .001. These additional misses are consistent with previous findings (Maxfield & Zelinsky, 2012) and reflect participants’ occasional failure to recognize a target as a member of the cued superordinate category (Murphy & Brownell, 1985). On target-absent trials, accuracy was lower at the subordinate level (M = 89.0%, 95% CI = [87.0, 91.0]) compared with the basic (M = 95.9%, 95% CI = [94.7, 97.3]) and superordinate (M = 95.4%, 95% CI = [93.2, 97.5]) levels, ps < .001. This increase in false positives was due to lures at the subordinate level being occasionally mistaken for members of the cued target category. Neither pattern of errors compromises our conclusions. Only trials responded to correctly were included in the subsequent analyses.

As in previous work (Castelhano, Pollatsek, & Cave, 2008; Maxfield & Zelinsky, 2012; Schmidt & Zelinsky, 2009), search performance was divided into target-guidance and -verification epochs that were analyzed separately. Target guidance was defined in two ways: as the time between the onset of the search display and the participant’s first fixation on the target (time to target) and as the proportion of trials in which the target was the first object fixated during search (immediate target fixations). Target verification was defined as the time between a participant’s first fixation on the target and his or her correct target-present manual response.

Analyses of the initial guidance epoch of search revealed significant differences in time to target between conditions, F(2, 24) = 22.08, p < .001, η² = .508. Targets cued at the subordinate level were fixated sooner on average than targets cued at the basic level, which were fixated sooner than targets cued at the superordinate level (ps ≤ .021; Fig. 4a). This same trend held for the proportion of immediate target fixations, F(2, 24) = 13.31, p < .001, η² = .456 (Fig. 4b), a more conservative measure of guidance. Subordinate-level targets were fixated first more often than basic-level targets (p < .001), and basic-level targets were fixated first more often than superordinate-level targets (p < .001). Initial saccade latency did not differ reliably between cuing conditions (p = .452), which suggests that these differences in time to target and proportion of immediate target fixations were not due to a speed-accuracy trade-off. Differences between conditions were also found during the verification epoch of search, F(2, 24) = 5.71, p = .006, η² = .215. As shown in Figure 4c, these differences took the form of a BSE; targets cued at the basic level were verified faster than those cued at the subordinate level (p = .01) and the superordinate level (p = .004). These findings not only extend previous work in showing that the hierarchical level at which a target is cued differentially affects target-guidance and -verification processes (Maxfield & Zelinsky, 2012), but also create a challenging guidance and verification behavioral ground truth against which our generative model of category representation can be evaluated.

Fig. 4.

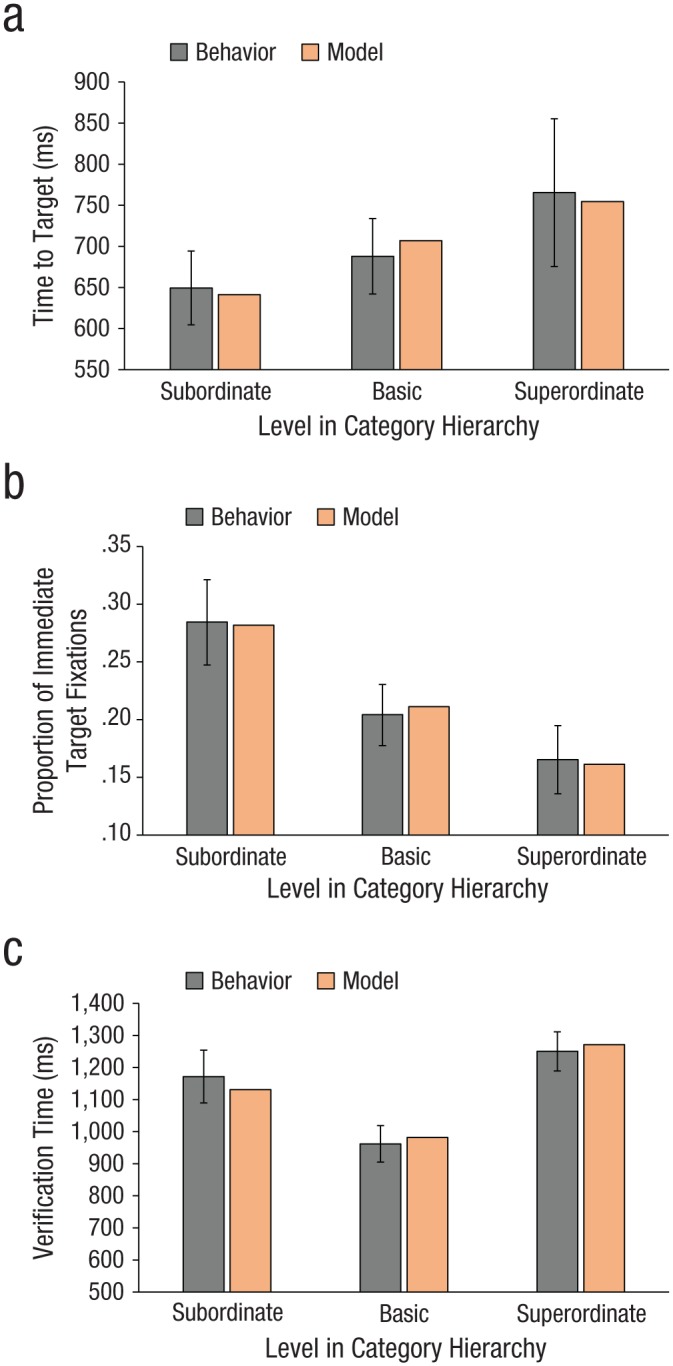
Mean behavioral results and output from the category-consistent feature model for (a) time to the first fixation on the target, (b) proportion of immediate fixations on the target, and (c) time from first fixation on the target until the correct target-present button press. Error bars indicate 95% confidence intervals.

Computational Experiment

Method

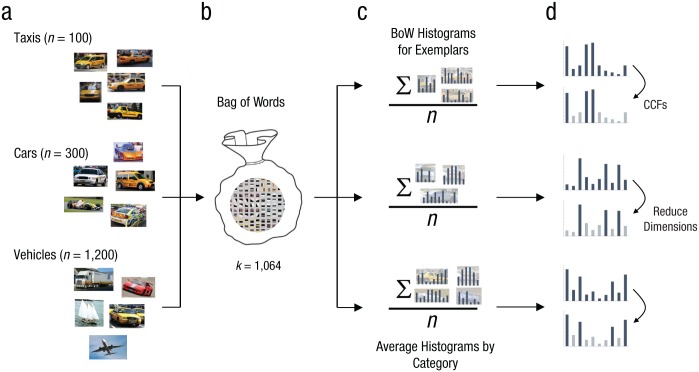
Two distinct effects of category hierarchy were found in the behavioral data: a subordinate-level advantage in target guidance and a basic-level advantage in target verification. In this section, we explain both of these behavioral patterns using a single unsupervised generative model that extracts features from images of category exemplars and then reduces the dimensionality of these representations to obtain what we refer to as category-consistent features (CCFs). Figure 5 provides an overview of this model.¹

Fig. 5.

Overview of the category-consistent features (CCF) model. One hundred images of object exemplars from each of 48 subordinate-level categories were used to build the model. These exemplars were also combined to create 16 basic-level categories (each with 300 exemplars) and 4 superordinate-level categories (each with 1,200 exemplars), for a total of 68 object categories across the three levels. Examples from the taxi, car, and vehicle categories are shown (a). Next, scale-invariant feature transform (SIFT) and color-histogram features were extracted from each exemplar, and the Bag-of-Words (BoW) method was used to create from these features a common feature space consisting of 1,064 visual words (b). For each exemplar, a 1,064-bin BoW histogram was obtained; each bin corresponded to a visual word, and its height indicated the frequency of that feature in the exemplar image. BoW histograms were averaged by category (c) to obtain 68 averaged histograms, each having a mean frequency and variability associated with each visual word. Features having too low a frequency or too high a variability were excluded, to create a lower-dimensional feature representation of each category consisting of its CCFs—those highly informative features that were present both frequently and consistently across the exemplars of that category (d). This dimensionality reduction is illustrated in each histogram pair by the darker shading of CCFs in the lower histogram.

Using the same category hierarchy as in the behavioral experiment, we built from ImageNet and Google Images (https://images.google.com/) an image data set for model learning. This set consisted of 100 exemplars for each of the 48 subordinate-level categories (4,800 images in total; see Fig. 1 for tiny views of most of these images). Each exemplar was an image patch closely cropped around the depicted object. Exemplars for basic-level and superordinate-level categories were the sets created by combining the subordinate, children, exemplars under the parent categories. For example, the basic-level “boat” category had 300 exemplars, consisting of 100 speed boats, 100 sailboats, and 100 cruise ships, and the superordinate-level “vehicle” category had 1,200 exemplars, consisting of the 300 exemplars each from the “boat,” “car,” “truck,” and “plane” sibling categories.

The first step in representing an object category was the extraction of features from its exemplars. Two types of features were used: scale-invariant feature transform (SIFT) and color-histogram features. SIFT features capture the structure of gradients in images using 16 spatially distributed histograms of scaled and normalized oriented-edge energy (Lowe, 2004). Color-histogram features (van de Weijer & Schmid, 2006) capture the distribution of hue in an image. In the current implementation, each color-histogram feature was represented by 64 bins of hue in 360° HSV (hue, saturation, value) color space. Using dense sampling (and discarding samples from uniform regions), we extracted five scales of SIFT descriptors, from patches of 12 × 12, 24 × 24, 36 × 36, 48 × 48, and 60 × 60 pixels, and a color-histogram feature from a fixed-size 20- × 20-pixel patch surrounding the center position of each SIFT descriptor in each of the 4,800 exemplars. Color histograms were pooled over patches within exemplars to create a single 64-bin color histogram for each exemplar. However, to compare SIFT features between exemplars it was necessary to find a common feature space, and for this we used the Bag-of-Words (BoW) method (Csurka, Dance, Fan, Willamowski, & Bray, 2004). The SIFT features extracted from all the exemplars were put into a metaphorical bag, and k-means clustering was performed on this bag to obtain a common vocabulary of 1,000 visual words (k = 1,000). The 64 hue features from the color histogram were concatenated to the end of the SIFT BoW histograms generated from this vocabulary to create a 1,064-dimensional feature space in which each of the 4,800 exemplars could be represented as a BoW histogram, with each bin of the histogram corresponding to 1 of the 1,064 visual-word features and the height of each bin indicating the frequency of that feature in that exemplar.

Having put all the category exemplars in a common feature space, we next found those features that were most representative of each target category. This process began by averaging the BoW exemplar histograms to obtain what might be called a prototype for each category (Rosch, 1973), although we avoid using this theoretically laden term so as not to associate a prototype with a particular step in the computation of CCFs. Each averaged category histogram captured the mean frequency of each of the 1,064 features in the category’s exemplars, along with the variance for each of these means (see Fig. S2 in the Supplemental Material for a partial averaged histogram for the “taxi” category, and see Fig. S3a for a visualization of every complete histogram contributing to the averaged histogram for that category).

Although methods for selecting features abound in the computer vision literature (e.g., R. T. Collins, Liu, & Leordeanu, 2005; Ullman, Vidal-Naquet, & Sali, 2002), most of these are tailored to finding features that discriminate between categories of objects for the purpose of classification. This makes them poorly aligned with our generative approach. Instead, feature selection under the CCF model is grounded in signal detection theory (Green & Swets, 1966). We assumed that features having a high frequency and a low variance were more important than the rest, and used these simple measures to prune away the other features. Specifically, we identified features having a high mean frequency over the category exemplars using the interquartile range rule: For a given category histogram, these features were those with an average frequency (X) greater than 1.5 * (Q₃(X) – Q₁(X)), where Q₁ and Q₃ are the first and third quartiles, respectively. The 1,000-dimensional SIFT features and the 64-dimensional color features were analyzed separately. For each of these frequently occurring features, we then computed the inverse of its coefficient of variation by dividing its mean frequency by its standard deviation, a commonly used method for quantifying a scale-invariant signal-to-noise ratio (SNR; Russ, 2011). Finally, k-means clustering, with k = 2, was performed on the SNRs of all features in the set to find a category-specific threshold to separate the important features from the less important features. The CCFs for a given category are defined as those features having SNRs falling above this threshold.

CCFs are therefore the features that occur both frequently and reliably across the exemplars of a category, and each category has different CCFs in this 1,064-dimensional feature space. These CCFs, and not the noisier category histogram formed by simply averaging exemplar histograms, are what we believe constitute the learned visual representation of an object category (see Fig. S3b in the Supplemental Material for the CCFs from the “taxi” category and note how they compare with the corresponding averaged category histogram in Fig. S3a).

Results

Can the CCF model capture the patterns of target guidance and verification observed in behavior? We show that these two very different patterns can be modeled as different properties of the same CCF category representations.

Target guidance

The behavioral data showed that target guidance got weaker as targets were cued at higher levels in the category hierarchy. Guidance was strongest following a subordinate-level cue, weaker following a basic-level cue, and weakest following a superordinate-level cue. How does the CCF model explain target guidance and its change across hierarchical levels?

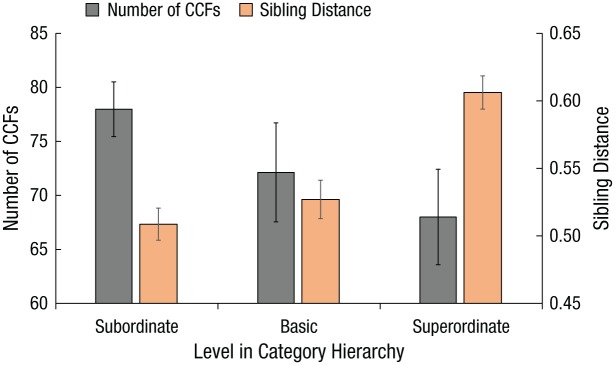
According to the CCF model, target guidance is proportional to the number of CCFs used to represent a target category. The logic underlying this prediction is straightforward. To the extent that CCFs are the important features in the representation of a category, more CCFs mean a better and more specific category representation (see also Schmidt, MacNamara, Proudfit, & Zelinsky, 2014). A target category having a larger number of CCFs would therefore be represented with a higher degree of specificity and, consequently, fixated more efficiently than a target having a sparser “template” (Schmidt & Zelinsky, 2009). As shown in Figure 6, the number of CCFs per category indeed varied with hierarchical level; the subordinate-level categories had the most CCFs, followed by the basic-level and finally the superordinate-level categories. This too was predicted. Subordinate-level categories have more details in common that can be represented and selected as CCFs, whereas at the higher levels, greater variability between exemplars causes features to be excluded as CCFs, so there is a smaller total number.

Fig. 6.

Mean number of category-consistent features (CCFs) and mean sibling distance from the CCF model by hierarchical level. Error bars indicate ±1 SEM, computed by treating the number of categories at each level as the number of sample observations (n).

Figure 4 shows that the effect of hierarchical level on target guidance can be captured simply by the mean numbers of CCFs extracted for the 48 subordinate-level target categories, the 16 basic-level categories, and the 4 categories at the superordinate level. Specifically, we linearly transformed the mean number of CCFs at each level to put these means into the same scale as the behavioral data and then plotted these transformed means in Figure 4b to capture the downward trend in the proportion of immediate target fixations. The multiplicative inverses (1/number of CCFs) of these transformed means are plotted in Figure 4a to capture the increase in time to target (poorer guidance) with movement up the category hierarchy. The model’s behavior fell within the 95% CIs surrounding all six of the behavioral means. This finding has implications for search theory. It suggests that the stronger target guidance reported for exemplar search (e.g., targets cued by picture preview) compared with categorical search (e.g., targets cued by category name) may be due, not to a qualitative difference in underlying processes, but rather to a quantitative difference in the number of “good” features in the target representations used to create the priority maps that ultimately guide search (Zelinsky & Bisley, 2015). Many strong guiding features can be extracted when the opportunity exists to preview a specific target exemplar, but strong guidance in a categorical search task requires a target category represented by many CCFs.

Target verification

If more CCFs enable greater specificity in the target representation, the converse is also true. With movement up the category hierarchy, decreasing numbers of CCFs incur a cost to specificity; this cost is greatest for superordinate-level categories, least for subordinate-level categories, and in between for basic-level categories. We show that target verification can be modeled by combining this trend with a second and opposing trend, one based on the distance to neighboring categories.

Sibling distance

In the context of a categorical search task, the target-verification epoch is the time between the first fixation on the target and the correct target-present judgment. The CCF model predicts that this time is proportional to the distance between the CCFs of the target category and the features of the exemplars composing the target’s categorical siblings, which are defined as categories sharing the same parent (one level up in the category hierarchy). This logic is also straightforward. Verification difficulty should depend on the distance between the target category and the most similar nontarget categories in the test set; as this distance increases, target verification should become easier. This follows from the fact that smaller distances create greater potential for feature overlap between categories, and to the extent that this happens, one category might become confused with another. In the present context, these least distant, most similar nontarget categories would be the categorical siblings of the target category. If the target was a police car, the nontarget objects creating the greatest potential for confusion would be exemplars of race cars and taxis, and these objects would largely determine the difficulty of verifying the presence of a police car. Indeed, members of these sibling categories were the same objects used as categorical lures in order to obtain our behavioral demonstration of a basic-level advantage.

To model the distance between a target category and its categorical siblings, we computed for each sibling category the mean chi-squared distance between its CCF histogram and the BoW histogram for every exemplar under the parent category. We denote the full set of BoW bins as F = {1, . . ., 1,064} and the CCFs for target category k as F′k, such that k ∈ {1, . . ., 68} and F′_k are indices to a subset of bins in F (i.e., F′_k ⊆ F). Chi-squared distance is defined as follows:

$${\mathrm{\chi }}^2\left(x,y\right)=\frac{1}{2}{\displaystyle \sum }_i\frac{{({\mathrm{\varphi }}_i\left(x\right)-{\mathrm{\varphi }}_i(y))}^2}{{\mathrm{\varphi }}_i\left(x\right)+{\mathrm{\varphi }}_i\left(y\right)},$$

where x and y are the two histograms to be compared, and φ_i is the value at the ith bin of the 1,064-bin feature histogram. Note, however, that following the dimensionality reduction that occurred in selecting the CCFs, the sibling CCF histograms may no longer be in the same feature space as the BoW histograms for the exemplars. To compute the distances, we therefore had to put the CCF and BoW histograms back into a common feature space, and we did this by adopting the following algorithm. For comparisons between a given CCF histogram of category k and the BoW histograms for the category’s exemplars, chi-squared distances were computed for only those bins in the BoW histograms for which there were corresponding bins in the CCF histogram, such that i ∈ F′_k. For comparisons between the exemplar histograms from category j and the CCF histogram from a sibling category, k, chi-squared distances were limited to the feature space formed by the union of the CCF histograms for the two categories, such that i ∈ ∪ (F′_j, F′_k).

For example, consider two sibling categories, A and B, that have nonidentical CCF bins (F′_A ≠ F′_B) forming CCF histograms µ(A) and µ(B) based on exemplars A_n and B_n, where n denotes all of the exemplars for a given category (in this study, n = 100, 300, or 1,200, depending on whether the category is at the subordinate, basic, or superordinate level). We compute the chi-squared distances between µ(A) and the BoW histograms obtained for all of A’s exemplars, A_n, for which there are corresponding bins in F′_A. If we denote the distance between the CCF histogram of A and all the A exemplar histograms as d_A,A, then

$$d_{\mathrm{A},\mathrm{A}}=\frac{1}{N}{{\displaystyle \sum }_{n=1}^N}^2{\mathrm{\chi }}^2(\mathrm{\mu }\left(\mathrm{A}\right),{\mathrm{A}}_n\mathrm{|}i\mathrm{ϵ}{\mathrm{F}}_{\mathrm{A}}^{\prime }).$$

We also compute the chi-squared distances between µ(A) and the BoW histograms obtained for all of B’s exemplars, d_A,B, with these comparisons limited to the bins forming the union of the F′_A and F′_B CCF histograms, such that

$$d_{\mathrm{A},\mathrm{B}}=\frac{1}{N}{{\displaystyle \sum }_{n=1}^N}^2{\mathrm{\chi }}^2(\mathrm{\mu }\left(\mathrm{A}\right),{\mathrm{B}}_n\mathrm{|}i{{\displaystyle \mathrm{ϵ}\cup }}^{}({\mathrm{F}}_{\mathrm{A}}^{\prime },{\mathrm{F}}_{\mathrm{B}}^{\prime })).$$

Doing the same for µ(B) and the BoW histograms of the B exemplars and the A exemplars, gives us d_B,B and d_B,A, respectively. Finally, taking the mean over the hundreds of distances in the sets d_A,A, d_A,B, d_B,B, and d_B,A, we obtain an estimate of the distance between sibling categories A and B, which we refer to as sibling distance.

To the extent that smaller sibling distances mean more difficult category-verification decisions, the CCF model predicts a verification benefit for target categories designated at higher levels in the hierarchy. Computing sibling distances for all 68 target categories, then averaging within hierarchical level, we found that subordinate-level categories were closest to their sibling exemplars and that superordinate-level categories had the largest mean sibling distance (Fig. 6). Verification times for race cars should therefore be relatively long because of the proximity of this category to taxi and police-car exemplars, whereas shorter verification times are predicted for vehicles because of this category’s greater mean distance to Oreo cookies and other sibling exemplars. The basic-level categories fall in between subordinate and superordinate categories with respect to sibling distance and should therefore have an intermediate level of verification difficulty.

Basic-level superiority effect

In our behavioral experiment, however, we did not find this predicted speedup in target-verification times with movement up the hierarchy. Instead, we found the often-observed BSE: faster verification for targets cued at the basic level compared with those cued at the subordinate or superordinate level. Our explanation of the BSE is consistent with early explanations (Murphy & Brownell, 1985) in suggesting that there is a trade-off between two interacting processes, specificity, which we operationalized as the number of CCFs for a given category, and distinctiveness, which we operationalized as the distance between the CCFs of a given category and the features of its sibling exemplars. Indeed, the countervailing trends illustrated in Figure 6 reflect these opposing processes. To model their net impact on target-verification time, we simply multiplied one by the other. Specifically, to obtain a (unit-less) estimate of each category’s verification difficulty, we multiplied its number of CCFs by its sibling distance. At each hierarchical level, we averaged these values to obtain a mean, and we then linearly transformed the three means for the three levels into the behavioral scale. The results are shown in Figure 4c. As was the case for target guidance, the model’s estimates fell within the 95% CIs surrounding the behavioral means. In a control experiment, we found that when the same numbers of visual-word features were randomly selected, the model did not predict the BSE observed in behavior (see Fig. S4 in the Supplemental Material). Any features will not do—these features have to be CCFs.

Although categories at the subordinate level have the most CCFs (a specificity benefit), they also have the smallest sibling distance (a distinctiveness cost). This results in an intermediate degree of verification difficulty. Superordinate-level categories have the opposite pattern, relatively few CCFs (a specificity cost) but a large sibling distance (a distinctiveness benefit). This, again, results in an intermediate degree of verification difficulty. Basic-level categories occupy a privileged position in the hierarchy that avoids these two extremes. They have a relatively high number of CCFs while also being relatively distant from their sibling exemplars. This favorable trade-off between distinctiveness and specificity produces the BSE, faster verification at the basic level relative to the levels above and below.

Predicting search behavior using the CCF model

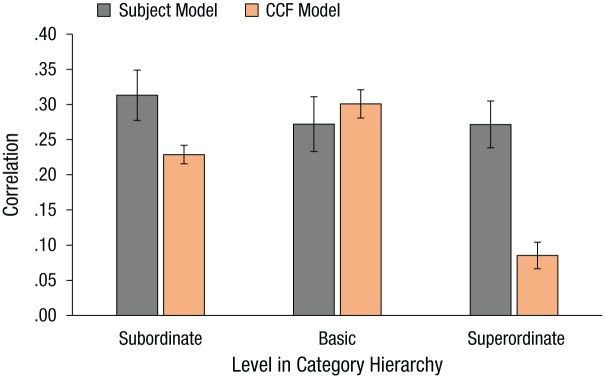
The analyses we have discussed thus far demonstrated that the CCF model captured trends observed in target guidance and verification across the superordinate, basic, and subordinate levels, but can this model also predict behavior within each of these categorical levels? As a first step toward answering this question, we conducted a trial-by-trial analysis to determine how well the model could predict search guidance to an exemplar of the target category. For each target-present trial in which the target was fixated and the response was correct, we computed the chi-squared distance between the CCF representation of the target category and the target exemplar appearing in the search display. We then correlated these distances with the time-to-target measure of target guidance obtained for these trials. To evaluate the CCF model’s predictions, we used the leave-one-out method to derive a subject model, which indicated how well the mean target guidance of n – 1 (N = 26) subjects predicted the guidance of the subject left out. This analysis provided a rough upper limit on the predictive success of the CCF model, as correlations higher than those of the subject model would not be expected given variability in participants’ guidance behavior.

Figure 7 plots the correlations between time to target and both the subject model and the CCF model at each hierarchical level. Paired-group t tests revealed that the correlations did not differ reliably between the CCF and subject models at the subordinate (p = .078) or basic (p = .334) level, but were significantly different at the superordinate level (p < .001). The poor correlation for the CCF model at the superordinate level is consistent with the absence of guidance at this level, as indicated by the chance-level proportion of immediate target fixations in the behavioral experiment (Fig. 4b). These findings suggest not only that the CCF model predicted the fine-grained search behavior occurring on individual trials, but also that the model’s predictions at the subordinate and basic levels were as good as could be expected given the level of agreement in the participants’ behavior.

Fig. 7.

Comparison of the trial-by-trial predictive success of the category-consistent features (CCF) model and a subject model at each hierarchical level. For the CCF model, the graph shows the averaged correlations (using Fisher’s r-to-z transformation) between the model’s predicted distances to the target exemplars and the time-to-target measures from the behavioral experiment. The correlations for the subject model capture the agreement among participants in their time-to-target guidance behavior. Error bars indicate ±1 SE.

Conclusion

Categories determine how people interact with the world. Understanding the forces that shape category representation is therefore essential to understanding behavior in every domain of psychological science. We have introduced a computational model of category representation, one that accepts image exemplars of common object categories and finds the features that appear frequently and consistently within each category’s exemplars—what we refer to as CCFs.

We validated the CCF model through comparison with behavior in a categorical search task. Categorical search is important and has diverse applications. When security screeners search for weapons, or radiologists search for tumors, they are engaging in categorical search. Categorical search is also unique in that this single task enables study of both the representations used to guide attention to categorically defined targets and the representations underlying the recognition of these objects as members of the target category. We manipulated the hierarchical level at which categorical targets were cued and found that these attention and recognition processes were expressed in very different behavioral patterns. A subordinate-level advantage was evident for target guidance; targets cued at the subordinate level were preferentially fixated compared with targets cued at the basic or superordinate level. In contrast, a basic-level advantage was evident for target verification; fixated objects were verified faster as members of the target category following a basic-level cue compared with a subordinate or superordinate-level cue.

In the CCF model, both patterns depend on the number of CCFs extracted from exemplars at each hierarchical level. Target guidance weakens with movement up the category hierarchy because exemplar variability at the higher levels restricts the formation of CCFs, which results in less effective target templates for guiding search (Olivers, Peters, Roos, & Roelfsema, 2011). The CCF model advances existing theory on search and visual working memory by making explicit the processes of extracting visual features from image exemplars of real-world categories and consolidating these features into lower-dimensional category representations (CCFs) that can be used to guide search. The CCF model also provides a theory for understanding effects of category hierarchy (Maxfield & Zelinsky, 2012) and target specificity (Schmidt & Zelinsky, 2009) on search behavior; search is guided more efficiently to targets specified lower in the category hierarchy because these objects would usually be represented using more CCFs.

Target verification was modeled as a multiplicative interaction between the number of CCFs and sibling distance, the latter a measure of similarity between the CCFs of a target category and the features of exemplars in its sibling categories. In this approach, we appealed to the core principles of specificity and distinctiveness that have been guiding categorization research for decades (Murphy & Brownell, 1985). The number of CCFs maps onto the idea of specificity. Subordinate-level categories are the most specific because they give rise to many CCFs. Sibling distance maps onto the idea of distinctiveness. Verification suffers with movement down the hierarchy because target representations start to share too many features with their closest categorical neighbors. The CCF model advances categorization theory by making these core principles computationally explicit and applicable to real-world object categories.

Of potentially even broader theoretical significance is the question of whether search and categorization share the same target representation: Are the visual features used to guide overt attention to a categorical target in a search display the same as those used to categorize the target once it is fixated? The CCF model suggests that they are, and to the extent that this suggestion is supported through converging evidence (Zelinsky, Peng, et al., 2013), a strong theoretical bridge will be built between the attention and categorization literatures. Future work using deep convolutional neural networks to extract CCFs will extend this bridge to the computer vision and computational neuroscience literatures. Supervision is a powerful learning tool (Khaligh-Razavi & Kriegeskorte, 2014), and combining it with the generative extraction of features from exemplars may lead to significant advances in the understanding of category representation.

The CCF model makes possible the rigorous study of how the features of visual object categories can be learned and represented from exposure to the vast numbers of diverse image exemplars accumulated throughout everyday experience. Recent decades have seen scientific doors to the real world open for many psychological processes. The CCF model opens another such door into categorization.