The effect of frequency-dependent attenuation on predicted histotripsy waveforms in tissue mimicking phantoms

Abstract

Tissue-mimicking phantoms are employed for the assessment of shocked histotripsy pulses in vitro. These broadband shockwaves are critical for tissue ablation, and are influenced by the frequency-dependent attenuation of the medium. The density, sound speed, and attenuation spectra (2–25 MHz) were measured for phantoms that mimic key histotripsy targets. The influence of nonlinear propagation relative to the attenuation was described in terms of the Gol’dberg number. An expression was derived to estimate the bandwidth of shocked histotripsy pulses for power law-dependent attenuation. The expression is independent of the fundamental frequency of the histotripsy pulse for linear frequency-dependent attenuation.

Introduction

Histotripsy is a focused ultrasound therapy that fractionates tissue mechanically through microbubble cloud formation (Xu et al. 2004). Microbubble clouds form through scattering of the shocked histotripsy pulse from a nucleated cavity at the focus combined with constructive interference with the incident shockwave (Maxwell et al. 2011). The degree of shockwave formation is influenced by the frequency-dependent attenuation of the medium (Hamilton and Blackstock 1998). Recent studies by Maruvada et al. (2015) indicate that accurate measurements of the frequency dependence of attenuation are critical for prediction of focused ultrasound fields. The bandwidth used for attenuation measurements of tissue and tissue-mimicking materials is typically less than 10 MHz (Bamber and Hill 1979; Duck 1990; Lin et al. 1987; Madsen et al. 1978), much less than the bandwidth of the shocked histotripsy pulse (Parsons et al. 2006).

The objective of this study was to ascertain the influence of frequency-dependent attenuation on the bandwidth of shocked histotripsy pulses. An insertion loss method was used to measure the frequency-dependent attenuation (2–25 MHz) for types of tissue-mimicking phantoms. Prostate and liver mimicking phantoms were manufactured following Madsen et al. (1998). An agar phantom used for in vitro assessment of histotripsy was manufactured following Maxwell et al. (2010). Density, sound speed, and frequency-dependent attenuation were measured for each phantom. The influence of nonlinear propagation relative to the attenuation was analyzed in terms of the Gol’dberg number for each phantom material. An expression was derived to estimate the bandwidth of shocked histotripsy pulses for power law-dependent attenuation.

Methods and Materials

Production of phantoms

Attenuation measurements were made for only tissue mimicking materials in this study. All three types of phantoms were composed of agar, n-propanol, and evaporated milk. The ratio of these components is reported in Table 1 for each phantom. For the prostate and liver phantoms, commercially available evaporated milk (Meijer Brand, Meijer, Inc., Grand Rapids, MI) was filtered (pore size 100 μm), and gently stirred on a hot plate to reach a final temperature of 55°C. Agar powder (A9539 Sigma-Aldrich Co. St. Louis, MO) was dissolved into 0.2 μm filtered, deionized water (NANOPure, Barnstead International, Dubuque, IA, USA) and n-propanol solution by heating in 30 s increments in a standard microwave until clear. The heated solution was then placed in a heated (50°C) ultrasonic cleaning bath for 30 min while continuously evacuating at 2 kPa. The degassed agar/n-propanol solution was combined with the heated evaporated milk, poured into a mold, and allowed to solidify at 5°C. Agar phantoms were manufactured in a similar fashion, but without the addition of evaporated milk or n-propanol. The phantoms were made in triplicate (N=3) for each measurement.

Table 1.

Ratio of components used for manufacturing tissue phantoms.

Component	Prostate phantom	Liver phantom	Agar phantom
deionized water (18-MΩ)	147.2 mL	184 mL	400 mL
Agarose	3.7 g	2 g	6 g
n-propanol	12.8 mL	16 mL	—
evaporated milk	240 mL	200 mL	—

Density and sound speed measurements

The phantom mass was measured using a standard laboratory balance (AE100, Mettler-Toledo, Columbus, OH, USA), and the volume was measured using a water displacement technique (Hughes 2005). The phantom density was calculated as the mass divided by the volume. The sound speed of each of the three phantoms were measured using a through-transmission substitution technique (Selfridge 1985; Zell et al. 2007).

Broadband attenuation measurements

The frequency-dependent attenuation spectra of the phantoms were measured using a broadband through-transmission technique (Marsh et al. 1997), as described in Raymond et al. (2013) Briefly, a pair of broadband polyvinylidene fluoride transducers (PI-20, Olympus NDT, Waltham, MA, USA) were employed to acquire the spectrum after passing through the phantom material. A pulser-receiver (Panametrics 5077 PR, Olympus NDT) generated the excitation pulse (pulse repetition frequency of 100 Hz) and amplified the received signal (25 dB gain).

The received waveforms were averaged (256 traces per acquisition) and digitized (LT572, LeCroy, Chestnut Ridge, NY, USA; 16 bits, 1-GHz sampling rate) for analysis offline. The frequency-dependent attenuation coefficient, α(f), was calculated as:

$${\alpha }_{\mathit{meas}}(f)=10{\mathit{log}}_{10}(\frac{\left|V_{\mathit{sample}}{(f)}^2\right|}{\left|V_{\mathit{ref}}{(f)}^2\right|})/d$$ (1)

Where V_ref and V_Sample are the received amplitude spectra of the measured voltage-time waveforms through the water path and phantom sample, respectively. The phantom thickness, d, was adjusted to ensure optimal signal to noise over the bandwidth of the measurement. The frequency-dependent attenuation was fit in the least squares sense to a power law of the form

$${\alpha }_{\mathit{meas}}(f)={\alpha }_0{f}^{\mathit{PL}}$$ (2)

where α₀ and PL were fitting parameters, and f was frequency in MHz.

Predicted bandwidth of shockwave for frequency-dependent attenuation

The presence of high frequency components during shockwave formation of the histotripsy pulse depends on the degree of nonlinearity and attenuation of the medium. The influence of nonlinear propagation relative to the attenuation can be described in terms of the Gol’dberg number (Hamilton and Blackstock 1998), Γ:

$$\Gamma =\frac{2\pi f\beta p}{\rho c^3\alpha }$$ (3)

where β is the coefficient of nonlinearity, ρ is the medium density, c is the medium sound speed, p is the pressure amplitude, and α is the attenuation at frequency f. The amplitude of the m^th harmonic of the fundamental frequency present in the shocked histotripsy pulse, P_m, can be expressed as (Hamilton and Blackstock 1998):

$$P_m=\frac{P_{\mathit{SHOCK}}}{m\pi }$$ (4)

where P_SHOCK is the positive pressure of the histotripsy pulse. The Gol’dberg number of the m^th harmonic of the shocked histotripsy pulse, Γ_m, is expressed by substituting eqns. (2) and (4) into eqn. (3):

$$\Gamma =\frac{2\beta P_{\mathit{SHOCK}}}{\rho c^{3}m{\alpha }_0{(m{f}_0)}^{\mathit{PL}-1}}$$ (5)

where f₀ is the fundamental frequency of the histotripsy pulse. Harmonics with Γ_m less than 1 will be readily attenuated, and will not contribute to shockwave formation. Setting Γ_m equal to 1 in eqn. (5) and solving for m, the critical harmonic that will be readily attenuated, m_crit, can be expressed as:

$$m_{\mathit{crit}}={\left[\frac{2\beta P_{\mathit{SHOCK}}}{\rho c^3{\alpha }_0{f}_0^{\mathit{PL}-1}}\right]}^{1/\mathit{PL}}$$ (6)

Results

Density and Sound Speed

The measured densities and sound speeds of each phantom are reported in Table 2. The prostate and liver phantoms had sound speeds of 1520 ± 30 m/s and 1530 ± 4 m/s, respectively. The agar phantom had a sound speed of 1500 ± 13 m/s. The nominal density of all the phantoms was 1.0 g/mL.

Table 2.

Measured physical properties of the three tissue phantoms in this study. Best-fit parameters for α₀ and PL were calculated over 2–25 MHz. The best-fit parameter α₀ was also calculated over 2–10MHz assuming a linear power law (PL = 1). The goodness of fit parameter coefficient of determination (r²) is also reported.

Material	Density [g/mL]	Sound speed [m/s]	α0 [dB cm−1 MHz−PL]	PL [A.U.]	r2
Prostate phantom	1.04 ± 0.03	1523 ± 30	0.36 ± 0.01	1.12 ± 0.01	0.999
			0.46 ± 0.01	1	0.993
Liver phantom	1.05 ± 0.03	1532 ± 4	0.32 ± 0.01	1.09 ± 0.01	0.999
			0.41 ± 0.003	1	0.995
Agar phantom	1.01 ± 0.07	1497 ± 13	0.02 ± 0.07	1.57 ± 0.01	0.999
			0.09 ± 0.003	1	0.922

Attenuation Spectra

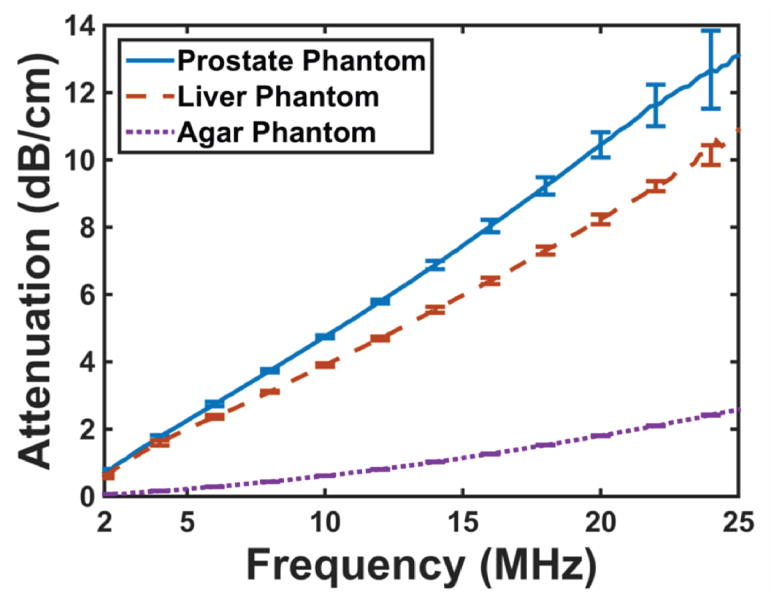
The frequency-dependent attenuation spectrum for each of the phantoms is shown in Figure 1a. The error bars represent the standard deviation (N = 3). The average attenuation spectra for each phantom were fit in the least-squares sense using the power law described by eqn. (2). Values for the fitting parameters in eqn. (2) are presented in Table 2. The power law fit for attenuation spectra agreed well with the measured attenuation spectra over the entire bandwidth of the measurement (Figure 1b), with a coefficient of determination greater than 0.99 for all three phantoms.

Figure 1.

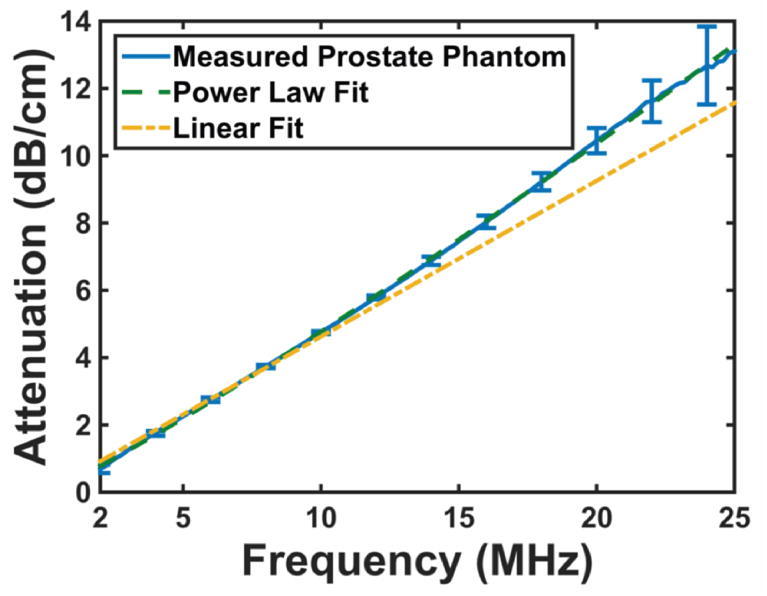
(a) Attenuation spectra for each of the tissue phantoms between 2 and 25 MHz. The error bars are representative of the standard deviation (N = 3). (b) Measured attenuation spectra for prostate phantom (solid blue line), along with a power law fit (long dashed green line). The short dashed yellow line is a linear fit to the attenuation data between 2 and 10 MHz. Less than 3% difference is observed between the data and both fits below 10 MHz. The linear fit underestimates the measured attenuation for frequencies above 10 MHz.

Measured attenuation spectra are typically assumed to have a linear frequency dependence (i.e. eqn. (2) with PL set to 1) (Duck 1990) over a bandwidth less than 10 MHz (Madsen et al. 1998). Attenuation spectra between 2 and 10 MHz were also fit to a linear power law (eqn. (2) with PL = 1). The best-fit slope parameter is also presented in Table 2. The linear fits agreed well with the measured data up to 10 MHz. However, the attenuation was underestimated at frequencies greater than 10 MHz (Figure 1b). The power law fit agreed well with the measured data over the entire 2 to 25 MHz measurement bandwidth.

Attenuation of Histotripsy Shockwave

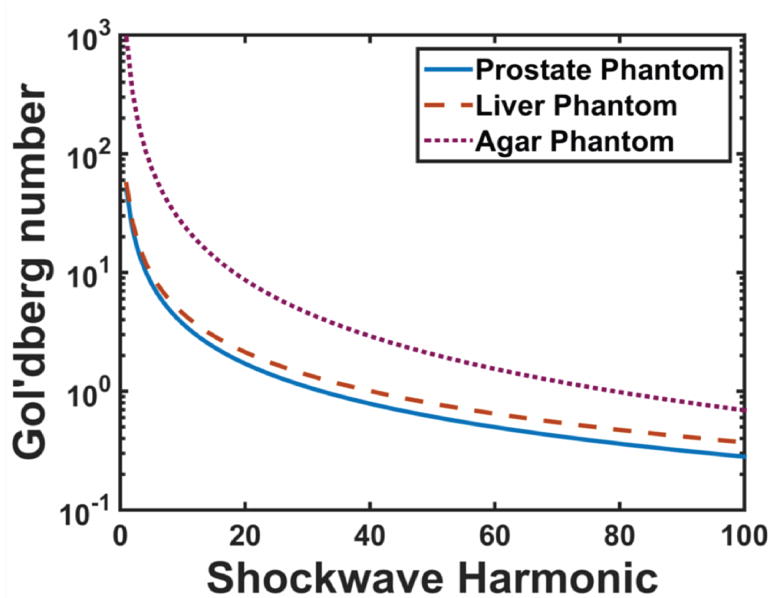
The harmonic-dependent Gol’dberg number calculated via eqn. (5) is shown in Figure 2a for each phantom, assuming a 1 MHz fundamental frequency histotripsy pulse with a 80 MPa peak positive pressure (Maxwell et al. 2012). The attenuation variables α₀ and PL used to evaluate eqn. (5) were the best-fit parameters for the power law fit for each of the phantoms (Table 2). The coefficient of nonlinearity was assumed to be 4.3 for the phantoms (Dong et al. 1999).

Figure 2.

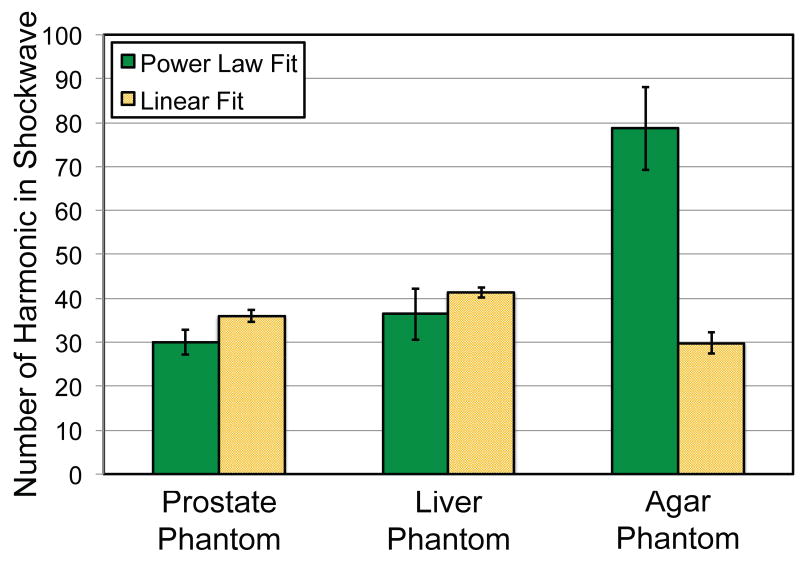
(a) The Gol’dberg number calculated via eqn. (5) for harmonics of a histotripsy pulse with a 1 MHz center frequency and 80 MPa peak positive pressure. The attenuation variables α₀ and PL used to evaluate eqn. (5) were the best-fit parameters for the power law fit for each of the phantoms (Table 2). (b) The number of harmonics present in the shockwave calculated via eqn. (6). For each of the phantoms, eqn. (6) was evaluated using best-fit parameters α₀ and PL in Table 2 for power law and linear power law (PL = 1) attenuation. Error bars indicate propagation of error due to the measured sound speed, density, and attenuation power law fitting parameters α₀ and PL.

The critical harmonic was calculated for each of the phantoms using eqn. (6), and is shown in Figure 2b. For each of the phantoms, eqn. (6) was evaluated using best-fit parameters α₀ and PL in Table 2 for power law and linear power law (PL = 1) attenuation. The linear power law for attenuation overestimates the bandwidth of the shockwave by 7 harmonics for the prostate and liver phantoms (PL ~ 1.1), but underestimates the number of harmonics by 48 for the agar phantom (PL = 1.57).

Discussion and Conclusions

The measured density and sound speed of these phantoms are similar to the target tissues (Fedewa et al. 2006; Mountford and Wells 1972; Parker et al. 1993; White et al. 1987), and are within an acceptable range for most soft tissue (D’Souza et al. 2001). The attenuation spectra fitting parameters are also consistent with previous measurements of ex vivo tissue found in the literature. The attenuation frequency power law, PL, for human prostate tissue is reported to be between 1 and 1.1, and α₀ ranges from 0.09 to 0.78 (Christopher 2005; Parker et al. 1993). For human liver, PL varies between 0.81 and 1.5 (Parker et al. 1984), and α₀ ranges from 0.40 to 0.7 (Lin et al. 1987). Maxwell et al. (2010) measured the attenuation of an agar phantom, and found a linear frequency dependence for attenuation between 1 and 5 MHz. Interestingly, the current study found the agar phantom exhibited a frequency exponent of 1.57, which is higher than either the prostate or liver phantoms, which were approximately 1.10. This frequency dependence indicates that the attenuation mechanisms in the agar phantom are closer to those in water (PL = 2). The agar phantom also had a lower attenuation coefficient over the bandwidth of the measurement (2–25 MHz) than either the prostate or liver phantoms.

A linear frequency dependence for the attenuation coefficient is valid up to approximately 10 MHz (see Fig. 1b). Beyond 10 MHz, the linear fit underestimates the attenuation coefficient. Frequency components above 10 MHz are present during histotripsy pulses, but their persistence depends on the relative degree of nonlinear propagation versus attenuation of the medium. Shock scattering histotripsy requires the formation of a microbubble cloud for tissue ablation (Xu et al. 2005). The precipitating event for microbubble cloud formation is the expansion of a single bubble, which scatters the shockwave geometrically (Maxwell et al. 2011). The portion of the incident shockwave that is scattered depends on the size of the bubble (Anderson 1950), which is dictated by the rarefactional pressure of the histotripsy pulse (Bader and Holland 2015). Equation (6) can be used to determine the number of harmonics that will contribute to shockwave formation, and potentially shockwave scattering. Note that if the frequency dependence of attenuation of the medium is linear (PL = 1), the bandwidth of the shockwave will independent of the fundamental frequency of the histotripsy pulse.

There are several aspects of this study that limit these findings. The attenuation measurement was done with an insertion loss technique, which neglected reflections of the incident pulse from the sample. Based on the measured acoustic impedance of the phantoms, the reflection coefficient (Pierce 1989) between the fluid and phantom was less than 4%. The influence of frequency-dependent attenuation on shockwave formation merits further investigation, and will require solving the Westervelt equation numerically for the highly focused fields require to generate histotripsy pulses (Soneson 2012). A finite-difference model will be employed in the future to study the influence of the frequency dependence of the attenuation on histotripsy shockwave formation in order to verify the predictions of eqn. (6) (Bader and Holland 2015).