Abstract
Multiple-demand (MD) regions of the human brain show coactivation during many different kinds of task performance. Previous work based on resting-state functional magnetic resonance imaging (fMRI) has shown that MD regions may be divided into two closely coupled subnetworks centered around the lateral frontoparietal (FP) and cingulo-opercular cortex. Here, we used on-task fMRI to test whether this division is apparent during the performance of an executive task. Furthermore, we investigated whether there is a difference in the encoding of task between the two subnetworks. Using connectivity methods, we found that activity across the entire MD cortex is correlated during task performance. Meanwhile, however, there was significantly stronger connectivity within each of the subnetworks than between them. Using multivoxel pattern analysis, we also found that, although we were able to decode task-relevant information from all regions of the MD cortex, classification accuracy scores were significantly higher in the FP subnetwork. These results suggest a nested picture with MD regions as a whole showing coactivation and broad rule representation, but with significant functional distinctions between component subnetworks.
SIGNIFICANCE STATEMENT Multiple-demand (MD) regions of frontal and parietal cortex appear essential for the orchestration of goal-directed behavior and problem solving. Understanding the relative specialization of regions within the MD cortex is crucial to understanding how we can coordinate and execute complex action plans. By examining functional connectivity during task performance, we extend previous findings suggesting that the MD cortex can be divided into two subnetworks centered around the frontoparietal (FP) and cingulo-opercular (CO) cortex. Furthermore, using multivoxel pattern analysis, we show that, compared with the CO subnetwork, the FP subnetwork manifests more differentiated coding of specific task events.
Keywords: cognitive control, dual networks, executive function, multiple demand
Introduction
The performance of many different tasks involves coordinated activity of a large-scale brain network variously termed the multiple-demand (MD) cortex or cognitive control network. Multiple studies have established that the same regions are coactivated when subjects are engaged in many kinds of goal-directed behavior: the dorsolateral prefrontal cortex (DLPFC), inferior frontal junction (IFJ), intraparietal sulcus (IPS), dorsal anterior cingulate cortex and presupplementary motor area (DACC), and the anterior insula (AI) (Cabeza and Nyberg, 2000; Duncan and Owen, 2000; Cole and Schneider, 2007; Duncan, 2010, 2013; Fedorenko et al., 2013).
An important requirement for goal-directed behavior is the maintenance and execution of the relevant steps that lead toward that goal. Within psychological paradigms, this often manifests as explicit task rules. The primate literature is rich with evidence suggesting that the DLPFC is particularly important in encoding task rules (Miller, 2000; Freedman et al., 2001; Kusunoki et al., 2010; Buschman et al., 2012; Stokes et al., 2013). Furthermore, through human functional magnetic resonance imaging (fMRI) studies in particular, evidence has accumulated that the wider MD cortex is also important in the learning and execution of rules (Cole et al., 2011; Dumontheil et al., 2011; Woolgar et al., 2011a, 2011b).
It is apparent, however, that the component regions of the MD cortex are far from homogeneous (Derrfuss et al., 2004; Ramnani and Owen, 2004; Menon and Uddin, 2010; Crittenden and Duncan, 2014; Matsuyoshi et al., 2012; Shenhav et al., 2013). Indeed, a particularly interesting line of investigation has indicated that the broad MD system may be further divided into two closely coupled subnetworks (Dosenbach et al., 2008). In proposing this dual-network architecture, Dosenbach et al., (2006) have argued for a distinction between a frontoparietal (FP) rapid adaptive control network and a CO sustained task-set maintenance network. They report that, across a variety of tasks, activation in the FP subnetwork (DLPFC, IFJ, and IPS) was strongly associated with trial-to-trial performance control, as demonstrated by significant activation associated with individual events of a mixed block-event-related design (Visscher et al., 2003). In contrast, the CO regions (DACC, AI, and anterior prefrontal cortex or APFC) showed additional sustained activity throughout a task block.
A potential distinction between the two subnetworks has further been demonstrated through analysis of temporal correlations in resting-state data (Dosenbach et al., 2007). Dosenbach et al. (2007) found that correlations between regions of interest (ROIs) within each of the FP and CO subnetworks were significantly stronger than between-network correlations. Furthermore, Nomura et al. (2010) found that lesion to an MD ROI reduced the network integrity of the subnetwork to which it belonged significantly more than the subnetwork to which it did not belong.
We also investigated whether separation of subnetworks is also apparent when subjects are engaged with a cognitive task. To test this, participants were required to perform an executive task composed of six rules (Fig. 1) during fMRI. Although the resting state is associated with unconstrained mind-wandering, the MD regions are most strongly engaged during executive task performance. Therefore, we performed a connectivity analysis over the entire task period to investigate the integrity of the MD network as a whole during task performance as well as the integrity of the CO and FP subnetworks within it. Furthermore, the present study used multivoxel pattern analysis (MVPA) on fMRI data to determine whether there are significant differences in the strength of rule representation within FP and CO subnetworks. We reasoned that, if the FP network is more engaged in the application of task rules to incoming sensory information, then this may require a stronger trial-specific representation of these rules, which would be apparent as a stronger decoding of task in the FP ROIs compared with the CO ROIs. A previous report based on the same data focused on the default mode network and its link to rule switching (Crittenden et al., 2015).
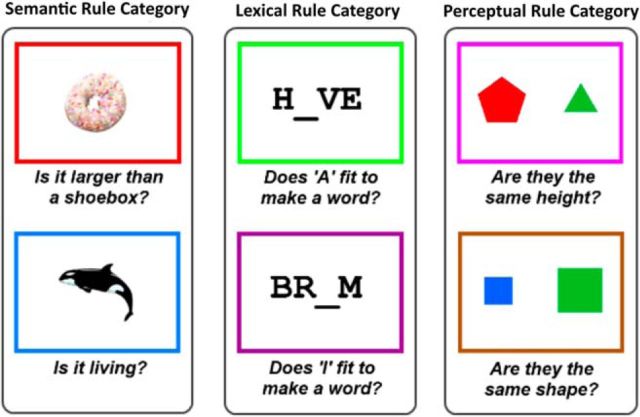
Figure 1.
Task rules. Subjects were trained to associate six different task rules with the color of a border surrounding the trial stimuli. Rules were grouped into three categories—semantic, lexical, and perceptual—with two alternative rules per category.
Materials and Methods
Subjects.
Eighteen right-handed subjects (10 females) between 18 and 40 years of age were recruited from the Medical Research Council Cognition and Brain Sciences Unit subject panel. Of 21 original subjects scanned, 3 had to be removed for excessive head movements (>10 mm translation and/or 6° rotation). None of the subjects was colorblind or had a history of neurological or psychiatric illness. The study was performed in accordance with ethical approval given by the Cambridge Psychology Research Ethics Committee. Subjects provided informed written consent and were reimbursed for their time.
Task description.
The task was created using the Psychophysics Toolbox (Brainard, 1997) for MATLAB. Within the scanner, the stimulus display was projected onto a mirror mounted to a 32-channel head coil. Stimuli were rendered on a light gray background and subtended a visual angle of ∼7.9°.
Subjects were required to learn six different tasks. Each task was associated with a different rule, with the appropriate rule determined by the color border in which the task stimulus appeared. The six task rules are shown in Figure 1. Rules were divided into three categories—semantic, lexical, and perceptual—with two alternative rules per category. For the semantic category, stimuli were pictures of real-world objects. A red border was associated with the rule: “Is it larger than a shoebox?,” blue with: “Is it living?” For the lexical category, stimuli were four-letter strings with an empty space. A green border was associated with the rule: “Does A in the empty space fit to make a word?,” purple with “Does I fit to make a word?” For the perceptual category, stimuli were pairs of geometric figures. A pink border was associated with the rule: “Are figures the same height?,” brown with “Are figures the same shape?” Shapes were regular polygons (triangle, square, pentagon, and hexagon), which varied in color (blue, green, red, and yellow), although color was always irrelevant. All questions were framed in a true/false format (right thumb button press = true, left thumb button press = false) so that arbitrary response mappings for each rule did not have to be learned in addition to the rules themselves. All categories included stimuli that required a positive answer for both potential rules (25%), for one rule but not the other (50%), or for neither rule (25%); therefore, subjects needed to remember and apply the correct rule on all trials.
Each trial began with the simultaneous appearance of the color border and the task stimulus, which both remained until the response. Subjects were requested to respond as quickly as possible. A low tone was played to subjects if they made an incorrect response. There was a jittered interval between the response to one trial and the onset of the next. Interval jittering followed an exponential distribution between 1 and 11 s, with a mean of 4.1 s.
Procedure.
Before scanning, subjects practiced the task until they had completed at least 20 trials with an accuracy exceeding 80%. Within the scanner, subjects then completed four runs of 73 trials each. Discarding the first trial, each run contained 12 trials with each task, divided equally between task repetitions, within-category switches, and between-category switches. The distinction between switch types has been described previously (Crittenden et al., 2015) and is not relevant here. After scanning, when questioned, no subjects reported having any sense of what task to expect from one trial to the next.
fMRI acquisition.
Scans were acquired with a 3T Siemens Trim Trio scanner; 32 3 mm slices (0.75 mm interslice gap) in axial orientation gave an inplane resolution of 3 × 3 mm and were acquired using a TR of 2 s. T2*-weighted echo-planar imaging (EPI) capturing blood oxygen level dependent (BOLD) contrast was used with a flip angle of 78°. For both experiments, the first 8 images were discarded to avoid T1 equilibration effects.
fMRI analysis.
Images were preprocessed and analyzed with SPM8 (Wellcome Department of Cognitive Neurology). In the first preprocessing step, individual data were checked visually to ensure that the acquisition window was appropriately placed and that there were no obvious artifacts or distortions, such as those caused by movement in either the structural or functional scans. All images were then realigned to the first image. Next, slice time correction and coregistration of the structural with the EPI images were performed. Finally, data were normalized to the standard Montreal Neurological Institute (MNI) template and subjected to a high-pass filter with cutoff at 128 s. For the connectivity analysis, data were smoothed with an 8 mm full-width-half-maximum Gaussian kernel. For MVPA, unsmoothed data were used.
ROIs were defined using data from Fedorenko et al. (2013), which are available online at imaging.mrc-cbu.cam.ac.uk/imaging/MDsystem. All were bilateral and included the DLPFC, IFJ, IPS, AI, DACC, and APFC.
Connectivity analyses were performed using the CONN toolbox (Whitfield-Gabrieli and Nieto-Castanon, 2012). Two sources of functional data were used for the connectivity analysis: in the first analysis, the EPI images that had been preprocessed as described but had undergone no further statistical analysis were used; in the second analysis, the residual images from a first-level general linear model performed in SPM8 were used (details in Results). Connectivity strength was calculated over the entire task period. Before subject-level analysis, standard preprocessing and denoising procedures using the default settings of the CONN toolbox were performed on the EPI data using the BOLD signal derived from white matter masks and CSF, as well as motion correction parameters from the realignment stage of the spatial preprocessing as covariates of no interest. The data were further band-pass filtered between 0.008 and 0.09 Hz. For each subject, the bivariate Fisher-transformed correlation was calculated for each pair of ROIs. Only ROI to ROI analyses were performed. Subsequent analysis compared Fisher-transformed correlation strengths within and between FP and CO subnetworks.
MVPA was performed using the Decoding Toolbox (Christophel et al., 2012; Hebart et al., 2015). Before MVPA, fixed-effects analyses were performed on each individual's data using a GLM with separate regressors for each of the six different rules. Each regressor was modeled as a rectangular function from the onset of each stimulus to the moment of response and convolved with the canonical HRF. The resulting β values from each task produced by the subject-wise fixed effects analyses were Z-scored across all voxels within each ROI. This step was intended to reduce any impact of task differences in overall ROI activity. Pattern discrimination between tasks was then estimated using pairwise classification; that is, only one of the 15 possible task pairs was decoded at a time. A support vector machine (LIBSVM) was used to train and classify data from three of the four runs, with the remaining run used to test the classifier. For each task pair, this procedure was repeated four times, once for each left-out run (fourfold cross-validation). The classification accuracy (CA) for a given ROI was averaged across test-train splits, yielding a single CA for each ROI, in each individual, for each task pair.
Results
Behavioral results
Performance accuracy on all tasks was high, with the median accuracy for all tasks >95% and an interquartile range of no more than 6% for any task. The mean and SD of the response times across the group for each task are shown in Table 1. By ANOVA with Greenhouse–Geisser correction for sphericity, tasks differed significantly in response time (F(3.1,53.1) = 8.86, p < 0.001). Table 2 shows the p-values resulting from two-tailed, paired t tests of all pairwise comparisons between tasks.
Table 1.
Mean response time (in milliseconds) of each task
| “shoebox” | “animal” | “A” | “I” | “shape” | “height” | |
|---|---|---|---|---|---|---|
| Mean | 1917 | 1514 | 1869 | 1852 | 1627 | 1790 |
| SD | 333 | 301 | 396 | 395 | 386 | 312 |
Table 2.
p-values from pairwise comparisons
| “shoebox” | “animal” | “A” | “I” | “shape” | “size” | |
|---|---|---|---|---|---|---|
| “shoebox” | — | |||||
| “animal” | <0.001 | — | ||||
| “A” | 0.58 | <0.001 | — | |||
| “I” | 0.35 | <0.001 | 0.76 | — | ||
| “shape” | 0.003 | 0.216 | 0.03 | 0.01 | — | |
| “size” | 0.067 | <0.001 | 0.035 | 0.331 | 0.002 | — |
The p-values resulting from 2-tailed, paired t test of all pairwise comparisons between tasks are shown. Numbers in bold represent significant differences after Bonferroni correction.
Connectivity results
We tested to what extent the MD network fractionated into the two subnetworks defined by Dosenbach et al. 2008 when subjects are in an active task state as opposed to a resting state. Fisher-transformed correlation values obtained for each ROI pair were averaged across subjects. The correlation matrix in Figure 2a shows the mean Z-value for each pair of ROIs. Two-tailed, paired t tests showed that all but eight pairs of ROIs were significantly positively correlated (Bonferonni corrected, p < 0.05). All eight of these nonsignificant pairs were between-subnetwork connections. Nonsignificant correlations are shown as gray squares in Figure 2a.
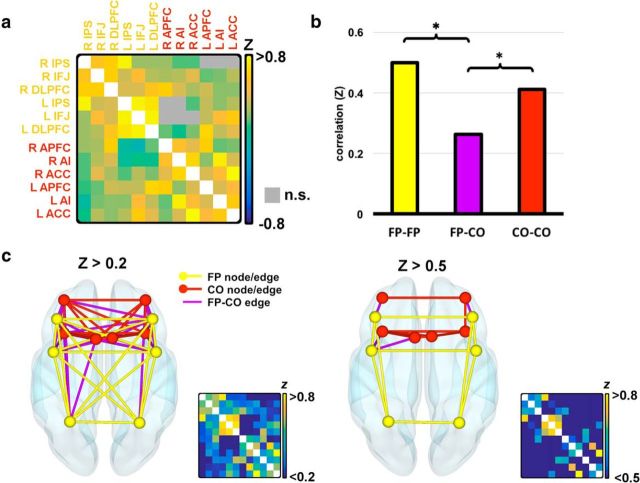
Figure 2.
Functional connectivity between MD ROIs. a, Fisher-transformed correlation values (Z) between all ROIs. Gray squares above the diagonal represent nonsignificant correlations. b, Mean connectivity strength within each subnetwork and between the two subnetworks. Connections between hemispheric homologs (e.g., DLPFC–DLPFC) were not included. Significant differences at the level p < 0.05 are shown. c, Graphs resulting from a threshold of Z > 0.2 and Z > 0.5. Yellow nodes and lines represent the FP ROIs and the surviving connections between them. Red nodes and lines represent the CO ROIs and the surviving connections between them. Purple lines represent surviving connections between the two subnetworks. The smaller correlation matrix is the thresholded and rescaled version of the matrix shown in a. All values below the threshold are shown as dark blue as given by the color scale.
To test for differences in connectivity strength within each subnetwork and between subnetworks, paired t tests were performed as follows. Within each subject, the mean connectivity between the FP ROIs was calculated, as was the mean connectivity between the CO ROIs and the mean connectivity of FP to COI ROIs. Because between-subnetwork correlations do not include any hemispheric homologs (e.g., right and left DLPFC), which we reasoned may be strong regardless of any subnetwork distinction, these correlations were not included in the within-subnetwork average correlation values. The mean strength of these three connection types is shown in Figure 2b. Two-tailed t tests found significantly stronger connectivity within than between subnetworks (FP vs between: t17 = 6.73, p < 0.001; CO vs between: t17 = 5.07, p < 0.001). Connectivity strength within the two networks did not differ significantly.
In accordance with previous studies, the overall group graph was thresholded at Z > 0.2 (Fig. 2c), as was done by Dosenbach et al. (2007). At this threshold, 64% of all possible between subnetwork connections remained intact (shown in purple), whereas 100% of connections between the FP ROIs (shown in yellow) and 93% of connections between the CO ROIs (shown in red) were intact. When a stricter threshold of Z > 0.5 was applied, only 11% of potential between-network connections were still present, whereas 60% and 46% of within-subnetwork connections were found for the FP and CO, respectively. These data suggest that the association of ROIs within the two subnetworks as defined in the dual-networks architecture is generally stronger than between the two subnetworks.
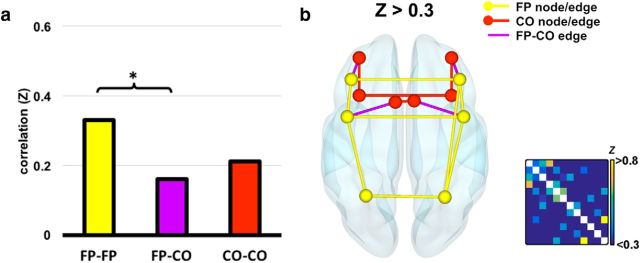
One concern with connectivity analysis on active task data is that connectivity values may largely reflect common univariate response to task events. To account for this, we performed the same connectivity analysis on the residual data produced by the SPM GLM described as part of the MVPA pipeline. In this analysis, responses to task events should be removed by event regressors. As shown in Figure 3a, using residual activity reduced overall connectivity strength compared with the previous method, but general trends were unchanged. Paired, two-tailed t tests revealed significantly greater connectivity within the FP subnetwork compared with between the two subnetworks (t17 = 3.03, p = 0.007), but no significant difference between the CO subnetwork connectivity and the between-networks connectivity nor between the two subnetworks. As before, when thresholded at Z > 0.2 (data not shown), the graph showed a strong connectivity pattern across the MD network, particularly within the FP subnetwork. However, because overall connectivity strengths were reduced by this method, the Z > 0.5 threshold was very strict, with only 3 connections surviving (data not shown). In Figure 3b, we show an intermediate threshold at Z = 0.3, which shows the FP network as 53% intact and the CO subnetwork as 27% intact, whereas only 11% of between-subnetwork connections survive.
Figure 3.
Functional connectivity of residual activity between MD ROIs. a, Mean connectivity within each subnetwork and between the two subnetworks. Significant differences at the level p < 0.05 are shown. b, Graph resulting from a threshold of Z > 0.3. For conventions, see Figure 2.
MVPA results
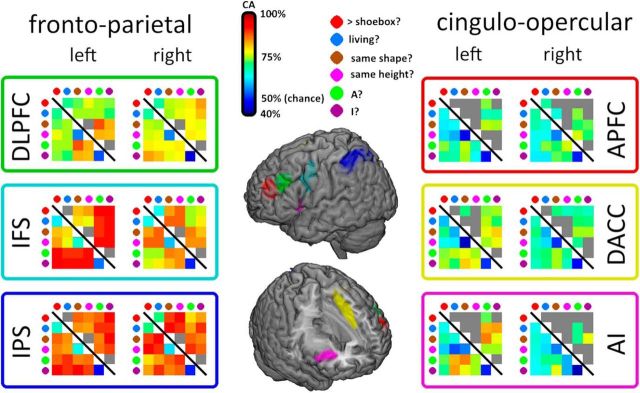
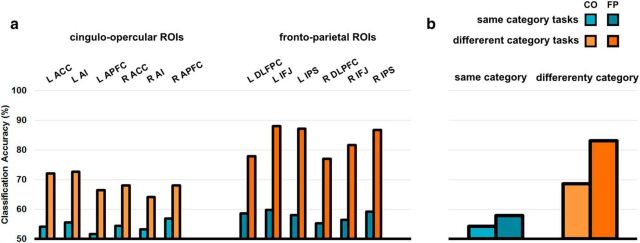
Mean CA for each task pair (15 task pairs in total) in each ROI is shown in Figure 4. Significance was determined by performing two-tailed Wilcoxon signed-rank tests against the chance level of 50%, separately each task pair in each ROI and correcting for multiple comparisons with a Bonferroni correction. Overall, there was relatively strong decoding of task pairs in the FP subnetwork (across ROIs, 84% of task pair discriminations significant), but comparatively weaker decoding in the CO subnetwork (46% of discriminations significant). It is apparent from Figure 4 that discrimination between task pairs from the same category was much weaker than discrimination between categories.
Figure 4.
Task decoding across the multiple demand ROIs. The MD ROIs are shown on the central brain rendering. Results for FP ROIs are shown on the left and those for CO ROIs on the right. Within each ROI, each colored matrix shows mean CA for all task pairs averaged across participants. The bottom left of each matrix shows all CAs; the top right shows the same CAs but with nonsignificant CAs greyed out.
To compare task encoding between the two subnetworks, the mean CA across task pairs was calculated separately for same-category and different-category task pairs. Mean CA for each ROI is shown in Figure 5a and the mean across all ROIs in each subnetwork is shown in Figure 5b. A mixed-model repeated-measures ANOVA was performed with hemisphere and subnetwork as within-groups factors and size of ROI as a nuisance covariate. This ANOVA was performed separately on the same-category and different-category data. There was a significant effect of subnetwork in both same-category pairs (F(1,196) = 7.8, p = 0.006) and different-category pairs (F(1,196) = 134.9, p < 0.001), with no significant effects of hemisphere or subnetwork × hemisphere interaction.
Figure 5.
Task decoding in FP and CO subnetworks. Blue indicates similar task decoding; orange dissimilar task decoding. Lighter colors indicate CO ROI and darker colors FP ROIs. a, Mean classification accuracy across subjects associated with each ROI separately for similar and dissimilar tasks. CO ROIs are shown on the left, FP ROIs on the right. b, Mean classification accuracies after averaging over CO and FP ROIs.
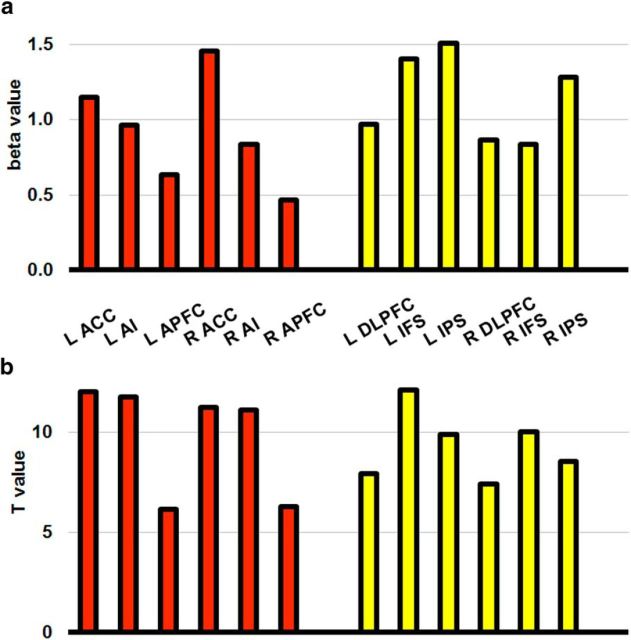
To determine whether the difference in pattern classification could be explained by a difference in the underlying signal-to-noise ratio between the two subnetworks rather than by a real cognitive difference, we looked at the univariate signal within each ROI. Performing a GLM on smoothed data gave β estimates of each task relative to the implicit baseline in each ROI. These are shown in Figure 6a. Paired, two-tailed t tests found each ROI to be significantly stronger than baseline across subjects. Figure 6a also demonstrates that the differences in decoding between the two subnetworks is not simply a reflection of an underlying univariate difference (Z-scoring before MVPA should largely account for this). As an estimate of the signal-to-noise within each ROI, Figure 6b shows the T-value associated with the comparison the t test of each β value against baseline. Again, the results imply that there was no systematic difference in signal-to-noise in the ROIs between the two subnetworks.
Figure 6.
Univariate activity across the MD ROIs. a, Mean task-related change in β values relative to baseline in each of the MD ROIs across participants. Results show that all regions were more active when engaged on the task, but there is no clear difference in activation between the two subnetworks. b, t-values from a two-tailed, paired t test of β values shown in a against the implicit baseline across participants. Similar t-values give an indication that the signal-to-noise ratio of the univariate signal is comparable across the two subnetworks.
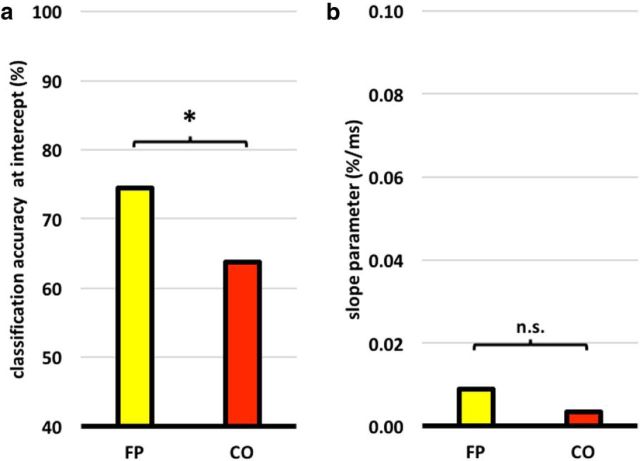
Recently, concern has arisen that reaction time (RT) may have a confounding influence on CA scores, with larger RT differences inflating CA (Todd et al., 2013). Others, however, have argued that, when treated appropriately, RT has little influence on CA (Woolgar et al., 2014). We investigated to what extent RT differences between different tasks, within each individual, may be contributing to the CA of that task pair and whether this was different for the FP and CO subnetworks. For each subnetwork, we performed a regression analysis of CA on absolute difference in RT. First, we extracted the CA associated with each task pair in each ROI in each subject. We then calculated the mean CA across the component ROIs of the two subnetworks in each individual, producing a 2D matrix of CA values for 2 subnetworks × 15 task pairs in each subject. A similar matrix was produced for absolute RT differences. Adopting the method described by Klauer et al. (1998), we regressed CA on RT within each subject separately for each subnetwork, thus obtaining an estimate of the slope (β) and intercept (α) for each subnetwork in each individual. Figure 7 shows the mean α and β values across participants. If RT is exerting a significant effect on classification accuracy, one would expect that the slope parameter would be positive and significantly greater than 0. Furthermore, if CA were wholly explained by RT, one may expect that, when there is a RT difference of 0 (i.e., at the intercept), then that classification accuracy would be close to chance (50%). The regression revealed α values of 74.4% and 63.8% (Fig. 7a) for the FP and CO subnetworks, respectively, which two-tailed, Wilcoxon signed rank tests showed to be significantly greater than 50% in both subnetworks (FP: p < 0.001; CO: p < 0.001). This indicates that, even with effectively no RT difference, decoding of task was strong. The regression also provided an estimate of β, the mean of which, across subjects, was positive for both the FP subnetwork (β = 0.009) and the CO subnetwork (β = 0.003), as shown in Figure 7b. This indicates, for example, that an RT difference of 100 ms contributes an ∼0.9% increase in CA score in the FP network and a 0.3% increase in the CO subnetwork. Because the mean RT difference between tasks in this experiment was 187 ms, this could suggest that RT may have inflated CA by ∼1.7% in the FP subnetwork and by 0.6% in the CO subnetwork. The slope was significantly greater than zero in the FP subnetwork (p = 0.047), but not in the CO subnetwork (p = 0.30). Two-tailed, paired t tests indicated a significant difference in α between the subnetworks (p < 0.001), but no significant difference in β (p = 0.17). In conclusion, although it is possible that RT differences may have contributed small increases in classification accuracy, we can be confident that any influence is far from accounting for the full effect.
Figure 7.
Mean parameter estimates of α and β after regression of classification accuracy on absolute response time differences. a, Mean value of α across participants for each of the two subnetworks. α values for both subnetworks were significantly greater than chance (50%) at the p < 0.05 level. b, Mean value of β across participants for each of the two subnetworks. Neither was significantly greater than 0.
Discussion
The dual-networks architecture of top-down control proposes that the MD system may be subdivided into two smaller subnetworks: the FP control and the CO maintenance subnetworks. Through a connectivity analysis of on-task fMRI data, we show that there is a pattern of strong interconnectivity across the MD system and that, as predicted by the dual-networks architecture, the within-subnetwork connectivity is stronger than the between subnetwork connectivity. In addition, we found very strong task decoding across the FP cortex, which is consistent with other studies (Woolgar et al., 2011a, 2011b), but we also found significantly stronger decoding of task across the FP subnetwork ROIs compared with the CO subnetwork ROIs.
According to the dual-networks model, activity in the FP subnetwork is linked closely to the processing operations of individual trials. In addition to trial-specific activity, the CO network has been associated with more sustained activation that is thought to represent the maintenance of general task set over the course of a block. Under this framework, it may be that stronger rule discrimination in the FP subnetwork indicates specialization for rapid and adaptive control, requiring precise encoding of particular rules and stimulus information bearing on a specific choice. In contrast, whereas there is also representation of trial-specific information across the CO ROIs, here, this representation may be more imprecise because these regions take on a broader or more temporally extended role.
Using a large test battery, Hampshire et al. (2012) have recently suggested that there are two major factors underlying human intelligence, which may be conceptualized as working memory and reasoning. Interestingly, they found that the working memory factor was more strongly associated with regions in the CO subnetwork, whereas the reasoning factor was more associated with the FP subnetwork. Although an exact mapping between the present data and the functional distinction of Hampshire et al. (2012) is not immediately clear, one possible link concerns the complexity of decision rules. In typical reasoning tasks, correct choices are often based on a complex set of considerations, somewhat resembling the current choice between six rules based on stimulus category and frame color and perhaps calling for strong involvement of the FP subnetwork. Again, it is important to appreciate that the distinction made by Hampshire et al. (2012) was relative because all MD regions (i.e., both subnetworks) showed activations even during the performance of tasks that loaded more on their “nonpreferred” factor.
Another perspective may be offered by the results of Seeley et al. (2007), who reported a correlation between connectivity strength and an anxiety score selectively in the CO subnetwork, whereas the FP subnetwork showed a correlation between connectivity strength and executive task performance. Seeley et al. (2007) concluded that the CO subnetwork may represent a “salience” network responsible for detecting important, behaviorally relevant information and, to some extent, the coordination of reward processing. In a different study, Sadaghiani et al. (2015) found that connectivity between the CO subnetwork (but not the FP subnetwork) and auditory cortex was positively correlated with performance in an auditory detection task. Like Seeley et al. (2007), Sadaghiani et al. (2015) reasoned that the increased correlation, before a correct detection of a (relatively rare) tone, was indicative of the CO engaging with salient external events.
In contrast to the CO subnetwork, Seeley et al. (2007) argue that the FP subnetwork could be responsible for acting on information that has been identified as salient, with responsibility for specific attentional control and other executive functions. The differential strength of rule decoding that we report here could therefore be explained by the CO ROIs only requiring a coarse representation of task information to detect the most salient details of the presented display, whereas the FP subnetwork requires a precise representation of specific task information and content. It is worth noting that the CO control network and the salience network may occupy different regions of cingulate and insular cortex (Power and Petersen, 2013) with different connectivity profiles (Touroutoglou et al., 2012) and similar but distinct cognitive roles (Sadaghiani and D'Esposito, 2015), although the MD ROIs used in this study overlap both of these subnetworks.
Previous studies looking at individual decoding of rules and other stimulus features in each MD ROI individually have not reported a clear distinction between the FP and CO ROIs in terms of decodability. For example, Woolgar et al. (2011b) show that, although the effect size of decoding stimulus position was stronger in DLPFC and IPS compared with AI and DACC, the effect size of decoding rule was approximately equal in the DLPFC, IPS, and AI and the effect size of decoding color was stronger in the AI than the DLPFC. Similar mixed results were also reported in another study (Woolgar et al., 2011a). Notably, the latter study found that classification accuracies in DLPFC and IPS were susceptible to practice effects, with the decoding of rule significantly weaker in a second test session. Conceivably, use of a complex six-rule task, assessed relatively early in practice, may have called for particularly strong involvement of FP control in the current study.
In addition to the MVPA, we performed an active-state functional connectivity analysis to assess whether fractionation of the MD system, previously found in resting-state functional connectivity analysis, is also apparent during task performance. The question is particularly pertinent for MD ROIs because they usually display a relative deactivation in the resting state and their function is associated with active engagement with the environment. Here, we found that our data converged toward a nested system of two more tightly coupled subnetworks that appeared to act together during task execution. At the lower threshold of Z > 0.2, many of the internetwork connections remained, suggesting a considerable degree of communication between all MD ROIs. However, at higher thresholds (Z > 0.3 and Z > 0.5), the greater segregation into FP and CO subnetworks became more apparent, although an absolute separation of the two networks was not found.
In conclusion, the current study replicates the finding of an integrated MD system with all regions coactivated and correlated while performing a cognitive task. These results also reaffirm the finding that the MD cortex may best be conceived as the coupling of two more tightly interconnected subnetworks centered around CO and FP cortex. Here, we also present fresh insight into the differentiation of the CO and FP subnetworks. Although both subnetworks code task rules, they do so differentially, with decoding consistently stronger in the FP subnetwork. Further work is needed to evaluate boundary conditions on this finding and its functional significance in terms of stronger FP involvement in moment-by-moment task operations (Dosenbach et al., 2008), CO emphasis on event salience (Seeley et al., 2007), specific FP involvement in complex choices (Hampshire et al., 2012), or some other distinction. Meanwhile, our data confirm that a broad distinction between FP and CO subnetworks provides one useful step forward in dissociating the parts of a broad MD system.
Footnotes
This work was supported by the Medical Research Council (United Kingdom) intramural research programme (Grant MC-A060-5PQ10). We thank Alfonso Nieto-Castanon for help with the CONN toolbox and Peter Watson for guidance with statistical analyses.
The authors declare no competing financial interests.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License Creative Commons Attribution 4.0 International, which permits unrestricted use, distribution and reproduction in any medium provided that the original work is properly attributed.
References
- Brainard DH. The Psychophysics Toolbox. Spat Vis. 1997;10:433–436. doi: 10.1163/156856897X00357. [DOI] [PubMed] [Google Scholar]
- Buschman TJ, Denovellis EL, Diogo C, Bullock D, Miller EK. Synchronous oscillatory neural ensembles for rules in the prefrontal cortex. Neuron. 2012;76:838–846. doi: 10.1016/j.neuron.2012.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cabeza R, Nyberg L. Imaging cognition II: An empirical review of 275 PET and fMRI studies. J Cogn Neurosci. 2000;12:1–47. doi: 10.1162/08989290051137585. [DOI] [PubMed] [Google Scholar]
- Christophel TB, Hebart MN, Haynes JD. Decoding the contents of visual short-term memory from human visual and parietal cortex. J Neurosci. 2012;32:12983–12989. doi: 10.1523/JNEUROSCI.0184-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole MW, Schneider W. The cognitive control network: Integrated cortical regions with dissociable functions. Neuroimage. 2007;37:343–360. doi: 10.1016/j.neuroimage.2007.03.071. [DOI] [PubMed] [Google Scholar]
- Cole MW, Etzel JA, Zacks JM, Schneider W, Braver TS. Rapid transfer of abstract rules to novel contexts in human lateral prefrontal cortex. Front Hum Neurosci. 2011;5:142. doi: 10.3389/fnhum.2011.00142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crittenden BM, Duncan J. Task difficulty manipulation reveals multiple demand activity but no frontal lobe hierarchy. Cereb Cortex. 2014;24:532–540. doi: 10.1093/cercor/bhs333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crittenden BM, Mitchell DJ, Duncan J. Recruitment of the default mode network during a demanding act of executive control. Elife. 2015;4:e06481. doi: 10.7554/eLife.06481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Derrfuss J, Brass M, von Cramon DY. Cognitive control in the posterior frontolateral cortex: evidence from common activations in task coordination, interference control, and working memory. Neuroimage. 2004;23:604–612. doi: 10.1016/j.neuroimage.2004.06.007. [DOI] [PubMed] [Google Scholar]
- Dosenbach NU, Visscher KM, Palmer ED, Miezin FM, Wenger KK, Kang HC, Burgund ED, Grimes AL, Schlaggar BL, Petersen SE. A core system for the implementation of task sets. Neuron. 2006;50:799–812. doi: 10.1016/j.neuron.2006.04.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dosenbach NU, Fair DA, Miezin FM, Cohen AL, Wenger KK, Dosenbach RA, Fox MD, Snyder AZ, Vincent JL, Raichle ME, Schlaggar BL, Petersen SE. Distinct brain networks for adaptive and stable task control in humans. Proc Natl Acad Sci U S A. 2007;104:11073–11078. doi: 10.1073/pnas.0704320104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dosenbach NU, Fair DA, Schlaggar BL, Cohen AL, Petersen SE. A dual-networks architecture of top-down control. Trends Cogn Sci. 2008;12:99–105. doi: 10.1016/j.tics.2008.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumontheil I, Thompson R, Duncan J. Assembly and use of new task rules in fronto-parietal cortex. J Cogn Neurosci. 2011;23:168–182. doi: 10.1162/jocn.2010.21439. [DOI] [PubMed] [Google Scholar]
- Duncan J. The multiple-demand (MD) system of the primate brain: mental programs for intelligent behaviour. Trends Cogn Sci. 2010;14:172–179. doi: 10.1016/j.tics.2010.01.004. [DOI] [PubMed] [Google Scholar]
- Duncan J. The structure of cognition: attentional episodes in mind and brain. Neuron. 2013;80:35–50. doi: 10.1016/j.neuron.2013.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duncan J, Owen AM. Common regions of the human frontal lobe recruited by diverse cognitive demands. Trends Neurosci. 2000;23:475–483. doi: 10.1016/S0166-2236(00)01633-7. [DOI] [PubMed] [Google Scholar]
- Fedorenko E, Duncan J, Kanwisher N. Broad domain generality in focal regions of frontal and parietal cortex. Proc Natl Acad Sci U S A. 2013;110:16616–16621. doi: 10.1073/pnas.1315235110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freedman DJ, Riesenhuber M, Poggio T, Miller EK. Categorical representation of visual stimuli in the primate prefrontal cortex. Science. 2001;291:312–316. doi: 10.1126/science.291.5502.312. [DOI] [PubMed] [Google Scholar]
- Hampshire A, Highfield RR, Parkin BL, Owen AM. Fractionating human intelligence. Neuron. 2012;76:1225–1237. doi: 10.1016/j.neuron.2012.06.022. [DOI] [PubMed] [Google Scholar]
- Hebart MN, Görgen K, Haynes JD. The Decoding Toolbox (TDT): a versatile software package for multivariate analyses of functional imaging data. Front Neuroinform. 2015;8:88. doi: 10.3389/fninf.2014.00088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klauer KC, Draine SC, Greenwald AG. An unbiased errors-in-variables approach to detecting unconscious cognition. Br J Math Stat Psychol. 1998;51:253–267. doi: 10.1111/j.2044-8317.1998.tb00680.x. [DOI] [PubMed] [Google Scholar]
- Kusunoki M, Sigala N, Nili H, Gaffan D, Duncan J. Target detection by opponent coding in monkey prefrontal cortex. J Cogn Neurosci. 2010;22:751–760. doi: 10.1162/jocn.2009.21216. [DOI] [PubMed] [Google Scholar]
- Matsuyoshi D, Ikeda T, Sawamoto N, Kakigi R, Fukuyama H, Osaka N. Differential roles for parietal and occipital cortices in visual working memory. PLoS One. 2012;7:e38623. doi: 10.1371/journal.pone.0038623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menon V, Uddin LQ. Saliency, switching, attention and control: a network model of insula function. Brain Struct Funct. 2010;214:655–667. doi: 10.1007/s00429-010-0262-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller EK. The prefrontal cortex and cognitive control. Nat Rev Neurosci. 2000;1:59–65. doi: 10.1038/35036228. [DOI] [PubMed] [Google Scholar]
- Nomura EM, Gratton C, Visser RM, Kayser A, Perez F, D'Esposito M. Double dissociation of two cognitive control networks in patients with focal brain lesions. Proc Natl Acad Sci U S A. 2010;107:12017–12022. doi: 10.1073/pnas.1002431107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Petersen SE. Control-related systems in the human brain. Curr Opin Neurobiol. 2013;23:223–228. doi: 10.1016/j.conb.2012.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramnani N, Owen AM. Anterior prefrontal cortex: insights into function from anatomy and neuroimaging. Nat Rev Neurosci. 2004;5:184–194. doi: 10.1038/nrn1343. [DOI] [PubMed] [Google Scholar]
- Sadaghiani S, D'Esposito M. Functional characterization of the cingulo-opercular network in the maintenance of tonic alertness. Cereb Cortex. 2015;25:2763–2773. doi: 10.1093/cercor/bhu072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadaghiani S, Poline JB, Kleinschmidt A, D'Esposito M. Ongoing dynamics in large-scale functional connectivity predict perception. Proc Natl Acad Sci U S A. 2015;112:8463–8468. doi: 10.1073/pnas.1420687112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seeley WW, Menon V, Schatzberg AF, Keller J, Glover GH, Kenna H, Reiss AL, Greicius MD. Dissociable intrinsic connectivity networks for salience processing and executive control. J Neurosci. 2007;27:2349–2356. doi: 10.1523/JNEUROSCI.5587-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shenhav A, Botvinick MM, Cohen JD. The expected value of control: an integrative theory of anterior cingulate cortex function. Neuron. 2013;79:217–240. doi: 10.1016/j.neuron.2013.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stokes MG, Kusunoki M, Sigala N, Nili H, Gaffan D, Duncan J. Dynamic coding for cognitive control in prefrontal cortex. Neuron. 2013;78:364–375. doi: 10.1016/j.neuron.2013.01.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todd MT, Nystrom LE, Cohen JD. Confounds in multivariate pattern analysis: theory and rule representation case study. Neuroimage. 2013;77:157–165. doi: 10.1016/j.neuroimage.2013.03.039. [DOI] [PubMed] [Google Scholar]
- Touroutoglou A, Hollenbeck M, Dickerson BC, Feldman Barrett L. Dissociable large-scale networks anchored in the right anterior insula subserve affective experience and attention. Neuroimage. 2012;60:1947–1958. doi: 10.1016/j.neuroimage.2012.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher KM, Miezin FM, Kelly JE, Buckner RL, Donaldson DI, McAvoy MP, Bhalodia VM, Petersen SE. Mixed blocked/event-related designs separate transient and sustained activity in fMRI. Neuroimage. 2003;19:1694–1708. doi: 10.1016/S1053-8119(03)00178-2. [DOI] [PubMed] [Google Scholar]
- Whitfield-Gabrieli S, Nieto-Castanon A. Conn: a functional connectivity toolbox for correlated and anticorrelated brain networks. Brain Connect. 2012;2:125–141. doi: 10.1089/brain.2012.0073. [DOI] [PubMed] [Google Scholar]
- Woolgar A, Hampshire A, Thompson R, Duncan J. Adaptive coding of task-relevant information in human frontoparietal cortex. J Neurosci. 2011a;31:14592–14599. doi: 10.1523/JNEUROSCI.2616-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woolgar A, Thompson R, Bor D, Duncan J. Multi-voxel coding of stimuli, rules, and responses in human frontoparietal cortex. Neuroimage. 2011b;56:744–752. doi: 10.1016/j.neuroimage.2010.04.035. [DOI] [PubMed] [Google Scholar]
- Woolgar A, Golland P, Bode S. Coping with confounds in multivoxel pattern analysis: what should we do about reaction time differences? A comment on Todd, Nystrom & Cohen 2013. Neuroimage. 2014;98:506–512. doi: 10.1016/j.neuroimage.2014.04.059. [DOI] [PMC free article] [PubMed] [Google Scholar]