Abstract
A key finding of human balance experiments has been that the integration of sensory information utilized for postural control appears to be dynamically regulated to adapt to changing environmental conditions and the available sensory information, a process referred to as “sensory re-weighting.” We propose a postural control model that includes automatic sensory re-weighting. This model is an adaptation of a previously reported model of sensory feedback that included manual sensory re-weighting. The new model achieves sensory re-weighting that is physiologically plausible and readily implemented. Model simulations are compared to previously reported experimental results to demonstrate the automated sensory reweighting strategy of the modified model. On the whole, the postural sway time series generated by the model with automatic sensory re-weighting show good agreement with experimental data, and are capable of producing patterns similar to those observed experimentally.
Keywords: Balance, Posture, Sensory re-weighting, Feedback, Modeling
1 Introduction
Humans utilize a variety of sensory systems to maintain balance, primary among them being the visual, vestibular, and proprioceptive systems. Several studies have demonstrated that human standing posture is affected by perturbations to these sensory systems [4, 7, 8, 9, 10, 16, 21, 22], suggesting that feedback control, based on perceived body motion, contributes to postural stability. There is redundancy across these sensory systems and the organization of these feedback control mechanisms is not fully known. There is some question as to whether feedback alone is sufficient for human postural control [5, 19], although recent studies have shown that a postural control strategy based solely on sensory feedback can account for experimental findings involving a variety of proprioceptive, visual, and vestibular perturbations to postural control [2, 22, 24].
The utility of each sensory system depends upon environmental conditions and the reliability of sensory orientation and movement information. A key finding of human postural control experiments has been that the integration of sensory information appears to be dynamically regulated to adapt to changing environmental conditions and the available sensory information, a process referred to as “sensory re-weighting” [2, 11, 15, 17, 22, 24, 26]. For example, during eyes-closed stance on a fixed, level surface, the primary sensory source for information about body orientation in space is proprioception, but under conditions where the platform moves, the primary source of sensory information shifts from proprioceptive to graviceptive/vestibular [22]. This dynamic regulation or re-weighting of the sensory cues enables the body to maintain upright stance under different environmental conditions [7].
Numerous models have been developed to describe and understand human postural control [1, 6, 12, 18, 22, 25]. While no single model currently explains all aspects of human postural control, the model we consider here [22] has been shown to accurately fit experimental data in a variety of conditions, both steady-state [22] and transient [24]. Of special interest are the results obtained experimentally [24], in which transient periods of low or high frequency oscillations in the body sway of healthy young adults were observed during sway-referencing of the support surface. Additional experimental support for the model has recently been obtained [2]. The model provides a conceptually simple view of sensory adaptation/re-weighting. However, it does not describe how sensory weights change nor does it actually implement an automatic sensory re-weighting strategy. Rather, Peterka and Loughlin [24] showed model simulations that exhibited similar time-varying characteristics to those seen experimentally, by using pre-programmed manual weight changes. However, left unanswered was how this re-weighting might be physiologically achieved or how sensory reweighting could be accomplished automatically in the model. In this paper, we develop and implement a simple mechanism for adaptive sensory re-weighting to extend the model and interpretation of experimental results on a swayreferenced platform reported in [24]. We present new model simulations, with comparison to the previously reported experimental results.
2 Methods
2.1 Postural control model
The feedback postural control model considered (Fig. 1) consists of a linearized (i.e., small angle) single-link inverted pendulum representation of body dynamics [22, 24]. Upright stance is maintained by a corrective torque applied about the ankle joint, generated by a proportional integral-derivative (PID) controller, with fixed gain parameters KP, KI and KD. Note that the model utilizes both position and velocity information to stabilize the inverted pendulum, consistent with control theory.
Fig. 1.
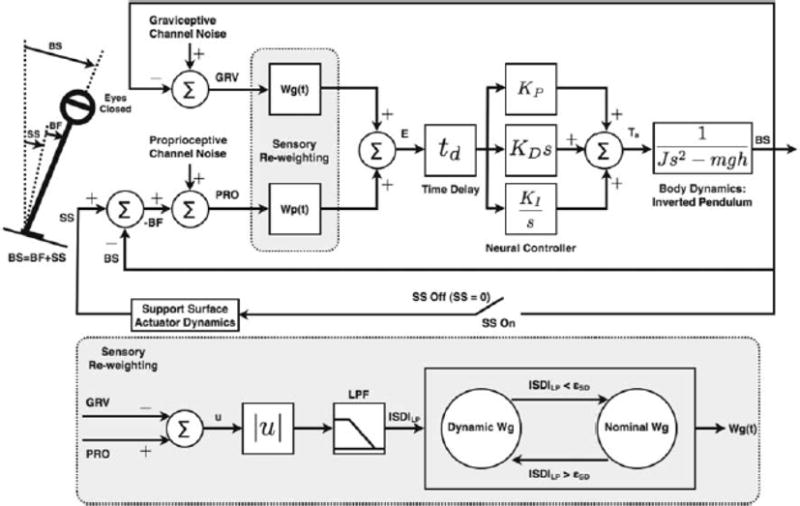
Feedback model of postural control (modified from [22, 24]). The body is modeled as a linearized inverted pendulum. The sensory pathways include variable sensory weights (Wg,Wp) that can change as environmental factors change (the “sensory re-weighting” hypothesis). BS and SS are angles, with respect to earth-vertical, of the body and support surface, respectively, as shown in the stick-figure. BF is the relative angle of the support surface with respect to the body. Corrective torque about the ankle, Ta, is generated by a proportional-integral-derivative (PID) controller with fixed gains KP, KD, KI, acting on the combined delayed sensory error signal E. To generate spontaneous body sway, filtered Gaussian white noise is added to both the graviceptive and proprioceptive channels. Also shown is a schematic representation of the dynamic sensory re-weighting algorithm
The parameters KP and KD represent the active stiffness and damping, respectively, of the postural control system. They are termed “active” because they generate neurally mediated corrective torque, in contrast to passive stiffness and damping of the muscles and tendons during quiet standing. Both active and passive mechanisms contribute to postural control and, while there is no general agreement on their relative contributions to postural control [13], previous experiments using small amplitude platform perturbations similar to ours have found the contribution of the passive stiffness and damping to torque generation to be negligible (ten times smaller than the active parameters) [22, 23]. Accordingly, the model presented here includes only active stiffness and damping parameters. The parameter td in the model represents the effective or lumped time delay of the system, which includes combined delays due to sensory transduction, neural transmission, nervous system processing, muscle activation, and force development. The gains Wp and Wg represent the relative contribution of proprioceptive and graviceptive sensory information to torque generation, Ta. Unlike the fixed PID gains of the controller, the sensory weights can change with environmental conditions (the “sensory re-weighting” strategy.) The model assumes that under steady-state conditions the sum of the sensory weights is unity (Wg + Wp = 1) [22], but can increase or decrease from this value during periods of transient changes in environmental conditions that impact the availability or reliability of sensory information for balance [24]. The means by which this may be accomplished is the topic of this paper.
For the model, the body sway (BS) in response to support surface (SS) motion is given in the Laplace domain by
| (1) |
where s is the Laplace variable and
| (2) |
A key concept of the model and the sensory reweighting hypothesis is the effective overall sensory weight, W, of the system, which is the sum of the sensory weights of those channels that contribute accurate sensory information about body sway. For example, for eyes-closed stance, the visual system does not contribute information about body sway, so the effective overall sensory weight in this case is W = Wp + Wg. For stance on a sway-referenced platform, wherein the support surface rotates in oneto-one proportion to body sway (SS = BS in Fig. 1), the proprioceptive channel does not contribute accurate information about body sway, so in this case the effective overall sensory weight is W = Wg under eyes closed condition. Thus, the sensory weights that contribute to the effective overall sensory weight are different under different environmental conditions (i.e., under different manipulations of the sensory inputs).
An important point to appreciate is that as the value of W changes, the dynamics of body sway will change. In particular, during transient conditions the system can be pushed towards instability if sensory re-weighting is not correct, causing W to be too large or too small. This effect of changes in the value of W on the body sway that develops is illustrated in the frequency response magnitude plots shown in Fig. 2. The figure shows a plot of the magnitude of WpH(s) versus frequency (s = jω) on a log–log scale. Note that the model predicts oscillatory body sway at specific frequencies if sensory reweighting is inappropriate (W less than or greater than one), as reflected by peaks (“resonances”) in the frequency response. Increased resonance is characteristic of a system nearing instability.
Fig. 2.
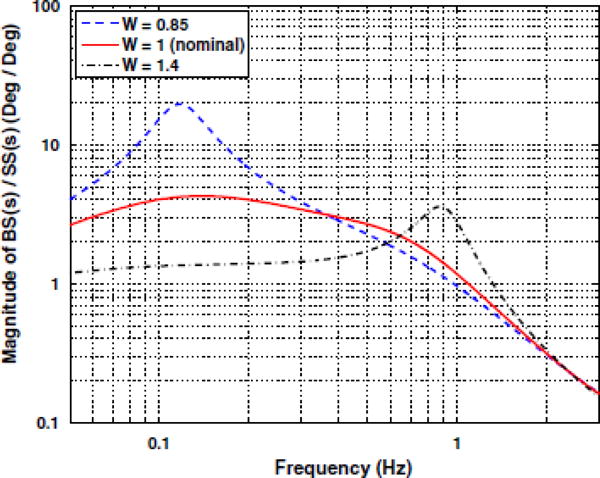
Frequency response plots, for the postural control model in Fig. 1, showing the effects of changes in the effective overall sensory weight, W. The curves correspond to plots of the magnitude frequency response from Eq. 2, i e., |WpH(S)|, with s = jω and Wp = 0.8, on a log-log scale. Dotted curve is for W = 0.85, solid is for W = 1, dotted-dashed is for W = 1.4. PID control parameters were the same in all cases (KP = 970 N m rad−1, KI = 86 N m s−1-rad−1, KD = 344 N m s rad−1), as were other physical parameters (g = 9.8 m/s2, m = 85 kg, h = 0.9 m, J = 81 kg m2 td = 175 ms). Note the changes in the frequency response as W changes, and in particular the development of resonances (peaks in the frequency response) at particular frequencies for W > 1 and W < 1
Simulations of body sway from the model for different values of W have been shown to be consistent with results obtained experimentally [24]. Shown in Fig. 3 are body sway measurements and the corresponding time-varying spectrum (or time–frequency distribution, TFD) obtained during eyes-closed stance on a platform that transitioned from fixed, to sway referenced for 60 s (labeled SR in Fig. 3), and then back to fixed (see [24] for details of the experimental protocol and data analysis). During the initial period of eyes-closed stance on the fixed platform, the effective overall sensory weight is W = Wp + Wg, and under the sensory re-weighting hypothesis, once steadystate has been reached we have Wp + Wg = 1. Following the transition to the sway-referenced platform (starting at 60 s in Fig. 3), the proprioceptive channel no longer provides accurate information about body sway. Hence the effective overall sensory weight becomes W = Wg which will be less than unity immediately after the transition to sway-referencing. This decrease in the value of W will cause a change in the frequency characteristics of body sway as predicted by the frequency response curve in Fig. 2 (dashed curve) and seen experimentally in the time-varying spectrum of Fig. 3 (note the band of energy in the TFD plot around 0.1 Hz that develops after t = 60 s).
Fig. 3.
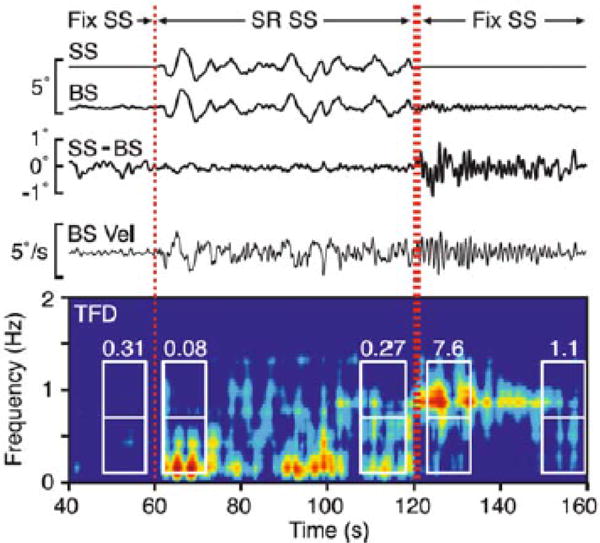
Time series and corresponding time-varying spectra [or time-frequency distribution (TFD), bottom plot] of postural sway from an example subject (Adapted from [24]). The support surface angle (SS) is sway-referenced (SR) during the period 60–120 s. After rapidly returning to a fired support surface within 1 s (denoted by the double vertical dotted lines at 120 s), body sway oscillations at ~ 1 Hz develop (bright band in the TFD around 1 Hz for t > 120 s), indicative of inadequate sensory re-weighting. Boxed areas in the TFD correspond to time-frequency regions of interest for which energy ratios (ER) of high-frequency (0.7–1.3 Hz) to low-fiequency (0.1–0.7 Hz) energy were analyzed; numbers above the box reflect the ER values
As the body adjusts to the sway-referenced condition over time, sensory re-weighting brings the effective sensory weight back to unity, i.e., the graviceptive weight Wg increases to near unity. Upon the transition back to a fixed platform (at t = 120 s), the effective sensory weight becomes W = Wp + Wg, but now the graviceptive weight is higher than it was during the initial fixed platform condition (t< 60 s), so that now W>1. According to the model, this should result in oscillatory sway near 1 Hz (Fig. 2, dot-dashed curve), which was observed experimentally (see the time-varying spectrum in Fig. 3 and in particular the band of energy that develops around 1 Hz after t = 120 s).
2.2 Dynamic sensory re-weighting algorithm
Our sensory re-weighting algorithm is based on two assumptions: (1) the graviceptive channel provides veridical but noisy orientation information, and (2) the central nervous system (CNS) can monitor differences between the sensory channels. Sensory re-weighting is achieved by monitoring the difference between the graviceptive channel and the other sensory channels, and adjusting sensory weights when the difference exceeds a threshold. To develop this sensory re-weighting strategy, consider the model depicted in Fig. 1. The proprioceptive (PRO) and graviceptive (GRV) channels measure body sway (BS) relative to the support surface (SS), and body sway relative to earth vertical, respectively,
| (3) |
Hence, the magnitude of the sensory difference, |SD|, is given by
| (4) |
| (5) |
where we have included sensory noise from the two channels. Hence, when the platform is not moving (SS = 0), the sensory difference is a low-level noise signal, which defines a threshold (eSD; see Appendix) below which no change to the sensory weights is made. However, when the platform moves, then the sensory difference will exceed the noise threshold. When that occurs, it is assumed that the information from the proprioceptive channel is corrupted, and more emphasis is placed on the graviceptive channel by altering the graviceptive sensory weight Wg. Because of the sensory noise, the sensory difference signal is low-pass filtered, |SD|LP = hLP(t)*|SD|, where * denotes convolution and hLP(t) is the filter impulse response. This filtering is applied in order to provide a smoother, less variable, sensory difference measure to compare to the threshold. The filter is a first order Butterworth low-pass filter with cut-off frequency fc = 0.24 Hz.
In our implementation, we augment Wg according to a nonlinear (sigmoidal) function, which ensures that it can not exceed a specified range. Specifically, the filtered sensory difference |SD|LP is continuously compared to the threshold eSD. If the sensory difference does not exceed this threshold, then no change is applied to the graviceptive sensory weight (Fig. 1, Sensory Re-weighting block, Nominal Wg). On the other hand, if |SD|LP exceeds the threshold, then an intermediate dynamic weight (denoted by Wgint) is computed as a function of |SD|LP,
| (6) |
where we chose the constant to be γ= 5 deg-1 in our simulations. To avoid system instability and ensure a sufficiently rapid change in Wg at the start of the platform transition, the difference between the current value obtained for the intermediate weight and its previous filtered value is computed and compared at each time step (set to 0.01 s here) to an arbitrary threshold δ (set to 0.3 in our simulations). If the difference exceeds this threshold, then Wg + Wgint, but if the threshold is not exceeded, then Wg + WgintLP (Fig. 1, Sensory Re-weighting block, Dynamic Wg). The additional low-pass filtering (first order filter with cut-off frequency fc = 0.04 Hz) applied to the intermediate weight is done to avoid abrupt jumps in Wg.
Experimental studies [24] showed that some subjects exhibited persistent sway following the platform transition from sway-referenced back to fixed, while other subjects more rapidly returned to nominal levels of sway. To simulate this range of experimental observations, two different time constants were used to return Wg in the model to its nominal value, representing subjects who return faster and slower, respectively, to their pre-sway-referenced state. This was implemented by low-pass filtering the graviceptive weight with a first order filter with a cut-off frequency of either fc = 0.04 Hz (fast adjustment time constant~4 s) or fc = 0.02 Hz (slow adjustment time constant ~8 s).
The above description of the dynamic sensory reweighting strategy is summarized by the following algorithm:
|
| |
| % initialize Wg to its nominal value (e.g., 0.2) | |
|
If
| |
| Compute According to Eq 6 | |
| If | |
| Else | |
| Else | |
| End | |
|
|
where in our implementation, eSD is set to 0.50° (see Appendix).
2.3 Simulations and analysis
The parameter values used in the model were: mass m = 85 kg; moment of inertia J = 81 kg m2; height to center-of-mass h = 0.9 m; stiffness KP = 970 N m rad−1; damping KD = 344 N m s rad−1; swiftness KI = 86 N m s−1 rad−1; and time delay td = 175 ms. These values are the same as reported in [24]. To generate spontaneous body sway in the model, filtered Gaussian white noise was added to both the graviceptive and proprioceptive channels (Fig. 1). The filter specifications are the same as described in [24]. In brief, the sensory channel noise is band-pass filtered at 0.05–2 and 0.2–2 Hz for graviceptive and proprioceptive channels, respectively, then low-pass filtered at 0.16 Hz using, for both the band-pass and low-pass filters, a first order (Butterworth) IIR digital filter. The proprioceptive and graviceptive channel noise variance, prior to filtering and as given in [24], were set to 1 deg2 and 6 deg2, respectively. After filtering, the noise variances were calculated to be 0.002 deg2 and 0.0215 deg2, which was also verified by simulations.
As in [24], the external perturbation to the model is a sway-referenced platform motion (ideally, SS = BS) [20]. Each simulation lasted 180 s, consisting of 60 s of no platform movement, i.e., a fixed support surface (SS = 0), followed by 60 s of sway-referenced movement, and then a final 60 s of fixed surface. Consistent with the experiments in [24], the transition at 60 s from the fixed to the swayreferenced platform was done instantaneously, while the transition at 120 s back to the fixed platform was done over 1 s, to avoid large torque perturbations of the support surface that could pitch the subject off the platform. Because, in practice, sway-referencing is not ideal, the dynamics of the support surface actuator, as derived in [24], are incorporated into the simulations (block labeled Support Surface Actuator Dynamics in Fig. 1). During the initial fixed support surface condition (prior to sway referencing), the initial values of the proprioceptive and graviceptive weights were set to Wp = 0.8 and Wg = 0.2, respectively [24] (Fig. 1, Sensory Re-weighting block, Nominal Wg).
The simulation has a time step of 0.01 s. The difference between successive samples was computed to generate a body sway velocity time series. This time series was then low-pass filtered at 5 Hz and down-sampled to 10 Hz for further analysis, similar to the data analysis described in [24]. The time-varying spectrum of the down-sampled body sway velocity was estimated by computing a positive TFD (see [3, 14, 24] for details).
Energy levels were computed from the TFDs over distinct frequency bands (high: 0.7–1.3 Hz; low: 0.1–0.7 Hz) at five different 10 s time intervals: end of fixed platform (End of Fix), start of sway-referencing (Start of SR), end of sway-referencing (End of SR), start of final fixed platform condition (Start of Final Fix), and end of trial (End of Trial). These correspond to the same frequency bands and time intervals used in [24], which were chosen because they capture the frequency ranges over which the low- and high-frequency resonances in body sway were experimentally observed, and predicted by the model as W changes. Energy ratios of high- to low-frequency bands were computed for each time interval to demonstrate changes in the body sway response to transient environmental conditions.
Twenty simulations were computed, consisting of ten simulations that modeled rapid adjustments of the graviceptive weight Wg (4 s time constant) and ten simulations that modeled slower adjustments (8 s time constant). Each simulation used different noise realizations. Energy ratios as above were extracted from each TFD per simulation and then averaged over the N = 20 simulations for comparison with experimental data. All simulations were performed using Simulink with Matlab version 7 (R14) (The Math- Works, Natick, MA).
3 Results
Example model simulation results are shown in Fig. 4 for fast (a) and slow (b) adjustments to transient environmental conditions. Plotted in the figure are the support surface (SS) rotation angle, body sway (BS) angle, the difference between these two (SS – BS), body sway velocity (BS Vel), graviceptive (GRV) and proprioceptive (PRO) sensory channels, filtered sensory difference |SD|LP, the intermediate graviceptive weight Wgint (Eq. 6), the effective sensory weight W = Wg + Wp, the individual weights Wg and Wp, and the corresponding body sway velocity TFD.
Fig. 4.
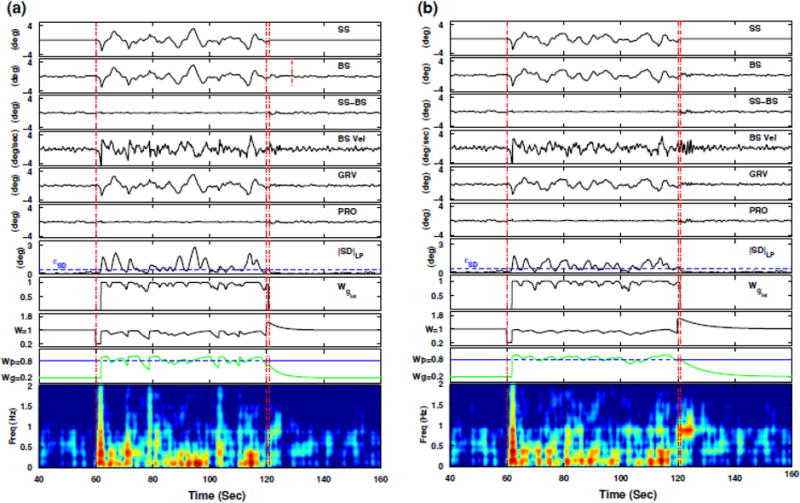
Example model simulations for fast (a) and slow (b) weight adjustments according to the sensory re-weighting hypothesis, where the top six panels in each plot show the time series for SS, BS, SS – BS, BS Vel, GRV, and PRO, the seventh panel shows the filtered sensory difference (|SD|LP) along with ɛSD set to 0.50°, the eighth panel shows the intermediate graviceptive weight Wgint (Eq. 6), and the last three panels show the effective sensory weight W = Wg + Wp, the individual weights Wg and Wp, and the corresponding TFD for body sway velocity (BS Vel), respectively
Figure 4 shows that the graviceptive weight Wg adaptively changes from its initial value (set to 0.2 at the beginning of the trial) to a value slightly higher than 0.8 when the support surface condition goes from fixed to sway-referenced (vertical dash-dotted line at 60 s). This increase is rapid, which is necessary to maintain stability. The proprioceptive weight Wp is kept constant at its initial value (0.8) throughout the entire trial duration, consistent with the assumptions in [24]. Note that even though Wp stays constant during sway-referencing, the proprioceptive channel does not contribute to torque generation during this period since no change in body sway relative to support surface is sensed when the body is sway-referenced.
Note that the effective sensory weight after the switch to sway-referencing is W = Wg, since no sensory information is coming through the proprioceptive channel during (ideal) sway-referencing [24]. Hence, the effective weight drops from W = Wp + Wg = 0.8 + 0.2 = 1 just prior to the transition to W = Wg = 0.2 immediately after the transition. A stability analysis of the closed-loop transfer function (Eq. 3) for W = 0.2 reveals that the system is unstable [24], hence a rapid increase in Wg is necessary to maintain stability.
After the platform is returned to the fixed condition over a 1 s interval (vertical dash-dotted lines at 120 s), the graviceptive weight decays either in a fast (Fig. 4a) fashion causing the overall effective sensory weight W to stay at 1, resulting in no resonant behavior in the system; or in a slow (Fig. 4b) fashion causing W to stay at a value greater than 1, inducing an oscillatory (i.e., resonant) behavior as indicated in the TFD plots at around 1 Hz, and as observed experimentally (Fig. 3).
As observed in Fig. 4, the change in Wg is slightly delayed in the model simulation at the onset of sway-referencing. This delay is a consequence of the temporal filtering and thresholding used to trigger sensory reweighting. For some trials, at the onset of sway-referencing the value of the sensory difference signal was below the threshold (eSD = 0.50°). Accordingly, sensory re-weighting did not begin right at the onset of sway-referencing, but began a short time after when the sensory difference increased to a level greater than the threshold. This delay causes a body sway velocity spike at the onset of sway referencing (Fig. 4, ~61–62 s). This behavior was not observed in experimental data.
In Fig. 5, the energy ratios (ER) from the TFDs of the model simulations are plotted (black bars), along with the ERs obtained experimentally (white bars) [24], which we have reproduced here for comparison. The simulation results are the mean ER (±SE) for 20 model simulations. As evident from the graph, the automatic sensory reweighting algorithm is capable of producing similar patterns observed experimentally.
Fig. 5.
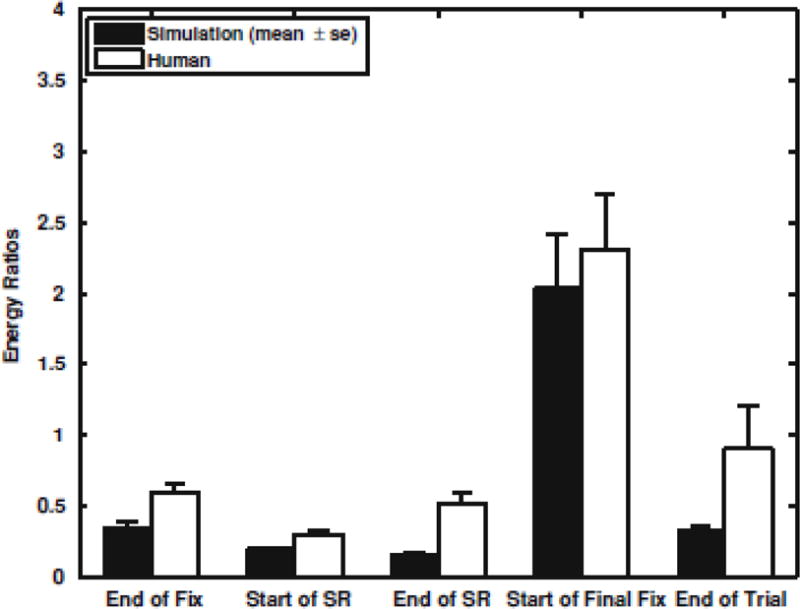
Bar graphs, of the high- to low-frequency energy ratios (ER), extracted from the TFDs, for the 10 s time windows. Each bar indicates, the mean ER (±SE) for 20 model simulation. (black bars) and 12 subjects (white bars) [24]]
4 Discussion
In a previous study [24] experimentally observed changes in postural sway during eyes-closed stance were qualitatively shown to be consistent with simulated postural sway time series from a feedback control model in which sensory feedback weights were manually changed over time. While the experimental results and model-based interpretation provided compelling evidence for sensory re-weighting in postural control, the question of how the sensory weight changes might occur was left unanswered. Our aim in this paper was to propose a physiologically plausible mechanism to accomplish sensory re-weighting in the model, under eyes-closed conditions, that generates postural sway time series that are consistent with the experimentally observed results reported in [24].
For these eyes-closed conditions, we based our sensory re-weighting strategy on a comparison of sensory information between the proprioceptive and graviceptive channels, which we referred to as the sensory difference (SD) signal. The rationale is that the graviceptive channel provides an absolute but noisy estimate of body sway (with respect to earth vertical), while the propriceptive channel provides a higher quality but relative estimate of body sway (with respect to the support surface). When the support surface is level and fixed, the two channels are in agreement, and hence the difference between them is small (ideally zero in the absence of sensory noise). However, when the platform becomes sway-referenced, the proprioceptive signal becomes small (ideally zero) while the graviceptive signal continues to reflect body sway, which usually increases during sway referencing. Hence under this condition, the sensory difference signal becomes large. If the CNS is able to monitor this difference, which seems physiologically plausible, then an increase above a certain threshold would indicate sensory disagreement and trigger corrective action. In the case of sway-referencing as explored here, this corrective action would be to increase the graviceptive weight to compensate for the degradation of proprioceptive information. Implementation of this strategy in the postural control model was able to produce simulations that were consistent with experimental results.
A difference observed between the simulations and the experimental trials was the existence of a body sway velocity spike at the onset of the sway-referenced platform condition in some of the simulations. This was a result of the sensory difference being below threshold at the onset of sway-referencing. Accordingly, the graviceptive weight is not increased until the sensory difference crosses the threshold. During this brief initial interval, the body accelerates from equilibrium, because the total effective sensory gain of the system drops from Wg + Wp just prior to sway-referencing to Wg just after the onset (since the proprioceptive channel is eliminated by sway-referencing), and this gain is inadequate to maintain stability [22, 24]. Lowering the threshold of course decreases this delay and reduces the body sway velocity spike, however, because there is sensory noise, the threshold must remain high enough so as not to trigger sensory re-weighting during quiet stance. Despite this difference between simulations and experimental data, on the whole, the postural sway time series generated by the model with sensory reweighting showed good agreement with experimental data, in terms of their TFDs and energy ratios.
Other sensory re-weighting strategies have been proposed [1, 18, 17, 26] which either use sensor fusion combined with detection thresholds to apply the reweighting or base their approach entirely on optimal estimation (Kalman gain). A distinction between our model and what others have proposed is the assumption that the CNS has knowledge of the true position and velocity of the body. In other words, the neural controller in our model is based on veridical signals, as opposed to an estimated version of these quantities. We believe that a sensory difference strategy as proposed here remains physiologically plausible even when estimated measures of body position and velocity are used, but this remains to be incorporated into the model and tested.
Although not explored here, sensory re-weighting has been experimentally reported for eyes-open conditions as well [7, 9, 15, 22]. The sensory-difference approach developed here could be extended to include vision. The visual system provides a relative measure of body sway with respect to the visual surround. Hence, when the visual surround is fixed (i.e., no visual perturbations are applied), the difference between the graviceptive and visual channels is small. However, under conditions where the visual surround is sway-referenced, then the difference between the two channels becomes large and sensory re-weighting could be activated when this difference exceeds a threshold. Further development of the model, including eyesopen stance and additional sensory comparisons, is under investigation.
Acknowledgments
The research of P. Loughlin, A. Mahboobin and M. Redfern was supported by the National Institutes of Health [R01 AG029546 (NIA)], and the Pittsburgh Claude D. Pepper Older Americans Independence Center [P30 AG024827 (NIA)]. The research of C. Atkeson was supported in part by the National Science Foundation under grants ECS-0325383 and EEC-0540865.
Appendix: Sensory difference threshold determination
To determine the threshold ɛSD (see Sect. 2.2), consider a Gaussian noise process x ~ N(0, σ2). We would like to find the probability that where ζ is a small number and ɛSD is the desired sensory difference threshold. Solving for ɛSD results in
| (7) |
where erf is the error function.
In our model simulations, we take the noise variance, i.e., σ2, as the sum of the sensory channel noise variances, with proprioceptive and graviceptive channel noise variances (post-filtering) set to 0.002 deg2 and 0.0215 deg2, respectively. With these values, and , Eq. 7 yields ɛSD ≥ 0.50°. We therefore took ɛSD = 0.50°.
Contributor Information
Arash Mahboobin, Email: arm19@pitt.edu, Department of Bioengineering, University of Pittsburgh, Pittsburgh, PA 15261, USA.
Patrick Loughlin, Department of Bioengineering, University of Pittsburgh, Pittsburgh, PA 15261, USA.
Chris Atkeson, Robotics Institute, Carnegie Mellon University, Pittsburgh, PA 15213, USA.
Mark Redfern, Department of Bioengineering, University of Pittsburgh, Pittsburgh, PA 15261, USA.
References
- 1.Carver S, Kiemel T, Van der Kooij H, Jeka JJ. Comparing internal models of the dynamics of the visual environment. Biol Cybern. 2006;92:147–163. doi: 10.1007/s00422-004-0535-x. [DOI] [PubMed] [Google Scholar]
- 2.Cenciarini M, Peterka RJ. Stimulus-dependent changes in the vestibular contribution to human postural control. J Neurophysiol. 2006;95:2733–2750. doi: 10.1152/jn.00856.2004. [DOI] [PubMed] [Google Scholar]
- 3.Cohen L. Time-Frequency Analysis. New York: Prentice-Hall; 1995. [Google Scholar]
- 4.Day BL, Severac Cauquil A, Bartolomei L, Pastor MA, Lyon IN. Human body-segment tilts induced by galvanic stimulation: A vestibularly driven balance protection mechanism. J Physiol. 1997;500:661–672. doi: 10.1113/jphysiol.1997.sp022051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fitzpatrick R, Burke D, Gandevia SC. Loop gain of reflexes controlling human standing measured with the use of postural and vestibular disturbances. J Neurophysiol. 1996;76:3994–4008. doi: 10.1152/jn.1996.76.6.3994. [DOI] [PubMed] [Google Scholar]
- 6.Fujisawa N, Masuda T, Inaoka H, Fukuoka Y, Ishida A, Minamitani H. Human standing posture control system depending on adopted strategies. Med Biol Eng Comput. 2005;43:107–114. doi: 10.1007/BF02345130. [DOI] [PubMed] [Google Scholar]
- 7.Horak FB, Macpherson JM. Postural orientation and equilibrium. In: Rowell LB, Shepherd JT, editors. Handbook of Physiology: Section 12: Exercise: Regulation and Integration of Multiple Systems. New York: Oxford University Press; 1996. pp. 255–292. [Google Scholar]
- 8.Ishida A, Masuda T, Inaoka H, Fukuoka Y. Stability of the human upright stance depending on the frequency of external disturbances. Med Biol Eng Comput. 2008;46(3):213–21. doi: 10.1007/s11517-007-0269-8. [DOI] [PubMed] [Google Scholar]
- 9.Jeka J, Allison L, Saffer M, Zhang Y, Carver S, Kiemel T. Sensory reweighting with translational and visual stimuli in young and elderly adults: the role of state-dependent noise. Exp Brain Res. 2006;174:517–527. doi: 10.1007/s00221-006-0502-y. [DOI] [PubMed] [Google Scholar]
- 10.Johansson R, Magnusson M. Human postural dynamics. Crit Rev Biomed Eng. 1991;18:413–437. [PubMed] [Google Scholar]
- 11.Kiemel T, Oie KS, Jeka JJ. Multisensory fusion and the stochastic structure of postural sway. Biol Cybern. 2002;87(4):262–77. doi: 10.1007/s00422-002-0333-2. [DOI] [PubMed] [Google Scholar]
- 12.Kuo AD. An optimal control model for analyzing human postural balance. IEEE T Bio-Med Eng. 1995;42:87–101. doi: 10.1109/10.362914. [DOI] [PubMed] [Google Scholar]
- 13.Loram ID, Maganaris CN, Lakie M. The passive, human calf muscles in relation to standing: the non-linear decrease from short range to long range stiffness. J Physiol. 2007;584:661–675. doi: 10.1113/jphysiol.2007.140046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Loughlin PJ, Pitton J, Atlas L. Construction of positive time-frequency distributions. IEEE T Signal Proces. 1994;42:2697–2705. [Google Scholar]
- 15.Mahboobin A, Loughlin P, Redfern MS, Sparto PJ. Sensory re-weighting in human postural control during moving-scene perturbations. Exp Brain Res. 2005;167(2):260–267. doi: 10.1007/s00221-005-0053-7. [DOI] [PubMed] [Google Scholar]
- 16.Maki BE. Selection of perturbation parameters for identification of the posture control system. Med Biol Eng Comput. 1986;24:561–568. doi: 10.1007/BF02446257. [DOI] [PubMed] [Google Scholar]
- 17.Maurer C, Mergner T, Peterka RJ. Multisensory control of human upright stance. Exp Brain Res. 2006;171(2):231–250. doi: 10.1007/s00221-005-0256-y. [DOI] [PubMed] [Google Scholar]
- 18.Mergner T, Maurer C, Peterka RJ. A multisensory posture control model of human upright stance. Prog Brain Res. 2003;142:189–201. doi: 10.1016/S0079-6123(03)42014-1. [DOI] [PubMed] [Google Scholar]
- 19.Morasso PG, Baratto L, Capra R, Spada G. Internal models in the control of posture. Neural Networks. 1999;12:1173–1180. doi: 10.1016/s0893-6080(99)00058-1. [DOI] [PubMed] [Google Scholar]
- 20.Nashner LM. Adaptation of human movement to altered environments. Trends Neurosci. 1982;5:358–361. [Google Scholar]
- 21.Peterka RJ, Benolken MS. Role of somatosensory and vestibular cues in attenuating visually induced human postural sway. Exp Brain Res. 1995;105:101–110. doi: 10.1007/BF00242186. [DOI] [PubMed] [Google Scholar]
- 22.Peterka RJ. Sensorimotor integration in human postural control. J Neurophysiol. 2002;88:1097–1118. doi: 10.1152/jn.2002.88.3.1097. [DOI] [PubMed] [Google Scholar]
- 23.Peterka RJ. Simplifying the complexities of maintaining balance. IEEE Eng Med Biol. 2003;22(2):63–68. doi: 10.1109/memb.2003.1195698. [DOI] [PubMed] [Google Scholar]
- 24.Peterka RJ, Loughlin PJ. Dynamic regulation of sensorimotor integration in human postural control. J Neurophysiol. 2004;91:410–423. doi: 10.1152/jn.00516.2003. [DOI] [PubMed] [Google Scholar]
- 25.Van der Kooij H, Jacobs R, Koopman B, Grootenboer H. A multisensory integration model of human stance control. Biol Cybern. 1999;80:299–308. doi: 10.1007/s004220050527. [DOI] [PubMed] [Google Scholar]
- 26.Van der Kooij H, Jacobs R, Koopman B, Van der Helm F. An adaptive model of sensory integration in dynamic environment applied to human stance control. Biol Cybern. 2001;84:103–115. doi: 10.1007/s004220000196. [DOI] [PubMed] [Google Scholar]


