A Modeling and Experimental Investigation of the Effects of Antigen Density, Binding Affinity, and Antigen Expression Ratio on Bispecific Antibody Binding to Cell Surface Targets

Abstract

Despite the increasing number of multivalent antibodies, bispecific antibodies, fusion proteins, and targeted nanoparticles that have been generated and studied, the mechanism of multivalent binding to cell surface targets is not well understood. Here, we describe a conceptual and mathematical model of multivalent antibody binding to cell surface antigens. Our model predicts that properties beyond 1:1 antibody:antigen affinity to target antigens have a strong influence on multivalent binding. Predicted crucial properties include the structure and flexibility of the antibody construct, the target antigen(s) and binding epitope(s), and the density of antigens on the cell surface. For bispecific antibodies, the ratio of the expression levels of the two target antigens is predicted to be critical to target binding, particularly for the lower expressed of the antigens. Using bispecific antibodies of different valencies to cell surface antigens including MET and EGF receptor, we have experimentally validated our modeling approach and its predictions and observed several nonintuitive effects of avidity related to antigen density, target ratio, and antibody affinity. In some biological circumstances, the effect we have predicted and measured varied from the monovalent binding interaction by several orders of magnitude. Moreover, our mathematical framework affords us a mechanistic interpretation of our observations and suggests strategies to achieve the desired antibody-antigen binding goals. These mechanistic insights have implications in antibody engineering and structure/activity relationship determination in a variety of biological contexts.

Introduction

Monoclonal antibodies and antibody-derived molecules, such as antibody conjugates and multispecific antibodies, are a large and growing class of therapeutics for a wide range of conditions (1). Building on these successes, a variety of other antibody-derived therapeutics and imaging agents are currently in development. These include antibody fragments, novel macromolecule binding scaffolds, fusion proteins, multispecific antibodies, and nanoparticles targeted by antibodies or fragments (2–9). There are now antibody-derived molecules in clinical trials that range from monovalent to one or more target(s), to bivalent such as IgGs, to tetravalent in the case of some bispecific antibody formats, and even higher valencies for some targeted nanoparticle reagents (10–13). Antibody fragments such as F(ab′)s and single-chain variable fragments are also in clinical development as therapeutics and imaging reagents (4, 5, 14).

With the increasing number and variety of antibody constructs in development, the science to select and engineer them, as well as to characterize their properties, has advanced in parallel. Innovations in screening and characterization techniques such as antibody display technologies and high throughput flow cytometry have allowed libraries of billions of antibody variants to be probed for the desired attributes or specificities (15, 16). Technologies such as surface plasmon resonance allow binding kinetics and affinity to be characterized with a high degree of precision and reproducibility (17). As a result, modern antibody engineering allows identification, characterization, and optimization of antibodies against an array of protein therapeutic targets. Recently there have been efforts made to use these engineering tools to create novel therapeutics that differ from natural IgGs in their structure (18–24).

The generation of these novel antibody-derived constructs results in a need to understand the structure-function relationship between affinity, valency, and binding to target(s). Regardless of the mechanism of action of a given construct, to exert its function it must first bind the intended molecular target(s), yet the mechanism of multiarm binding to cell surface targets remains poorly understood. Antibodies are multivalent and so avidity, the accumulated strength of multiple 1:1 binding events, is believed to play a strong role in antibody binding, but a mechanistic understanding of avidity in cell surface target binding is lacking. The impact of avidity on antibody binding has been demonstrated and shown to be potentially strong in certain contexts, but to date these studies have been purely empirical in nature (25, 26). A rationally designed model of how molecular structure affects the binding properties of these molecules to cell surface target antigens can improve understanding to aid engineering and selection efforts. In this work we applied a simple model to better understand how molecular structure, valency, and monovalent binding kinetics influence the binding of multivalent molecules to one or more cell surface targets. A conceptual framework to place these interactions into context is outlined and incorporated into a mathematical model to describe multiple binding events. This simplified depiction of biomolecular interactions and kinetics allows us to then make predictions about how antibody affinity, valency, and antigen density affect binding to cell surface antigens.

Using a number of different bispecific antibodies to cell surface antigens (Fig. 1), we have experimentally validated our mathematical model on multiple cell lines spanning a wide range of biologically relevant antigen densities and demonstrated its predictive capabilities. This work has led to insights into how multivalent and multispecific antibody constructs may have dramatically different binding properties than their monovalent affinities would have otherwise predicted. The conceptual framework that we have used to model the binding interactions further allows the observations to be interpreted mechanistically and leads to actionable hypotheses and guidance for antibody selection and engineering goals. These observations may present important additional considerations to take into account when determining the binding properties of antibodies and novel constructs to cell-associated antigens.

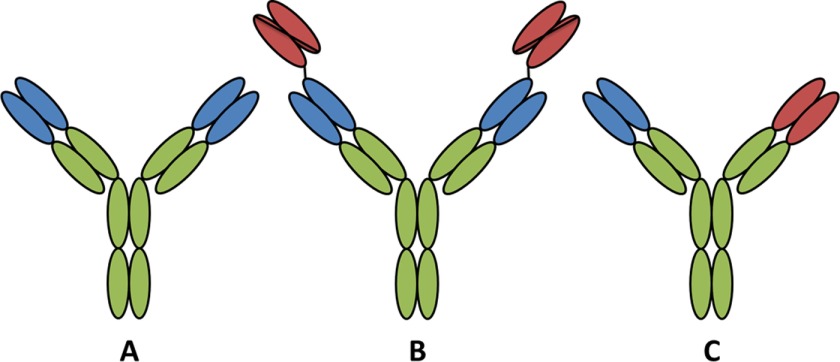
FIGURE 1.

Antibody formats tested in the MET/EGFR occupancy assay. Antibodies (A) against either MET (blue) or EGFR (red) or an equimolar combination of the two were tested against either a tetravalent bispecific heavy chain N-terminal fusion of an anti-EGFR single-chain variable fragment on the MET Ab (B) or a “knob in hole” design bispecific antibody (C).

Experimental Procedures

Mathematical Model Development

A mathematical model of bivalent binding to cell surface receptors was implemented in MATLAB R2015a (Mathworks). The antibody-antigen interactions were based upon those described in the literature and are depicted below,

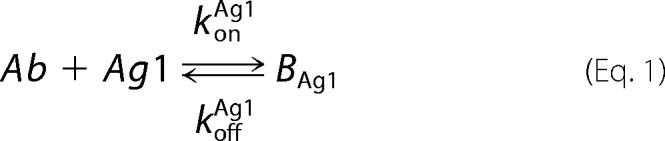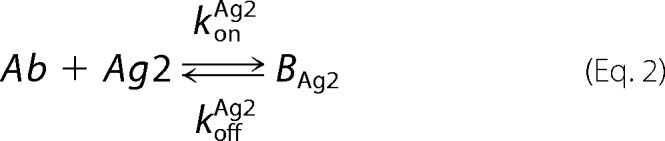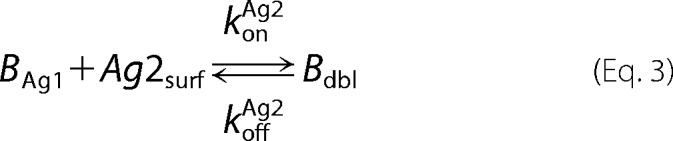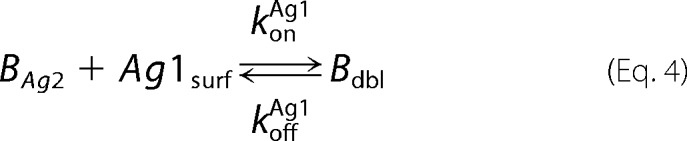where Ab denotes the antibody or bispecific, Ag1 and Ag2 refer to the antigens targeted by each of the two arms of the antibody, B_Ag refers to a bound Ab-Ag complex, B_dbl refers to an antibody bound to both antigens, and Ag_surf denotes the accessible antigen when an antibody is confined to the cell surface through binding to another cell surface antigen.

Antibody-antigen interactions as shown were translated into a set of ordinary differential equations based upon mass action kinetics (27). Antigen kinetics, e.g. synthesis, internalization, and degradation, were assumed negligible for the purposes of the model. The equations as depicted below were solved numerically using the MATLAB built-in solvers.

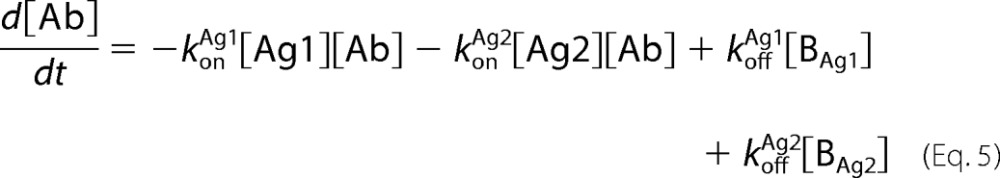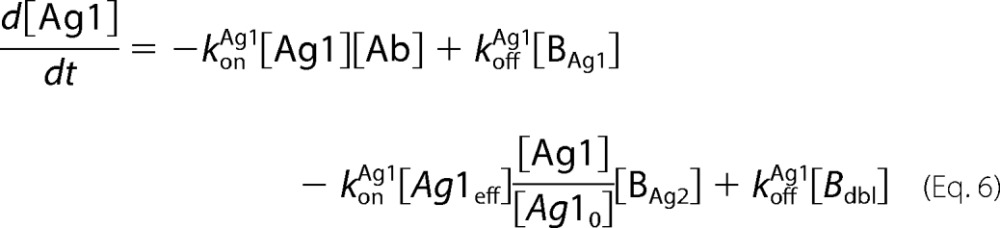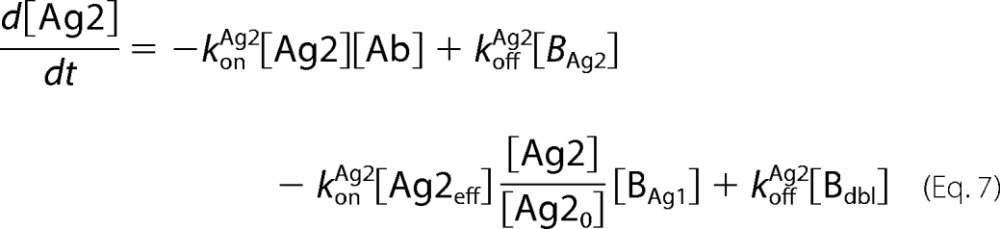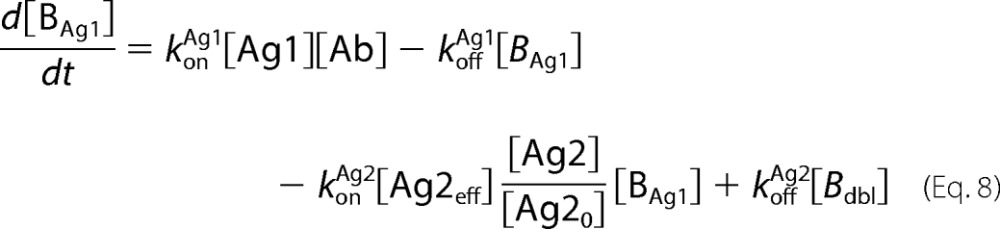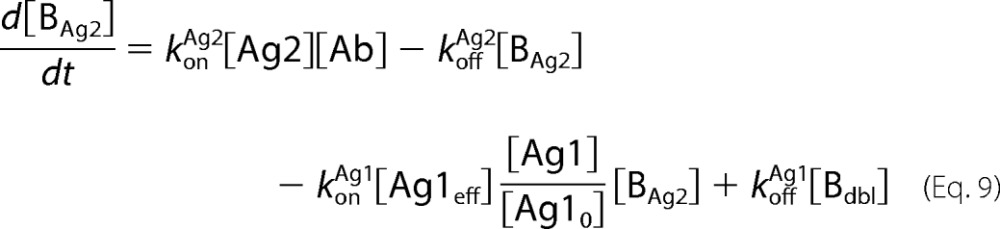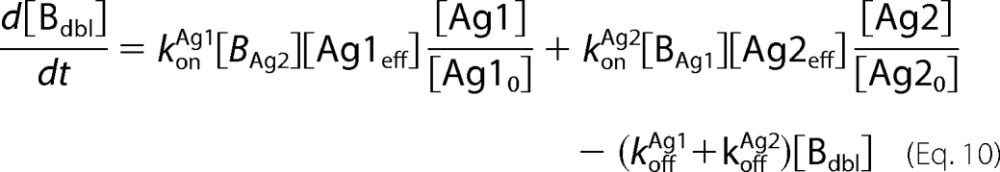In the equations above, Ag_eff refers to the effective antigen concentration once bound to the cell surface, and Ag₀ refers to the initial available antigen concentration.

Cell Lines

The cell lines A431 (catalog no. CRL-1555), H1993 (catalog no. CRL-5909), H441 (catalog no. CRM-HTB-174), BxPC-3 (catalog no. CRL-1687), and A253 (catalog no. HTB-41) were purchased from American Type Culture Collection. MKN45 cells were purchased from the National Institute of Biomedical Innovation in Japan. MKN45, H1993, H441, and BxPC-3 cells were cultured in RPMI 1640 basal medium (Life Technologies, catalog no. 11875-093) supplemented with 10% heat-inactivated FBS (Life Technologies, catalog no. 10082-147) and 100IU penicillin with 100 μg/ml streptomycin (HyClone, catalog no. SV30010). A431 cells were cultured in DMEM high glucose basal medium (HyClone, catalog no. SH30022.01) with the same supplements. A253 cells were cultured in McCoy's 5a medium (Life Technologies, catalog no. 16600-082) with the same supplements.

MET and EGFR Quantitation

Median MET and EGFR² numbers on each cell line were determined using the Quantum Simply Cellular anti-human IgG cytometry kit by Bangs Laboratories (Fishers, IN). The fluorescence of cells and a set of calibrated control cytometry beads with a known number of antibody binding sites were compared using an antibody specific for each receptor. Identical concentrations of the same antibodies were bound to cells and beads, analyzed by flow cytometry, and quantitated by fitting the median fluorescence intensity shift to that of the control beads.

Unbound Receptor Detection

Unbound receptor levels were determined by binding titrated concentrations of an antibody construct of interest to its ligand(s) on live cells chilled on ice in suspension in PBS, 1% BSA for 30 min; quickly washing away any excess antibody; and then fixing for 5 min with PBS, 4% paraformaldehyde to cross-link the antibody with ligand(s). Fixed cells with antibody bound were then blocked with PBS, 1% BSA 0.1% sodium azide, and unbound ligand were detected with a fluorophore-conjugated antibody binding the same ligand epitope. All antibodies and bispecific antibodies used for binding and detection to MET and EGFR were developed internally. Antibody binding and occupancy of both MET and EGFR binding epitopes were determined simultaneously using separate antibody-fluorophore conjugates. 5 μg/ml of anti-MET Alexa Fluor 555 conjugate was used to detect unbound MET with 5 μg/ml anti-EGFR Alexa Fluor 647 conjugate being used to detect unbound EGFR. Fluorophore conjugates were made using TFP or succinimidyl ester antibody labeling kits as appropriate (Invitrogen, catalog nos. A30006, A30007, and A30009) to label primary amines on binding and detection antibodies. In some experiments, to detect bound antibody, separate identical sets of treated samples were stained with anti-human IgG phycoerythrin conjugate (Life Technologies, catalog no. H10104).

Cytometry measurements were performed on either a BD FACSCalibur cytometer running CellQuest Pro version 5.2.1 for Mac OS X (BD Biosciences) or a BD LSR Fortessa cytometer running FACSDiva version 8.0.1 for Windows. The cells were gated as single events by forward and side scatter and analyzed with appropriate, empirically determined compensation between signal channels.

Unbound Receptor Quantitation and Data Analysis

Bound antibody signal was normalized between maximal median fluorescence intensity signal at the highest concentration tested and signal in a no-antibody control. Unbound receptor signal was normalized between the maximal signal in a no-antibody control, and the baseline signal in the presence of the highest concentration of antibody was tested, which was far above the concentration required to saturate estimated cell surface antigen levels. All data analyses were performed using GraphPad Prism version 6.04 for Windows (GraphPad Software).

Murine A253 Tumor Xenograft Model

A murine tumor xenograft model was developed to compare the in vivo effects of tetravalent bispecific constructs with lower versus higher affinity to a low expressed target antigen. Athymic nude mice (Harlan Laboratories) used in the study were kept in normal environmental conditions and fed ad libitum throughout the study. First, the animals were randomized by weight and inoculated with 5 × 10⁶ A253 cells in Matrigel (Corning, catalog no. 354248) in the hind flank. One week after inoculation, twice per week tumor volume measurement was initiated and continued through the course of the study. 6 weeks after inoculation, the animals were randomized by tumor volume into three groups of eight animals each with a mean tumor volume of 500–600 mm³. Each group was then treated with either a nonbinding negative control antibody at 20 mg/ml or a lower or higher affinity tetravalent bispecific construct at 27 mg/ml, each dosed twice a week for 4 weeks.

Results

Mathematical Model of Antibody Binding

Antibodies in a bivalent or tetravalent IgG-like format are assumed to be capable of engaging both binding arms simultaneously. To conceptualize and mathematically simulate the binding of a two-armed antibody, we adapted a model from the literature that was previously used to simulate bivalent binding of an IgG to two antigens on a surface (27). This model is based upon straightforward and logical geometric constraints and assumptions. It is informed by parameters that are routinely measured in biopharmaceutical discovery and selection efforts, antibody engineering, and cell-based assays, such as the number of target antigens expressed on the cell surface and the monovalent antibody-antigen association (k_on) and dissociation (k_off) rates. The model does not require any fitting to estimate parameters. Table 1 lists and defines the required parameters to fully inform the model. The model's depiction of bivalent binding to cell surface antigens treats the binding of each arm of an antibody to an antigen as an independent event (Fig. 2). These independent binding events are assumed to occur with monovalent on and off rate kinetics as measured by techniques such as surface plasmon resonance and were informed in our model by Biacore surface plasmon resonance measurements. The binding of the first arm of an antibody is modeled as binding to a soluble target, with the concentrations of antibody and antigen assumed to be evenly distributed in the available volume. Following the binding of the first arm of the antibody, the microenvironment that the molecule is able to access is dramatically altered (Fig. 2B). At this point, the antibody is assumed to be fixed to a region near the cell surface by the initial binding event. Instead of being able to freely sample the entire available volume, the unbound arm of the antibody is now confined to a volume defined by the size, flexibility, and structure of the antibody. Antibodies are known to be flexible, and so in the absence of available data, the bound antibody is assumed to sample a hemispheric space with a radius equal to the length of a typical IgG (27–29). Consequently, the concentration of the antigen within that hemispherical volume is calculated from the available receptor number per cell data (Table 2) and by assuming that the antigen is evenly distributed on the surface of the cell. The concentration of antigen that exists in the microenvironment of a bound antibody is termed the effective antigen concentration in our model ([Ag_eff]).

TABLE 1.

Model parameter definitions and parameter values in baseline simulations

Parameter	Model baseline value	Definition
kon	105 m−1s−1	Kinetic rate constant for Ab-Ag association
koff	10−4 s−1	Kinetic rate constant for Ab-Ag dissociation
[Ag0]	Calculated based on receptor number/cell	Initial antigen concentration; estimated as solution phase concentration
[Ageff]	Calculated as described in Fig. 2 and “Experimental Procedures”	Effective antigen concentration experienced by antibody bound to cell surface receptor(s)
rIgG	125 Å (28, 29)	Arm to arm distance of an IgG
rcell	8 μm (37)	Radius of an average cell

FIGURE 2.

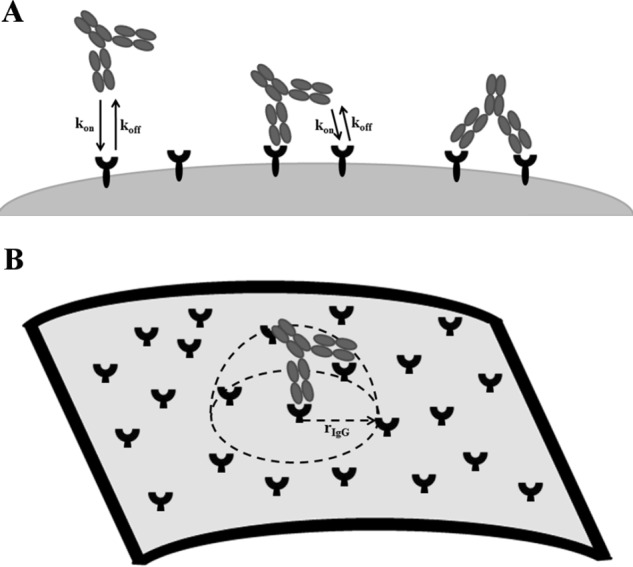
Schematic of framework for multivalent antibody binding model. A, assumed process for antibody binding to cell surface antigens assuming that each arm binds independently with monovalent binding kinetics parameters k_on (association) and k_off (dissociation). B, cartoon illustrating steric assumption of the constrained volume accessible to unbound arms(s) of a multivalent construct following binding of the first arm. The parameter r_IgG denotes the radius of the IgG or binding molecule.

TABLE 2.

Cell surface EGFR and MET levels on selected cell lines

Cell line	Tissue	EGFR/cell ± S.D.	MET/cell ± S.D.	EGFR:MET ratio
MKN45	Gastric	220,000 ± 100,000	1,700,000 ± 640,000	1:7.7
A431	Epidermal	6,700,000 ± 2,400,000	100,000 ± 39,000	67:1
H1993	Lung	560,000 ± 250,000	2,400,000 ± 800,000	1:4.3
H441	Lung	400,000 ± 170,000	320,000 ± 140,000	1.3:1

Mathematical Modeling of Varying Antigen Density

We employed our mathematical model of bivalent IgG binding to cell surface antigens to explore the binding properties of bispecific antibodies to a pair of cell surface targets. Receptor density can vary between cell lines by orders of magnitude, and for bispecific antibodies this means that the ratio between targets can vary over an even greater range. The implications of varying ratios of antigen for target binding and for the affinity that is required to efficiently engage each target were explored in detail by mathematical modeling. MET and EGFR were used as model antigens for this study because of the availability of bispecific antibodies targeting these two receptors.

A hypothetical cell expressing varying amounts of surface MET and EGFR was simulated in our model (Fig. 3). In each case, surface EGFR expression was maintained constant at 10⁶ molecules of EGFR/cell, and surface MET receptor expression was varied from 10⁶ receptors (equimolar to EGFR) to 10⁴ receptors/cell (an EGFR:MET receptor ratio of 100:1). Assuming “typical” properties for a cell and antibody as described in Table 1, the binding behavior toward each receptor of a bispecific IgG-like molecule can be predicted. Fig. 3 summarizes the predicted binding curve of a representative bispecific antibody on the cell surface.

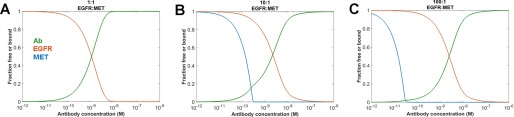
FIGURE 3.

Model predictions as a function of EGFR:MET antigen ratio with representative antibody and cellular parameters as detailed in Table 1. EGFR antigen density was held constant at 10⁶ receptors/cells, whereas MET was varied at 10⁶ (A), 10⁵ (B), and 10⁴ (C) receptors/cell. Green lines, simulated antibody binding curve; red lines, simulated unbound EGFR; blue lines, simulated unbound MET receptor.

At equimolar antigen expression levels (Fig. 3A), binding to both receptors is predicted to occur equivalently; this is unsurprising because binding to each receptor is modeled as having identical kinetics. However, as the expression of the antigens is altered and the ratio of EGFR:MET expression rises to 10:1 (Fig. 3B) or 100:1 (Fig. 3C), the model predicted binding curves to each antigen increasingly diverge. The binding to the predominant antigen is minimally affected, but the proportion of binding to the lower expressed antigen is predicted to be strongly impacted. As the ratio of EGFR:MET increases, binding to the MET receptor occurs at progressively lower concentrations of antibody. Although the simulated K_d of MET binding is 1 nm, when EGFR is present in excess over MET, the simulated binding to the Met receptor occurs at a much higher apparent affinity. In the case of 100-fold excess EGFR over MET, the apparent binding K_d of the cell surface MET is predicted to be ∼10 pm.

Measurement of Cell Surface Ligand Binding and Receptor Occupancy

It is difficult to independently measure the individual binding events of a conventional IgG, both arms of which bind identical epitopes on the same target. A previous report approached this problem by fitting a mathematical model to estimate the effect of avidity on cell surface binding (30). Although informative, this approach is empirical and not mechanistic in nature and does not distinguish the binding of the two arms from one another. Here we utilized bispecific antibodies targeting the growth factor receptors MET and EGFR (Fig. 1) to directly measure binding to two different antigens simultaneously. Because the constructs target two different receptors, we were able to develop a quantitative flow cytometry method to measure the receptor occupancy on the cell surface for each receptor independently as a function of bispecific antibody concentration. Employing this method on a number of cell lines expressing a range of MET and EGFRs (Table 2), we tested the predictions of our mathematical model and evaluated the impact of antigen ratio on binding to each target.

First, we demonstrated that the procedure we developed to measure receptor occupancy of each receptor was specific for the chosen receptor. Using the parental antibodies from which the bispecific construct was derived, we showed that each parental antibody bound and occupied its target antigen without a measurable effect on the untargeted antigen (Fig. 4). In contrast, when a combination of the two antibodies or the bispecific antibody was added, both antigens were affected (Fig. 5, A and D).

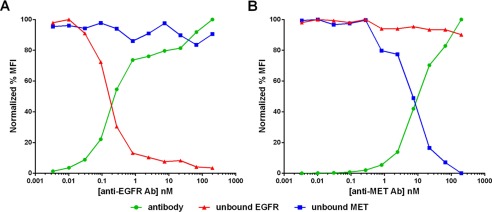
FIGURE 4.

Comparison of antibody binding (green circles) versus unbound EGFR (red triangles) or MET (blue squares) receptors on MKN45 cells in the presence of anti-EGFR monoclonal antibody (A) or anti-MET monoclonal antibody (B). MFI, median fluorescence intensity.

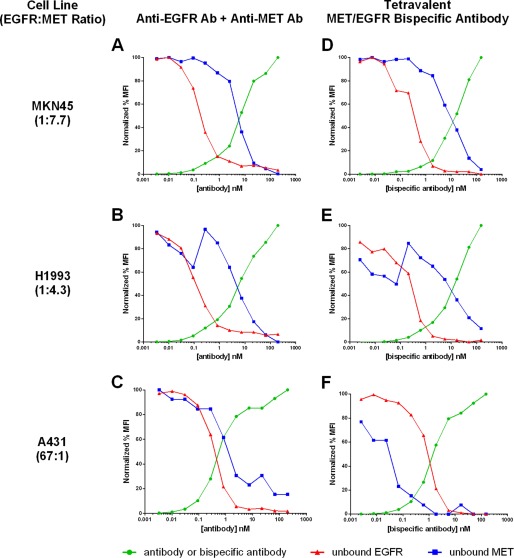
FIGURE 5.

Comparison of antibody binding (green circles) versus unbound EGFR (red triangles) and MET (blue squares) receptors on MKN45 (A and D), H1993 (B and E), and A431 (C and F) cell lines in the presence of anti-EGFR monoclonal antibody and anti-MET monoclonal antibody combination (A–C) and anti-MET/EGFR tetravalent bispecific antibody construct (D–F). MFI, median fluorescence intensity.

We next explored the antigen binding characteristics of the MET/EGFR bispecific antibody on several cell lines chosen to have a wide range of antigen expression (Table 2). In addition to expressing a range of MET and EGFR, the cell lines also vary in the ratio of the expression of these two receptors. The cell lines chosen for this study have antigen expression ratios ranging from nearly 70-fold higher expression of EGFR than MET in the case of A431 to nearly 8-fold higher MET expression than EGFR for MKN45.

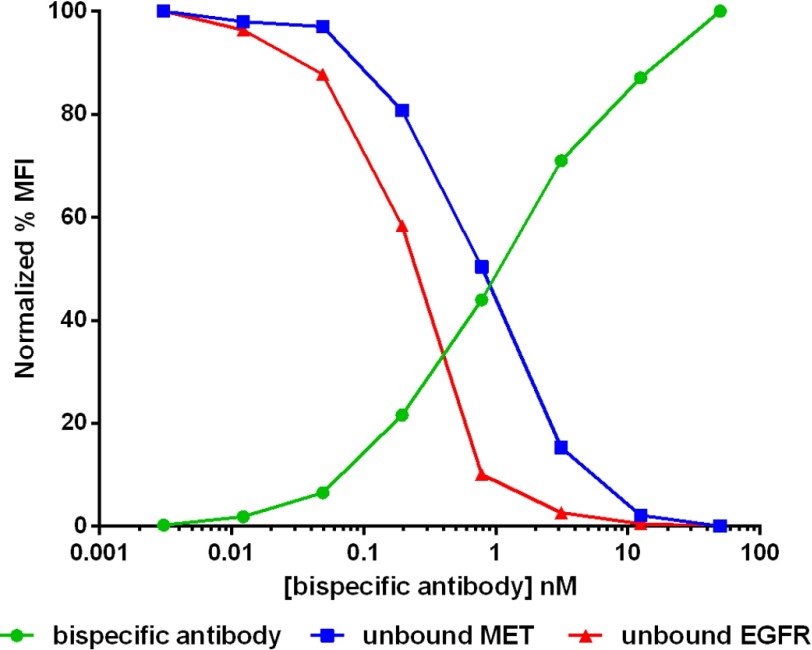
When measuring the tetravalent bispecific binding and target receptor occupancy curves for the cell line H441, which has similar, moderate amounts of both MET and EGFR (Table 2), the receptor occupancy curves for both receptors were measured to be within a few fold of one another in agreement with the mathematical model (Fig. 6). The antibody binding curve was also shown to be the converse of the occupancies of both receptors, indicating that as the tetravalent bispecific construct binds to the cell surface, it occupies both receptors similarly. By contrast, in other cell lines such as MKN45 (Fig. 5, A and D) and H1993 (Fig. 5, B and E), which express ∼4–8-fold more MET than EGFR, the receptor occupancy curves of the two ligands diverged to a greater degree. In these cell lines, EGFR becomes completely occupied at considerably lower tetravalent bispecific concentrations than the predominant MET antigen (Table 3). In addition, the bispecific binding curve matches more closely with the MET antigen occupancy curve, whereas the EGFR occupancy diminishes at much lower bispecific concentrations.

FIGURE 6.

Comparison of antibody binding (green circles) versus unbound EGFR (red triangles) and MET receptor (blue squares) on the cell line H441 in the presence of anti-MET/EGFR tetravalent bispecific antibody construct. MFI, median fluorescence intensity.

TABLE 3.

Bound antibody EC₅₀ and unbound receptor IC₅₀ values

Cell line	Antibody	Bound antibody EC50	Unbound MET IC50	Unbound EGFR IC50
		nm	nm	nm
MKN45	Combination	7.3	5.4	0.17
	Bispecific	21.7	10.3	0.32
H1993	Combination	8.7	6.5	0.12
	Bispecific	25.0	15.2	0.32
A431	Combination	0.5	0.93	0.38
	Bispecific	1.4	0.05	0.92

The A431 cell line conversely expresses ∼70-fold more EGFR than MET, the highest antigen ratio of the cell lines tested (Fig. 5, C and F). Combined antibody binding on this cell line shows that both antigens are occupied at a similar concentration of the antibody combination (Table 3). However, when the bispecific construct is titrated over this cell line, the MET antigen was measured to be completely occupied at much lower antibody concentrations than seen with the combination, followed at higher concentrations by the more highly expressed EGFR antigen. This order of antigen binding is in reverse order from that observed for the MET-predominant cell lines. In this case, with the predominant expression of EGFR, the antibody binding curve more closely followed the EGFR occupancy result, and the MET occupancy was shifted to lower concentrations. For all cell lines where one receptor predominates, the bispecific construct binding curve more closely followed the loss of receptor occupancy of that predominant receptor, and the lesser expressed receptor was bound at lower concentrations of the bispecific antibody. For the lower expressed antigen, receptor occupancy occurred at lower concentrations of the bispecific relative to the combination of antibodies and also lower than the monovalent binding affinity would have predicted. The magnitude of this effect appeared proportional to the antigen ratio.

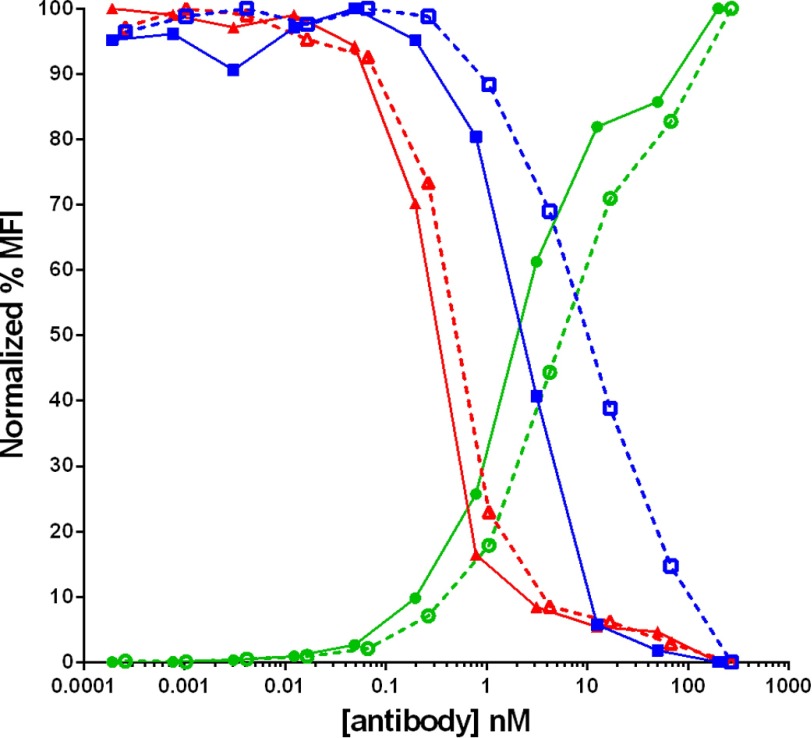
We also analyzed whether receptor occupancy at similar concentrations was increased by using bispecific molecules of different valencies. The tetravalent MET/EGFR bispecific construct (Fig. 1B) was compared with a bivalent “knobs into holes” MET/EGFR bispecific construct (Fig. 1C) using similar ligand binding domains with comparable monomeric affinity to their respective target antigens. When compared, both the antibody binding and receptor occupancy curves appeared similar to within a few fold of each other, indicating that any differences between a tetravalent and divalent MET-EGFR bispecific construct in this assessment were minimal (Fig. 7).

FIGURE 7.

Comparison of antibody binding (green circles) versus unbound EGFR (red triangles) and MET (blue squares) receptors on MKN45 cells in the presence of anti-MET/EGFR tetravalent bispecific antibody construct (solid symbols, solid lines) or anti-MET/EGFR bivalent bispecific antibody construct (open symbols, dashed lines). MFI, median fluorescence intensity.

Affinity and Avidity in a High Antigen Ratio Cell Line

With a bispecific molecule, it is often the case that affinity to one target differs from affinity to the second target. Potential effects of this imbalanced affinity on cell surface target binding are unclear, as is the impact that varying receptor densities and/or ratios may have on binding of bispecifics with unbalanced affinity. We conducted additional simulations and quantitative flow cytometry experiments to understand this issue.

First, we simulated the binding of an existing tetravalent bispecific molecule to two cell surface receptors (antigens A and B) that are often coexpressed with a high antigen ratio. In general, the expression of antigen A is considerably lower than the expression of antigen B. For the model, the expression ratio was set at 1:100, because a representative cell line exists with this antigen A:B ratio. The affinity of this tetravalent bispecific construct is imbalanced; although the single-arm affinity to antigen B is ∼700 pm, the affinity to antigen A is a considerably weaker 20 nm. This was initially anticipated to impair the ability of the construct to bind antigen A, but surprisingly the cell binding model predicted a very strong avidity effect and enhanced binding into the low to mid picomolar range (similar to Fig. 3C). Even when the anti-A affinity was increased to 1 nm in the model, very little effect was predicted on the binding curve to antigen A.

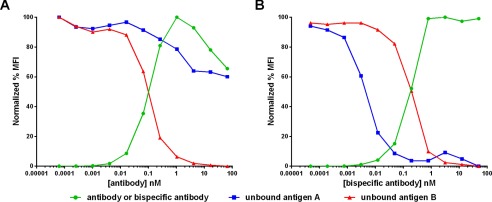
To investigate this prediction experimentally, the quantitative flow cytometry approach used to measure EGFR and MET receptor occupancy was adapted to measure antigens A and B on the cell line BxPC3, which has an antigen A:B ratio of ∼1:25. When a combination of the parental antibodies was titrated on these cells, antigen B binding occurred as expected with binding at approximately the measured K_d (Fig. 8A). The anti-A antibody, however, bound extremely poorly and was unable to saturate cell surface antigen even at very high antibody concentrations. We suspect that this failure to saturate is an experimental artifact caused by the low affinity of the anti-A antibody, which may dissociate from the cell during the wash steps and before it can be fixed to its ligand. When the tetravalent bispecific construct was titrated over the same cell line, the antigen B binding behavior was minimally affected relative to the parental antibody combination, but the antigen A binding shifted several orders of magnitude toward a higher affinity interaction (Fig. 8B).

FIGURE 8.

Comparison of antibody binding (green circles) versus unbound antigen B (red triangles) and antigen A (blue squares) on BxPC3 cells in the presence of a combination of equal concentrations of anti-B antibody and an anti-A antibody (A) or anti-B/A tetravalent bispecific antibody construct (B). MFI, median fluorescence intensity.

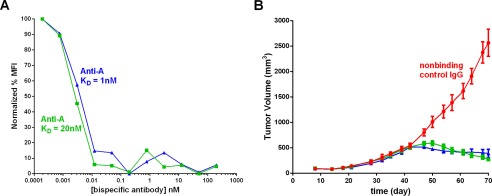
Our cell surface binding model had predicted that a higher affinity to antigen A would have little effect on binding to the target. To test this experimentally, the anti-A binding portion of the tetravalent bispecific construct was engineered to have a binding affinity of 1–2 nm, a 10–20-fold higher affinity than the original bispecific, bringing it in balance with the affinity to antigen B. When this higher affinity construct with an otherwise similar molecular structure was compared directly against the lower affinity bispecific construct for antigen A binding on the cell surface, the two were indistinguishable. Both bound antigen A at very low concentrations (Fig. 9A). Consistent with this binding data, a mouse xenograft study conducted using the same cell line compared the two bispecific antibodies and revealed no significant difference in efficacy between the imbalanced and balanced affinity tetravalent bispecifics (Fig. 9B).

FIGURE 9.

Comparison of antigen A receptor occupancy in response to either low antigen A affinity (green squares) or high antigen A affinity (blue triangles) tetravalent bispecific constructs on A253 cells (A) and tumor volume over time in an A253 mouse tumor xenograft model comparing a nonbinding control IgG (red circles) with the same low antigen A affinity (green squares) or high antigen A affinity (blue triangle) tetravalent bispecific constructs (B). The error bars represent means ± S.D. MFI, median fluorescence intensity.

Discussion

In this work, we present a simple and generalizable conceptual and mathematical framework for multivalent binding to two or more cell surface targets. Starting from straightforward geometric constraints and routinely measured biological data, we have crafted a mathematical representation of the process by which an IgG-like molecule may interact with and bind to cell surface antigens. Using this simplified framework as a model for avidity, we ran a series of binding simulations to elucidate the effects that varying antigen densities could have on the binding of bispecific constructs. Intriguingly, the model predicted that for bispecific constructs targeting two cell surface targets, antigen density may have a very strong effect on binding to the less predominant antigen. The magnitude of this effect was predicted to be dependent upon the antigen expression ratio. Additionally, the model predicted that binding curves of the lesser expressed antigen may exceed the monovalent affinity of the antibody-antigen interaction by orders of magnitude at high antigen ratios.

Using a tetravalent MET/EGFR bispecific antibody, we developed a flow cytometry-based assay enabling the direct measurement of cell surface receptor occupancy for both the MET and EGFR antigens. This method was shown to be robust and specific over a wide range of cell lines and antigen expression levels. Then using a MET/EGFR bispecific antibody construct, we probed the model predictions by generating in vitro binding and receptor occupancy curves on cell lines expressing a range of receptor numbers and EGFR:MET receptor ratios (Table 2).

For a cell line with similar amounts of surface MET and EGFR, both receptor occupancy curves appeared similar to one another and in line with the monovalent affinities of the antibody-antigen interactions as measured by Biacore (Fig. 6). However, for cell lines that expressed more MET than EGFR, the EGFR occupancy curve shifted and available receptor was measured to be bound essentially completely at concentrations considerably lower than the monovalent EGFR affinity (Fig. 5 and Table 3). Conversely, in a cell line with far more EGFR than MET, the MET receptor occupancy was measured to be near complete at concentrations far lower than predicted based upon its affinity. By contrast, in both cases the occupancy of the predominant receptor was measured to occur in the range that would be expected based upon the monovalent affinity to that receptor.

This effect of cell surface receptor ratio on binding to a lower expressed antigen was predicted by our mathematical model (Fig. 3). In an effort to probe the mechanism for observed enhanced binding to a lower abundance cell surface antigen, we investigated some of the assumptions and predictions of the model. Interestingly, the geometric assumption of steric restriction following the binding of one arm of the bispecific leads to an estimate of the effective concentration of antigen [Ag_eff] accessible by the unbound arm of the bispecific. This concentration is calculated to be very high relative to the binding affinity of most antibodies. For the case of a cell with 10⁵ receptors on the cell surface, the calculated value of [Ag_eff] is greater than 1 μm. Because [Ag_eff] ≫ K_d, the binding of the second arm of the antibody is predicted to occur quickly. For the vast majority of multivalent binding events, all arms are bound shortly after a single arm binds. Another consequence of the high predicted [Ag_eff] is that dependence on affinity for binding of the second arm of an antibody construct in the K_d range of most therapeutic antibodies is greatly reduced. For [Ag_eff] concentrations near the micromolar range, antibody affinity changes in the low nanomolar range have very little effect on the binding, as shown by our model and verified experimentally (Fig. 9A).

The straightforward assumptions that were made in the model are likely not accurate in many cases. In particular, the assumption that antigen is evenly distributed over the cell surface is probably not accurate for antigens that are known to have patterns in their distribution, such as antigens associated with cell polarization or lipid rafts (31–34). Furthermore, the model treats antigen, which is confined to the two-dimensional cell surface, as if it were evenly distributed in the volume in which the cells are confined, making antigen concentration a function of both cell density and receptor number per cell. A similar assumption is made for the modeling of the singly bound antibody at the cell surface. In this case, the antigen confined to the cell surface is treated as though distributed in a hemispherical volume accessible to the other arm of the antibody.

The assumption that the antibody is flexible such that it can freely sample a hemisphere centered on one arm is also probably a poor approximation in some cases. For example, some antibodies likely bind epitopes that limit their flexibility. Other antibodies may inherently vary in their flexibility and affect the accuracy of this prediction (35).

Despite the uncertainty around the model assumptions, the model was successful in quantitatively predicting the effects of receptor ratio and the lack of dependence on affinity. In part, this is likely because although there is uncertainty regarding some assumptions, the model predictions are due primarily to the very high [Ag_eff] that it computes for the second arm binding. Although there is quantitative uncertainty regarding the value of [Ag_eff] because of the assumptions made, its value is typically in the >1 μm range. This value is orders of magnitude higher than the affinity of most therapeutic antibodies, and so even if a more appropriate value for [Ag_eff] was considerably different from the calculated value, the model predictions are simply not sensitive to this difference. Therefore, we feel that the simplistic geometric assumptions made in our model are appropriate to capture the fundamental biology while requiring minimal measurements and with no parameter fitting required.

The conceptual outline of multivalent binding described in Fig. 2 and the quantitative simulations in Fig. 3 predict that it is the initial binding to an antigen that subsequently drives bivalent binding and gives rise to an apparent enhancement of targeting to lower expressed antigens. For the initial binding event, the antibody is more likely to bind to the higher expressed antigen simply because of its abundance. Following this initial binding, the effective antigen concentration that the second arm of the antibody is able to access in its constrained volume near the cell surface is very high, leading to rapid binding of the second arm and a multivalently bound antibody-antigen complex. Because the second binding event is dependent on the first, only a fraction of the higher expressed antigen must be bound to result in near complete binding of the lower expressed antigen. As the antigen ratio increases, a progressively smaller amount of the highly expressed antigen must be bound to drive antibody cross-linking and near complete binding of the lower expressed antigen (Figs. 3 and 5). It is important to note that because the second arm binding event is dependent on a cell surface geometric constraint, this model does not apply in cases in which either antigen is not cell-associated.

The effect of antigen ratio on targeting and binding to a lower expressed antigen is potentially very significant. When the antigen ratio is high, the binding benefit to the lower expressed antigen is also very high and can result in interactions with modest monovalent affinity occurring at far lower concentrations or to a far greater extent than predicted. For some targets and expression patterns, we have shown that this apparent affinity boost can have an effect of several orders of magnitude. This could be a potential benefit in some situations, such as for binding to antigens that may be expressed at low levels that would otherwise require a very high affinity antibody to efficiently engage the target. It also has interesting implications for antibody discovery and engineering. Because the model predictions are strongly based on the geometry of the binding and subsequent ability of the bispecific antibody to sample the surrounding volume, any parameters that affect those attributes could alter the binding profile. Binding to an epitope on an antigen that restricts subsequent binding to additional antigens would dramatically reduce the avidity effect. In addition, antibody constructs with greater size or flexibility to their binding components could strongly impact the ability of the construct to bind multivalently. There is literature evidence that this occurs and that antibodies can be categorized by their propensity to efficiently bind bivalently (36). Although the bispecific antibody constructs used in these experiments are primarily tetravalent and not bivalent as depicted in our mathematical model, we reason that our simplified framework and mathematical model is still a useful approximation of multivalent binding in general. The bivalent approach is the simplest possible multivalent binding strategy to model and requires fewer assumptions or data to parameterize the model. In the multiple cell lines probed in this study and for the various bispecific constructs examined, our model of bivalent binding was able to capture the effect we measured experimentally.

Depending upon the biology and the desired properties of the antibody-antigen interaction, this modeling and experimental approach could be used to guide antibody engineering and selection approaches. Additionally, our framework for bivalent binding provides insight into the mechanism of binding and the key parameters that may affect the degree to which a multivalent construct productively engages multiple cell surface targets. It also suggests situations in which multispecific antibodies may provide mechanistic advantages over alternative approaches such as combinations of monoclonal antibodies. For example, the model suggests and we show experimentally that targeting to a poorly expressed antigen can be dramatically enhanced and the target saturated even by a low affinity antibody when designed as a bispecific but not as a combination of two monoclonal antibodies. The simplicity and flexibility of our modeling approach allows the exploration of the biological and biophysical parameter space to make quantitative predictions regarding multivalent binding and can help direct antibody engineering and selection efforts.

Author Contributions

J. J. R. and V. J. W. conceived and designed the study. J. J. R. and G. L. D. wrote the paper and prepared the figures. G. L. D. designed, performed, and analyzed the flow cytometry experiments. J. J. R. developed and implemented the mathematical model of receptor binding. All authors reviewed the results and approved the final version of the manuscript.