Abstract
The biggest challenge for jatropha breeding is to identify superior genotypes that present high seed yield and seed oil content with reduced toxicity levels. Therefore, the objective of this study was to estimate genetic parameters for three important traits (weight of 100 seed, oil seed content, and phorbol ester concentration), and to select superior genotypes to be used as progenitors in jatropha breeding. Additionally, the genotypic values and the genetic parameters estimated under the Bayesian multi-trait approach were used to evaluate different selection indices scenarios of 179 half-sib families. Three different scenarios and economic weights were considered. It was possible to simultaneously reduce toxicity and increase seed oil content and weight of 100 seed by using index selection based on genotypic value estimated by the Bayesian multi-trait approach. Indeed, we identified two families that present these characteristics by evaluating genetic diversity using the Ward clustering method, which suggested nine homogenous clusters. Future researches must integrate the Bayesian multi-trait methods with realized relationship matrix, aiming to build accurate selection indices models.
Introduction
Jatropha (Jatropha curcas L.) has many economically interesting characteristics, and nowadays, it has been considered as the most important shrub for biodiesel production, mainly due to the large amount of oil content it produces [1]. Additionally, jatropha stands out due to premature production period, when it is compared with other palms commonly used for biofuel production [2]. Moreover, this culture presents drought resistance [3], low seed cost [4], high seed oil content [5], and easy adaptation [2].
Approximately 35% of seeds’ content is composed of oil, of which 24.6% is crude protein and 47.2% is crude fat [6]. Moreover, jatropha’s oil presents higher oxidation stability than soybean’s oil; lower viscosity than castor’s oil; and lower pour point than other palms [7].
Despite the large amount of oil and crude protein content, consumption of seeds can represent a risk for animal health [8]. Indeed, the use of jatropha’s cake (by-product of seeds industrial processing) as animal feed, and consequently the crop cultivation economic viability are conditioned by the low toxicity content [9]. Phorbol ester has been considered as the main substance for jatropha’s seeds toxicity [10], and has been differently reported in toxic genotypes (2 to 6 mg/g of dry matter) and in non toxic genotypes (0 to 1.8 mg/g) [9]. Thus, there is the need to achieve highly productive genotypes with respect to high seed oil content and low level of toxicity. Therefore, the use of breeding techniques must be adopted in order to identify superior genotypes aiming at the improvement for these traits.
Bayesian multi-trait models have become useful statistics method for plant and animal genetic evaluations. Many authors have shown that this model is more flexible and effective than the least squares method, since it is not only based on the likelihood function, but it also allows a priori knowledge assumption when defining prior distribution [11].
Many previous studies have estimated variance components and genetic parameters under different statistical methods in jatropha [12–15]. However, none of them carried out multi-trait analysis using a Bayesian approach for seed oil content (SOC, %), weight of 100 seeds (W100S, g), and phorbol ester concentration (PEC, mg/g). Therefore, the Bayesian multi-trait analysis was carried out in order to estimate variance components and genetic parameters, which were used to evaluate genetic diversity and selection indices, aiming to identify superior genotypes for SOC, W100S and PEC traits.
Materials and Methods
Experimental design
The experiment considered the evaluation of 179 jatropha half-sib families from the Embrapa Cerrados germplasm bank [samples were collected in different Brazilian regions (S1 Table)]. It is settled in the experimental field of Embrapa Cerrados, Planaltina, Distrito Federal, Brazil (15°35’30”S and 47°42’30”W; 1007 m asl). The experiment was implemented in November, 2008, in a complete randomized block design with 2 replications, and 5 plants per plot, arranged in rows, spaced 4 m between rows, and 2 m between plants. All management practices were based on Dias et al. [16], and they were adapted according to recent research advances regarding jatropha in Brazil [17–19]. The half-sib families were evaluated over 5 crop years (2010 to 2014) for W100S, while SOC and PEC were evaluated only in 2014. All data used in this study are available in Table in S2 Table.
Phorbol ester was extracted according to procedure described by Makkar et al. [20]. Milled seeds was carried on in accelerated solvent extraction equipment called Dionex (model ASE 350). Tetrahydrofuran was used as solvent, and posteriorly, it was evaporated under nitrogen flow. The Oily residual was transferred to a test tube (10 mL), and extracted repeatedly (four times) using methanol (once using 2mL and three using 1mL). Finally, the oily residual was transferred to volumetric flask (5 mL). The work solution was filtered using VertiPure PTFE Syringe (13 mm, 0.2 μm) and 1oo mL of this solution was injected into High Performance Liquid Chromatography (HPLC). A typical column (C18 250 x 4.6 mm) was used, with the temperature around 25°C. A UV detector allowed on-column detection operated from 200 nm to 340 nm. The standard curve was built using 12-myristate 13—phorbol Acetate.
The oil extraction was performed crushing seeds and albumens, and weighing epicarp and mesocarp separately. Analyses were performed according to Adolfo Lutz Institute protocols. Sample (200 g of seeds) for each plant and replicated twice. Soxhlet was used to extract the oil and the hexane was used as solvent.
Despite the five consecutive years of evaluations of W100S, only the records of 2014 were used because SOC and PEC traits were recorded only in this specific year. Additionally, mean phenotypes were used for W100S, and these records were adjusted according to the number of replications within genotypes and blocks. Also, all analyses were carried out using 358 phenotypic records for each trait of the 179 half-sib families.
Statistical model and analysis
Variance components and genetic parameter estimates were obtained under the Bayesian approach, via Gibbs sampling, using the Gibbs2f90 software, as described by Misztal et al. [21]. We considered a total of 100,000 cycles after discarding the 40,000 initial samples used for burn-in and thinned every tenth iteration, resulting in a total of 6,000 samples. The convergence of Markov Chain Monte Carlo (MCMC) was tested by the Geweke criterion [22], using two packages: boa [23], and CODA [24], implemented in the R software [25]. Posterior means, key percentiles and standard deviations (SD) for estimated parameters were obtained from MCMC samples. Multi-trait mixed model was:
| [1] |
where yijkl is the lth = {1,2,…,358} phenotypic value of ith = {1,2,3} trait, on jth = {1,2,…,179} genotype, within kth = {1,2} blocks; μi is the overall mean of ith trait; and eijkl is the residual term.
Under the Bayesian approach, the following joint distribution of data (likelihood function) were:
| [2] |
where β is the vector of a prior probability of systematic effects (overall mean and blocks for each trait from Eq [1]); g = {gij}∼N(0,I⨂G0) is the vector of a prior probability of genotypic values, where I is the identity matrix and is the genotypic variance matrix; e = {eijkl}∼N(0,I⨂R0) is the vector of a prior probability of residual values with normal independent identical distribution; where ; x′ij and z′ij are incidence rows that relates systematic and genotypes effects within traits to the respective phenotypic value; and is residual variance assumed as homogeneous.
The following a priori probability distributions for the location parameters of interest were given by:
| [3] |
where Vb is a diagonal matrix of the a priori variance of β, assuming Vb → ∞;
Three-dimensional scaled inverted Wishart distributions are assigned as prior process for each of the G0 and R0 covariance matrices:
| [4] |
| [5] |
Where Σg and Σe are scale matrices, and n = 5 is the degree of freedom parameter.
The joint posterior density of all parameters, which are dependent on the genotypic effects of the corresponding matrix, but which take over prior independence, is given by
| [6] |
Clustering and genetic diversity
A cluster analysis was carried out aiming to understand the genotypic relationship between traits, and to identify genotypes that expressed genetically similar performance. Hence, we intended to cluster homogeneous genotypes. The first step of cluster analysis is to calculate dissimilarity (D) matrix. In this study, we adopted the Mahalanobis distance, which can be defined as follows:
| [7] |
Where g1 and g2 are genotypic values for SOC, W100S or PEC traits; Ψ = S−1 is the Mahalanobis generalized distance; and S−1 is the three-dimensional inverse of variance matrix. This metric was used to consider the covariance between genotypes evaluated in different blocks.
Thus, the Ward cluster hierarchy method was applied, and it was chosen aiming to maximize the homogeneity within clusters so that the sum of square of error (SSE) is minimum. SSE of each cluster can be achieved as follows:
| [8] |
where nm is the number of individuals on mth cluster; and
Mojena criteria was used to set the optimal number of clusters, and the method is based on computing the highest amplitude between clusters that maximizes the quality of the clustering [26].
| [9] |
where j = (1,2,…,n) is the number of clusters; αj is the correspondence joint point to n − j + 1 clusters; and Sα are the mean and the standard deviation of α′s; and ω is a constant equal to 1.25, as suggest by [27].
Selection index calculations
Selection indices procedures were constructed according to Hazel [28]. Overall genetic gain can be achieved by selecting individuals by the sum of its several genotypes for each trait weighted by its relative economic value. This aggregate genotype (H) can by defined as:
| [10] |
Where gi, i = {1,2,…,n} is the vector of genotypic values for the nth trait; and wi, i = {1,2,…,n} is the relative economic value.
In this study, three different scenarios were used, and they included different traits in the selection indices. Additionally, three different weights (w) of the traits in the breeding goal were taken into account. In the first situation, all traits had weight of 1 monetary unit per genetic standard deviation. In the second situation, SOC received weight of 2 and 1 monetary units for the other traits. Finally, we set weight of 4 monetary units for SOC, 2 for W100S, and 1 for PEC, in the third scenario. Traits contemplated in these scenarios were defined to depict a situation in which an established breeding program already working on selection for SOC intends to incorporate W100S and PEC in its breeding goal. As a trait of major importance, only SOC was used as target in the first scenario. The next two scenarios gradually included W100S and PEC in selection indices.
The set up matrices P, G and C contains phenotypic (co)variance between all components in a given scenario; covariance between traits of selection index and additive genetic values for traits of the breeding goal; and genetic (co)variance between traits in the breeding goal, respectively. Selection indices coefficients were calculated by b = P−1Gw, where w is the vector of relative economic weights expressed in monetary units per measurement units of the traits. Variances of the index (I) and of the H were calculated by and . Correlation between the index and the genotypic aggregate (accuracy of the index) was calculated by .
Monetary overall genetic gain per generation was calculated by ΔG = (i)RIHσH, and the response to selection per generation (S) for each trait was calculated by:
| [11] |
where i is the selection intensity assumed to be 1.75, considering the selection of the 10% superior genotypes.
Results
In this study, we evaluated 179 genotypes for the three important traits in jatropha breeding program: seed oil content (SOC), weight of 100 seeds (W100S) and phorbol ester concentration (PEC) aiming to identify superior half-sib families under a Bayesian multi-trait model, using selection indices procedures.
Phenotypic evaluation
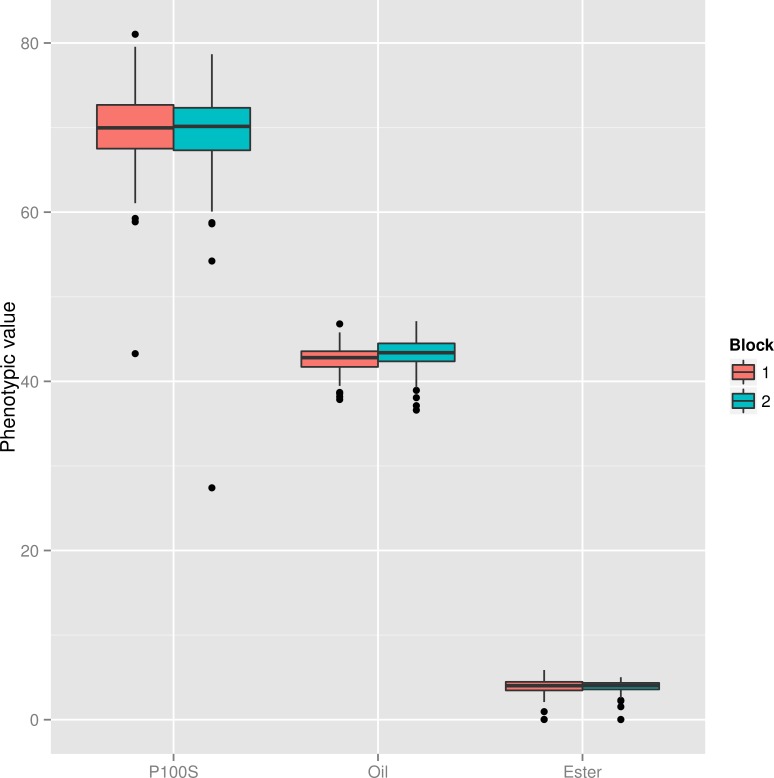
We observed that there are no differences between blocks within traits (Fig 1). The highest standard deviation value was observed for W100S, followed by SOC and PEC. We observed a few outlier records for each trait.
Fig 1. Phenotypic trait evaluation using the Boxplot analysis.
Vertical bars are second and third quantiles, and the dots outside the bars are outliers. Each block was evaluated separately, allowing their individual evaluation. W100S –weight of 100 seeds; SOC–seed oil content; PEC–phorbol ester concentration.
Convergence criterion
Geweke convergence criterion indicates convergence for all dispersion parameters when generating 100,000 MCMC chains, 40,000 samples for burn-in and a sampling interval of 10, totaling 6,000 effective samples used for variance component estimate. Similar posterior mean, median and mode estimates were obtained for variance components, suggesting density with normal shape appearance. Effective sample size (ESS) estimated the number of independent samples with information equivalent to that contained within the dependent sampling. Thus, it was observed that the length of the generated chain was adequate since the smallest ESS was 1991.
Variance components and genetic parameters
Genotypic variance estimated under the Bayesian multi-trait model for W100S () was about 43 times greater than for SOC (), or for PEC () (Table 1). The genotypic variances for SOC and PEC were approximately of the same magnitude. We observed negative covariance between W100S and PEC, which is a desirable relationship. Covariance between W100S and SOC was positive, and HPD interval evidences statistical significance of this parameter.
Table 1. Variance components and genetic parameters estimated under the Bayesian multi-trait analysis via Gibbs sampling of weight of 100 seeds (W100S), seed oil content (SOC) and phorbol ester concentration (PEC) traits.
| Parameter1 | PM2 | PMD | PMO | PSD | HPD | Z | ESS |
|---|---|---|---|---|---|---|---|
| 15.522 | 15.390 | 14.708 | 2.061 | 11.73, 19.65 | 0.19 | 5200 | |
| 0.891 | 0.884 | 0.823 | 0.408 | 0.10, 1.69 | -0.07 | 4187 | |
| -0.319 | -0.318 | -0.305 | 0.247 | -0.80, 0.17 | 0.13 | 5706 | |
| 0.359 | 0.337 | 0.299 | 0.132 | 0.15, 0.63 | 0.15 | 1991 | |
| -0.004 | -0.003 | 0.003 | 0.067 | -0.13, 0.13 | 0.18 | 3175 | |
| 0.373 | 0.369 | 0.386 | 0.059 | 0.26, 0.49 | 0.03 | 6000 | |
| 7.498 | 7.446 | 7.430 | 0.799 | 5.95, 9.02 | -0.04 | 6000 | |
| 0.008 | 0.004 | 0.113 | 0.317 | -0.62, 0.63 | -0.07 | 5426 | |
| -0.080 | -0.079 | -0.063 | 0.116 | -0.32, 0.13 | -0.21 | 5203 | |
| 2.416 | 2.409 | 2.452 | 0.214 | 1.98, 2.82 | -0.11 | 4190 | |
| 0.016 | 0.015 | 0.020 | 0.016 | -0.11, 0.14 | -0.02 | 4790 | |
| 0.312 | 0.310 | 0.305 | 0.033 | 0.25, 0.37 | -0.08 | 5995 | |
| 0.672 | 0. 674 | 0.684 | 0.040 | 0.586, 0.745 | 0.131 | 6000 | |
| 0.129 | 0.122 | 0.105 | 0.045 | 0.059, 0.232 | 0.679 | 2055 | |
| 0.545 | 0.544 | 0.551 | 0.052 | 0.436, 0.640 | -1.573 | 6000 |
1 Genetic variance of ith trait (); genetic covariance between traits i and j (); residual variance of ith trait (); residual covariance between traits i and j (); and heritability of ith trait ().
2 Posterior mean (PM), posterior median (PMD), posterior mode (PMO), posterior standard deviation (PSD), posterior high density interval (HPD), Z-Geweke (Z) and effective sample size (ESS).
W100S presented the highest residual variance (lower certainty), possibly due to a scale effect, followed by SOC and PEC, respectively (Table 1). Residual covariance estimates among all traits can be considered as not statistically significant when analyzing HPD interval; thus, residual correlations can be considered as absent.
W100S and PEC presented higher estimated heritabilities than SOC. Despite the higher certainty in these estimates being associated to W100S, amplitude of HPD intervals was relatively close for all traits (Table 1).
We verified desirable association between SOC and W100S (positive correlation) for phenotypic and genotypic correlation, being the latter stronger than the former (Table 2). Besides the moderate genotypic association between SOC and W100S, all the other correlations were of low magnitude for both genotypic and phenotypic correlations. Additionally, desirable negative genotypic correlation was observed between PEC and SOC, and between PEC and W100S.
Table 2. Heritability (diagonal), genotypic (above) and phenotypic (below) correlation between traits.
| Trait | SOC | W100S | PEC |
|---|---|---|---|
| Seed oil content (SOC) | 0.129 | 0.544 | -0.010 |
| Weight of 100 seeds (W100S) | 0.113 | 0.674 | -0.130 |
| Phorbol ester concentration (PEC) | 0.009 | -0.101 | 0.545 |
| Phenotypic variance | 2.774 | 23.019 | 0.685 |
Genetic diversity
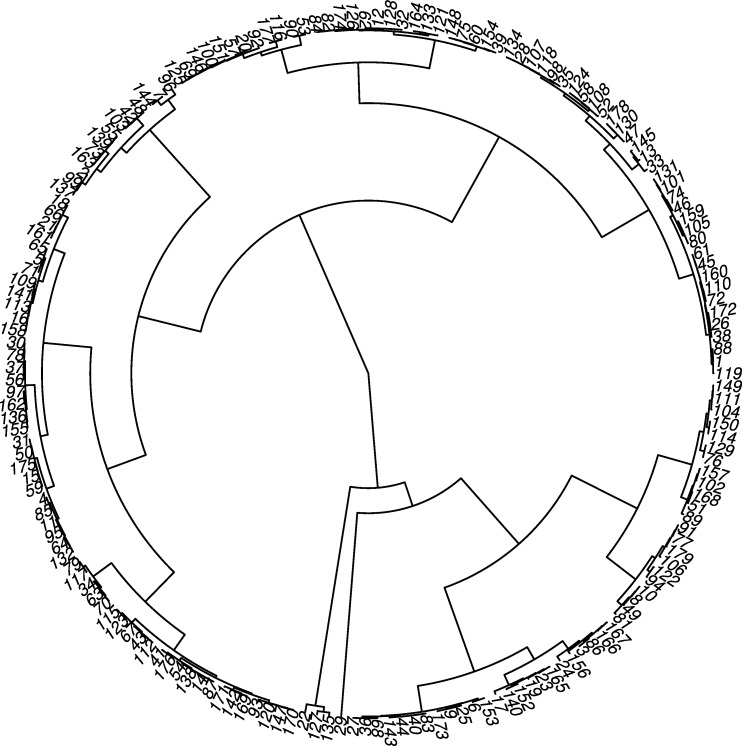
Genetic diversity analysis aimed to evaluate how the genotypes were distributed between the clusters. In this analysis we used the Ward clustering method based on the Mahalanobis distance, which was calculated using the genotypic values estimated under a Bayesian multi-trait mixed models.
Nine clusters were suggested according to the Ward method: six big clusters with 35, 31, 28, 23, 24 and 22 half-sib families; one cluster with 13 half-sib families; and two small clusters with 3 and 1 half-sib families (Fig 2).
Fig 2. Ward cluster method based on the Mahalanobis distance, calculated using genotypic values estimated by the Bayesian multi-trait analysis.
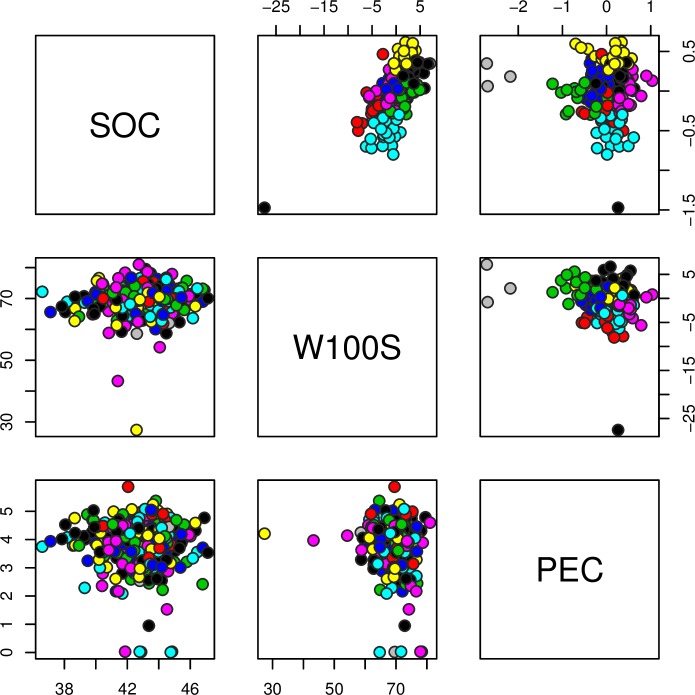
Phenotypic and genotypic distribution of the nine clusters suggested by the Ward clustering method can be verified in Fig 3. We observed that the use of genotypic values enables a well-defined clustering of genotypes, which is not observed when evaluating the phenotypic values using the clusters suggested by the clustering method. In other words, despite the high heritability, selection of plants based only on phenotypic information could not provide genetic gain for all traits simultaneously.
Fig 3. Genotypic values (above diagonal) and phenotypic values (below diagonal) distributions between seed oil content (SOC, g), weight of 100 seed (W100S, %) and phorbol ester concentration (PEC, mg/g).
Genetic gain and genotype selection based on selection index
After the study of trait’s behavior and after verifying that simultaneous genetic gain will hardly be achieved for all traits, we evaluated several different selection index scenarios (Table 3) aiming to select superior genotypes.
Table 3. Scenarios with the respective traits considered by the selection criteria.
| Scenario | Traits considered in the selection index1 |
|---|---|
| 1 | SOC |
| 2 | SOC + W100S |
| 3 | SOC + W100S + PEC |
1 Weight of 100 seeds (W100S, g), Seed oil content (SOC, %), and phorbol ester concentration (PEC) in seeds (mg/g)
Table 4 shows the results of response to selection per generation (S), accuracy of the index, and overall genetic gain among different scenarios and weights. The highest accuracy values were achieved under scenario 3 (all traits were used in selection criteria) regardless of the assessed weights. A different trend was observed for the monetary overall genetic gain per generation (ΔG), which was higher when adopting w3 (quadruple for SOC, double for W100S, and one for PEC) strategies. Additionally, it was possible to obtain simultaneous economically interesting response to selection in scenarios 1 and 2, considering different weighting strategies.
Table 4. Response to selection per generation (S), accuracy of the index (RIH), and monetary overall genetic gain per generation (ΔG) for weight of 100 seeds (W100S, g), seed oil content (SOC, %) and phorbol ester concentration in seeds (PEC, mg/g) using selection index.
| S for each trait | |||||
|---|---|---|---|---|---|
| Scenario1 | RIH | ΔG | SOC | W100S | PEC |
| w1 | |||||
| 1 | 0.2641 | 0.8647 | 0.37806 | 0.94490 | -0.00377 |
| 2 | 0.5866 | 1.9206 | 0.42677 | 5.43193 | -0.10412 |
| 3 | 0.7064 | 2.3128 | 0.36474 | 4.45593 | 0.34990 |
| w2 | |||||
| 1 | 0.3172 | 1.4959 | 0.37806 | 0.94490 | -0.00377 |
| 2 | 0.5631 | 2.6559 | 0.45034 | 5.16525 | -0.09691 |
| 3 | 0.6288 | 2.9657 | 0.41157 | 4.58196 | 0.26170 |
| w3 | |||||
| 1 | 0.3319 | 2.9980 | 0.37806 | 0.94490 | -0.00377 |
| 2 | 0.6058 | 5.4716 | 0.44750 | 5.20812 | -0.09802 |
| 3 | 0.6241 | 5,6372 | 0.43881 | 5.03137 | 0.09332 |
1 In scenario 1 only SOC was used as selection criteria. W100S was incorporated into the selection index in scenario 2, and PEC was added to scenario 3. Economic relative weights (w) were defined as w1 = same, w2 = double for SOC, and w3 = 4(SOC), 2(W100S) and 1(PEC).
Discussion
Phenotypic evaluation
Boxplot analysis was carried out to verify how phenotypic data were distributed among blocks. Previous phenotypic analyses are always important for the understanding of each trait, and it helps the researcher in choosing the best way of data evaluation.
Phenotypic variance estimates for seed oil content (SOC) and phorbol ester concentration (PEC) presented low magnitudes. Different authors have shown the absence of genetic diversity between accessions [13, 29, 30], suggesting that traits’ improvement could be restricted.
The success of the evaluation of a breeding program is related to the accurate prediction of genotypic values, which is closely related to the adoption of proper models. Thus, in this research, we applied a novel statistic approach for variance components estimate under plant breeding schemes. Implementation of the Bayesian multi-trait models is straightforward, and nowadays it has been widely used due to the possibility of considering a prior knowledge when modeling. Despite its wide application in animal breeding [31, 32], Bayesian multi-trait analysis has never been reported in plant breeding.
Variance components and genetic parameters
Genetic and environment parameters estimated under the Bayesian multi-trait approach were similar to SOC estimates reported by Peixoto et al. [33], while carrying out analysis of variance (ANOVA). Rosado et al. [30] used information of molecular markers and reported low genetic variance estimates among jatropha families. These authors argue that a possible cause would be a common ancestor origin and the selection pressure that this species has suffered in recent years. Indeed, these causes would explain the low genotypic variance observed for SOC, and consequently its low heritability. Thereby, selecting superior genotypes based on phenotypic values would not provide an expected overall genetic gain since approximately 83% of the phenotypic variance is not genetic. Thus, it is necessary the adoption of appropriate methodologies to accurately predict genetic effects. Therefore, based on these results and on previous researches, we suggest that the Bayesian multi-trait analysis is more appropriate than ANOVA to perform analysis and select superior genotypes for jatropha breeding, since the Bayesian model can capture minor genetic differences between families, while ANOVA cannot.
The success of a breeding program, which usually aims to improve multiple traits simultaneously, is influenced by the correlation between traits, and mainly by the breeding goal. We observed a non-significant difference for all covariance estimates, except for SOC and W100S (Table 1), which suggests that selection based on information of a specific trait will not provide correlated gain to another trait (Table 2). However, it is expected and necessary that multiple traits are improved simultaneously due to the large generation interval of jatropha. Thus, it is necessary the use of statistics techniques that would help breeders to select superior families, and consequently result in reasonable overall gain. Thereby, the use of selection index strategies seems to be a good alternative.
Genetic diversity
To evaluate the diversity between Jatropha half-sib families, the Ward method was used for clustering, resulting in nine clusters. Singh et al. [34] reported that one of the main problems of jatropha breeding programs is the little genetic variability between genotypes. Moreover, it was reported that the genetic variance is high within families and low between families [29, 35].
We observed low correlation estimates between W100S and SOC with PEC, which is similar to the reports of Peixoto et al. [33]. They estimated correlation based on ANOVA and BLUP results, and observed that there was only significant correlation between W100S and SOC. Thus, these results mean that when we select for W100S we are also selecting for SOC, and vice versa. Otherwise, when we select for W100S and SOC, we are not selecting for PEC. Thereby, an option to improve all traits simultaneously is the use of selection index procedures.
Genetic gain and genotype selection based on selection index
Genotypic values estimated under the Bayesian multi-trait analysis was used to apply selection index procedures, and superior genotypes were selected based on different scenarios.
Despite the low correlation estimates observed between SOC, W100S and PEC, it was possible to achieve overall genetic gain for all traits simultaneously by using selection index. Peixoto et al. [33] used different selection index methods and concluded that a multiplicative index provided genetic gain for all the evaluated traits. Therefore, our work confirms that it is possible to increase SOC and reduce PEC. This is an important result for jatropha’s breeding, mainly because PEC is a limiting factor to the cultivation of this crop.
Simultaneous genetic gain can be achieved by correlated response, which can be maximized with several crossing cycles in order to increase the frequency of favorable alleles for all traits [33]. In this study, we presented a different strategy to achieve simultaneous genetic gain when using the Bayesian multi-traits analysis to estimate genotypic values, and we used them to build a selection index aiming to select superior genotypes.
Implications and future perspectives
Jatropha is a perennial plant which has been used to produce biofuel, and it has been reported that it is possible to increase its performance by selecting plants based on genetic information. Indeed, the use data of traditional jatropha breeding techniques, novel statistics methods, and molecular markers (i.e. single nucleotide polymorphism, SNP) would be the key to improve the accuracy of selection, to reduce the time per cycle, and to decrease the costs per cycle.
In future researches, the use of SNP should be exploited aiming to improve prediction accuracy. Recent developments in next-generation sequencing have enabled researchers to quickly and cost-effectively carry out genotyping-by-sequencing of entire breeding populations to discover genetic markers of an entire genome. Therefore, the use of molecular markers for the selection of the best genotypes in breeding populations under field evaluation has recently emerged as the foundation of plant breeding, mainly forest species, since the cycle is too long [36]. Based on theoretical studies and on practical considerations, genomic wide selection (GWS) is likely to increase efficiency of breeding programs by shortening the duration of the breeding cycle. Today, progeny testing phase could potentially be omitted, since breeders are able to carry out early selection for yet-to-be observed phenotypes at seedling stage. This early selection would then allow selected individuals being immediately propagated, if micropropagation protocols are available for the immediate establishment of optimized clonal trials with several years of anticipation, compared to the classical breeding scheme [37].
Integration between genomic selection and multi-trait Bayesian approach can increase prediction accuracy. Therefore, selection indices will be more powerful and reliable. Moreover, the identification of chromosome regions that are related to genetic control of multiple traits (pleiotropic genes) would be a useful tool aiming to increase the overall genetic gain during selection. Additionally, the use of molecular data will provide the realized genetic diversity among families since the evaluation will be based on the identical by state (IBS) information [38].
Conclusion
The Bayesian multi-traits analysis integrated with selection indices allowed obtaining selection gain for all traits simultaneously, i.e., it is possible to reduce Jatropha seeds toxicity caused by phorbol ester concentration (PEC) and to increase seed oil content (SOC).
Based on the estimated genotypic values under the Bayesian multi-trait approach, and on the evaluation of genetic gain when applying the selection index methods, 169 and 170 half-sib families presented high genotypic values for W100S and for SOC, and low estimates for PEC. Thus, these families should be used in future diallel crossings.
Supporting Information
(DOCX)
(DOCX)
Acknowledgments
We also thank the Biometric Lab of the Federal University of Viçosa, Brazil, where all analyses were carries out.
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
CAPES—Coordenação de Aperfeiçoamento de Pessoal de Nível Superior http://www.capes.gov.br/ and Cnpq—Conselho Nacional de Desenvolvimento Cientifico e Tecnológico http://cnpq.br/.
References
- 1.Openshaw K. A review of Jatropha curcas: an oil plant of unfulfilled promise. Biomass and Bioenergy. 2000;19(1):1–15. [Google Scholar]
- 2.Basha SD, Sujatha M. Inter and intra-population variability of Jatropha curcas (L.) characterized by RAPD and ISSR markers and development of population-specific SCAR markers. Euphytica. 2007;156(3):375–86. [Google Scholar]
- 3.Laviola BG, Rosado TB, Bhering LL, Kobayashi AK, Resende MDVd. Genetic parameters and variability in physic nut accessions during early developmental stages. Pesquisa Agropecuária Brasileira. 2010;45(10):1117–23. [Google Scholar]
- 4.Franco J, Crossa J, Ribaut JM, Bertran J, Warburton ML, Khairallah M. A method for combining molecular markers and phenotypic attributes for classifying plant genotypes. Theoretical and Applied Genetics. 2001;103(6–7):944–52. [Google Scholar]
- 5.Laviola BG, Alves AA, Gurgel FdL, Rosado TB, Rocha RB, Albrecht JC. Estimates of genetic parameters for physic nut traits based in the germplasm two years evaluation. Ciência Rural. 2012;42(3):429–35. [Google Scholar]
- 6.Akintayo ET. Characteristics and composition of Parkia biglobbossa and Jatropha curcas oils and cakes. Bioresource technology. 2004;92(3):307–10. [DOI] [PubMed] [Google Scholar]
- 7.Bailis R, Mccarthy H. Carbon impacts of direct land use change in semiarid woodlands converted to biofuel plantations in India and Brazil. GCB Bioenergy. 2011;3(6):449–60. [Google Scholar]
- 8.Liberalino AAA, Bambirra EA, Moraes-Santos T, Vieira EC. Jatropha curcas L. seeds: chemical analysis and toxicity. Arquivos de biologia e tecnologia. 1988;31(4):539–50. [Google Scholar]
- 9.Nithiyanantham S, Siddhuraju P, Francis G. Potential of Jatropha curcas as a biofuel, animal feed and health products. Journal of the American Oil Chemists' Society. 2012;89(6):961–72. [Google Scholar]
- 10.Adolf W, Opferkuch H, Hecker E. Irritant phorbol derivatives from four Jatropha species. Phytochemistry. 1984;23(1):129–32. [Google Scholar]
- 11.Hayashi T, Iwata H. A Bayesian method and its variational approximation for prediction of genomic breeding values in multiple traits. BMC bioinformatics. 2013;14(1):34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gomes RA Jr, de Lima Gurgel F, de Azevedo Peixoto L, Bhering LL, da Cunha RNV, Lopes R, et al. Evaluation of interspecific hybrids of palm oil reveals great genetic variability and potential selection gain. Industrial Crops and Products. 2014;52:512–8. [Google Scholar]
- 13.Bhering LL, Barrera CF, Ortega D, Laviola BG, Alves AA, Rosado TB, et al. Differential response of Jatropha genotypes to different selection methods indicates that combined selection is more suited than other methods for rapid improvement of the species. Industrial Crops and Products. 2013;41:260–5. [Google Scholar]
- 14.Bhering LL, Laviola BG, Salgado CC, Sanchez CFB, Rosado TB, Alves AA. Genetic gains in physic nut using selection indexes. Pesquisa Agropecuária Brasileira. 2012;47(3):402–8. [Google Scholar]
- 15.Spinelli VM, Dias LAS, Rocha RB, Resende MDV. Estimates of genetic parameters with selection within and between half-sib families of Jatropha curcas L. Industrial Crops and Products. 2015;69:355–61. [Google Scholar]
- 16.Dias LAS, Leme LP, Laviola BG, Pallini Filho A, Pereira OL, Carvalho M, et al. Cultivo de pinhão-manso (Jatropha curcas L.) para produção de óleo combustível Viçosa, MG: UFV; 2007. 40 p. [Google Scholar]
- 17.Carels N, Sujatha M, Bahadur B. Jatropha, Challenges for a New Energy Crop: Farming, Economics and Biofuel: Springer Verlag; 2013. 599 p. [Google Scholar]
- 18.Resende JCF, Londe LN, Neves WS. Pinhão-manso. Nova Poerteirinha-MG: Epamig; 2013. 524 p. [Google Scholar]
- 19.Bahadur B, Sujatha M, Carels N. Jatropha, Challenges for a New Energy Crop: Genetic Improvement and Biotechnology: Springer Science & Business Media; 2012. 601 p. [Google Scholar]
- 20.Makkar HPS, Aderibigbe AO, Becker K. Comparative evaluation of non-toxic and toxic varieties of Jatropha curcas for chemical composition, digestibility, protein degradability and toxic factors. Food chemistry. 1998;62(2):207–15. [Google Scholar]
- 21.Misztal I, Tsuruta S, Strabel T, Auvray B, Druet T, Lee D, editors. BLUPF90 and related programs (BGF90). World Congress on Genetics Applied to Livestock Production; 2002.
- 22.Geweke J. Evaluating the accuracy of sampling-based approaches to the calculation of posterior moments: Federal Reserve Bank of Minneapolis, Research Department; 1991. [Google Scholar]
- 23.Smith BJ. boa: an R package for MCMC output convergence assessment and posterior inference. Journal of Statistical Software. 2007;21(11):1–37. [Google Scholar]
- 24.Plummer M, Best N, Cowles K, Vines K. CODA: Convergence diagnosis and output analysis for MCMC. R news. 2006;6(1):7–11. [Google Scholar]
- 25.Team RC. R: A language and environment for statistical computing. 2012.
- 26.Mojena R. Hierarchical grouping methods and stopping rules: an evaluation. The Computer Journal. 1977;20(4):359–63. [Google Scholar]
- 27.Milligan GW, Cooper MC. An examination of procedures for determining the number of clusters in a data set. Psychometrika. 1985;50(2):159–79. [Google Scholar]
- 28.Hazel LN. The Genetic Basis for Constructing Selection Indexes. Genetics. 1943;28(6):476–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bhering LL, Peixoto LdA, Leite NLSF, Laviola BG. Molecular analysis reveals new strategy for data collection in order to explore variability in Jatropha. Industrial Crops and Products. 2015;74:898–902. [Google Scholar]
- 30.Rosado TB, Laviola BG, Faria DA, Pappas MR, Bhering LL, Quirino B, et al. Molecular Markers Reveal Limited Genetic Diversity in a Large Germplasm Collection of the Biofuel Crop L. in Brazil. Crop Science. 2010;50(6):2372–82. [Google Scholar]
- 31.Ventura HT, Silva FF, Varona L, de Figueiredo EAP, Costa EV, da Silva LP, et al. Comparing multi-trait Poisson and Gaussian Bayesian models for genetic evaluation of litter traits in pigs. Livestock Science. 2015;176:47–53. [Google Scholar]
- 32.Rolf MM, Garrick DJ, Fountain T, Ramey HR, Weaber RL, Decker JE, et al. Comparison of Bayesian models to estimate direct genomic values in multi-breed commercial beef cattle. Genetics Selection Evolution. 2015;47(1):23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Peixoto LdA, Laviola BG, Bhering LL, Mendonça S, Costa TdSA, Antoniassi R. Oil content increase and toxicity reduction in jatropha seeds through family selection. Industrial Crops and Products. 2016;80:70–6. [Google Scholar]
- 34.Singh P, Singh S, Mishra SP, Bhatia SK. Molecular characterization of genetic diversity in Jatropha curcas L. Genes Genome Genomics. 2010;4:1–8. [Google Scholar]
- 35.Gupta P, Idris A, Mantri S, Asif MH, Yadav HK, Roy JK, et al. Discovery and use of single nucleotide polymorphic (SNP) markers in Jatropha curcas L. Molecular Breeding. 2012;30(3):1325–35. [Google Scholar]
- 36.Grattapaglia D, Resende MD. Genomic selection in forest tree breeding. Tree Genetics & Genomes. 2011;7(2):241–55. [Google Scholar]
- 37.Alves AA, Laviola BG, Formighieri EF, Carels N. Perennial plants for biofuel production: Bridging genomics and field research. Biotechnology journal. 2015;10(4):505–7. doi: 10.1002/biot.201400201 [DOI] [PubMed] [Google Scholar]
- 38.Rafalski A. Applications of single nucleotide polymorphisms in crop genetics. Current opinion in plant biology. 2002;5(2):94–100. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX)
(DOCX)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.