Analysis of multi-domain protein dynamics

Abstract

Proteins with a modular architecture of multiple domains connected by linkers often exhibit diversity in the relative positions of domains while the domain tertiary structure remains unchanged. The biological function of these modular proteins, or the regulation of their activity depends on the variation in domain orientation and separation. Accordingly, careful characterization of inter-domain motion and correlated fluctuations of multi-domain systems is relevant for understanding the functional behavior of modular proteins. Molecular dynamics (MD) simulations provides a powerful approach to study these motions in atomic detail. Nevertheless, the common procedure for analyzing fluctuations from MD simulations after overall rigid-body alignment fails for multi-domain proteins; it greatly overestimates correlated positional fluctuations in the presence of relative domain motion. We show here that expressing the atomic motions of a multi-domain protein as a combination of displacement within the domain reference frame and motion of the relative domains correctly separates the internal motions to allow a useful description of correlated fluctuations. We illustrate the methodology of separating the domain fluctuations and local fluctuations by application to the tandem SH2 domains of human Syk protein kinase and by characterizing an effect of phosphorylation on the dynamics. Correlated motions are assessed from a distance covariance rather than the more common vector-coordinate covariance. The approach makes it possible to calculate the proper correlations in fluctuations internal to a domain as well as between domains.

1 Introduction

Changes in domain structure are fundamental to the biological function of certain proteins with a modular architecture of multiple domains connected by linkers. The essence of molecular machines, signaling proteins, and some allosteric proteins lies in the motions that alter the relative orientation between domains.^1–5 Further, for enzymes in which the active site is formed from multiple domains, concerted domain motions can greatly influence the positioning of catalytic residues and thus regulate catalytic activity.³ In another example, the modular structure of a protein can serve to form a binding surface across domains so that variation in domain structure is the basis for regulating the interaction with binding partners.^1,6

Characterizing the dynamics of multi-domain proteins in terms of positional fluctuations and correlated motions using molecular dynamics (MD) simulation is a powerful and often-practiced first step toward elucidating molecular behavior and function, mechanisms of regulation of modular proteins, and allostery. For the case of allosteric function of modular proteins in particular, discovering correlations in atomic fluctuations and domain motions detected over a long distance would be a key component in a description of the molecular mechanism of allostery. While changes in motional timescales over a set of amino acids due to a conformational perturbation of the protein can be determined from NMR relaxation studies,⁷ these experiments cannot determine correlations in motions. MD studies can directly assess possible correlation networks that might form the basis of allostery.^4,8,9 Nevertheless, even though fluctuations and correlated motions in single domain proteins are readily analyzed, assessment of motions in a multi-domain protein is complicated due to the presence of both local motions internal to the framework of an individual domain and changes in domain-domain separation and relative domain orientation, so that estimating fluctuations following the same analysis fails. One tactic that can be taken toward understanding dynamics of multi-domain proteins is to account for the collective motion of a modular protein using a description of changes in the relative domain orientation plus changes in the atomic positions internal to a given domain. Such an approach is motivated by the rationale that concerted motions derived from local fluctuations translate into larger-scale domain-domain motion. To implement such an approach, and to properly assess the dynamics of multi-domain proteins in general, it is essential to identify fluctuations in local structure and domain structure independently to effectively characterize the dynamics of multi-domain protein.

A difficulty in general with evaluating conformational flexibility of a protein from a MD trajectory is separating overall rigid-body motion from fluctuations in the internal structure^10–13 because there is no unambiguous way to remove the external degrees of freedom from internal dynamics of a flexible protein.^11,12 Separating rigid body motions from local fluctuations in the time evolution of atomic positions of a protein is an under-determined problem (discussed in more detail in the Supporting Information (SI)), so that the result for the local fluctuation amplitudes depends on the assumptions made to define the rigid-body molecule frame. The most popular assumption is to remove the overall motion by a single rigid body alignment that minimizes the difference in coordinates of all atoms, or a relatively rigid subset of atoms, between the flexible protein conformation (a trajectory snapshot) and a reference structure.^10,11,14 While this common approach is reasonable for a single domain protein where the choice for a structural core is readily apparent, further thought is needed to characterize internal motions of a modular multi-domain protein. In the case that relative domain orientation varies in a multi-domain protein, a single alignment step to minimize the difference between the reference structure and a trajectory snapshot does not separate motions within a domain from motions between domains.

We introduce here a procedure with two alignment steps that gives accurate fluctuation values and therefore reasonable estimates for a correlation analysis of internal motions and rigid-body domain motions as validated with a known system (see SI). We demonstrate its application to the tandem SH2 protein, a multi-domain protein fragment from the human spleen tyrosine kinase, Syk. Correlated motion is assessed using a metric based on changes in atomic positions rather than absolute atomic positions. In what follows, we first describe the overestimate of correlated motion that arises with a typical single alignment procedure for analyzing the fluctuations and covariance of the tandem SH2 protein. Next, we present a procedure that more accurately describes the fluctuations of multi-domain proteins by including two rigid-body alignment steps and the resulting correlation coefficients. Finally, we apply the approach to characterize the effect of tyrosine phosphorylation on correlated internal motions and relative domain motions, and thus, illustrate how correlation analysis of multi-domain proteins can give insight into their biological function.

2 Methods

2.1 Molecular dynamics simulations

Simulations of the unphosphorylated and phosphorylated forms of the Syk tandem SH2 protein

Two 0.5 μs trajectories of the 254-residue, multi-domain Syk tandem SH2 fragment in the unphosphorylated tSH2 and Tyr131-phosphorylated ptSH2 forms were calculated with the NAMD program using the CHARMM22/CMAP force field. The initial coordinates for tSH2 and ptSH2 simulations were taken from chain A of the asymmetric unit of the crystal structure (PDB ID: 1A81). The two proteins tSH2 and ptSH2 were solvated in octahedral boxes with 15043 TIP3P water molecules as well as Na⁺ and Cl⁻ ions so that the distance from the protein edge to the box edge was at least 12 Å and the salt concentration was maintained at 0.15 M. The non-bonded list was generated with a 14 Å cutoff. A switching function was applied to the van der Waals potential energy from 10 Å to 12 Å to calculate non-bonded interactions. Particle Mesh Ewald (PME) algorithm was used to calculate electrostatic interactions.

The energy of the solvated proteins was minimized first with the positions of the protein atoms fixed, then with harmonic restraints on protein backbone heavy atoms (N, C, C_α atoms), and lastly, without restraints using the steepest descent and Powell algorithms.

All trajectories were calculated using the leapfrog integrator with a 2-fs time step. The SHAKE constraint was applied to fix the lengths of bonds involving hydrogen atoms. The systems were heated from 100K to 298K and equilibrated at 298K in the NVE ensemble for a total of 500 ps. The appropriate system volumes of the two species were established with a 1-ns equilibration in the NPT ensemble using constant pressure and temperature (CPT) dynamics. The Nose-Hoover thermostat and Langevin barostat were used to maintain a reference temperature of 298K and a reference pressure of 1 atm. The NPT-equilibrated systems with the proper volumes were equilibrated for 2 ns in the NVT ensemble at 298K using a Langevin heat bath with a friction coefficient of 1 ps⁻¹. Production runs were carried out for 0.5 μs with coordinates saved every 1 ps, yielding one trajectory of 0.5 μs for each form of the tandem SH2 fragment.

Simulations of the isolated SH2 domain

An isolated 96-residue SH2 domain was simulated using the NAMD program with the CHARMM22/CMAP force field. The initial coordinates of the isolated SH2 domain were taken from chain A, residues 167–262, of the asymmetric unit of the crystal structure (PDB ID: 1A81). The isolated SH2 domain was solvated in an octahedral box filled with 7817 TIP3P water molecules and Na⁺ and Cl⁻ ions so that the distance between the protein and box edges was at least 12 Å and the salt concentration was 0.15 M.

A 0.1 μs trajectory of the isolated SH2 domain was calculated using the same simulation conditions as those used to calculate the trajectories of the unphosphorylated and phosphorylated tandem SH2 fragments.

2.2 Separation of motions

We provide a mathematical description for the separation of motions and first present the common approach of modeling atomic displacements as a combination of rigid-body motion and deviations from it. Let us assume R_t represents position vectors of N atoms in tth snapshot of a MD trajectory, with ${\mathbf{R}}_t^i$ being the position vector of the ith atom, at time t. Then without any loss of generality we can write for time t

$$\begin{array}{cc}\hfill {\mathbf{R}}_t& ={\mathbf{T}}_t+{\mathrm{U}}_t{\mathbf{R}}_0+{\delta }_t\hfill \\ \hfill {\mathrm{U}}_t^{-1}{\delta }_t& ={\mathrm{U}}_t^{-1}({\mathbf{R}}_t-{\mathbf{T}}_t)-{\mathbf{R}}_0.\hfill \end{array}$$ (1)

where T_t is the overall translation vector, R₀ is the position of the N atoms in the reference structure, U_t is the matrix representing overall rotation of the protein molecule with respect to the reference structure, and δ_t is the deviation of ith atom from the rigid-body motion of T_t and U_t. ${\mathrm{U}}_t^{-1}$ is the inverse matrix of U_t. Overall translation is removed by aligning the center of mass (COM) of the conformation at time t with that of the reference structure. Typically for a single domain protein, ${\mathrm{U}}_t^{-1}$ is found by aligning the flexible structure to the reference structure to minimize ${\sum }_{i\subset \mathrm{M}}{\Vert {\mathbf{R}}_t^i-{\mathrm{U}}_t{\mathbf{R}}_0^i-{\mathbf{T}}_t\Vert }^2$, where {M} is a subset of atoms spanning the whole protein.^10,11,14 The time series δ_t represents the deviation of the atoms from the rigid body motion. Once U_t and subsequently ${\mathrm{U}}_t^{-1}{\delta }_t$ are estimated, cross correlation or other properties, such as root mean square fluctuation (RMSF), can be calculated from δ_t.

In the case of multi-domain protein, changes in the relative orientation of domains also contribute to the total atomic displacements; the overall motion, relative domain fluctuations (DF) and local fluctuations within a domain (LF) can be separated following a procedure in the spirit of eqn.1. Let us consider a protein with D domains. We can write the position of the ith atom at time t as a combination of overall motion, LF and DF with the constraint that DF does not give rise to overall rotation or translation:

$${\mathbf{R}}_t={\mathbf{T}}_t+{\mathrm{U}}_t[{\mathbf{S}}_t^1+{\mathrm{W}}_t^1{\mathbf{R}}_0^1\dots {\mathbf{S}}_t^D+{\mathrm{W}}_t^D{\mathbf{R}}_0^D]+{\delta }_t$$ (2)

In the above equations ${\mathbf{S}}_t^d$ and ${\mathrm{W}}_t^d$ represent the independent translation and rotation of the dth domain within the overall molecular frame at time t, respectively. ${\mathbf{R}}_0^d$ in the above equation represents the position vector of the atoms in the dth domain of the reference structure. Any rotation matrix, other than the identity matrix, leaves only the center point unchanged. Since the ${\mathrm{W}}_t^d$ matrices leave the centers of the domains unchanged, the domain rotations in eqn.2 can not contribute to overall rotation. Furthermore, ${\mathbf{S}}_t^d$ matrices in eqn.2 represent relative translations of the domains and do not contribute to overall translation. We can rewrite eqn.2 as

$$\begin{array}{cc}\hfill & {\mathrm{U}}_t^{-1}{\delta }_t^i={\mathrm{U}}_t^{-1}({\mathbf{R}}_t-{\mathbf{T}}_t)-{\mathbf{R}}_{t^{\prime }}\hfill \\ \hfill & \mathrm{where}{\mathbf{R}}_{t^{\prime }}=[{\mathbf{S}}_t^1+{\mathrm{W}}_t^1{\mathbf{R}}_0^1\dots {\mathbf{S}}_t^d+{\mathrm{W}}_t^d{\mathbf{R}}_0^d]\hfill \end{array}$$ (3)

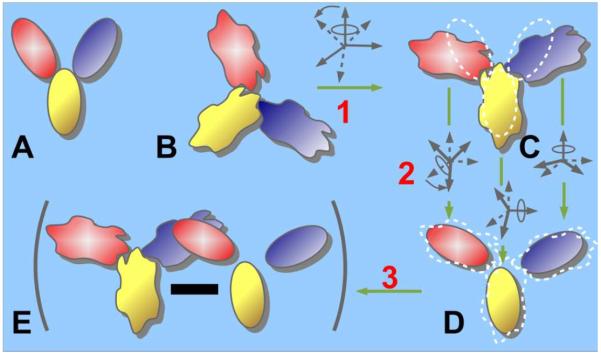
To separate LF and DF according to eqn.3 the following protocol is applied to each snapshot of the original trajectory to generate two trajectories, as schematically illustrated in Figure 2.

1. Remove the molecule translation and rotation by least-square superposition of the snapshot with respect to the reference structure using atoms selected over the whole protein (step 1 in Figure 2 and ${\mathrm{U}}_t^{-1}({\mathbf{R}}^t-{\mathbf{T}}^t)$ in eqn.3).

2. Obtain the rigid-domain trajectory by independently aligning individual domains of the reference structure to the corresponding domain of the oriented snapshot (step 2 in Figure 2 and R_t′ in eqn.3), and keeping coordinates of the aligned reference domains.

3. Obtain the LF trajectory from the coordinate difference between the oriented reference domains and the oriented snapshot domain (step 3 in Figure 2 and ${\mathrm{U}}_t^{-1}{\delta }_t$ in eqn.3).

   The rigid-domain trajectory generated in step 2 is used to estimate domain-domain correlation, while the LF trajectory obtained in step 3 is used to calculate correlations in the local atomic fluctuations.

Figure 2.

Schematic to illustrate the separation of LF and DF in a flexible multi-domain protein. (A) and (B) show the reference and the flexible structure (trajectory snapshot), respectively. (C) In step (1) the flexible structure is aligned with the reference structure to remove the overall motion and generate the oriented structure. (D) In step (2) individual domains of the reference structure are aligned with (C) to specify the domain fluctuation, DF. (E) In step (3), the coordinate difference between the oriented structure C and the structure D with rigid domain motion gives the local fluctuation, LF.

2.3 Distance Correlation

In this work, we calculated correlation using a distance correlation coefficient, DCOR.¹⁵ Previously, we showed that among Pearson's correlation coefficient (PCC), a generalized correlation coefficient (GCC)¹⁶ and DCOR, DCOR is the most appropriate parameter to find association in atomic motions because it is least sensitive to angular dependence while reflecting variability in covariance.¹⁷

Calculation of DCOR between two vector series is straightforward to implement. Let {A} and {B} be two vector series with m entries each and the ith entry in {A} is denoted by Aⁱ. To calculate distance covariance between {A} and {B} the following five steps are needed.

1. Calculate the m×m matrix, a, from {A}, where a_ij is the Euclidean distance between the ith and jth entries of {A}:

   $$a_{ij}=a_{ji}=\mid {\mathbf{A}}^i-{\mathbf{A}}^j\mid$$

2. Average the rows of a: $a_{i.}=\frac{1}{m}{\sum }_j{a}_{ij}$

3. Average the columns of a: $a_{.j}=\frac{1}{m}{\sum }_i{a}_{ij}$

4. Average all elements of a: $a_{..}=\frac{1}{m^2}{\sum }_{ij}{a}_{ij}$

5. Build the m×m matrix α from a where α_ij = a_ij − a_i. − a._j +a..

Then the distance covariance is

$$\mathit{cov}\left(A,B\right)\equiv \sqrt{\frac{1}{m^2}\sum _{ij}{\alpha }_{ij}{\beta }_{ij}}$$ (4)

where β_ij is defined similarly from B.

The distance correlation coefficient, DCOR, is defined as

$$\mathit{DCOR}\equiv \frac{\mathit{cov}\left(A,B\right)}{\sqrt{\mathit{cov}\left(A,A\right)\mathit{cov}\left(B,B\right)}}.$$ (5)

DCOR was found to capture both linear and non-linear correlation between positional vectors.¹⁷ In an earlier study we observed long-distance concerted motions in a protein using DCOR that was not revealed by PCC or GCC.¹⁷

3 Results and Discussion

3.1 Single alignment overestimates domain fluctuation in tandem SH2

The effect of relative domain fluctuations on estimates correlation coefficients using the common procedure of a single rigid-body alignment step is illustrated for the Syk tandem SH2 (tSH2), a multi-domain protein comprising two SH2 domains, SH2_N and SH2_C, connected by a flexible linker A (see Figure 1A). The cross correlations in dynamics between 254 C_α atoms were calculated from a 0.5 μs trajectory of the tSH2 (see Methods section). We used a distance correlation coefficient, DCOR,¹⁵ rather than the more common vector coordinate, Pearson's correlation coefficient (PCC) to evaluate the correlated motion. DCOR measures the correlation in the change in atomic positions over a time period, that is the correlation in Euclidean distance of the atomic position at time t and t +δt. DCOR is the most powerful parameter among conventional metrics for assessing correlated fluctuation in protein motion because it can capture the true correlation, both linear and non-linear, between positional vectors.^17,18 The mathematical definition of DCOR is provided in the Methods section.

Figure 1.

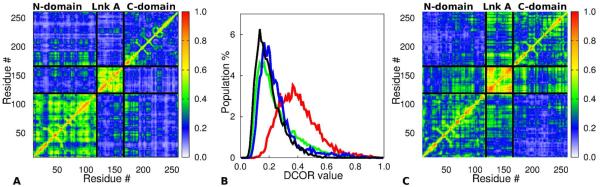
Covariance analysis of C_α -C_α positions of tSH2 protein using a single overall alignment and the distance correlation coefficients, DCOR, calculated from a 0.5 μs trajectory. (A) Ribbon representation of Syk tSH2 protein (PDB ID 1A81) with the SH2_N (residues 9-119) in red, linker A (residues 120-166) in gold, and SH2_C (residues 167 to 262) in blue. Residue numbering is for the human Syk protein. (B) DCOR values between C_α atoms calculated after whole-molecule least squares alignment with respect to all C_α atoms. The presence of domain fluctuations gives rise to the apparent high DCOR values. (C) Histograms of DCOR values after a single alignment with respect to either C_α atoms of all residues (green) or residues in the SH2_N (red), or SH2_C (blue). The green curve corresponds to the cross correlation values in B. That the histogram profile changes drastically depending on how the structures are aligned is unsatisfactory and indicates the presence of domain fluctuation. (D) DCOR values after alignment with respect to the SH2_N plotted in the red histogram in C.

To characterize covariation in internal motions of the tSH2 protein, we first consider positional correlations calculated following a single overall alignment. Conformations obtained from 0.5 μs trajectory were aligned following the common procedure of least-square superposition to minimize the difference in all C_α coordinates of each snapshot with the coordinates of a reference structure, the initial structure in this case. DCOR values after a single alignment of the whole molecule are shown in Figure 1B, and the histogram of these DCOR values is shown in Figure 1C (green curve). All correlation coefficients are unreasonably high for covariance of fluctuations within a domain with a mean value around 0.6, compared to 0.3 calculated from a MD trajectory of a single SH2 domain in a previous study.¹⁷ The unusually high correlation arises from the presence of domain-domain motions that are not separated from the motion internal to a domain by a single overall alignment of the flexible target with the reference structure.

Another approach that has been taken in previous studies is to align the trajectory ensemble with respect to a single domain and then examine correlations between atoms in two domains.¹⁹ This approach shows that correlation values for atoms within the chosen domain to agree with expected values; however, this approach greatly overestimates the correlation between and within the remaining domains. This behavior is demonstrated here by a single alignment of the tSH2 conformational ensemble with the SH2_N domain (residues 9-119) (Figure 1D). Although the cross correlations between C_α atoms within SH2_N or between SH2_N and other domains are small and most are less than 0.6, correlations between atom pairs that are either intra-domain or inter-domain pairs from the other two domains, linker A (residues 120-166) and SH2_C (residues 162–262), are generally greater than 0.8, again indicating much stronger covariance in motions overall than anticipated for proteins. A histogram of these DCOR values (Figure 1C, red) further illustrates the strong sensitivity to the selection of atoms for a single-alignment procedure. In comparison to the histogram of DCOR values calculated after a single alignment of all C_α atoms (Figure 1C, green curve), the distributions calculated by aligning to C_α atoms of either the SH2_N (Figure 1C, red curve) or the SH2_C (blue curve) domain are highly populated at a smaller DCOR value, yet, the population with DCOR value greater than 0.8 increases substantially. The variability in DCOR distributions shown in Figure 1C is clearly unsatisfactoryfor characterizing any kind of relative domain-domain motion; correlations between domains can not be characterized reliably with any choice of atoms using a single alignment.

3.2 Approach to separate local and domain fluctuation

We propose a simple procedure that better describes positional fluctuations in the internal structure of modular proteins by separating the relative domain fluctuations, DF, and the local fluctuations within a domain, LF, under the assumption that these internal motions and the over-all rigid-body motion are independent. Details of the mathematical formulation for our protocol are given in the Methods section. The procedure involves two alignment steps, shown schemati-cally in Figure 2. The whole protein structure taken from trajectory snapshots are superposed with the reference structure to remove overall translation and rotation (step 1, first alignment). Each domain of the reference structure is then aligned to the corresponding domain of the superposed snapshot structures to obtain the relative domain fluctuation (step 2, second alignment). The difference in coordinates generated from the two alignment steps is the local fluctuations (LF) within a domain (step 3). The accuracy in the description of the total atomic motion using this approach is demonstrated by application to a model trajectory in which the local fluctuation amplitudes and fluctuations in relative domain positions are known (discussed in the SI).

We recognize that there are situations in which the assumption that protein internal motions are independent of overall rotation is invalid. For example, changes in the shape of a flexible body with zero angular momentum can induce changes in external orientation.²⁰ Consequently, rotation cannot be completely separated from internal motion of a flexible object without a priori knowledge of the deformability of the object during rotation.²⁰ Zhou et al. demonstrated that, in simulating a microcanonical ensemble, a protein molecule undergoes larger rigid body motion than allowed from the conservation of angular momentum as a consequence of the flexibility of the pro-tein molecule.¹³ The dependency of the internal fluctuation and the overall rigid-body motion has also been pointed out in calculation of NMR variables related to global and local motions.²¹ These cases indicate that overall rigid-body motion and internal fluctuations are not entirely independent. Nevertheless, the coupling is difficult to quantify, but certainly weaker for less deformable bodies. We note that this independence is implicitly assumed in general for the removal of overall rota-tion from single-domain proteins. Here, we extend the same assumption to multi-domain proteins eventhough the assumption is not strictly valid. We do so in order to provide a more robust pro-tocol for describing correlated motions between all regions of the protein than using the current single-alignment approach.

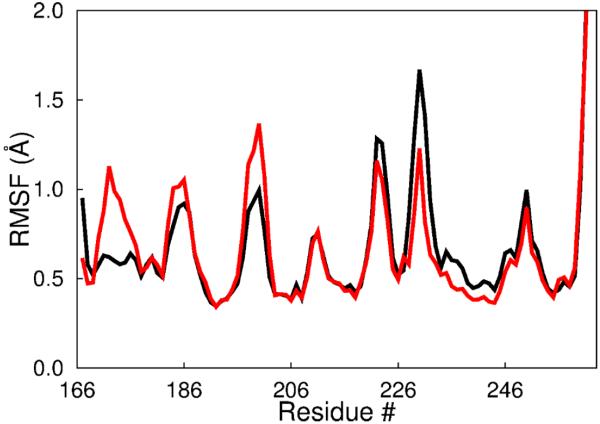
Following our approach to decompose the total atomic displacements, the final step 3 captures the displacements due to motions internal to a domain framework. Accordingly, the rms fluctuations calculated from this difference LF trajectory in the case of tSH2 should be similar to fluctuations determined from a trajectory of an isolated SH2 domain if there are no effects on motions due to the presence of the other domains. We therefore compare the values of the rms fluctuations calculated from the LF trajectory of tSH2 with the values calculated from a trajectory of an isolated domain. The results for the main chain rms fluctuations are plotted in Figure 3 as a function of residue number for the isolated C-terminal SH2 domain (red) and from the LF trajectory of tSH2 (black). Examination of Figure 3 finds that the fluctuation profiles are indeed highly similar with the same pattern of larger fluctuations for the loops and smaller values near 0.5 Å corresponding to the helical and strand regions. The low fluctuation amplitude for the residues 172-177 seen with the tandem SH2 is a result of interactions with the linker region. The absence of the linker region in the simulation of the isolated SH2 domain, therefore, resulted in a large difference in fluctuation amplitude for the residues 172-177. Overall, the close agreement between the rms fluctuations calculated from the LF trajectory of tSH2 and the trajectory of the same SH2 domain in isolation validates the approach to separate local and domain motions.

Figure 3.

Comparison of positional fluctuations calculated from the LF trajectory of tSH2 with fluctuations calculated from an isolated SH2 domain trajectory. Residue averages of the backbone heavy atoms (N, C, and Cα atoms) positional fluctuations calculated from the LF trajectory of the tandem SH2 (black) show similar profiles as those from the trajectory of an isolated SH2 domain (red). The large difference in fluctuation amplitude for the residues 172-177 is a result of interactions with the linker region of the tandem SH2, which is not present in the simulation of the isolated SH2 domain.

To demonstrate the effectiveness of separating relative domain motion in a protein from local fluctuations using two rigid-body alignment steps, we compare the values for a C_α-C_α covariance analysis of tSH2 after separation of domain fluctuations and local fluctuations (Figure 4A) obtained with the results using a single alignment shown in Figure 1. The DCOR values for local fluctuations determined from the LF trajectory (step 3, Figure 2) are overall smaller. In particular the inter-domain DCOR values are found to be in the range 0.2 to 0.3 compared to 0.5 to 0.7 without separation of motions (Figure 1B). The average difference between the inter-domain cross correlation values of Figure 1B and Figure 4A is 0.38±0.31. The distribution of LF DCOR values of tSH2 after removing DF is in Figure 4B (green). Most correlation values are < 0.4 and the DCOR distribution is unlike any of the distributions in Figure 1C. Subsets of the histogram shown by the green line are for DCOR values within the SH2_N (red) and SH2_C (blue). All three histograms have been normalized independently and show similar patterns of peaks near 0.3 and long tails after 0.6 corresponding to a small set of C_α-C_α pairs with highly correlated motions. Together, these characteristics of the DCOR distributions are as expected for proteins.

Figure 4.

Covariance analysis of C_α -C_α positions of tSH2 with separation of local and domain fluctuations using two alignment steps (Figure 1) and calculated from the same trajectory used for calculations shown in Figure 1. (A) DCOR values of C_α atoms from the LF trajectory of tSH2. These values show cross correlation of local fluctuations between two atoms within a domain as well as atoms in two different domains. (B) Histograms of DCOR values from the LF trajectory of tSH2 for all C_α atoms (green), for C_α atoms within SH2_N (red), within SH2_C (blue) and C_α atoms between domains (black). Red, blue and black histograms are subset of the green histogram. Each of them has been independently normalized. The profiles are very similar as might be expected. (C) DCOR values of C_α atoms from the LF trajectory of ptSH2. The effect of phosphorylation on local fluctuations is shown by comparison with panel A. values show cross correlation of local fluctuations between two atoms within a domain as well as in two different domains.

3.3 Effect of phosphorylation on tSH2 dynamics

We demonstrate that differences in domain-domain motions can be assessed using the two-alignment procedure (eqn.2, Figure 2) to evaluate the effect of phosphorylation on tSH2 dynamics. The SH2_N, SH2_C and linker A are tightly associated in tSH2, but NMR measurements show that, upon phosphorylation of the residue Tyr-131 of linker A, the relative SH2-SH2 domain orientation changes and their rotational tumbling time diminishes, indicating the interactions between the SH2_N and SH2_C domains are weakened and the domains become partially decoupled,¹ which results in decreased affinity for the receptor in immune signaling. The resonances for linker A are too broad to be detected and the physical basis for this effect of phosphorylation on tSH2 conformation and dynamics is unknown. How phosphorylation of a residue in the linker region might cause these changes in SH2-SH2 coupling can be investigated using MD simulations following the reasoning that differences in domain coupling would be manifest in the dynamics on the timescale of MD trajectories. The two-alignment approach separating rigid-body domain motions from local motions internal to a domain would enable a reliable comparison of correlations in local motions and inter-domain motions of unphosphorylated tSH2 with phosphorylated tSH2 (ptSH2). We therefore compare correlated motions from 0.5 μs trajectories of tSH2 and ptSH2 to demonstrate the value of the approach for assessing MD trajectories, although it should be recognized that longer sampling times are needed before drawing conclusions in quantitative terms about the effects of phosphorylation.

The domain motions were characterized from the displacements of the center of mass (COM) of the three domains calculated from the DF trajectories. The covariance of the COM was computed with DCOR as a means to estimate the degree of association between two domains. Separation of the rigid body motions using the two-alignment approach allowed us to compare the associa-tion between domains and the change in association due to phosphorylation at Tyr-131 (Table 1). The correlation between the between the linker A and the SH2_C domain is increased significantly (DCOR = 0.60 ± 0.12 to DCOR = 0.78 ± 0.06), indicating that a localized modification to the protein - phosphorylation at Tyr-131 - can effectively alter the global domain-domain interactions.

Table 1.

DCOR between SH2_N, SH2_C and linker A^a

	SH2N-SH2C	SH2N-Linker	SH2C-Linker
tSH2	0.74 ± 0.17	0.79 ± 0.08	0.60 ± 0.12
ptSH2	0.88 ± 0.05	0.85 ± 0.05	0.78 ± 0.06

^aDistance correlation between centers of mass of SH2_N, SH2_C and linker A calculated from the domain-domain motion after removal of local fluctuations. Coupling between linker A and SH2_C increases upon phosphorylation of Tyr-131. The error is calculated using the moving-block bootstrap method,²² which is explained in details in SI.

The effect of Tyr-131 phosphorylation on the intra-domain motion of tSH2 can also be examined from the local fluctuation patterns of residues. DCOR values calculated from LF (Figure 3C) indicate that correlations in C_α displacements from local fluctuations of residues within linker A are diminished and the couplings between local fluctuations of residues within SH2_N are enhanced upon phosphorylation.

4 Conclusion

Results here demonstrate that effective analysis of the motion of modular, multi-domain proteins includes the separation of domain motions from the total atomic displacements, and a rigid-body rotation and translation of individual domains in addition to the typical overall alignment of the whole molecule extracts relative domain dynamics from local fluctuations internal to each domain. The approach enables characterization of the conformational states of multi-domain proteins following a description of domain motions and local fluctuation magnitudes to relate structure and function. Functional changes in dynamics of multi-domain proteins due to factors such as effector binding or phosphorylation can be effectively assessed from MD simulations with this two alignment approach. In particular, accurate estimation of LF will allow identification of possible allosteric pathways as traced from correlated fluctuations of residues^4,8 in multi-domain proteins. We illustrated the approach here by application to the Syk tSH2 to examine the change in dynamics upon phosphorylation of Tyr-131. This chemical modification regulates the association of Syk with membrane immunoreceptors. Differences in domain-domain motion and C_α covariance were detected between the unphosphorylated and phosphorylated forms of the Syk tSH2. Efforts are underway with more extensive sampling to understand how concerted motions internal to linker A influence, or not, the coupling of the two SH2 domains of Syk tyrosine kinase and the effects of Tyr131 phosphorylation.