The contribution of dominance to phenotype prediction in a pine breeding and simulated population

Abstract

Pedigrees and dense marker panels have been used to predict the genetic merit of individuals in plant and animal breeding, accounting primarily for the contribution of additive effects. However, nonadditive effects may also affect trait variation in many breeding systems, particularly when specific combining ability is explored. Here we used models with different priors, and including additive-only and additive plus dominance effects, to predict polygenic (height) and oligogenic (fusiform rust resistance) traits in a structured breeding population of loblolly pine (Pinus taeda L.). Models were largely similar in predictive ability, and the inclusion of dominance only improved modestly the predictions for tree height. Next, we simulated a genetically similar population to assess the ability of predicting polygenic and oligogenic traits controlled by different levels of dominance. The simulation showed an overall decrease in the accuracy of total genomic predictions as dominance increases, regardless of the method used for prediction. Thus, dominance effects may not be accounted for as effectively in prediction models compared with traits controlled by additive alleles only. When the ratio of dominance to total phenotypic variance reached 0.2, the additive–dominance prediction models were significantly better than the additive-only models. However, in the prediction of the subsequent progeny population, this accuracy increase was only observed for the oligogenic trait.

Introduction

Genomic prediction of complex traits can increase genetic gains per unit of time in plant and animal breeding by allowing early and more accurate selection than traditional approaches (Heffner et al., 2010; Wiggans et al., 2011; Resende et al., 2012b). In human genetics, the same methods may be applicable to predict propensity to disease, and response to drug treatments (de los Campos et al., 2010; Yang et al., 2010; Wray et al., 2013). Most of the early development of genomic prediction methods occurred in dairy cattle with the aim of selecting sires with high breeding value. Thus, prediction models were developed to account for the contribution of additive effects to phenotypic traits, whereas nonadditive effects were typically not considered. Considering nonadditive effects in the model could improve predictions as the genetic architecture of traits is a factor that contributes to the accuracy of models (Hayes et al., 2009). In addition, dominance and epistasis may be confounded with the additive effect in genomic predictions. Thus, their specific contribution should be accounted for to avoid the overestimation of genetic parameters in downstream applications (Muñoz et al., 2014).

Prediction of dominance effects is needed in advanced breeding programs that explore specific combining ability. In these programs, seeds from a small number of crosses known to have superior specific combining ability can be scaled up through controlled mass pollination and deployed in large scale (White et al., 2007). When dominance contributes to the complex trait, these strategies increase the yield and genetic gain when compared with half-sib, open-pollinated families (McKeand et al., 2006). Recent studies in plants and animals have reported a significant contribution from nonadditive effects to phenotypes, adding to a considerable proportion of the genetic variance and improving the accuracy of predictions (Su et al., 2012; Vitezica et al., 2013; Muñoz et al., 2014; Nishio and Satoh, 2014). Analysis of simulated data indicated that including dominance is recommended to achieve higher genetic gains in crossbred population (Zeng et al., 2013) and would also allow the application of mate allocation (Toro and Varona, 2010; Sun et al., 2013; Ertl et al., 2014). When only additive effects are considered, predicting the best combination of parents that generate superior families equals the average of their breeding values. Thus, inclusion of dominance is critical to identify complementary individuals and explore heterosis.

Numerous whole-genome regression (WGR) approaches have been proposed for genomic prediction of additive effects. These approaches generally share the same linear model but differ in their assumptions regarding the prior information of marker effects (de los Campos et al., 2013; Gianola, 2013). For instance, priors implemented in Bayesian ridge regression (BRR) assume that marker effects follow a normal distribution with a common variance component. This assumption is suitable under the infinitesimal model where the trait is controlled by a large number of genes with small effect. Others models implement more complex (parameterized) priors that can fit traits with major-effect genes that explain a significant proportion of the genetic variation. These models rely on variable selection (for example, Bayes B) to remove markers that are not in linkage disequilibrium with any quantitative trait loci (QTLs), and modeling variance heterogeneity of marker effect (for example, Bayes A, Bayes B, Bayesian Lasso (BL)) that assumes that each marker explains a distinct part of genotypic variation. In polygenic traits it was previously observed that the different WGR models and priors usually result in similar accuracies (Heslot et al., 2012; Pérez et al., 2012; Resende et al., 2012a). However, when WGR was applied to traits that are expected to be oligogenic, such as rust resistance (Resende et al., 2012a) and milk fat (Habier et al., 2013), the accuracies were superior under priors that assume variable selection, variance heterogeneity or both.

Despite the relevance of different priors in the performance of additive whole-genome prediction models, their contribution to the accuracy of models that incorporate dominance effects, and for traits with distinct genetic architecture, have not been extensively explored. The objective of this study is to address this limitation. We evaluate additive and additive–dominance models in the prediction of traits with a relatively simple (disease resistance) and complex (growth) genetic architecture, measured in a standard breeding population of loblolly pine (Resende et al., 2012a). Furthermore, to fully explore the advantages and limitations of different models in the prediction of dominance, we extend the analysis to a simulated population with traits controlled by contrasting levels of dominance.

Materials and methods

Loblolly pine population data

The reference loblolly pine (Pinus taeda L.) breeding population CCLONES (Comparing Clonal Lines On Experimental Sites) was used in this study. The population was created by crossing 42 parents representing a wide range of accessions from the US Atlantic coastal plain in a circular mating design with additional off-diagonal crosses (Baltunis et al., 2007). In total, 923 individuals from 71 full-sib families (average of 13 individuals per family, s.d.=5) were genotyped for 7216 single-nucleotide polymorphism (SNP) loci using an Illumina Infinium assay (Illumina, San Diego, CA, USA; Eckert et al., 2010). All 4722 loci that were polymorphic in the population were used in this study, regardless of their minor allele frequency. Missing data were low (<1%) and missing values were replaced by the marker expected value (de los Campos and Perez, 2014). Three traits with contrasting genetic architecture were analyzed. Tree height (HT) is a polygenic trait, and was measured in field trials when the trees were 6 years old in eight clonal replicates distributed in an α-lattice design (Baltunis et al., 2007). Fusiform rust is an oligogenic trait, controlled by a number of loci of large effect (Resende et al., 2012a). Fusiform rust incidence was measured as gall volume (RFgall) and as a binary (presence/absence) trait (RFbin) (Quesada et al., 2014). Plants were phenotyped for rust in a greenhouse experiment that followed a randomized complete block design, with three repetitions, as described previously (Resende et al., 2012a). The estimated narrow-sense heritability of these traits was previously reported as 0.31, 0.21 and 0.12 for HT, RFbin and RFgall, respectively (Resende et al., 2012a).

Simulated data

The parametric contribution of dominance to trait variation, and the ratio of dominance to additive effects, are unknown in the CCLONES population. In order to fully evaluate the ability of models in predicting dominance effects of different architectures and degrees, we proceeded to simulate a population with similar genetic properties as CCLONES, except that trait QTLs were manipulated to include dominance and regulation by different numbers of loci. The simulation of a population with similar properties as CCLONES was carried out in two steps. First, 1000 diploid individuals were created by randomly sampling 2000 haplotypes generated after 1000 generations of a neutral coalescence model from a population with effective size (N_e) of 10 000 and mutation rate of 2.5 × 10⁻⁸ (Willyard et al., 2007). The simulated genome had 12 chromosomes, each with 100 cM, and 10 000 polymorphic loci were randomly selected. This first step was simulated using Macs (Chen et al., 2009). In the second step of the simulation, the 1000 diploid individuals generated previously were subject to selection and recombination and used to generate a loblolly pine improvement program in its second breeding cycle (Figure 1). The simulation of the population generated a total of 196 303 656 polymorphic sites. As commonly observed in pine tree breeding populations, the majority of loci had very low minor allele frequencies (Supplementary Figure S1).

Figure 1.

Breeding scheme applied to create the simulated CCLONES population used for analysis of all traits.

Six traits with different genetic architectures (polygenic and oligogenic) and levels of dominance (none, medium or high dominance) were simulated. For the polygenic traits, 1000 QTLs were used in the analysis, and their additive effects were sampled from a standard normal distribution (Hickey and Gorjanc, 2012). For the oligogenic traits, 30 QTLs were sampled from a gamma distribution with rate 1.66 and shape 0.4, and the QTL effects were sampled to be positive or negative with equal probability (Meuwissen et al., 2001). The dominance effect of the ith QTL, when present, was determined by: d_i=a_i × ϕ_i, where ϕ_i was sampled from a normal distribution with mean zero and s.d. of 1 (moderate dominance) and 2 (high dominance) (Table 1). The additive effect (a_i) of the ith QTL was defined as half of the difference between alternative homozygote categories, and the dominance effect (d_i) as the deviation of the heterozygote from the mean of two homozygote classes. The heritability was calculated as h²=V_A/V_P, and d²=V_D/V_P, where V_P=V_A+V_D+V_E (additive–dominance scenario) or V_P=V_A+V_E (additive scenario). V_P, V_A, V_D and V_E are the phenotypic, additive, dominance deviation and residual variances, respectively (Falconer and Mackay, 1996). The error was simulated from a normal distribution with mean zero, and the variance was defined to result in an h² equal to 0.25. The simulation of dominance traits was supervised in order to achieve a d² of 0.1 and 0.2 for traits with moderate and large dominance effects, respectively. For traits with moderate dominance, we accepted d² between 0.09 and 0.11; for traits with large dominance, we accepted d² between 0.19 and 0.21. When d² fell outside the desired range the simulation was discarded.

Table 1. Summary of simulated traits.

Traits description	Number of genes (QTLs)	d2	d2/h2
Oligogenic with no dominance	30	0	0
Polygenic with no dominance	1000	0	0
Oligogenic with medium dominance	30	0.1	0.4
Polygenic with medium dominance	1000	0.1	0.4
Oligogenic with high dominance	30	0.2	0.8
Polygenic with high dominance	1000	0.2	0.8

Abbreviation: QTL, quantitative trait locus.

A heritability of 0.25 was used in all simulated conditions.

After sampling individuals from the natural population and creating the base population (G0), two discrete generations of selection and mating were simulated. From 1000 individuals in the base population (G0), the 10% highest phenotypic values were selected and randomly mated to generate 1000 individuals that compose the first breeding generation (G1). From G1, 42 individuals were selected and used in a mating design that reproduced the same pedigree as the CCLONES population (G2). The breeding populations from G2 were simulated with 10 replicates for each trait using the R software (R Development Core Team, 2014). In addition, the 42 individuals with highest phenotypic value from each replicate of G2 were selected to be parents in the subsequent generation (G3). The mating followed again the same design as CCLONES and the top selected individuals were randomly crossed.

Statistical methods

We used Bayesian WGR models with SNPs as covariates and common priors, including BRR (also called SNP-BLUP), Bayes A, Bayes B and BL. All methods used here can be represented by the following base model:

Where y_j is the phenotype (clonal mean) of individual j; μ is the intercept; e_j is the error of observation j; and g_j is the genotypic value. In all models it was assumed that:

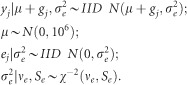For each prior, either additive only or additive–dominance effects were considered. Thus, the general additive–dominance WGR model was replaced by:

Where x_ij and w_ij are the functions of SNP i in individual j, for genotypes AA, Aa and aa. We parameterized x_ij with values 1 (AA), 0 (Aa) and −1 (aa) and w_ij with 0 (AA), 1 (Aa) and 0 (aa) (Toro and Varona, 2010). The additive and dominance effects of the ith marker were represented by a_i and d_i, respectively. The dominance effect was fitted only in the additive–dominance model. The priors used in linear regression coefficients for additive–dominance and additive models are described below.

Bayesian ridge regression

The BRR is a Bayesian method in which it is assumed that all regression coefficients have common variance. Thus, for an additive–dominance model, all markers with the same allele frequency explain the same proportion of the additive and dominance variances, and have the same shrinkage effect (Gianola, 2013). For BRR it was assumed that:

Bayes A

Bayes A was proposed by Meuwissen et al. (2001) and, contrary to BRR, it considers that markers have heterogeneous variances. Bayes A was further modified (de los Campos and Perez, 2014) to estimate the shape parameter of the inverted χ² distribution. This modification is expected to reduce the influence of the hyperparameter and improve the learning process (Gianola et al., 2009). For Bayes A it was assumed that:

Bayes B

Bayes B differs from Bayes A in that it includes the selection of covariates (SNPs) that do not contribute to genetic variance (Meuwissen et al., 2001). Similar to Bayes A, we adopted a modified version of Bayes B (de los Campos and Perez, 2014), where the shape parameter follows a gamma distribution and π is an estimated parameter (Gianola et al., 2009). This implementation of Bayes B is very similar to Bayes Dπ (Habier et al., 2011), and it assumes:

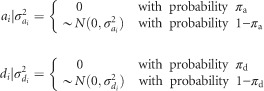Bayesian lasso

The Bayesian version of Lasso regression was proposed by Park and Casella (2008), and the application in whole genomic prediction was proposed by de los Campos et al. (2009). As in Bayes A and Bayes B, BL presupposes that covariates do not have homogeneous variance. Furthermore, it promotes an indirect marker selection with strong shrinkage in the regression coefficients, as the marginal prior of regression coefficients follows a double exponential distribution (Park and Casella, 2008) that drive many marker effects to zero or near zero. The BL assumes:

All analysis with the WGR models were carried out with the R package BGLR (de los Campos and Perez, 2014) with default hyperparameter (Supplementary Tables S1 and S2) values described previously (de los Campos et al., 2013; de los Campos and Perez, 2014; Pérez and de los Campos, 2014). In total, 30 000 Markov chain Monte Carlo iterations were used, of which the first 10 000 were discarded as burn-in and every third sample was kept for parameter estimation. We also evaluated the accuracy of additive and additive–dominance models based exclusively on pedigree information by generating the expected relationship matrix. Although the additive–dominance pedigree model was more accurate for dominance deviation, the genomic models were more accurate for parent and clonal selection (Table 2 and Supplementary Table S3). Thus, this study focused on genomic prediction models only.

Table 2. Average of accuracies of phenotype prediction with pedigree base line models with only additive effect (Ped-Add), with additive and dominance effects (Ped-Add-dom) and mean accuracy of all genomic models.

Models	HT	RFbin	RFgall
Ped-Add	0.371	0.335	0.264
Ped-Add-Dom	0.398	0.325	0.259
Genomic	0.407	0.355	0.293
Gen vs Ped	0.023a	0.025a	0.031a

Abbreviations: Add, additive; Dom, dominance; Gen, genomic; HT, tree height; Ped, pedigree; RFbin, fusiform rust incidence measured as a binary (presence/absence) trait; RFgall, fusiform rust incidence measured as gall volume.

The comparison between genomic and pedigree base models were made by contrast estimated as weighted mean of accuracy of genomic models minus pedigree models. The traits evaluated were HT and two measures of rust resistance (RFbin and RFgall).

^aContrast significant at P<0.01.

Breeding value and dominance deviation

After fitting each WGR model, the breeding values (u) and dominance deviation of the additive–dominance models (δ) were estimated (Falconer and Mackay, 1996) as described below.

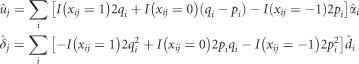Where p_i is allele frequency of allele A of SNP i, q_i=1−p_i, 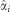is the average effect of substitution, 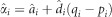, and I is an indicator function of SNPs.

Variance components and heritability estimation

For estimation of variance components, linkage equilibrium, absence of epistasis and Hardy–Weinberg equilibrium was assumed (Gianola et al., 2009). Considering these assumptions, the additive variance 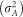and the variance due to dominance deviation 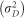were estimated as described previously (Zeng et al., 2013; Ertl et al., 2014):

and

These estimates were used to calculate h² and d², as previously described.

Validation

A 10-fold cross-validation was used to compare results in the real and simulated populations (Ertl et al., 2014). Briefly, the data set was separated into 10 subsets. In each cycle, a subset was excluded before models were fitted with the remaining data, and the model was used to predict the excluded subset. The process was repeated 10 times, and in each cycle the prediction accuracy was estimated (Pearson's correlation) and regression coefficients of parametric values on predicted validation data were calculated. For the simulated population, the accuracies were calculated for breeding values, dominance deviations, total genotypic values and phenotype values of individuals. The results reported are means (and s.e.) of accuracies and regression coefficients of parametric values on estimated values across folds. Because in the nonsimulated population the true genotypic values are unknown, we used the prediction ability (accuracy of phenotype prediction 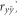), the correlation between predicted whole genotypic value and phenotype.

Results

Heritability

BRR was used to estimate the narrow-sense heritability using additive and additive–dominance models. Estimates of h² were higher in additive models, for all traits, in the real (Table 3) and the simulated population (Supplementary Table S4). For traits measured in the real population, estimates of d² ranged from 0.09 to 0.15, whereas 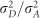(or d²/h²) varied from 0.31 to 0.42. Because the parametric values are known in the simulated population, it was possible to evaluate the impact of model selection in the estimation of genetic parameters. For traits without dominance, the estimates of h² were similar to the parametric value for additive and additive–dominance models. The dominance component of the additive–dominance model captured dominance variability and overestimated d² as 0.07. For simulated traits with low dominance (d²=0.1), estimates of d² and h² were similar to the parametric value. However, in the case of higher dominance (d²=0.2), these estimates were underestimated for d² and modestly overestimated for h².

Table 3. Narrow- and broad-sense heritability and proportion of variance of dominant deviations relative to total genetic variance explained by markers using BRR for height (HT) and rust resistance evaluated as gall volume (RFgall) and presence or absence (RFbin) in Pinus taeda.

Trait	Additive model	Additive–dominance model
	h2	h2	d2	H2	d2/h2
HT	0.40 (0.30–0.51)	0.35 (0.26–0.45)	0.15 (0.08–0.22)	0.49 (0.38–0.60)	0.42 (0.22–0.68)
RFbin	0.37 (0.26–0.49)	0.32 (0.23–0.44)	0.10 (0.05–0.17)	0.42 (0.32–0.55)	0.31 (0.12–0.57)
RFgall	0.29 (0.19–0.41)	0.27 (0.18–0.38)	0.09 (0.05–0.14)	0.36 (0.25–0.48)	0.33 (0.16–0.56)

Abbreviations: BRR, Bayesian ridge regression; HT, tree height; RFbin, fusiform rust incidence measured as a binary (presence/absence) trait; RFgall, fusiform rust incidence measured as gall volume.

Values between parenthesis are Bayesian credibility interval (95%).

Additive and additive–dominance model prediction in the CCLONES population

We contrasted the predictive ability of linear models with different assumptions regarding prior information of marker effects, and accounting for only additive or additive–dominance contributions. The models with different priors were similar in absolute value of the predictive ability (Table 4). However, an analysis of variance indicated that the results were statistically different for HT and RFbin (Supplementary Table S5). The inclusion of dominance effects only increased modestly the predictive ability for HT. For instance, additive Bayes B showed the highest accuracies for RFgall (0.299) and RFbin (0.376). In contrast, the highest accuracies with additive–dominance models were 0.292 and 0.369 for RFgall and RFbin, respectively (Table 4). These results suggest a minor contribution of dominance to tree height. On the other hand, prediction of rust resistance traits show no improvement in accuracy when dominance is considered, possibly because this effect is absent or negligible. Other factors, such as limited marker coverage of rust QTLs or insufficient population size to estimate the dominance effect, may have also contributed to the observed results. Overall, the results are in agreement with the proportion of variance of dominant deviations relative to total genetic variance that was estimated to be 50% higher for HT as compared with RFgall and RFbin (Table 4).

Table 4. Results of predictive ability and slope of whole-genome regressions using different priors and including dominance effects for height (HT) and rust resistance evaluated as gall volume (RFgall) and presence or absence (RFbin) in Pinus taeda.

Model	Prior	HT		RFgall		RFbin
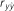		(s.e.)	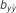(s.e.)	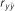(s.e.)	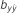(s.e.)	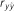(s.e.)	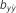(s.e.)
Add-Dom	Bayes A	0.415 (0.04)ab	1.002 (0.10)	0.291 (0.03)a	1.008 (0.10)	0.367 (0.02)ab	0.968 (0.08)
	Bayes B	0.414 (0.04)ab	1.020 (0.10)	0.291 (0.03)a	0.994 (0.09)	0.369 (0.02)a	0.985 (0.07)
	BL	0.415 (0.04)ab	1.054 (0.10)	0.288 (0.03)a	1.148 (0.14)	0.338 (0.02)c	1.024 (0.08)
	BRR	0.418 (0.04)a	0.999 (0.09)	0.292 (0.03)a	0.960 (0.10)	0.329 (0.02)c	0.908 (0.06)
Additive	Bayes A	0.401 (0.03)bc	1.025 (0.10)	0.296 (0.03)a	1.069 (0.11)	0.375 (0.02)a	0.997 (0.08)
	Bayes B	0.401 (0.03)bc	1.019 (0.10)	0.299 (0.03)a	1.044 (0.10)	0.376 (0.02)a	0.988 (0.08)
	BL	0.392 (0.03)bc	1.038 (0.11)	0.292 (0.03)a	1.134 (0.13)	0.345 (0.02)bc	1.028 (0.09)
	BRR	0.402 (0.03)abc	1.003 (0.10)	0.291 (0.03)a	0.981 (0.10)	0.336 (0.02)c	0.947 (0.08)

Abbreviations: Add, additive; BRR, Bayesian ridge regression; Dom, dominance; HT, tree height; Ped, pedigree; RFbin, fusiform rust incidence measured as a binary (presence/absence) trait; RFgall, fusiform rust incidence measured as gall volume.

All slope coefficients were statistically equal to 1. Average of predict ability with same letter are statistically equal by Tukey's test. All inferences used type 1 error=0.05.

Genetic properties of the simulated population

To assess the effect of the trait genetic architecture on prediction models that include additive and additive–dominance effects, scenarios considering a polygenic trait (1000 QTLs) and an oligogenic trait (30 QTLs) were evaluated. For both types of traits, three dominance levels were simulated: no dominance (d²=0; d²/h²=0), moderate dominance (d²=0.1; d²/h²=0.4) and high dominance (d²=0.2; d²/h²=0.8). A set of 10 000 markers randomly distributed across the genome (expected 8.33 markers per cM) and polymorphic in the base population were included in the analysis. In the population that simulated CCLONES (G2), approximately half of QTLs (mean=53.92% s.d.=1.18%) and markers (mean=55.45% s.d.=0.56%) were fixed. Thus, the two cycles of breeding and selection reduced (or fixed) the frequency of alleles in a large number of loci. The allele frequency distributions of polymorphic SNPs were similar between CCLONES and the simulated population (Supplementary Figure S1). In the simulated base population, the linkage disequilibrium among markers and QTLs was low. As expected, the linkage disequilibrium increased over successive generations, reflecting the lower effective population size relative to the base population (Supplementary Figure S2). On average, two or more markers had an r² >0.4 with any QTL for all simulated traits.

Dominance reduces the overall accuracy of prediction models

The suitability of additive and additive–dominance prediction models was assessed by estimating the total genomic accuracy (Figure 2), breeding value (Figure 3), dominance deviation (Figure 4) and phenotypic accuracy (Supplementary Figure S3). In all scenarios, the different WGR provided statistically different results (Supplementary Tables S6–S9). Overall there was a decrease in the accuracy of total genomic predictions as the dominance increased, regardless of the method used for model development. Thus, the data indicate that dominance effects may not be accounted for as effectively in the prediction models as traits controlled by loci that contribute additive effects only.

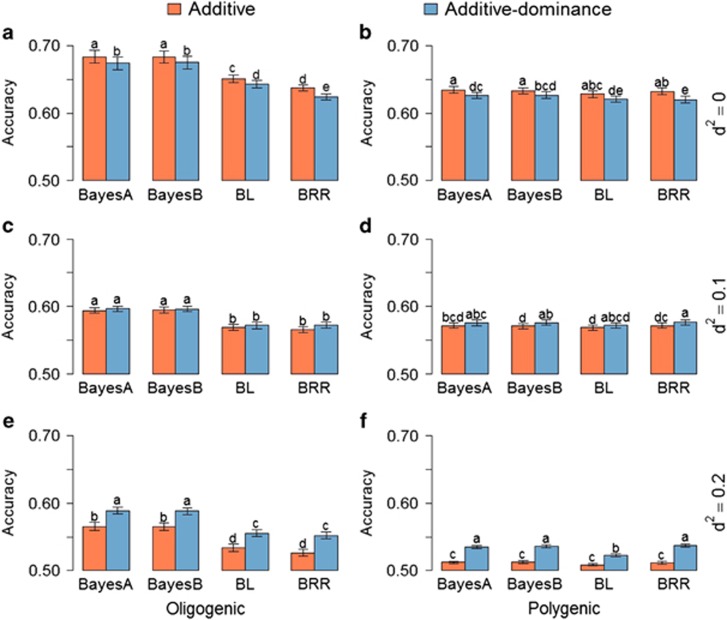
Figure 2.

Average of accuracies of whole genotypic predictions with additive and additive–dominance WGRs using different priors for six different simulated traits: (a) oligogenic and (b) polygenic traits with h²=0.25 and nondominance effects; (c) oligogenic and (d) polygenic traits with h²=0.25 and d²=0.1; and (e) oligogenic and (f) polygenic traits with h²=0.25 and d²=0.2. Error bars are s.e. among 10 replicates. Means with same letter are statistically equal by Tukey's test (P<0.05).

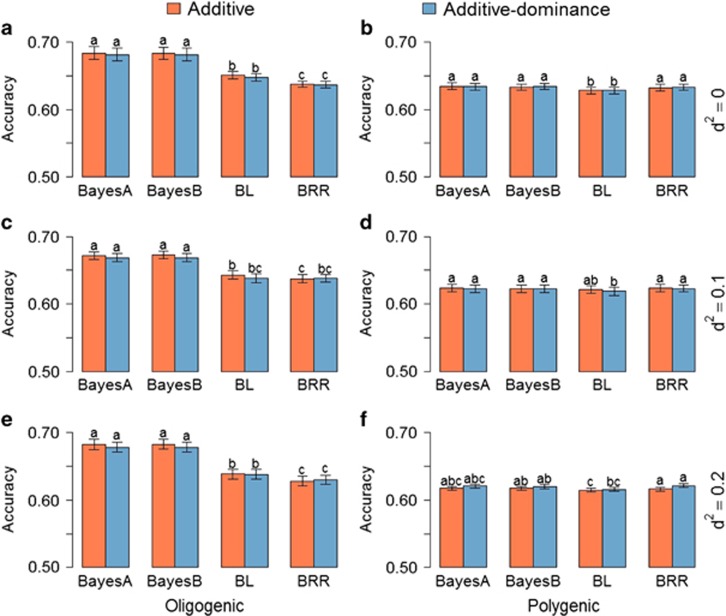
Figure 3.

Average of accuracies of breeding value predictions with additive and additive–dominance WGRs using different priors for six different simulated traits: (a) oligogenic and (b) polygenic traits with h²=0.25 and nondominance effects; (c) oligogenic and (d) polygenic traits with h²=0.25 and d²=0.1; and (e) oligogenic and (f) polygenic traits with h²=0.25 and d²=0.2. Error bars are s.e. among 10 replicates. Means with same letter are statistically equal by Tukey's test (P<0.05).

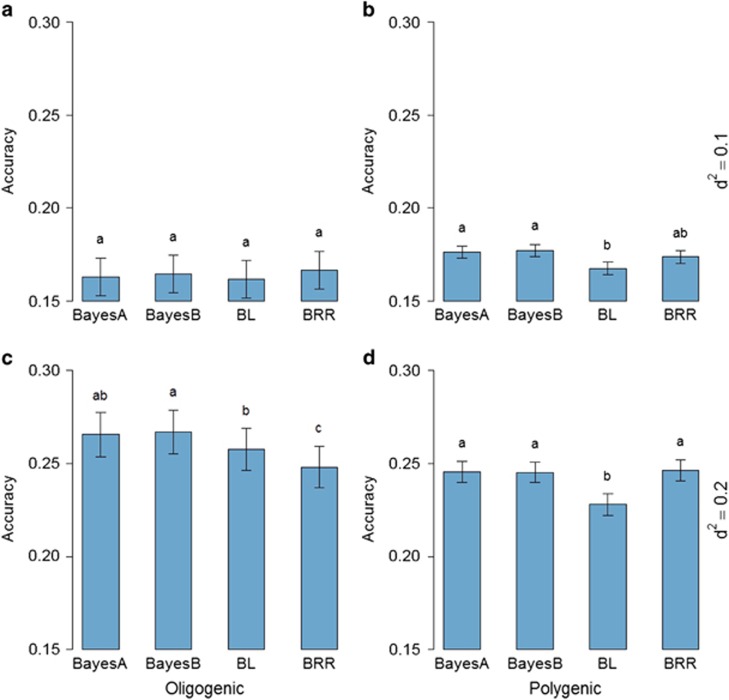
Figure 4.

Average of accuracies of dominance deviation predictions with additive–dominance WGRs using different priors for four different simulated traits: (a) oligogenic and (b) polygenic traits with h²=0.25 and d²=0.1; and (c) oligogenic and (d) polygenic traits with h²=0.25 and d²=0.2. Error bars are s.e. among 10 replicates. Means with same letter are statistically equal by Tukey's test (P<0.05).

Models that incorporate dominance are only more accurate when d² is high

In the simulated population we detected a very small (mostly nonsignificant) improvement in accuracy of genomic prediction from additive–dominance models, when d² was equal to 0.1 (Figure 2). A much larger and significant improvement was only observed as d² increased to 0.2, a relatively high dominance to additive effect ratio. The s.e. values were generally higher among oligogenic traits as compared with polygenic traits. This difference was accentuated when dominance was high. This may occur because the oligogenic architecture can exacerbate the inaccuracy in the estimation of dominance. Random sampling of individuals from the population in the cross-validation can result in subsamples with different representations of heterozygous individuals between the training and validation subpopulations.

The accuracy of the total genomic prediction was similar across different methods for polygenic traits, regardless of the presence of dominance (Figure 2). However, Bayes A and Bayes B had higher accuracy than BL and BRR for oligogenic traits in all scenarios. This observation is similar to previous reports (Resende et al., 2012a; Daetwyler et al., 2013) that have shown the limitation of BL and RR-BLUP (frequentist version of BRR) in accounting for few loci of large effect in the predictive model. It suggests that when the trait architecture is unknown, it may be suitable to evaluate multiple models before adoption of one approach for trait prediction in future generations.

Accuracy of predicting additive and dominance effects and phenotypes

The inclusion of dominance in the prediction model did not affect the prediction of breeding values, as expected (Figure 3). There was no difference among models in the accuracy of prediction of additive effects in polygenic traits. However, similar to the prediction of total genetic effects, a significant improvement was detected when Bayes A and Bayes B were used for prediction of oligogenic traits over BL and BRR.

The accuracy of dominance prediction improved significantly (over 50%) when its contribution to traits increased from d²=0.1 to 0.2 (Figure 4). Thus, as the contribution of dominance is higher, the ability to accurately capture it in prediction models improves. However, the overall genetic accuracy decreases as the d² increases, as those effects may not be estimated adequately. Accuracies were observed to be more accurate for oligogenic traits predicted with Bayes A and Bayes B models.

Finally, the accuracy derived by the correlation of phenotypes to the estimated genetic effect (Supplementary Figure S3) showed that as dominance increases in oligogenic and polygenic traits, accuracy of phenotype prediction also increases. As d² increased from 0 to 0.2, the prediction accuracy improved 22%. However, there is only a significant difference in the prediction using the additive–dominance model when d² is 0.2. We expect this difference to increase as dominance increases.

Additive–dominance models improve accuracy of progeny selection only for oligogenic traits with high dominance

Progeny derived from the real CCLONES population are currently not available, preventing the evaluation of prediction models in generations following the population used for model estimation. However, such progeny can be generated for the simulated population. The first generation (G3) derived from the simulated CCLONES population was generated by selecting 42 individuals with the highest phenotypic value that were crossed following the same matting design as CCLONES. The results showed that the accuracy of the prediction in the next generation (Supplementary Figure S4) decreased significantly when compared with the accuracy in the CCLONES (G2) population (Figures 2, 3, 4 and Supplementary Figure S3). The accuracy of the prediction of dominance deviation was almost zero for all characteristics, except for oligogenic trait with high dominance. In all other traits the additive models provided better predictions.

Discussion

Dominance was formulated by Mendel as one of the first concepts of genetics (Wilkie, 1994). In quantitative genetics, dominance is defined as the interaction between different alleles of a gene, and is measured as the difference of heterozygotes and mean of homozygotes (Falconer and Mackay, 1996). Dominance effects contribute to inbreeding depression, and may also play a role in heterosis (or hybrid vigor) (Falconer and Mackay, 1996; Hallauer et al., 2010). Expectedly, the presence of dominance is dependent on the trait under consideration and allele frequencies in the population. Here we analyzed the contribution of dominance effects in the accuracy of genomic prediction with models that assume different priors and for traits with different genetic architectures. The assessment was made for traits measured in the reference CCLONES population of loblolly pine that was previously genotyped and extensively phenotyped for height growth and rust resistance. Next we extended the analysis to a simulated population with similar genetic properties to CCLONES, where traits with different genetic architectures and degrees of dominance were considered. In this study, additive and dominance effects were simultaneously adjusted in genomic prediction models. Epistasis, however, was not considered in the model. Hence, the presence of any epistatic effect could have acted as a confounding effect and affect prediction accuracy.

Previous quantitative genetic analysis of height measured in pine breeding populations indicated that the trait is highly polygenic, and that nonadditive effects contribute to its variance (Isik et al., 2003; Muñoz et al., 2014). In the analysis of height measured in the CCLONES population, models that accounted for both additive and dominance effects had higher predictive ability. The analysis of the simulated population supports these results, as polygenic traits with dominance effects were predicted with significantly higher accuracy in models that included additive and dominance effects. Previous analysis of complex traits reported that inclusion of dominance (and epistasis in some cases) was advantageous for breeding programs when compared with using models that accounted for only additive effects (Su et al., 2012; Lopes et al., 2014; Muñoz et al., 2014; Nishio and Satoh, 2014). The same was observed in simulated populations (Toro and Varona, 2010; Denis and Bouvet, 2012; Zeng et al., 2013). Contrary to height, the inclusion of dominance effects did not improve the predictive ability of rust resistance-related traits in the real population. Other studies previously reported that dominace deviation was not significant for this characteristic in a pine breeding population (Isik et al., 2003) and in our analysis the additive models were marginally more accurate than additive–dominance models. In summary, the additive–dominance prediction models improved considerably the accuracies in simulated traits with large dominance effects, but showed limited or no improvement when these effects are modest. Thus, inclusion of dominance in genomic prediction will depend on the trait's genetic architecture in each specific population.

Another goal of this study was to evaluate the effect of using WGR methods that adopt distinct priors in the prediction of traits that include dominance effects. These methods differ in their approach to variable selection and the variance of regressions coefficients. As a consequence, WGR differ in the marginal prior of regression coefficients (markers effects) that control the shrinkage of markers effects (de los Campos et al., 2013; Gianola, 2013). The identification of the best model or prior is trait dependent (Resende et al., 2012a). In the present study, models with different priors did not differ significantly for the trait height measured in the CCLONES population, and for the polygenic traits in the simulated population. In contrast, the accuracy of prediction models for rust resistance traits were higher for Bayes A and Bayes B as compared with BRR. The same pattern was observed for the simulated oligogenic traits. These results are expected, as the marginal priors of Bayes A and Bayes B provide more shrinkage than BRR, and Bayes B also incorporates variable selection.

The use of dominance in forest breeding programs is desirable for species that are clonally propagated because their entire genotypic value can be translated to commercial plantations. An accurate estimation of dominance effects can also improve the genetic gain in improvement programs (Falconer and Mackay, 1996). Finally, the incorporation of dominance effects is critical for introduction of breeding approaches that aim to create crosses with complementary alleles in mate-pair allocation (Toro and Varona, 2010). Here we showed that including dominance effects in the prediction of traits controlled by loci with additive and dominance effects can result in more accurate models. Improved models will increase genetic gains for clonal selection and in reciprocal recurrent selection of superior mate-pairs. It has to be noted that in the breeding values estimation, the additive–dominance WGR models were not more accurate, even in the presence of a dominance component (see Figure 3). This limitation is likely to occur because dominance variance estimations is less accurate and demands much more information (Toro and Varona, 2010). Estimating the contribution of dominance relies on the measurement of phenotypes in heterozygous individuals. In the simulated population, where more than a third of loci have a minor allele frequency below 5%, >10% of the individuals are expected to have the heterozygote genotype. Furthermore, with only 923 individuals, the simulated population used to train the models may not be sufficiently large to support the accurate estimation of these dominance effects. These results suggest that as dominance increases, the accuracy of predictions will become less suitable for genomic selection. Others have recently reported that the prediction of dominance deviation from SNP information is not as accurate as that reported for breeding values (Nishio and Satoh, 2014). However, the use of larger training populations (Ertl et al., 2014; Wittenburg et al., 2015) or the adoption of training populations where loci with higher minor allele frequency occur (and therefore more heterozygotes are available for dominance estimation) may improve predictions. Further investigation is necessary to identify the factors that most improve the accuracy of predicting dominance effects.

Finally, we evaluated the performance of the models estimated in G2 to predict the simulated progeny (G3). The additive–dominance models outperformed the additive models only for simulated oligogenic trait with high dominance effects. Toro and Varona (2010) also reported that additive–dominance models outperformed additive models only in the first generation for polygenic simulated traits. These results suggest that the use of additive–dominance models would only be recommended in species that can be vegetative propagated. Further studies combining the use of additive–dominance models with mate-pair allocation are required to evaluate whether the prediction of dominance can improve the accuracy of subsequent generations under sexual propagation schemes.

Data archiving

All phenotypic and genotypic data utilized in this study have been previously published as a standard data set for development of genomic prediction methods (Resende et al., 2012a). Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.3126v.

The authors declare no conflict of interest.