Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 May 16;138(22):7161–7170. doi: 10.1021/jacs.6b03680

Selective, Tunable O2 Binding in Cobalt(II)–Triazolate/Pyrazolate Metal–Organic Frameworks

Dianne J Xiao †, Miguel I Gonzalez †, Lucy E Darago †, Konstantinos D Vogiatzis ‡, Emmanuel Haldoupis ‡, Laura Gagliardi ‡, Jeffrey R Long †,§,∥,*
PMCID: PMC4901364  PMID: 27180991

Abstract

graphic file with name ja-2016-03680b_0009.jpg

The air-free reaction of CoCl2 with 1,3,5-tri(1H-1,2,3-triazol-5-yl)benzene (H3BTTri) in N,N-dimethylformamide (DMF) and methanol leads to the formation of Co-BTTri (Co3[(Co4Cl)3(BTTri)8]2·DMF), a sodalite-type metal–organic framework. Desolvation of this material generates coordinatively unsaturated low-spin cobalt(II) centers that exhibit a strong preference for binding O2 over N2, with isosteric heats of adsorption (Qst) of −34(1) and −12(1) kJ/mol, respectively. The low-spin (S = 1/2) electronic configuration of the metal centers in the desolvated framework is supported by structural, magnetic susceptibility, and computational studies. A single-crystal X-ray structure determination reveals that O2 binds end-on to each framework cobalt center in a 1:1 ratio with a Co–O2 bond distance of 1.973(6) Å. Replacement of one of the triazolate linkers with a more electron-donating pyrazolate group leads to the isostructural framework Co-BDTriP (Co3[(Co4Cl)3(BDTriP)8]2·DMF; H3BDTriP = 5,5′-(5-(1H-pyrazol-4-yl)-1,3-phenylene)bis(1H-1,2,3-triazole)), which demonstrates markedly higher yet still fully reversible O2 affinities (Qst = −47(1) kJ/mol at low loadings). Electronic structure calculations suggest that the O2 adducts in Co-BTTri are best described as cobalt(II)–dioxygen species with partial electron transfer, while the stronger binding sites in Co-BDTriP form cobalt(III)–superoxo moieties. The stability, selectivity, and high O2 adsorption capacity of these materials render them promising new adsorbents for air separation processes.

Introduction

Decades after their discovery in the mid-19th century,1 synthetic transition metal–dioxygen compounds continue to command widespread interest due to their relevance as models of biological oxygen carriers and metalloenzymes,2 catalysts in oxidation chemistry,3 and adsorbents for industrial air separation applications.4 Recently, rising atmospheric CO2 levels have generated increasing impetus for research efforts in this last area, as several proposed carbon capture and sequestration technologies require the use of high-purity oxygen.5 Briefly, precombustion CO2 capture utilizes O2 for the gasification of coal, while oxyfuel combustion systems burn fuel in the presence of pure O2 diluted in CO2. As high-purity oxygen is currently produced on a large scale via energetically demanding cryogenic distillation,6 there is a need for alternative, lower-cost air separation technologies.

Metal–organic frameworks, a relatively new class of highly crystalline and porous materials, have the potential to transform a variety of gas separation and storage processes,5b,7 including oxygen purification from air. For example, frameworks containing coordinatively unsaturated redox-active metal centers that can reversibly bind and reduce oxygen, such as Cr3(btc)2, Cr-BTT, and Fe2(dobdc), exhibit much higher selectivities and total capacities than the ion-exchanged zeolites currently used in adsorbent-based air separation plants and devices.4c,4d,8,9 Furthermore, most ion-exchanged zeolites are N2-selective, as their extra-framework cations (e.g., Li+) are generally redox-inactive and interact preferentially with the larger quadrupole moment of nitrogen. Because oxygen constitutes a smaller fraction of air than nitrogen (21% versus 78%), O2-selective materials such as the aforementioned metal–organic frameworks are inherently more efficient than N2-selective adsorbents. In spite of these advantages, however, many improvements are still necessary with respect to the thermal stability and cyclability of metal–organic frameworks. Indeed, Fe2(dobdc) irreversibly oxidizes at temperatures above 222 K, while chromium frameworks can exhibit gradual capacity losses over multiple cycles. Significantly, all of these framework materials decompose over time when exposed to humid air.

While molecular complexes of cobalt(II) comprise some of the earliest,10 prototypical examples of synthetic oxygen carriers, cobalt-based metal–organic frameworks with a strong affinity for O2 are noticeably absent from the literature. This discrepancy may be due to the widespread use of weak-field carboxylate-based bridging ligands as framework struts, leading to electron-poor cobalt(II) nodes that exhibit only weak O2 binding. Additionally, cobalt(III)-superoxo and peroxo species, like most cobalt(III) compounds, adopt low-spin electronic configurations with short equatorial metal–ligand bonds ranging from ∼1.9 to 2.0 Å.11 These geometric requirements may be incompatible with certain framework structures. For example, it has been shown that transition-metal ions in the M2(dobdc) (also known as M-MOF-74) series maintain a high-spin configuration even in the presence of strong-field ligands such as CO as well as in high oxidation states.12,13 Due to the combination of weak ligand field and structural rigidity, the metal centers in Co2(dobdc) have been demonstrated to be redox-inactive in the presence of O2.14 Thus, while cobalt(II)-based metal–organic frameworks are appealing targets in the pursuit of new adsorbents for air separations, development of such materials requires the design of new frameworks possessing both strong-field ligands and some degree of structural flexibility.

Herein, we present two such metal–organic frameworks, Co-BTTri and Co-BDTriP, which feature coordinatively unsaturated cobalt(II) centers supported by a combination of electron-donating triazolate and pyrazolate linkers. Gas adsorption measurements reveal that both materials exhibit a strong preference for binding O2 over N2. Electronic structure calculations further show that the extent of charge transfer between the cobalt(II) nodes and dioxygen is highly dependent on the primary coordination sphere of the metal center.

Experimental Section

Synthesis of Co-BTTri

A 100 mL Schlenk flask was charged with 200 mg of H3BTTri (0.716 mmol, 1.00 equiv) dissolved in 50 mL of N,N-dimethylformamide and methanol (10:1 DMF:MeOH). To this mixture was added 319 mg dimethylformamidium trifluoromethanesulfonate (1.43 mmol, 2.00 equiv) followed by 163 mg CoCl2 (1.26 mmol, 1.75 equiv). The Schlenk flask was sealed using a high-vacuum grease suitable for high temperatures, degassed by freeze–pump–thawing three times, and stirred at 393 K for 7 days and 413 K for 2 days. The resulting pink solid was filtered, and under an inert atmosphere washed with DMF (6 × 50 mL, each wash 12 h at 393 K) and exchanged with methanol (6 × 50 mL, each wash 12 h at 343 K). The solid was fully activated by heating at 423 K under dynamic vacuum for 24 h to produce 158 mg of a tan solid (49% yield). The reaction can also be scaled up and concentrated to 1.60 g of H3BTTri in 200 mL of the same solvent mixture, 1.75 equiv of CoCl2, and 1.00 equiv of acid (note reduced acid equivalents) to produce 1.70 g of material (66% yield). Anal. calcd for Co3[(Co4Cl)3(BTTri)8]2·14DMF (C234H194Cl6Co27N158O14): C, 38.78; H, 2.70; N, 30.54. Found: C, 39.03; H, 2.59; N, 30.53.

Single-Crystal Synthesis of Co-BTTri

A 20 mL vial was charged with 10 mg of H3BTTri (0.036 mmol, 1.0 equiv) and 8 mL of solvent (4:1 DMF:MeOH). After the ligand had fully dissolved, 2.2 equiv of concentrated HCl (12 M) was added, followed by 3.0 mg of CoCl2 (0.023 mmol, 0.65 equiv) and 150 μL of water. The solution was separated into several pyrex tubes, freeze–pump–thawed, and flame-sealed. Heating the sealed tubes at 423 K for 4 days led to the formation of pink, cubic crystals of Co-BTTri.

Single-Crystal Synthesis of Co-BDTriP

A 20 mL vial was charged with 20 mg of H3BDTriP (0.072 mmol, 1.0 equiv) and 4 mL of solvent (4:1 DMF:MeOH). After the ligand had fully dissolved, 1.1 equiv of concentrated HCl (12 M) was added (0.079 mmol) along with 250 μL of water, followed by 9.3 mg of CoCl2 (0.072 mmol, 1.0 equiv). The solution was separated into several pyrex tubes, freeze–pump–thawed, and flame-sealed. Heating the sealed tubes at 423 K for 1 week led to the formation of pink, cubic crystals of Co-BDTriP. The crystals were isolated, transferred into a glovebox, and then washed with DMF (6 × 50 mL, each wash 12 h at 393 K), exchanged with methanol (6 × 50 mL, each wash 12 h at 343 K), and activated at 453 K for 24 h to give 20 mg of activated Co-BDTriP (60% yield). Anal. calcd for Co3[(Co4Cl)3(BDTriP)8]2·17DMF (C259H231Cl6Co27N145O17): C 41.75, ; H, 3.13; N, 27.26. Found: C, 42.94; H, 3.15; N, 27.35.

Low-Pressure Gas Adsorption Measurements

For all gas adsorption measurements, 50–100 mg of sample was transferred to a preweighed glass sample tube under an atmosphere of nitrogen and capped with a Transeal. Samples were then transferred to a Micromeritics ASAP 2020 gas adsorption analyzer and heated under dynamic vacuum until the outgas rate at the degassing temperature was <2 μbar/min and were subsequently weighed to determine the mass of sample. Adsorption isotherms for the uptake of O2 at 195 K were measured using a dry ice/isopropanol cold bath. Temperatures between 195 and 273 K were maintained using a Julabo FT902 immersion cooler.

Isotherm Fitting

Adsorption isotherms for O2 and N2 in Co-BTTri and Co-BDTriP were fit with a multisite Langmuir equation (eq 1), where n is the total amount adsorbed in mmol/g, P is the pressure in bar, nsat,I is the saturation capacity in mmol/g, and bi is the Langmuir parameter in bar–1. While all isotherm data for Co-BTTri could be adequately fit by a dual-site Langmuir equation, the O2 data for Co-BDTriP required at least a quadruple-site equation due to the mixture of coordination environments for the metal centers.

graphic file with name ja-2016-03680b_m001.jpg 1
graphic file with name ja-2016-03680b_m002.jpg 2

The Langmuir parameter can be expressed using eq 2, where Si is the site-specific molar entropy of adsorption in J/mol·K, Ei is the site-specific binding energy in kJ/mol, R is the gas constant in J/mol·K, and T is the temperature in K. The variable temperature isotherms for N2 and O2 were each fit simultaneously with a single set of parameters.

Isosteric Heat of Adsorption Calculations

Using the Langmuir fits, the isosteric heat of adsorption, Qst, can be calculated as a function of the total amount of gas adsorbed, n, by using the integrated form of the Clausius–Clapeyron equation (eq 3):

graphic file with name ja-2016-03680b_m003.jpg 3

For example, the O2 Langmuir fits for Co-BTTri were used to obtain the exact pressures that correspond to specific loadings at 195, 213, and 223 K. This was done at loading intervals of 0.1 mmol/g. At each loading, the slope of ln(P) versus 1/T was calculated to obtain the isosteric heat.

Ideal Adsorbed Solution Theory Calculations

Ideal adsorbed solution theory (IAST)15 was used to predict mixed gas behavior (e.g., 0.21 bar O2, 0.79 bar N2) from single-component adsorption isotherms. Plots showing IAST selectivities as a function of temperature were calculated using the Langmuir fits for O2 and N2 in Co-BTTri and Co-BDTriP. The selectivity factor, S, is defined according to eq 4, where ni is the amount adsorbed for each component as determined from IAST and xi is the mole fraction of each component in the gas phase at equilibrium.

graphic file with name ja-2016-03680b_m004.jpg 4

Single Crystal X-ray Diffraction

For all solvated structures, X-ray diffraction analyses were performed on single crystals coated with Paratone-N oil and mounted on Kapton or MiTeGen loops. For activated and gas-dosed structures, a single crystal was epoxied onto a thin glass fiber and carefully inserted into a 1.0 mm borosilicate capillary. The capillary was then attached to a Micromeritics ASAP 2020 instrument via a custom designed gas cell, degassed at a specified temperature using a sand bath, and then dosed with 400 mbar of a specific gas (He or O2). After dosing, the capillary was flame-sealed. X-ray data for all Co-BTTri samples were collected at Beamline 11.3.1 at the Advanced Light Source, Lawrence Berkeley National Laboratory using synchrotron radiation (λ = 0.7749 or 0.8856 Å) and a Bruker PHOTON100 CMOS diffractometer equipped with a Bruker AXS APEX II CCD detector. X-ray data for the Co-BDTriP samples were collected using a Bruker APEX-II QUAZAR diffractometer (Mo–Kα, λ = 0.71073 Å) equipped with a Bruker APEX II detector. For more details on treatment of X-ray data, please see the Supporting Information.

Magnetic Susceptibility

Magnetic susceptibility measurements were performed on Co-BTTri and DMF-solvated Co-BTTri using a Quantum Design MPMS2 SQUID magnetometer. DC magnetic susceptibility measurements were collected in the temperature range 2–300 K under applied magnetic fields of 0.1, 0.5, and 1 T. Diamagnetic corrections were applied to the data using Pascal’s constants. For the activated Co-BTTri sample, data in the temperature range of 50–300 K were simulated using the software program PHI using the simplex method.16 For more details on sample preparation and data treatment, please see the Supporting Information.

Quantum Chemical Calculations

Two different cluster models were used in this study. The first was crafted from the X-ray crystal structures of the activated and O2-bound Co-BTTri compounds. The [Co4Cl(Tri)8]1– models (HTri =1,2,3-triazole) were saturated with H atoms to keep the correct total charge. Geometry optimizations were performed where the position of H atoms was relaxed, while the key atoms (Co, Cl, N) were kept fixed. The amount of charge transferred from Co to O2 and the magnetic exchange coupling constants were computed. These properties directly depend on the geometry, and for that reason the experimental bond distances and angles of Co, Cl, and triazolate were employed. These calculations were performed by means of density functional theory (DFT) and multiconfigurational wave function theory. All cluster DFT calculations were performed with the M0617 functional as implemented in the Gaussian 0918 program package and the def2-TZVP all-electron basis sets.19

Multiconfigurational calculations with the complete active space self-consistent field20 (CASSCF) method, and its extension through second-order perturbation theory21 (CASPT2), were performed on both activated and O2-bound complexes. A minimal active space composed of four electrons in the four 3dz2 orbitals (abbreviated as CAS(4,4)) was used for the calculation of the exchange coupling constants J and J′. A spin ladder of one quintet, three triplets and one singlet states was formed by considering the spin couplings of four S = 1/2 centers. CASPT2(4,4) energies were used for the calculation of the J and J′ constants. For an in-depth understanding of the local properties of one, noncoupled Co center, CASSCF/CASPT2 calculations were performed on a monocobalt model, i.e., three out of four CoII centers were substituted by closed-shell MgII centers. A CAS(9,11) composed of the five 3d orbitals of Co, the five orbitals of the second d-shell of Co, and the bonding component between the 3dx2–y2 orbital and four 2p orbitals of the Co-coordinated N atoms was used for the activated node. For the Co–O2 node, a CAS(11,13) was employed, which included the same orbitals of CAS(9,11) augmented with the two singly occupied π* orbitals of O2. The triple-ζ quality ANO-RCC-VTZP basis set was used for Co and O atoms, a double-ζ quality ANO-RCC-VDZP basis set for the atoms forming the first coordination sphere of Co, and a minimal ANO-RCC-MB basis set for all other atoms. All multiconfigurational calculations were performed using the MOLCAS 8.0 program package.22

The second cluster model was crafted from the Co-BTTri structure optimized with periodic DFT. The effect of the countercation was considered for the periodic DFT geometry optimizations of the activated Co-BTTri material. The negative charge of the framework was balanced with protons placed at the noncoordinated N atoms of the triazolate group. This approach is similar to the work of Poloni et al.23 in which the M-BTT family of materials was optimized using periodic DFT with protonated frameworks. The pyrazolate group of the BTP3– ligand possesses no uncoordinated N atoms, and therefore periodic DFT geometry optimizations were not performed on the Co-BTP structure. We also considered cluster models of the isostructural Co-BTT and Co-BTP systems to investigate the effect of the different ligands (BTT3–, BTTri3–, BTP3–) on the Co–O2 binding. Three out of four CoII centers were substituted by closed-shell MgII centers. The positions of the modified atoms in the three systems, the Co and its first coordination sphere, and the O2 molecule bound to Co were relaxed at the M06/def2-TZVP level of theory.

All periodic DFT calculations were performed with the Vienna Ab Initio Simulation Package (VASP) version 5.3.5.24,25 The Perdew–Burke–Ernzerhof (PBE) gradient-corrected, exchange–correlation functional,26 combined with Grimme’s D3 dispersion correction (PBE-D3),27 was used for all periodic calculations. The electronic self-consistency loop was converged within 10–5 eV, and the ionic positions and lattice constants were fully relaxed until forces were converged within 0.05 eV/Å. Finally, a plane wave energy cutoff of 400 eV was used, while the Brillouin zone was sampled at the Gamma point only.

Results and Discussion

Synthesis of Co-BTTri

Solvated Co-BTTri, or Co3[(Co4Cl)3(BTTri)8]2·58DMF, can be readily synthesized under air-free conditions through the reaction of H3BTTri, CoCl2, and dimethylformamidium trifluoromethanesulfonate in a mixture of DMF and methanol at 393 K. The powder X-ray diffraction pattern of this product (see Figure S1) is in good agreement with a family of cubic, sodalite-type frameworks whose general structure consists of square [M4Cl]7+ clusters linked by tritopic bridging ligands to form an overall anionic framework (Figure 1). To maintain charge balance, there are three extra-framework Co2+ cations for every 24 framework cobalt centers. In solvated Co-BTTri, the framework metal cations are ligated by four equatorial triazolates, one chloride anion, and a solvent molecule. The axial solvent molecule can be removed by heating to 423 K under dynamic vacuum, leading to a porous material with coordinatively unsaturated cobalt(II) centers and a Brunauer–Emmett–Teller (BET) surface area of 1595(4) m2/g (Langmuir surface area of 1853(7) m2/g). Even after activation, elemental and infrared analyses indicate that residual DMF remains within the material, the majority of which is likely ligated to the extra-framework cations (Figure S2). The overall formula of activated Co-BTTri is thus Co3[(Co4Cl)3(BTTri)8]2·14DMF.

Figure 1.

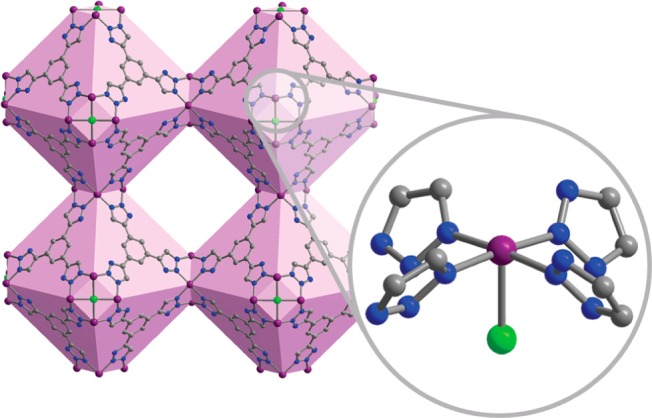
Figure 1

Open in a new tab

Structure of Co-BTTri, with the truncated octahedral cages highlighted in light purple. Expanded view: Local coordination environment of the framework cobalt(II) centers. Each metal is ligated by four equatorial triazolates and one axial chloride, while the sixth coordination site is occupied by a solvent molecule that can be removed by pulling vacuum at 423 K. Purple, gray, blue, and green spheres represent Co, C, N, and Cl atoms, respectively; H atoms are omitted for clarity.

Analogues of Co-BTTri have previously been synthesized with a variety of nitrogen heterocycle-containing linkers and transition metals. These systems include tetrazolates (M-BTT; H3BTT = 1,3,5-tri(1H-tetrazol-5-yl)benzene; M = Cr, Mn, Fe, Co, Ni, Cu, Cd),8,28 triazolates (M-BTTri; H3BTTri = 1,3,5-tri(1H-1,2,3-triazol-5-yl)benzene; M = Fe, Cu),29 and pyrazolates (M-BTP; H3BTP = 1,3,5-tri(1H-pyrazol-4-yl)benzene; M = Cu, Ni).30 The pKa of the protonated form of the bridging ligand, which increases in the order of H3BTT < H3BTTri < H3BTP, was found to be positively correlated with the chemical stability of the overall framework and inversely related to the Lewis acidity of the open metal site. Due to the high basicity and donating ability of pyrazolate linkers, the metal ions in Ni-BTP adopt low-spin configurations.30 On the other hand, it has been shown that the intermediate basicity of triazolates allows the iron(II) centers in Fe-BTTri to convert between high-spin and low-spin configurations, depending on the identity of the axial guest molecule.29b Intriguingly, these examples suggest that this structure type should be able to accommodate other low-spin metal ions, such as low-spin cobalt(III).

Adsorption of O2 and N2 in Co-BTTri

Initial low-temperature gas adsorption measurements indicated that the cobalt(II) centers in Co-BTTri interact much more strongly with O2 than with N2. At 195 K, the O2 loading rapidly rises to 3.3 mmol/g at 0.21 bar and reaches a maximum of 4.8 mmol/g at 1 bar, while the N2 isotherm is much flatter, achieving only 2.0 mmol/g at 1 bar (Figure 2). To further quantify the gas adsorption properties of Co-BTTri, O2 and N2 isotherms were collected at three different temperatures between 195 and 223 K (Figure S3). Each set of three isotherms was simultaneously modeled by a dual-site Langmuir equation, and isosteric heats of adsorption, as well as IAST15 selectivities, were then calculated from these fits (Figures S4 and S5). At low loadings, the isosteric heat (Qst) of O2 adsorption is −34(1) kJ/mol, which turns over near 2.8 mmol/g and subsequently decreases to −5(1) kJ/mol (Figure S4). The large isosteric heat at low loadings is due to interactions between O2 and the coordinatively unsaturated cobalt(II) centers, while the lower isosteric heat at higher loadings is a result of weak physisorption to the framework surface. The amount of strongly bound O2, as determined from the inflection point in the Qst plot, corresponds to roughly 0.85 per framework cobalt center, suggesting the formation of a 1:1 cobalt-dioxygen adduct. In comparison, the framework interaction with N2 is significantly weaker, with an isosteric heat that is relatively constant at −12(1) kJ/mol (see Figure S4).

Figure 2.

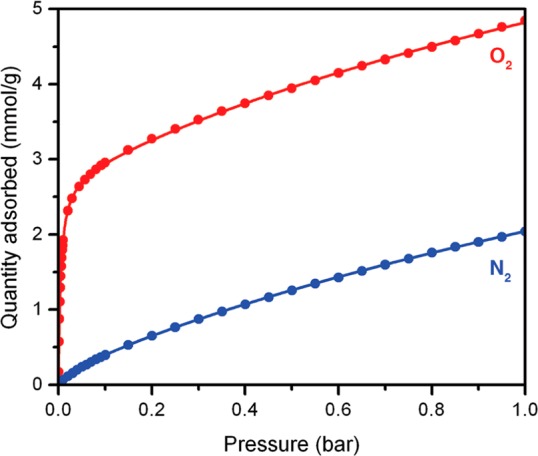
Figure 2

Open in a new tab

Adsorption isotherms for the uptake of O2 and N2 in Co-BTTri at 195 K. The filled circles and solid lines represent experimental data and corresponding dual-site Langmuir fits, respectively.

We subsequently employed IAST to model mixed-gas behavior and predict the purity of O2 gas that can be achieved from air using Co-BTTri. The resulting selectivities, calculated for a mixture of 0.21 bar O2 and 0.79 bar N2, reach 41 at 195 K and gradually drop to 13 by 243 K (see Figure S5). These values correspond to O2 purities of 92% and 77%, respectively. While lower than Cr3(btc)2 and Cr-BTT, these selectivities are significantly higher than Fe2(dobdc), which reaches a maximum selectivity of only 11 at 201 K.4d Notably, the higher O2/N2 selectivities displayed by Co-BTTri are not the result of a particularly strong interaction with O2, as previously reported iron and chromium frameworks exhibit much larger O2 isosteric heats. Rather, the selectivities are due to the combination of moderate O2 affinities coupled with exceptionally weak N2 binding. Indeed, the isosteric heat of N2 adsorption in Co-BTTri is nearly three times lower in magnitude than that of Fe2(dobdc) (Qst = −12(1) versus −35 kJ/mol). This distinction is important, because while large O2 isosteric heats often lead to high selectivity, they also result in punitive regeneration energies and highly exothermic adsorption processes that can, quite literally, spark framework decomposition. For example, Fe2(dobdc), Cr3(btc)2, and Cr-BTT have all been shown to lose crystallinity and capacity if the O2 adsorption temperature and/or adsorption rate are not carefully regulated. As a result of this strong interaction and corresponding sensitivity, these materials cannot be easily handled in air without significant reductions in their gas adsorption properties, hindering their utilization in practical processes. On the other hand, materials such as Co-BTTri, which exhibit weaker interactions with O2 and also significantly more robust framework architectures, can be regenerated under mild conditions and are much more likely to be stable over many adsorption/desorption cycles.

To illustrate this concept, we performed multiple O2 adsorption/desorption cycles at 195 K/323 K and 0.21 bar to investigate the reversibility of O2 binding in Co-BTTri. Gratifyingly, no change in O2 uptake, crystallinity, or surface area was observed after 10 cycles (Figure 3). In addition, the framework can be exposed to room temperature air at 90% relative humidity for 24 h, reactivated at 423 K, and still exhibit no loss in adsorption properties. This stability greatly exceeds that of iron- and chromium-based metal–organic frameworks. Co-BTTri also surpasses the performance of many cobalt-based molecular complexes, which are susceptible to irreversible ligand and metal oxidation (the latter occurring via predominantly bimolecular pathways).31 This remarkable stability, combined with a high O2/N2 selectivity, makes Co-BTTri an excellent candidate adsorbent for air purification applications.

Figure 3.

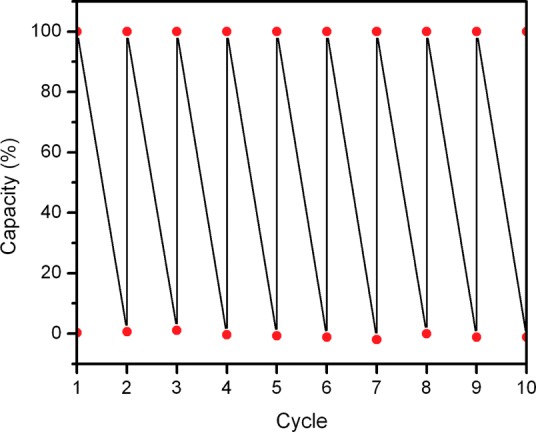
Figure 3

Open in a new tab

Uptake and release of O2 in Co-BTTri. Adsorption was carried out at 195 K and 0.21 bar, while desorption was performed by quickly heating the sample to 323 K for 5 min. Note that before the last cycle, the sample was exposed to humid air (90% relative humidity) for 24 h and then reactivated at 423 K for 6 h.

Structural Characterization of Co-BTTri

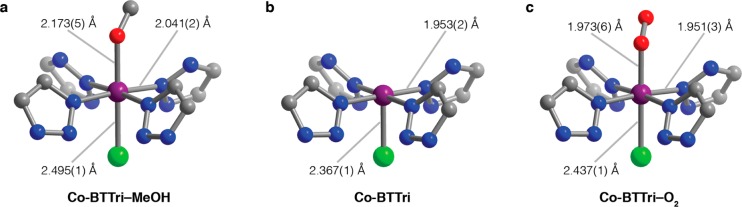
In order to structurally probe the Co–O2 interaction in Co-BTTri, pink crystals of Co-BTTri were grown at 423 K inside sealed tubes. Methanol-solvated Co-BTTri (Co-BTTri–MeOH) adopts the primitive space group Pm3̅m, much like previously reported frameworks of this structure type. Analysis of the bond lengths in the solvated structure reveals Co–N bond distances of 2.041(2) Å, which are slightly shorter than bond lengths observed in the tetrazolate congeners of this framework (2.06–2.32 Å) (Figure 4a).8,28 We note that the extra-framework cobalt centers, which are likely ligated by solvent, could not be located in Co-BTTri–MeOH.

Figure 4.

Figure 4

Open in a new tab

Structural changes observed in Co-BTTri upon (a) methanol solvation, (b) desolvation, and (c) O2 binding. Purple, gray, blue, and green spheres represent Co, C, N, and Cl atoms, respectively; H atoms are omitted for clarity. Note that in the structure of Co-BTTri–O2 the bound O2 units are disordered over two positions with slightly differing tilt angles, only one of which is depicted here.

To obtain a desolvated structure, a single crystal was heated to 453 K under dynamic vacuum inside a glass capillary and then subsequently flame-sealed under 400 mbar of helium. Note that roughly 38(2)% of the cobalt centers remain solvated in the activated single crystal, as determined by X-ray crystallography. Because gas adsorption experiments revealed that at least 85% of the framework sites are accessible to O2, this incomplete activation is likely a reflection of imperfect capillary sealing and the sensitivity of a single crystal to adventitious water.

Surprisingly, upon heat and vacuum treatment, the crystal structure distorts from Pm3̅m to face-centered Fm3̅c symmetry. In this lower symmetry space group, the opposing [Co4Cl]7+ squares of each truncated octahedral cage are slightly twisted with respect to each other (Figure S7a). In addition, the triazolate rings are ordered, such that the noncoordinating nitrogen atoms of neighboring heterocycles are pointed away from each other (Figure 4b). However, there is almost certainly a small amount of disorder in the triazolate orientations, as residual electron density corresponding to the extra-framework Co2+ cations was located in between adjacent heterocycles (Figure S7c). Presumably, as the crystal is activated, the extra-framework cations lose some of the coordinated solvent, migrate, and bridge adjacent triazolate nitrogen atoms.

In addition to the symmetry reduction, upon activation the Co–N and Co–Cl bond lengths within Co-BTTri each decrease by ∼0.1 Å, to 1.953(2) Å and 2.367(1) Å, respectively (Figure 4b). While it was not possible to definitively assign a spin state using the Co–N bond distances in Co-BTTri–MeOH, the much shorter bond lengths observed in the activated material strongly suggest the presence of low-spin cobalt(II).

To gain insight into the Co–O2 interaction within the activated material, an activated crystal was dosed with 400 mbar of O2 and cooled to 100 K. The Fm3̅c symmetry is maintained, and O2 was found to coordinate to each metal in an end-on fashion with a Co–O2 bond length of 1.973(6) Å. This distance is somewhat longer than previously reported octahedral cobalt–superoxide complexes, which possess Co–O2 bond lengths between 1.86 and 1.90 Å.11,32 In Co-BTTri, the O2 is further disordered over two positions, with bent Co–O–O angles of 122(1)° and 130(2)° and occupancies of 42(3)% and 58(3)%, respectively (Figure 4c). Due to this disorder, the O–O bond length could not be accurately determined and was constrained to values near 1.21 Å. The relatively long Co–O separation, combined with the essentially unchanged Co–N bond lengths, suggests partial electron transfer to O2 rather than full reduction to superoxide. This hypothesis is fully consistent with the moderate O2 binding energies observed in the gas adsorption studies and indicates only very slight activation of the O–O bond.

Spin-State Characterization of Co-BTTri

To further probe the cobalt(II) spin state in these materials, DC magnetic susceptibility measurements were carried out on both activated and DMF-solvated Co-BTTri (Co-BTTri–DMF) samples under an applied magnetic field of 1 T. As some solvent loss was observed during the preparation of methanol-soaked Co-BTTri samples, DMF was used instead to solvate Co-BTTri due to its lower volatility.

The Co–N bond lengths observed in the activated crystal structure suggest that the 24 CoII centers per formula unit are low-spin (S = 1/2), while the three charge-balancing extra-framework CoII centers are likely high-spin (S = 3/2). The expected χMT value for such a spin system, if all metal centers are magnetically noninteracting with g = 2, is 14.63 emu·K/mol. As shown in Figure 5 (red circles), the χMT value observed at 300 K and Hdc = 1 T for Co-BTTri is notably higher at 18.99 emu·K/mol. This value can be rationalized in part by considering that the g values for high-spin cobalt(II) complexes are typically substantially higher than 2.33 Furthermore, the linear shape of the susceptibility curve suggests a temperature-independent paramagnetism contribution to the susceptibility, which would also contribute to a larger than predicted room temperature χMT value.

Figure 5.

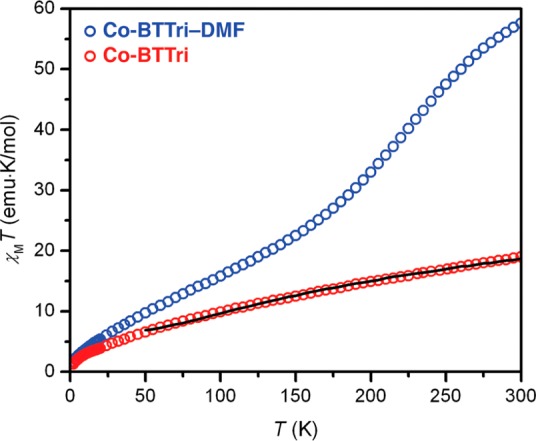
Figure 5

Open in a new tab

Variable-temperature magnetic susceptibility data collected under an applied field of 1 T for samples of Co-BTTri solvated in DMF (blue circles) and activated Co-BTTri (red circles). The black line represents a fit to the data using the Hamiltonian and parameters described in the text.

A fit to the magnetic susceptibility data for activated Co-BTTri was obtained using the Hamiltonian in eq 5 in order to further understand the magnetic exchange interactions within the [Co4Cl]7+ clusters. The magnetic data were corrected by subtracting the expected contributions from the extra-framework CoII centers and should thus reflect the magnetic behavior of a single [Co4Cl]7+ square (see Supporting Information for details).

graphic file with name ja-2016-03680b_m005.jpg 5

In eq 5, J reflects the magnetic coupling between two low-spin (S = 1/2) CoII centers through a triazolate bridge (i.e., the coupling between nearest-neighbor metals) and J′ reflects the magnetic coupling between two low-spin (S = 1/2) CoII centers across the μ4-chloride bridge. In addition, an unfixed temperature-independent paramagnetism parameter, χTIP, was included during fitting. This Hamiltonian provided a good fit to the data in the temperature range 50–300 K using the parameters J = −10 cm–1, J′ = −98 cm–1, and χTIP = 0.0038 emu/mol. The large negative value of J′ is not unreasonable, as halide-bridged low-spin CoII centers have been previously shown to exhibit large antiferromagnetic coupling.34 It was not possible to fit magnetic data below 50 K, possibly due to the presence of additional magnetic coupling pathways that are favored at lower temperatures. The fitting parameters obtained should be considered as approximate, since neither zero-field splitting nor spin–orbit coupling of the CoII centers were included, and only the primary magnetic coupling pathways have been modeled. Mixing of the S = 1/2 state of the CoII centers with a high-spin excited state is also possible and may be reflected in the large value of χTIP extracted from fitting.

Compared to the activated sample, in which the framework cations maintain a low-spin configuration over the entire observed temperature range, Co-BTTri–DMF shows markedly different magnetic behavior that is suggestive of a broad spin-crossover transition (Figure 5, blue circles). At 300 K the χMT product is 57.64 emu·K/mol, which is larger than the 50.65 emu·K/mol anticipated for 27 noninteracting S = 3/2 centers with g = 2. Again, this larger value is expected, given that the magnetic moment for octahedral high-spin cobalt(II) centers is generally higher than the spin-only value. The χMT value smoothly decreases with temperature until it approaches a value consistent with 24 noninteracting S = 1/2 centers and three noninteracting S = 3/2 centers at about 90 K. Further decreases in the χMT product below 90 K are attributed to antiferromagnetic coupling between CoII centers. The spin-crossover behavior of the CoII centers within the [Co4Cl]7+ squares is likely solvent dependent,35 although solvents aside from DMF were not investigated.

Electronic Structure of Co-BTTri and Co-BTTri–O2

The extent of charge transfer in metal–O2 adducts is typically probed by vibrational spectroscopy via the O–O stretching frequency.36 However, due to the weak binding of O2 in this system, it was not possible to identify this stretch in the infrared spectra collected for Co-BTTri–O2 at room temperature. For this reason, quantum chemical calculations were performed to gain insight into the electronic structures of both Co-BTTri and Co-BTTri–O2. These calculations were carried out on a simplified model of the [Co4Cl]7+ building unit, in which each ligand was truncated into a simple triazolate ring (Figure 6). Geometry optimizations were performed keeping the Co, Cl, and N atoms fixed at coordinates experimentally observed in the single crystal structures (for more details, see the Experimental Section above).

Figure 6.

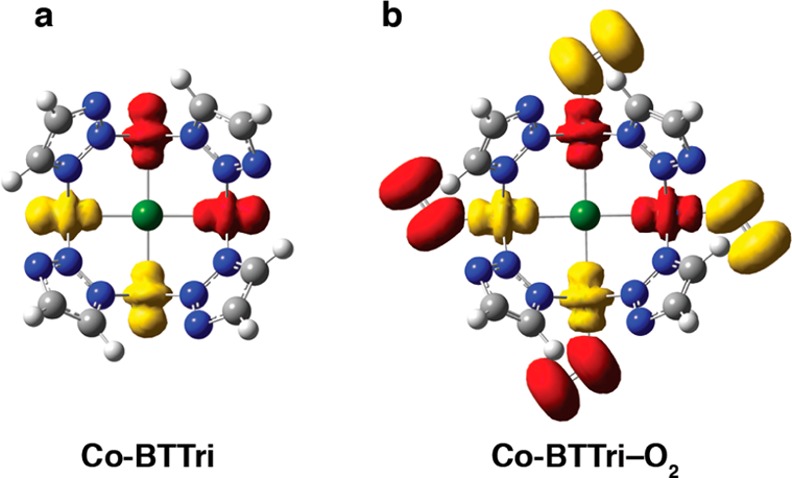
Figure 6

Open in a new tab

Spin density of (a) the activated [Co4Cl(Tri)8]1– node and (b) the [Co4(O2)4Cl(Tri)8]1– node. The positions of the Co, N, and Cl atoms are fixed according to the experimental crystal structures. Red density corresponds to alpha electron excess, yellow density to beta electron excess (isosurface: 0.01 au). Gray, blue, green, and white spheres represent C, N, Cl, and H atoms, respectively.

For the activated framework, both DFT, CASSCF, and CASPT2 methods predict an open-shell singlet for the ground state of the [Co4Cl]7+ node, consistent with experimental measurements. The spin density of the broken symmetry singlet (Figure 6a) shows antiferromagnetic coupling between the four metal centers. Each cobalt(II) center has an unpaired electron in the 3dz2 orbital, and these are antiferromagnetically coupled across the μ4-chloride bridge. The energy levels obtained from the Hamiltonian shown in eq 5 are given as

graphic file with name ja-2016-03680b_m006.jpg 6

Here, S1 is the spin on each of the metal centers, S13 and S24 are intermediate spins with values of 1 or 0, and S is the total spin of the Co4 node. Solving eq 6 using the CASPT2(4,4) energies for S = 2, 1, and 0 gives the ratio J/J′ = 0.1, which is in agreement with the exchange coupling constants obtained from fitting the magnetic susceptibility data.

The character of the Co–O2 bonding interaction was subsequently examined by means of electronic structure theory. As in the case of the activated node, the open-shell singlet state was found to be the ground state of the [Co4(O2)4Cl]7+ node (Figure 6b). The spin density on each CoII center suggests that little oxidation occurs upon O2 binding. The extent of electron transfer from cobalt to dioxygen is about 0.25 electrons (M06 functional), and the partial occupation numbers of the CASSCF multiconfigurational wave function verified this weak charge transfer (0.20 electrons). Therefore, the Co–O2 adduct in Co-BTTri has more Co(II)–dioxygen character than Co(III)–superoxo (O2–) character. This conclusion is in agreement with previous EPR measurements on molecular 1:1 cobalt–dioxygen complexes, which showed that the extent of electron transfer to O2 can vary between 0 and 1 electrons, and depends heavily upon the ligand field.37 Finally, the DFT-calculated enthalpy of O2 adsorption is −32.8 kJ/mol (M06), within error of the experimental value of −34(1) kJ/mol.

Synthesis of Co-BDTriP

While Co-BTTri represents the first cobalt-based metal–organic framework to show appreciable O2 binding at pressures below 1 bar and demonstrates excellent air stability, its isosteric heat of −34(1) kJ/mol is relatively low. For comparison, enthalpies of oxygenation for cobalt(II) molecular complexes typically range between −40 and −75 kJ/mol.11 As a result of the low binding energy exhibited by Co-BTTri, low O2 adsorption and poor selectivity are observed for this material at room temperature. In principle, however, it should be possible to tune the ligand environment around the metal centers in Co-BTTri to facilitate a greater O2 uptake and greater selectivity at higher temperatures.

Toward this end, we sought to synthesize an analogous framework with H3BTP, a tritopic linker containing only pyrazole moieties. However, various synthetic conditions led only to the formation of alternate phases featuring tetrahedral cobalt centers. All attempts to access a mixed-ligand framework, wherein H3BTP and H3BTTri were added simultaneously in various ratios, led to poorly crystalline material with low surface areas and poor O2 uptake. We succeeded, however, in synthesizing the new ligand H3BDTriP (5,5′-(5-(1H-pyrazol-4-yl)-1,3-phenylene)bis(1H-1,2,3-triazole)), wherein one of the triazole moieties is replaced with a pyrazole (Figure 7a). Gratifyingly, single crystals of Co-BDTriP can be grown following similar procedures as Co-BTTri, and desolvation of the material under vacuum at 453 K leads to a porous material with a BET surface area of 1332(4) m2/g (Langmuir surface area = 1517(2) m2/g). Note that the lower surface area is likely due to a small amount of ligand or solvent remaining in the pores, which could not be removed by high-temperature DMF and methanol washes or prolonged evacuation.

Figure 7.

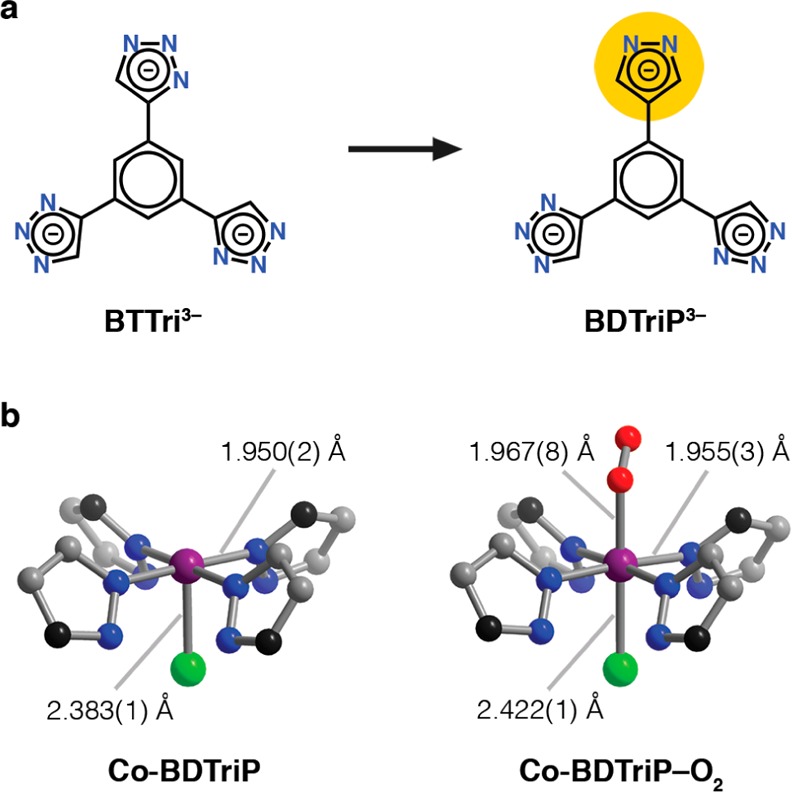
Figure 7

Open in a new tab

(a) Structure of the ligands used in this work, BTTri3– and BDTriP3–. In BDTriP3–, one of the bridging triazolates is replaced with a more electron-donating pyrazolate. (b) Structural changes observed for Co-BDTriP upon O2 binding. Purple, gray, blue, and green spheres represent Co, C, N, and Cl atoms, respectively; due to ligand disorder, the black spheres represent either C or N atoms; H atoms are omitted for clarity. Note that in the structure of Co-BBDTriP–O2, the bound O2 units are disordered over two positions, which are related by a mirror plane.

Crystals of Co-BDTriP form in the space group Pm3̅m, with all heterocycle moieties randomly distributed. The orientations of the triazolate groups are similarly disordered. The compound is thus expected to contain a statistical distribution of five distinct cobalt centers ligated by a combination of triazolate and pyrazolate rings. Because of this disorder, the metal–ligand bond lengths in this structure are the weighted average of five different coordination environments and may not necessarily reflect any individual cobalt center. Finally, as with Co-BTTri, the extra-framework cation in Co-BDTriP was found to reside in between the nitrogen atoms of two neighboring triazolate ligands.

Overall, the solvated, activated, and O2-dosed structures of Co-BDTriP closely resemble those of Co-BTTri (Figure 7b). This similarity is not unexpected, due to the only minor change in the ligand composition. The Co–N and Co–Cl bond lengths in methanol-solvated Co-BDTriP are very slightly shorter than those in Co-BTTri–MeOH (1.983(3) and 2.451(1) Å, respectively). As was the case with Co-BTTri, a completely activated crystal structure could not be obtained for Co-BDTriP due to difficulties in single-crystal sample preparation. However, in the 60% desolvated material the Co–N and Co–Cl distances significantly contract to 1.950(2) and 2.383(1) Å. Finally, the Co–O2 distance in Co-BDTriP is within error to that found in Co-BTTri (1.967(8) Å), with a similarly bent Co–O–O angle of 128(1)°. Note that the O2 is disordered over two positions related by a mirror plane.

Adsorption of O2 and N2 in Co-BDTriP

While the O2-dosed crystal structures of Co-BDTriP and Co-BTTri are quite similar, a qualitative comparison of the steepness of their 195 K O2 isotherms indicates that Co-BDTriP has a much higher affinity for O2 (Figure 8). To quantify this difference, O2 and N2 isotherms were measured at three different temperatures and fit to a Langmuir model to obtain isosteric heats of adsorption (Figure S8). Because of the asymmetry of the BDTriP3– linker and the presence of many different metal coordination environments within the framework, at least a quadruple-site Langmuir equation was needed to accurately fit the O2 isotherms for Co-BDTriP.

Figure 8.

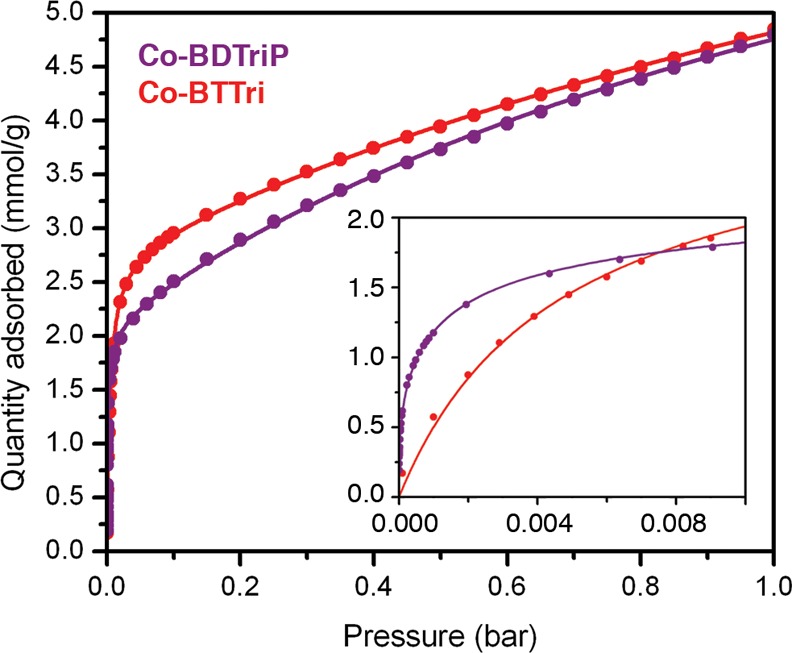
Figure 8

Open in a new tab

Comparison of O2 adsorption isotherms collected for Co-BTTri (red) and Co-BDTriP (purple) at 195 K. The filled circles and solid lines represent experimental data and their corresponding Langmuir fits, respectively. Inset: Low-pressure region of the 195 K O2 isotherms. The Co-BDTriP–O2 uptake is significantly steeper at these low pressures than Co-BTTri.

From chemical intuition, one would expect a fraction of the binding sites in Co-BDTriP to be significantly stronger than Co-BTTri, with the remainder possessing either moderately higher or similar binding energies. Indeed, roughly 12% of the accessible open metal sites have an extremely high affinity for O2, with an isosteric heat of −47(1) kJ/mol (Figure 9). This strong binding at low loadings is attributed to interactions with cobalt centers bound by three or more pyrazolate ligands, which, in a purely statistical mixture, should account for 11% of the total metal sites. The isosteric heat then gradually decreases in magnitude to −32(1) kJ/mol, a value very close to that determined for Co-BTTri, before turning over at 2.1 mmol/g (Figure 9). This saturation capacity is lower than observed for Co-BTTri (2.8 mmol/g) and is likely due to incomplete activation of the framework or unreacted ligand in the pores, which is also consistent with the comparatively lower surface area of Co-BDTriP. In addition to an increased O2 affinity at low loadings, Co-BDTriP also exhibits a lower N2 isosteric heat that gradually plateaus to −9(1) kJ/mol (Figure 9). This decrease is expected, given the weaker Lewis acidity of pyrazolate-bound metal centers, and should also contribute to a higher O2/N2 selectivity.

Figure 9.

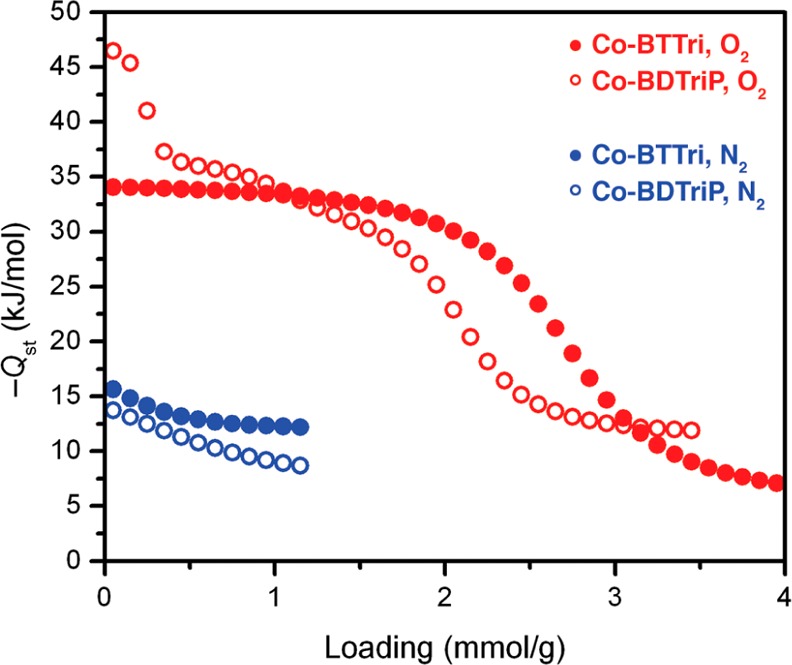
Figure 9

Open in a new tab

Comparison of O2 and N2 isosteric heats for Co-BTTri (filled red and blue circles, respectively) and Co-BDTriP (open red and blue circles, respectively).

Although the chemical change between Co-BTTri and Co-BDTriP is modest, the IAST selectivities for Co-BDTriP are dramatically improved due to the combination of higher O2 and lower N2 binding energies observed for this framework (Figure 10). Indeed, the IAST selectivity more than doubles to 105 (97% purity) at 195 K and drops only to 40 at 243 K (91% purity). Notably, even with these higher O2 binding affinities, no loss in stability is observed, and Co-BDTriP can also be cycled multiple times without any loss in adsorption capacity (Figure S10).

Figure 10.

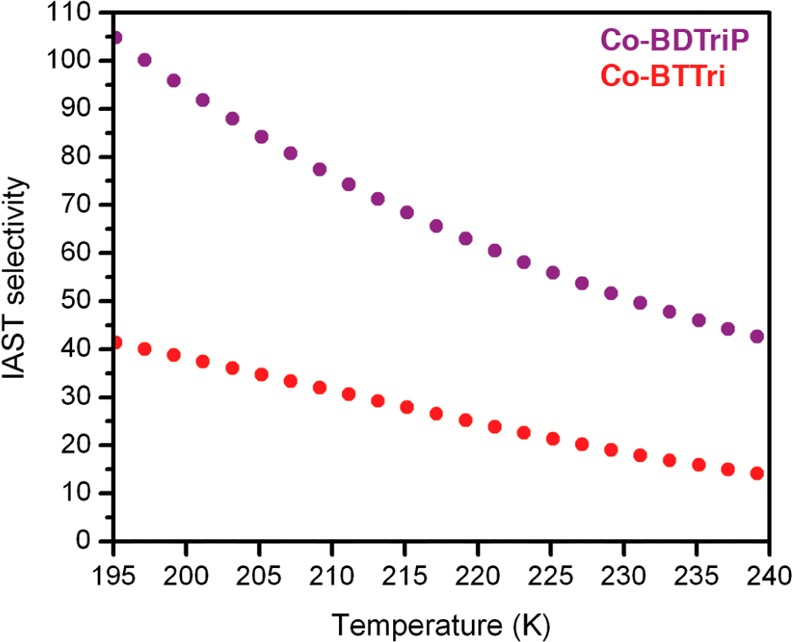
Figure 10

Open in a new tab

IAST selectivities for Co-BTTri and Co-BDTriP calculated for a mixture of 0.21 bar O2 and 0.79 bar N2. Co-BDTriP is significantly more selective at all temperatures between 195 and 240 K.

In addition to selectivity and stability, another important metric used to evaluate adsorbents is their working capacity, or the amount of gas that can be recovered during one adsorption and desorption cycle. Regeneration of commercial, zeolite-based air separation units is typically accomplished through vacuum swing adsorption (VSA).9 In this scenario, the adsorbent bed is held at a constant temperature and cycled between ambient pressure and a lower desorption pressure, PD. For a VSA air separation process, the working capacities can be roughly estimated from single component O2 isotherms as the difference between the quantity of O2 adsorbed at 0.21 bar and the quantity adsorbed at PD. Depending on the shape and steepness of the O2 isotherm, this value can be much less than the total O2 uptake of a material at 0.21 bar.

For PD = 0.05 bar, the working capacities of Co-BTTri and Co-BDTriP are both maximized at a bed temperature of ∼230 K. At this temperature the calculated O2 capacities of Co-BTTri and Co-BDTriP are 1.2 mmol/g and 0.6 mmol/g, respectively, while the resulting O2 purity is 83% and 93%, respectively (see Figure S11). Interestingly, although Fe2(dobdc) exhibits a significantly higher total O2 uptake than Co-BTTri at 211 K (5.8 versus 3.0 mmol/g at 0.21 bar), its working capacity is only slightly higher, at 1.4 mmol/g.4d Because of its higher working capacity, Co-BTTri may be better suited for processes where large volumes of O2 are needed, while Co-BDTriP may be preferable if high O2 purities are important. Although significantly higher working capacities can be achieved in both of these materials with lower desorption pressures, at a certain point the cost of achieving deeper vacuum levels will outweigh the benefits of increased capacity. Alternative regeneration conditions, such as temperature swing adsorption or a combined temperature and pressure swing process, can also be envisioned and might lead to greater O2 recovery.

Effect of Ligand Field on O2 Adducts of Cobalt-Azolate Frameworks

While the experimental results above demonstrate that a small change in the organic linker can lead to large increases in the O2 heat of adsorption, more detailed characterization of the Co–O2 adducts in Co-BDTriP is hindered by its inherent structural disorder. A deeper understanding of the effect of ligand field on Co–O2 interactions in metal–organic frameworks is desirable, however, as it may lead to the identification of new synthetic targets for O2/N2 separation applications. Thus, O2 binding in the isostructural series Co-BTT, Co-BTTri, and Co-BTP was explored systematically by computational methods to probe the relationship between equatorial ligand field, electronic structure, and heat of adsorption.

Because experimental structures of activated Co-BTT and Co-BTP and their oxygen-bound derivatives are not available, the cluster models used for this study were carved from the Co-BTTri structure optimized by periodic DFT (see experimental methods section for more details). While this approach leads to structural parameters that are slightly different from what is experimentally observed in Co-BTTri, particularly with respect to the Co–Cl bond distances (Table 1), the trends found in this series should hold nonetheless. Table 1 summarizes the results obtained from the geometry optimizations of the three models of the nodes within Co-BTT, Co-BTTri, and Co-BTP upon binding O2. The Co–O, Co–N, and Co–Cl bond distances decrease according to the series Co-BTT > Co-BTTri > Co-BTP, while the extent of charge transfer and the strength of the Co–O2 interaction follows the opposite trend. In addition, unlike Co-BTTri, the hypothetical Co-BTP dioxygen adduct can be more accurately thought of as a Co(III)–superoxo species. Such a material, if it can be synthesized, may be intriguing for both higher temperature air separation applications as well as aerobic oxidation catalysis. Remarkably, despite the simplicity of the three models, the calculated enthalpies of O2 adsorption for the triazolate and pyrazolate clusters are in agreement with the measured O2 heats of adsorption (at low loadings) for Co-BTTri and Co-BDTriP, respectively.

Table 1. Key Bond Distances (in Å), Charge Transfer (in electrons), and O2 Enthalpies of Adsorption (in kJ/mol, M06/def2-TZVP level of theory) for the Three Cluster Models of the Co-BTT, Co-BTTri, and Co-BTP Metal–Organic Frameworks.a.

  Co-BTT Co-BTTri Co-BTP
Co–O 2.182 2.053 1.917
Co–Navg 1.954 1.924 1.904
Co–Cl 2.355 2.321 2.273
Charge transfer 0.14 0.31 0.72
ΔHads –28.6 –33.0 –47.5
Open in a new tab
a

Note that these cluster models were carved from periodic DFT-optimized structure of Co-BTTri and not from experimental data.

Conclusions and Outlook

One of the most promising aspects of metal–organic frameworks is their structural diversity and chemical tunability, both of which facilitate the rational design of materials with specifically tailored properties.38 Indeed, we have shown here how the judicious choice of both framework structure and ligand basicity results in two cobalt-based frameworks that not only exhibit exceptional oxidative stability but also display some of the highest O2/N2 selectivities reported to date. Deeper insights into the nature of the Co–O2 bond gained by electronic structure calculations reveal that tuning the ligand field changes the O2 heats of adsorption and also drastically alters the extent of electron transfer from cobalt to O2 (from ∼0.3 to 0.7 electrons). Finally, while not the focus of this work, the temperature- and solvent-dependent spin-state changes in Co-BTTri are of fundamental interest and could be of potential use in sensing applications. Future work will focus on further development of pyrazolate-containing cobalt frameworks and evaluation of such materials as catalysts for aerobic oxidation processes.

Acknowledgments

The synthetic chemistry, crystal structure determinations, and characterization of the fundamental gas adsorption properties were supported through the Center for Gas Separations Relevant to Clean Energy Technologies, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under award DE-SC0001015. The measurement and analysis of magnetic susceptibility data and the computational work were supported by the Nanoporous Materials Genome Center, funded by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences and Biosciences under award DE-FG02-12ER16362. The Minnesota Supercomputing Institute provided the computational resources for this work. Stability and adsorption/desorption cycling measurements, as well as assessments of the suitability of these materials for a practical air separation, were funded by IHI Corporation. This research used resources of the Advanced Light Source, which is supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under contract no. DE-AC02-05CH11231. This research also used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under contract no. DE-AC02-06CH11357. We thank Dr. Antonio DiPasquale and the Chexray Facility for assistance with X-ray crystallographic analysis (NIH shared Instrumentation Grant S10-RR027172). We further thank Dr. Jarad A. Mason, David Gygi, Julia Oktawiec, and Douglas Reed for helpful discussions and Dr. Zoey Herm and Rebecca Siegelman for experimental assistance. We also thank NSF for providing graduate fellowship support for D.J.X. and L.E.D. Dr. Katie R. Meihaus is acknowledged for editorial assistance.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.6b03680.

  • Crystallographic data (CIF)

  • Crystallographic data (CIF)

  • Additional experimental details, including ligand synthesis, gas sorption data and analysis (PDF)

The authors declare no competing financial interest.

Supplementary Material

ja6b03680_si_001.cif (4.8MB, cif)
ja6b03680_si_002.cif (20.4MB, cif)
ja6b03680_si_003.pdf (13MB, pdf)

References

  1. a Barreswil L. C. A. Ann. Chim. Phys. 1847, 20, 364. [Google Scholar]; b Werner A.; Mylius A. Z. Anorg. Allg. Chem. 1898, 16, 245. 10.1002/zaac.18980160133. [DOI] [Google Scholar]; c Gubelmann M. H.; Williams A. F. Struct. Bonding (Berlin) 1984, 55, 1. 10.1007/BFb0111572. [DOI] [Google Scholar]
  2. a Pecoraro V. L.; Baldwin M. J.; Gelasco A. Chem. Rev. 1994, 94, 807. 10.1021/cr00027a012. [DOI] [Google Scholar]; b Feig A. L.; Lippard S. J. Chem. Rev. 1994, 94, 759. 10.1021/cr00027a011. [DOI] [Google Scholar]; c Wallar B. J.; Lipscomb J. D. Chem. Rev. 1996, 96, 2625. 10.1021/cr9500489. [DOI] [PubMed] [Google Scholar]; d Costas M.; Mehn M. P.; Jensen M. P.; Que L. Jr. Chem. Rev. 2004, 104, 939. 10.1021/cr020628n. [DOI] [PubMed] [Google Scholar]; e Lewis E. A.; Tolman W. B. Chem. Rev. 2004, 104, 1047. 10.1021/cr020633r. [DOI] [PubMed] [Google Scholar]; f Borovik A. S. Acc. Chem. Res. 2005, 38, 54. 10.1021/ar030160q. [DOI] [PubMed] [Google Scholar]; g Groves J. T. J. Inorg. Biochem. 2006, 100, 434. 10.1016/j.jinorgbio.2006.01.012. [DOI] [PubMed] [Google Scholar]
  3. a Brégeault J. – M. Dalton Trans. 2003, 3289. 10.1039/B303073N. [DOI] [Google Scholar]; b Que L. Jr.; Tolman W. B. Nature 2008, 455, 333. 10.1038/nature07371. [DOI] [PubMed] [Google Scholar]; c Campbell A. N.; Stahl S. S. Acc. Chem. Res. 2012, 45, 851. 10.1021/ar2002045. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. a Norman J. A. T.; Pez G. P.; Roberts D. A.. Reversible Complexes for the Recovery of Dioxygen. In Oxygen Complexes and Oxygen Activation by Transition Metals; Martell A. E., Sawyer D. T., Eds.; Plenum Press: New York, 1988; pp 107–125. [Google Scholar]; b Li G. Q.; Govind R. Ind. Eng. Chem. Res. 1994, 33, 755. 10.1021/ie00028a001. [DOI] [Google Scholar]; c Murray L. J.; Dincă M.; Yano J.; Chavan S.; Bordiga S.; Brown C. M.; Long J. R. J. Am. Chem. Soc. 2010, 132, 7856. 10.1021/ja1027925. [DOI] [PubMed] [Google Scholar]; d Bloch E. D.; Murray L. J.; Queen W. L.; Chavan S.; Maximoff S. N.; Bigi J. P.; Krishna R.; Peterson V. K.; Grandjean F.; Long G. J.; Smit B.; Bordiga S.; Brown C. M.; Long J. R. J. Am. Chem. Soc. 2011, 133, 14814. 10.1021/ja205976v. [DOI] [PubMed] [Google Scholar]
  5. a Olajire A. A. Energy 2010, 35, 2610. 10.1016/j.energy.2010.02.030. [DOI] [Google Scholar]; b Sumida K.; Rogow D. L.; Mason J. A.; McDonald T. M.; Bloch E. D.; Herm Z. R.; Bae T. – H.; Long J. R. Chem. Rev. 2012, 112, 724. 10.1021/cr2003272. [DOI] [PubMed] [Google Scholar]
  6. Smith A. R.; Klosek J. Fuel Process. Technol. 2001, 70, 115. 10.1016/S0378-3820(01)00131-X. [DOI] [Google Scholar]
  7. a Li J. – R.; Kuppler R. J.; Zhou H. – C. Chem. Soc. Rev. 2009, 38, 1477. 10.1039/b802426j. [DOI] [PubMed] [Google Scholar]; b Murray L. J.; Dincă M.; Long J. R. Chem. Soc. Rev. 2009, 38, 1294. 10.1039/b802256a. [DOI] [PubMed] [Google Scholar]; c Suh M. P.; Park H. J.; Prasad T. K.; Lim D. – W. Chem. Rev. 2012, 112, 782. 10.1021/cr200274s. [DOI] [PubMed] [Google Scholar]; d Herm Z. R.; Bloch E. D.; Long J. R. Chem. Mater. 2014, 26, 323. 10.1021/cm402897c. [DOI] [Google Scholar]; e Mason J. A.; Veenstra M.; Long J. R. Chem. Sci. 2014, 5, 32. 10.1039/C3SC52633J. [DOI] [Google Scholar]; f DeCoste J. B.; Weston M. H.; Fuller P. E.; Tovar T. M.; Peterson G. W.; LeVan M. D.; Farha O. K. Angew. Chem., Int. Ed. 2014, 53, 14092. 10.1002/anie.201408464. [DOI] [PubMed] [Google Scholar]; g Barea E.; Montoro C.; Navarro J. A. R. Chem. Soc. Rev. 2014, 43, 5419. 10.1039/C3CS60475F. [DOI] [PubMed] [Google Scholar]
  8. Bloch E. D.; Queen W. L.; Hudson M. R.; Mason J. A.; Xiao D. J.; Murray L. J.; Flacau R.; Brown C. M.; Long J. R.. Angew. Chem. Int. Ed. (DOI: 10.1002/anie.201602950R1). [DOI] [PubMed] [Google Scholar]
  9. Gaffney T. R. Curr. Opin. Solid State Mater. Sci. 1996, 1, 69. 10.1016/S1359-0286(96)80013-1. [DOI] [Google Scholar]
  10. Tsumaki T. Bull. Chem. Soc. Jpn. 1938, 13, 252. 10.1246/bcsj.13.252. [DOI] [Google Scholar]
  11. Niederhoffer E. C.; Timmons J. H.; Martell A. E. Chem. Rev. 1984, 84, 137. 10.1021/cr00060a003. [DOI] [Google Scholar]
  12. Bloch E. D.; Hudson M. R.; Mason J. A.; Chavan S.; Crocellà V.; Howe J. D.; Lee K.; Dzubak A. L.; Queen W. L.; Zadrozny J. M.; Geier S. J.; Lin L. – C.; Gagliardi L.; Smit B.; Neaton J. B.; Bordiga S.; Brown C. M.; Long J. R. J. Am. Chem. Soc. 2014, 136, 10752. 10.1021/ja505318p. [DOI] [PubMed] [Google Scholar]
  13. Xiao D. J.; Bloch E. D.; Mason J. A.; Queen W. L.; Hudson M. R.; Planas N.; Borycz J.; Dzubak A. L.; Verma P.; Lee K.; Bonino F.; Crocellà V.; Yano J.; Bordiga S.; Truhlar D. G.; Gagliardi L.; Brown C. M.; Long J. R. Nat. Chem. 2014, 6, 590. 10.1038/nchem.1956. [DOI] [PubMed] [Google Scholar]
  14. Weston M. H.Metal–Organic Frameworks for Oxygen Storage and Air Separation. U.S. Patent 20150105250, April 16, 2015.
  15. Myers A. L.; Prausnitz J. M. AIChE J. 1965, 11, 121. 10.1002/aic.690110125. [DOI] [Google Scholar]
  16. Chilton N. F.; Anderson R. P.; Turner L. D.; Soncini A.; Murray K. S. J. Comput. Chem. 2013, 34, 1164. 10.1002/jcc.23234. [DOI] [PubMed] [Google Scholar]
  17. Zhao Y.; Truhlar D. G. Theor. Chem. Acc. 2008, 120, 215. 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
  18. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas Ö.; Foresman B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09, Revision D.01, Gaussian, Inc.: Wallingford, CT, 2009.
  19. a Weigend F.; Ahlrichs R. Phys. Chem. Chem. Phys. 2005, 7, 3297. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]; b Weigend F. Phys. Chem. Chem. Phys. 2006, 8, 1057. 10.1039/b515623h. [DOI] [PubMed] [Google Scholar]
  20. a Roos B. O. Adv. Chem. Phys. 1987, 69, 399. 10.1002/9780470142943.ch7. [DOI] [Google Scholar]; b Ruedenberg K.; Cheung L. M.; Elbert S. T. Int. J. Quantum Chem. 1979, 16, 1069. 10.1002/qua.560160511. [DOI] [Google Scholar]
  21. Andersson K.; Malmqvist P. – Å.; Roos B. O. J. Chem. Phys. 1992, 96, 1218. 10.1063/1.462209. [DOI] [Google Scholar]
  22. Aquilante F.; De Vico L.; Ferré N.; Ghigo G.; Malmqvist P.-Å.; Neogrády P.; Pedersen T. B.; Pitonak M.; Reiher M.; Roos B. O.; Serrano-Andrés L.; Urban M.; Veryazov V.; Lindh R. J. Comput. Chem. 2010, 31, 224. 10.1002/jcc.21318. [DOI] [PubMed] [Google Scholar]
  23. Poloni R.; Lee K.; Berger R. F.; Smit B.; Neaton J. B. J. Phys. Chem. Lett. 2014, 5, 861. 10.1021/jz500202x. [DOI] [PubMed] [Google Scholar]
  24. Kresse G.; Furthmüller Comput. Mater. Sci. 1996, 6, 15. 10.1016/0927-0256(96)00008-0. [DOI] [Google Scholar]
  25. Blöchl P. E. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  26. Perdew J. P.; Burke K.; Ernzerhof M. Phys. Rev. Lett. 1996, 77, 3865. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  27. Grimme S.; Antony J.; Ehrlich S.; Krieg H. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  28. a Dincă M.; Dailly A.; Liu Y.; Brown C. M.; Neumann D. A.; Long J. R. J. Am. Chem. Soc. 2006, 128, 16876. 10.1021/ja0656853. [DOI] [PubMed] [Google Scholar]; b Dincă M.; Han W. S.; Liu Y.; Dailly A.; Brown C. M.; Long J. R. Angew. Chem., Int. Ed. 2007, 46, 1419. 10.1002/anie.200604362. [DOI] [PubMed] [Google Scholar]; c Sumida K.; Horike S.; Kaye S. S.; Herm Z. R.; Queen W. L.; Brown C. M.; Grandjean F.; Long G. J.; Dailly A.; Long J. R. Chem. Sci. 2010, 1, 184. 10.1039/c0sc00179a. [DOI] [Google Scholar]; g Liao J.–H.; Chen W. – T.; Tsai C.–S.; Wang C. – C. CrystEngComm 2013, 15, 3377. 10.1039/c3ce27063g. [DOI] [Google Scholar]
  29. a Demessence A.; D’Alessandro D. M.; Foo M. L.; Long J. R. J. Am. Chem. Soc. 2009, 131, 8784. 10.1021/ja903411w. [DOI] [PubMed] [Google Scholar]; b Reed D. A.; Xiao D. J.; Gonzalez M. I.; Darago L. E.; Herm Z. R.; Grandjean F.; Long J. R. J. Am. Chem. Soc. 2016, 138, 5594. 10.1021/jacs.6b00248. [DOI] [PubMed] [Google Scholar]
  30. Colombo V.; Galli S.; Choi H. J.; Han G. D.; Maspero A.; Palmisano G.; Masciocchi N.; Long J. R. Chem. Sci. 2011, 2, 1311. 10.1039/c1sc00136a. [DOI] [Google Scholar]
  31. a Busch D. H.; Alcock N. W. Chem. Rev. 1994, 94, 585–623. 10.1021/cr00027a003. [DOI] [Google Scholar]; b Kolchinski A. G.; Korybut-Daszkiewicz B.; Rybak-Akimova E. V.; Busch D. H.; Alcock N. W.; Clase H. J. J. Am. Chem. Soc. 1997, 119, 4160. 10.1021/ja9624477. [DOI] [Google Scholar]
  32. Li J.; Noll B. C.; Oliver A. G.; Scheidt W. R. J. Am. Chem. Soc. 2012, 134, 10595. 10.1021/ja303475a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Boča R. Coord. Chem. Rev. 2004, 248, 757. 10.1016/j.ccr.2004.03.001. [DOI] [Google Scholar]
  34. Mealli C.; Midollini S.; Sacconi L. Inorg. Chem. 1975, 14, 2513. 10.1021/ic50152a044. [DOI] [Google Scholar]
  35. a Halder G. J.; Kepert C. M.; Moubaraki B.; Murray K. S.; Cashion J. D. Science 2002, 298, 1762. 10.1126/science.1075948. [DOI] [PubMed] [Google Scholar]; b Southon P. D.; Liu L.; Fellows E. A.; Price D. J.; Halder G. J.; Chapman K. W.; Moubaraki B.; Murray K. S.; Létard J. – F.; Kepert C. J. J. Am. Chem. Soc. 2009, 131, 10998. 10.1021/ja902187d. [DOI] [PubMed] [Google Scholar]
  36. Holland P. L. Dalton Trans. 2010, 39, 5415. 10.1039/c001397h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. a Tovrog B. S.; Kitko D. J.; Drago R. S. J. Am. Chem. Soc. 1976, 98, 5144. 10.1021/ja00433a016. [DOI] [Google Scholar]; b Drago R. S.; Corden B. B. Acc. Chem. Res. 1980, 13, 353. 10.1021/ar50154a003. [DOI] [Google Scholar]
  38. a Eddaoudi M.; Moler D. B.; Li H.; Chen B.; Reineke T. M.; O’Keeffe M.; Yaghi O. M. Acc. Chem. Res. 2001, 34, 319. 10.1021/ar000034b. [DOI] [PubMed] [Google Scholar]; b Qiu S.; Zhu G. Coord. Chem. Rev. 2009, 253, 2891. 10.1016/j.ccr.2009.07.020. [DOI] [Google Scholar]; c Farha O. K.; Hupp J. T. Acc. Chem. Res. 2010, 43, 1166. 10.1021/ar1000617. [DOI] [PubMed] [Google Scholar]; d Cook T. R.; Zheng Y. – R.; Stang P. J. Chem. Rev. 2013, 113, 734. 10.1021/cr3002824. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja6b03680_si_001.cif (4.8MB, cif)
ja6b03680_si_002.cif (20.4MB, cif)
ja6b03680_si_003.pdf (13MB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES