Disparity processing in primary visual cortex

Abstract

The first step in binocular stereopsis is to match features on the left retina with the correct features on the right retina, discarding ‘false’ matches. The physiological processing of these signals starts in the primary visual cortex, where the binocular energy model has been a powerful framework for understanding the underlying computation. For this reason, it is often used when thinking about how binocular matching might be performed beyond striate cortex. But this step depends critically on the accuracy of the model, and real V1 neurons show several properties that suggest they may be less sensitive to false matches than the energy model predicts. Several recent studies provide empirical support for an extended version of the energy model, in which the same principles are used, but the responses of single neurons are described as the sum of several subunits, each of which follows the principles of the energy model. These studies have significantly improved our understanding of the role played by striate cortex in the stereo correspondence problem.

This article is part of the themed issue ‘Vision in our three-dimensional world’.

1. Introduction

One of the most significant advantages of having two eyes with overlapping visual fields is that it provides a unique source of visual information about the three-dimensional structure of our surroundings. Objects will fall at different locations on the two retinae, generating a binocular disparity, in a way that reflects the distance from the observer to that object. In order to measure the binocular disparity generated by an object, it is first necessary to identify which image features on the left retina correspond to features on the right retina (‘correspond’ in the sense that they both represent light coming from the same point in the three-dimensional world). This problem is called the stereo correspondence problem and has been widely investigated in both computational and psychophysical studies. Indeed, there are now many algorithms that work robustly in artificial systems (see [1] for a review), which have revealed how the constraints imposed by the geometry and the structure of the natural world make this problem tractable.

Here, we explore how computations performed by neurons in the visual cortex deal with the correspondence problem. An important constraint on the solutions available to the brain is that considerable processing of the visual inputs occurs in the retina of each eye, before any binocular comparisons can be made. Although some neurons in the lateral geniculate nucleus receive binocular inputs [2,3], no disparity selectivity has ever been reported there. The first site in the mammalian brain where disparity selectivity has been observed is in the primary visual cortex (V1). This initial coding of binocular information profoundly constrains what will be necessary or even possible at subsequent stages. Although considerable progress has been made in understanding this important step, the remaining uncertainties make it difficult to elucidate what computations are required beyond striate cortex. Here, we discuss recent changes in our understanding of how disparity is computed in V1, and its implications for subsequent processing.

2. The binocular energy model and the stereo correspondence problem

The binocular energy model (BEM) remains central to our understanding of how disparity is computed in binocular neurons. The idea was first suggested by Ohzawa & Freeman [4] to account for a striking observation in binocular complex cells. When stimulated with sinusoidal luminance gratings, these neurons are not selective for the spatial phase of monocular gratings presented to either eye, and yet are selective for the difference in phase between the eyes. The quantitative model was first explicitly described and tested in the classic paper by Ohzawa et al. [5]. The model was able to account for the disparity-selective properties of both simple and complex cells with a very simple mechanism.

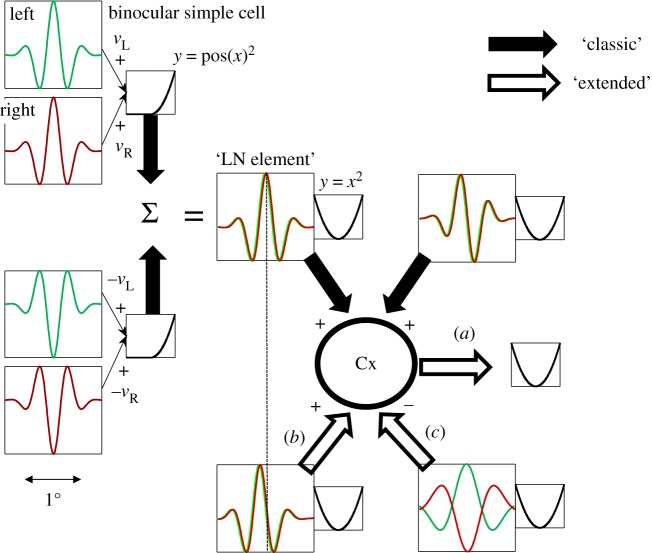
Figure 1 illustrates the principles of the model. For simple cells, it postulates that monocular processing in each eye can be described by a linear filter (the receptive field, RF), and the results from the two eyes are linearly summed before passing through an output nonlinearity. That is, for any image the monocular response in the left (right) eye is given simply by the inner product of the image with the monocular RF, resulting in a scalar which we denote with 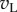(left eye) and 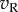(right eye). The output nonlinearity is typically modelled with a squaring operator as this has several convenient properties. The response of one binocular simple cell is then given by 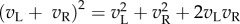. The first two terms in this equation depend only on the monocular images and RFs, but the final term computes the covariance between the monocular responses. This term confers disparity selectivity on the model neuron, since the magnitude of 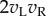depends on the correlation¹ between the images after filtering. Because all processing prior to the output nonlinearity is linear, the BEM is an instance of the class of ‘linear–nonlinear’ (LN) models that have been widely used to describe responses in early visual cortex [8–10].

Figure 1.

The classic BEM and recent extensions that are discussed in this review. A disparity-selective simple cell (upper left) is constructed from two monocular RFs (labelled ‘left’ and ‘right’). Each RF computes the dot product (a weighted sum) of the image and the RF, and the results from each eye (scalars 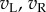) are linearly summed. In this example, the RFs are identical in the two eyes, and are both Gabor functions. (Two cycles per degree sinusoidal carrier, Gaussian envelope 0.25°. While the scaling of all these figures is arbitrary, we include a scale bar that indicates a plausible size, and that was used for simulations.) After summation, the response is half-wave rectified and squared (y = pos(x)²). A second simple cell (lower left) has monocular RFs that are exact inversions of the first simple cell, thus the monocular responses are 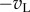and 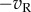(since both simple cells are presented with the same image). The summed response of these two simple cells can be described as a single binocular ‘LN element’ that has one binocular RF followed by squaring. The classic BEM complex cell (Cx) is constructed from two LN elements in quadrature. That is, the phase of all Fourier components is shifted by π/2 between the RFs of the two LN elements. In this diagram, the filled arrows show all of the summation steps required to produce the classic BEM with physiologically plausible components. Note that once one monocular RF is defined (upper left), every other step required to generate a complex cell selective for zero disparity is determined. The open arrows show modifications that are minor in the sense that they use exactly the same principles, but they can nonetheless significantly change the behaviour of the model. Modification (a) is simply to add a squaring nonlinearity at the output of the complex cell, identical to that postulated for simple cells (since the complex cell response is always positive, half-squaring and full-squaring are indistinguishable). Modification (b) creates a complex cell with more than two LN elements. Here, the additional element has a slightly different RF location (but left and right components are still identical to each other), but is otherwise identical. The dashed line marks a corresponding point in both RFs. This is similar to the elements identified by Sasaki et al. [6]. Modification (c) shows an LN element whose output is subtracted from the complex cell response (as if it released inhibitory neurotransmitters). In this example, the binocular RF is also different, so that zero disparity now produces a response minimum, and it has a broader RF. These are all characteristic of the elements identified by Tanabe et al. [7]. In modifications (b,c), the additional elements are not in quadrature with the LN elements of the classic BEM. Once the requirement for quadrature is relaxed, there are a large number of possible LN elements that could be introduced—these are just two examples for which empirical support will be discussed later.

The squaring used for this simple description is not a realistic model of real simple cells, which are better described by a half-squaring. But the sum of two binocular simple cells, with RFs that are related by inversion (figure 1), is a physiologically natural way to produce these squared responses. We refer to this slightly abstract construct as an ‘LN element’ (figure 1) to distinguish it from simple cells. The response of a single LN element will still depend upon the spatial phase of a luminance grating, and so to build model complex cells it is usual to combine two LN elements that have RFs in quadrature (the RF in the second element is obtained by shifting all of the Fourier components through 90°). The fact that the two LN elements are in quadrature confers phase invariance on the model complex cell. The fact that the response of both LN elements depends on disparity makes the model sensitive to interocular phase difference.

Note that once a single monocular RF has been defined (of any shape), these rules completely define a model complex cell selective for zero disparity (with identical RFs in each eye, as in figure 1). Thus, BEMs can be built with any shape of RF, although almost all studies have used Gabor functions to describe the monocular RFs. Although it has always been recognized that this compact description is bound to be an oversimplification, it nonetheless provided a powerful framework for understanding both the responses of individual neurons and the nature of the correspondence problem faced by the brain.

The traditional way to challenge correspondence algorithms is to use them to decode the disparity of random dot stereograms (RDS). The BEM produces a tuning curve for disparity in RDS that closely reflects the shape of the monocular RF, provided the tuning curve is constructed by averaging the response to many different RDS patterns. In response to a single RDS pattern, the response of a BEM to changes in disparity will also depend upon how each image displacement (necessary to produce disparity) changes the stimulus within the monocular RFs. These are the signals that the brain must deal with when trying to detect disparity in a single image. Figure 2 illustrates a simple way to view this problem from the perspective of a downstream visual area. The rules for constructing BEM complex cells tuned to zero disparity (above) may be generalized to produce a model population of BEMs, each selective for a different disparity. This generalization step can be done in several ways, but the most intuitive is to produce model neurons selective for different disparities by simply translating the RF in one eye (termed an RF with ‘position disparity’ [11,12]). One advantage of generating a population in this way is that there is a symmetry between disparity in the stimulus and disparity in the RFs: the response of a BEM with zero RF disparity (figure 1) to a stimulus disparity x, is the same as the response of a BEM with RF disparity –x to a stimulus with zero disparity. Figure 2a shows the response of a population of such disparity detectors to a single RDS at zero disparity (equivalent to the response of the BEM shown in figure 1 to a single RDS stimulus shown at different disparities). Figure 2a shows four important properties of such a population response:

• (i) There is a local maximum in the response where the RF disparity matches the stimulus disparity.²

• (ii) There are additional local maxima at other disparities (false matches).

• (iii) The response map is much smoother than the pixelation of the original image (reducing the number of false matches), which simply reflects the fact that the monocular RFs pool over a finite spatial extent.

• (iv) The peaks associated with false matches can be larger than those for the true match. So a simple rule that found the maximum response in this population would frequently report the incorrect disparity. Note, however, that the locations of the false matches depend on the particular dot pattern, and so if responses like these are averaged across enough different dot patterns (or equivalently, across enough neurons with no-overlapping RFs), the mean response will have a global maximum at the stimulus disparity.

Figure 2.

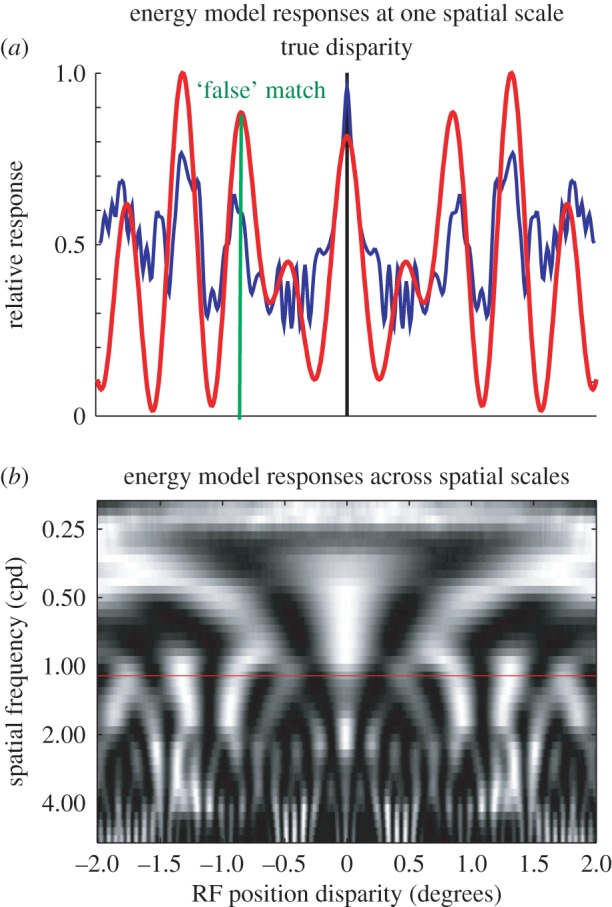
The correspondence problem after filtering with the binocular BEM, represented by considering the response of a population of model complex cells to a single binary noise pattern. This pattern has zero disparity—the image is identical in both eyes. This simulation was run using the one-dimensional RFs shown in figure 1, with one-dimensional images. The image pixel size was 0.005° (100 pixels per cycle of the carrier). (a) The response profile across a population of neurons that differ only in their position disparity (smooth red curve; equivalent to the responses of the complex cell shown in figure 1 to different disparities). The position disparities were introduced by displacing the RFs in each eye symmetrically, so the mean (cyclopean) RF position is constant. There is a local maximum at the true disparity, but several other local maxima—‘false’ matches. The false matches can have a greater magnitude than the response to the true disparity. (b) A population differing in both position disparity and spatial scale (quantified by the preferred spatial frequency). The colour scale shows relative response (like the ordinate in (a)), in which each horizontal row has been normalized to a maximum of unity. The red horizontal line marks the set of model cells used in (a). Note that while every row in this image has a local maximum at the true disparity, the locations of the false matches depend on the spatial scale of the filters. Consequently, a simple summation across spatial scales can extract the correct disparity in most cases. The blue (less smooth) line in (a) shows this sum normalized (like the smoother red curve) to a maximum of unity. Note that here the global maximum is at the true disparity.

The response profiles in figure 2a illustrate how the correspondence problem might appear to a visual area downstream of striate cortex. What rule applied to this response profile will yield a correct disparity estimate? Using only the population of neurons shown in figure 2a, this is still a challenging problem [13]. But recall that this population was generated from a single monocular Gabor RF. If a similar map is generated for the same stimulus, but using Gabor RFs of a different sizes (corresponding to neurons with different spatial frequency preferences, figure 2b), a simple readout becomes possible. While there is a local maximum at the true disparity for all frequencies, the locations of the false matches are different across spatial frequency preferences. Consequently, simply summing these responses across V1 neurons with different spatial frequency preferences might be an effective but simple way for extrastriate cortex to solve for stereo correspondence. An appropriately weighted summation of BEMs can perform even better [14]. This is closely related to the ‘coarse-to-fine’ principle identified in the earliest correspondence algorithms [15]. The summation of responses shown here is simpler than those early algorithms, which proposed a nonlinear interaction between scales with a progression from coarse scales to fine scales over time. The summation in figure 2 might better be described as ‘coarse AND fine’. But both methods exploit the same principle that the false matches are different at different scales, while the correct matches are aligned.

3. The matching problem in V1 neurons: similar to the binocular energy model

Note that this description is based entirely on simulation results with the BEM. The response of a large population of real V1 neurons to a single random dot stimulus has not been studied. As a result, our current understanding of the problem faced by extrastriate cortex (which has access to a response map like figure 2b) depends critically on the BEM providing an accurate account of the responses of V1 neurons. Many lines of evidence indicate that the basic architecture of the model is approximately correct, and accounts for several aspects of perception. The size of the monocular RF should limit the finest detectable modulation in disparity [16]. This is true for single neurons, and appears to explain the poor spatial resolution for disparity that is found psychophysically [16,17]. Similarly, the temporal integration of the monocular RF limits the ability to detect temporal modulation in disparity, again in line with human psychophysics [18]. Perhaps the most striking confirmation of the principles of the BEM is the effect of presenting images of opposite contrast to the two eyes (anticorrelation). Inverting the contrast of an image is equivalent to multiplication by −1 (if the image is described with deviations from mean luminance). Since monocular processing in the BEM is linear, this means that the monocular response must also be multiplied by −1. In the BEM, this means that the term 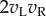above (§2) must become 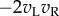(only one eye's image is inverted). Since it is this term alone that produces the disparity-selective response, this predicts that the disparity-selective response should be inverted when anticorrelated stimuli are presented. This inversion is indeed found [5,19].

However, while the inversion observed with anticorrelated stimuli provided strong evidence for the model architecture, it also revealed a quantitative failure: the magnitude of the response modulation was substantially weaker for anticorrelated stimuli than for correlated stimuli [19]. This discrepancy is particularly interesting as it suggests that neurons are specialized for realistic inputs, in a way that the model does not explain. The anticorrelated stimuli do not have the properties of correct disparity matches (e.g. in figure 2b no disparity would produce consistent peaks across spatial frequencies, although they would produce consistent troughs [20]). These stimuli are ‘unnatural’ in the sense that it is impossible to achieve anticorrelation in natural viewing.³ The viewing geometry imposes some close relationships between spatial frequency and interocular phase difference [11,13,21], and anticorrelation represents the largest possible deviation from these naturally occurring relationships [21]. It is presumably the ‘unnatural’ binocular structure that produces the weak responses in real neurons, but the BEM is not sensitive to this. That suggests some specialization at the level of V1 that helps to eliminate false matches, and this in turn implies that extrastriate cortex may face a simpler problem than is suggested by figure 2b. Thus, the BEM provides an excellent starting point for describing V1, but requires some modification before we can understand the role of V1 in stereo correspondence.

4. Extending the energy model

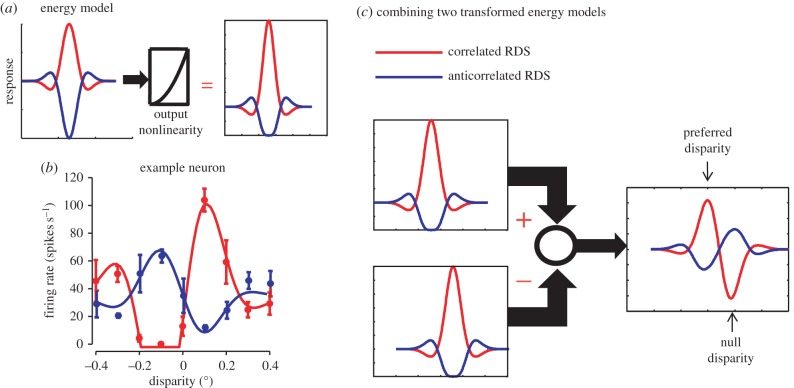
Identifying what mechanism is responsible for these attenuated responses is therefore an important step in understanding how the cortex deals with the correspondence problem. For many cells, this could in principle be explained by proposing that the complex cell response also passes through an output nonlinearity [22,23] as illustrated in figure 3a. (Although note there is not yet any evidence that this is the correct explanation.) However, for neurons with odd-symmetric tuning (‘near–far’ types, figure 3b), a simple output nonlinearity cannot generate the asymmetry seen in real cells [23]. The responses in odd-symmetric cells can be explained without changing the underlying structure of the model if the neuron receives inputs from a broader range of simple cells than the quadrature pairs used in the classic model and the simple cell nonlinearities are not just half-squaring (illustrated in figure 3c) [21,24].

Figure 3.

Simple ways to explain attenuated responses to anticorrelated RDS. (a) A traditional BEM, which shows a symmetry between responses to correlated RDS (red) and anticorrelated RDS (blue). If the output of this model complex cell is then passed through an expansive nonlinearity (e.g. squaring) the responses to correlated RDS are increased, while those to anticorrelated RDS are attenuated (this is modification (a) in figure 1). However, this approach cannot explain attenuation in odd-symmetric neurons like the example shown in (b). In these neurons, the response to the preferred disparity (a term often used to describe the correlated disparity that produces the maximal firing rate) and to the null disparity (the correlated disparity that produces the minimum firing rate) are both more extreme than the corresponding responses to anticorrelated RDS. Consequently, no point nonlinearity applied to the correlated (red) data can produce the anticorrelated data (blue). If odd symmetry is constructed by combining multiple subunits, and each subunit has an additional nonlinearity, it is possible to produce odd-symmetric responses for anticorrelation that are attenuated. (c) Here, the two subunits have different preferred disparities, but are otherwise identical. Subtracting one from the other then produces odd-symmetric tuning. Note that these two subunits do not form a quadrature pair, so that (c) represents another instance of the extended BEM.

This extended model is still very similar to the BEM, which also proposes that disparity-selective complex cells are the sum of several LN elements. The original model used a squaring nonlinearity and just two LN elements that were in quadrature. Real neurons do not behave exactly as predicted by this model, but may be explained by a more general form of the same mechanism: a sum of more than two LN elements, with a mixture of nonlinearities. Despite the subtlety of this change, the behaviour of this extended model, e.g. in simulations like those shown in figure 2, can be quite different from the classic version. This makes the extended model more flexible, but until recently the evidence supporting the idea was indirect. Determining the extent to which the responses of real V1 neurons are captured with the extended model remains an essential step in understanding the structure of the stereo correspondence problem in visual cortex.

5. Physiological evidence in favour of the extended energy model: multiple subunits

A number of recent studies have provided clear evidence in favour of the extended model. The most ‘hands-off’ of these used independent white noise stimuli presented to the two eyes. From a large set of these random images, only a fraction will produce spikes. This ‘spike-triggered ensemble’ of images is identified by picking all images that occurred at a fixed time delay before each spike. Given a large set of images that produce spikes, and a large set that do not, it is possible to infer the set of LN elements that explain which images fall into the spike-triggered ensemble. This can be done simply by applying principal component analysis to the spike-triggered ensemble (a technique known as spike-triggered analysis of covariance, STC [10,25]). When applied to disparity-selective neurons recorded in monkey striate cortex, this revealed that most neurons do require more than two LN elements to describe their responses adequately [7]. It also revealed that the majority of neurons require that some LN inputs be suppressive—certain stimulus features reduced the probability of spiking. There were several systematic relationships between the suppressive and excitatory LN elements (illustrated by modification (c) in figure 1). First, they had complementary disparity selectivity—disparities that caused the strongest excitation also produce the weakest inhibition. That is, they seem to have a ‘push–pull’ organization. Second, the inhibitory elements were at a coarser spatial scale (with a peak frequency approx. one octave lower than the excitatory elements). This interaction between spatial scales has much in common with the coarse-to-fine computation that reduces false matches as described in §2. Because the suppressive inputs have inverted disparity selectivity, they produce ‘disinhibition’ at the preferred disparity of the excitatory subunits, so the effect is similar to summation over spatial scales (illustrated in figure 2). Finally, the effects of the suppressive images are slightly delayed, by about 7 ms [26]. The origin of this delay is unknown, but it is tempting to speculate that it represents the delay introduced by passing excitatory inputs through inhibitory interneurons in the cortex. In classic coarse-to-fine algorithms, the coarse scale is represented earlier in time, so the summation over scales in V1 neurons does not implement exactly those algorithms. But they clearly exploit the same principle that combining over coarse and fine scales helps to resolve ambiguity. It is also important to note that combining excitation at one scale with inhibition over a broader scale has the effect of ‘sharpening’ the disparity tuned response of the sum. Consequently, the responses of single neurons do move from coding coarser scales to finer scales over a period of 20–50 ms [7,26–28]. The early coarse-to-fine algorithms imagined this combination happening at a stage after the initial binocular filtering [15]. That so many components of this are visible in the responses of V1 neurons indicates a surprisingly sophisticated computation, and yet one that can be performed by the extended BEM.

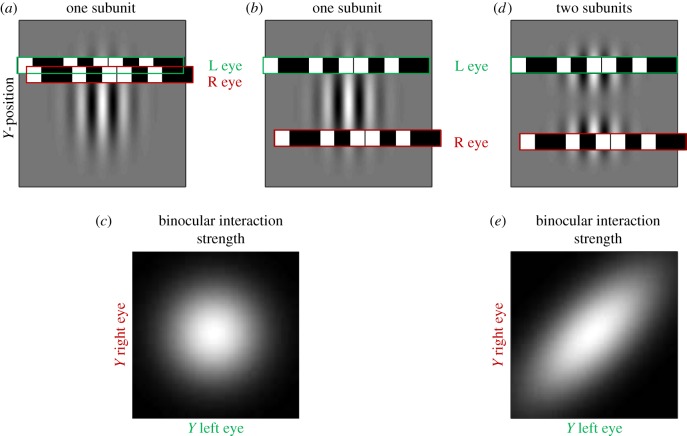
The contribution of multiple subunits can be demonstrated in a more direct way if a sufficiently large stimulus set is used to probe disparity signals in different sub-regions of the RF [6]. Figure 4 illustrates the principle used. Suppose a thin strip of random dots is placed at one end of the RF in both eyes—figure 4a shows them in the upper half. The classic BEM will signal disparity in these dots, regardless of whether these are presented in the upper half, or at the symmetrical location in the lower half. Now suppose the dots are placed in the upper half of the RF in the left eye, but the lower half in the right eye. The classic BEM still displays selectivity, because the dots produce the same response in the monocular RF at both ends. That is, because the terms 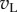and 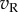are the same in all three cases, the model response must be identical. However, if the cell were composed of two distinct subunits as illustrated in figure 4d, then no disparity selectivity will be seen when the dots are at different locations in the two eyes, because they activate different subunits. That is, if 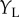and 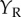indicate the vertical position of the dots, a classic BEM will show disparity selectivity that is a separable function of 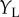and 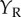(figure 4c). If the cell is composed of two subunits, each of which is a BEM, and they have different Y locations, then the cell's response will be an inseparable function of 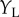, , 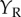elongated along the diagonal (figure 4e). The extent of this elongation can be used to estimate a minimum number of subunits, and a substantial number of neurons recorded by Sasaki et al. [6] needed more than three subunits to account for the responses. This combination of spatially offset subunits was illustrated by modification (b) in figure 1.

Figure 4.

Binocular interactions across different locations in the RF can be used to identify different subunits (after Sasaki et al. [6]). (a,b) An RF (for simplicity, it is identical in right and left eyes), with a row of random dots superimposed. In (b), the dots in the right eye are at a different location along the long axis of the RF (Y-position), but this is chosen such that a horizontal cross section through the RF is the same at these two locations. Consequently, despite the fact that the right eye stimulus is in a different location in (a,b), it produces identical activation of the right RF (i.e the inner product of stimulus and RF is the same). This ensures that the binocular interactions will also be the same—both configurations result in the same disparity selectivity. (c) The magnitude of disparity selectivity as a function of Y-position in the left and right eyes. A single subunit produces a separable response. (d) Two subunits. Here the two locations of dots in the right eye have very different effects. When each eye stimulates a separate subunit, there is no binocular interaction. The result (e) is that disparity selectivity is an inseparable function of Y-position in the two eyes.

These two methods complement one another in important ways. The major strength of STC is that it gives a full description of the RF properties of each subunit. However, this comes at a significant price: the conclusion only holds under the assumptions of the model—that the cell really is composed of a set of LN subunits. If other nonlinear processes influenced the firing rate (e.g. if some dot patterns led to changes in the contrast gain), the set of LN filters recovered by STC may be quite different from the true RF subunits of a given cell. The method of Sasaki et al. [6] requires far fewer assumptions—the fact that dots that are separated but still within the RF show no binocular interaction clearly indicates that the RF is divided into subunits with distinct binocular RFs, regardless of any nonlinearities within those sub-regions. The disadvantage of this method is that it gives a much less complete picture of the properties of those subunits. It is clear that they occupy different spatial locations, but little else can be said about their properties.

Fortunately, the same principle can be extended to explore other differences between subunits, such as differences in selectivity for spatial frequency [29]. Here, the stimuli were sinusoidal luminance gratings in which the spatial frequency was manipulated separately in the two eyes (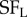, 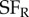), and for each frequency combination the strength of disparity modulation was measured. This requires a very large number of grating stimuli, that exhaustively explored all combinations of four parameters: spatial frequency (left and right) and spatial phase (left and right). By the same logic as illustrated in figure 4 for location, their finding that disparity modulation is an inseparable function of 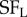, 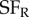indicates the presence of multiple binocular subunits selective for different frequencies. As in the study by Tanabe et al. [7], this also provides a substrate for a ‘coarse-to-fine’ interaction that helps to reduce false matches. Thus, all of these studies support the same general conclusion—typical V1 complex cells behave as if they receive input from more than two LN elements, and the effect of this combination is to reduce the problem of false matches.

In addition to revealing multiple subunits, Baba et al. [29] found that some cells shared an interesting property across the subunits. As in an earlier study [30], some cells responded best when the SF presented to the two eyes was different. In these cells, Baba et al. showed that the interocular difference in preferred SF was preserved across subunits. This provides an ideal arrangement for detecting surfaces that are tilted around a vertical axis, which produces interocular SF differences in the stimulus [31]. Having multiple subunits helps both to sharpen the selectivity for slant in these neurons and reduce the number of false matches produced by slanted surfaces. More recently, Kato et al. [32] extended this analysis to explore different orientations between the eyes, and again found evidence for multiple subunits, with matched interocular differences in preferred orientation. This seems to be a specialization for detecting surfaces tilted around a horizontal axis [33]. Thus, the extended model helps to eliminate false matches not only for stimuli with uniform disparity, but also for more natural surfaces with a variety of slants.

6. Testing the extended energy model: suppressive subunits?

Although it is possible that these studies reveal the same underlying mechanism, at first sight the descriptions differ in one important respect. Tanabe et al. [7] identified a suppressive contribution from lower SFs, whereas Baba et al. [29] did not find evidence for suppressive inputs. Because the conclusions of Baba et al. are derived from measures of disparity modulation, it might be that the modulation at lower SFs was produced by suppressive mechanisms, while that at higher SFs derives mainly from excitatory mechanisms. Although this is a possible resolution, Baba et al. present some compelling arguments against such a simple account.

The stimulus used by Tanabe & Cumming [26] was constructed by adding together a number of sinusoidal gratings, and in each image a random number of these components were included (this construction was performed independently for the two eyes). This allowed them to demonstrate the presence of disparity-selective suppression in a more direct way. They compared the mean response for two subsets of the stimuli: (i) all stimuli containing a given component in both eyes at the null disparity, and (ii) all stimuli in which this component was absent in both eyes. For most neurons, it was possible to identify a component for which (i) was a lower rate than (ii), clearly indicating suppression. If the neuron's response represents the sum of many LN elements, then this observation clearly indicates the presence of LN elements with a suppressive effect. But once again, if more complex nonlinearities are present, this is less clear. An important candidate here is cross-frequency suppression—when a cell is stimulated with its preferred SF, adding a second SF to the stimulus is often suppressive [34]. This may reflect the inputs to a contrast gain mechanism [35]. If this suppression occurred monocularly, in a cell where there was an excitatory binocular interaction, it would be compatible with the data of both studies above. When a binocular stimulus is presented, raising responses above baseline, suppressive effects of adding a single frequency to one eye are often seen [36]. It is therefore possible that over the range of stimuli explored in all these studies, the two descriptions are functionally equivalent. Put another way, if there were monocular regulation of contrast gain, the best fitting LN model is likely to account for these effects with suppressive elements. Consequently, it is possible that a version of the extended model that also includes contrast gain control would account for the data in all of these studies with the same model. This in turn means these studies do not imply that that disparity processing is fundamentally different in cats (used by Baba et al.) and monkeys (used by Tanabe et al.).

7. The extended model resolves one longstanding puzzle

In the classic BEM, the shape of the monocular RF largely determines the shape of the disparity tuning curve [37]. For example, if the monocular RFs are Gabors, the disparity tuning will also be a Gabor, and its parameters are determined by the parameters of the monocular RFs.⁴ As a result, some simple measures made monocularly predict properties of the disparity tuning curve. For example, the preferred spatial frequency measured monocularly determines the spatial scale (distance between preferred and null disparities) of the disparity tuning to RDS.⁵ It has been recognized for many years that this is not true in real neurons [38,39], but this mismatch remained unresolved. One hallmark of a mechanism that combines BEM subunits is that these simple relationships need no longer hold. This can be appreciated from figure 3c, where the two BEM subunits could be constructed with elements that have identical monocular spatial frequency tuning. The preferred disparity of one subunit can be changed (simply by applying a translation to one monocular RF) without altering spatial frequency tuning. These changes in preferred disparity of the subunits lead to changes in the spatial scale of the disparity tuning curve, without changing the monocular spatial frequency tuning. Thus, in principle, the extended BEM might account for the observed neuronal properties [38,39]. Two recent studies suggest that this explanation is correct: the observed mismatch is largely explained by the effects of summing across the inferred set of LN subunits. One [26] used the ‘push–pull’ model reconstructed with STC that best described the responses of each cell [7], and showed that this did account quantitatively both for the tuning to spatial frequency observed monocularly, and for the spatial scale of disparity selectivity. Baba et al. [29] also found that a model based on the subunits they identified reproduced this property. Thus, these methods for identifying multiple subunits seem finally to have resolved a longstanding discrepancy between real disparity-selective neurons and the BEM. They have improved our description of the mechanism by which disparity selectivity is generated, and show that this allows real neurons to be less sensitive to ‘false’ matches than the classic BEM.

8. The extended model does not explain the effects of anticorrelation

These successes, combined with the theoretical principle illustrated in figure 3, suggest that the extended model might also provide a good description of the attenuated responses shown by V1 neurons to anticorrelated stimuli. The LN elements reconstructed with STC allow this to be tested directly. For each individual cell, this method yields a reconstructed model that is the best estimate of the extended model describing that cell. If the extended model correctly describes the responses of V1 neurons, the model reconstructed by STC should then correctly predict all responses. The responses to anticorrelated stimuli are then a good test of the model's success. However, the reconstructed model systematically fails to reproduce this feature of the responses in real neurons—the reconstructed models all showed very similar modulation for correlated and anticorrelated stimuli [7]. Interestingly, further analysis of the responses of the neurons themselves may explain why. The study presented a forward correlation analysis⁶ to estimate responses to positive and negative correlations that occurred by chance in the uncorrelated random sequence. Neuronal responses here were equally strong to negative correlations and positive correlations—there was no attenuation of responses to negative correlation. If this attenuation is absent in the data used to reconstruct the model, it may explain why the reconstructed model also does not predict any attenuation for anticorrelated RDS. The random stimulus produces a limited range of correlation strengths (correlations of +1 and −1 are extremely rare by chance), so it is possible the same analysis applied to stimuli covering a wider range of binocular correlation would reveal an extended model that explains the attenuation for anticorrelation. It is hard to imagine how the extended model could produce this change purely as a function of dynamic range (of binocular correlation), but we cannot currently exclude this possibility with certainty. Importantly, Tanabe et al. [7] showed that the same neurons did exhibit this attenuation in traditional tuning curves. That is, individual neurons that showed attenuation in traditional tuning curves did not show that attenuation when tested with forward correlation in the binocularly uncorrelated noise stimulus.

This observation itself is informative about how neurons might produce attenuated responses to anticorrelation. In a traditional tuning curve, responses are attenuated, but in the forward correlation analysis they are not. There are only two differences between traditional tuning curves and the forward correlation—one (or both) of these differences must be responsible. The first is that, as noted above, the range of binocular correlation values contained in the forward correlation is small. If the attenuation is only produced by correlations close to −1, it would be absent in the forward correlation analysis. The second difference is that the forward correlation measures responses to single video frames (with a duration of only 10 ms in [7]). It may be that the process responsible for attenuation develops too slowly to be engaged by such brief stimuli. Indeed, there is some evidence that the response attenuation gets a little stronger over time [40]. Both of these explanations seem like nonlinearities that are difficult to produce with a summation of LN elements, but more experiments are required before it is clear which of these factors is important.

9. Going beyond the linear–nonlinear framework

(a). A possible role for gain control

Whichever factor is responsible, this suggests that the mechanism producing attenuated responses to anticorrelated stimuli is not encompassed by the extended model—neurons producing the attenuation in this way should have shown attenuation in the forward correlation analysis. This carries the implication that some other nonlinearity plays an important role in shaping disparity selectivity. One possibility is that recurrent processing is important, as suggested by Samonds et al. [40], who demonstrated that the attenuated responses to anticorrelation show some changes on long timescales. It may also be that more well-documented processes play an important role. A potentially important factor is contrast gain control—when the contrast of a visual stimulus is reduced, neuronal responses are not reduced proportionally, but compensate for the low contrast by increasing their gain [35,41]. In disparity-selective simple cells, this has been shown to be a largely monocular phenomenon [42], which may have profound consequences for disparity-selective responses, even when contrast is not explicitly manipulated. This depends critically upon what aspects of an image regulate monocular contrast gain. If the gain in each eye is determined by the RMS contrast of a large area, then it should have little consequence for responses to random patterns. If the gain is determined by the contrast energy over a small range of spatial frequencies in a restricted part of the image, then there could be substantial fluctuations in monocular contrast gain when neurons are stimulated with RDS.

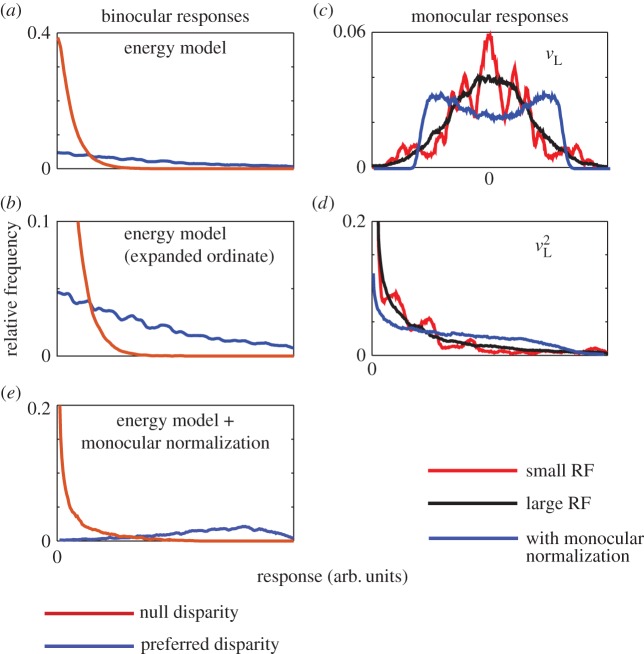
The lack of any contrast gain control in the BEM leads to a curious property in the variability of model responses (figure 5). If a random dot stimulus has little contrast energy in the spatial frequencies that activate the RF, then the binocular response will be weak regardless of the disparity. When the relevant contrast energy is present, responses will be much larger at the preferred disparity than the null disparity. This results in enormous overlap between the response distributions for different disparities, and a variability in model responses changes substantially with disparity (figure 5a). The reason why the BEM produces these particular distributions it not important for the argument here, but for completeness it is described in the next paragraph.

Figure 5.

The distribution of responses to different random dot patterns in the BEM. The responses of a BEM complex cell to 10 000 different instances of an RDS were computed. The stimulus was 100% correlated and presented at one of two disparities—preferred and null (as defined in figure 3). This uses the classical complex cell exactly as shown in figure 1, using a pixel size of 0.005° for simulations (as in figure 2). (a) The frequency histogram of these responses when the stimulus was at the preferred disparity (blue) or the null disparity (red). Both distributions are ‘heavy tailed’, but the main effect of disparity is to increase this. That is, the difference in mean response between preferred and null disparities is largely driven by a small fraction of images that produce very large responses. (b) The same data with an expanded ordinate, where the difference in the tails of the distributions is more clearly visible. These distributions follow directly from the distributions of the monocular responses, shown in (c). In almost all cases, the monocular responses follow a nearly Gaussian distribution, with a mean of zero. If the stimulus were Gaussian noise, the stimulus would dictate this Gaussian distribution. Were the stimulus a single point that was either black or white, this distribution would reflect only the RF shape (full-wave rectified). With binary noise, the central limit theorem ensures this approximates a Gaussian, provided there are sufficient noise elements in the RF. If the noise pattern has large elements or the RF is very small, so that each RF contains very few dots, deviations from a Gaussian can be seen. The red line (with multiple peaks) shows responses where the width of the noise elements is 0.25°—half of the spatial period of the RF, and 50 times larger than used for the simulation shown in black (nearly Gaussian distribution). This change in noise element size is equivalent to using an unchanged stimulus with an RF that is 50 times smaller than that illustrated in figure 1. The multiple peaks here are not the result of random fluctuations in the simulation. With very large elements, the details of RF shape give rise to this structure. (d) The same values after squaring. Thus, the shape seen in (a) is largely the result simply of squaring a set of Gaussian responses, producing a χ² distribution. (e) The response of a modified BEM in which there was a simple monocular normalization. Here, the monocular response in the right eye was given by 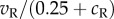, where 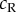is the response of a monocular complex cell with quadrature RFs that are identical to those in the binocular complex cell. This term simply estimates contrast energy in the monocular RF. The monocular responses of this model are shown with blue lines in (c,d). The bimodal distribution of the raw responses means that the squared responses show less kurtosis. This then makes the binocular response distribution less heavy tailed, especially at the preferred disparity, and hence this version of the model predicts smaller changes in variability with stimulus disparity in RDS. The exact shape of these distributions is quite sensitive to the equation used for normalization, so this figure illustrates the principle that normalization might play an important role, rather than providing a definitive account of that role.

(b). Explanation for afficionados

The major effect of disparity is to change the kurtosis of the response distributions. This is a consequence of three factors. First, the distribution of monocular responses (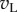 and 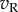) to RDS is close to Gaussian with zero mean (figure 5c). Second, squaring these responses produces a χ² distribution (with 1 d.f.) that is kurtotic and skewed (figure 5d). Third, at the preferred disparity, 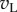and 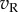are perfectly correlated, so the sum shows the same distribution as the monocular responses. That is, one LN element stimulated with RDS at the preferred disparity generates responses described by a χ² distribution with 1 d.f. As disparity is moved towards the null disparity (as defined in figure 2), this correlation becomes weaker. At the null disparity, 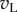and 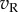are negatively correlated (but with a correlation greater than −1). When the stimulus is binocularly uncorrelated, the distribution of the term 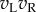resembles a χ² distribution with a lower mean than that for 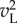. Disparities on the flanks of the disparity tuning curve, which place non-overlapping parts of the image in the left and right RFs, behave exactly like an uncorrelated stimulus.

(c). Stimulus-related variability

When we examined BEM responses to RDS across all disparities, we found that the predicted variance is equal to the square of the mean response. Note that this is a steeper dependence than the proportionality of variance and mean (not mean squared) typical of cortical neurons [43,44]. It is also important to note that this variability is all caused by stimulus variation—the model used here has no noise added that is independent of the stimulus. The model therefore shows no variability when stimulated with deterministic stimuli (e.g. gratings), while neurons have variance proportional to mean even with deterministic stimuli. It appears that this stimulus-driven variance predicted by the BEM is greatly reduced in cortical neurons, although currently available data do not permit a simple test of this prediction. In a traditional tuning curve, measured with RDS, multiple different frames are presented, so that the neuron's mean response is the mean of many samples from the distributions shown in figure 5. This results in a stimulus-driven variance which is proportional to the mean, but with a slope less than unity (the exact value depends on the stimulus duration, framerate, and the temporal integration in the neuron). Nonetheless, the model clearly predicts higher response variability in response to random dot patterns than deterministic stimuli (where the stimulus-driven variance is zero). No published study has explicitly examined this question for disparity-selective neurons. We therefore re-examined data from neurons recorded in previously published studies [37,45,46] where disparity tuning had been measured with RDS and with sinusoidal gratings in the same neurons. The relationship between variance and mean was no steeper for RDS stimuli compared with gratings (B. Cumming 2000, 2001, unpublished data).

This then suggests that much of the variability that different dot patterns should produce, according to the BEM, is not observed in real neurons. What properties of real neurons might explain this? The extended model itself may explain some of this. Each additional LN element adds a new pick from the distribution of responses shown in figure 5a, so the sum becomes more Gaussian (central limit theorem). A second possibility is contrast gain control. Dot patterns at the preferred disparity that produce weak responses in model complex cells do so because that pattern lacks contrast energy in the spatial passband of the RF. If these dot patterns produced compensatory changes in contrast gain, then while the BEM predicts a weak response, the increase in contrast gain makes the neuron's response stronger than predicted by the BEM. This produces monocular responses that are not Gaussian, and so can produce less kurtosis in the squared responses (figure 5c,e).

The changes produced by contrast gain control in figure 5 are modest, and certainly not sufficient to remove a disparity-dependent change in response variability. Equally, the control of contrast gain in real neurons is probably more complex than the very simple scheme used to make figure 5. This simulation does, however, illustrate the principle that monocular regulation of gain can substantially alter the binocular responses, especially their variability across random dot patterns. As this type of variability is an important part of what produces the false peaks in figure 2, it seems possible that contrast gain control will reduce the magnitude of false peaks in the V1 population response. Given the empirical observation that there is substantial monocular regulation of contrast gain [42], this suggests that incorporating this process into future models of disparity selectivity will be important to understand how the population activity in V1 can be used to solve the correspondence problem.

Introducing monocular contrast gain control has a second interesting consequence. If it normalizes responses on the basis of RMS contrast in each eye, it would mean that responses do not simply represent covariance, but come closer to representing normalized cross-correlation. It is clear that they do not do exactly this—perfect normalization would imply that neuronal responses do not increase with contrast. Nonetheless, normalizing the responses with a term that is related to the monocular contrast comes closer to calculating a normalized correlation coefficient than the classic BEM.

10. Summary and implications

The BEM provides an elegant account of a simple, physiologically plausible, mechanism that produces disparity-selective signals. It does this using subunits that perform linear operations on the binocular image (a dot product of the image and the RF) and pass the result through a mathematically simple nonlinearity (squaring). Thus, it belongs to the class of LN models that have been widely used in describing responses of sensory neurons. It achieves something very similar to computing the binocular cross-correlation between two filtered image patches. Recent advances in analytical tools have allowed neuronal responses to be described by extended versions of the model, incorporating multiple LN subunits. These provide a more precise description of the properties of single neurons. Importantly, they also show that the LN subunits are related in ways which help to reduce the problem of identifying false matches when decoding disparity from a population of neurons. This allows us to build a more realistic description of the correspondence problem faced by extrastriate cortex, which has the task of determining disparity from a population of activity like that shown in figure 2.

However, even the extended model fails to explain some properties of real neurons, and two of these unexplained properties are likely to play an important role in shaping the population response. First, it is clear that real neurons show considerable regulation of contrast gain that is a monocular property [42], and this could substantially alter the binocular responses. A better understanding of exactly what features of an arbitrary image set the contrast gain is needed in order to evaluate how this influences the correspondence problem. Second, the attenuated responses seen in response to anticorrelated stimuli remain challenging to explain. Although several explanations are possible in principle (ranging from the use of multiple LN elements to nonlinear recurrent processes), there is no clear evidence that any of these is the correct explanation for real neurons.

Because there is not yet a consensus on how best to replace the BEM, it remains widely used as a way of representing the information available about stereopsis in V1. While this may be a good enough approximation for some purposes, it is important to recognize how the approximation fails. V1 neurons approximately implement a ‘correlation-based’ computation, but the results with anticorrelated dots indicate that their response is not a linear function of binocular correlation—it is not a ‘pure correlation’ computation. Recently, an ingenious series of psychophysical experiments by Doi et al. [47,48] have demonstrated that human stereo matching in some stimuli cannot be explained by a matching scheme based on pure correlation. They have suggested that this requires two separate matching mechanisms, and show that a model with two mechanisms neatly describes the data [49]. One of these mechanisms is a pure correlation detector (linear response to correlation), similar to the BEM, but not to V1 neurons. If observations explained by pure correlation detectors can also be explained by correlation detectors that are not perfectly linear, it remains possible that a single mechanism, based on elements whose response is not a linear function of correlation, can also account for human responses. Once we have a good model of that single mechanism, it will be simpler to devise psychophysical tests that distinguish it from two separate mechanisms. Because there is no agreed upon alternative model, Doi et al. did not test any models based on a single mechanism (other than the classic BEM). It therefore remains possible that a single computation, based on an extended model, might explain their results.

There is little doubt that further processing downstream of V1 plays an important role in refining responses to false matches. But until we have a clearer picture of how V1 responds to false matches, it will be difficult to construct and test specific models that describe how connections between neurons beyond V1 allow the brain to solve the stereo correspondence problem.

Competing interests

The authors declare that they have no competing financial interests.

Funding

This work was supported by the Intramural Research Program of the National Institutes of Health, National Eye Institute.