Molecular dynamics study of human carbonic anhydrase II in complex with Zn²⁺ and acetazolamide on the basis of all-atom force field simulations

Abstract

Human carbonic anhydrase II (hCAII) represents an ultimate example of the perfectly efficient metalloenzymes, which is capable of catalyzing the hydration of carbon dioxide with a rate approaching the diffusion controlled limit. Extensive experimental studies of this physiologically important metalloprotein have been done to elucidate the fundamentals of its enzymatic actions: what residues anchor the Zn²⁺ (or another divalent cation) at the bottom of the binding pocket; how the relevant residues work concertedly with the divalent cation in the reversible conversions between CO₂ and HCO₃^−, what are the protonation states of the relevant residues and acetazolamide, an inhibitor complexed with hCAII, etc. In this article, we present a detailed computational study on the basis of the all-atom CHARMM force field where Zn²⁺ is represented with a simple model of divalent cation using the transferrable parameters available from the current literature. We compute the hydration free energy of Zn²⁺, the characteristics of hCAII-Zn²⁺ complexation, and the absolute free energy of binding acetazolamide to the hCAII-Zn²⁺ complex. In each of these three problems, our computed results agree with the experimental data within the known margin of error without making any case-by-case adjustments to the parameters. The quantitatively accurate insights we gain in this all-atom molecular dynamics study should be helpful in the search and design of more specific inhibitors of this and other carbonic anhydrases.

Graphical abstract

INTRODUCTION

Carbonic anhydrases (CAs), [1] a ubiquitous group of zinc-bound proteins (metalloenzymes),[2, 3] have long been known to catalyze the hydration of carbon dioxide at an extremely high rate.[4] This colorless metalloprotein has one zinc ion per molecule,[5] but a substitution of zinc with cobalt, in bovine carbonic anhydrase, gives a colored enzyme with 45% of the native enzyme activity.[6] Human carbonic anhydrase II (hCAII), in particular, is a cytosolic and monomeric protein with a molecular weight of 30 kDa.[7] Its tertiary structure (illustrated in Fig. 1) is represented by a 15Å deep conical binding pocket [8] formed largely with 10-stranded beta-sheets, [9] which is lined, on one side, with hydrophobic residues and, on the other side, with hydrophilic residues. At the bottom of the pocket, a zinc ion is tetrahedrally coordinated with three histidine residues (HIS 94, 96 and 119) and a bound water/hydroxyl (H₂O/OH⁻) or the NH group of an inhibitor, acetazolamide (AZM), lodged in the pocket of the enzyme’s active site.[10]

Fig. 1.

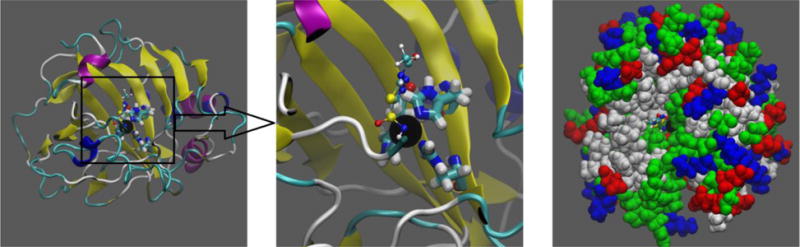
Structure of the hCAII-Zn²⁺-AZM complex. Shown in the left panel and the center panel (zoom into the active site) are the protein in ribbons colored by its secondary structures (beta sheets, yellow; helices, blue and purple; and coils, cyan and white). Also shown in these two panels are the zinc finger residues His 94, 96, and 119 (in licorices, colored by atom names) that tetrahedrally coordinate Zn²⁺ (large black sphere) along with AZM (in balls and sticks, colored by atom names). The color-by-atom names scheme: H, white; O, red; C, cyan; N, blue; S, yellow. Shown in the right panel are the protein and Zn²⁺ (in large spheres, colored by residue types: hydrophilic, green; hydrophobic, white; positively charged, blue; negatively charged, red) and AZM (in balls and sticks, colored as in the left panels) to illustrate the binding pocket. All molecular graphics in the paper were rendered with VMD.[11] The initial structure of the complex was from the RCSB Protein Data Bank (PDB code: 3HS4 [12]).

Human carbonic anhydrase II plays very fundamental roles in human physiology/pathology. It is essential in keeping the adequate balance between carbon dioxide and bicarbonate and thus controlling the pH level in cells. Mutations of hCAII have been found to cause carbonic anhydrase deficiency syndrome [13–15] leading to diseases such as osteopetrosis, renal tubular acidosis,[13, 16] and cerebral calcification.[17, 18] On the other hand, overexpression of hCAII was found to favor glaucoma.[19] An inhibitor of hCAII, N-(5-sulfamoyl-1,3,4-thiadiazol-2-yl)acetamide (namely, acetazolamide), was found to bind hCAII with a dissociation constant of 6.8 nM[20, 21] and an inhibition constant in the range of 3.3–12nM.[22–25] Near the physiological pH, AZM has multiple protonation states (shown in Fig. 2). Two pKa values (7.19 and 8.65) were experimentally determined.[26–28] These four and other protonation states can coexist as determined by several factors.[28] It should be noted that the protonation state of AZM in complex hCAII was revealed in a very interesting recent experiment employing the technique of neutron diffraction.[26] State (AZM-1a) of Fig. 2 was the observed state, which is consistent with the fact that Zn²⁺ very effectively lowers the pKa of even H₂O. Zn²⁺ can readily force the deprotonation of the sulfamoyl group when a neutral AZM falls into the binding pocket of hCAII (Fig. 1).

Fig. 2.

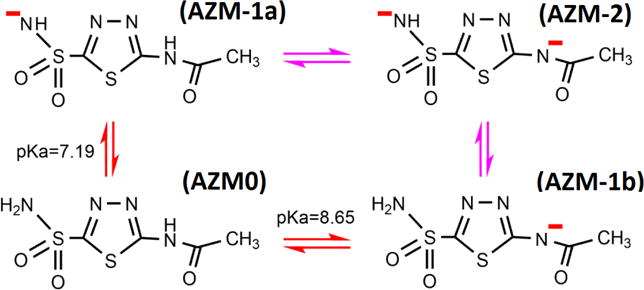
Four protonation states of AZM. State (AZM0) and State (AZM-1a) are the two states we study in this paper.

Although numerous experimental studies are available on hCAII and its inhibitors, systematic molecular dynamic (MD) simulations have not yet been done to gain the atomistic, dynamics insights and quantitative understanding of the interactions between hCAII and the available inhibitors. One of the difficulties for the theoretical/computational studies is how to accurately represent the key role played by the metal ion Zn²⁺. Now we have the experimentally determined values of the AZM-hCAII binding affinity, the structure of the AZM-hCAII complex resolved to atomistic resolutions, and even the protonation state of the metalloenzyme complex. It is time for us to obtain a quantitative computational/theoretical understanding of this fundamentally important metalloprotein-inhibitor complex in a systematic and self-consistent investigation. It is needless to note that a good understanding of these interactions will be helpful in the pursuit of new or improved inhibitors/modulators of hCAII and other carbonic anhydrases.

In this article, we present a detailed, quantitative characterization of the AZM-hCAII-Zn²⁺ binding problems on the basis of all-atom MD simulations. First, we address one of the currently debated issues by testing the non-bonded model of Zn²⁺, in which the metal ion is simply represented by two van der Waals parameters. With such a simple model, we compute the free energy of hydration of Zn²⁺. We further compute the binding characteristics of Zn²⁺ to the hCAII protein in the uninhibited and inhibited states. In all cases, our computed values agree with the experimental measurements when we use the recently refined Zn²⁺ parameters of Li et al.[29] along with the standard CHARMM parameters other than those for the divalent metal ion. Then, we compute the free energies of binding the charged form (State AZM-1a, Fig. 2) and the neutral form (State AZM0, Fig. 2) of AZM to hCAII. In this comparative study, we provide detailed, quantitative insights about the binding interactions between AZM-1a, Zn²⁺, and hCAII, all in agreement with the experimental data within the known margin of error.

METHODS

Simulation parameters

In all the equilibrium MD and nonequilibrium steered molecular dynamics (SMD) runs, we use the CHARMM36 force field [30, 31] for all the intra-and intermolecular interactions except for Zn²⁺. For Zn²⁺, we use two sets of van der Waals (vdW) parameters (shown in Table 1) in the computation of its free energy of hydration. On the basis of a better agreement between our computed and the experimentally measured values of the hydration free energy, we choose the recently refined parameter set of Li et al (Set 2 in Table 1) in the other computations: the characteristics of binding Zn²⁺ to hCAII and the absolute free energies of binding Forms (AZM0) and (AZM-1a) of AZM (Fig. 2) to hCAII-Zn²⁺.

Table 1.

vdW parameters for Zn²⁺

Parameter Sets	Rmin/2 (Å)	ε (kcal/mol)
Set 1, CHARMM default [32]	1.090	0.25
Set 2, Refined by Li et al [29]	1.271	0.0033

We implement the Langevin stochastic dynamics with NAMD[33] to simulate the systems at a constant temperature of 298 K and a constant pressure of 1 bar. The time step is 1 fs for short-range and 2 fs for long-range interactions. The PME is updated every 4 fs. The damping constant is 5/ps. Explicit solvent is represented with the TIP3P model.[34] Selected alpha carbons on the alpha helices and the beta sheets far away from the binding site are fixed to their crystal structure coordinates, fully respecting the experimentally determined metalloprotein structures. The protein complex is rotated so that the pulling is along the z-axis in the SMD runs. The pulling velocity v_d = (0, 0, ± 2.5Å/ns) unless explicitly stated otherwise.

For the AZM-hCAII binding problems, we use periodic boundary conditions in all three dimensions. Full electrostatics is implemented by the means of particle mesh Ewald (PME)[35] at the grids of 128×128×128. For the Zn²⁺ ion-hydration problem, we use periodic boundary conditions only in two dimensions (on the xy-plane that is parallel to the vacuum water interface) but not along the z-axis that is perpendicular to the water-vacuum interface.

Computing the hydration free energy of Zn²⁺

We follow the multi-sectional procedure of SMD detailed in Ref. [36]. In essence, we build a cubic box of water with each side at 80 Å; choose the coordinates so that the top side of the cube is on the xy-plane (z=0); bring a Zn²⁺ ion along the z-axis from z₀ = ∞ to z_A =10Å (outside the water box, shown in supplementary information (SI) Fig. S1(A)) and then to z_B = −8Å (deep inside the water box, shown in SI Fig. S1(B)). We compute the free energy difference (the change in the potential of mean force, PMF[37–39]) from z₀ = ∞ to z_A =10Å analytically by approximating water as a continuous medium. For this range, the attraction on the ion by the water box can be accurately approximated by the force from its image charge q′ − (ε/ε₀ −1/(ε/ε₀+1)q. Consequently,

$$G_A-G_{\infty }=\frac{q^2}{16\pi {\epsilon }_0\left|z_{\mathrm{A}}\right|}\frac{\epsilon /{\epsilon }_0-1}{\epsilon /{\epsilon }_0+1}$$ (1)

where q=2e is the charge of the ion. ε₀ is the vacuum dielectric constant. ε = 81 ε₀ is the experimentally measured dielectric constant of water.

From z_A =10Å (outside the water box) to z_B = −8Å (deep inside the water box), we conduct 18 sections (1 Å each in width) of SMD runs and use the Brownian Dynamics Fluctuation Dissipation Theorem (BD-FDT)[40] to compute the PMF difference between two states from the work measurements along the pulling paths. Pulling from State A to State B, we have the difference as follows:

$$G_{\mathrm{B}}-G_{\mathrm{A}}=\mathrm{\Delta }\mathit{PMF}=-k_{\mathrm{B}}T\text{ln}\frac{\langle \exp (-W_{\mathrm{A}\to \mathrm{B}}/2k_{\mathrm{B}}T)\rangle }{\langle \exp (-W_{\mathrm{B}\to \mathrm{A}}/2k_{\mathrm{B}}T\rangle }.$$ (2)

Here the brackets in the numerator and the same in the denominator represent the statistical averages along the forward and the reverse pulling paths, respectively. W_A→B and W_B→A are, respectively, the work done along the forward and the reverse pulling paths. k_B is the Boltzmann constant and T, the absolute temperature.

Put altogether, we have the hydration free energy of the zinc ion,

$$\mathrm{\Delta }{G}_{\text{hydration}}=G_{\mathrm{B}}-G_{\infty }=(G_{\mathrm{B}}-G_{\mathrm{A}})+(G_{\mathrm{A}}-G_{\infty }),$$ (3)

which consists of an analytical formula in Eq. (1) and a numerical evaluation in Eq. (2) involving work values obtained in the SMD runs.

It is noted here that ion hydration has long been in focus of various studies and that multiple correction factors were involved in computational approaches.[41, 42] In contrast, our approach is a straightforward way to pull an ion from vacuum into a bulk of water and measure the reversible work (the difference in potential of mean force) along the pulling path. In this simple approach, only two correction factors need to be estimated: (1) the continuous medium approximation of water when the ion is far from the water-vacuum interface (>10 Å) and (2) the finite size of the system (which is 80 Å). Our computed results, in agreement with the experimentally measured values, indicate that neither of these two factors would give rise to an error above the inevitable errors from the force field parameters. Therefore, we argue that our simple approach (pulling an ion into water) is a preferable way of hydration-energy computation.

Computing the binding affinities

We follow the procedure of the hybrid SMD (hSMD) detailed in Refs. [43, 44]. Briefly, we conduct MD runs to sample the fluctuations of the metalloprotein (hCAII-Zn²⁺) and the “ligand” (AZM) in the bound state and in the dissociated state. We conduct SMD runs to pull the ligand from the one chosen bound state (the SMD starting point) along a chosen dissociation path to the one corresponding dissociated state (the SMD end point), disallowing any fluctuations of the pulling centers along the pulling paths. In this way, we compute the PMF difference between the one dissociated state and the corresponding one bound state via BD-FDT in Eq. (2). We compute the partial partitions in the bound state from the fluctuations around the one chosen bound state which is the starting point of the SMD runs and the partial partition functions in the dissociated state from the fluctuations around the one dissociated state which is the end point of the SMD runs. Note that the PMF difference depends on the choice of the one state (the SMD starting point) and so do the two partial partitions of the bound and the dissociated states. When the three factors are combined to give the free energy of binding, however, the final result is independent of the choice of the one SMD-starting-point state as long as it is taken from within the equilibrium ensemble of the bound state.

Specifically, we choose three pulling centers illustrated in Fig. 3. The first center is the Zn²⁺ ion whose pulling velocity is kept at zero. This choice allows for an easy way to take into account the fact that the ion fluctuates in significantly different degrees when AZM is present or absent in the binding pocket. The second and the third pulling centers are the N1 and the N4 atoms of AZM (Fig. 3). The coordinates of these three pulling centers are grouped into a single row 1×9 matrix (r₁,r₂,r₃) whose transpose (r₁, r₂, r₃)^T is a single-column 9×1 matrix.

Fig. 3.

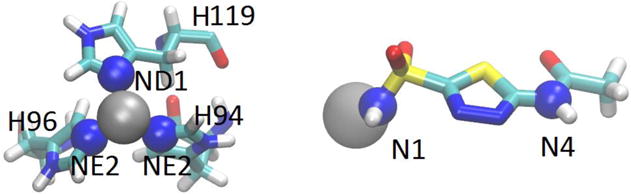
Key players of the metalloprotein and the pulling centers for SMD runs. Shown in the left panel are the zinc ion and three aromatic nitrogens of His 94, 96, and 119, represented as spheres for the computation of Zn²⁺ binding interactions. The three zinc-coordinating residues are shown in licorices colored by atom names. Shown in the right panel are the three pulling centers [the zinc ion and the N1 and N4 atoms of AZM represented as spheres] for the computation of AZM binding affinity. Colors: H, white; C, cyan; N, blue; O, red; S, yellow; and Zn, gray.

It is proven in Ref. [43] that the free energy of binding is related to the PMF difference (ΔPMF_0, ∞) and the two partial partitions as follows:

$$\mathrm{\Delta }{G}_{\text{binding}}=\mathrm{\Delta }PM{F}_{0,\infty }-k_{\mathrm{B}}T\ln (c_0{Z}_{30}/Z_{3\infty }).$$ (4)

Here c₀ =1M = 6.02×10⁻⁴ Å⁻³ is the standard concentration. The subscripts 0 and ∞ indicate the bound and the dissociated states respectively. The subscript 3 of the partial partitions indicates that three pulling centers are chosen in our study. The bound state partial partition can be well approximated as Gaussian,

$$\begin{array}{l}{Z}_{30}={\displaystyle {\int }_{\text{site}}{d}^3{x}_1{d}^3{x}_2{d}^3{x}_3\exp \left[-(\mathit{PMF}[{\mathbf{r}}_1,{\mathbf{r}}_2,{\mathbf{r}}_3]-\mathit{PMF}[{\mathbf{r}}_{10},{\mathbf{r}}_{20},{\mathbf{r}}_{30}])/k_{B}T\right]}\\ \simeq {(2\pi )}^{9/2}De{t}^{1/2}\left({\sum }_3\right)\exp \left[{\mathrm{\Delta }}_3/k_{B}T\right].\end{array}$$ (5)

Here the dimensionless quantity Δ_3/k_B^T gives a measure of how far (r₁₀,r₂₀,r₃₀), the initial state chosen for SMD, is from the PMF minimum (〈r₁〉, 〈r₂〉, 〈r₃〉)

$${\mathrm{\Delta }}_3/k_{B}T=\frac{1}{2}\left(\langle {\mathbf{r}}_1\rangle -{\mathbf{r}}_{10},\langle {\mathbf{r}}_2\rangle -{\mathbf{r}}_{20},\langle {\mathbf{r}}_3\rangle -{\mathbf{r}}_{30}\right){\sum }_3^{-1}{\left(\langle {\mathbf{r}}_1\rangle -{\mathbf{r}}_{10},\langle {\mathbf{r}}_2\rangle -{\mathbf{r}}_{20},\langle {\mathbf{r}}_3\rangle -{\mathbf{r}}_{30}\right)}^T.$$ (6)

Det represents the determinant. Σ₃ is the 9×9 matrix of the fluctuations/deviations of the pulling center coordinates r₁ − 〈r₁〉 etc. in the bound state ensemble,

$${\sum }_3=\langle {({\mathbf{r}}_1-\langle {\mathbf{r}}_1\rangle ,{\mathbf{r}}_2-\langle {\mathbf{r}}_2\rangle ,{\mathbf{r}}_3-\langle {\mathbf{r}}_3\rangle )}^T({\mathbf{r}}_1-\langle {\mathbf{r}}_1\rangle ,{\mathbf{r}}_2-\langle {\mathbf{r}}_2\rangle ,{\mathbf{r}}_3-\langle {\mathbf{r}}_3\rangle )\rangle .$$ (7)

Σ₃⁻¹ is the inverse matrix of Σ₃ which can be accurately evaluated by running equilibrium MD in the bound state of the ligand-protein complex. This approximation is valid because the pulling centers do not deviate much from the binding site. The brackets represent the ensemble average throughout this paper.

The partial partition function Z_3∞ of the dissociated state has the integration over 2 (=3−1) centers,

$$Z_{3\infty }={\displaystyle \int d^3{x}_1\int d^3{x}_2\exp }\left[-(\mathit{PMF}[{\mathbf{r}}_1,{\mathbf{r}}_2,{\mathbf{r}}_{3\infty }]-\mathit{PMF}[{\mathbf{r}}_{1\infty },{\mathbf{r}}_{2\infty },{\mathbf{r}}_{3\infty }]/k_{B}T\right].$$ (8)

Note that, in the dissociated state, the third pulling center (the N4 atom of AZM) is fixed in a position far outside the binding pocket while the two other centers (the Zn²⁺ ion and the N1 atom of AZM) freely sample the space available to them, which are represented in the double 3D integrals in Eq. (8). In this case, AZM is far away from Zn²⁺ and, therefore, the two 3D integrations can be carried out independently. The fluctuations of the first center (Zn²⁺ ion) can be approximated as Gaussian and thus the corresponding partial partition Z_1∞ can be easily evaluated by sampling the fluctuations of the Zn²⁺ ion in the dissociated state. The fluctuations of the second center (the N1 atom of AZM) are not small and cannot be approximated as Gaussian but they are isotropic around the third center (N4 which is far away from the protein). The 3D integration can be readily reduced into a 1D integral. In this, we have the following approximation:

$$Z_{3\infty }-Z_{1\infty }{Z}_{2\infty },Z_{2\infty }=4\pi \int dr{r}^2{e}^{-(\text{PMF}(\mathrm{r})-\text{PMF}({\mathrm{r}}_0))/k_{\mathrm{B}}T}.$$ (9)

Here, r₀ is the N1-N4 distance in the dissociated state (which is identical to the value in the bound state as N1 and N4 are pulled with identical velocities during the SMD runs).

Simulation systems of AZM-metalloenzyme complexes

We take Sippel et al’s high-resolution crystallographic structure of human carbonic anhydrase II complexed with AZM (PDB code: 3HS4),[12] rotate it so that the opening of the enzyme’s binding pocket is approximately along the z-axis (Fig. 1, right panel) for the convenience of SMD runs, place the complex (which happens to be neutral) in a box of water whose dimensions are 80 Å along the x- or y-axis but 100 Å along the z-axis, and salinate the system with 150 mM NaCl. In this way, we build an all-atom system for the charged AZM (AZM-1a) consisting of 60300 atoms.

RESULTS AND DISCUSSION

H₂O-Zn²⁺ interactions

Foremost among all ion interactions in a biological system are the interactions with water molecules. For the purpose of choosing an optimum set of parameters, we computed the free energy of zinc hydration using both sets of parameters in Table 1. The PMF curves along the Zn²⁺ hydration path are shown in Fig. 4(A). Note that, from z = ∞ to z_A =10Å, the reversible work [Eq. (1)] is equal to −32.7 kcal/mol. Combining this analytical approximation with the numerical values in Fig. 4(A), the computed hydration energy is −427 kcal/mol for Set 1 and −471 kcal/mol for Set 2. The latter value is in close agreement with the accepted experimental data in the literature, −468 kcal/mol of Marcus.[45]

Fig. 4.

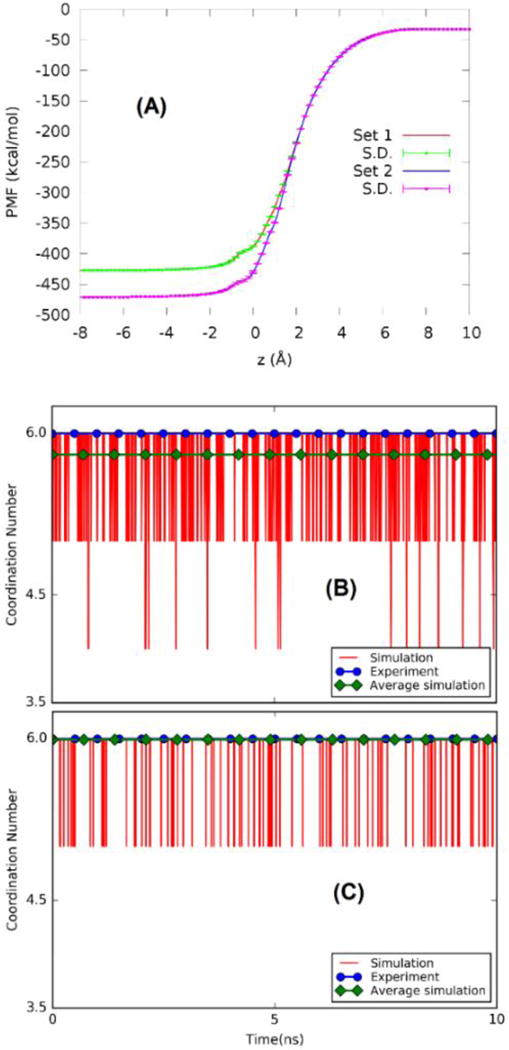
Ion-water interactions. (A) PMF curves along the path of Zn²⁺ hydration for vdW parameters Set 1 vs Set 2 (Table 1). (B) Coordination numbers for Set 1. (C) Coordination numbers for Set 2.

Furthermore, we computed the coordination numbers of waters around the Zn²⁺ ion using both sets of parameters. The coordination number of waters at a given instant was computed as the number of water molecules whose oxygen atoms are within 2.2 Å from the Zn²⁺ ion. In Fig. 4 (B) and (C), we illustrate the instantaneous fluctuations where deviations from the value of 6.0 are explicitly shown along with the time averages and the experimentally measured value. Again, the parameter Set 2 of Li et al[29] corresponds extremely well with the experimental measurements.[46] Therefore, in the rest of this study, we use only this set of parameters.

hCAII-Zn²⁺ interactions

The key players in hCAII-Zn²⁺ interactions are the three histidine residues (His 94, 96, 119) that coordinate the zinc ion. In particular, NE2 of HSD 94, NE2 of HSD 96, and ND1 of HSE 119 are bonded to Zn²⁺. Therefore, the distances from these three nitrogen atoms to the zinc ion fluctuate around their mean values in small amplitudes. The computed values of these distances are shown in Fig. 5 as functions of time for the last 10 ns of the equilibrium MD runs. The fourth partner of the zinc coordination is H₂O or OH⁻ when the enzyme is not inhibited by AZM (“apo” in Fig. 5), or the NH-end of AZM when inhibited (“holo” in Fig. 5). The Zn-N1 and the Zn-O distances are also shown in Fig. 5. It is noted that our computed values on the basis of parameter Set 2 are all within 10% of experimentally measured geometries of the crystal structures.[12, 47] The fluctuations are indeed small in our stochastic dynamics simulations.

Fig. 5.

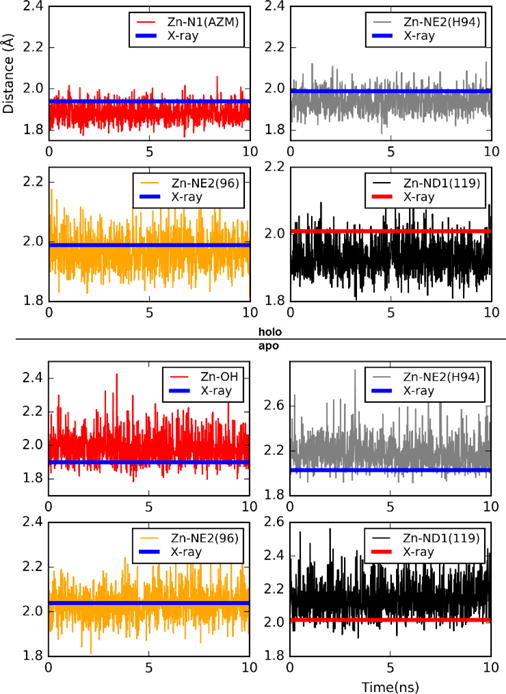
Zn²⁺ distances from directly interacting atoms when AZM is bound to the protein (top four panels, marked as “holo”) and when AZM is away from the protein (bottom four panels, marked as “apo”). The X-ray structure of AZM-hCAII-Zn²⁺ (holo) was taken from Ref. [12] and the same of hCAII-Zn²⁺ (apo) from Ref. [47].

AZM-hCAII-Zn²⁺ interactions

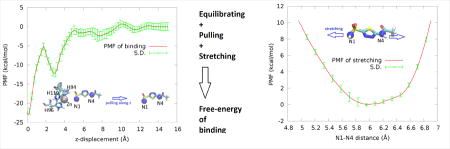
In order to quantify the binding affinity of AZM to the metalloenzyme, we took the charged form shown in Fig. 2 (AZM-1a). We conducted hSMD runs with three pulling centers (Fig. 6, top panel inset) and computed the PMF along the AZM dissociation path (Fig. 6, top panel). These hSMD runs gave us a PMF difference between the starting point, one state chosen from the ensemble of bound states and the corresponding one state in the ensemble of dissociated states,

$$\mathrm{\Delta }PM{F}_{0,\infty }=-22.0\pm 1.8\text{kcal/mol}.$$ (10)

Fig. 6.

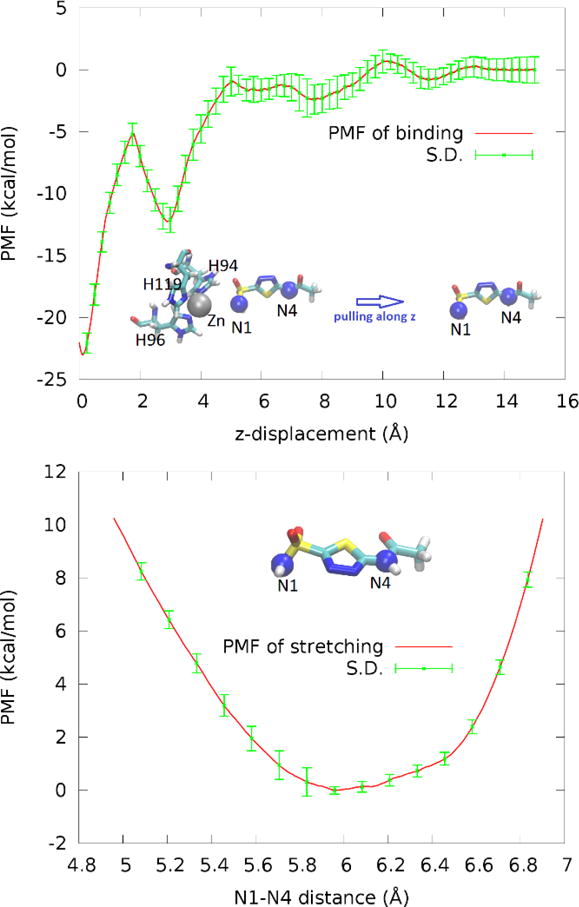
PMF along the dissociation path of pulling AZM from hCAII-Zn²⁺ (top panel) and PMF as a function of the distance between two pulling centers (N1 and N4) of AZM in the dissociated state (bottom panel). In the insets, the pulling centers are shown as spheres (N1, N4, blue; Zn²⁺, gray). AZM and the zinc coordinating residues are shown in licorices.

We sampled the fluctuations of the three puling centers in the bound state ensemble (SI, Figs. S2) and computed the partial partition of the bound state ensemble,

$$Z_{30}=1.01\times {10}^{-3}{\stackrel{\circ }{\mathrm{A}}}^9.$$ (11)

Here the subscript 3 represents the number of pulling centers and the subscript 0 indicates the bound (holo) state.

In the apo state when AZM is far out of the binding pocket, we conducted hSMD runs with two pulling centers (Fig. 6, bottom panel) stretching and compressing AZM and thus determined the PMF as a function of the N1-N4 distance r. Integrating the PMF of stretching/compressing AZM, we obtained the partial partition of AZM in the dissociated state,

$$Z_{2\infty }=205.15{\stackrel{\circ }{\mathit{A}}}^3.$$ (12)

In the meantime, we also sampled the fluctuations of the other pulling center Zn²⁺ when AZM is far away. The Zn²⁺ fluctuations gave us a partial partition of

$$Z_{1\infty }=0.08508{\stackrel{\circ }{\mathrm{A}}}^3.$$ (13)

Putting these factors together, we obtained the partial partition of the dissociated state ensemble,

$$Z_{3\infty }=Z_{1\infty }{Z}_{2\infty }=17.45{\stackrel{\circ }{\mathrm{A}}}^6.$$ (14)

Pulling the results in Eqs. (10), (11), and (14) together into Eq. (4) as formulated in Refs. [43, 44], we obtained the absolute free energy of binding AZM⁻ to hCAII-Zn²⁺,

$$\mathrm{\Delta }{G}_{\text{binding}}=-11.87\pm 1.8\text{kcal/mol}.$$ (15)

The error bar can be estimated from those in the PMF curves (Fig. 6) to be ±1.8 kcal/mol. This computed value of binding free energy does agree with the experimentally measured value of −10.8 kcal/mol.[21] For a clear contrast, we also computed the absolute binding free energy of neutral AZM (Fig. 2(AZM0)) to hCAII-Zn²⁺. The computed value of the binding free energy is −2.4±1.8 kcal/mol (dissociation constant 15 mM) which is very far from the experimentally measured value of −10.8 kcal/mol.[21] The details of the hSMD study of the neutral AZM are included in the SI. This large deviation, in light of the fact that our computed value of −11.9±1.8 kcal/mol for the charged AZM (Fig. 2(AZM-1a)) agrees with the experimental measurements, leads us to conclude that AZM bound to the metalloenzyme hCAII-Zn²⁺ is confirms the findings of the neutron diffraction experiments by Fisher et al.[26]

CONCLUSIONS

On the basis of the all-atom CHARMM force field parameters including the recently refined zinc parameters, our extensive simulations lead us to these conclusions: The key biophysical/biochemical interactions of the divalent zinc ion with the aqueous environmental factors, with the protein, and with the hCAII inhibitor, AZM, can all be well approximated with a simple ion model using the refined vdW parameters of Li et al.[29] The existence of the divalent zinc ion at the active site causes the three coordinating residues of hCAII to have different protonation states: Residues 94 and 96 are HSDs and Residue 119 is HSE as shown in Fig. 3, left panel. In the uninhibited state of the metalloprotein, the zinc ion also causes a decrease in the pKa of a water bound to it, from 14 in the bulk to approximately 7, and thus facilitates the reversible conversion between H₂ O and OH⁻+H⁺ In the inhibited state of hCAII, the divalent zinc can readily cause the deprotonation of the amino end of AZM, significantly lowering its pKa from its free form value of 7.18. The inhibitor lodged in the binding pocket is indeed in the charged form (carrying a negative charge) instead of being neutral. We expect that the atomistic and dynamic insights from our systematic all-atom simulations will be useful in the pursuit of better hCA inhibitors.

HIGHLIGHTS.

All-atom molecular dynamics of the most efficient metalloenzyme in agreement with experimental data; A simple representation of the divalent cation Zn²⁺ shown to be accurate enough for its hydration, its complexation with hCAII, and the binding affinity of an inhibitor it co-effects.