Effect of Solvent Evaporation on Fiber Morphology in Rotary Jet-Spinning

Abstract

The bulk production of polymeric nanofibers is important for fabricating high performance, nano-scale materials. Rotary Jet-Spinning (RJS) enables the mass production of nanostructured fibers by centrifugal forces but may result in inconsistent surface morphologies. Because nanofiber performance is dependent on its surface features, we asked which parameters must be optimized during production to control fiber morphology. We developed and tested a mathematical model that describes how the competition between fluid instability and solvent removal in RJS regulates the degree of beading in fibers. Our data suggests that solvent evaporation during the spinning process causes an increase in jet viscosity and that these changes inhibit both bead formation and jet thinning. The RJS was used to vary experimental parameters showing that fiber beading can be reduced by increasing solvent volatility, solution viscosity, and spinning velocity. Collectively, our results demonstrate that nanofiber morphology and diameter can be precisely controlled during RJS manufacturing.

Graphical abstract

Introduction

Nanofibers are utilized for applications ranging from energy^{1, 2} to tissue engineering^{3, 4} due to their large surface area to volume ratio. For example, the energy harvesting efficiency within nanofibers is proportional to its exposed surface area, which is maximized in fine, defect-free fibers.² Defects within a nanofiber-based scaffold for biological tissues may degrade cell migration and tissuegenesis.^{5, 6, 7} Although there has been a significant effort to understand nanofiber geometry and surface topography through empirical studies^{8, 9, 10} and modeling,^{11, 12, 13, 14} methods to control surface malformations, or beading, during bulk manufacturing remain elusive. In order to optimize nanomaterials for specialized applications, it is necessary to first identify and then control the parameter space used in fiber production.

Rotary Jet-Spinning (RJS)^{14, 15, 16, 17, 18} is an efficient and reproducible manufacturing technique developed for the bulk nanofiber production. In this system, a high speed, rotating reservoir projects a fluid jet from a micron-sized orifice towards a collector. The high speed rotation and solvent evaporation enables production of nanoscale polymer fibers. RJS surpasses the electrospinning technique^{11, 12, 15} in both production rate and utility,¹⁹ with a speeds up to 5–6 times higher while eliminating the requirements of an external electric field or a charged solution.¹⁶ We asked how nanofiber morphology, including beading and fiber diameter, is regulated during RJS manufacturing. Previous analytical, empirical, and numerical studies suggest that fiber diameter is reduced by decreasing viscosity or by increasing rotation speed.^{13, 14} However, decreasing either viscosity or rotation speed independently increases the incidence of surface defects, such as beading.¹³

We hypothesize that bead formation occurs due to Rayleigh instabilities within fluid jets and that smooth, bead-free fibers form as a result of faster solvent evaporation. We developed an analytical model that balances this fluid instability and fiber drying. To test the model, we manufactured fibers using solutions with a range of viscosities and solvent volatilities. Our results suggest a mechanism of bead reduction that depends not only on tuning viscosity and rotation speed as formerly suggested,¹³ but also due to inhibition of Rayleigh instabilities via solvent evaporation.

Methods Section

Solution Preparation

Polylactic acid (PLA) (polymer 2002D, NatureWorks®, Minnetonka, MN) was dissolved in chloroform (99.8%, Mallinckrodt Chemicals, Phillipsburg, NJ) and dimethylformamide (DMF) (Sigma Aldrich, St. Louis, MO) at room temperature by stirring.

Fiber Fabrication

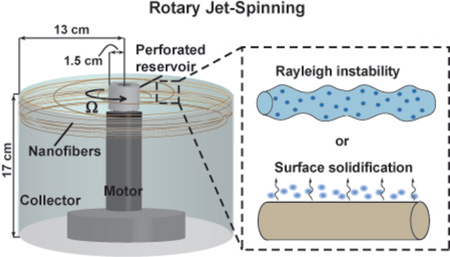
The RJS system used to manufacture fibers is depicted in Figure 1a. The RJS consisted of a brushless DC servo motor (Maxon Motor Company, Fall River, MA) attached to a custom fabricated reservoir with a 343 µm sidewall orifice. Solutions (1 ml) were spun at angular speeds, Ω, up to 75,000 rpm and collected at the spinning midpoint to ensure sample uniformity. Samples were Pt/Pd coated using a sputter coater (Cressington 208HR, Watford, England) and imaged using a Zeiss SUPRA field-emission scanning electron microscope (SEM) (Carl Zeiss, Dresden, Germany).

Figure 1.

Variable fiber morphologies of RJS. (a) Schematic of the RJS setup. A solution of polylactic acid (4 wt% in chloroform) is spun using RJS. Fibers collected have variable morphologies including (b) beads and malformations, (c) beads on a string (beaded fiber), or (d) continuous, defect-free fibers. (b–d) Scale bars are 20 µm.

Solution Properties

Polymer solution surface tension was measured with a Sigma700 Tensiometer (KSV instruments, Espoo, Finland). Solution viscosity was measured in a rheometer (Model AR-G2, TA instruments, New Castle, DE) fitted with a standard-size recessed end concentric cylinder geometry (model 988339, outer radius 14 mm, inner radius 15 mm, 4000 µm gap) under steady state shear rate from 0.1 – 3000 s⁻¹.

Analysis

Number of beads or malformations in each experiment was calculated by manually thresholding SEM images in ImageJ (National Institute of Health, Bethesda, MD) and measuring polymer area in beads or malformations. Phase diagrams consist of points marking the transition from samples consisting of non-uniform fibers (samples with >5% beads or malformations) to samples consisting of continuous fibers (samples with <5% beads or malformations). A threshold value of 5% was chosen for consistency with previously published work.¹³ A total of n = 24 fields of view at 2500× (~0.01mm²) and 7500× (~10⁻³mm²) magnification were analyzed per condition.

The flux of mass transfer of solvent at the jet surface

The local steady state convection-diffusion equation for the solvent mass concentration ρ near the jet surface can be approximated as: $V_x\frac{\partial \rho }{\partial x}=D_{\mathit{\text{air}}}\frac{{\partial }^2\rho }{\partial y^2}$, where D_air is the solvent diffusion constant in air, x axis is tangential to the local surface and y axis is perpendicular to the local surface, V_x is the air flow speed relative to the jet. A length scale of mass diffusion L_y near the local surface can be determined by scale analysis: $V_x\frac{\rho }{L_x}=D_{\mathit{\text{air}}}\frac{\rho }{L_y{}^2}$. Assuming V_x ~ ΩS₀, and L_x ~ R, where R is the jet radius and S₀ is the reservoir radius, one has $L_y~{\left(\frac{D_{\mathit{\text{air}}}R}{\Omega S_0}\right)}^{1/2}$. The flux J for surface mass transfer can then be written as $J=D_{\mathit{\text{air}}}\frac{\partial \rho }{\partial y}~D_{\mathit{\text{air}}}\frac{{\rho }_a}{L_y}$, where ρ_a is the solvent vapor concentration in the air near the fiber surface. Substituting L_y into the flux equation $J~D_{\mathit{\text{air}}}\frac{{\rho }_a}{L_y}$ gives

$$J~{\rho }_a{(\frac{D_{\mathit{\text{air}}}{s}_0}{R})}^{1/2}{\Omega }^{1/2}.$$ (1)

Here ρ_a can be related to solvent vapor pressure P by the ideal gas equation as ${\rho }_{\mathrm{a}}=\frac{PM}{R_{\mathit{\text{gas}}}T}$, where M is the solvent molecule molar mass, R_gas is the ideal gas constant, and T is temperature. Substituting this expression of ρ_a into equation (1), solvent removal flux J can be approximated as

$$J~\frac{PM}{R_{\mathit{\text{gas}}}T}{\left(\frac{D_{\mathit{\text{air}}}{s}_0}{R}\right)}^{1/2}{\Omega }^{1/2}.$$ (2)

Time scale of surface layer solidification

The time scale of surface layer solidification is much shorter than that of complete solvent evaporation. The surface layer solidification time scale is governed by two physical processes: (1) solvent evaporation at the boundary and (2) solvent diffusion from the fiber center to the boundary. The mass transport by diffusion in the long cylindrical jet can be treated as radially symmetric. Therefore, the solvent density ρ is a function of the radial coordinate r and time t only. The diffusion equation²⁰ can then be written as $\frac{\partial \rho }{\partial t}=\frac{1}{r}\frac{\partial }{\partial r}\left(rD\frac{\partial \rho }{\partial r}\right)$, where D ~ 10⁻⁷cm²/s is the solvent diffusion constant in the polymer solution.²¹ The initial condition is ρ(r, t) = 0 = ρ₀. The boundary conditions are ${D\frac{\partial \rho }{\partial r}|}_{r=R}=J$, and ${\frac{\partial \rho }{\partial r}|}_{r=0}=0$, where ρ₀ is the initial solvent mass concentration in the jet, the flux J is given by equation (2). The solvent density at the jet surface (r = R) as a function of time can be written²⁰ as $\rho (R,t)={\rho }_0-\frac{JR}{D}\{\frac{2Dt}{R^2}+\frac{1}{4}-2{\sum }_{n=1}^{\infty }\frac{\mathit{\text{exp}}(-D{\alpha }_n^{2}t/R^2)}{{\alpha }_n^2}\}$, when α_n > 0 and satisfies J₁(α_n) = 0, where J₁ is the Bessel function of the first kind. Assuming that the solidification occurs at the surface when ρ(R, t) = ρ̄, then the time scale τ_s can be obtained using the following equation,

$$\overline{\rho }={\rho }_0-\frac{JR}{D}\{\frac{2D{\tau }_s}{R^2}+\frac{1}{4}-2{\sum }_{n=1}^{\infty }\frac{\mathit{\text{exp}}(-\frac{D{\alpha }_n^2{\tau }_s}{R^2})}{{\alpha }_n^2}\}.$$ (3)

It can be numerically shown that the sum, $\frac{2D{\tau }_s}{R^2}+\frac{1}{4}-2{\sum }_{n=1}^{\infty }\frac{\mathit{\text{exp}}(-D{\alpha }_n^2{\tau }_s/R^2)}{{\alpha }_n^2}$, is approximately equal to $\sqrt{\frac{D{\tau }_s}{R^2}}$ when ${\tau }_s\ll \frac{R^2}{D}$. The diffusion time scale, $\frac{R^2}{D}$, is in the range of 10⁻¹ – 10⁻³ s by estimating R as 10⁻⁷ – 10⁻⁶ m. For successful fiber formation, τ_s should be less than the spinning time scale, the reciprocal of angular spinning speed, which is ~ 10⁻³ s. Therefore, the condition ${\tau }_s\ll \frac{R^2}{D}$ is satisfied, and equation (3) can be simplified as $\overline{\rho }={\rho }_0-\frac{JR}{D}\sqrt{\frac{D{\tau }_s}{R^2}}$. Solving for τ_s, we have ${\tau }_s=D{\left(\frac{{\rho }_0-\overline{\rho }}{J}\right)}^2$. Substituting equation (2) into it, we obtain the timescale of surface layer solidification as

$${\tau }_s={\left(\frac{R_{\mathit{\text{gas}}}T}{PM}\right)}^2\frac{DR{({\rho }_0-\overline{\rho })}^2}{D_{\mathit{\text{air}}}{s}_o\Omega }.$$ (4)

Equation (4) is used to illustrate the effect of solvent evaporation on fiber diameter and to derive the condition for production of continuous fibers.

Results and Discussion

The RJS system consists of a rotating reservoir that extrudes a fluid jet from a micron sized orifice towards a collector to form solid nanofibers (Figure 1a). To initiate fiber formation, polymer solutions are injected into the reservoir spinning at speeds, Ω, up to 75,000 rpm, projecting the jet through the 343µm diameter orifice. The jet is elongated, traveling in a spiral trajectory towards a stationary cylindrical wall ~10 cm from the reservoir. During this stage, polymer chains extend and entangle while the solvent evaporates to yield a combination of malformed (Figure 1b), beaded (Figure 1c), and continuous (Figure 1d) nanofibers.

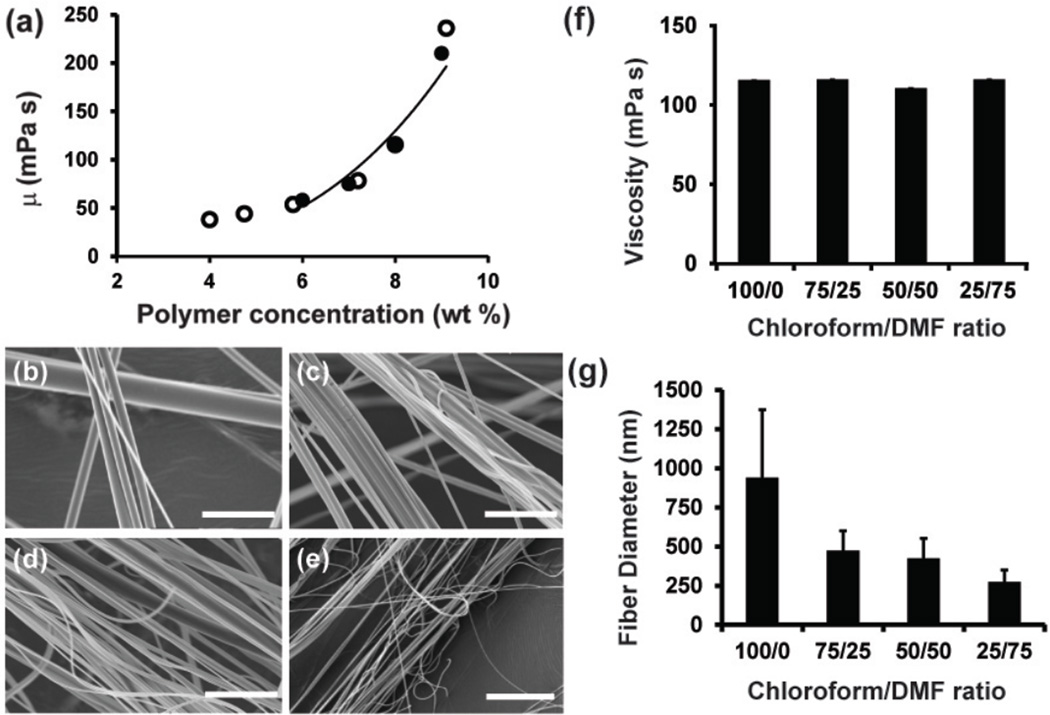
We first asked how the solvent evaporation rate of extruded polymer solutions impacts final fiber diameter. The solvent removal process can be divided into two stages. In stage I, the jet travels in air resulting in forced convective mass transfer of solvent at the jet surface. In this stage, the solvent evaporation rate is dependent on spinning speed. In stage II, the remaining solvent diffuses through the polymer matrix and evaporates after the fibers land on the collector. Because nanoscale fibers are collected immediately after spinning, we assume fiber diameter is determined during jet elongation in stage I. Therefore, we focus on solvent evaporation in stage I. The solution viscosity remains nearly constant when polymer concentration c < 6% g/ml as shown in Figure 2a. Viscosity also increases with polymer concentration by a power law (μ ~ μ_i(c/c_i)^3.2) when c ≥ 6% g/ml, where c_i ~ 6% g/ml, μ_i ~ 58 mPa · s. Only a small amount of solvent evaporation is necessary in stage I to bring polymer concentration at the jet surface to a viscosity high enough such that the polymer solution becomes solid-like. A previously obtained scaling relation between fiber radius R, viscosity μ, and angular spinning speed Ω¹³ suggested that fiber diameter increases with solution viscosity. However, the relationship between solvent evaporation and diameter has not been determined.

Figure 2. Effect of solvent volatility on fiber diameter.

(a) Viscosity as a function of polymer concentration for solutions of PLA in 100/0 Chloroform/DMF (open circles) and 75/25 Chloroform/DMF (closed circles). The line is fitted by a power law for c ≥ 6% g/ml using chloroform and chloroform/DMF data points. (b) SEM images of PLA fibers spun from a 8 wt% solution in 100/0 (c) 75/25 (d) 50/50 and (e) 25/75 Chloroform/DMF. (f) Viscosity of 8 wt% PLA solutions of 100/0 Chloroform/DMF, 75/25 Chloroform/DMF, 50/50 Chloroform/DMF, and 25/75 Chloroform/DMF (n=3 solutions measured per condition) (g) Graph of PLA nanofiber diameters with varying solvent conditions (n=5 ROIs, 200 measurements per image). Error is standard deviation. Scale bars are (b–e) 5µm.

We hypothesize that faster solvent evaporation leads to increased jet viscosity and hence larger fiber diameters. To test this hypothesis empirically, we varied the ratios of chloroform and dimethylformamide (DMF) to tune the evaporation rate and measured fiber diameter using SEM and image analysis. Chloroform (vapor partial pressure P =21.2 kPa) is a more volatile organic solvent than DMF (vapor partial pressure P =0.36 kPa). Thus, increasing the ratio of chloroform to DMF increases the amount of solvent evaporation. Here, PLA nanofibers were formed from composite solutions containing chloroform/DMF ratios ranging from 100/0 to 25/75 (Figure 2b–e). To determine the effect of solvent volatility on viscosity, we measured the viscosity for 8 wt% PLA solutions dissolved in chloroform/DMF ratios of 100/0, 75/25, 50/50, and 25/75. We observed no significant differences in viscosities as a function of solvent composition (Figure 2f). However, we found that fiber diameter increases with increasing solvent volatility (Figure 2g). These results suggest that a more volatile solvent leads to faster solvent evaporation, which increases polymer concentration and viscosity during drying, resulting in larger fiber diameters. These results suggest that fiber diameter can vary independently of solution viscosity and rotation speed; specifically, increasing the solvent volatility leads to increased polymer concentration and hence fluid jet viscosity during stage I, resulting in larger diameter fibers.

In order to better illustrate the effect of solvent evaporation on fiber production, we derived a scaling relationship describing the time scale of jet surface solidification in stage I as a function of experimental parameters. In RJS, fibers move with a speed ~ ΩS₀ relative to ambient air, where Ω is the angular spinning speed of the reservoir and S₀ ~ 1.4 cm is the radius of the reservoir. Solvent removal occurs by forced convective mass transfer at the jet surface. The Reynolds number Re of the air flow relative to fiber is $\mathit{\text{Re}}=\frac{\Omega S_{0}R}{{\upsilon }_{\mathit{\text{air}}}}~1$, where the kinematic viscosity of air at room temperature is ${\upsilon }_{\mathit{\text{air}}}~1.6\times \frac{{10}^{-5}{m}^2}{s}$. Assuming for low Reynolds numbers Re ~ 1, we derived the mass transfer flux of solvent from the jet to air based on the convection-diffusion equation and the surface solidification time scale as ${\tau }_s={\left(\frac{R_{\mathit{\text{gas}}}T}{PM}\right)}^2\frac{DR{({\rho }_0-\overline{\rho })}^2}{D_{\mathit{\text{air}}}{S}_0\Omega }$ (which is equation (4) in methods). Equation (4) shows that higher volatility solvent results in larger fiber diameters as a consequence of jet surface solidification due to solvent evaporation slowing jet elongation. The theoretical result obtained here agrees qualitatively with the experimental data in Figure 2(g), in which fiber radius decreases as the solvent becomes less volatile.

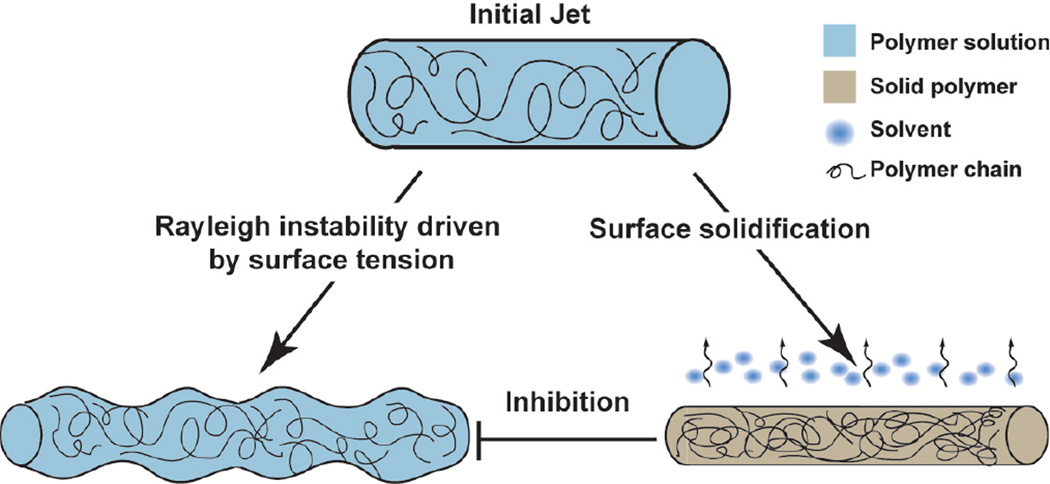
Next, we asked if decreased solvent volatility decreased the number of surface defects. We sought to determine how the rate of solvent removal scaled with Rayleigh instability and subsequent bead formation using a theoretical approach. Rayleigh instability theory states that cylindrical threads of viscous fluid will develop instabilities or varicose morphology within a certain time scale.²² This theory has been applied to polymer solutions in rheology,²³ threads of human saliva,²⁴ and electrospun jets,²⁵ but has not been applied to RJS formed fibers. In RJS, bead formation occurs because the surface tension is minimized in a spherical geometry subsequently resulting in a minimized surface area. A simple geometric calculation shows that when a long cylindrical jet breaks into spherical beads with diameter larger than 1.5 times of the initial jet diameter, the total surface area decreases. While surface tension drives bead formation, the surface solidification occurring in RJS inhibits beading when the jet becomes too viscous to flow into a varicose morphology, as depicted in Figure 3. A cylindrical polymer jet ejected from the RJS orifice results in a smooth or beaded nanofiber. This result is potentiated by the competition between solvent removal and surface tension-driven Rayleigh instabilities.

Figure 3.

Schematic of forces acting on polymer solutions upon exiting the RJS orifice. Cylindrical polymer jets ejected from the spinning reservoir result in beaded or smooth fibers when the jet elongation stage is dominated by surface tension driven Rayleigh instabilities or solvent evaporation, respectively.

The time scale τ_b of beading for a cylindrical column of viscous fluid can be obtained by considering the force equilibrium between the viscosity $\mu \frac{(R/{\tau }_b)}{R^2}$ and surface tension $\frac{\sigma }{R^2}$. Equating these two terms yields

$${\tau }_b~\frac{R\mu }{\sigma }.$$ (5)

The number of beads in RJS can be estimated by comparing the time scale of Rayleigh instability and that of surface solidification. Beaded fibers form when the timescale of Rayleigh instability, τ_b, is less than the timescale of surface solidification, τ_s. On the other hand, continuous fibers form when τ_b > τ_s, because the jet surface becomes solid-like before the fiber develops beads. Substituting equations (4) and (5) into the inequality τ_b > τ_s, we obtain the condition for the production of continuous fibers:

$$\Omega \mu P^2>C_{\text{fit}}\sigma {(\frac{R_{\mathit{\text{gas}}}T}{M})}^2\frac{D{({\rho }_0-\overline{\rho })}^2}{D_{\mathit{\text{air}}}{s}_o},$$ (6)

where C_fit is added as a numerical factor to be fitted. Equation (6) predicts that beading can be reduced either by decreasing the rate of Rayleigh instability, or by increasing viscosity μ, or by increasing the rate of surface solidification.

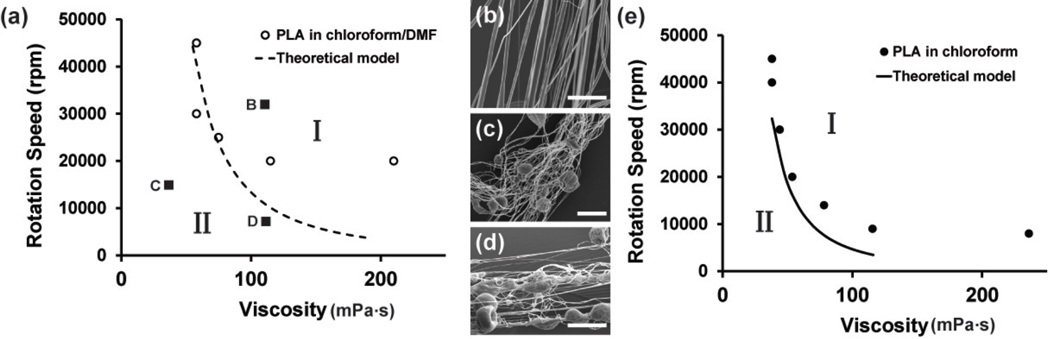
To test whether our model can predict bead formation, we used the RJS to spin fibers from varying solutions of PLA dissolved in chloroform and chloroform/DMF (75/25) solvents (Figure 4). The resulting fiber morphologies were analyzed within a phase diagram in the Ω − μ space, as shown in Figure 4. The circles mark the transition from continuous fibers with less than 5% beads to beaded fibers for PLA spun in chloroform/DMF (75/25) (Figure 4a). For example, fibers spun at 35,000 rpm from 7.5% PLA in chloroform/DMF (75/25) have <5% beads (Figure 4b). However, samples spun at low viscosity and moderate speed (2.5 wt% at 25,000 rpm, Figure 4C) or high viscosity and low speed (7.5 wt% at 10,000 rpm, Figure 4d) have significantly more beading present. The curve in Figure 4a marks the transition boundaries from the model predictions, plotting $\Omega =\frac{1}{P^2}{C}_{\text{fit}}\sigma {\left(\frac{R_{\mathit{\text{gas}}}T}{M}\right)}^2\frac{D{({\rho }_0-\overline{\rho })}^2}{D_{\mathit{\text{air}}}{S}_0}{\mu }^{-1}$. In Figure 4a, region I above the transition curve indicates the continuous-fiber phase (Figure 4b), while the regions below the transition curves are the beaded phase (Figure 4c and d). The trend of the experimentally determined transition boundaries (open circles in Figure 4(a) and closed circles in Figure 4(e)) match with the model predictions (dashed line in Figure 4(a) and solid line in Figure 4(e)) that show increasing Ω or μ reduces beading.

Figure 4.

(a) Phase diagram of PLA nanofibers spun in chloroform/DMF 75/25 is plotted in the angular speed, Ω - solution viscosity, μ plane. Circles represent the experimentally determined transition between fibers with <5% beads (regime I) and >5% beads (regime II). (b) Fibers spun at 35,000 rpm from 7.5% PLA in chloroform/DMF (75/25) (c) Fibers spun at 25,000 rpm from 2.5% PLA in chloroform/DMF (75/25) (d) Fibers spun at 10,000 rpm from 7.5% PLA in chloroform/DMF (75/25). (e) Phase diagram of PLA nanofibers spun in chloroform is plotted in the Ω-μ plane. Closed circles represent the transition from <5% beads (regime I) and regime II >5% beads (regime II). Equation (6) is plotted for both (a) and (e) and qualitatively agrees with the experimental data.

To further demonstrate the utility of our model for multiple solvent volatilities, we compared it to an empirical phase diagram for PLA in chloroform only. We show that our model similarly matches our experimental data (Figure 4e) repeated from empirical phase diagrams previously published.¹³ In addition, equation (6) predicts that when the solvent volatility P increases, the transition curve will move downward in the Ω − μ space. This is suggested by comparing the experimental data in Figure 4a with Figure 4e, suggesting that the beading transition curve shifts downward as the solvent becomes less volatile (chloroform in Figure 4e compared to chloroform/DMF(75/25) in Figure 4a, respectively). Additionally, this data suggests that lower spinning speeds are required to form continuous fibers using highly volatile solvents and other common solutions including less volatile, aqueous solvents would require higher spinning speeds to form defect-free fibers. In other words, more volatile solvents increase the range of the continuous-fiber phase in the Ω − μ space meaning a broader range of fiber diameters can be obtained. This addition enables the production of continuous fibers and less beaded structures during nanofiber production.

Conclusion

From our results, we conclude that the physical mechanism of bead formation in RJS is a competition between the timescales of Rayleigh instability and solvent evaporation rate. Our experimental data and theoretical analysis reveal that fiber drying, a result of solvent evaporation, plays an important role in determining nanofiber morphology in RJS. Solvent evaporation rate can be controlled by changing solvent volatility and rotation speed. Increasing solvent volatility, while holding viscosity constant, produces larger fiber diameters by inhibiting jet thinning. However, increasing both solvent volatility and spinning speed prohibits bead formation in RJS fibers by increasing the polymer concentration in the jet and drying fibers before Rayleigh instabilities develop. The analytical model we derived here can be used for precise morphology control during production. These findings may increase the utility of RJS when forming nano-scale materials with applications that require defect-free fibers such as energy harvesting and tissue engineering.