Frequency Domain Ultrasound Waveform Tomography: Breast Imaging Using a Ring Transducer

Abstract

Application of the frequency domain acoustic wave equation on data acquired from ultrasound tomography scans is shown to yield high resolution sound speed images on the order of the wavelength of the highest reconstructed frequency. Using a signal bandwidth of 0.4–1 MHz and an average sound speed of 1500 m/s, the resolution is approximately 1.5 mm. The quantitative sound speed values and morphology provided by these images have the potential to inform diagnosis and classification of breast disease. In this study, we present the formalism, practical application, and in vivo results of waveform tomography applied to breast data gathered by two different ultrasound tomography scanners that utilize ring transducers. The formalism includes a review of frequency domain modeling of the wave equation using finite difference operators as well as a review of the gradient descent method for the iterative reconstruction scheme. It is shown that the practical application of waveform tomography requires an accurate starting model, careful data processing, and a method to gradually incorporate higher frequency information into the sound speed reconstruction. Following these steps resulted in high resolution quantitative sound speed images of the breast. These images show marked improvement relative to commonly used ray tomography reconstruction methods. The robustness of the method is demonstrated by obtaining similar results from two different ultrasound tomography devices. We also compare our method to MRI to demonstrate concordant findings. The clinical data used in this work was obtained from a HIPAA compliant clinical study (IRB 040912M1F).

1. Introduction

The purpose of this work is to produce high resolution quantitative in vivo sound speed images of the human breast for aiding in the detection and diagnosis of breast cancer. Ultrasound tomography is an ideal technique for obtaining 3D images of breast structures since the breast is comprised of soft tissues without bones or other materials which would strongly scatter and attenuate transmitted signal energy (Greenleaf et al., 1977). Potential clinical benefits of ultrasound tomography include safety, comfort, and 3D imaging. This is in contrast to existing clinically accepted modalities such as x-ray mammography which only provides planar projections, involves ionizing radiation, and uses uncomfortable compression.

The two ultrasound tomography devices used to generate data for this work (Duric et al., 2007, 2013) operate in a similar fashion. During an exam, the patient lies prone on a table and inserts a breast into a ring transducer which is immersed in a water filled chamber (figure 1(a)). The water is heated to just below body temperature (approximately 32°C) to yield a sound speed that is intermediate to the range of sound speeds found in breast issues. Furthermore, the warm water provides patient comfort, and it is degassed to reduce noise and scattering produced by air bubbles. The ring transducer then scans the entire breast acquiring coronal slices from the chest wall to the nipple region. Tomographic B-mode images are then reconstructed from the reflected signals while sound speed and attenuation images are reconstructed from the transmitted signals. The three image types can then be used to evaluate the presence of breast disease. The B-mode images are qualitative reconstructions which measure the variations in the impedance properties of the breast tissue (Schmidt et al., 2011). They provide useful contrast and morphological information. The sound speed and attenuation images map the sound speed (m/s) and attenuation (dB/mm) of the reconstructed breast volume. In addition to providing contrast and morphological information, this quantitative data helps in the identification of unknown structures in an absolute and consistent way (Li et al., 2008a,b).

Figure 1.

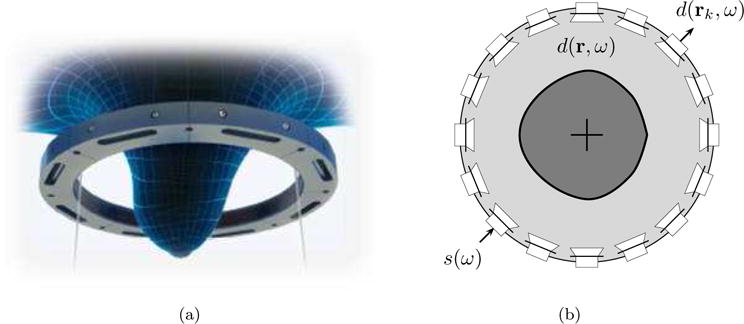
Ultrasound tomography transducer acquisition setup. (a) Placement of breast in ring. (b) Transducer ring configuration.

In this work, we focus on the reconstruction of the sound speed in breast tissue using waveform tomography techniques. Waveform tomography reconstruction algorithms model the propagating wave fields using the full wave equation, hence taking into account higher order effects such as diffraction and multiple scattering (Virieux and Operto, 2009). This is in contrast to more common ray tomography techniques which only consider the arrival times of transmitted wavefronts (Li et al., 2008a). A limitation of our approach is that we model 2D wave propagation which neglects the out of plane scattering present in real data acquisition. However, this approach has significant advantages in terms of computational speed, complexity of hardware, and chest wall access. It is also motivated by the fact that the considered transducer ring focuses most of the acoustic energy into the coronal plane. It will be seen that the 2D approach still significantly improves upon ray tomography methods which are also 2D. By careful data-fitting of the numerical wave fields to real acoustic data, we use an iterative gradient search algorithm to produce sound speed models of the breast. We highlight the robustness and practicality of our approach by reconstructing data acquired by two different ultrasound tomography units using ring transducers. The improved image quality enabled by waveform tomography has the potential to significantly increase the clinical value of sound speed images for the detection and diagnosis of breast cancer.

In the preceding decades, various research teams have made significant advances in waveform tomography. A growing body of geophysics research has demonstrated the potential of waveform tomography to image the earth subsurface with greater accuracy (Tarantola, 1984; Song et al., 1995; Pratt, 1999). See (Virieux and Operto, 2009) for a review. Of these methods, the approach and techniques used in (Pratt, 1999) was crucial in developing our algorithm. While some research has investigated medical applications using numerical data sets (Natterer, 2008; Roy et al., 2010; Huang et al., 2014; Li et al., 2014), to the best of our knowledge, very few have successfully applied these techniques to clinical in vivo data. The work in (Borup et al., 1999; Wiskin et al., 2007) was a major pioneering contribution using an ultrasound tomography device with planar transducer arrays. Their reconstruction technique contrasts sharply with ours. While (Borup et al., 1999) used an implicit integral equation technique to find the scattered wave fields, we use finite difference and matrix inversion methods using data acquired from a ring transducer. Another important contribution to waveform tomography for breast imaging is given in (Pratt et al., 2007). The authors use a very similar waveform tomography algorithm to produce sound speed and attenuation images of a physical tissue mimicking breast phantom and in vivo data obtained using our older ultrasound tomography unit. Their work relies on manual travel time picking to build the initial sound speed model. Manual travel time picking requires a user to look at a received waveform and decide the time of arrival of the acoustic signal. Due to the vast amount of data collected, this approach is not suitable for practical clinical applications. By contrast, our method utilizes a completely automatic time-of-flight picker which is capable of separating system noise and the arrival of the acoustic signal. We also use different preprocessing techniques in the implementation of our algorithm.

The outline of the paper is as follows. We present the inverse problem in section 2. In section 3, we review the steps needed to numerically model acoustic wave propagation. We also show how simulated and real wave field measurements are used to solve the inverse problem of obtaining a sound speed model of the breast. In section 4, we explain the main steps necessary to process the acquired data to a form that can be used by the inversion process. In section 5, we present and discuss reconstructed sound speed images of a numerical simulation, tissue mimicking breast phantom, and several in vivo data sets. We also show a comparison of our method to MRI. We summarize the discussion with our conclusions in section 6. We acknowledge our funding sources and potential conflicts of interest in section 7.

2. Problem Statement

Let us consider the ultrasound tomography acquisition setup depicted in figure 1(b). The breast is immersed in water and surrounded by an ultrasound transducer ring with n elements. The positions of the transducer elements are given by r_k for k = 1, 2, …, n.

Our goal is to estimate the sound speed model c(r) as a means to quantitatively characterize breast tissue. The sound speed is assumed to be independent of the frequency (no dispersion). Note that attenuation can easily be included by adding an imaginary component to the sound speed model (Aki and Richards, 2002; Song et al., 1995). Attenuation reconstruction is beyond the scope of the current work and will not be addressed. The sound speed model is sampled on an uniform m × m reconstruction grid and stacked into an m² dimensional vector c.

The acquisition works as follows. Each transducer element sequentially emits an ultrasound pulse which propagates throughout the medium. In the frequency domain, the transmitting pulse of the transducer operating at frequency ω is given by complex valued quantity s(ω), and the resulting complex wave field at position r is denoted d(r, ω). The wave field is measured at the transducer locations r_k, giving complex valued experimental measurements d(r_k, ω). The measurements obtained for all emitter-receiver pairs can be stacked into an n² dimensional vector d_obs(ω). The expected numerical wave field obtained at position r for a given operating frequency ω and sound speed model c is denoted u(r, ω, c). Similar to the experimental measurements, the simulated wave field is sampled at the transducer locations and the values are stacked in an n² dimensional vector u_obs(ω, c).

The problem that we would like to solve is to estimate the sound speed model c that generates, upon numerical simulation, simulated measurements u_obs(ω, c) that best match the experimental measurements d_obs(ω). More specifically, we would like to minimize the real valued mean squared error cost function

$$E(\omega ,\mathbf{c}){=}_2^1{\mathbf{e}}^H(\omega ,\mathbf{c})\mathbf{e}(\omega ,\mathbf{c}),$$ (1)

where^H denotes the Hermitian transpose, and e is the residual mismatch defined as

$$\mathbf{e}(\omega ,\mathbf{c})={\mathbf{u}}_{\mathit{\text{obs}}}(\omega ,\mathbf{c})-{\mathbf{d}}_{\mathit{\text{obs}}}(\omega ).$$ (2)

A regularization term can easily be added to smooth the reconstructed sound speed images in order to stabilize the inversion process. Note that the dependence on the frequency ω and the sound speed model c is explicitly given in the above expressions to emphasize that the optimization is performed on one frequency at a time, and that the simulated wave field depends on the assumed sound speed model. In other words, if the sound speed model is updated, the simulated wave field needs to be reevaluated. In the rest of the paper, however, the dependency on these two parameters will be implicit.

3. Sound Speed Reconstruction

The optimization problem stated in the previous section is solved in an iterative manner. We start from an initial estimate of the sound speed model and update it using conventional gradient descent methods. The iterations stop when a convergence criterion is satisfied. The computation of the simulated wave field for a given sound speed model is achieved through forward modeling. The update of the sound speed model based on the computed measurement mismatch is obtained by solving the corresponding inverse problem. We explain below the approach taken in this work to address these two key aspects of the reconstruction process.

3.1. Forward Modeling

We assume that the propagation of acoustic waves in the human breast is governed by the acoustic wave equation with constant density. Because of the high computation cost of time domain modeling and the efficiency of the frequency domain approach for a multi-source problem, we model the propagation of ultrasound within the breast in the frequency domain using the Helmhotz equation

$$\left({\nabla }^2+\frac{{\omega }^2}{c{(\mathbf{r})}^2}\right)u(\mathbf{r},\omega )=s\left(\mathbf{r},\omega \right),$$ (3)

where ∇² is the Laplacian operator. Equation 3 describes the wave field u at location r originating from a spatial source s. In the case s is a point source at position r_k, it can be expressed as s(r, ω) = s(ω) δ (r − r_k), where δ denotes the delta distribution.

In order to use computer programs to numerically solve the above differential equation, we sample the wave field values on an uniform m × m forward modeling grid. The grid size is computed as λ/n_λ, where λ is the wavelength at the chosen optimization frequency, and n_λ = 5 is the number of grid points per wavelength chosen to balance the computation cost, the quality of the reconstructed image, and the mitigation of numerical dispersion. Choosing n_λ ≤ 4 leads to a complete breakdown of the algorithm as this is a limiting value for our chosen finite difference stencil. Choosing a value n_λ > 5 increases the computation time without providing a substantial increase in the quality of the reconstructed image. To compute the wavelength, we use the mean sound speed of the water bath as a reference value. The wave field values are stacked into an m² dimensional vector u. Similarly, we define the m² dimensional vector s that has non-zero values only at the grid indices that correspond to the position of the transmitting transducer element. The Helmholtz operator that appears in equation 3 is discretized using a finite difference stencil whose values are stored in a matrix S with dimensions m² × m². The matrix S is large but very sparse. Its entries depend on the assumed sound speed model c and the chosen absorbing boundary conditions. In this work, we choose the optimal nine-point finite difference stencils detailed in (Jo et al., 1996) and the absorbing boundary conditions exposed in (Engquist and Majda, 1977). With the above discretization, the Helmholtz equation can be written in matrix form as

$$\mathbf{S}\mathbf{u}=\mathbf{s}.$$ (4)

Note that the above equation needs to be solved for each source which we have grouped in the source vector s. Since the matrix S does not change unless the sound speed model is updated, these systems of equations can be efficiently solved using LU factorization (Marfurt, 1984; Li, 2005). Once S has been factored, its LU constituents can be re-used to rapidly solve the system of equations corresponding to each source. We note that the solution u of equation 4 depends on the source vector s for which we can make an arbitrary initial guess. The guess is scaled by a complex scalar using a method to estimate the source signal (see section 4.3). The field values u are also scaled by the same factor.

3.2. Inverse Problem

To solve the inverse problem for sound speed reconstruction, we use an iterative approach. The starting sound speed model c⁽⁰⁾ is created using a travel time reconstruction method (Li et al., 2008a). For each frequency ω, we define a stopping criterion by updating the sound speed a configurable number of times. This is based on balancing computation cost with the quality of the reconstructed image. The quality of the image is a subjective metric which balances the interpretation of the apparent ability of the algorithm to correctly image structures and the introduction of noise and artifacts into the reconstructed image. Often times, the quality can be improved by taking more iterations at a particular frequency or by incorporating higher frequency information. However, there is a point where the improvements in quality by making further iterations or moving to higher frequencies are negligible when compared to the additional computation cost. An optimal frequency and iteration schedule is a topic of current and ongoing investigation.

In the inversion process, we start at the lowest frequency in the set of selected frequencies, and then we move to the next frequency until all frequencies have been used. Given a current estimate c⁽ⁱ⁾ of the sound speed model, we find the gradient of the cost function defined in equation 1. We then update the sound speed in the direction of the steepest descent to obtain a new estimate c⁽ⁱ⁺¹⁾. The sound speed update can be written as

$${\mathbf{c}}^{(i+1)}={\mathbf{c}}^{(i)}-\alpha \nabla E(\omega ,{\mathbf{c}}^{(i)}),$$ (5)

where α is the step size as determined by a line search method (Nocedal and Wright, 1999), and the gradient ∇ is taken with respect to the sound speed. A derivation of a practical computer implementation of the gradient of the cost function is given in (Pratt, 1999). The gradient is then given by

$$\nabla E=Re\left\{{\mathbf{F}}^H\mathbf{v}\right\},$$ (6)

where the back-propagated data residuals $\mathbf{v}={\left[{\mathbf{S}}^{-1}\right]}^H\widehat{\mathrm{e}}$ are multiplied by virtual source terms F. The vector ê is the residual mismatch vector e appended with zeros to match the dimensions of S. Also, the j-th column f_j of the virtual source matrix F is given by f_j = (−∂S/∂c_j) u. Examples of the cost function gradients are shown in figure 2.

Figure 2.

The gradient of the cost function. (a) Gradient for one emitter and one receiver. (b) Accumulated gradient for one emitter and all receivers. (c) Accumulated gradient for all emitters and all receivers.

4. Processing of Experimental Data

In this section, we describe the steps needed for the successful inversion of experimental data. The same steps are applied to data acquired by the two considered tomographic ultrasound units. These include: computing a low resolution sound speed starting model using ray tomography, applying digital signal processing to the raw signals to extract the frequency components used for the optimization, compensating for the transducer response, and estimating the unknown source signal.

4.1. Acquisition Hardware

Two ultrasound tomography devices were used to gather clinical data. The first device (Duric et al., 2007), an early prototype developed at the Karmanos Cancer Institute, has a ring array transducer with a 100 millimeter radius, 256 transducer elements, and a signal bandwidth centered at 1.5 MHz. The second device (Duric et al., 2013), a recent prototype developed by Delphinus Medical Technologies, Inc., has a transducer with a 110 millimeter radius, 2048 transducer elements, and a signal bandwidth centered at 2.75 MHz. For further details, see (Roy et al., 2013). Only 256 transducer elements were used in this work to facilitate comparison with the older prototype and to minimize reconstruction time. The two devices, uniquely different in their manufacturing, have different performance properties and provide excellent test cases to assess the robustness of the proposed waveform tomography reconstruction scheme.

4.2. Starting Model

In order to ensure that the waveform tomography algorithm converges to a solution close to the global minimum, an accurate starting sound speed model is needed to avoid cycle skipping phase mismatch between the simulated measurement u_obs and the experimental measurements d_obs (Brossier et al., 2008). For example, let the true phase of a discrete frequency component of the received waveform be ϕ_d = 0. If an initial sound speed model c₁ predicts a phase ϕ₁ such that −π < ϕ₁ ≤ π, then the algorithm will update the sound speed model to ${\mathbf{c}}_1^{\prime }$ in order to minimize the phase mismatch: ϕ₁ → ϕ_d. However, if another initial sound speed model c₂ predicts a phase ϕ₂ such that −3π < ϕ₂ ≤ −π, then the algorithm will update the sound speed model to the wrong local minimum ${\mathbf{c}}_2^{\prime }$ to minimize the phase mismatch: ϕ₂ → ϕ_d − 2π. We generate our starting model using the ray tomography method detailed in (Li et al., 2008a). The travel time (or ray) reconstruction algorithm is iterated sufficiently to output a high enough resolution image that avoids phase mismatch due to cycle skipping. However, overiteration is avoided as it introduces strong ray artifacts which are retained throughout the waveform tomography inversion process. Paralleling the need for an accurate starting model, once the inversion process begins, each subsequent update of the sound speed needs to adequately avoid the cycle skipping problem in order to converge in the direction of the global minimum. This requirement becomes stricter as higher frequencies are incorporated into the inversion process.

4.3. Frequency Component Extraction

The proposed algorithm works on the frequency components extracted from the raw time series (figure 3(a)) acquired by the hardware. The raw time series is preprocessed before the frequency selection (figure 3(b)). This is achieved by applying the steps below.

Figure 3.

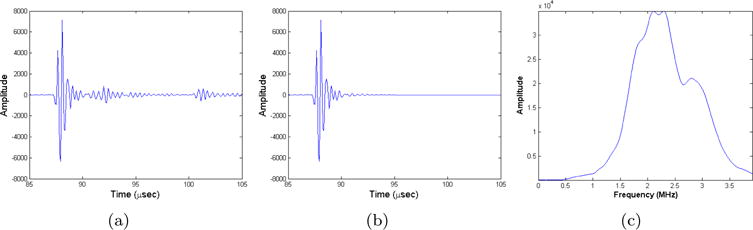
Processing of raw ultrasound signal generated by newer prototype. (a) Original waveform. (b) Processed waveform. (c) Magnitude spectrum of processed waveform.

Time Windowing

The time of first arrival for each waveform is evaluated using an automatic travel time estimation method described in (Zhang et al., 2003). These travel times allow us to define windows which extract the primary transmitted portion of the received waveforms and reject reflected and multi-scattered signals. This is done to force the algorithm to match the primary features of the true sound speed model (Pratt et al., 2007). The length of the window is chosen so that it includes the contribution of the primary transmitted waveform. Short cosine tapers (approx. 0.5 μs) are applied to both sides of the window before to avoid leakage in the Fourier domain.

Exponential Damping

We dampen the tail of the signal for the same reason we window. A damping profile of the form max {1, exp [− (t − t₀ − t_d)/τ]} is applied to every waveform as a means to further focus the inversion process on information contained in the primary transmitted signal. We use a value of t_d that begins damping the signal after the main transmitted portion of the waveform (approx. 5 μs after the travel time t₀), and a short scaling factor τ (approx. 1 μs) to quickly attenuate the later portion of the signal that is contaminated by non-transmitted components.

Waveform Selection

A calibration of the ring array transducer (Roy et al., 2011) and the determination of travel time statistical outliers in the clinical data set allow us to detect faulty transducer elements and discard waveforms that are too noisy to be included in the reconstruction process. We use an automated calibration method which estimates the position of the transducer elements using a travel time measurements done in water bath at controlled temperature. The calibration method also analyses the power of the transmitted signals to flag faulty transducer elements. For example, the transducer element directional beam profiles make small angle emitter-receiver contributions unreliable. For this reason, we omit waveforms that do not lie within an arc of approximately 270 degrees with respect to the source transducer.

Fourier Transformation

The processed waveforms are then Fourier transformed to extract the frequency components given as input to the optimization process. A typical magnitude spectrum for the new device is shown in figure 3(c). We start the iterative optimization procedure with the lowest frequency that has enough energy (around 400 kHz for the older unit and 500 kHz for the newer unit). We iterate multiple times on that frequency and then move to the next frequency using an increment of 30 kHz up to a maximum frequency of 1 MHz. Since computation cost is not linearly proportional to the size of mesh, and thus, the chosen frequency, the maximum reconstruction frequency of 1 MHz was found to be an appropriate maximum frequency since further improvements in the quality of the reconstructed image were overshadowed by significant increases in computation cost and model mismatch. The chosen optimization process allows us to gradually incorporate shorter wavelength features to prevent the algorithm from being stuck in a local minimum. Experiments have shown that this optimization schedule performs well across all considered data sets. Note that the current transducer ring has not been optimized to operate at such low frequencies. The energy available in the considered frequency range is significantly lower than what is available near the central frequency (figure 3(c)). Thus, further optimization of the acquisition hardware holds great promise for even better image reconstruction quality.

Transducer Response

For the simulated data set to best match the experimental one, we must also take the characteristics of the transducer beam profile into account. This can be achieved either by including the transducer response in our propagation model or by modifying the waveforms to best match a simple numerical model that assumes omni-directional point sources. For simplicity, we have chosen the latter approach. We normalize the magnitude spectrum of both the simulated and experimental data sets. In other words, we only match the phase of the frequency components in the inversion process. However, neglecting amplitude information may lead to residual artifacts. This is true especially in a propagation medium rich with scattering.

Source Signal Estimation

In order to solve our forward problem, the input signal s must be known. We could calibrate our transducers and obtain the signal, but that would add an additional layer of complexity to our algorithm. In addition, by estimating the source, we provide an additional degree of freedom to the inversion problem. For a given sound speed model, the estimation of a source signal is a linear estimation task. We need to find the optimal complex valued source scaling factor γ such that the simulated and experimental measurements best match in a mean squared sense. The optimal value is obtained through orthogonal projection (Pratt, 1999) and is given by

$$\gamma =\frac{{\mathbf{d}}_{\mathit{\text{obs}}}^H{\mathbf{u}}_{\mathit{\text{obs}}}}{{\mathbf{u}}_{\mathit{\text{obs}}}^H{\mathbf{u}}_{\mathit{\text{obs}}}}.$$ (7)

In our case, a single scaling factor is computed by matching the data gathered from all emitters. Using this scaling factor, the source vector and field values are scaled to s → γs, and u → γu, respectively. The reconstruction algorithm alternates between updating the source signal using the above scaling factor for a known sound speed model and estimating the sound speed model for a given source signal.

5. Results and Discussion

In this section, we present numerical, physical breast phantom, and in vivo reconstruction results. We also make a comparison of our waveform tomography method to MRI. We highlight the improvements made upon existing travel time imaging methods and the robustness of the proposed algorithm to data acquired by the two considered ultrasound tomography units. Note that our goal is not to compare the two units in terms of image reconstruction quality, but to demonstrate the applicability of the algorithm to data sets acquired with different devices. A detailed discussion on numerical results that includes numerical phantom reconstructions, resolution assessment, accuracy analysis, and computational cost can be found in our previous work (Li et al., 2014).

5.1. Numerical Simulation Results

A numerical phantom with various lesions of different sizes and sound speeds was reconstructed using both travel time and waveform tomography methods. The reconstructions along with the true model are shown in figure 4. It can be seen that the waveform reconstruction is nearly identical to the true model while the travel time reconstruction is smooth with diffuse boundaries. This is due to the fact that ray tomography methods only partially compensate for refraction and do not model diffraction effects. Critical diagnostic information contained in the morphological features of tumors is unveiled using the waveform tomography reconstruction method. For example, the margins of the star shaped lesion are not visible with the travel time reconstruction.

Figure 4.

Reconstruction of numerical phantom. (a) ray tomography reconstruction. (b) Waveform tomography reconstruction. (c) True Model.

5.2. Physical Phantom Results

A physical tissue mimicking breast phantom, built by Dr. Ernest Madsen of the University of Wisconsin, was used to assess the real-world reconstruction ability of our algorithm. It has been previously used in the studies presented in (Duric et al., 2007; Li et al., 2008a). An x-ray computed tomography (CT) image of the phantom is shown in figure 5(c). The phantom has scanning characteristics of a highly scattering predominantly parenchymal breast, and it has two embedded high speed tumors and two low sound speed fat inclusions which are surrounded by a cascading subcutaneous fat layer that is further surrounded by a layer of skin. The travel time and waveform tomography reconstruction results of data obtained from the old prototype are shown in figure 5. An x-ray computed tomography (CT) scan is also shown in figure 5(c) to highlight concordant findings. Note that the phantom images have been manually masked so that the reader can focus on the contained lesions instead of artifacts outside the field of view. Also, in contrast to in vivo patients scans, the temperature of the water bath was approximately 22°C.

Figure 5.

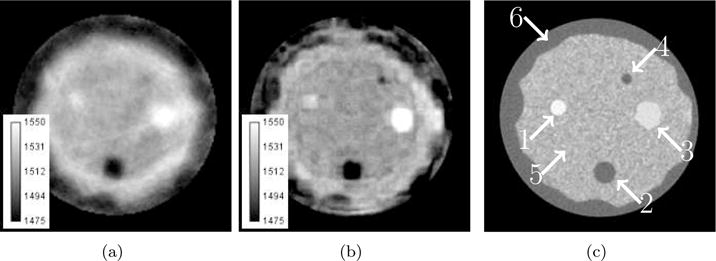
Reconstruction of physical breast phantom using older ultrasound tomography unit. Gray scale values in the sound speed images correspond to a range of 1475–1550 m/s. Brighter areas correspond to higher sound speed. (a) Ray tomography method. (b) Waveform tomography method. (c) Computed tomography reference with arrow overlays labeling structures: (1) small tumor, (2) large fat deposit, (3) large tumor, (4) small fat deposit, (5) glandular tissue, (6) subcutaneous fat layer.

The waveform tomography reconstruction method show significant improvements in the morphological quality of the reconstructed image over the method based on travel times. For example, the inclusion at 1 o’clock is clearly visible in the higher resolution waveform image while it is barely visible in the ray tomography image. In addition to finding smaller lesions, the shape and margins of the larger lesions in the waveform image are better delineated and match more closely the CT reconstruction. Since the shape and margins of tissues, including tumors, cysts, and parencyhma have critical diagnostic value in the assessment of disease (Stavros et al., 1995), an observer would be able to make a more accurate diagnosis with the additional information present in the waveform reconstruction.

We assess the accuracy of the reconstructed sound speed values by selecting a region of interest (ROI) around the structures labeled in figure 5(c). Each ROI is contoured to match the morphological feature of the imaged lesion. For an ROI of N pixels, we obtain the mean sound speed $\mu =1/N{\displaystyle {\sum }_{i=1}^{N}c(i)}$ and unbiased variance ${\sigma }^2=1/(N-1){\displaystyle {\sum }_{i=1}^N{\left[c(i)-\mu \right]}^2}$. We then compare the obtained sound speeds to reference values reported by the manufacturer. Table 1 summarizes these results. In most cases, the reconstructed sound speed values are very similar, especially within the error of the measurements, and close to the reference values. However, there was a significant lapse in time between the creation of the phantom and its scanning using our older ultrasound tomography unit. It is likely that the phantom degraded over that time. Thus, the reference values are not reliable estimates of the true sound speed of the phantom at the time of scanning. What is of importance is the trend in sound speed. For example, the large tumor should have greater sound speed than the small tumor. We can see that both the waveform and travel time methods agree with these trends. The recovered sound speed of the small tumor and fat deposit is most problematic. Due to their small size, we approach the resolution limitations of waveform tomography when the highest reconstructed frequency is 1 MHz. Due to volume averaging effects and convergence issues, the reconstructed sound speeds of the lesions are averaged with the adjacent glandular tissue leading to skewed sound speed values. By looking at the values in table 1, we see that the waveform reconstructions have significant variance in the reported sound speed values. This could be reduced and smoothed by incorporating a regularization penalty to the cost function. For example, a Tikhonov penalty would help balance data fitting and image roughness by prohibiting updates which significantly change the sound speed (Golub et al., 1999).

Table 1.

Comparison to ground truth of sound speed values (m/s) of travel time and waveform tomography reconstructions. Values are reported using the mean sound speed μ in the ROI and the corresponding standard deviation σ.

Structure	Reference Values	Travel Time Rec. (μ ± σ)	Waveform Rec. (μ ± σ)
Large tumor	1559	1551 ± 10	1551 ± 5
Small tumor	1549	1542 ± 2	1535 ± 3
Large fat deposit	1470	1501 ± 10	1490 ± 9
Small fat deposit	1470	1524 ± 3	1511 ± 4
Glandular tissue	1515	1528 ± 3	1521 ± 3

Artifacts are present in both the travel time and waveform reconstruction. The most significant artifact in the travel time sound speed images are streaks or ray artifacts arising around regions of higher tissue contrast. This is seen to some degree in the phantom reconstruction in figure 5(a), but are more clearly seen in the in vivo reconstructions in figures 6 and 7 (top row). The ray artifacts are distracting because they mask the true morphology contained in the margins of the tumor.

Figure 6.

Comparison of travel time (top row) and waveform (bottom row) reconstruction methods using older ultrasound tomography unit. Gray scale values in the sound speed images correspond to a range of 1400–1575 m/s. Brighter areas correspond to higher sound speed. (a) Complex parenchyma shape. (b) 1.5 cm tumor. (c) 4 cm tumor (1 o’clock) and parenchyma (9 o’clock).

Figure 7.

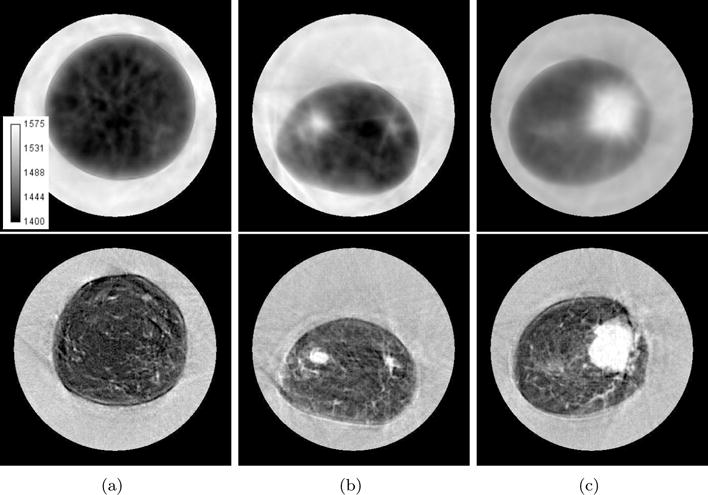
Comparison of travel time (top row) and waveform (bottom row) reconstruction methods using newer ultrasound tomography unit. Gray scale values in the sound speed images correspond to a range of 1400–1575 m/s. Brighter areas correspond to higher sound speed. (a) Very fine parenchyma patterns. (b) 1 cm tumor (10 o’clock). (c) 4 cm tumor (3 o’clock).

The waveform results contain other artifacts. They arise from the hardware, phase mismatching, and the inaccuracy of the starting model. The waveform images reconstructed by the older prototype have significantly more artifacts than the newer prototype. The artifacts are readily seen within the regions corresponding to water in figures 6 and 7 (bottom rows). This can lead to problems in imaging the skin contour of the breast. The artifacts are present due to defective transducer elements whose corrupted data is discarded by the calibration process (see section 4.3) which discards noisy waveforms whose time-of-flight cannot be found using an automatic process. Due to poor signal quality, other problems exist near the chest wall or when the imaging ring is filled to capacity. Also, the presence of more signal energy at 400 kHz and the different acquisition hardware alters the overall perception of the old prototype images. A phase mismatch also results in artifacts within the reconstructed image. For example, the waveform phantom image in figure 5(b) contains aberrations which look like false contours or clouds on the outer portions of the cascading skin layer (11, 1, and 6 o’clock positions). They arise from a phase offset induced on the reconstructed wavelets. This phase mismatch occurs as a result of the impedance mismatch between the water and the outer skin layer of the tissue mimicking breast phantom and the finite vertical dimension of the ultrasound transducer which confuses the origins of received signals from the sloping edges of the insonified object. Problems pertaining to the imaging of the outer skin is not as important as the success of imaging clinically relevant features (tumors, cysts, parenchmya, etc.) which are better resolved by using the waveform technique. Ray artifacts inherited from the travel time starting model also corrupt the waveform images. An example is seen in figure 6(a). This issue will be addressed in future work.

5.3. In Vivo Results

The usefulness of the waveform tomography method is most clearly seen in the improvements made in imaging the sound speed of in vivo structures. To highlight the robustness of the method, we present images reconstructed from data acquired by both the old and new ultrasound tomography units. These reconstructions include examples of the bulk breast tissue and parenchyma, small tumors, and large tumors. Note that each reconstructed image corresponds uniquely to a different patient. We also demonstrate the accuracy of our in vivo sound speed reconstructions by imaging a saline breast implant with known sound speed. Last, we show the validity of our waveform tomography method by demonstrating concordant findings with MRI.

The sound speed reconstructions of data recorded by the older prototype are shown in figure 6. The top row corresponds to the travel time reconstruction method while the bottom corresponds to the waveform method. In figure 6(a), we see an example of parenchymal tissue (white) embedded in fat (black). Improvements are made with the waveform reconstruction (bottom row). The cascading layers of the parenchymal tissue are revealed with great clarity in the waveform image where only a fuzzy image marred with ray artifacts is revealed by the travel time reconstruction method (top row). In addition, ray artifacts are clearly seen in the travel time reconstructions. In figures 6(b) and 6(c), we see examples of a smaller (approx. 1.5 cm at 6 o’clock) and larger (approx. 4 cm at 1 o’clock) tumors, respectively. As stated before, many structures in the breast can be uniquely identified by their sound speed. However, when dealing with structures with similar sound speed, the improvements made in the delineating the margins of unknown breast structures are of utmost importance (Stavros et al., 1995). These margins facilitate the differentiation of parencyhma and other breast structures from malignant and benign masses. The improvements made with the waveform reconstruction allows an observer to better classify the unknown lesions as tumors when, for example, an identification of parenchyma might have resulted from the travel time reconstruction image.

The sound speed reconstructions of data recorded by the newer prototype is shown in figure 7. In figure 7(a), we see another example of breast parenchyma. Unlike the big cascading layers in figure 6(a), figure 7(a) shows a patient with very fine parenchymal strands. When compared to the ray tomography reconstruction in figure 7, which only has a faint hint of some of these detailed structure, the delineation of these fine strands is a testament to the resolving power of waveform tomography. In figures 7(b) and 7(c), we see examples of a smaller (approx. 1 cm at 9 o’clock) and larger (approx. 4 cm at 3 o’clock) tumors, respectively. As was stated before, a proper reconstruction of the margins of a tumors aids in the best identification of unknown masses. Note the very fine structures resolved in all the cases shown in figure 7. From figures 6 and 7, it can be seen that the sound speed of waveform reconstructions tend to be lower in fatty regions while being accentuated in tumors and parenchyma. As in section 5.2, this can partially be explained by volume averaging effects and convergence issues. An explicit comparison of waveform and ray sound speeds is shown in figure 8 where a vertical line profile has been taken through the tumor in figure 7(c). From the profiles, it can be seen that ray tomography tends to overestimate fat sound speeds while underestimating tumor sound speeds. In addition, the improvements in resolution are apparent through the increased sharpness of the edge response of the line profiles.

Figure 8.

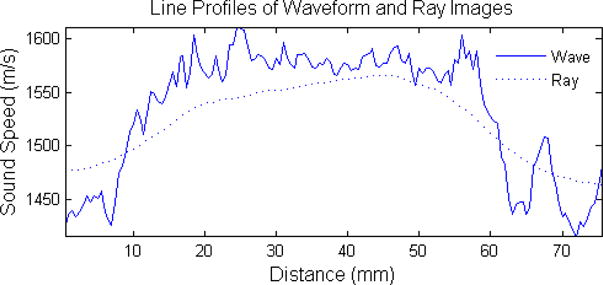
Vertical line profile through the tumor in figure 7(c).

In section 5.2, we presented quantitative sounds speed measurements for a tissue mimicking phantom. We demonstrate the in vivo accuracy of quantitative sound speed measurements by imaging a saline breast implant as shown in Figure 9. Saline breast implants contain an outer silicone shell filled with a sterile saline solution (U.S. FDA, 2014). Typical saline is composed of 0.9% NaCl solution. Using an empirical formula (Wilson, 1960), we calculated the sound speed of the saline breast implant assuming a body temperature of 37°C, a salinity of 0.9%, and a pressure of 1 atm to predict a sound speed of 1535 m/s. Drawing a 25 mm radius circular ROI within the center of the implant gives an average sound speed μ with error σ of 1533 ± 3 m/s and 1528 ± 1 m/s for waveform and travel time reconstructions, respectively. Thus, we see that sounds speed of the breast implant is fairly uniform across measurements from three different modalities. This should give some verification to the quantitative capabilities of waveform tomography sound speed imaging and clear up some of the inconsistencies in the measured sound speed values reported in section 5.2.

Figure 9.

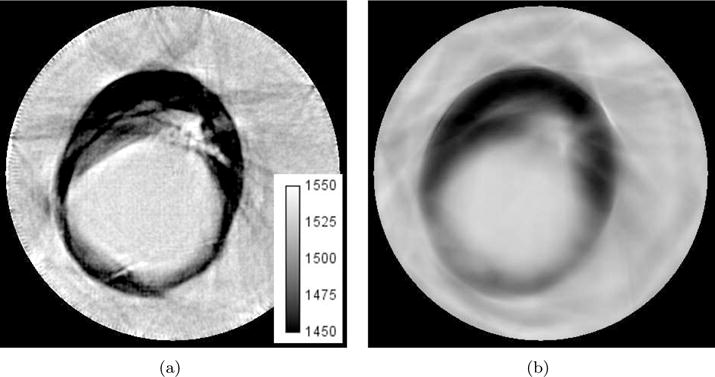
Saline breast implant reconstructions. Gray scale values in the sound speed images correspond to a range of 1450–1550 m/s. Brighter areas correspond to higher sound speed. (a) Waveform Tomography Method. (b) Travel time tomography method.

In order to verify morphological comparison, we also present a corresponding MRI slice to the image of very fine parenchymal structures in figure 7(a). This is seen in figure 10. Note that the gray scale values of the sound speed reconstruction have been inverted to match the gray scale convention of the T1 weighted MRI image. Also, it is hard to perfectly register MRI and our ultrasound tomography images due to the differences in the data acquisition procedure. For example, the breast is freely suspended in air during MRI acquisition. From figure 10, we see many concordant findings between our waveform tomography sound speed method and that of MRI. In particular, the x-shaped lesions at 9 o’clock is nearly identical in both images and the general parenchymal patterns on the right hand side of the images are similar.

Figure 10.

Comparison of waveform tomography reconstruction method using new ultrasound tomography unit to T1 weighted MRI. Gray scale values in the sound speed image have been inverted to match the gray scale convention of T1 MRI. The gray scale corresponds to a range of 1575–1400 m/s. (a) Waveform tomography sound speed reconstruction. (b) T1 weighted MRI.

6. Conclusions

We have developed and presented an ultrasound tomography algorithm to estimate the sound speed of breast tissue to aid with the detection and diagnosis of breast cancer. The adopted method is based on the principles of full waveform inversion and operates in the frequency domain. The robustness of the scheme has been demonstrated using carefully processed data sets obtained from different ultrasound tomography devices with ring transducers. Our reconstruction results using a physical tissue mimicking breast phantom and in vivo data sets have shown that the proposed method is a marked improvement over ray tomography. The apparent improved contrast, better resolution, and more accurate margin delineation have the potential to greatly increase the clinical value of breast sound speed images. Furthermore, by comparing our method to MRI, we demonstrate concordant findings of very fine parenchymal structures. Current research is focusing on optimizing the algorithm, reducing the reconstruction time, and improving the reconstruction accuracy by reducing artifacts, investigating a more optimal transducer design, and using more transducers in the reconstruction process. In addition, we are investigating reconstruction of attenuation via the inversion of a complex valued sound speed. The clinical implications of sound speed imaging derived from waveform tomography will be discussed in a future paper.