Abstract
Probabilistic topic models provide an unsupervised method for analyzing unstructured text, which have the potential to be integrated into clinical automatic summarization systems. Clinical documents are accompanied by metadata in a patient’s medical history and frequently contains multiword concepts that can be valuable for accurately interpreting the included text. While existing methods have attempted to address these problems individually, we present a unified model for free-text clinical documents that integrates contextual patient- and document-level data, and discovers multi-word concepts. In the proposed model, phrases are represented by chained n-grams and a Dirichlet hyper-parameter is weighted by both document-level and patient-level context. This method and three other Latent Dirichlet allocation models were fit to a large collection of clinical reports. Examples of resulting topics demonstrate the results of the new model and the quality of the representations are evaluated using empirical log likelihood. The proposed model was able to create informative prior probabilities based on patient and document information, and captured phrases that represented various clinical concepts. The representation using the proposed model had a significantly higher empirical log likelihood than the compared methods. Integrating document metadata and capturing phrases in clinical text greatly improves the topic representation of clinical documents. The resulting clinically informative topics may effectively serve as the basis for an automatic summarization system for clinical reports.
Keywords: Topic modeling, LDA, n-grams, document metadata
Graphical Abstract
1. Introduction
Much of the information contained in a patient’s medical report is stored as free text in physician’s clinical reports. Clinical narrative contained in these reports can be challenging to make sense of computationally due to the variability in author reporting styles, differences in clinical practice, and the inherent complexity of language. Nonetheless, these documents can provide valuable information for clinical applications such as case-based reasoning [1] and automatic summarization.[2] Topic models provide a means for indexing large, unstructured corpora with inferred semantics,[3] but incorporating these methods in clinical text has begun only recently. While these techniques have yielded promising results, they have generally been limited to basic methods that have not incorporated more recent advances in the topic modelling field. Development of new topic modeling methods that incorporate diverse clinical information and structure have the potential to unlock the information contained in clinical reports for use in developing clinical tools.
Probabilistic topic models for language have been widely explored in the literature as unsupervised, generative methods for quantitatively characterizing unstructured free-text with semantic topics. There are many possible configurations for topic models, but in general they define a semantic topic as a multinomial distribution over the dictionary of tokens (e.g., words, n-grams, concepts, etc.) that make up a collection. These multinomial distributions are learned through the contextual co-occurrence of tokens in documents. Documents are modeled as multinomial mixtures of topics, which allows for efficient search by topics of interest, as well as document-document comparison. These models have been largely discussed for general corpora (e.g., newspaper articles), and have been developed for many uses, including word-sense disambiguation,[4] topic correlation,[5] learning information hierarchies,[6] and tracking themes over time.[7,8] In the clinical domain, work has investigated the use of topic models in cased-based retrieval,[1] characterizing clinical concepts over time,[9] and the impact of copy and pasted text on topic learning.[10] Topics have also been used as features in classifiers in order to predict patient satisfaction,[11] depression,[12] infection,[13] and mortality.[14]
The goal of this project is to develop a topic model designed specifically for capturing information from the electronic health record (EHR). In particular, whereas previous work has captured document-level information, the proposed model will additionally incorporate patient-level metadata. Both document and patient-level data will influence how topics are distributed in a document. To capture focused clinical language, the model is capable of learning multiword concepts (e.g., “abnormal enhancement”). The topics generated by the proposed model are compared with those created using existing topic models. Finally, we show that disease classification is possible using the distribution of topics in a patient’s record, illustrating that topics capture distinguishing clinical information, which can be important for clinical applications such as clinical document summarization.
1.1. Background
Latent semantic indexing (LSI) provides a seminal method for exploring latent semantics in free-text.[15] It involves creating a weighted term-document matrix and applying singular value decomposition (SVD) to generate a lower-rank factorization, used for comparing terms or documents. LSI is able to address common problems such as synonymy and polysemy by exploiting the contextual co-occurrence patterns of words in the matrix. Probabilistic LSI (PLSI) extends the traditional LSI model by using a set of latent classes to models the joint distribution of documents and words.[16] PLSI represents each document as a mixture model of latent multinomial distributions over words (“topics”). Generating a word requires the selection of a topic based on its proportion in the document and then drawing a word from that latent class’s word distribution. Model parameters may be optimized using the Expectation Maximization (EM) algorithm.[17]
The latent Dirichlet allocation (LDA) topic model is a generative model that can be applied to a corpus of documents composed of categorical data.[3] In LDA, each document is represented as a random mixture of latent topics, which are multinomial distributions over the unique words in a corpus. The generative process for a document involves selecting a topic distribution from the corpus-level Dirichlet distribution. Then, for each word in the document, a topic is chosen and a word is drawn from the corresponding multinomial distribution. Documents’ topic distributions may be used for search, prediction, and comparison. Work has illustrated the potential of extending LDA for specialized text collections, with examples including modeling time,[7,8,18] finding correlations between topics,[5] learning annotations,[19–21] performing automatic translation,[22,23] and learning topic hierarchies.[6,24,25] LDA is often fit to data using Gibbs sampling, a Markov Chain Monte Carlo (MCMC) method. The number of topics in the LDA model must be specified prior to model fitting, with more semantically granular topics discovered as the number of topics increases.
Two extension to the LDA framework are relevant to this work: Topical N-grams (TNG) and Dirichlet multinomial regression (DMR). TNG removes the bag-of-words assumption and describes a model for learning both topics and topical phrases.[26] It is shown to be a more powerful generalization of previous n-gram-based models such as the Bigram Topic Model and the LDA Collocation Model.[27,28] Rather than treating each word independently, the model includes Bernoulli distributed variables indicating if sequential words constitute a bigram. A word selected from a given topic has a prior probability of becoming a bigram based on how often it is used as part of a phrase when discussing that topic. Subsequent words are then chosen based on the common completions of that phrase. Phrases can then be built by chaining bigrams together.
DMR offers a technique that can capture relationships between topics and features specific to each document.[29] Identification of these relationships is accomplished by weighting each document’s Dirichlet hyper-parameter, α, based on document-specific metadata. The document’s topic distribution is then drawn from a distribution that is tailored based on prior document-specific knowledge, rather than from a single corpus-level distribution. This method better models the topics in a given document by incorporating the known context of that document, and is therefore particularly apt in the medical domain as clinical documents are generally accompanied by encounter (e.g., physician name) and patient (e.g., demographics) information.
While the TNG and DMR models have separately been shown to improve on the traditional LDA model, the use of document metadata and phrase information in a topic model have not been implemented together. Here, we present a model that combines the benefits of these two methods, called the metadata and phrase driven topic model (MPT). We hypothesize that the gains achieved by each of these methods are from incorporating separate sources of information into the model and that combining the methods will result in a superior model than either of the methods implemented alone. We further believe that medical reports are particularly appropriate for both of these methods due to the associated metadata and the use of common phrases in clinical jargon, and thus implementation of the combined model will provide useful topics for the clinical domain.
2. Materials and Methods
2.1. Data Collection
Medical reports for patients with glioblastoma multiforme (GBM), lung cancer, or acute ischemic stroke were collected from an institutional review board (IRB)-approved disease-coded research database. The data set contained 936 patients, with a total of 84,201 medical reports. As we were primarily interested in uncontrolled free-text that summarizes a patient’s episode of care, the collection was then filtered by report type. Progress Notes, Consultation Notes, History and Physicals (H&Ps), Discharge Summaries, and Operative Reports/Procedures/Post-op Notes were selected, resulting in 20,120 reports that were used to fit topic models. Preprocessing of these reports removed all punctuation, stop words, words that occurred in fewer than five documents, and words that occur in every document. Protected health information (including names, dates, locations, and identifying numbers) and numbers were also removed, resulting in a final dataset consisting of 5,820,160 total tokens (17,993 unique).
The research database also contained metadata for each document regarding details about the associated visit, including the date, signing physician, and report type. Similarly, demographic information was associated with each document including the patient’s age, gender, race, and ethnicity. All of this information was made available to the model to use as a prior for generating topics specific to the current document.
2.2. Model
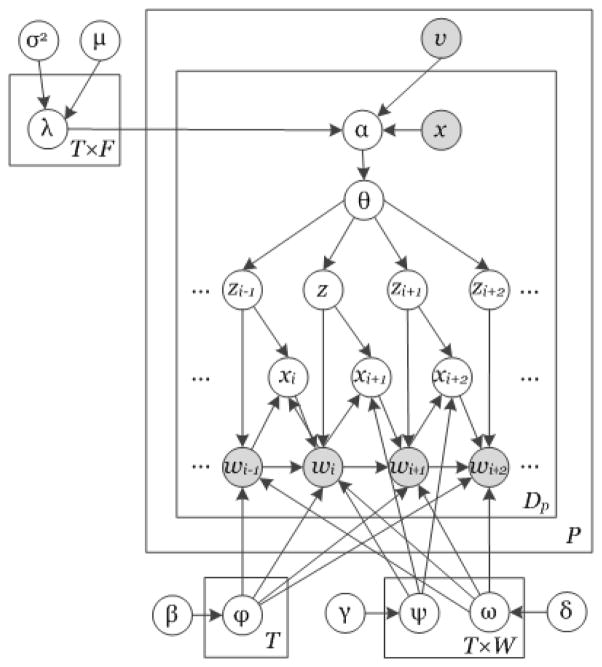
Building upon our previous work and the aforementioned TNG and DMR models, Figure 1 shows the proposed model (corresponding notation can be found in supplementary table 1).[1,9] As clinical text frequently contains multiword concepts, following previous work, the model is capable of discovering n-gram phrases.[26] To account for patient and document context, the document-topic Dirichlet hyper-parameter is weighted by both document-level and patient-level context.[29] The latter weighting is unique to the clinical domain and may be observed in Figure 1 by plate P (plates are boxes in the graphical model diagram and represent replication of a function across a given set), indicated by the outermost box, which contains observable information (v) associated with each patient. Importantly, as denoted by the topic plate T, which falls outside of the patient plate, topics are learned from the entire collection of patient documents.
Figure 1.
Proposed topic model introducing a patient plate P. Boxes denote replication of a function across a set. For instance, everything contained in plate P is performed for every patient. All elements within a plate are computed for each replication and additional subscripts/superscripts are omitted for simplicity. Shaded nodes represent observed data.
Given a set of model hyperparameters, 〈μ, σ2; β, γ, δ〉, the generative process for creating a set of topics, T, for a population of patients, P, each with a set of documents, Dp, is defined as follows:
-
For each topic t ∈ T,
-
1.1
Draw a distribution over words φt ~ D(β)
-
1.2
For each metadata feature f ∈ F,
-
1.2.1
Draw the feature prior distribution parameter λtf ~ N(μ, σ2)
-
1.2.1
-
1.3
For each word w in the vocabulary W
-
1.3.1
Draw the status distribution parameter ψtw ~ Beta(γ)
-
1.3.2
Draw the bigram distribution parameter ωtw ~ D(δ)
-
1.3.1
-
1.1
-
For each patient p ∈ P and document d ∈ Dp,
-
2.1
For each topic t ∈ T
-
2.1.1
Let the hyperparameter for topics be
-
2.1.1
-
2.2
Draw the distribution of topics θ(pd) ~ D(α(pd))
-
2.3
For each token i,
-
2.3.1
Draw topic
-
2.3.2
Draw the bigram status
-
2.3.3
If
-
2.3.1.1
Draw a word from the bigram distribution
-
2.3.1.1
-
2.3.4
If
-
2.3.4.1
Draw a word from the word-topic distribution
-
2.3.4.1
-
2.3.1
-
2.1
While it is possible to derive a model that includes explicit parameters for patient-specific topic-time relationships, in the domain of clinical reporting estimating such parameters is impeded by limited observations over time [9]. Generally, topic models are fit to data using variational or Markov chain Monte Carlo (MCMC) methods,[30–32] in particular Gibbs sampling.[33,34] In this work we used a stochastic expectation-maximization (EM) scheme combining Gibbs sampling [35–37] and L-BFGS optimization.[8,38–40] A fixed parameter in the proposed model is the number of topics, which is set to 100 based on prior studies involving topic models in clinical literature.[41]
Information specific to the document and the patient was used to generate each document’s Dirichlet hyperparameter. The meta-information set used consists of: report type, signing physician name, age, ethnicity, race, and gender. Because of inconsistency in physician name format (e.g., including first name versus including only the first initial or no first name), only last names were used. Possible values for report type and signing physician name were limited to those that occurred in at least 100 documents. After the cutoff, five report types and 23 signing physician names were used in the analysis. Age was discretized by decade and, while the DMR model allows for the use of integer valued variables, each decade was treated as a separate binary variable in order to represent nonlinear trends in topic association.
2.3. Empirical Log Likelihood
To evaluate the generalization capability of the model we use the empirical likelihood (EL) method advocated for topic model evaluation by Li and McCallum.[42] Evaluating the probability of held-out documents in topic models is difficult because there are an exponential number of possible topic assignments for the words. EL solves this problem by sampling topic distributions from the trained model. EL measures a combination of how good the topic-word distributions are and how well the model can guess which combinations of topics will appear in a given document.
For the traditional LDA model, |S| unconditional word distributions are sampled for a given held-out document d by sampling a topic distribution θpds from a Dirichlet distribution with parameter α defined by the training set. The probability of each of the observed word tokens wi is then calculated from the marginal probability over each topic t.
where p(wi|t) is calculated from the topic-word counts.
For the DMR topic model, word distributions are sampled by first calculating the αpd parameters of the Dirichlet prior over topics specific to a patient and document given the observed metadata features (a(p), b(pd))T in the previously described manner. A topic distribution θpds is then sampled from that Dirichlet distribution. Finally, we calculate the probability of each of the observed word tokens, wi, by calculating the marginal probability over each topic t of that type using the current point estimates of p(wi|t) given the topic-word counts.
When using topical n-grams, the probability of a word occurring is the sum of its probability of being drawn from its topic distribution and being selected as the completion of a bigram.
where xt,wi−1 is the total probability that the previous word is the beginning of a bigram.
The data set was split into a training set (60%, 12,072 total documents) and a testing set (40%, 8,048 documents). The training set was used to train the model hyperparameters and EL values were computed for each document in the testing set. The EL values obtained for each document were then compared across the four models using a two-way ANOVA test with three degrees of freedom and paired t-tests were used to determine whether the proposed model consistently yielded higher values than the other three models.
2.4. Disease and Document Author Classification
To investigate the information captured by topics, we set out to classify patients by their disease based on the topic distributions in their documents and to determine the author of individual documents based on their topic distributions. In all models, topics were trained on 60% of the total documents. The remaining 40% were then used as a testing set for evaluation. Only those documents from the 10 most frequent physicians in the data set were used for author classification. For each word in the testing documents, 100 topic assignments were independently sampled using the generative process defined by the model. The number of times each topic occurs over all the samples was then summed for each document to get a vector of topic counts, n1…n|T|, which was used as a feature vector for each document.
For classification in the MPT and DMR models, we followed the method outlined by Mimno and McCallum.[29] For each potential author i, a prior over topics, αi, was created for each document d given only that author name as a metadata feature. The likelihood for the author is the Dirichlet-multinomial probability of the nt counts using that prior.
They author with the highest likelihood is then chosen. Similarly, documents are classified among the three disease types were assigned priors over topics based on the disease metadata feature and the highest resulting likelihood was chosen.
In the TNG and LDA models, this method is not appropriate because document metadata is not taken into account in the topic distribution. In these models, classification was performed using an all versus all (AVA) multiclass support vector machine (SVM) classifier using the nt counts normalized by the total number of labelled words as features. The AVA approach extends the traditional binary SVM classifier to make a decision between N classes by independently training N(N−1) classifiers, fij, for each pair of classes i and j. The classification is then found by computing
Ties were broken by randomly assigning to one of the tied classes. Classifications were performed using ten-fold cross validation, and overall accuracy as well as recall and precision values were calculated for each of the classes.
3. Results
In the proposed model, the Dirichlet parameter is tailored to the types of words that are likely to occur given the document and patient metadata. Table 1 shows three examples using different document types, signing physicians, patient ages, and patient genders. Changing these parameters drastically changes the Dirichlet hyperparameter. A similar effect is seen when using DMR, but including phrase information allows for a more targeted prior than using metadata alone (table 2).
Table 1.
Hyperparameter values for the top five topics in three example documents. Report author names have been replaced with the physician’s area of specialty.
| Report type | Author | Patient age | Patient gender | |
|---|---|---|---|---|
| Consultation | Neuro oncologist | 30 | Male | |
| 7.481 | temodar, cycle, days, cycles, brain | |||
| 5.977556 | intact, year-old, normal, seen, mri_scan | |||
| 5.396355 | mri_scan, change, comes, nerves, outpatient | |||
| 4.248921 | surgery, ct_scan, revealed, performed, mri_scan | |||
| 4.193324 | glioblastoma_multiforme, tumor, brain, resection, mri | |||
| Report type | Author | Patient age | Patient gender | |
| Progress report | Cardiologist | 70 | Male | |
| 2.61905 | blood_pressure, normal, illness, months, pulse | |||
| 2.460163 | stroke, given, prior, acute, evidence | |||
| 2.374758 | blood_pressure, stenosis, significant, coronary_artery_disease, status_post | |||
| 1.522354 | course, continued, home, hospitalization, follow-up | |||
| 1.435546 | course, follow, discharged, instructed, pain | |||
| Report type | Author | Patient age | Patient gender | |
| Progress report | Thoracic surgeon | 50 | Female | |
| 0.969474 | underwent, lung, negative, revealed, performed | |||
| 0.906682 | plan, year-old, clear, edema, currently | |||
| 0.599339 | chemotherapy, lesion, lesions, size, parietal_lobe | |||
| 0.553506 | plan, agree, seen, discussed, lower_lobe | |||
| 0.532509 | continue, plan, bid, inpatient, hr | |||
Table 2.
Ranked topics for different document types using the four models (MPT, DMR, TNG, and LDA) based on the topic hyperparameters. TNG and LDA do not use document metadata, so the prior for the topic distribution is the same for every document type. Incorporating phrases into the model results in more targeted topics and higher weighting for these topics based on document metadata. Incorporating document metadata allows for patient- and document-specific topics, while models without metadata use only one document distribution for all document types.
| MPT | DMR | ||
|---|---|---|---|
| Operative report | Operative report | ||
| 3.93281 | catheter, prepped, using, draped, inserted | 1.814893 | catheter, needle, using, vein, placement |
| 1.692049 | placed, operation, cranial_nerve, taken, used | 1.66272 | operation, placed, surgeon, incision, anesthesia |
| 1.05243 | placed, removed, using, performed, operation | 0.843987 | normal, csf, stomach, endoscope, consent |
| 0.777849 | tumor, using, dura, resection, resection_cavity | 0.753292 | tumor, using, resection, flap, intraoperative |
| 0.666869 | approximately, appeared, obtained, performed, felt | 0.338279 | eye, lens, anterior, tube, chamber |
| Discharge summary | Discharge summary | ||
| 3.182792 | course, continued, home, hospitalization, follow-up | 3.451551 | course, started, continued, therapy, home |
| 2.972885 | course, follow, discharged, instructed, pain | 1.947799 | surgery, pain, stable, home, postoperative |
| 1.716823 | stroke, given, prior, acute, evidence | 0.805114 | stroke, cerebral, artery, ct, middle |
| 1.55142 | transfer, course, started, tube, continued | 0.653268 | tumor, glioblastoma, resection, radiation, multiforme |
| 1.273632 | able, daily, therapy, activities, improved | 0.572004 | stroke, mri, mca, tpa, arm |
| Progress note | Progress note | ||
| 1.327833 | continue, plan, bid, inpatient, hr | 0.671341 | continue, plan, bid, bp, hr |
| 1.09157 | plan, year-old, clear, edema, currently | 0.357264 | plan, inpatient, stroke, seen, discussed |
| 0.766955 | bid, given, continue, qd, old | 0.347626 | outpatient, able, therapy, good, having |
| 0.685851 | intact, year-old, normal, seen, mri_scan | 0.340108 | medicine, stable, continue, htn, pain |
| 0.674692 | likely, given, iv, blood_pressure, inpatient | 0.286204 | clear, abdomen, extremities, rate, regular |
| TNG | LDA | ||
| All report types | All report types | ||
| 0.52712 | given, lower_extremity, stroke, upper_extremity, approximately | 0.10219 | given, evidence, therapy, significant, possible |
| 0.42026 | able, normal_limits, daily, acute_distress, therapy | 0.09007 | able, having, problems, normal, days |
| 0.40148 | glioblastoma_multiforme, brain, decadron, mri, dilantin | 0.08062 | clear, rate, abdomen, extremities, regular |
| 0.37318 | denies, pain, clear, shortness, systems | 0.05552 | continue, plan, stable, inpatient, bp |
| 0.32127 | currently, negative, plan, continue, year-old | 0.05437 | allergies, family, social, systems, denies |
Incorporating TNG into the model allows for the detection of several salient phrases. These phrases include anatomical phrases (e.g., “lower extremity,” “cranial nerve”), tests (e.g., “mri scan,” “blood pressure”), symptoms (e.g., “acute distress”), and diseases (e.g., “glioblastoma multiforme,” “coronary artery disease”). TNG also allows for disambiguation of several words. For instance, the word “scan” appears in the top 10 words of five different topics in the LDA model, but none of the topics in the MPT model. Instead, it is split into more specific tests “mri scan” and “ct scan,” which appear in four topics and two topics, respectively. The word “lobe” appears in four topics in the LDA model: two involving the brain, and two involving the lung. In the MPT model, it is split into several different phrases: the “parietal lobe,” “frontal lobe,” and “temporal lobe” of the brain and the “lower lobe” of the lung. These phrases are treated as separate elements, with the brain phrases appearing together in one topic, but never co-occurring with the lung phrase.
3.1. Disease and Document Author Classification
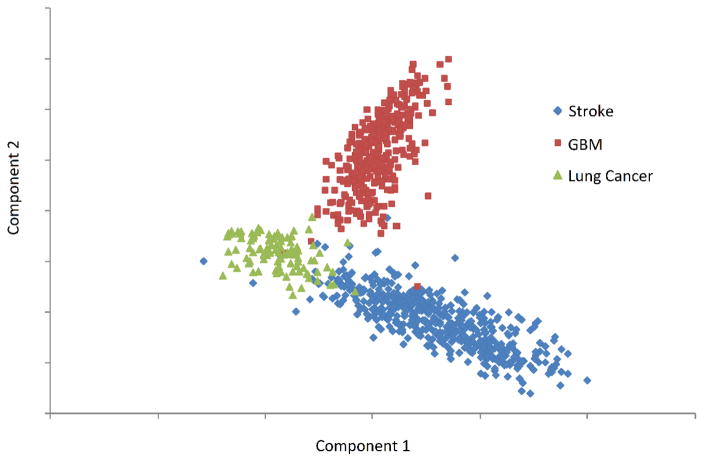
Projecting patients onto their first two spectral components yielded clearly separable clusters for each disease (Figure 2). In general, the first component represented part of the body, with higher values representing brain and lower values representing lung. The second component generally represented disease type, with higher values representing cancer and lower values representing stroke.
Figure 2.
Scatter plot of the first two principal components of the topic distribution of each patient’s medical documents.
The overall accuracy for disease classification was 99.8%. The recall values for all three disease classifications were at least 0.99 (0.999, 0.998, and 0.996 for GBM, lung cancer, and stroke, respectively). The precision values for all three disease classifications were at least 0.99 as well (1.000, 0.998, and 0.995 for GBM, lung cancer, and stroke, respectively).
The overall classification accuracy for document authors was 83.2%. The recall values were between 0.13 (physician I) and 1.00 (physician G) (Table 3). The precision values ranged from 0.30 (physician I) to 1.00 (physician C). The majority of errors occurred within groups of physicians with similar specialties. For instance, physicians A, B, and F are all neuro-oncologists, and physicians G, H, and I are stroke specialists. Author D was actually a combination of two physicians with similar names. The majority (61%) of the documents belonged to a lung cancer specialist and were correctly assigned. The remainder belonged to a stroke specialist and were incorrectly assigned to other authors with stroke specialty.
Table 3.
Confusion matrix for report author classification based on topic distributions.
| A | B | C | D | E | F | G | H | I | J | total | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1223 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 1225 |
| B | 44 | 161 | 0 | 0 | 0 | 4 | 4 | 0 | 1 | 0 | 214 |
| C | 0 | 0 | 141 | 0 | 0 | 1 | 1 | 0 | 0 | 29 | 172 |
| D | 0 | 0 | 0 | 103 | 0 | 2 | 27 | 8 | 13 | 9 | 162 |
| E | 4 | 1 | 0 | 0 | 96 | 12 | 0 | 0 | 0 | 1 | 114 |
| F | 63 | 0 | 0 | 0 | 0 | 43 | 3 | 1 | 0 | 0 | 110 |
| G | 0 | 0 | 0 | 0 | 0 | 0 | 111 | 0 | 0 | 0 | 111 |
| H | 0 | 0 | 0 | 1 | 2 | 9 | 38 | 20 | 5 | 9 | 84 |
| I | 0 | 0 | 0 | 0 | 0 | 0 | 58 | 0 | 9 | 0 | 67 |
| J | 5 | 3 | 0 | 0 | 10 | 18 | 4 | 0 | 0 | 33 | 73 |
|
| |||||||||||
| total | 1339 | 165 | 141 | 104 | 108 | 89 | 246 | 29 | 30 | 81 | 2332 |
In disease classification, the TNG and LDA models achieved significantly lower accuracies (p<0.001) than the MPT and DMR models (table 4). There was no significant difference between the accuracies of the MPT and DMR methods in this classification (p=0.22). In author classification, the MPT method achieved significantly higher classification accuracy than DMR, TNG, and LDA (p<0.001, p=0.002, and p<0.001, respectively). The low performance of some of the methods was due in part to the data imbalance as author A signed substantially more documents than the other authors. To account for this imbalance, classification was performed again excluding documents signed by author A. In this analysis, MPT’s accuracy fell and the other three saw improved accuracy. However, MPT still achieved significantly better accuracy than the other models (p=0.002, p=0.002, and p<0.001, respectively).
Table 4.
Comparison of disease and author classification accuracies for the four methods. Author classification is performed with and without inclusion of author A. Values marked with an asterisk are significantly lower than the corresponding accuracy for MPT (p<0.01).
| Disease | Author | ||
|---|---|---|---|
| With Author A | Without Author A | ||
| MPT | 0.9981 | 0.8319 | 0.7471 |
| DMR | 0.9976 | 0.3742* | 0.6910* |
| TNG | 0.8252* | 0.6759* | 0.6931* |
| LDA | 0.7974* | 0.5288* | 0.5858* |
3.2. Empirical Log Likelihood
The two-way ANOVA test showed that there were significant differences between the EL values produced by the four models (p<0.001). Both the TNG (-21724232.7) and DMR (-22373494.3) models had higher empirical log likelihoods than the standard LDA model (-23019060.3; p<0.001). The MPT (-21036105.8) model had a significantly higher empirical log likelihood than the TNG, DMR, and LDA models (p<0.001). Of the 8,048 documents in the data set, MPT had a higher EL than the TNG, DMR, and LDA models for 92.9%, 92.5%, and 96.1% of the documents, respectively.
4. Discussion
Knowing information about the patient or the physician writing the document can provide insight into the type of information contained in the document, and using this information is valuable for creating a model. DMR assigns prior probabilities to topics based on the data associated with the document, thereby biasing towards topics that are in line with the document’s metadata. When DMR is not used, every document has the same Dirichlet hyperparameter and the weights for the topics are based on the overall prevalence of the topics throughout the entire data set. Thus, in this clinical document dataset, the high probability topics represent different diseases (Table 2). However, for a given document, these topics are unlikely to co-occur because one patient is unlikely to have each of these diseases. This can result in ambiguous words incorrectly being labelled as a different disease from much of the remaining document.
The disease classification results indicate that the proposed topic model is able to learn salient dimensions that distinguish different diseases. Disease classification based on topic distributions achieved almost perfect classification accuracy (99.8%). The high classification accuracy using a relatively simple classifier demonstrates the amount of clinical information captured by the topics. While this classification was fairly rudimentary, it can possibly be extended in future work for tasks such as case-based retrieval or outcome prediction. Additionally, the proposed model provides a method for utilizing free-text in an unsupervised manner to extract electronic health record phenotypes, which may prove useful in discovering disease subtypes, or in supporting phenome-wide association studies that generally rely on coded data or pre-specified concepts.
In the disease classification, many of the misclassified patients had other diseases in their medical histories that could explain the prevalence of topics more commonly associated with other classes. For example, a GBM patient that was misclassified as a lung cancer patient had several lung issues in their history, including a pulmonary embolism. Similarly, a lung cancer patient that was classified as a stroke patient was primarily being treated for an aneurysm and only later had lung nodules discovered. Finally, a stroke patient who was classified as a lung cancer patient was being treated for chronic depression and later had a stroke. The majority (74%) of the documents in this patient’s record predated the stroke and many subsequent documents were about depression and obesity. These examples represent one of the challenges of analyzing EHR data: patients have a large and diverse set of co-morbidities that can make them difficult to classify. Furthermore, we looked at the entirety of each patient’s medical record, rather than a fixed number of previous encounters. Thus, our primary care patients generally have a much longer history than those receiving only specialty care, which leads to noise in the outlined classification task.
Author prediction was a more difficult task given the higher number of possibilities. The classifier was able to correctly classify 83.2% of the documents with the majority of the errors occurring between physicians with similar specialties. Among those with a similar specialty, the classifier was still able to correctly classify the majority of the time, indicating that it was able to capture more subtle physician-specific information beyond the primary specialty.
4.1. Future Directions
A fixed parameter in all LDA-based topic models is the number of topics, which is important because it affects the granularity of the topics generated. If the number it too low, it is not able to distinguish between distinct concepts, while a value too high will result in overly specific topics that are hard to interpret. The optimal number of topics is largely dependent on the type of text being modeled and the intended application of the results. In this study, the value is set to 100 based on prior studies involving LDA topic models in clinical literature.[41] Because the optimal value for LDA is not necessarily optimal for the proposed model, future work could further improve the presented results by optimizing the number of topics.
The current model represents text using bigrams, which could potentially be improved with more complicated language models. While going beyond bigrams may yield a better-fitting model, it would add significant complexity to the model. Currently, the model finds a Dirichlet distribution across all words in the vocabulary for each bigram completion, which results in a number of variables equal to the square of the size of the vocabulary. Increasing beyond bigrams increases this number of variables exponentially, which quickly becomes hard to train. Given a large enough training corpus, however, the larger model could potentially be trained effectively and therefore yield better results. Smoothing methods could also account for this added complexity by using the larger model when training data is available and relying on a simpler model in cases where the larger one is undertrained.[43]
The goal of the current study was to demonstrate the ability of the proposed model to capture important clinical information. The next step will be to implement this method in a health informatics application and measure its potential clinical impact. In particular, we plan to investigate how topics created using the proposed model can be used to drive an application for automatically summarizing patient records. Such an application may include a visualization that displays a list of the top topics for each patient, enabling a concept-oriented information view.
5. Conclusions
Integrating patient and document metadata, as well as capturing phrases in clinical text, greatly improves the topic representation of clinical reports. Incorporating topical n-grams into the model captures common anatomical concepts, tests, and diseases while also differentiating words that are ambiguous in a bag-of-words model. Including patient- and document-level information creates a more informative prior on the topics in a document, resulting in topics that better represent the contained text. Our future work includes using the topics discovered in this study to drive a web application that automatically summarizes a patient’s medical records, including concept, source, and time oriented views.
Supplementary Material
Highlights.
A topic model is proposed that incorporates document metadata and phrase information
The model is applied to a clinical report dataset to capture medical information
Comparison with existing models shows improved clinical document representation
Document classification shows the model’s ability to capture clinical information
Acknowledgments
Funding Statement:
This work was supported by a grant from the National Library of Medicine of the National Institutes of Health under award number R21LM011937 (PI Arnold). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Arnold CW, El-Saden SM, Bui AAT, Taira R. Clinical Case-based Retrieval Using Latent Topic Analysis. AMIA Annu Symp Proc. 2010;2010:26–30. [PMC free article] [PubMed] [Google Scholar]
- 2.Feblowitz JC, Wright A, Singh H, Samal L, Sittig DF. Summarization of clinical information: a conceptual model. J Biomed Inform. 2011;44:688–699. doi: 10.1016/j.jbi.2011.03.008. [DOI] [PubMed] [Google Scholar]
- 3.Blei DM, Ng AY, Jordan MI. Latent Dirichlet Allocation. J Mach Learn Res. 2012;3:993–1022. doi: 10.1162/jmlr.2003.3.4-5.993. [DOI] [Google Scholar]
- 4.Boyd-Graber J, Blei DM, Zhu X. A Topic Model for Word Sense Disambiguation. Proc. 2007 Jt. Conf. Empir. Methods Nat. Lang. Process. Comput. Nat. Lang. Learn; 2007. pp. 1024–1033. [Google Scholar]
- 5.Blei DM, Lafferty JD. A correlated topic model of Science. 2007:17–35. doi: 10.1214/07-AOAS114. [DOI] [Google Scholar]
- 6.Blei DM, Griffiths TL, Jordan MI, Tenenbaum JB. Hierarchical Topic Models and the Nested Chinese Restaurant Process. n.d [Google Scholar]
- 7.Wang C, Blei D, Heckerman D. Continuous time dynamic topic models. 2012 arXiv Prepr. arXiv1206.3298. [Google Scholar]
- 8.Wang X, McCallum A. Topics over time: a non-Markov continuous-time model of topical trends. Proc. 12th ACM SIGKDD Int. Conf. Knowl. Discov. Data Min; ACM; 2006. pp. 424–433. [Google Scholar]
- 9.Arnold C, Speier W. A Topic Model of Clinical Reports. Proc 35th Int ACM SIGIR Conf Res Dev Inf Retr. 2012:1031–1032. doi: 10.1145/2348283.2348454. [DOI] [Google Scholar]
- 10.Cohen R, Aviram I, Elhadad M, Elhadad N. Redundancy-Aware Topic Modeling for Patient Record Notes. PLoS One. 2014;9:e87555. doi: 10.1371/journal.pone.0087555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Howes C, Purver M, McCabe R. Investigating topic modelling for therapy dialogue analysis. Proc. IWCS Work. Comput. Semant. Clin. Text; 2013. pp. 7–16. [Google Scholar]
- 12.Resnik P, Armstrong W, Claudino L, Nguyen T, Nguyen V-A, Boyd-Graber J. Beyond LDA: Exploring Supervised Topic Modeling for Depression-Related Language in Twitter. Proc. 2nd Work. Comput. Linguist. Clin. Psychol; 2015. [Google Scholar]
- 13.Halpern Y, Horng S, Nathanson LA, Shapiro NI, Sontag D. A comparison of dimensionality reduction techniques for unstructured clinical text. Icml 2012 Work. Clin. Data Anal; 2012. [Google Scholar]
- 14.Ghassemi M, Naumann T, Doshi-Velez F, Brimmer N, Joshi R, Rumshisky A, et al. Unfolding physiological state: Mortality modelling in intensive care units. Proc. 20th ACM SIGKDD Int. Conf. Knowl. Discov. Data Min; ACM; 2014. pp. 75–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Deerwester S, Dumais ST, Furnas GW, Landauer TK, Harshman R. Indexing by latent semantic analysis. J Am Soc Inf Sci. 1990;41:391–407. doi: 10.1002/(SICI)1097-4571(199009)41:6<391::AID-ASI1>3.0.CO;2-9. [DOI] [Google Scholar]
- 16.Hofmann T. Probabilistic latent semantic indexing. Sigir. 1999:50–57. doi: 10.1145/312624.312649. [DOI] [Google Scholar]
- 17.Dempster a, Laird N, Rubin D. Maximum Likelihood from Incomplete Data via the EM Algorithm. J R Stat Soc Ser B. 1977;39:1–38. [Google Scholar]
- 18.Blei DM, Lafferty JD. Dynamic topic models. Proc. 23rd Int. Conf. Mach. Learn; ACM; 2006. pp. 113–120. [Google Scholar]
- 19.Blei DM, Jordan MI. Modeling annotated data. Proc. 26th Annu. Int. ACM SIGIR Conf. Res. Dev. Informaion Retr; ACM; 2003. pp. 127–134. [Google Scholar]
- 20.Barnard K, Duygulu P, Forsyth D, De Freitas N, Blei DM, Jordan MI. Matching words and pictures. J Mach Learn Res. 2003;3:1107–1135. [Google Scholar]
- 21.Carrivick L, Prabhu S, Goddard P, Rossiter J. Unsupervised learning in radiology using novel latent variable models. Comput. Vis. Pattern Recognition, 2005. CVPR 2005. IEEE Comput. Soc. Conf; IEEE; 2005. pp. 854–859. [Google Scholar]
- 22.Mimno D, Wallach HM, Naradowsky J, Smith DA, McCallum A. Polylingual topic models. Proc. 2009 Conf. Empir. Methods Nat. Lang. Process; Association for Computational Linguistics; 2009. pp. 880–889. [Google Scholar]
- 23.Crain SP, Yang S-H, Zha H, Jiao Y. Dialect topic modeling for improved consumer medical search. AMIA Annu. Symp. Proc; American Medical Informatics Association; 2010. p. 132. [PMC free article] [PubMed] [Google Scholar]
- 24.Li W, McCallum A. Pachinko allocation: DAG-structured mixture models of topic correlations. Proc. 23rd Int. Conf. Mach. Learn; ACM; 2006. pp. 577–584. [Google Scholar]
- 25.Teh YW, Jordan MI, Beal MJ, Blei DM. Hierarchical dirichlet processes. J Am Stat Assoc. 2006;101 [Google Scholar]
- 26.Wang X, McCallum A, Wei X. Topical n-grams: Phrase and topic discovery, with an application to information retrieval. Data Mining, 2007. ICDM 2007. Seventh IEEE Int. Conf; IEEE; 2007. pp. 697–702. [Google Scholar]
- 27.Steyvers M, Griffiths T. Matlab topic modeling toolbox. 2013 May 20; Http//psiexp.Ss.Uci.Edu/research/programs_Data/toolbox.Htm(2005)
- 28.Wallach HM. Topic modeling: beyond bag-of-words. Proc. 23rd Int. Conf. Mach. Learn; ACM; 2006. pp. 977–984. [Google Scholar]
- 29.Mimno D, McCallum A. Topic models conditioned on arbitrary features with dirichlet-multinomial regression. 2012 arXiv Prepr. arXiv1206.3278. [Google Scholar]
- 30.Jordan MI. Learning in Graphical Models. proceedings of the NATO Advanced Study Institute...: Ettore Mairona Center; Erice, Italy. September 27–October 7, 1996; Springer Science & Business Media; 1998. [Google Scholar]
- 31.Jordan MI, Ghahramani Z, Jaakkola TS, Saul LK. An introduction to variational methods for graphical models. Mach Learn. 1999;37:183–233. [Google Scholar]
- 32.Wainwright MJ, Jordan MI. Graphical models, exponential families, and variational inference. Found Trends® Mach Learn. 2008;1:1–305. [Google Scholar]
- 33.Bishop CM. Pattern recognition and machine learning. springer; New York: 2006. [Google Scholar]
- 34.Gelman A, Carlin JB, Stern HS, Rubin DB. Bayesian data analysis. Taylor & Francis; 2014. [Google Scholar]
- 35.Steyvers M, Griffiths T. Probabilistic topic models. Handb Latent Semant Anal. 2007;427:424–440. [Google Scholar]
- 36.Resnik P, Hardisty E. Gibbs sampling for the uninitiated. DTIC Document. 2010 [Google Scholar]
- 37.Griffiths TL, Steyvers M. Finding scientific topics. Proc Natl Acad Sci. 2004;101:5228–5235. doi: 10.1073/pnas.0307752101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Liu DC, Nocedal J. On the limited memory BFGS method for large scale optimization. Math Program. 1989;45:503–528. [Google Scholar]
- 39.Wright SJ, Nocedal J. Numerical optimization. Springer; New York: 1999. [Google Scholar]
- 40.McCallum AK. MALLET: A Machine Learning for Language Toolkit. 2002. [Google Scholar]
- 41.Arnold CW, Oh A, Chen S, Speier W. Evaluating topic model interpretability from a primary care physician perspective. Comput Methods Programs Biomed. 2015 doi: 10.1016/j.cmpb.2015.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wei L, McCallum A. Pachinko allocation: DAG-structured mixture models of topic correlations, ICML ’06. Proc 23rd Int Conf Mach Learn. 2006:577–584. doi: 10.1145/1143844.1143917. [DOI] [Google Scholar]
- 43.Witten IH, Bell T. The zero-frequency problem: Estimating the probabilities of novel events in adaptive text compression. Inf Theory, IEEE Trans. 1991;37:1085–1094. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.