Time-domain comparisons of power law attenuation in causal and noncausal time-fractional wave equations

Abstract

The attenuation of ultrasound propagating in human tissue follows a power law with respect to frequency that is modeled by several different causal and noncausal fractional partial differential equations. To demonstrate some of the similarities and differences that are observed in three related time-fractional partial differential equations, time-domain Green's functions are calculated numerically for the power law wave equation, the Szabo wave equation, and for the Caputo wave equation. These Green's functions are evaluated for water with a power law exponent of y = 2, breast with a power law exponent of y = 1.5, and liver with a power law exponent of y = 1.139. Simulation results show that the noncausal features of the numerically calculated time-domain response are only evident very close to the source and that these causal and noncausal time-domain Green's functions converge to the same result away from the source. When noncausal time-domain Green's functions are convolved with a short pulse, no evidence of noncausal behavior remains in the time-domain, which suggests that these causal and noncausal time-fractional models are equally effective for these numerical calculations.

I. INTRODUCTION

The attenuation of compressional ultrasound waves in soft tissue is described by a power law of the form α(f) = ${\alpha }_0{\left|f\right|}^y$, where f is the frequency in MHz, α₀ is the attenuation constant in Np/m/Hz^y or dB/m/Hz^y, and y is the power law exponent. Examples of measured values for the power law exponent are y = 1.139 in human liver¹ and y = 1.5 in human breast.² Additional examples of mammalian tissues with various power law exponents are tabulated in the book by Duck,³ and other compiled lists of attenuation values are found in papers by Goss et al.^4,5

The corresponding wave equations that describe power law attenuation in soft tissue utilize fractional derivatives, which are non-integer order derivatives. These fractional derivatives are often time-fractional,^6–8 although space-fractional derivatives are also used.^9,10 Examples of time-fractional lossy wave equations that model attenuation and dispersion of ultrasound in soft tissue include the Szabo wave equation,⁶ the Caputo wave equation,¹¹ and the power law wave equation.⁷ The Szabo and power law wave equations were developed for medical ultrasound applications, and the Caputo wave equation¹¹ was originally defined for applications in geophysics and then independently evaluated by Wismer as a model for attenuation and dispersion in soft tissue.⁸

The time-fractional wave equations are particularly amenable to analytical methods of causality analysis, including the Paley-Wiener criterion,¹² Kramers-Kronig analysis,¹³ and a time causal theory;⁶ however, inconsistent conclusions are often reached with different methods, especially for power law exponents y ≥ 1. In an effort to resolve some of these apparent inconsistencies, time-domain Green's functions are calculated numerically for the Blackstock wave equation, the Stokes wave equation, the Szabo wave equation, the Caputo wave equation, and the power law wave equation. In addition, a three-cycle Hanning-weighted pulse is convolved with each of these to show the effects of causal and noncausal Green's functions on the calculated signals. The results show that noncausal behavior is only evident very close to the source in time-domain Green's function calculations, that this noncausal behavior is no longer evident after convolution with a short pulse, and that the time-domain calculations with these causal and noncausal time-fractional models converge a short distance from the source.

II. TIME-FRACTIONAL WAVE EQUATIONS

A. Power law attenuation and dispersion

The frequency-dependent attenuation α(ω) of ultrasound in soft tissue is described by the power law¹⁴

$$\alpha (\omega )={\alpha }_0{|\omega |}^y,$$ (1)

where y is the power-law exponent, α₀ is the attenuation constant, and ω is the angular frequency in radians/s. The corresponding frequency-dependent sound speed (dispersion) c(ω) satisfies¹⁴

$$\frac{1}{c(\omega )}=\frac{1}{c_0}+{\alpha }_0\hspace{0.17em}\text{tan}\left(\frac{\pi y}{2}\right){|\omega |}^{y-1}.$$ (2)

In Eq. (2), c₀ is the sound speed at ω = 0, and when y = 2, Eq. (2) is nondispersive because the ω dependence disappears. For the numerical calculations that follow, the attenuation constant α₀ with units Np/cm/MHz^y is multiplied by 100 and divided by 10^6y and (2π)^y to convert cm into m, MHz into Hz, and frequency in Hz into angular frequency in radians/s, respectively.

B. Szabo wave equation

For an attenuation constant α₀ with units Np/m/Hz^y, the Szabo wave equation⁶ is given by

$${\nabla }^{2}p-\frac{1}{c_0^2}\frac{{\partial }^{2}p}{\partial t^2}-\frac{2{\alpha }_0}{c_0\hspace{0.17em}\text{cos}\left(\pi y/2\right)}\frac{{\partial }^{y+1}p}{\partial t^{y+1}}=0,$$ (3)

where p represents the pressure in Pa and t is the time in seconds. The Szabo wave equation is a time-fractional extension of the Blackstock wave equation,¹⁵

$${\nabla }^{2}p-\frac{1}{c_0^2}\frac{{\partial }^{2}p}{\partial t^2}+\frac{2{\alpha }_0}{c_0}\frac{{\partial }^{3}p}{\partial t^3}=0,$$ (4)

where the third term in Eq. (3) approximately describes the effects of power law attenuation and dispersion in Eqs. (1) and (2) over the range of frequencies where the smallness approximation⁶ holds. When the Fourier transform in time of a function f(t) is defined as $\mathcal{F}\{f(t)\}={\int }_{-\infty }^{\infty }f(t)e^{-j\omega t}dt$, the 3D frequency-domain Green's function for the Szabo wave equation is

$$G\left(r,\omega \right)=\frac{\exp (-\frac{r}{c_0}\sqrt{-{\omega }^2+\frac{2{\alpha }_0{c}_0}{\hspace{0.17em}\text{cos}\left(\pi y/2\right)}{\left(j\omega \right)}^{y+1}})}{4\pi r}$$ (5)

for frequencies ω ≥ 0, where r = $\sqrt{x^2+y^2+z^2}$ is the distance from a point source at the origin to an observation point at (x, y, z). There is no known exact time-domain Green's function for the Szabo wave equation.

C. Power law wave equation

The power-law wave equation,⁷ which is closely related to the Szabo wave equation in Eq. (3), is given by

$${\nabla }^{2}p-\frac{1}{c_0^2}\frac{{\partial }^{2}p}{\partial t^2}-\frac{2{\alpha }_0}{c_0\hspace{0.17em}\text{cos}\left(\pi y/2\right)}\frac{{\partial }^{y+1}p}{\partial t^{y+1}}-\frac{{\alpha }_0^2}{\hspace{0.17em}{\text{cos}}^2\left(\pi y/2\right)}\frac{{\partial }^{2y}p}{\partial t^{2y}}=0.$$ (6)

Only the power law wave equation yields a complex wavenumber that exactly satisfies Eqs. (1) and (2) for all frequencies ω, whereas the Szabo and Caputo time-fractional wave equations approximately satisfy these expressions. The 3D frequency-domain Green's function for the power law wave equation is

$$G\left(r,\omega \right)=\frac{e^{-j\omega r/c_0}{e}^{-{\alpha }_0{\left(j\omega \right)}^{y}r/\hspace{0.17em}\text{cos}\left(\pi y/2\right)}}{4\pi r}.$$ (7)

By expanding the second exponential term with j^y = e^jπy/2 and collecting the real and imaginary parts from the two exponential terms in the numerator of Eq. (7), the attenuation and dispersion relations in Eqs. (1) and (2) are exactly recovered. Furthermore, unlike the other time-fractional wave equations evaluated here, the power law wave equation has an exact closed form 3D time-domain Green's function, which is

$$g\left(r,t\right)=\frac{1}{4\pi r}\frac{1}{{\left({\alpha }_{0}r\right)}^{1/y}}{\tilde{f}}_y\left[\frac{t-\frac{r}{c_0}}{{\left({\alpha }_{0}r\right)}^{1/y}}\right].$$ (8)

In Eq. (8), ${\tilde{f}}_y$ is the probability density function (pdf) for a maximally skewed stable distribution¹⁶ with parameter y. Since the power law wave equation exactly satisfies Eqs. (1) and (2), demonstrating whether the time-domain Green's function in Eq. (8) is causal or noncausal is equivalent to demonstrating whether the expressions in Eqs. (1) and (2) are causal or noncausal.

For the power law exponent y = 2, the 3D frequency-domain Green's function in Eq. (7) reduces to

$$G\left(r,\omega \right)=\frac{e^{-j\omega r/c_0}{e}^{-{\alpha }_0{\omega }^{2}r}}{4\pi r},$$ (9)

which is a Gaussian function multiplied by the 1/(4πr) geometric spreading factor and a complex exponential delay term. The inverse Fourier transform of Eq. (9) is exactly equal to the time-shifted Gaussian function

$$g\left(r,t\right)=\frac{1}{4\pi r}\frac{1}{\sqrt{4\pi {\alpha }_{0}r}}{e}^{-{\left(t-r/c_0\right)}^2/\left(4{\alpha }_{0}r\right)},$$ (10)

which is equivalent to the time-domain Green's function in Eq. (8) with y = 2.

D. Caputo wave equation

The Caputo wave equation¹¹ is given by

$${\nabla }^{2}p-\frac{1}{c_0^2}\frac{{\partial }^{2}p}{\partial t^2}+{\tau }^{y-1}\frac{{\partial }^{y-1}}{\partial t^{y-1}}{\nabla }^{2}p=0,$$ (11)

where τ is the fractional relaxation time. The Caputo wave equation, which is a time-fractional extension of the Stokes wave equation¹⁷

$${\nabla }^{2}p-\frac{1}{c_0^2}\frac{{\partial }^{2}p}{\partial t^2}+\tau \frac{\partial }{\partial t}{\nabla }^{2}p=0,$$ (12)

approximately satisfies the attenuation and dispersion relations in Eqs. (1) and (2), and no exact closed form time-domain Green's function is available for the Caputo wave equation. However, the 3D frequency-domain Green's function for the Caputo wave equation is

$$G\left(r,\omega \right)=\frac{1}{1+{\left(j\omega \tau \right)}^{y-1}}\frac{\exp (-\frac{j\omega r}{c_0}\frac{1}{\sqrt{1+{\left(j\omega \tau \right)}^{y-1}}})}{4\pi r}$$ (13)

for frequencies ω ≥ 0.

E. Conversion factor

The conversion factor

$${\tau }^{y-1}=-2{\alpha }_0{c}_0/\text{cos}\hspace{0.17em}(\pi y/2),$$ (14)

which relates the power law attenuation constant α₀ to the fractional relaxation time τ, is obtained by Fourier-transforming the power law wave equation and the Caputo wave equation in time and space. After solving for the square of the wavenumber and taking the square root of both sides, the smallness approximation⁶ yields Eq. (14). This expression is singular at y = 1, the Szabo and power law wave equations are also singular at y = 1, and the Caputo wave equation is non-attenuating at y = 1, so only values of the power law exponent that satisfy 1 < y ≤ 2 are considered in the following numerical evaluations.

III. CAUSALITY FOR ACOUSTIC PROPAGATION

In a causal system, the effect does not precede the cause.⁶ Causality in the context of signal analysis¹⁸ requires that the impulse response h(t) is causal if h(t) = 0 for all t < 0, and when this definition is extended to the attenuation and dispersion relations that describe acoustic propagation in soft tissue, the time-domain Green's function g(r, t) is causal if g(r, t) = 0 for all t < 0 and noncausal if g(r, t) ≠ 0 for any t < 0. Although these are time-domain definitions, efforts to determine whether a model that describes the attenuation and dispersion of ultrasound in soft tissue is causal or noncausal are often performed in the frequency-domain,^12,13,19,20 and definitive demonstrations of noncausal behavior in the time-domain according to the definitions above are generally not provided, presumably because guidelines for evaluating time-domain models of acoustic propagation that clearly demonstrate noncausal effects have not yet been established. Distinguishing between causal and noncausal models in the time-domain is further complicated by noncausal partial differential equations that yield causal time-domain Green's functions at the origin (i.e., at r = 0) and by noncausal partial differential equations that yield time-domain results that appear causal away from the origin, which motivates the following time-domain comparisons and evaluations.

IV. METHODS

Time-domain Green's functions for the power law wave equation are rapidly and accurately evaluated in matlab with the STABLE toolbox.^16,21 In these calculations, which numerically evaluate stable probability distribution functions (pdf's), the index parameter is defined as the power law exponent y, the skewness parameter is equal to 1, the scale parameter is (α₀r)^1/y, and the location parameter is equal to zero. The STABLE toolbox evaluates stable pdf's at single points in time or limited ranges of time values without numerical artifacts, which is advantageous for time-domain Green's function calculations.

The time-domain Green's functions for the Blackstock, Stokes, Caputo, and Szabo wave equations are computed in matlab with inverse fast Fourier transforms (IFFTs). For these calculations, a time window T is defined as an integer multiple of the scale factor (α₀r)^1/y such that the error is 1% or less. The time window T is then extended as needed to fill a larger display window for comparisons with other materials at the same distance. Other parameters that are required for these calculations include the frequency sampling, which is defined as Δf = 1/T, and the center of each time window, which is located at t = r/c. Each time-domain Green's function is computed with 100 time samples per scale parameter, which consistently yields smooth time-domain waveforms for each result. If the time window defined for the time-domain Green's function calculation is larger than the desired display window, then the computed waveform is cropped after the IFFT is evaluated.

In calculations of time-domain Green's functions for the Blackstock and Stokes wave equations with the IFFT, the time window is defined as T ≫ (α₀r)^1/y, and even larger time windows are needed for IFFT-based calculations of the time-domain Green's functions for the Caputo and Szabo wave equations to avoid problems with frequency-domain aliasing. Similar to the time-domain Green's functions for the power law wave equation, the time-domain Green's functions for the Caputo and Szabo wave equations have “heavy tails” that decay as 1/t^y+1 when 0 < y < 2. These heavy tails cause undesirable wrap-around artifacts in the time-domain unless the time window T is sufficiently large and the frequency sampling Δf = 1/T is sufficiently small. Also, for IFFT calculations with nonzero start time t₀, the frequency-domain Green's function is multiplied by e^jωt₀. This accounts for start times before t = 0 when noncausal results are shown close to the source and also for calculations at larger distances with later start times.

V. RESULTS

A. Time-domain Green's functions for acoustic propagation in water

Time-domain Green's functions multiplied by 4πr are shown in Figs. 1(a)–1(d) for acoustic propagation in water with y = 2. The results in these figures are calculated with c₀ = 1500 m/s and α₀ = 2.5328 × 10⁻⁴ Np/cm/MHz². In Figs. 1(a)–1(d), the time-domain Green's function for the Stokes wave equation is indicated by a solid line, the time-domain Green's function for the Blackstock wave equation [Eq. (4)] is represented by a dashed line, and the time-domain Green's function for the power law wave equation is indicated by a dash-dot line. The time-domain Green's function for the power law wave equation is directly calculated from the Gaussian function in Eq. (10), and the time-domain Green's functions for the Blackstock and Stokes wave equations apply IFFTs to the values obtained from the frequency-domain Green's functions in Eqs. (5) and (13), respectively, with y = 2. A thin dashed line is also included as a reference in each of the subfigures in Fig. 1 to indicate the arrival time t = r/c₀ for a lossless medium with a constant sound speed c₀.

FIG. 1.

Simulated time-domain Green's functions of the Caputo, Szabo, and power law wave equations calculated for water with y = 2, α₀ = 2.5328 × 10⁻⁴ Np/cm/MHz², and c₀ = 1500 m/s and scaled by 4πr at (a) r = 1 nm, (b) r = 100 nm, (c) r = 1 cm, and (d) r = 10 cm. Simulated time-domain Green's functions of the Caputo, Szabo, and power law wave equations calculated for breast with y = 1.5, α₀ = 0.086 Np/cm/MHz^1.5, and c₀ = 1450 m/s and scaled by 4πr at (e) r = 10 nm, (f) r = 1 μm, (g) r = 1 cm, and (h) r = 10 cm. Simulated time-domain Green's functions of the Caputo, Szabo, and power law wave equations calculated for liver with y = 1.139, α₀ = 0.0459 Np/cm/MHz^1.139, and c₀ = 1540 m/s and scaled by 4πr at (i) r = 100 zm, (j) r = 100 am, (k) r = 1 cm, and (l) r = 10 cm.

The time-domain Green's functions for the Stokes, Blackstock, and power law wave equations evaluated in water are shown in Figs. 1(a)–1(d) at distances of r = 1 nm, r = 100 nm, r = 1 cm, and r = 10 cm. The computed Green's functions are multiplied by 4πr so that the spherical spreading contribution is eliminated and only the effects of propagation, dispersion, and attenuation as a function of time are included in these plots. The units defined for the horizontal axis are picoseconds, nanoseconds, or microseconds. Figure 1(a) shows the result evaluated at a distance r = 10⁻ⁿ m for the smallest integer value of n, specifically n = 9, that clearly demonstrates noncausal behavior in the time-domain Green's functions for both the Blackstock and power law wave equations. Figure 1(b) shows the result at a distance r = 10⁻ⁿ m for the largest integer value of n, namely, n = 7, where the noncausal behavior is not clearly evident in plots of the time-domain Green's functions for the Blackstock and power law wave equations when displayed on a linear vertical scale. Figures 1(c)–1(d) show the results at r = 1 cm and r = 10 cm, respectively, which are representative distances for applications of diagnostic and therapeutic ultrasound. The time-domain Green's functions for the Blackstock and Stokes wave equations define time windows T for IFFT calculations as 40, 40, 300, and 500 times the scale factor (α₀r)^1/y calculated for each respective plot in Figs. 1(a)–1(d). The results in Figs. 1(a)–1(d) are then cropped and displayed in windows that are approximately 25, 25, 197, and 312 scale factors wide, respectively. Figures 1(a)–1(d) demonstrate that the time-domain Green's functions for the Blackstock and power law wave equations produce noncausal time-domain waveforms very close to the source and that these transition over a short distance to waveforms that are difficult to distinguish from causal waveforms in the time-domain.

Figure 1(a) indicates that the time-domain Green's functions for the Blackstock and power law wave equations with y = 2 evaluated at r = 1 nm yield similar, yet distinct, results, where both of these are clearly noncausal with significant nonzero contributions between t = −5 ps and t = 0. Whereas the time-domain Green's function for the power law wave equation is a Gaussian function in time, the time-domain Green's function for the Blackstock wave equation is slightly skewed to the right in this location. The time-domain Green's function for the Stokes wave equation evaluated at r = 1 nm first demonstrates nonzero values after time t = 0, and the shape of the time-domain Green's function for the Stokes wave equation is clearly different from the other two time-domain Green's functions.

The time-domain Green's functions evaluated at r = 100 nm in Fig. 1(b) have nearly converged to the same result. All three waveforms are now clearly offset from t = 0, where some small differences remain, and all three waveforms appear to be causal in these plots. However, since the time-domain Green's function for the power law wave equation is a time-shifted Gaussian function, even though the result appears to be causal, the time-domain result is nonzero for all values of t < 0, so the Green's function for the power law wave equation is noncausal. In Figs. 1(c)–1(d), all three time-domain Green's functions evaluated at r = 1 cm and at r = 10 cm agree closely, which indicates that as the distance r increases, the time-domain Green's functions for the Blackstock and Stokes wave equations converge to the Gaussian function in Eq. (10).

B. Time-domain Green's functions for acoustic propagation in breast

Figures 1(e)–1(h) show the time-domain Green's functions multiplied by 4πr for the Caputo wave equation (solid line), the Szabo wave equation (dashed line), and the power law wave equation (dot-dashed line) calculated for human breast with y = 1.5, α₀ = 0.086 Np/cm/MHz^1.5, and c₀ = 1450 m/s. The results are computed at r = 10 nm, r = 1 μm, r = 1 cm, and r = 10 cm. The units defined for the horizontal axis in Figs. 1(e)–1(h) are again picoseconds, nanoseconds, or microseconds. Figure 1(e) contains the result evaluated at a distance r = 10⁻ⁿ m for the smallest integer value of n, specifically n = 8, that clearly demonstrates noncausal behavior in the time-domain Green's functions for both the Szabo and power law wave equations. Figure 1(f) displays the result at a distance r = 10⁻ⁿ m for the largest integer value of n, namely, n = 6, where the noncausal behavior is not clearly evident in plots of the time-domain Green's functions for both the Szabo and power law wave equations when displayed on a linear vertical scale. Figures 1(g) and 1(h) show the results at r = 1 cm and r = 10 cm, respectively. The time-domain Green's functions for the Szabo and Caputo wave equations define time windows T for IFFT calculations as 300, 60, 30, and 30 times the scale factor (α₀r)^1/y calculated at each distance r for each respective plot in Figs. 1(e)–1(h). The results in Figs. 1(e)–1(h) are then cropped and displayed in windows that are approximately 23, 30, 16, and 17 scale factors wide, respectively.

Figure 1(e), which shows the time-domain Green's functions calculated for breast at r = 10 nm, indicates that the Szabo and power law wave equations are noncausal and that the Caputo wave equation is causal. In this location, the time-domain Green's functions for the Szabo and power law wave equations are clearly nonzero before time t = 0, and the time-domain Green's function for the Caputo wave equation first demonstrates nonzero values after time t = 0. The shapes of the three time-domain waveforms also demonstrate significant differences at this distance.

Figure 1(f), which is evaluated at r = 1 μm, shows that the three waveforms calculated for breast are starting to converge at this distance. However, at r = 1 μm, identifying the noncausal contributions is difficult in the time-domain when these are plotted on a linear scale. Similar to the Gaussian function, the stable pdf in the numerator of Eq. (8) is strictly positive⁷ for all values of t when y = 1.5, so the power law wave equation is noncausal at all distances for y = 1.5.

Figures 1(g) and 1(h), which are evaluated at r = 1 cm and r = 10 cm, respectively, show that the time-domain Green's functions for the three time-fractional wave equations in Eqs. (3), (6), and (11) converge to the same result at these distances. Unlike the results shown in Figs. 1(b)–1(d), which are either approximately or exactly represented by symmetric, time-shifted Gaussian functions, the time-domain Green's functions in Figs. 1(f)–1(h) are skewed (asymmetric) with a heavy tail, which are characteristics of the maximally-skewed stable pdf in Eq. (8).

C. Time-domain Green's functions for acoustic propagation in liver

Figures 1(i)–1(l) show the simulated Green's functions for Caputo wave equation (solid line), the Szabo wave equation (dashed line), and the power law wave equation (dot-dashed line) for human liver with y = 1.139, α₀ = 0.0459 Np/cm/MHz^1.139, and c₀ = 1540 m/s. In Figs. 1(i)–1(l), the three time-domain Green's functions are multiplied by 4πr and then evaluated at r = 100 zm, r = 100 am, r = 1 cm, and r = 10 cm. The units defined for the horizontal axis in Figs. 1(i)–1(l) are yoctoseconds (ys or 10⁻²⁴ seconds), zeptoseconds (zs or 10⁻²¹ seconds), or microseconds (μs). Figure 1(i) contains the result evaluated at a distance r = 10⁻ⁿ m for the smallest integer value of n, specifically n = 19, that clearly demonstrates noncausal behavior in the time-domain Green's functions for both the Szabo and power law wave equations, and Fig. 1(j) displays the result at a distance r = 10⁻ⁿ m for the largest integer value of n, namely, n = 16, where the noncausal behavior is not clearly evident in any of the three time-domain Green's functions when shown on a linear scale. Figures 1(k) and 1(l) show the results at r = 1 cm and r = 10 cm, respectively. The time-domain Green's functions for the Szabo and Caputo wave equations define time windows T for IFFT calculations as 12 000, 4000, 60, and 40 times the scale factor (α₀r)^1/y calculated at each distance r for each respective plot in Figs. 1(i)–1(l). The results in Figs. 1(i)–1(l) are then cropped and displayed in windows that are approximately 55, 37, 47, and 31 scale factors wide, respectively.

Figure 1(i) shows the time-domain Green's functions calculated for human liver at r = 100 zm (where 1 zeptometer = 1 zm = 10⁻²¹ m). In Fig. 1(i), the time-domain Green's functions for the Szabo and power law wave equations are clearly noncausal, and the time-domain Green's function for the Caputo wave equation begins a short time after t = 0. In Fig. 1(j), which is evaluated at r = 100 am, all three time-domain Green's functions are still distinct, and all three appear to start after t = 0.

Figures 1(k) and 1(l) display the time-domain Green's function calculated for human liver at r = 1 cm and at r = 10 cm, respectively. These figures show that the three time-domain Green's functions again converge to the same result as the distance increases. The waveforms in Figs. 1(k) and 1(l) are distinct from the waveforms shown in Figs. 1(g) and 1(h) in terms of both the overall shape and the temporal extent. Also, the power law wave equation maintains the same shape for the time-domain Green's function at all distances, but the shapes of the time-domain Green's functions for the Szabo and Caputo wave equations are noticeably different at shorter distances.

D. Vertical axis scaling

In each subfigure of Fig. 1, the maximum value of the vertical axis is determined by the largest of the three peak values in that subfigure. The peak value of 4πrg(r, t) for the power law wave equation when y = 2, which is the Gaussian function in Eq. (10), is equal to $1/\sqrt{4\pi {\alpha }_{0}r}$. Similarly, the peak value of the scaled stable pdf in Eq. (8) is approximately equal to $1/[2\sqrt{\pi }({\alpha }_0{r}^{1/y})]$. Thus, when the peaks of the three time-domain Green's functions start to converge, each decays as r^–1/y, and the limits of the vertical axes are proportional to the peak of the scaled stable pdf. Before the peak values converge, the axes are autoscaled.

E. Comparisons between time-domain Green's functions for acoustic propagation

To enable comparisons between the time-domain Green's functions calculated in water, breast, and liver, Figs. 1(c), 1(g), and 1(k), which occupy the third column of Fig. 1, are all calculated at r = 1 cm, and Figs. 1(d), 1(h), and 1(l), which occupy the fourth column of Fig. 1, are all calculated at r = 10 cm. Figures 1(a), 1(b), 1(e), 1(f), 1(i), and 1(j) are all computed at different distances, so the figures in the first two columns of Fig. 1 are not compared. Figures 1(c), 1(g), and 1(k) are all shown in a 0.5 μs wide time window, and Figs. 1(d), 1(h), and 1(l) are all shown in a 2.5 μs wide time window, where the size of each time window is determined by the temporal extent of the time-domain Green's functions calculated in breast.

When displayed in these two time windows, the time-domain Green's function for acoustic propagation in water exhibits nearly negligible dispersion, the time-domain Green's function for acoustic propagation in liver shows moderate dispersion, and the time-domain Green's function for acoustic propagation in breast is much more dispersive than water or liver. Furthermore, the time-domain Green's function for acoustic propagation in water is nearly impulsive relative to breast and liver. Also, each figure in Fig. 1 exhibits different arrival times. This is in part due to the different values for c₀ in water, breast, and liver, where the thin dashed lines that indicate the arrival time for a lossless medium with sound speed c₀ each occur at a different time, as observed along the third and fourth columns of Fig. 1. The time-domain Green's functions for acoustic propagation in breast and liver also demonstrate much earlier arrival times than the time t = r/c₀ predicted for lossless propagation due to dispersion. Among these, the peak value of the time-domain Green's function for acoustic propagation is largest in water and smallest in breast, as indicated by comparisons between the values on the vertical axes (noting the exponents in the upper left hand corner of each subfigure) in Figs. 1(c), 1(g), and 1(k) (r = 1 cm) and Figs. 1(d), 1(h), and 1(l) (r = 10 cm). Comparisons along the third and fourth columns of Fig. 1 also show that the shapes and extents of the time-domain Green's functions for acoustic propagation in water, breast, and liver differ significantly, as determined by the values of the power law exponent y and the scale factor (α₀r)^1/y.

F. Convergence of the Green's functions for acoustic propagation in the time domain

Figures 1(a)–1(d) demonstrate that the time-domain Green's functions for the Blackstock and Stokes wave equations multiplied by 4πr converge to a Gaussian function, and Figs. 1(e)–1(h) and 1(i)–1(l) show that the time-domain Green's functions for the Szabo and Caputo wave equations multiplied by 4πr converge to maximally skewed stable pdf's. This suggests that the time-domain Green's function for the power law wave equation is an effective approximation for the time-domain Green's functions of the Blackstock and Stokes wave equations when y = 2 and the Szabo and Caputo wave equations when 1 < y < 2. To characterize the convergence of these time-domain Green's functions, the percent difference between g(r, t) and a reference $g_{\mathit{r}\mathit{e}\mathit{f}}(r,t)$ is defined as ${\Vert g(r,t)-g_{\mathit{r}\mathit{e}\mathit{f}}(r,t)\Vert }_2/{\Vert g_{\mathit{r}\mathit{e}\mathit{f}}(r,t)\Vert }_2\times 100\%$, where g(r, t) is the time-domain Green's function calculated at a given distance r for the Blackstock, Stokes, Szabo, or Caputo wave equation, and the reference time-domain Green's function $g_{\mathit{r}\mathit{e}\mathit{f}}(r,t)$ for these calculations is the time-domain Green's function for the power law wave equation. In Fig. 2, these percent differences are calculated from r = 1 nm to r = 1 m for each material. Figure 2(a) shows the convergence of the time-domain Green's functions for the Stokes and Blackstock wave equations to the time-domain Green's function of the power law wave equation calculated for water with y = 2, α₀ = 2.5328 × 10⁻⁴ Np/cm/MHz², and c₀ = 1500 m/s. Figure 2(b) shows the convergence of the time-domain Green's functions for the Szabo and Caputo wave equations to the time-domain Green's function of the power law wave equation calculated for breast with y = 1.5, α₀ = 0.086 Np/cm/MHz^1.5, and c₀ = 1450 m/s. Figure 2(c) shows the convergence of the time-domain Green's functions for the Szabo and Caputo wave equations to the time-domain Green's function of the power law wave equation calculated for liver with y = 1.139, α₀ = 0.0459 Np/cm/MHz^1.139, and c₀ = 1540 m/s.

FIG. 2.

(a) The percent difference between the time-domain Green's functions for the Blackstock and Stokes wave equations and the time-domain Green's function for the power law wave equation as a function of distance calculated for water with y = 2, α₀ = 2.5328 × 10⁻⁴ Np/cm/MHz², and c₀ = 1500 m/s. (b),(c) The percent difference between the time-domain Green's functions for the Szabo and Caputo wave equation and the time-domain Green's functions for the power law wave equation as a function of distance calculated for breast with y = 1.5, α₀ = 0.086 Np/cm/MHz^1.5, and c₀ = 1450 m/s and calculated for liver with y = 1.139, α₀ = 0.0459 Np/cm/MHz^1.139, and c₀ = 1540 m/s.

In each medium, the percent differences calculated with the time-domain Green's functions for the Blackstock and Szabo wave equations are consistently smaller than those calculated for the Stokes and Caputo wave equations, respectively. In Fig. 2(a), the percent difference for the time-domain Green's function of the Blackstock wave equation calculated for water is 23% at r = 1 nm, and the percent difference for the time-domain Green's function of the Stokes wave equation calculated for water is 59% at r = 1 nm. Both time-domain Green's functions achieve rapid reductions in the percent difference calculated for water between 1 nm and 1 μm, and then the percent difference for the time-domain Green's function of the Blackstock wave equation calculated for water reaches 0.0009% at r = 1 m, and the percent difference for the time-domain Green's function of the Stokes wave equation calculated for water reaches 0.0024% at r = 1 m. In Fig. 2(b), the percent difference for the time-domain Green's function of the Szabo wave equation calculated for breast is 35% at r = 1 nm, and the percent difference for the time-domain Green's function of the Caputo wave equation calculated for breast is 77% at r = 1 nm. The time-domain Green's functions calculated for breast converge more slowly than those calculated for water, where the percent difference for the time-domain Green's function of the Szabo wave equation calculated for breast reaches 0.055% at r = 1 m, and the percent difference for the time-domain Green's function of the Caputo wave equation calculated for breast reaches 0.17% at r = 1 m. In Fig. 2(c), the percent difference for the time-domain Green's function of the Szabo wave equation calculated for liver is 8% at r = 1 nm, and the percent difference for the time-domain Green's function of the Caputo wave equation calculated for liver is 24% at r = 1 nm. Although the percent differences evaluated at r = 1 nm are smaller in liver than in water, the rate of convergence of these time-domain Green's functions is slower in liver than in water or breast, where the percent difference for the time-domain Green's function of the Szabo wave equation calculated for liver reaches 0.66% at r = 1 m, and the percent difference for the time-domain Green's function of the Caputo wave equation calculated for breast reaches 2% at r = 1 m.

G. Characterizing the noncausal component of the time-domain Green's functions for the Blackstock, Szabo, and power law wave equations

In numerical calculations with the Blackstock, Szabo, and power law wave equations, there is a threshold distance above which the noncausal time-domain Green's function is very small for all times t ≤ 0. The distance beyond which the noncausal component of the time-domain Green's functions for the Blackstock, Szabo, and power law wave equation becomes negligible is characterized here with an approach similar to that in⁶ by computing the quantity 20log₁₀{g(r, t = 0)/max[g(r, t)]}, which calculates the value of g(r, t) evaluated at time t = 0 divided by the maximum value of g(r, t) in dB, where the time-domain Green's functions in the numerator and the denominator are each calculated with a fixed value of r, and the maximum value of g(r, t) is evaluated with respect to the time t. In Fig. 3, this expression is evaluated across nine decades at ten equally spaced samples within each decade. The time-domain Green's functions for the Stokes and Caputo wave equations are not characterized with this approach because both of these are always causal for the y values considered here (i.e., 2, 1.5, and 1.139).

FIG. 3.

Relative noncausal contributions of the Blackstock, Szabo, and power law wave equations characterized with 20log₁₀{g(r, t = 0)/max [g(r, t)]} as a function of distance r. This quantity is calculated for (a) water with y = 2, α₀ = 2.5328 × 10⁻⁴ Np/cm/MHz², and c₀ = 1500 m/s from r = 1 nm to r = 1 m, (b) breast with y = 1.5, α₀ = 0.086 Np/cm/MHz^1.5, and c₀ = 1450 m/s from r = 1 nm to r = 1 m, and (c) liver with y = 1.139, α₀ = 0.0459 Np/cm/MHz^1.139, and c₀ = 1540 m/s from r = 1 zm to r = 1 pm.

The results of this calculation are shown in Figs. 3(a)–3(c) for water, breast, and liver. Figures 3(a) and 3(b) show that 20log₁₀{g(r, t = 0)/max[g(r, t)]} evaluated for water and for breast with the time-domain Green's function of the power law wave equation rapidly drops from approximately 0 to −400 dB between r = 1 nm and 1 μm. Figure 3(c) shows that 20log₁₀{g(r, t = 0)/max[g(r, t)]} calculated for liver with the time-domain Green's function of the power law wave equation rapidly decays from approximately 0 to −400 dB between r = 10 am and 100 fm. Figure 3(a) shows that 20log₁₀{g(r, t = 0)/max[g(r, t)]} calculated for water with the time-domain Green's function of the Blackstock wave equation closely tracks the same curve for the time-domain Green's function of the power law wave equation until a threshold between −200 and −300 dB is reached. Figure 3(b) shows that 20log₁₀{g(r, t = 0)/ max[g(r, t)]} calculated for breast with the time-domain Green's function of the Szabo wave equation follows the same trend as the same curve for the time-domain Green's function of the power law wave equation until a threshold near −200 dB is reached. Also, there is a greater difference between the two curves in Fig. 3(b) than in Fig. 3(a). Figure 3(c) shows that, for calculations with the time-domain Green's function of the Szabo wave equation evaluated for liver, the value of 20log₁₀{g(r, t = 0)/max[g(r, t)]} rapidly decays from approximately 0 dB to a value between −100 and −200 dB between r = 1 am and 1 fm. There is a much larger difference between the values of 20log₁₀{g(r, t = 0)/max[g(r, t)]} calculated for liver with the Szabo and power law wave equations than for water or breast. In each calculation of 20log₁₀{g(r, t = 0)/max[g(r, t)]} that evaluates g(r, t) for the Blackstock and Szabo wave equations, the lower threshold is a limitation of numerical calculations with the IFFT, whereas the STABLE toolbox avoids these problems with a numerical approach that is optimized for calculations of stable pdf's.¹⁶

H. Time-domain Green's functions convolved with a three cycle Hanning-weighted pulse

To demonstrate the effects of power law attenuation and dispersion on transient excitations, three cycle Hanning-weighted pulses^22,23 are convolved with time-domain Green's functions multiplied by 4πr, and the results are shown in Fig. 4. In each medium, the convolved waveforms are evaluated at (a) r = 100 μm, (b) r = 1 mm, (c) r = 1 cm, and (d) r = 10 cm. In Fig. 4, the center frequency of the Hanning-weighted pulse is f₀ = 7.5 MHz, which is a representative frequency for medical ultrasound that highlights some of the differences between the waveforms computed for these three materials.

FIG. 4.

Simulated three-cycle Hanning-weighted pulse with a center frequency of f₀ = 7.5 MHz convolved with time-domain Green's functions multiplied by 4πr calculated for water at (a) r = 100 μm, (b) r = 1 mm, (c) r = 1 cm, and (d) r = 10 cm, calculated for breast at (e) r = 100 μm, (f) r = 1 mm, (g) r = 1 cm, and (h) r = 10 cm, and calculated for liver at (i) r = 100 μm, (j) r = 1 mm, (k) r = 1 cm, and (l) r = 10 cm.

In Figs. 4(a)–4(d), which show the convolved waveforms for water, there is no attenuation or dispersion of the pulse at all four distances, and the results obtained from the Stokes, Blackstock, and power law wave equations are nearly identical. The only differences in Figs. 4(a)–4(d) are due to the differences in propagation delays and the different time scale that is employed in Fig. 4(d) to facilitate comparisons with Figs. 4(h) and 4(l). Figures 4(a)–4(d) demonstrate that, at these distances, the time-domain Green's functions for the Blackstock, Stokes, and power law wave equation are effectively delta functions for a three cycle Hanning-weighted pulse with a 7.5 MHz center frequency and that dispersion in water is only observed over much longer distances in water for this short pulse.

Figures 4(e)–4(h) show time-domain Green's functions for acoustic propagation in breast convolved with a three-cycle Hanning-weighted pulse with center frequency f₀ = 7.5 MHz evaluated at the same four distances. At r = 100 μm, r = 1 mm, and at shorter distances, the causal and noncausal time-domain Green's functions evaluated at these distances are all effectively equivalent to delta functions in these convolutions, so at r = 100 μm, r = 1 mm, and at shorter distances, there is minimal attenuation and dispersion of this short pulse. In Fig. 4(g), there is a slight difference between the three waveforms at r = 1 cm, and some attenuation and dispersion is also observed in Fig. 4(g) at r = 1 cm. Figure 4(h) shows that the three convolution results are approximately the same and that the attenuation and dispersion are significant for breast at r = 10 cm. The signal amplitude drops off considerably in Fig. 4(h), and there is also considerable filtering and spreading of the signal in the time domain in Fig. 4(h) relative to Figs. 4(e)–4(g). Figure 4(h) also shows that, unlike the result shown in water at r = 10 cm in Fig. 4(d), the 7.5 MHz center frequency has been completely removed by the effects of power law attenuation and dispersion at r = 10 cm.

Figures 4(i)–4(l) show the results obtained when the time-domain Green's functions for acoustic propagation in liver are convolved with a three-cycle Hanning-weighted pulse with a f₀ = 7.5 MHz center frequency. Figures 4(i) and 4(j) demonstrate that the three convolution results are nearly equivalent and that there is minimal attenuation or dispersion at r = 100 μm and at r = 1 mm. Figure 4(k) indicates that there is a small difference between the three waveforms at r = 1 cm, and there is minimal attenuation and dispersion observed in Fig. 4(k) relative to Figs. 4(i)–4(j). In Fig. 4(l), which is evaluated at r = 10 cm, some differences are observed in the three convolution results because of the differences that are observed at this distance in Fig. 2(c), and there is a moderate amount of attenuation and dispersion relative to that observed at shorter distances in Figs. 4(i)–4(k).

Some interesting trends are also observed when the waveforms evaluated at the same distance are compared for different media. For example, the waveforms in Figs. 4(a), 4(e), and 4(i), which are calculated at r = 100 μm, are all displayed within the same time window. These three figures are all very similar, and no attenuation or dispersion is evident in any of these. The waveforms in Figs. 4(b), 4(f), and 4(j), which are calcuated at r = 1 mm, are also evaluated in the same time window. These three figures are also very similar, again with no attenuation or dispersion, although the waveform locations vary due to the differences in the sound speeds c₀ for the three media. The waveforms in Figs. 4(c), 4(g), and 4(k), which are evaluated at r = 1 cm, are all shown in 0.6 μs wide time windows with different start times. These figures demonstrate more obvious shifts in the waveform locations due to sound speed differences, show some variation in the attenuation in the three media, and indicate the onset of dispersion in the signal calculated for breast. The convolution results in Figs. 4(d), 4(h), and 4(l), which are evaluated at r = 10 cm, are all shown in 2.5 μs wide time windows with different start times. At r = 10 cm, the waveform calculated for water still shows no evidence of attenuation and dispersion, the waveform calculated for liver demonstrates some attenuation and dispersion, and the waveform calculated for breast demonstrates the most attenuation and dispersion of these three materials.

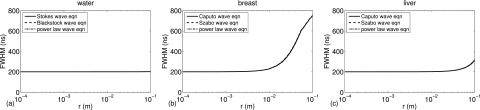
I. Characterizing the dispersion of $\mathit{v}\left(t\right)$ $\ast$ 4πrg(r, t) with the full width at half maximum (FWHM) of the envelope

Figure 5 characterizes the dispersion by evaluating the FWHM of the envelope of the convolution v(t) $\ast$ 4πrg(r, t) for each time-domain Green's function. The FWHM are shown in Figs. 5(a)–5(c) for water, breast, and liver, respectively, where the results are evaluated for distances r between 100 μm and 10 cm. The FWHM in Fig. 5 is calculated by evaluating the Hilbert transform of v(t) $\ast$ 4πg(r, t) and taking the absolute value of the result to obtain the envelope of the waveform. Then, the time at which the peak value of the envelope occurs is determined, the times at which half the peak value is reached are extracted, and then the difference between the largest and the smallest times at which half the peak value occurs determines the FWHM.

FIG. 5.

The FWHM of the envelope of v(t) $\ast$ 4πrg(r, t) calculated for (a) water, (b) breast, and (c) liver, where v(t) is a three cycle Hanning-weighted pulse and g(r, t) is the time-domain Green's function for the Stokes, Blackstock, Caputo, Szabo, or power law wave equation.

In Figs. 5(a)–5(c), the FWHM is calculated for the envelope of v(t) $\ast$ 4πrg(r, t), where v(t) is a three cycle Hanning-weighted pulse with a center frequency of 7.5 MHz, and g(r, t) represents the time-domain Green's function for the Stokes, Blackstock, Caputo, Szabo, or power law wave equation. In Fig. 5(a), the FWHM values calculated with the time-domain Green's functions of the Stokes, Blackstock, and power law wave equations for water are all equal to 200.42 ns at r = 100 μm and are all equal to 201.76 ns at r = 10 cm. The FWHM of the three cycle Hanning-weighted pulse with a center frequency of 7.5 MHz is equal to 200 ns, which suggests that the dispersion is negligible in water for a pulse with 7.5 MHz center frequency for all distances r between 100 μm and 10 cm. In Fig. 5(b), the FWHM values calculated with the time-domain Green's functions of the Caputo, Szabo, and power law wave equations for breast are equal to 200.49, 200.5, and 200.5 ns, respectively, at r = 100 μm and are equal to 750.81, 753.56, and 752.82 ns, respectively, at r = 10 cm. Thus, for all three convolution calculations in breast, the dispersion is negligible at r = 100 μm, but there is significant dispersion at r = 10 cm. In Fig. 5(c), the FWHM values calculated with the time-domain Green's functions of the Caputo, Szabo, and power law wave equations for liver are equal to 200.46, 200.44, and 200.44 ns, respectively, at r = 100 μm and are equal to 311.28, 318.23, and 316.41 ns, respectively, at r = 10 cm. Thus, for all three convolution calculations in liver, the dispersion is negligible at r = 100 μm, and there is moderate dispersion at r = 10 cm. Also, as indicated by the results shown in Figs. 5(a)–5(c) and by the FWHM values given above, the FWHM of the envelope of each convolution calculation are in close agreement in all three materials and for all three time-domain Green's functions when v(t) is represented by a 7.5 MHz center frequency pulse.

VI. DISCUSSION

A. Causal and noncausal time-domain Green's functions for acoustic propagation

Although the Blackstock, Szabo, and power law wave equations are all noncausal, clear demonstrations of noncausal behavior are challenging to find in locations far from the source, as shown in Fig. 1 for time-domain Green's function calculations in water, breast, and liver, especially when the results are plotted on a linear scale. However, in locations very close to the source, i.e., for water with r ≤ 1 nm, for breast with r ≤ 10 nm, and for liver with r ≤ 100 zm, the noncausal contributions are clearly evident in each of these time-domain Green's function calculations. This suggests that successfully observing obvious examples of noncausal time-domain behavior produced by the Blackstock, Szabo, and power law wave equations involves knowing where to look.

Figure 2(a) shows that the time-domain Green's functions for the Stokes and Blackstock wave equations converge to the time-domain Green's function for the power law wave equation in calculations for water, and Figs. 2(b) and 2(c) shows that the time-domain Green's functions for the Caputo and Szabo wave equations converge to the time-domain Green's function for the power law wave equation in calculations for breast and water, respectively, albeit at different rates. Figures 1(c), 1(d), and 2(a) indicate that the time-domain Green's function for the Stokes and Blackstock wave equations converge to a Gaussian function, which is the time-domain Green's function for the power law wave equation when y = 2. Figures 1(g), 1(h), and 2(b) indicate that the time-domain Green's function for the Caputo and Szabo wave equations converge to a maximally skewed stable distribution, and Figs. 1(k), 1(l), and 2(c) also indicate that the time-domain Green's function for the Caputo and Szabo wave equations converge to a maximally skewed stable distribution, which is the time-domain Green's function for the power law wave equation when 0 < y < 2. These figures show that, beyond a certain distance, the time-domain Green's function for the power law wave equation is an effective approximation for the time-domain Green's functions of the Stokes, Blackstock, Caputo, and Szabo wave equations.

Figure 3, which plots 20log₁₀{g(r, t = 0)/max[g(r, t)]} for the Blackstock, Szabo, and power law wave equations, demonstrates that the noncausal contributions to these noncausal time-domain Green's functions are miniscule beyond a certain distance. Figure 3 also demonstrates that calculations of time-domain Green's functions at t = 0 with the IFFT quickly reaches a lower limit beyond a certain distance that depends on the material and on the simulation parameters. Our experience is that the STABLE toolbox achieves much better accuracy than the IFFT and is much more convenient for calculating stable pdf's and for calculating 20log₁₀{g(r, t = 0)/max[g(r, t)]}, since there is no need to compute the entire time-domain Green's function for either of these with the STABLE toolbox.

B. Convolving time-domain Green's functions with three cycle Hanning-weighted pulses

In Fig. 4, noncausal time-domain contributions are not evident in any of the numerical calculations performed with the noncausal time-domain Green's functions. This suggests that the noncausal contributions are effectively “filtered out” by the three cycle Hanning-weighted pulse with a center frequency of 7.5 MHz and that the causal and noncausal models for 4πrg(r, t) considered here are equally effective for these calculations. Figure 5 also suggests that convolutions between the 7.5 MHz center frequency pulse and the noncausal and the causal models for 4πrg(r, t) are all effectively represented by delta functions at the origin in all three materials for distances r ≤ 100 μm. Furthermore, Fig. 5 indicates that there is very little difference between the FWHM of the envelope of 4πrg(r, t) $\ast$ v(t) for the causal and noncausal wave equations evaluated in these three materials, which suggests that convergence of the FWHM is achieved in all materials and at all distances shown. This is in contrast to the results shown in Figs. 1 and 2, which suggest that convergence in the norm of the difference is achieved around 5%.

C. Causality in acoustic wave propagation

Figure 1 indicates that the concept of causality, when distinguishing between the time-domain Green's functions for the Stokes, Blackstock, and power law wave equations when y = 2 and also for the Caputo, Szabo, and power law wave equations when 1 < y < 2, is only important very close to the source. Elsewhere, establishing the absence or presence of causality of these wave equations appears to be a purely academic exercise, because the Stokes, Blackstock, and power law wave equations generate very similar results for y = 2 and the Caputo, Szabo, and power law wave equations also generate very similar results for 1 < y < 2 beyond a certain distance where the noncausal contributions are negligible. However, causality is still a very important concept for acoustic wave propagation, especially for distinguishing incoming noncausal Green's functions from outgoing causal Green's functions and for maintaining consistency between the attenuation and dispersion in acoustic wave propagation, which suggests that the importance of causality in acoustic wave propagation depends on the context. The results presented in Figs. 1–5 suggest that, except for locations very close to the source, the Stokes, Blackstock, and power law wave equations are all effective models for acoustic propagation in water and that the Caputo, Szabo, and power law wave equations are all effective models for acoustic propagation in soft tissue that either exactly or approximately satisfy the attenuation and dispersion relations in Eqs. (1) and (2), respectively.

VII. CONCLUSION

Time-domain Green's functions for three time-fractional wave equations are numerically evaluated and the results are compared at different distances for water, breast, and liver. The results demonstrate that the Szabo and power law wave equations are noncausal and that the Caputo wave equation is causal, where the Szabo wave equation is a time-fractional extension of the noncausal Blackstock wave equation, and the Caputo wave equation is a time-fractional extension of the causal Stokes wave equation. Examples of noncausal behavior are readily observed in time-domain Green's functions for the Blackstock, Szabo, and power law wave equations when these are evaluated very close to the source, i.e., at r ≤ 1 nm for water, at r ≤ 10 nm for breast, and at r ≤ 100 zm for liver, but at much larger distances, the noncausal components of these time-domain Green's functions drop off rapidly. Comparisons also show that the time-domain Green's functions for the Caputo, Szabo, and power law wave equations with 1 < y < 2 converge to the same result and that the time-domain Green's functions for the Stokes, Blackstock, and power law wave equation with y = 2 converge to the same result.

When these time-domain Green's functions are convolved with a three-cycle Hanning-weighted pulse, no noncausal behavior is observed in the time-domain results, and the FWHMs of the envelopes of the convolution results are all approximately the same, which indicates that the Caputo, Szabo, and power law wave equations are equally effective for these time-domain calculations.