Explicit-water theory for the salt-specific effects and Hofmeister series in protein solutions

Abstract

Effects of addition of salts on stability of aqueous protein solutions are studied theoretically and the results are compared with experimental data. In our approach, all the interacting species, proteins, ions, and water molecules, are accounted for explicitly. Water molecules are modeled as hard spheres with four off-center attractive square-well sites. These sites serve to bind either another water or to solvate the ions or protein charges. The ions are represented as charged hard spheres, and decorated by attractive sites to allow solvation. Spherical proteins simultaneously possess positive and negative groups, represented by charged hard spheres, attached to the surface of the protein. The attractive square-well sites, mimicking the protein–protein van der Waals interaction, are located on the surface of the protein. To obtain numerical results, we utilized the energy route of Wertheim’s associative mean spherical approximation. From measurable properties, we choose to calculate the second virial coefficient B₂, which is closely related to the tendency of proteins to aggregate and eventually crystalize. Calculations are in agreement with experimental trends: (i) For low concentration of added salt, the alkali halide salts follow the inverse Hofmeister series. (ii) At higher concentration of added salt, the trend is reversed. (iii) When cations are varied, the salts follow the direct Hofmeister series. (iv) In contrast to the colloidal theories, our approach correctly predicts the non-monotonic behavior of B₂ upon addition of salts. (v) With respect to anions, the theory predicts for the B₂ values to follow different sequences below and above the iso-ionic point, as also confirmed experimentally. (vi) A semi-quantitative agreement between measured and calculated values for the second virial coefficient, as functions of pH of solution and added salt type and concentration, is obtained.

I. INTRODUCTION

Understanding the physical and chemical properties of mixtures of proteins with electrolytes in water^1–10 is of importance to the evaluation of the cellular functions, helps to understand the stability of such mixtures, and may yield improvements of methods for protein precipitation and crystallization.^11–17 For review of earlier studies see Ref. 18. It is well known that protein aggregation is posing a problem in pharmaceutical industry; the bio-pharmaceutical formulations must be free of aggregates, so their formation can be inhibited during storage.¹⁹ We also know that pathological protein aggregation is connected with several diseases.²⁰ On the other hand, in the downstream processing, the proteins have to be salted-out in such a way that their native form is preserved.

Many theories, used to analyze experimental results for protein–salt mixtures in water, are based on the models which treat water and salt as a structureless medium modifying the protein interaction.^18,21–24 Exceptions are the computer simulations, which are more detailed in treating of solvent and salt ions (see, for example, Refs. 25–29). As an alternative to the one-component models on one side and computer simulations on the other, we propose the theory where all the participating species, water, proteins, and salt ions are treated explicitly. We model water molecules as hard spheres with four off-center square-well sites. These sites serve to bind another water molecule or to solvate the ions and protein charges. This model of water, though missing explicit charges, exhibits many properties of real water.³⁰ The ions are depicted as hard spheres with charges in the centers and ability to bind water through discrete attractive square-well sites.^31–33 Two basic premises followed in choosing the interaction parameters for electrolyte ions were as follows: (i) strength of the ion site-water attraction was inversely proportional to the ion diameter, and (ii) the number of available attractive sites on an ion, where waters can coordinate, was proportional to its surface area.³² In summary, small ions bind water molecules strongly, but few of them. Large ions bind water molecules weakly but can coordinate many of them. We proved that this model is able to correctly reproduce the nontrivial ionic size dependence of the osmotic coefficient of alkali halide solutions found experimentally.³² The resulting ion–water interaction parameters, leading good agreement with experimental data, were strongly correlated with the hydration free energies of the individual ions. Protein is modeled as a large hard sphere with small charged spheres, representing charged groups, attached to the surface. The number of charges is set in accordance with the pH of the solution. The short-range van der Waals interaction between proteins is described by the square-well sites distributed over the surface of the protein. Notice that such rigid body models can only be useful if during the experiment the protein retains its native shape.^34,35

The main quantity calculated in the present work is the osmotic pressure of the solution at low protein concentration, where the second virial coefficient values (B₂) can easily be extracted. Notice that this quantity is an indicator of stability of the macroion–salt mixtures,^36–40 positive B₂ values indicate predominantly repulsive intermolecular interactions, while negative values reflect (predominantly) attractive interactions. As shown in several previous papers,^14,40–43 the second virial coefficient is directly correlated with the solubility of the protein in a given ionic environment.

While the model and theory were outlined in Ref. 33, here the numerical results are presented for various low-molecular-mass salts added to protein in water, for different salt concentrations, and pH values of the model solution. The calculations are compared with experimental and also with some simulation results. The main purpose of this study is to investigate how the nature of added salts influences the second virial coefficient of protein solutions. In other words, this work makes an effort toward explaining stability of protein solutions with an emphasize on the salt-specific effects as reflected in Hofmeister series.

II. MODELING THE MIXTURES OF PROTEIN, SALT AND WATER

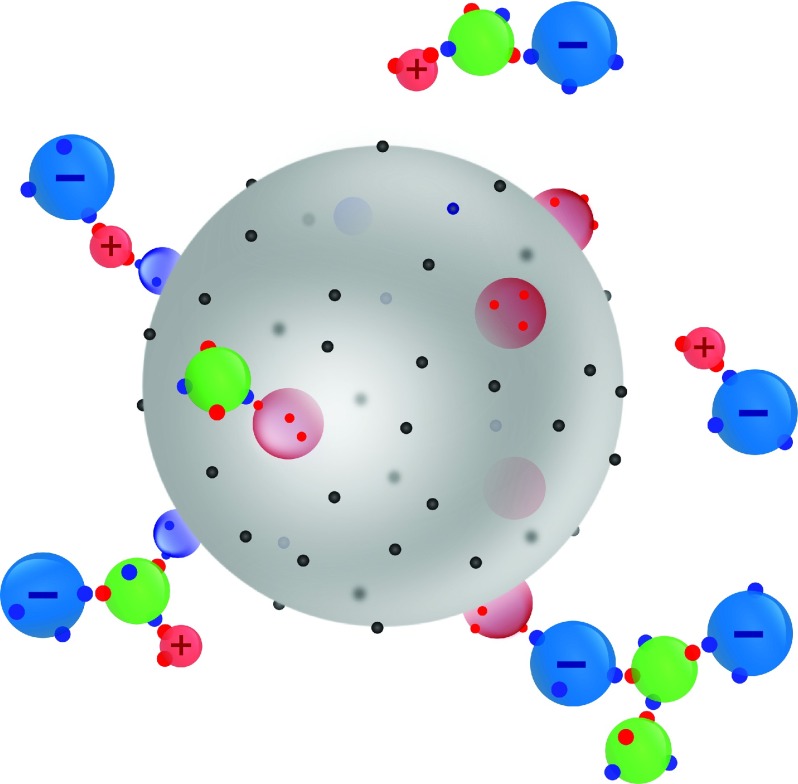
For a protein to model, we choose lysozyme. It is described by a hard sphere of diameter σ = 34 Å, and with Z₊ positive and Z₋ negative charges, pictured as charged hard spheres attached to the surface;^25,33,44,45 see Figure 1. These numbers are set in accordance with the net charges corresponding to the pH values of solutions.⁴⁶ The attractive sites, describing the lysozyme–lysozyme van der Waals attraction, are randomly distributed over the protein surface (Figure 1). As mentioned above the water molecules are pictured as hard spheres (diameter 3.099 Å) with four off-center square-well sites: two sites are mimicking hydrogens and two sites represent the lone-pair electrons. In the calculation we assume Coulomb interaction between the ions in solution and charges sticking out of the protein surface, while the ion–water and water–water interactions are approximated by the attractive square-well site–site potentials.³² Different salts were considered: for alkali halides the hard-sphere sizes of ions were chosen to be equal to their crystal sizes, exactly as in our previous publications.^32,33 The diameters for Li⁺, Na⁺, K⁺, and Cs⁺ ions are taken to be 1.2 Å, 1.9 Å, 2.66 Å, and 3.38 Å, respectively. The diameters of halide ions are 4.32 Å for I⁻, 3.90 Å for Br⁻, and 3.62 Å for Cl⁻.

FIG. 1.

Black dots on the protein’s surface symbolize the van der Waals attractive sites. The positive charges on the protein (and cations in solution) are depicted by red and the negative ones by blue colors. Water molecules are shown in green, with two binding sites mimicking positive charges (red) and the other two lone electron pair (blue).

To mimic the weakly hydrated $-{\mathit{NH}}_3^{+}$ group we choose its diameter to be 4.57 Å.³³ In the Hofmeister series, the carboxylic group occupies the place near F⁻; the position reflects its strongly negative hydration free energy.⁴⁷ To account for this, we choose its diameter to be equal to 1.6 Å. The number of attractive square-well sites on the protein, representing the van der Waals interaction between the proteins, was arbitrary set to 40. Variation of this number in a relatively broad limits does not affect the conclusions.⁴⁸ Numerical values of all the parameters used in the present calculation are the same as in our previous publications^32,33 (see also the supplementary material⁴⁹).

To determine the properties of this complex system, we use the associative mean spherical approximation (AMSA),^32,33,50 based on Wertheim’s multi-density integral equation theory.^51,52 The numerical results were obtained via the energy route, which involves the calculation of the excess free energy and consecutive differentiations to obtain measurable quantities. The virial route to thermodynamic properties, most often used in numerical calculations and simulations, is, namely, in case of the mean spherical approximation much less accurate.⁵³ The osmotic pressure, Π, is then calculated by assuming an equilibrium between the aqueous electrolyte solution on one, and protein–water–electrolyte mixture, on the other side of the membrane, which is not permeable for protein species.³³ The osmotic second virial coefficient, B₂, is defined,

$${\displaystyle B_2=\underset{\rho \to 0}{lim}\left[\frac{1}{\rho }\left(\frac{\beta \mathrm{\Pi }}{\rho }-1\right)\right],}$$ (1)

where β = 1/k_BT, ρ is the protein number concentration, k_B Boltzmann’s constant, and T absolute temperature. The limit in Eq. (1) was taken numerically, extrapolating the values of (βΠ/ρ − 1)/ρ obtained for a set of sufficiently small values of ρ. Experimentally determined second virial coefficient, most often denoted B₂₂, is related to B₂ as

$${\displaystyle B_2=B_{22}{M}_2^2/N_A,}$$ (2)

where N_A is the Avogadro number and M₂ the molecular mass of a protein. B₂₂, which has units cm³ mol/g² and is often of the magnitude around 10⁻⁴, can be determined by various experimental techniques.¹⁸ In theoretical studies, the reduced second virial coefficient $B_2^{\ast }=B_2/B_2^{\left(hs\right)}$, where $B_2^{\left(hs\right)}=(2/3)\pi {\sigma }^3$ (assuming that protein is spherical), is most often presented. The AMSA integral equation theory, including the calculations of the individual activities and osmotic pressure, was in detail explained in the preceding publication.³³ No convergence problems were encountered for this range of parameters. Numerical uncertainties in $B_2^{\ast }$ calculations are smaller than sizes of the symbols (about the width of the lines) in Figs. 2–4 and can be ignored in comparison with the experimental errors in $B_2^{\ast }$ determinations.

FIG. 2.

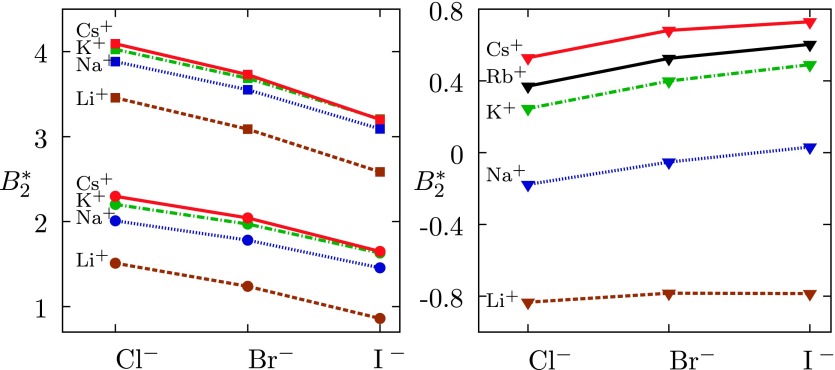
Left panel: $B_2^{\ast }$ for the model lysozyme (the lines are to guide the eyes) with Z₊ = 21 and Z₋ = 10 (pH = 4.0) in aqueous solution of alkali halide salts with concentrations equal to 0.10M (squares) and 0.15M (circles). The Rb⁺ curve practically coincides with Cs⁺ results and is for better clarity not shown here. Legend: Cs⁺ red solid lines, K⁺ green dashed-dotted lines, Na⁺ blue dotted lines, and Li⁺ brown dashed lines. Right panel: The same but for salt concentration equal to 0.40M. Black line applies to Rb⁺ ion.

FIG. 3.

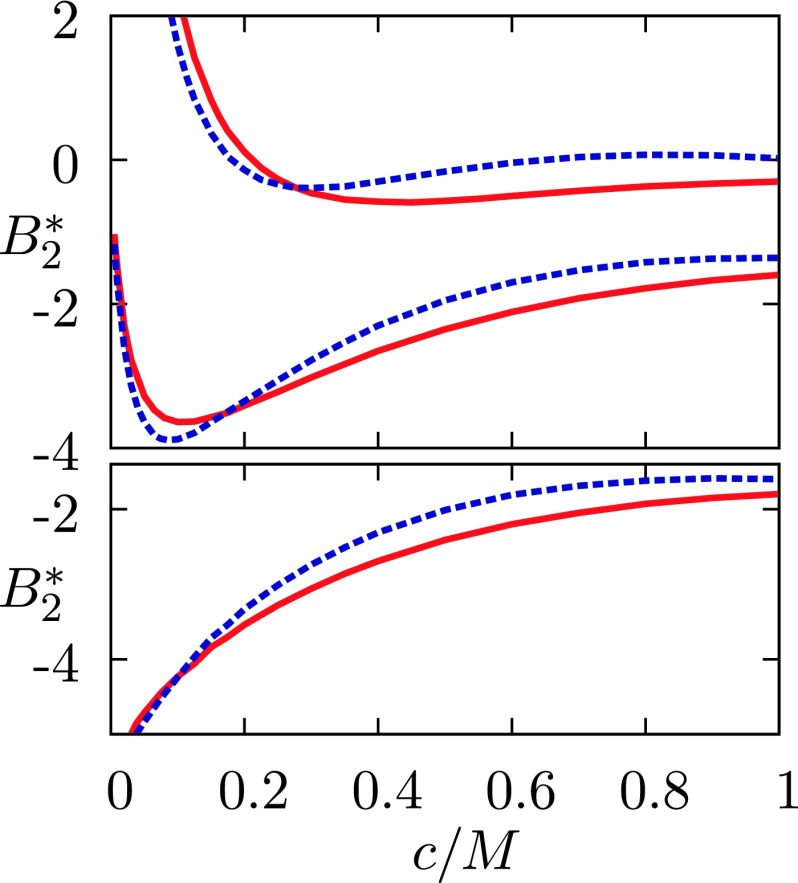
$B_2^{\ast }$ as a function of the molar salt concentration M for lysozyme–alkali halide salts mixtures in water. The top family of curves applies to Z₊ = 21 (Z₋ = 11), the middle one to Z₊ = 18 (Z₋ = 14), and the lowest one to Z₊ = Z₋ = 16. Red solid lines denote results for NaCl and blue dashed lines for NaI solutions.

FIG. 4.

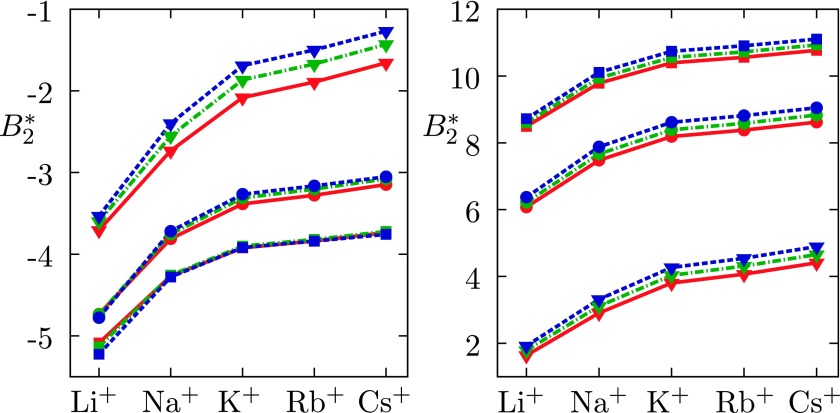
Left: $B_2^{\ast }$ for the model lysozyme with Z₊ = Z₋ = 16 in aqueous solution of alkali halides. Right: $B_2^{\ast }$ for Z₊ = 10, Z₋ = 21. Legend: Cl⁻ red solid lines, Br⁻ green dashed-dotted lines, and I⁻ blue dashed lines. The salt concentrations are 0.1M (triangles), 0.15M (spheres), and 0.40M (squares).

III. RESULTS AND DISCUSSION

A. Numerical results for the second virial coefficient

The second virial coefficient, B₂, is a critical parameter in controlling the protein aggregation and its solubility.^{14,19,40–43} Wilson and co-workers discovered that in order to grow well-defined crystals, the second virial coefficient must be slightly negative.^36,37 Numerical results for the reduced second virial coefficient $B_2^{\ast }$, presented in Figures 2–6, apply to T = 298 K and relative permittivity ε_r = 78.3. To orient the reader, we repeat that small values of $B_2^{\ast }$ indicate low stability of the solution.

FIG. 5.

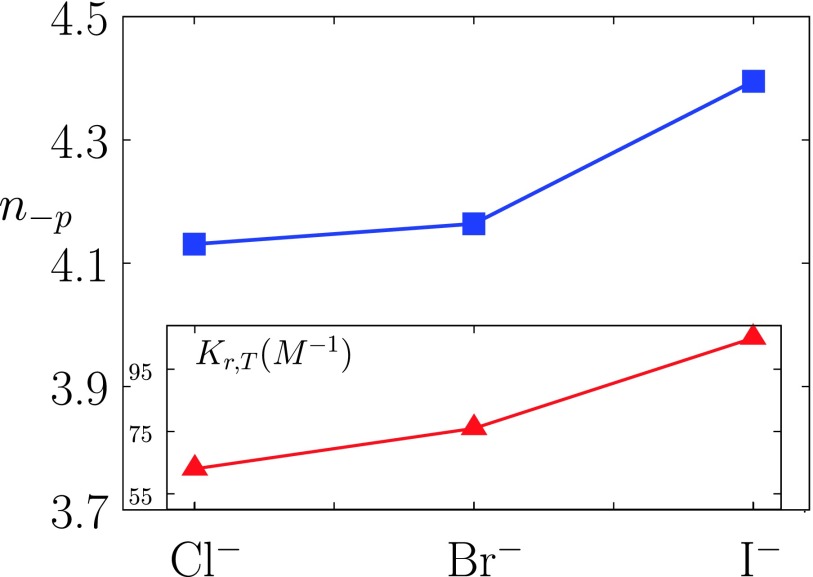
Coordination number n_−p of anions (counterions) around model lysozyme molecule with Z₊ = 21 and Z₋ = 10 (pH = 4.0) (blue squares) for aqueous solution of sodium halides at salt concentration 0.3 M and T = 298 K. Inset shows experimental values of the apparent binding constants K_r,T, as given in Ref. 55 (red triangles).

FIG. 6.

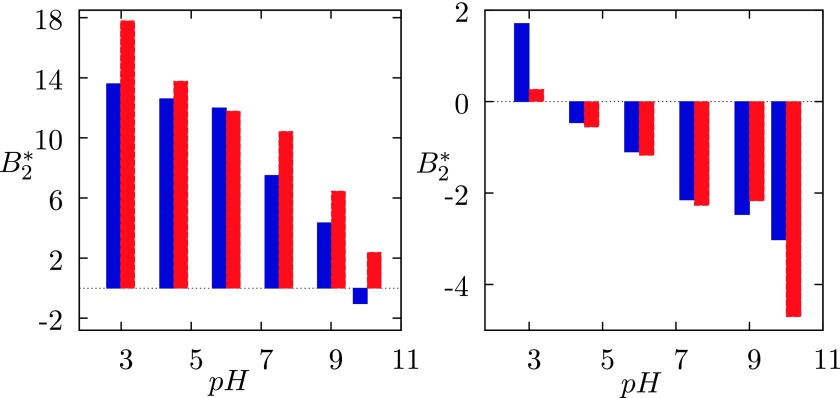
$B_2^{\ast }$ for lysozyme–NaCl mixtures in water as a function of pH: blue columns denote calculations and the red ones experiments.³⁸ Left panel: ionic strength is 0.005M, and the right panel, I = 0.3 M. Theoretical $B_2^{\ast }$ values are calculated from experimental B₂₂ data by Eq. (2). For the pH-net charge dependence see Ref. 46.

As we see from Figure 2, $B_2^{\ast }$ decreases in the order Cl⁻ > Br⁻ > I⁻ and the trend applies to all the cations studied here. The ordering is in agreement with experimental results for solubility of lysozyme; the effectiveness of anions follows the inverse Hofmeister series (from I⁻ toward Cl⁻).^5,54 The apparent binding constants for anions at this pH, determined in our recent experimental study of lysozyme (see also inset in Figure 5), confirm this ordering.⁵⁵

In the right panel of Figure 2, we show the results for higher concentration of added salt. The ordering of salts is reversed here: $B_2^{\ast }$ increases (and so does the stability of the system) in the sequence Cl⁻ < Br⁻ < I⁻. The result is consistent with experimental data for T_cloud and is explained by an increased absorption of the salts at higher concentrations.⁵ From Figure 2, we also see that $B_2^{\ast }$ increases in the direction from Li⁺ to Cs⁺, following experimental observations which suggest direct Hofmeister series.⁵⁴

Theoretical^39,56 and experimental studies^57–60 have provided evidence of non-monotonic behavior of $B_2^{\ast }$ with respect to concentration of added salt. Our calculations (Figure 3) confirm these findings. Decrease of the net charge causes a shift of the minimum toward smaller salt concentrations. Notice that such behavior cannot be captured by the traditional Deryaguin-Landau-Verwey-Overbeek (DLVO) theory.^39,56

The results in Figure 4 (left) correspond to the so-called iso-ionic point, where the net charge is zero. The $B_2^{\ast }$ values are more negative and the protein has, consistently with experimental observations, stronger tendency to precipitate. The stability increases from Li⁺ toward Cs⁺ ion and in agreement with the results shown in the bottom panel of Figure 3, the salt concentration dependence is reversed here.

The calculation presented on the right panel of this figure applies to the net charge −11 and is for lysozyme, which is unstable under these conditions, merely of theoretical value. On the basis of the DLVO theory, one would expect identical behaviour as shown in Figure 2.^21,22 In reality this is not true because negative surface groups have different solvation properties than the positive ones. COO⁻ group in our experience holds its waters tightly and has large negative free energy of hydration.⁴⁷ This would suggest to pair with ions of similar properties, such as lithium and sodium.¹ As shown in Figure 4, the stability measured by the $B_2^{\ast }$ values is indeed the lowest for solution with lithium counterions.

Unlike lysozyme, the barstar protein is stable under conditions when its net charge is negative. The cation binding to carboxylic charges of this protein (net charge −6) has recently been simulated.²⁷ The binding affinity was found to vary as K⁺ < Na⁺ < Li⁺, consistently with the present and previous studies.⁶¹ Experimental results do not confirm this sequence completely; the position of Li⁺ ion seems to be misplaced by calculations.^62,63 It is of interest to discuss also the anion effects under such conditions: as pointed out by experiments and calculations, the anions now follow an opposite ordering as the iso-ionic point.^3,64 Also this important experimental observation is correctly reproduced by our calculations [compare Figures 4 (right) and 2 (left)].

B. Ion–protein correlation

As we already mentioned in Section II, a deficiency of the mean spherical approximation is that it does not yield accurate pair distribution functions. In particular the like-ion distribution functions may assume negative values for small interionic distances. This un-physical result prevents accurate determination of the equation of state. For this reason, the recommended route for calculating the thermodynamic properties, utilized also in this paper, is via the excess energy.⁵³

Of course there will always be an interest for structural information, which could be helpful in explaining the results on a microscopic level. In the next figure, we present the coordination number of ions around the model lysozyme. This quantity is calculated using the following expression:⁵³

$${\displaystyle n_{ip}=4\pi {\rho }_i{\int }_{{\sigma }_{ip}}^{r_{ip}^{\left(\mathit{min}\right)}}{r}^2{g}_{ip}\left(r\right)dr,}$$ (3)

where i denote either anion (i = − ) or cation (i = + ), p denote protein, g_ip(r) denote particle–protein(centre) radial distribution function, $r_{ip}^{\left(\mathit{min}\right)}$ denote position of its first minimum, σ_ip = (σ_i + σ_p)/2, and σ_i and σ_p are the hard-sphere diameters of particles of species i and p, respectively. The distribution functions g_ip(r) used in the calculations are shown in the supplementary material.⁴⁹

As we see from Figure 5 (see inset), the apparent equilibrium constant of anion-binding (K_r,T) to the protein residues⁵⁵ increases in the direction from NaCl to NaI solution. Our theoretical results (blue symbols) follow this trend but the ion-specific effect appears to be less pronounced as found experimentally. Corresponding value of the coordination number of the sodium ions is in all cases equal to 2.8. We expected for these calculations to be, due to the shortcomings in determination of the pair distribution functions, only qualitatively correct. Notice again that such distributions do not enter in the evaluation of the second virial coefficient presented in this work. Additional calculations (results are not shown here) indicate that the number of bound counterions increases with the increasing salt concentration, while the number of solvating water molecules decreases in this direction. The influence of nature of the co-ion species (cations) is small under these conditions.

C. Comparison with experimental data

The proposed theory yields correct trends for the salt-specific and salt-concentration effects as seen in the solubility and the cloud-point temperature measurements. Though there is a strong correlation between $B_2^{\ast }$ and solubility,⁴⁰ it is of interest to confront the calculations with experimental data for the second virial coefficient directly. Unfortunately, there are several aspects which can make such a comparison indeterminate. First, different experimental methods like static light scattering, small angle neutron scattering, osmotic measurements, and more recent self-interaction chromatography⁶⁵ do not yield (within the accuracy of methods) the same result. For the chosen experimental method, the data collected in different Laboratories may scatter considerably more than suggested by the precision of a single measurement (see Table 4 in Ref. 66). Further, the measurements are rarely systematic: sometimes salts are added in addition to buffer, sometimes alone, forming the protein–salt mixture. For a comparison with the DLVO type of models, where only ionic strength is important, this is fine but insufficient to examine the more subtle salt-specific effects. The latter, namely, strongly depend on the electrolyte composition. In addition, the molar mass of the protein in solution, which can be obtained during the same measurement as B₂₂, is needed to calculate $B_2^{\ast }$. If no data are given, one assumes the monomer value. Finally, the details of protein solution preparation are not unimportant. Taking all these into account, it is difficult to expect better than semi-quantitative agreement of theory with experimental data for this quantity.

For the confrontation of the theory with measurements, we choose the B₂₂ results, obtained by the static light scattering (see Fig. 2 of Ref. 38). Original data were transformed to $B_2^{\ast }$ values by Eq. (2) using the relative molecular mass M₂ = 14 300 and the diameter of protein equal to 34 Å. In Fig. 6, we show the experimental results presented as functions of pH and added salt concentration by red columns. The left panel applies to ionic strength I = 0.005 M and the right one to I = 0.3 M. Our AMSA calculations, based on the parameters for Na⁺ and Cl⁻ ions as given in the modeling part and used before for alkali halide calculations,³² are in these histograms presented by blue columns. As we see, the model calculations are in semi-quantitative agreement with experimental data. The calculations, performed for concentrations I = 0.03 M and 0.5M, are in similarly good agreement with measurements,³⁸ but they are not shown here.

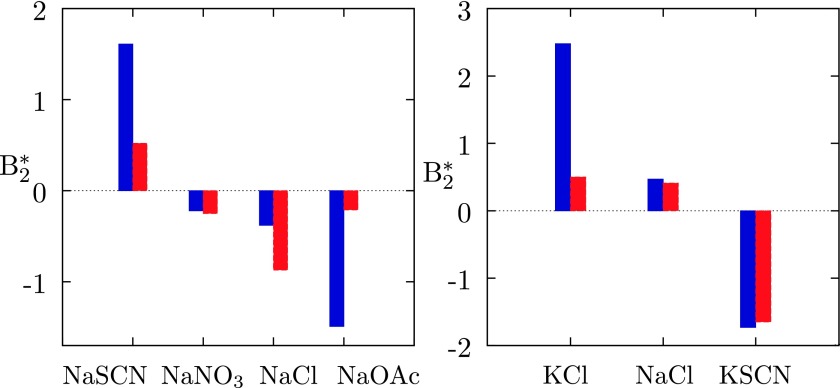
The purpose of this paper is to contribute toward better understanding of the ion-specific effects. For a comparison with experiment, we choose the small angle X-ray scattering data for aqueous lysozyme solutions in presence of various salts published by Bonnete et al.¹¹ These authors studied effects of the complex salts, such as, nitrates and thiocyanates on B₂₂. In absence of calculation for pure salts in water, the apparent diameters (these ions are not spherical) of the ${\mathit{NO}}_3^{-}$ and SCN⁻ ions were taken to be 6.0 and 8.0 Å. The values are close to the largest dimensions of the ions as estimated by the density functional theory within the B3LYP/6-31++G** approximation.⁶⁷ For smaller values of diameters the qualitative agreement between calculations and experiments is preserved, but the theoretical $B_2^{\ast }$ values become systematically too large. As yet another set of the B₂₂ measurements to be compared with the model calculations, we choose the data of Curtis et al.⁶⁸ This comparison is given on the right panel of Fig. 7. The agreement is qualitative.

FIG. 7.

$B_2^{\ast }$ for various lysozyme–salt mixtures in water: blue columns denote calculations and the red ones experiments. Left panel — data from Ref. 11; pH = 4.5, the relative permittivity value of water at T = 293 K is ε_r = 80.1. Right panel — data from Ref. 68, Table Ia. Experimental results for B₂₂ were transformed to $B_2^{\ast }$ as described before.

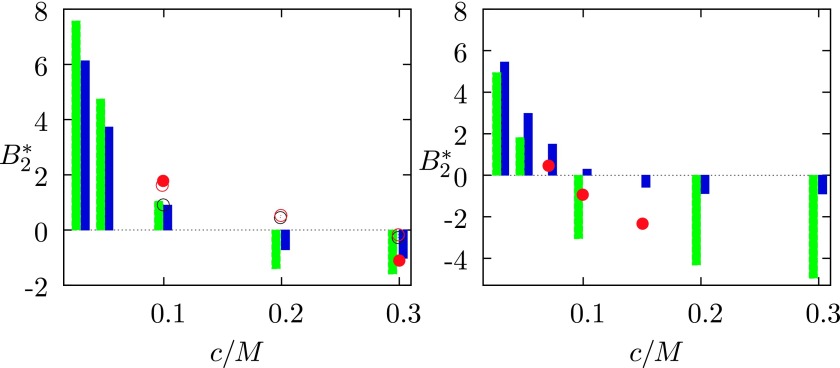
Molecular dynamics simulations are important tool of computational physical chemistry. Using a combination of explicit solvent and continuum model simulations, Lund et al.²⁶ calculated the potentials of mean force for lysozyme molecules in presence of NaI and NaCl salts in water. The resulting second virial coefficients corresponded well to the experimental data. It is of some interest to see how our model calculation performs vis-a-vis a numerically more demanding approach presented in Ref. 26.

For low concentrations of added electrolytes, in agreement with experiments,^38,69 both approaches suggest for the solution to be less stable in presence of NaI than in presence of NaCl salt. A quantitative comparison between these two totally different approaches is shown in Fig. 8, where our results are given in blue and those of Lund et al.²⁶ in green color. Red symbols denote experimental data.^38,69 For the clarity of the graph, we do not show the results for the lowest salt concentration (0.005 M). For this concentration of added salt, both methods suggest large positive value for $B_2^{\ast }$, with the molecular dynamics result being in better agreement with the experimental value.

FIG. 8.

$B_2^{\ast }$ for lysozyme–NaCl (left panel) and lysozyme–NaI (right panel) mixtures in water as a function of the salt concentration: blue columns denote results of our theory, green columns denote results of simulations,²⁶ and symbols denote experimental results from Refs. 38 and 69. Results apply to solution with pH = 4.7 (Z₊ = 21 and Z₋ = 12) at T = 298 K.

IV. CONCLUSIONS

The study presented here is concerned with the salt effects, taking place in electrolyte-protein mixtures in water. We propose the model, which explicitly accounts for all the species present in solution: protein molecules, salt ions, and water molecules. This is in contrast with lots of other studies, which treat the composed solvent (water plus salt) as a structureless continuum. In our calculation, we allow for the model water molecules to solvate different interacting species differently. Notice that all the interactions are local: the protein–ion and protein–water interactions take place in contact of protein with solution. Further the model protein is not characterized only by its net charge, but has simultaneously present positive and negative charges on the surface.

The model calculation is able to qualitatively correctly account for the pH and salt concentration dependencies, including the subtle reversal of the Hofmeister series at higher concentrations of added salt.⁵ Moreover, the model can predict correct ordering of salts in lyotropic series under various experimental conditions. The study suggests that solvation abilities of the protein charges and ions in the solution are among crucial factors determining properties of these systems. The approach presented here, though approximate in its treatment of solvent, allows systematic investigation of how the nature of charged groups on the protein and electrolyte ions affect thermodynamic properties of protein solutions. This is, to best of our knowledge, the first theoretical study of protein solution, which explicitly includes solvent in the consideration.