A GPU-accelerated Monte Carlo dose calculation platform and its application toward validating an MRI-guided radiation therapy beam model

Abstract

Purpose:

The clinical commissioning of IMRT subject to a magnetic field is challenging. The purpose of this work is to develop a GPU-accelerated Monte Carlo dose calculation platform based on penelope and then use the platform to validate a vendor-provided MRIdian head model toward quality assurance of clinical IMRT treatment plans subject to a 0.35 T magnetic field.

Methods:

penelope was first translated from fortran to c++ and the result was confirmed to produce equivalent results to the original code. The c++ code was then adapted to cuda in a workflow optimized for GPU architecture. The original code was expanded to include voxelized transport with Woodcock tracking, faster electron/positron propagation in a magnetic field, and several features that make gpenelope highly user-friendly. Moreover, the vendor-provided MRIdian head model was incorporated into the code in an effort to apply gpenelope as both an accurate and rapid dose validation system. A set of experimental measurements were performed on the MRIdian system to examine the accuracy of both the head model and gpenelope. Ultimately, gpenelope was applied toward independent validation of patient doses calculated by MRIdian’s kmc.

Results:

An acceleration factor of 152 was achieved in comparison to the original single-thread fortran implementation with the original accuracy being preserved. For 16 treatment plans including stomach (4), lung (2), liver (3), adrenal gland (2), pancreas (2), spleen(1), mediastinum (1), and breast (1), the MRIdian dose calculation engine agrees with gpenelope with a mean gamma passing rate of 99.1% ± 0.6% (2%/2 mm).

Conclusions:

A Monte Carlo simulation platform was developed based on a GPU- accelerated version of penelope. This platform was used to validate that both the vendor-provided head model and fast Monte Carlo engine used by the MRIdian system are accurate in modeling radiation transport in a patient using 2%/2 mm gamma criteria. Future applications of this platform will include dose validation and accumulation, IMRT optimization, and dosimetry system modeling for next generation MR-IGRT systems.

1. INTRODUCTION

Monte Carlo radiation transport simulation is generally considered to be the most accurate method for dose calculation in radiation therapy.^1,2 Well-known Monte Carlo packages such as mcnp,³ geant4,⁴ egs4/EGSnrc,^5,6 and penelope (Refs. ⁷ and ⁸) have been demonstrated to agree excellently with experimental data under a wide range of conditions. For example, EGSnrc was shown to pass the Fano cavity test at the 0.1% level.² Here, we categorize these platforms as “accuracy-oriented.” While these packages are highly accurate, they typically require long simulation time to finish a sufficient number of histories in order to achieve adequate statistical uncertainty.

Three approaches have been considered for accelerating Monte Carlo calculations: (1) simplifying particle transport mechanisms, thus reducing the necessary time for each particle history; (2) using variance reduction techniques such as particle splitting, Russian roulette, and interaction forcing to reduce the total history number required to achieve a given uncertainty; and (3) enhancing the computational capability by parallelizing the simulation on multiple CPU or GPU threads.⁹ Packages like vmc (Refs. ^10–12) and dpm (Ref. ¹³) applied approaches (1) and (2) to achieve clinically desired speeds, but sacrificed generality and absolute accuracy by dropping simulation of positrons and using simpler cross section profiles, among other simplifications. gDPM (Refs. ¹⁴ and ¹⁵) further utilized approach (3) (i.e., GPU parallelism) to obtain higher efficiency compared to the original dpm, while gpumcd (Ref. ¹⁶) performed similar simplification to dpm and was directly oriented to GPU implementation. gmc (Ref. ¹⁷) was developed based on geant4 but it results in larger discrepancy from geant4 than expected (2%/2 mm gamma passing rate is 91.74% for IMRT plans). Accuracy was possibly compromised for gmc by the fact that geant4 uses a lot of virtual functions and class inheritances that make implementing a faithful adaptation from c++ to cuda difficult. Here, we categorize these implementations as “efficiency-oriented.”

Fast Monte Carlo implementations like vmc and gDPM perform admirably for applications that require quick response to user changes such as treatment planning. Most recent developments include online IMRT planning using gpumcd for the MRI-linear accelerator¹⁸ and the clinical use of kmc on the MRIdian system (ViewRay, Inc., Cleveland, OH). The MRIdian system integrates a 0.35 T whole-body MR imaging system into an RT delivery system consisting of a rotating gantry with three ⁶⁰Co heads spaced 120° apart that can provide a maximum combined dose rate of 550 cGy/min at the isocenter. Its treatment planning system uses an optimized Monte Carlo code based on vmc to achieve clinically acceptable speed at the expense of accuracy to some extent. kmc is able to complete an IMRT plan calculation subject to a magnetic field within a few minutes, thus rendering online adaptive treatment a clinical reality. Commissioning such a clinical system, however, is challenging and relies largely upon complex experimental validations. The limited availability of quantitative, MRI-compatible, water-equivalent dosimeters makes accurate, multidimensional measurements quite difficult.^19,20 Therefore, a computational system needs to be developed to complement the experimental approach that enables dose comparison in the patient geometry and dosimeter modeling, among other things. Without a viable alternative on a parallel platform, physicists to date have relied on the stalwart, accuracy-oriented Monte Carlo implementations,^21,22 mostly without taking magnetic fields into account, to accomplish these tasks in their practices. In certain cases, such as dose validation for adaptive treatments and dose accumulation using large volumetric data over the treatment course, calculation speed is an important factor to be considered. These applications requiring both high accuracy and clinically acceptable computation time motivated us to develop a GPU-accelerated Monte Carlo engine derived from penelope by applying approach (3) only.

penelope is an experimentally well-validated Monte Carlo platform for simulating photon, electron, and positron transport in various supported materials.^23–28 Its kernel (version 2006) is relatively compact including roughly 3000 lines of fortran code. The code is well-documented with extensive detail on the theory underlying all scattering processes, thus readily enabling its adaptation on a GPU, namely, our implementation gpenlelope presented in this work. Beyond just implementing the kernel on a GPU, we expanded upon the original code to include voxelized tracking, charged particle propagation in magnetic fields, and several key features that make gpenlelope highly user-friendly.

Our primary application of gpenlelope in this work is to perform an accurate and independent check of clinical treatment plans within a clinically desired time. First, we verified that the source head is correctly modeled by integrating it into gpenlelope (noting that a dose calculation system includes both a head model and calculation engine) and comparing simulation results with experiments. Our measurements indicate that the head model provided by the vendor describes the hardware accurately. Then, the head model together with gpenelope can serve as an accurate dose calculation system for the MRIdian platform. We therefore can use this system to check clinical treatment plans generated by MRIdian’s treatment planning system (which uses the same head model and the kmc engine) independently and quickly.

2. METHODS

2.A. penelope in c++

We first translated the penelope kernel from fortran to c++. penelope was implemented in fortran 77 with an archaic programming style (e.g., many antiquated “GOTO” statements). Although GPU programming for fortran has been enabled by the PGI (Ref. ²⁹) compiler (via collaboration with NVIDIA), it lacks good object-oriented programming support and some general libraries, so convenient features like batch work and file compression cannot be implemented easily. Moreover, as the MRIdian head model was developed in c++, rewriting the penelope kernel in c++ first will more readily enable its application to MRIdian validation.

To build penelope in c++, we first extracted all relevant material data tables to a class called Material and assigned shared data to global variables. All “jump” and “knock” functions were rewritten as member functions of this class in an optimized logic sequence. The lengthy code for generating data tables (over 7000 lines) did not need to be translated to c++; instead, we added an interface function in penelope that we compiled to a DLL module. We can call this DLL in c++ to preprocess materials and export the relevant data table to a file that will be addressed to memory by the c++ code later.

The original penelope only supports single-thread processes, while multithreading through OpenMP is necessary to fully exploit modern multicore CPUs. We ensure that all kernel functions are thread-safe by managing thread-related variables accordingly in a single class. We additionally exploit mpi (with a set of workload balancing functions for optimizing overall performance) to enable parallel simulation on a distributed network. The random number generators (RNGs) are kept thread-private and are initiated with independent seeds, which are provided by a different type of RNG [e.g., 16 807 RNG (Ref. ³⁰)] in our implementation.

2.B. Validating the c++ version of penelope

Before adapting the c++ implementation onto a GPU, we validated that the c++ version produced identical results to the original fortran code. We set up a simple cone beam incident on a cubic water phantom, ran the two versions with various incident energies, angles, and cutoff energies in single-thread mode, and then exported the particle status of 10⁸ serial steps for comparison. Considering the possible runtime library differences between c++ and fortran, we set the allowed error of position, direction, and energy for each step to be 10⁻¹⁰ cm, 10⁻¹⁰, and 10⁻¹⁰ keV, respectively. We obtained 100% identical step-status outputs, suggesting that our c++ code is completely equivalent to the original fortran code.

2.C. User-friendly features

The original penelope configuration file has strict formatting restrictions that consequently require changes to the source code when adding or deleting certain configuration items. We thus developed an elegant script module that supports “c”-style free writing, declaring nested cells, and macrodefinitions for ease of use. A powerful log module was also developed to manage file records, run batch tasks, implement dose reuse, and provide e-mail notifications. We also developed a binary file manager module powered by a real-time compressing/decompressing algorithm³¹ to handle large phantom and dose output files that would otherwise cost a lot of storage space and bandwidth for synchronizing remote simulations.

2.D. Adapting to GPU

Upon confirming the integrity of our c++ code, we proceeded to port the c++ code to cuda, which is a c-extended GPU programming language that was introduced by NVIDIA in 2007.³² Though cuda greatly simplified parallel programming on GPUs, it suffers from two main restrictions in comparison to CPU programming.

First, modern GPUs are designed in single instruction multiple data (SIMD) architecture instead of multiple instruction multiple data (MIMD) due to efficiency and complexity reasons.³³ If threads diverge to different instruction flows through “if” or “switch” statements, the GPU work scheduler will simply execute the instruction flow in series and become less efficient. In general, more deeply nested diverging statements will result in lower efficiency.

Second, the largest device memory (∼GB) is only cached by a very small L2 cache, and so cache miss happens frequently and thus causes a long memory accessing latency. Shared and constant memories are hundreds of times faster than device memory, but have a size (∼KB) far less than that is necessary for Monte Carlo simulation with large material data tables. To deal with these shortcomings, we designed a dedicated workflow and allocated the scarce fast memory carefully to improve the efficiency of gpenelope.

2.D.1. Workflow

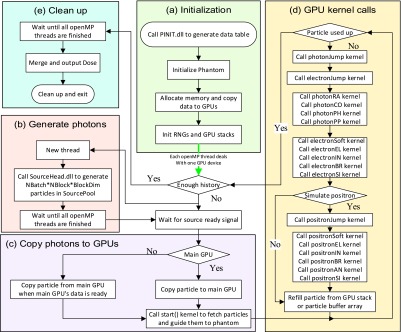
In all Monte Carlo codes, instruction divergence is common so we aim to improve efficiency by minimizing the number of nested diverging statements in each cuda kernel function. Instead of organizing all the simulation codes in one kernel function, we decided to split the code into several independent kernel functions which process different types of scattering events and let the CPU call these kernel functions in a loop within a main function as shown in Fig. 1.

FIG. 1.

Workflow of gpenelope including (a) initialization, (b) generate photons, (c) copy photons to GPUs, and (d) GPU kernel calls: RA, CO, PH, and PP are short for Rayleigh, Compton, photoelectric, and pair production while EL, IN, BR, SI, and AN are short for elastic, inelastic, bremsstrahlung, shell ionization, and annihilation, respectively. The “kernel-by-kernel” calls in sequence can help reducing instruction divergence. (e) Clean up.

As shown in Fig. 1(a), the program reads and parses the configuration file which includes details regarding the GPU devices, phantom (geometry and materials), and source head. The program then calls a DLL (see Sec. 2.A) to generate necessary data tables for relevant materials. These data and phantom information are then copied to GPU device memory with pointers to large arrays and some small data tables being copied to constant memory on the GPU instead for improving accessing speed. In addition, a random number generator and particle stack are initiated for each GPU thread. As our workstation includes multiple GPU cards, we next launch multiple threads through OpenMP to call GPU kernel functions on each card simultaneously.

Meanwhile, the main thread launches another thread calling the vender-provided head source module to prepare incident photons as shown in Fig. 1(b). As specified in Fig. 1(c), photons are then copied to the main GPU and in turn transferred to other GPUs in order to save I/O time. The GPU kernel function start() is then called to guide photons to the phantom via free propagation. As summarized in Fig. 1(d), distinct “jumping” kernels for photons and charged particles are called to advance relevant particles and label them with the type of interaction that will happen next. These interaction kernel functions are called sequentially such that particles labeled with a different interaction type will simply exit their threads. Though this schedule does not completely resolve the instruction divergence problem, it lowers the level of nested diverging statements and thus reduces the total pausing time. After all interaction kernels finish, we refill the current particle variable either from the stack storing secondary particles or the incident photon buffer array, thus improving the efficiency by enabling constant renewal of particles on all threads.

In addition, we provide an option for toggling positron simulation as the primary photon energy of ⁶⁰Co is just slightly higher than the threshold for pair production (twice the electron rest mass). We also allow for source particle reuse as occasionally the head model lags the GPU and cannot provide new particles at a sufficient rate. Our simulation comparisons show that the dose differences in “hot areas” (D > 10% × D_max) caused by reusing source particles are almost totally (99.73%) within the targeted 1% uncertainty for a large (10⁹) history number. Moreover, we set up the RNGs to refill their buffers after N loops in order to reduce instruction divergence, where N is the average number of loop iterations when an RNG buffer is exhausted.

2.D.2. Heterogeneous or voxelized tracking

For photon simulation, we added Woodcock tracking³⁴ to the original penelope to treat a heterogeneous phantom as uniform. In order to obtain an invariant mean free path λ = m₀/(ρ_iσ) across the whole phantom (m₀ is the molecular mass, ρ_i is the voxel density, and σ is the total scattering cross section), we add a virtual scattering cross section σ_i in each voxel i to maintain ${\rho }_i\left(\sigma +{\sigma }_i\right)={\rho }_{max}\sigma$ constant everywhere. Then the probability for this virtual scattering to happen is

$${\displaystyle p\left({\sigma }_i\right)=\frac{{\sigma }_i}{\sigma +{\sigma }_i}=1-\frac{{\rho }_i}{{\rho }_{max}}.}$$ (1)

If this virtual interaction is sampled during a knock event, we just continue to propagate the photon without changing direction or losing energy since the virtual event is not real. A shortcoming of this technique is that it could result in low efficiency for a phantom composed mainly of low density material (e.g., lung) because the virtual interaction will most likely be sampled thus wasting random numbers without any energy transfer. We thus instead try to improve the sampling efficiency by forcing the real interactions to always happen, with the secondary particles’ weight reduced by factor ρ_i/ρ_max and only ρ_i/ρ_max of the primary photons’ status (energy and direction) being changed. This ensures that the probability distribution of deposited energy is unbiased.

For electron and positron simulation, penelope applied the “mixed” condensed history scheme, which treats large energy transfer collisions in an analogue way and uses the continuous slowing down approximation (CSDA)³⁵ to model small-loss collisions. Since the CSDA range $\overline{s}$ is much smaller than the photon’s mean free path λ, we implemented a simple grid detection algorithm to trace the CSDA jump between heterogeneous voxels. Unlike photons, electrons and positrons will cross just a few voxels before being completely stopped. Though soft collisions occur at a high frequency, most of these are determined not to cross the voxel boundary by a rapid test that roughly estimates the nearest distance to the boundary, and so the necessary time for calculating exact crossing points at voxel boundaries is actually not expensive.

2.D.3. Magnetic field

Given that the CSDA range $\overline{s}$ of electrons and positrons is typically very small, the magnetic field in each voxel can be treated as uniform in most applications. The particles will undergo spiral motion in a uniform field B at the relativistic angular velocity

$${\displaystyle \overrightarrow{\omega }=-\frac{e\overrightarrow{B}}{\gamma m_e},}$$ (2)

where e denotes the elementary charge, m_e is the electron mass, and γ is the Lorentz factor. The corresponding location after advancing length s in a uniform phantom can be easily evaluated as shown in the penelope user manual to be¹

$${\displaystyle \overrightarrow{r}\left(s\right)={\overrightarrow{r}}_0+s{\hat{v}}_0-\frac{s}{v_0}{\overrightarrow{v}}_{0\perp }+\frac{1}{\omega }\left[1-\cos \left(s\omega /v_0\right)\right]\left(\hat{\omega }\times {\overrightarrow{v}}_{0\perp }\right)+\frac{1}{\omega }\sin \left(s\omega /v_0\right){\overrightarrow{v}}_{0\perp },}$$ (3)

where r₀ is the initial particle location and v₀ is the particle velocity (with v_0⊥ being the velocity component perpendicular to B). For a heterogeneous voxelized phantom, however, the intersection between the spiral curve and the voxel boundary must be calculated due to the variation of the density in each voxel. Accurate evaluation is messy and inefficient due to many inverse trigonometric function calls. As the CSDA range $\overline{s}$ is relatively small in comparison to the spiral radius R, we can approximate the spiral motion by small straight line segments that change direction gradually. Taking the allowed error in one segment move to be Δ_max, the maximum segment length s_m is expressed as

$${\displaystyle s_m=\sqrt{{(R+{\mathrm{\Delta }}_{max})}^2-R^2}\approx \sqrt{2R{\mathrm{\Delta }}_{max}}.}$$ (4)

If s > s_m, we only advance a distance s_m and change direction by angle θ ≈ s_m/R (continuing until s is exhausted). This straight-line advancing procedure uses the same voxel tracking implementation as the situation without magnetic field. While moving a distance, s may cross a voxel boundary, the particle direction may point back to the original voxel when v ⋅ (v + dv) < 0, and so the current voxel index must be corrected accordingly.

2.E. MRIdian head model

The vendor-provided MRIdian head model provides phase space data including the energy spectrum and flux for a given solid angle for the ⁶⁰Co source. Each IMRT beam consists of a collection of segments configuring the MLC shape and beam-on time. In our code, each segment is treated as a simulation unit and the history number assigned to each unit is weighted by its beam-on time. The MLC shape determines how many photons will be exported from the ⁶⁰Co head for each history, which is a nonfixed number due to the patient-specific MLC configuration.

To maximize its efficiency, the GPU should process a fixed number N of photons per batch. Therefore we designed a class to buffer the photons supplied by the head in a multithreading queue such that N photons are fetched in a batch by the GPU when the class is filled with slightly over N photons. The excess photons are then moved to the head of the queue to continue the buffering.

2.F. 3D dose comparisons

For 3D dosimetric evaluation, we considered both gamma indices and statistical histograms to reveal differences between two Monte Carlo systems. The gamma index for each voxel $\overrightarrow{r}$ is defined as

$${\displaystyle \gamma \left(\overrightarrow{r}\right)=min\left\{\mathrm{\Gamma }\left(\overrightarrow{r},{\overrightarrow{r}}^{\prime }\right)\right\}\forall \left\{{\overrightarrow{r}}^{\prime }\right\},\mathrm{\Gamma }\left(\overrightarrow{r},{\overrightarrow{r}}^{\prime }\right)=\sqrt{\frac{{\left|\overrightarrow{r}-{\overrightarrow{r}}^{\prime }\right|}^2}{\mathrm{\Delta }{d}^2}+\frac{{\left(D\left(\overrightarrow{r}\right)-D^{\prime }\left({\overrightarrow{r}}^{\prime }\right)\right)}^2}{\mathrm{\Delta }{D}^2}},}$$ (5)

where $|\overrightarrow{r}-{\overrightarrow{r}}^{\prime }|$ represents the distance between voxels $\overrightarrow{r}$ and ${\overrightarrow{r}}^{\prime }$, Δd is the distance-to-agreement (DTA) value, and ΔD is the dose tolerance value. We label a gamma index at voxel $\overrightarrow{r}$ as passing if $\gamma \left(\overrightarrow{r}\right)\le 1.0$ and count the passing rate for those voxels where $D\left(\overrightarrow{r}\right)>t\times D_{max}$, where t is a dose threshold. Higher gamma passing rates for smaller Δd and ΔD tolerances usually suggest stronger agreement between two dose distributions.

A statistical histogram, on the other hand, directly indicates the distribution of dose differences spanning all voxels. Here we define a statistical variable z-score for each voxel as

$${\displaystyle z\left(\overrightarrow{r}\right)=\frac{D_{\mathrm{test}}\left(\overrightarrow{r}\right)-D_{\mathrm{ref}}\left(\overrightarrow{r}\right)}{D_{\mathrm{ref}}\left(\overrightarrow{r}\right)\times {\sigma }_{\mathrm{tot}}},}$$ (6)

where $D_{\mathrm{test}}\left(\overrightarrow{r}\right)$ and $D_{\mathrm{ref}}\left(\overrightarrow{r}\right)$ are the test dose and reference dose at voxel $\overrightarrow{r}$, respectively, and σ_tot is the standard deviation of the distribution $\left(D_{\mathrm{test}}\left(\overrightarrow{r}\right)-D_{\mathrm{ref}}\left(\overrightarrow{r}\right)\right)/D_{\mathrm{ref}}\left(\overrightarrow{r}\right)$ spanning all voxels. The resultant z-scores are compared to a standard Gaussian distribution in the form of a normalized frequency histogram.

3. RESULTS

3.A. Comparison to c++ penelope

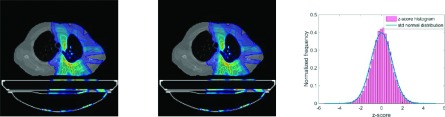
In Sec. 2.B, we showed that c++ penelope performs equivalently to the original code written in fortran by a detailed step-by-step comparison. Here we apply a similar approach to convincingly show that gpenelope performs equivalently to c++ penelope in single-thread operation. We simulate a complex lung IMRT plan (shown in Fig. 2) using both platforms and output particle statuses (position, velocity, and energy) in 10⁷ knocking steps for comparison. The maximum and average differences are summarized in Table I. The energy difference |dE| is actually negligible in comparison to the incident energy (>1 MeV).

FIG. 2.

Dose distributions for a lung case calculated by c++ penelope (left) and gpenelope (middle). The two distributions are identical within 1%. The frequency distribution of z-scores in comparison to a standard normal distribution (right).

TABLE I.

Particle status differences of 10⁷ steps between gpenelope and c++ penelope.

$max\left(\left|\mathrm{d}\overrightarrow{x}\right|\right)=1.42\times 10^{-8}\mathrm{cm}$	$max\left(\left|\mathrm{d}\hat{v}\right|\right)=1.82\times 10^{-9}$	$max\left(\left|dE\right|\right)=2.25\times 10^{-5}\mathrm{eV}$
$\mathrm{mean}\left(\left|\mathrm{d}\overrightarrow{x}\right|\right)=4.54\times 10^{-14}\mathrm{cm}$	$\mathrm{mean}\left(\left|\mathrm{d}\hat{v}\right|\right)=1.26\times 10^{-14}$	$\mathrm{mean}\left(\left|dE\right|\right)=7.29\times 10^{-9}\mathrm{eV}$

We additionally run 10⁶ histories to check differences in dose distributions directly, which turn out to be max(|dD|) = 7.63 × 10⁻⁵ Gy, mean(|dD|) = 6.78 × 10⁻⁸ Gy, σ(dD) = 7.17 × 10⁻⁷ Gy. The prescription dose for this patient is 50 Gy. That is, the maximum relative dose error is 1.36 × 10⁻⁹. Considering the possible runtime library differences between the GPU and CPU, the status tracking and dose deposition comparisons together show that gpenelope and c++ penelope can effectively be considered to be identical in single-thread mode.

Though impractical to compare particle status with gpenelope in multithreaded operation (considering thousands of threads simultaneously), we can compare dose distributions generated by gpenelope and c++ penelope directly. We thus run a large number of histories (4 × 10⁹) to ensure that the target area (D > 10% × D_max region) reaches less than 0.5% uncertainty so that the maximum allowed difference would be less than 1% if gpenelope behaves equivalently to c++ penelope. Comparing doses in these voxels, we found that

$${\displaystyle \frac{max\left(\left|dD\right|\right)}{max\left(D_{\text{ref}}\right)}=0.93\%,\frac{\text{mean}\left(\left|dD\right|\right)}{max\left(D_{\text{ref}}\right)}=0.12\%,\frac{\sigma \left(dD\right)}{max\left(D_{\text{ref}}\right)}=0.15\%,}$$ (7)

where D_ref is the dose calculated by c++ penelope. The results indicate that the equivalency assertion between gpenelope and penelope is valid. In addition, we compared the frequency distribution of z-scores (as defined in Sec. 2.F) to a standard normal distribution as shown in Fig. 2 (right). This comparison indicates that the z-score distribution follows a standard normal distribution.

Since gpenelope is effectively equivalent to c++ penelope in single-thread mode, and dose distributions generated by the two agree well within expected statistical uncertainties in multithread operation, we safely deduce that gpenelope is a faithful adaptation of penelope that does not compromise accuracy.

The hardware for our tests is a server that includes an Intel Xeon E5 2630 v3 CPU and an NVIDIA Tesla K80 GPU card. The CPU can provide 16 true simultaneous threads, giving an overall processing rate of 1.842 × 10⁵ histories/s. The GPU achieves a simulation rate of 1.756 × 10⁶ histories/s, which is almost 10 times faster than that of the CPU platform. Considering the original penelope engine only supports one thread, our GPU code can actually accelerate penelope by a factor of 152.

For the lung IMRT example above (phantom size 51.3 × 50.7 × 52.8 cm³, voxel size 3 × 3 × 3 mm³), gpenelope requires 9.5 min to finish simulating 10⁹ histories to achieve 0.5% uncertainty in the D > 50% × D_max region. If such a rigorous accuracy is not required, a lot of time could be saved by reducing the history number N as the accuracy is proportional to $\sqrt{N}$. As a platform designed for accurate dose calculation, verification, and accumulation over the treatment course, both the speed and accuracy meet the requirements of clinical applications.

3.B. Magnetic field effects

By integrating an MR scanner into the radiation delivery system, the MRIdian system must consider magnetic field effects on dose distributions. Raaijmakers³⁶ performed a detailed simulation study using geant4 of magnetic field effects on dose distributions for a 6 MV LINAC beam. Although the field strength of the MR scanner on MRIdian is relatively weak (0.35 T), the electron return effect (ERE) might still be nontrivial because the lower energy of a primary photon from the ⁶⁰Co source tends to result in a smaller spiral radius.

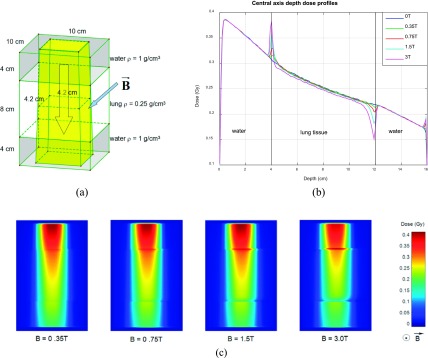
In homogeneous phantoms, dose distortion caused by ERE is generally negligible; however, it will become apparent in heterogeneous phantoms at the interfaces. Here we simulate the radiation delivery for a 10 × 10 × 16 cm³ water–lung–water phantom, where the lung tissue is represented by an 8 cm slab of water with a density of 0.25 g/cm³ [Fig. 3(a)]. A 4.2 × 4.2 cm^{2 60}Co beam consisting of 10⁹ photons was incident on the phantom, and a small dose scoring voxel size was set to 1 × 1 × 1 mm³ to probe for dose distortion. The simulation was repeated with 0.35, 0.75, 1.5, and 3 T magnetic field strengths and the corresponding central axis depth dose profiles were compared as shown in Fig. 3(b). The results are similar to those of Raaijmakers³⁶ except that the distortion layer is much thinner than for the 6 MV LINAC beam. The dose wash images in the x–z plane are presented in Fig. 3(c). Besides stronger dose accumulation effect, the lateral dose shift will also become more obvious as the magnetic field strength goes up.

FIG. 3.

(a) Water–lung–water phantom, ⁶⁰Co beam, and magnetic field configuration. Voxel size is 1 × 1 × 1 mm³. (b) Central axis depth dose profiles. Larger magnetic field results in larger dose distortion. (c) Dose distributions for configuration in (a) at indicated magnetic field strengths.

The simulation suggests that the 0.35 T magnetic field has a minor effect on the dose distribution in a heterogeneous phantom (spike-shape dose accumulation <3% of max dose within a 3 mm thin layer accompanied by a 1 mm lateral shift), which is consistent with the experimental results of Wooten et al. using radiographic film.²⁰ Wooten et al. noted that such perturbation effect would be mitigated by multiple overlapping beams, as in the case of an IMRT plan, for instance. It is interesting that this effect would become almost imperceptible when the voxel size increases to 3 × 3 × 3 mm³, which is the voxel size that most clinics use in treatment planning.

3.C. Experimental measurements

Beyond demonstrating that the gpenelope simulation kernel is both fast and accurate, we must confirm that the entire validation system is correctly modeled (especially the ⁶⁰Co head) in order to ensure safe deployment in the clinic. We thus investigate several vital comparisons to experimental measurements to validate its overall accuracy.

3.C.1. Depth dose

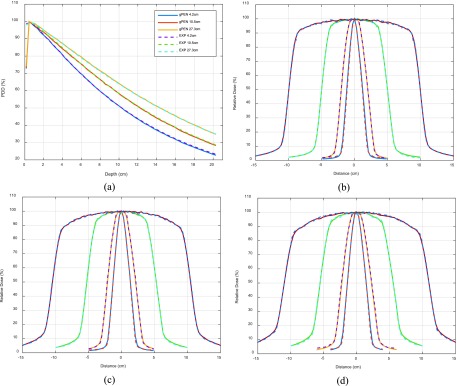
Measurements were performed in a cubic water phantom (30 × 30 × 30 cm³) placed at SSD = 100 cm using small, medium, and large field sizes (4.2 × 4.2, 10.5 × 10.5, and 27.3 × 27.3 cm²). The data were collected using an Extradin A18 ion chamber. Note that the chamber is manually positioned at different depths as an MRI compatible beam scanning device is not commercially available now. Considering the cylindrical dimensions of the ion chamber (radius = 2.5 mm, height = 6.4 mm), we set the voxel size of the phantom to be 3 × 3 × 3 mm³ in simulation and run 10⁹ histories to ensure sufficiently small statistical uncertainty (<0.5% for D > 50% × D_max region). Figure 4(a) shows comparisons between simulation and experimental data, yielding less than 1% difference.

FIG. 4.

Percentage-depth-dose comparisons between gpenelope and ionization chamber measurement (spline interpolated) for field sizes 4.2 × 4.2, 10.5 × 10.5, and 27.3 × 27.3 cm² at 100 cm SSD (a). Off-axis profile comparisons between gpenelope and radiochromic film measurement for field sizes 2.1 × 2.1, 4.2 × 4.2, 10.5 × 10.5, and 21.0 × 21.0 cm² at depths of 5 (b), 10 (c), and 15 cm (d) at 100 cm SSD.

3.C.2. Off-axis profile

We used EBT2 radiochromic films placed at depths of 5, 10, and 15 cm to sample planar doses for comparisons to simulation results. As shown in Figs. 4(b)–4(d), the simulated dose profiles agree well with measured data to within 2% or 2 mm DTA.

3.C.3. Output factor

Both square and rectangular field output factor measurements were performed in a cubic water phantom (30 × 30 × 30 cm³) placed at SSD =100 cm. The Extradin A18 ion chamber was placed at 5 cm below the surface, i.e., the isocenter. Note that in order to verify the small field output factor, we closed the central ten leaves incrementally from 10.5 to 0.6 cm, as recommended by ViewRay. As shown in Table II, the calculated output factors match well with the experimental data (<2%).

TABLE II.

Output factor comparison for square and rectangular fields.

Field shape	Size (cm2)	OF (gPEN)	OF (expt.)	Diff. (%)
Square field	4.2  ×  4.2	0.8839	0.8780	0.67
	6.3  ×  6.3	0.9414	0.9380	0.36
	10.5  ×  10.5	1.0000	1.0000	NA
	14.7  ×  14.7	1.0293	1.0410	−1.12
	27.3  ×  27.3	1.0624	1.0700	−0.71
Rectangular field	0.6  ×  10.5	0.2103	0.2070	1.58
	0.8  ×  10.5	0.2839	0.2825	0.51
	1.0  ×  10.5	0.3607	0.3568	1.08
	1.5  ×  10.5	0.5256	0.5246	0.19
	2.0  ×  10.5	0.6741	0.6721	0.30
	2.5  ×  10.5	0.7953	0.7859	1.19
	3.0  ×  10.5	0.8730	0.8583	1.71
	4.0  ×  10.5	0.9222	0.9119	1.13
	6.0  ×  10.5	0.9636	0.9582	0.56
	8.0  ×  10.5	0.9837	0.9822	0.16
	10.5  ×  10.5	1.0000	1.0000	NA

3.C.4. AAPM TG-119

The AAPM Task Group 119 (TG-119)³⁷ recommends that six cases be considered (two non-IMRT and four IMRT) for IMRT commissioning, including AP-PA, Bands, Multitarget, C-shape, Head and Neck, and Prostate. These treatment plans were planned using MRIdian’s inverse treatment planning system and delivered to a 30 × 30 × 15 cm³ water-equivalent plastic phantom containing ionization chambers (ICs) and EDR2 radiographic film.

3.C.4.a. TG-119 point dose.

All point dose measurements were made using an ADCL calibrated ionization chamber (Extradin A18). The dose at each plan’s isocenter (except C-shape) is measured to evaluate high dose accuracy while a few adjacent points are chosen to examine low dose accuracy.

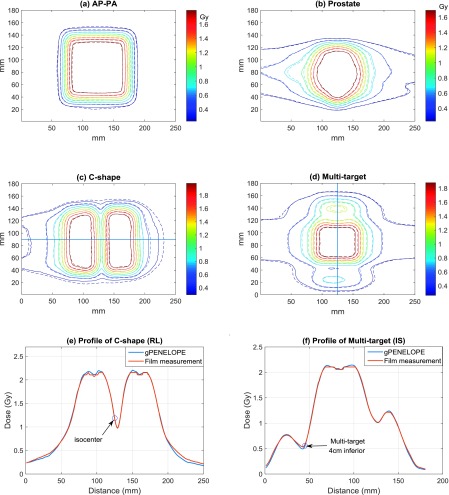
Table III compares calculated doses from gpenelope to experimental measurements. For flat high-dose regions, gpenelope gives excellent agreement with measurements (error < 0.31% for non-IMRT plans and error < 2.26% for IMRT plans). All results for the low-dose points are within the TG-119 confidence limit of 4.5%, with Multitarget (4 cm inferior) and C-shape (1 cm posterior) yielding the largest discrepancies. By examining the dose distributions, we find that the two points are located in high-gradient regions [cf. Figs. 5(e) and 5(f)] where small chamber positioning error could induce large measurement difference. For these two cases, we use DTA instead to evaluate gpenelope performance where we search around the dose matrix grid with interpolation to find the nearest point that has the exact same dose as measurement, with DTA defined as the distance from this point to the measurement point. Calculated DTAs are less than half of the voxel size (0.91 and 1.42 mm, respectively).

TABLE III.

TG-119 point dose comparisons: gpenelope vs IC.

TG-119 plans	Location	IC (Gy)	gpenelope (Gy)	Diff. (%)
AP-PA	Isocenter	1.988	1.991	0.16
Bands	Isocenter	1.422	1.426	0.31
Multitarget	Isocenter	2.085	2.058	−1.29
Multitarget	4 cm superior	1.062	1.038	−2.22
Multitarget	4 cm inferior	0.621	0.593	−4.43
C-shape	2.5 cm anterior	2.152	2.131	−0.96
C-shape	1 cm posterior	0.917	0.882	−3.77
Head and neck	Isocenter	2.215	2.265	2.26
Head and neck	5 cm posterior	0.917	0.919	0.27
Prostate	Isocenter	1.817	1.85	1.82
Prostate	4.5 cm posterior	0.372	0.374	0.62

FIG. 5.

Isodose and profile comparison between gpenelope and radiographic film measurements: (a) AP-PA, (b) Prostate, (c) C-shape, and (d) Multitarget, where solid lines represent gpenelope and dashed lines represent film measurement. (e) Profile of C-shape along the right-to-left central axis. (f) Profile of Multitarget along the inferior-to-superior central axis. Note that the circled points are located in the high gradient region.

3.C.4.b. TG-119 film dose.

For the six plans listed above, radiographic film measurements were made at the isocenter parallel to the coronal plane. Films were digitized and then exported to perform gamma analysis using gamma parameters recommended by TG-119: (a) absolute dose comparison, (b) 3% dose difference threshold, (c) global normalization for percent dose difference, (d) 3 mm DTA threshold, and (e) 10% low dose threshold. The gamma passing rates are 100.0%, 96.2%, 95.5%, 97.7%, 99.9%, and 94.4% for AP-PA, Bands, C-shape, Head and neck, Multitarget, and Prostate cases, respectively, yielding a mean value of 97.3% ± 2.3% (1 SD), which is within the TG-119 recommended confidence limit of 88%. Figure 5 summarizes the agreement between gpenelope and experiment using isodose line overlay. For IMRT plans, only the low dose contours (around 10%) show relatively obvious disagreements.

3.D. Comparison to MRIdian treatment planning system

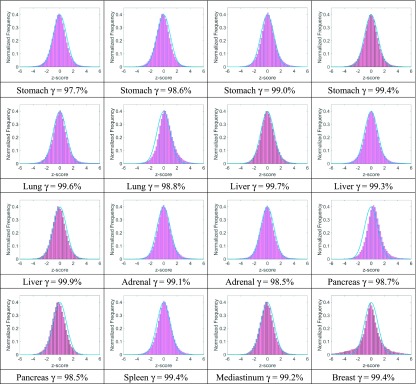
The kmc algorithm on the MRIdian TPS adopted many approximations and variance reductions³⁸ to increase calculation speed. kmc’s accuracy should thus be confirmed using a third-party Monte Carlo system devoid of approximations through 3D dose comparisons. Thus we selected 16 recent patient plans (from the ViewRay patient registry at Washington University in St. Louis) created by the MRIdian TPS with treatment sites including stomach (4), lung (2), liver (3), adrenal gland (2), pancreas (2), spleen (1), mediastinum (1), and breast (1). Three-dimensional gamma analysis results (2%/2 mm DTA and 10% threshold criteria) and histograms of z-scores (in comparison to standard normal distributions) are listed in Table IV. The table shows that kmc matches gpenelope well (15 out of 16 plans with dose gamma passing rates ≥98% and most closely fitting Gaussian distributions) except that kmc occasionally tends to result in a little higher dose than gpenelope. Some z-score distributions (second lung case, first pancreas case, and the breast case) are noticeably offset from the standard distribution, thus indicating that the physical modeling is somewhat affected by the approximations and variance reductions implemented by kmc for calculating a complex ⁶⁰Co IMRT plan. The statistical gamma passing rates are as high as 99.1% ± 0.6% for the two dose distribution, proving that kmc generally predicts dose consistent with our accuracy-oriented Monte Carlo engine. During MRIdian’s commissioning, Wooten et al. designed a custom heterogeneity phantom to acquire ionization chamber measurements.²⁰ They report that the mean ionization chamber measured dose for 27 measurements for 5 plans is within 1% vs kmc.

TABLE IV.

Gamma passing rates (2%/2 mm and 10% threshold) and z-score distributions comparing gpenelope and MRIdian’s kmc.

4. DISCUSSION AND CONCLUSION

The recent clinical use of the MRIdian radiation therapy system represents a significant advance in cancer care, enabling clinicians, for the first time, to deliver highly conformal IMRT with real-time MRI guidance. However, the rapid advances in the technology to deliver such radiation treatments seem to have not been paralleled by corresponding advances in the ability to verify these treatments subject to a permanent magnetic field. For conventional IMRT, despite its widespread utilization at modern radiation therapy clinics, precise dosimetric commissioning remains a challenge.³⁹ In the era of MRI-guided IMRT, the permanent magnetic field is augmenting another dimension of error and uncertainty to the already error-prone IMRT process.

As a result of many limitations to experimental approaches, largely due to the dearth of appropriate multidimensional water-equivalent dosimeters, a hybrid approach that includes a computational component is needed for MRI-IMRT commissioning and validation. For example, Ding et al.⁴⁰ studied the feasibility of using a Monte Carlo method to commission stereotactic radiosurgery beams shaped by micro multileaf collimators. This hybrid approach is especially valuable for MRI-IMRT where the Monte Carlo method may be the only method that is capable of dealing with complex dose deposition in a heterogeneous medium subject to a magnetic field.^18,41 The Monte Carlo methods like kmc, on the other hand, may require many approximations in order to be practical in the clinic, and these approximations may not be thoroughly communicated to an end-user for proprietary reasons. We therefore developed a fast, GPU-accelerated Monte Carlo dose calculation system based on penelope. Unlike some other GPU implementations, the accuracy of our adaptation is at the same level as the original code. Our implementation achieved 152 times faster speed than that of the original penelope implementation. Furthermore, we integrated the ⁶⁰Co head model of the MRIdian system into our system and performed a series of experimental benchmarks to examine the accuracy of the entire system. Finally, when comparing to MRIdian’s kmc for a number of patients that span multiple disease sites, an average of 99.1% ± 0.6% gamma passing rates at 2%/2 mm provides another layer of confidence in treating patients that may benefit from IMRT with simultaneous MRI guidance.

In the clinic, gpenelope should be applicable to nearly any application requiring high dose accuracy, such as beam modeling,²¹ IMRT optimization,⁴² dosimeter response modeling,^28,43 dose validation,¹⁹ dose accumulation,⁴⁴ among others. As an example, due to the three-source nature of the MRIdian system, quasi-3D dosimeters, such as ArcCHECK (Sun Nuclear Corp., Melbourne, FL), are quite useful for dosimetry measurements. However, the combined field size dependence and angular dependence of an ArcCHECK have been reported to be on the order of 10%–15% for a LINAC delivery. This can be corrected by using look-up tables as a function of beam angle and field size, for which the beam angle must first be determined using a virtual inclinometer in the ArcCHECK software. However, this cannot be corrected for the MRIdian system due to the simultaneous delivery of all three sources. One possibility to solve this problem is to model the dosimeter response using gpenelope so that the radiation transport in the diodes and surrounding buildup/backscatter material can be explicitly simulated. As a result, dose to individual diodes instead of to water can be calculated and subsequently compared to diode’s raw response during measurements. By doing this, we cannot only convert the ArcCHECK from a relative, 3D dosimeter to an absolute one; more importantly, tighter criteria can be used for the gamma analysis, for example, 2%/2 mm. Nelms et al.⁴⁵ have recently made a convincing case that adoption of more sensitive metrics/tighter tolerances enables continual improvement of the accuracy of radiation therapy dose delivery not only at the end-user level but also at the level of product design by the manufacturer. This is especially important for MRI-guided IMRT which is at the early stage of its clinical implementation.

In conclusion, a GPU version of penelope has been developed with its accuracy completely faithful to the original code. The comparisons with MRIdian dose calculation results suggest that MRIdian’s fast dose calculation for the ⁶⁰Co source subject to a 0.35 T magnetic field is accurate using 2%/2 mm criteria. gpenelope will be useful for many MRI–IMRT applications including dose validation and accumulation, IMRT optimization, and dosimetry system modeling.

CONFLICT OF INTEREST DISCLOSURE

The authors have no COI to report.