Landmark Based Shape Analysis for Cerebellar Ataxia Classification and Cerebellar Atrophy Pattern Visualization

Abstract

Cerebellar dysfunction can lead to a wide range of movement disorders. Studying the cerebellar atrophy pattern associated with different cerebellar disease types can potentially help in diagnosis, prognosis, and treatment planning. In this paper, we present a landmark based shape analysis pipeline to classify healthy control and different ataxia types and to visualize the characteristic cerebellar atrophy patterns associated with different types. A highly informative feature representation of the cerebellar structure is constructed by extracting dense homologous landmarks on the boundary surfaces of cerebellar sub-structures. A diagnosis group classifier based on this representation is built using partial least square dimension reduction and regularized linear discriminant analysis. The characteristic atrophy pattern for an ataxia type is visualized by sampling along the discriminant direction between healthy controls and the ataxia type. Experimental results show that the proposed method can successfully classify healthy controls and different ataxia types. The visualized cerebellar atrophy patterns were consistent with the regional volume decreases observed in previous studies, but the proposed method provides intuitive and detailed understanding about changes of overall size and shape of the cerebellum, as well as that of individual lobules.

1. Introduction

The cerebellum plays an important part in motor control, and is also involved in cognitive functions such as attention and language¹. Cerebellar dysfunction can lead to a wide range of movement disorders including incoordination, reduced manual dexterity, postural instability, and gait disturbances¹. Despite the significant impact of cerebellar diseases on patients' lives, the current standard of diagnosis and treatment of cerebellar diseases is inadequate^2,3. Magnetic resonance (MR) imaging provide potentials to improve the understanding and evaluation of cerebellar neuro-degeneration by revealing the structural changes of the cerebellum. Figure 1 shows example coronal sections of the cerebellum from healthy control (HC), spinocerebellar ataxia type 2 (SCA2), spinocerebellar ataxia type 6 (SCA6), and ataxia-telangiectasia (AT). We can see that the three ataxia types show cerebellar atrophy as compared to the healthy control, each has different regional atrophy patterns. It is of great interest to study the cerebellar structural pattern associated with each disease type, and to correlate the structural change with specific functional degeneration. On the scientific side, it helps researchers further understand the localized function map of the cerebellum. On the clinical side, it may help in the development of disease-modifying therapy, designing efficient therapeutic trials, and monitoring individual patient progress.

Figure 1.

Example coronal sections of the cerebellum from a HC and three ataxia types.

Various methods have been proposed to study structural changes of the brain based on MR images⁴. Region of interest (ROI) volumetry has been traditionally used to obtain regional measurement of anatomical volumes and to investigate abnormal tissue structures with disease⁵. ROI volumetric measure is simple and reliable, but it often cannot capture localized structural change patterns. Voxel-based analysis (VBA) overcome the limitations of ROI volumetry. It maps a subject image to a standard template space and applies a voxel-wise linear statistical test on voxel morphometric measures, such as a Jacobian determinant of the deformation and tissue density⁶. To overcome the limitations of mass-univariate analysis in VBA, high-dimensional pattern classification methods have been proposed^7–10. These methods aim to capture multivariate nonlinear relationships in the data and seek to achieve high classification accuracy at the individual level. Statistical shape analysis also plays an important role in structural analysis^11–13, where the complete shape of the anatomical structure is encoded in a vector and statistical analysis methods are designed to study the population distribution in high-dimensional shape space.

Our approach is closely related to statistical shape analysis and high-dimensional pattern classification methods. In particular, we propose a method to classify cerebellar ataxia types and visualize the cerebellar atrophy patterns associated with different disease types based on landmark shape representation of cerebellar lobules. Dense homologous landmarks are generated on the boundary surfaces of cerebellar sub-structures and a high-dimensional feature vector is generated by stacking the spatial coordinates of all the landmarks. This shape representation provides a highly informative feature representation of cerebellar structure. Partial least squares is used to reduce the data dimension, and regularized linear discriminant analysis is carried out in the dimension-reduced space to classify different ataxia types. Due to the linear properties of both dimension-reduction and discriminant analysis, the characteristic cerebellar atrophy patterns for different ataxia types can be visualized by sampling along the discriminant direction between healthy controls and the ataxia types and reprojecting to the high-dimension shape space.

2. Method

2.1 Cerebellar lobules and lobes

The cerebellum includes a central mass of white matter called the corpus medullare (CM) and surrounding gray matter branches, called lobules, numbered from I to X¹⁴. Specific groups of lobules are referred to as lobes; for example, lobules I through V make up the anterior lobe. Figure 2 shows a surface rendering of the cerebellar lobules and their names.

Figure 2.

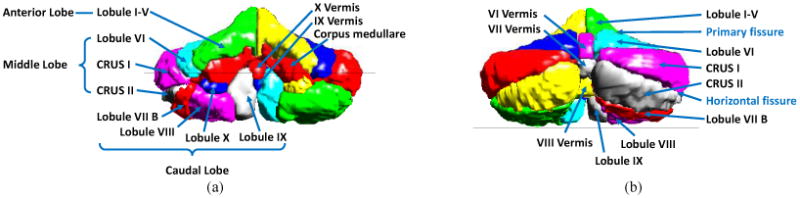
Cerebellar lobules and lobes. (a) Anterior view; (b) Posterior view.

2.2 Materials and preprocessing

T1-weighted magnetization prepared rapid gradient echo (MPRAGE) images of 123 subjects were acquired on a 3.0T MR scanner (Intera, Phillips Medical Systems, Netherlands). There are 65 healthy controls (HC) and 58 patients with four types of cerebellar ataxia. The subjects were diagnosed by blood test. Demographic information is provided in Table 1. The cerebellum was segmented from the MR image and parcellated into 22 cerebellar sub-structures defined in Sec. 2.1, using the method proposed in Yang et al. (2013)¹⁵. A dense triangulation of the boundary surface of each lobule was generated by the marching cubes algorithm¹⁶. Figure 3 shows the input MR image, the lobule segmentation, and the generated triangular meshes of lobules.

Table 1.

Demographic information on the 123 subjects being studied. Key: N number of subjects; m/f is the male/female ratio; Age is the mean age; SD is the standard deviation of the age; healthy controls (HC); spinocerebellar ataxia type 2 (SCA2), type 3 (SCA3), type 6 (SCA6) and type 8 (SCA8); ataxia-telangiectasia (AT).

	N	(m/f)	Age	(SD)
HC	65	(28/37)	50.7	(17.7)
SCA2	4	(3/1)	48.8	(8.8)
SCA3	7	(2/5)	51.7	(9.3)
SCA6	27	(7/20)	58.4	(9.3)
SCA8	2	(2/0)	43.5	(16.3)
AT	18	(12/6)	18.3	(6.2)

Figure 3.

From MR image to lobule meshes: (a) MR image of the cerebellum; (b) Lobule segmentation; (c) Triangular meshes of all lobules; (d) Vertices of the lobule meshes.

2.3 Landmark based shape representation

The landmark representation describes a shape by locating a set of landmarks on the outline, where a landmark is defined as “a point of correspondence on each object that matches between and within the populations”¹⁷. Landmark has been widely used in modeling shape priors in segmenting anatomical structures^18–20 and in studying the structural changes associated with growth and diseases^{12, 13}. A challenge of using the landmark representation to model anatomical structures, especially 3D structures, is establishing dense corresponding landmarks across different subjects. Multi-structure shape (as in the collection of lobules comprising a cerebellum) adds another level of complexity²¹. We address the correspondence building problem for multiple structures by applying a two-step nonrigid point set registration between the template point set and the subject point set, with the first step registering all lobules as a whole and the second step registering each lobule separately. The deformed template point set is then used as the landmarks of the subject. The steps for generating landmark representation is described in detail next.

Let P_k be the ordered set of points from the kth lobule mesh of a subject, generated as described in Sec. 2.2. P = {P₁, P₂, …, P_k} is the ordered set of points from all lobules, where K is the number of lobules, and K = 22. P is called the point set of a subject or subject point set. An arbitrary subject was selected as the template, and the template point set is denoted by P⁰. First, each subject point set P is aligned to P⁰ by a rigid transformation in order to remove its rotation and translation, resulting in P^r. Then, the two-step nonrigid registration is carried out for each subject: 1) P⁰ is registered to P^r through a nonrigid registration, resulting in P¹. Coherent point drift (CPD)²² is used to implement the nonrigid point set registration. 2) For each lobule k, $P_k^1$ (the set of points in P¹ that belongs to lobule k) is registered to $P_k^r$ (the set of points in P^r that belongs to lobule k) through a nonrigid transformation, resulting in $P_k^2$.

$P^2=\{P_1^2,P_2^2,\dots ,P_K^2\}$ is therefore the set of landmarks for the subject, since it outlines the shape of the subject and at the same time has one-to-one point correspondence with the template point set P⁰, and thus with all the other subject point sets. Figure 4 shows the initial template point set P⁰, and the template point set after each step of nonrigid registration, i.e., P¹ and P², overlaid with subject point set P^r. Let {x_i, y_i, z_i} be the spatial coordinates of the ith landmark. The landmark representation of the subject is the vector

Figure 4.

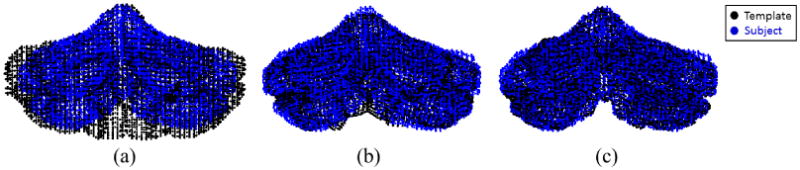
Two-step nonrigid point set registration: (a) Template point set and subject point set before nonrigid registration; (b) after whole cerebellum nonrigid registration; (c) after individual lobule nonrigid registration.

$$\mathbf{s}={[x_1,y_1,z_1,x_2,y_2,z_2,\dots ,x_M,y_M,z_M]}^T,$$ (1)

where $M={\sum }_{k=1}^K{M}_K$ is the number of landmarks from all lobules. In our case M ≈ 15000. The landmark representation s will be used as the feature vector for each subject in the following analysis.

2.4 Dimension reduction and discriminant analysis

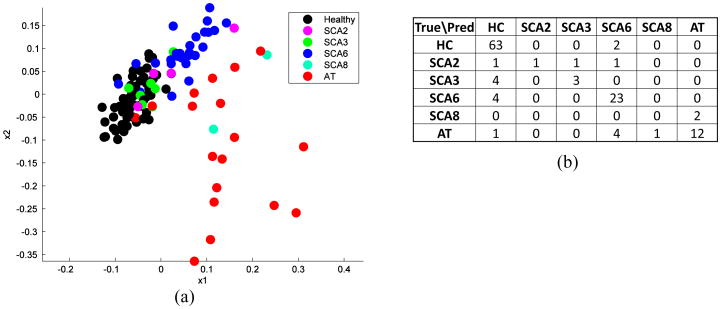
The high-dimensional feature vector s (the spatial coordinates of 15000 landmarks) and the small sample size N (∼100 subjects) make the discriminant analysis ill-posed. A critical step before analysis is dimension reduction. We use partial least squares (PLS), a supervised linear dimension-reduction method²³. PLS constructs new predictor variables as linear combinations of the original predictor variables; it is closely related to principal component analysis (PCA). PCA finds combinations of the predictors with large variance, while PLS finds combinations of the predictors that have a large covariance with the response values. PLS therefore combines information about the variances of both the predictors and the responses while also considering the correlations among them. Figure 5(a) shows the subject shape representations projected to the first two components of PLS. We can see that HC, SCA6, and AT form clusters.

Figure 5.

Dimension reduction and discriminant analysis: (a) Subject points in the first two dimension after PLS dimension reduction; (b) Confusion matrix between the true diagnosis and predicted diagnosis from leave-one-out experiment.

After dimension reduction, linear discriminant analysis (LDA)²⁴ is used to classify the diagnosis groups and to find the discriminant pattern between any two diagnosis groups. LDA finds a linear combination of features that characterizes or separates two or more classes of objects. The resulting combination is often used as a linear classifier. Let x denote the feature vector of a sample in the dimension-reduced space associated with a class label y ∈ {0, 1, …, C}. LDA assumes that the conditional probability density functions p(x|y = c), c = 0, 1, …, C, are normally distributed with common covariance Σ and different mean vectors μ_c, c = 0, 1, …, C. The class prediction problem is solved by maximizing the posterior probability that the observation belongs to a particular class p(y|x). In the case of two classes, the decision criterion becomes a threshold on the dot product

$$\mathit{\omega }\cdot \mathbf{x}>h,$$ (2)

for some threshold constant h, where

$$\mathit{\omega }={\sum }^{-1}({\mathit{\mu }}_1-{\mathit{\mu }}_2).$$ (3)

ω, called the discriminant direction, is the direction that the data from the two classes are most separated when projected on a line in this direction.

In this work, we use the shrunken centroids regularized discriminant analysis²⁵, a modified version of LDA. Instead of using the sample covariance matrix estimation Σ̂ in the discriminant function, they use a shrunken version of the sample covariance matrix

$$\widehat{\sum }=\alpha \widehat{\sum }+(1-\alpha ){\mathbf{I}}_p,$$ (4)

where I_p is the p × p identity matrix and 0 ≤ α ≤ 1. By introducing a slightly biased covariance matrix, it stabilizes the sample covariance estimates. It also stabilizes the variance and reduces the bias of the discriminant function, leading to an improved prediction accuracy²⁵.

2.5 Characteristic atrophy pattern visualization

Visualization of the anatomical shapes and shape differences between different diagnosis groups are key elements in the exploration of data, formulating and testing of hypotheses. In this section, we aim to visualize the characteristic cerebellar atrophy patterns as they change from HC to a particular ataxia type. We visualize the cerebellar atrophy pattern of a particular ataxia type as a series of synthetic shapes sampled along a line in the discriminant direction ω between HC and the ataxia type.

Given the discriminant direction ω, as computed in Sec. 2.4, in the dimension-reduced space, the corresponding direction in high-dimensional shape space can be computed as

$$\mathbf{w}=\mathbf{V}\mathit{\omega },$$ (5)

where V = [v₁, v₂, …, v_d] and v_i is the ith component computed from PLS. In order to be representative of the data, we select the line trajectory in the direction w that passes through the point μ, the mean of all subjects, and we call it the discriminant line. The parametric representation of the discriminant line s_l can then be written as

$$\begin{array}{cc}{\mathbf{s}}_l(t)=\mathit{\mu }+t\mathbf{w},& t\in \mathbb{R}.\end{array}$$ (6)

To visualize the line trajectory, we sample five equidistant points s_l(t₀ + kΔt), k = 0, 1, …, 4 on the line, and reconstruct the cerebellar lobule surfaces from the points. The points are sampled so that the first and third ones are the projection of the HC mean, μ_HC, and the mean of the ataxia type of interest, μ_Ataxia, respectively. The shape corresponding to the fifth point s_l(t₀ + 4Δt) depicts a conjectured extreme disease subject of the ataxia type, so that the cerebellar atrophy can be observed more evidently.

3. Result

3.1 Diagnosis group classification

In this experiment, we tested the proposed method on classifying HC and different ataxia types, i.e., SCA2, SCA3, SCA6, SCA8, and AT. See Table 1 for the number and demographic information for each diagnosis group. A leave-one-out experiment was carried out to evaluate the classification performance, where each of the 123 subjects was used as a test subject while the remaining 122 were used to compute the PLS projection and train the linear discriminant classifier. The average leave-one-out classification successful rate is 0.829, which is computed as the number of correctly predicted diagnosis prediction divided by the number of subjects used. Figure 5(b) is the confusion matrix between the true diagnosis and predicted diagnosis. We can see that the classifier predicts the majority diagnosis groups well (HC, SCA6, and AT), proving the representational and discriminant power of the proposed shape representation. The classifier did not predict SCA2, SCA3, and SCA8 well, we believe due to the limited training samples. A major source of error is classifying ataxia types as HC. This may be because that the cerebellum of patients with a short disease duration have mild cerebellar atrophy, and it is therefore difficult to distinguish their cerebella from healthy subjects.

3.2 Disease-specific atrophy pattern visualization

In this section, we show the characteristic atrophy patterns associated with different cerebellar ataxia types, as described in Sec. 2.5. Figures 6 and 7 shows the cerebellar atrophy patterns for SCA2, SCA3, SCA6, and AT, viewed from the front and back of the cerebellum. We can see that noticeable cerebellar atrophy is observed for all ataxia types, but different ataxia types have different patterns of shape changes.

Figure 6.

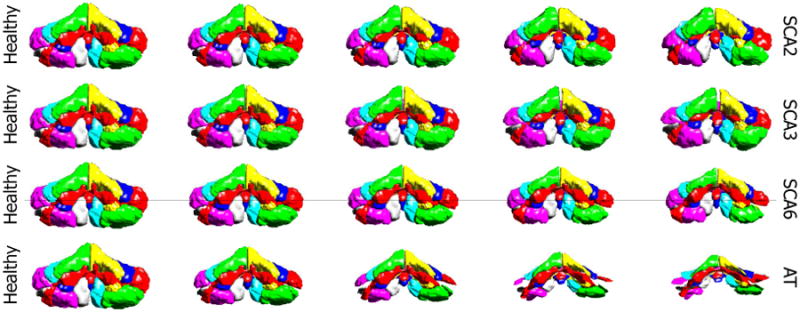
Characteristic cerebellar atrophy patterns for four different ataxia types, viewing from the front of the cerebellum. The columns show in turn the five equidistant points sampled on the discriminant line, with the first column being the projection of the HC mean and the third being the projection of ataxia mean.

Figure 7.

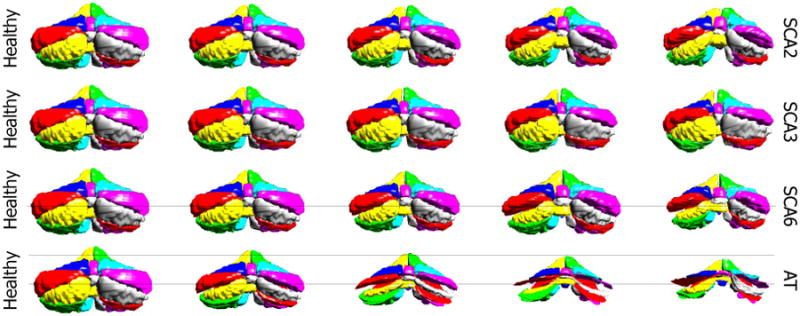
Characteristic cerebellar atrophy patterns for four different ataxia types, viewing from the back of the cerebellum. The columns show in turn the five equidistant points sampled on the discriminant line, with the first column being the projection of the HC mean and the third being the projection of ataxia mean.

SCA2 has the biggest atrophy in the corpus medullare among the four ataxia types (see the shrinking corpus medullare in Fig. 7), indicating large white matter atrophy. There is significant atrophy in the anterior and middle lobes (see the primary and horizontal fissure become wider from Fig. 7), while the caudal lobes do not change much. These observations agree with the observations in Jung et al. (2012)⁵ that the volume of corpus medullare, the anterior lobe, middle lobe of SCA2 patients were reduced compared to controls, while the caudal lobes are relatively preserved. The visualization also suggests that although there is atrophy in most of the cerebellum, the overall size of the cerebellum does not change too much.

SCA3 has the mildest cerebellar atrophy among the four, with no significant change in size. There is still noticeable lobule atrophy, as we can see that left and right CRUS I lobules become smaller in Fig. 7, but the degree of atrophy is less than the other three types. SCA3 has more WM loss compared to SCA6 and AT. These observations agree with the observations in Burk et al. (1996)²⁶ and Lukas et al. (2006)²⁷.

SCA6 has significant atrophy in almost all parts of the cerebellum and decrease in the overall size of the cerebellum. SCA6 has less atrophy in the corpus medullare than SCA2 and SCA3 (Fig. 6). These observations agree with the observations in Jung et al. (2012)²⁸ that compared to SCA2, SCA6 has larger atrophy in posterior-inferior regions of the cerebellum but less atrophy in the corpus medullare. They also agree with the voxel-based morphometry study on SCA3 and SCA6 in Lukas et al. (2006)²⁷, in which significant grey matter loss was found in SCA6 in hemispheric lobules bilaterally as well as in the vermis. White matter analysis revealed significant changes in SCA3, whereas no significant white matter reduction was found in SCA6 patients.

AT has the most significant whole cerebellum atrophy. The size of the cerebellum decreases rapidly when moving from healthy to AT. All lobules shrink, especially the middle lobes. These observations agree with the observations in Tavani et al. (2003)²⁹ that all parts of the cerebellar hemispheres and vermis undergo moderate to severe atrophy in AT patients in the age range 9 to 40, and the lateral part of the cerebellar hemispheres has the most severe atrophy.

4. Conclusion

In this paper, we present a landmark based cerebellar shape analysis pipeline to discriminate and visualize the differences in cerebellar structure associated with different cerebellar ataxia types. A leave-one-out experiment demonstrates the effectiveness of the proposed analysis in classifying diagnosis. The visualized disease-specific atrophy patterns associated with different ataxia types were consistent with the regional volume decreases observed in previous studies, and they provide more intuitive and detailed understanding about the shape changes of the whole cerebellum as well as the sub-structures. In addition to studying disease-specific cerebellar atrophy patterns, the proposed shape analysis pipeline can be adapted to study function-specific atrophy patterns.