Multivariate dynamical systems-based estimation of causal brain interactions in fMRI: Group-level validation using benchmark data, neurophysiological models and human connectome project data

Abstract

Background

Causal estimation methods are increasingly being used to investigate functional brain networks in fMRI, but there are continuing concerns about the validity of these methods.

New Method

Multivariate Dynamical Systems (MDS) is a state-space method for estimating dynamic causal interactions in fMRI data. Here we validate MDS using benchmark simulations as well as simulations from a more realistic stochastic neurophysiological model. Finally, we applied MDS to investigate dynamic casual interactions in a fronto-cingulate-parietal control network using Human Connectome Project (HCP) data acquired during performance of a working memory task. Crucially, since the ground truth in experimental data is unknown, we conducted novel stability analysis to determine robust causal interactions within this network.

Results

MDS accurately recovered dynamic causal interactions with an area under receiver operating characteristic (AUC) above 0.7 for benchmark datasets and AUC above 0.9 for datasets generated using the neurophysiological model. In experimental fMRI data, bootstrap procedures revealed a stable pattern of causal influences from the anterior insula to other nodes of the fronto-cingulate-parietal network.

Comparison with Existing Methods

MDS is effective in estimating dynamic causal interactions in both the benchmark and neurophysiological model based datasets in terms of AUC, sensitivity and false positive rates.

Conclusions

Our findings demonstrate that MDS can accurately estimate causal interactions in fMRI data. Neurophysiological models and stability analysis provide a general framework for validating computational methods designed to estimate causal interactions in fMRI. The right anterior insula functions as a causal hub during working memory.

Introduction

There is a growing interest in examining how cognitive functions emerge as a result of dynamic causal interactions among distributed brain regions. Computational methods for estimating dynamic causal interactions from fMRI data include state-space dynamical models (Daunizeau et al., 2009; Friston et al., 2003; Li et al., 2011; Ryali et al., 2011; Smith et al., 2009), Granger causal analysis (GCA) (Barnett and Seth, 2013; Deshpande et al., 2008; Goebel et al., 2003; Jiao et al., 2011; Roebroeck et al., 2005; Seth, 2010; Wen et al., 2012), structural equation modeling (SEM) (Gates and Molenaar, 2012; Gates et al., 2010; Gates et al., 2011; McIntosh, 1994) and Bayesian network methods (Ramsey et al., 2011; Ramsey et al., 2009). Despite much progress in the field, there is a growing debate about the validity of these methods. In an attempt to address this issue, Smith and colleagues (Smith et al., 2011) evaluated the performance of several methods, including GCA and Bayesian network methods, on several simulated datasets at a single-subject level. The performance of these methods was, however, not assessed at the group level. This remains a critical gap in the literature as almost all human fMRI studies are based on inferences on data from multiple participants (Gates and Molenaar, 2012; Ramsey et al., 2011; Schippers et al., 2011).

The performance of state-space based causal estimation methods (Cai et al., 2015; Chen et al., 2014; Ryali et al., 2011; Supekar and Menon, 2012) that overcome limitations of existing methods has not been validated using benchmark datasets or other more biologically plausible datasets generated independent of the methods used to test them. Critically, estimating causal interactions in fMRI is challenging because (a) neuronal interactions occur in the range of 20–50 ms while fMRI signals are sampled at 2–3 s, and (b) different brain regions have varying hemodynamic response (HRFs) that link neuronal signals to the observed fMRI response (Friston et al., 2003; Ryali et al., 2011; Seth et al., 2013; Smith et al., 2009). These factors represent a major challenge for computational methods designed to infer causal interactions in experimental fMRI data. Here we use extensive simulations and stability analysis to evaluate the performance of our previously developed multivariate dynamical systems (MDS) state-space methods (Ryali et al., 2011) at the group level on three different types of datasets: (1) benchmark data provided by Smith and colleagues (Smith et al., 2011), (2) fMRI datasets simulated using a stochastic neurophysiological model (Holcman and Tsodyks, 2006; Testa-Silva et al., 2012) that improves upon the models implemented by Smith and colleagues (Smith et al., 2011), and (3) experimental fMRI data on a working memory task from a group of 63 participants, acquired as part of the Human Connectome Project (HCP).

MDS is a state-space approach for estimating dynamic causal interactions in fMRI data at both single subject and group level. MDS estimates event-specific causal interactions in fMRI while accounting for regional variations in HRF across brain areas and individuals (Ryali et al., 2011). Previously, we evaluated the performance of MDS using data as a function of signal to noise ratio (SNR), regional variation in HRF characteristics, network size, number of observations and experimental design (Ryali et al., 2011). We found that MDS accurately estimates causal interactions and that its performance is much better than GCA. However, our use of MDS-based models for generating simulated test datasets could potentially have biased the evaluation of its performance. This is a common problem in many studies seeking to validate new computational methods in the neuroimaging literature. For example, in a recent analysis of group level GCA, model performance was evaluated using a very simplistic two-node network (Schippers et al., 2011). The simulated datasets were generated using a bivariate autoregressive (AR) model which in turn was used for estimating the Granger causality between the two nodes. It is therefore not clear how group level GCA performs when the simulation model is different from the model used for estimating the causal interactions; for example, when a more realistic neuronal mass model is used to stimulate the fMRI data. To avoid potential biases when evaluating the performance of individual methods, it is critical to use data that is generated independently from the models used to estimate dynamical causal interactions (Seth et al., 2013; Smith et al., 2011).

Here we address three critical issues associated with the validation of MDS: (1) unbiased evaluation using simulated data generated from models different from MDS, (2) simulation of more realistic datasets with causal interactions occurring at a 20–50 ms time resolution at the neuronal level with BOLD-fMRI signals downsampled to 2–3 s, and (3) validation of MDS at the group level, similar to experimental fMRI studies. We used datasets generated using two simulation models: (i) previously published benchmark datasets generated using a deterministic bi-linear DCM model (Friston et al., 2003; Smith et al., 2011) and (ii) new datasets generated using a more biologically realistic neurophysiological model that incorporates nonlinear interactions between neuronal populations, conduction delays and saturation effects (Holcman and Tsodyks, 2006; Testa-Silva et al., 2012). In the latter case, a reduced stochastic dynamical system is used to model an interconnected network of excitatory neurons with activity-dependent synaptic depression (Holcman and Tsodyks, 2006). Crucially, this model system reproduces key aspects of intrinsic cortical dynamics, including spontaneous state transitions, and is well suited to examining brain dynamics in experimental preparations with both typical and atypical synaptic connections (Holcman and Tsodyks, 2006; Testa-Silva et al., 2012). Here we extend the original neurophysiological model by creating 5, 10 and 15 node networks and incorporating biologically realistic delays into inter-node signaling to generate casual interactions within a stochastic dynamical system framework. We show through extensive simulations, using both deterministic DCM and stochastic neurophysiological models, that MDS can accurately recover dynamic causal networks in simulated fMRI data.

Despite their advantages, in principle, simulations cannot model all aspects of fMRI data. To address this issue and further validate MDS, we applied MDS on fMRI data acquired during performance of a working memory task and examined causal interactions within a fronto-cingulate-parietal network important for cognitive control (Cai et al., 2015; Chen et al., 2014; Dosenbach et al., 2008; Dosenbach et al., 2007; Menon, 2011; Menon and Uddin, 2010; Supekar and Menon, 2012). This control network includes anterior insula (AI), anterior cingulate cortex (ACC), ventrolateral prefrontal cortex (VLPFC), dorsolateral prefrontal cortex (DLPFC) and posterior parietal cortex (PPC) regions that are co-activated across a wide range of cognitive tasks (Menon, 2011; Menon and Uddin, 2010). Critically, the AI node of this network is thought to play a key role in switching between large-scale brain networks and facilitating access to attention and working memory resources (Sridharan et al., 2007; Sridharan et al., 2008). Previous studies using a variety of different computational methods have reported that the AI has a dominant causal influence on other prefrontal, cingulate and parietal regions during tasks involving orienting attention and response inhibition (Cai et al., 2015; Chen et al., 2014; Ham et al., 2013; Sridharan et al., 2008; Supekar and Menon, 2012). Here, we use open-source task fMRI data (Van Essen et al., 2012) acquired during a working memory task which required participants to continually encode, maintain and update information in mind (Baddeley, 1996). Based on the research reviewed above, we predicted that the AI would play a dominant causal role during working memory task performance with significant influence on other nodes of the fronto-cingulate-parietal network. Crucially, because the ground truth in experimental data is not known, we used novel stability analysis of data from 63 participants to identify robust causal influences within this network. In sum, we demonstrate that MDS can reliably identify causal interactions in simulated as well as experimental data.

Methods

In this section, we describe two different forward models for generating simulated datasets as well as MDS (Ryali et al., 2011) for estimating causal networks from “fMRI” signals generated using these datasets.

Simulated Data

(a) Dataset 1: DCM forward model

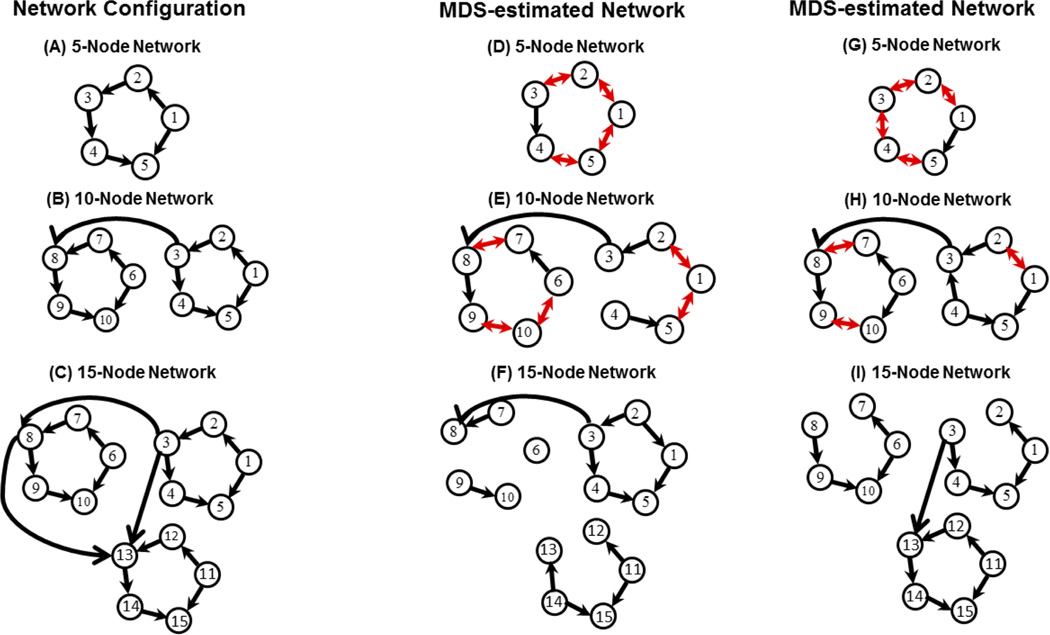
Dataset 1 was based on “benchmark” datasets generated by Smith and colleagues using a DCM model (Smith et al., 2011). Figure 1A–C respectively shows the 5, 10 and 15 node network configurations used in this study. We use a subset of the 28 available simulated datasets selected using the following criteria: (a) number of nodes less than or equal to 15, (b) session duration of 10 min, and (c) TR = 3 s (Supplementary Table S1). We chose these criteria because the sensitivity of MDS in estimating causal networks decreases for networks of size greater than 15 nodes and criteria (b) and (c) are typical in experimental fMRI data acquisitions. Based on these criteria we identified 12 simulations for use here: Sim1, Sim2, Sim3, Sim8, Sim10, Sim12, Sim13, Sim14, Sim15, Sim16, Sim17 and Sim18 as defined previously (Smith et al., 2011). The rationale for not including the other datasets is given in the Supplementary Material. For each simulation, 50 datasets were generated representing 50 different participants. Additional details are described in the Supplementary Materials, and all the datasets used in this study are available from www.fmrib.ox.ac.uk/analysis/netsim.

Figure 1.

Network architectures: (A) 5, (B) 10, and (C) 15 node causal networks (Smith et al. 2011) used for simulating fMRI signals using benchmark deterministic and stochastic neurophysiological models. Estimated causal networks on benchmark datasets: (D) 5, (E) 10 and (F) 15 node causal networks estimated using MDS. Group level results for Sim1, Sim2 and Sim3 are shown (p = 0.05, Bonferroni corrected). The sensitivity of MDS in estimating causal networks is high, but it decreases with increase in network size (Table 2). GCA resulted in disconnected networks for these datasets with sensitivity of 0. Estimated causal networks on neurophysiological model datasets: (G) 5, (H) 10 and (I) 15 node causal networks estimated using MDS. Group level results for Sim1, Sim2 and Sim3 are shown (p = 0.05, Bonferroni corrected). The sensitivity of MDS in estimating causal networks is high, but it decreases with increase in network size (Table 4). GCA resulted in disconnected networks for these datasets with sensitivity of 0.

(b) Dataset 2: Neurophysiological Model

We employed a neurophysiologically realistic neuronal network model to simulate neural dynamics within brain networks. The simulated brain network comprises 5, 10 and 15 nodes, with the same network structures in the DCM simulations shown in Figure 1A–C, in which each node’s dynamics are defined by a synaptic network model (Holcman and Tsodyks, 2006; Testa-Silva et al., 2012).

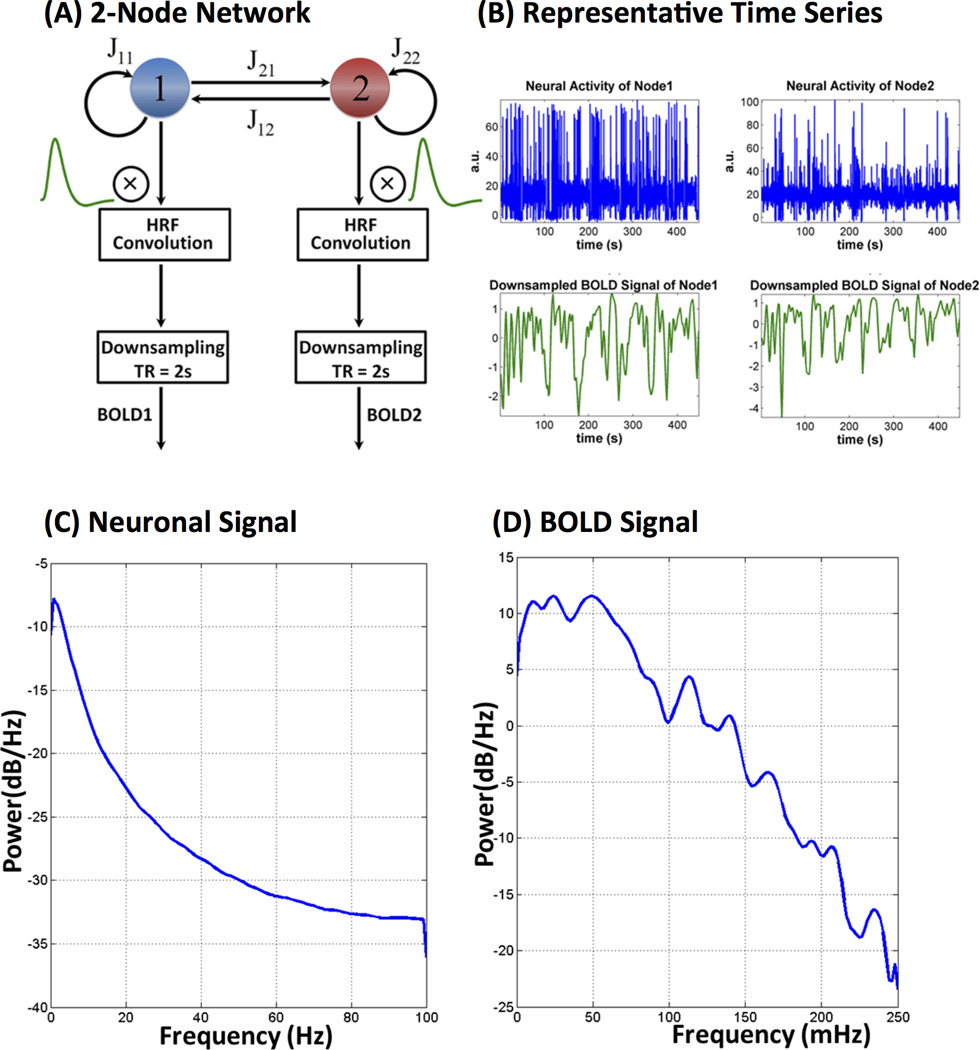
Briefly, following are the procedures similar to the ones used for simulating Dataset 1: The simulated neural dynamics were synthesized with a time step of 5 ms with an overall duration of 750 s. The first 150 s of data were discarded to account for the effects of initialization. The resulting 600 s (10 min) BOLD signals were then obtained by convolving the neural activity with the canonical HRF function (default in SPM8) and downsampling to TR = 2 s. Consistent with simulations in the DCM model (Smith et al., 2011), we generated data for 50 subjects by adding jitters to connectivity strength and neuronal delay (Supplementary Table S2). Hence, each simulation contains datasets for 50 subjects with an effective duration of 10 min for each subject. The mean neuronal delay leading to causality between two nodes is set to 35 ms, which lies in a normal physiological range of 20 – 50 ms. The HRF confounding delays were also taken into account by varying the time-to-peak delay of HRF functions with a standard deviation of 0.5 s. Finally, independent Gaussian white noise with a standard deviation of 1% (of mean signal level) was added to the downsampled BOLD signals to simulate different levels of measurement noise. These parameters (mean neuronal delay, HRF standard deviation and noise levels) are similar to the ones used in the DCM forward model simulations reported in (Smith et al., 2011). Figure 2A shows the flow chart for simulating BOLD signals for a given architecture using the biophysical model. Figure 2B shows the representative neuronal and BOLD fMRI time series for a node. Figure 2C–D shows the power spectra for one representative simulated neural and downsampled BOLD signals, respectively. As expected, the power spectra show 1/f profiles with higher power at low frequencies for both neuronal and fMRI signals.

Figure 2.

(A) Flow chart illustrating key steps in simulation of fMRI signals using the neurophysiological model. Latent neural signals were convolved with an fMRI hemodynamic response function and then downsampled to TR = 2 s. (B) Representative neuronal and BOLD fMRI time series for node 1. Power spectra of representative (C) neuronal and (D) fMRI signals simulated using the neurophysiological model. Both power spectra have 1/f characteristics with higher power at lower frequencies.

(c) Dataset 3: Experimental fMRI data

MDS performance on experimental fMRI data was investigated using a working memory fMRI task data from the Human Connectome Project (HCP, http://www.humanconnectome.org/). Previous research has demonstrated that SN and CEN nodes are consistently activated during performance of this task (Nee et al., 2013; Owen et al., 2005; Wager and Smith, 2003). Here we investigate a frontal-cingulate-parietal network model encompassing the SN and CEN and examine dynamic causal interactions during working memory task performance. The nodes in the SN and CEN were identified using an unbiased approach similar to our previous studies (Chen et al., 2014; Supekar and Menon, 2012; Uddin et al., 2011). First, we conducted an independent component analysis (ICA) on resting-state fMRI data from a different group of participants to identify the SN and CEN. ICA is a model-free, data-driven approach and has the flexibility to identify various independent spatial patterns and their associated temporal fluctuations (Beckmann and Smith, 2004). From the SN ICA map, we identified nodes in the right AI, ACC and VLPFC. From the CEN ICA map, we identified nodes in the right DLPFC and PPC.

Working memory task

Participants were presented with blocks of trials that consisted of pictures of places, tools, faces and body parts and were instructed to perform a 0-back or a 2-back task in randomly alternating blocks (Barch et al., 2013). Within each run, the four different stimulus types were presented in separate blocks. Each run had eight N-back task blocks (27.5 s each), consisting of four 0-back task blocks and four 2-back task blocks, and four fixation blocks (15 s each). A 2.5 s cue was presented in the beginning of each block to inform participants of the nature of the task (0-back versus 2-back), followed by 10 trials of 2.5 s each, including 2 targets and 2–3 non-target lures in the 2-back task. On each trial, the stimulus was presented for 2 s, followed by a 500 ms inter-trial interval. In 0-back task blocks, a target cue was presented at the start of each block and the subject was required to identify any stimuli that matched the target. In 2-back task blocks, the subject was required to identify stimuli that matched the one presented back 2 trials.

Participants

fMRI task data from the HCP Q1 release, which included a total 68 adult participants, were used in this study. We excluded 5 participants because their total head movement exceeded the size of 1 voxel. The final analysis therefore included data from 63 participants (47 female, 16 male, 22–35 years old).

fMRI Data preprocessing

We used minimally preprocessed data provided by the HCP Consortium (Glasser et al., 2013). Briefly, the preprocessing included a “PreFreeSurfer” pipeline to correct MR gradient-nonlinearity-induced distortion on structural MRI data, align T1w and T2w images with a 6 degree of freedom (DOF) rigid body transformation using FSL’s FLIRT and perform registration of structural data to a standard MNI space template. A “fMRIVolume” pipeline was also used to correct MR gradient-nonlinearity-induced distortion on fMRI data, correct head motion with a 6 DOF rigid body transformation using FSL’s FLIRT and 12 motion parameters including x, y, z translation in mm, x, y, z rotation in degrees and their first derivatives and perform registration of the fMRI data to T1w and to a standard MNI space template. We applied a 5 mm FWHM Gaussian smoothing kernel on the top of the preprocessed data to take into account spatial noise and individual variation in anatomy.

MDS Methods for Causal Estimation

MDS is a state-space model (Ryali et al., 2011) consisting of a state equation to model the latent “neuronal–like” states of the dynamic network and an observation equation to model BOLD-fMRI signals as a linear convolution of latent neural dynamics and HRF responses. Like DCM, it estimates causal interactions between brain regions while accounting for variations in hemodynamic responses in these regions.

The state equation in MDS is a multivariate linear difference equation or a first order multivariate auto regressive (MVAR) model that defines the state dynamics

$$\mathit{s}(t)={\sum }_{j=1}^J{v}_j(t)C_j\mathit{s}(t-1)+\mathit{w}(t)$$ (1)

The model for the observed BOLD responses is a linear convolution model

$${\mathit{x}}_m(t)={[{\mathit{s}}_m(t){\mathit{s}}_m(t-1)\dots .{\mathit{s}}_m(t-L+1)]}^{\prime }$$ (2)

$$y_m(t)=b_m\Phi {\mathit{x}}_m(t)+{\mathit{e}}_m(t)$$ (3)

In Equation (1), s(t) is a M × 1 vector of latent signals at time t of M regions, C_j is a connection matrix ensued by modulatory input v_j(t), and J is the number of conditions in a given fMRI experiment. The non-diagonal elements of C_j represent the coupling of brain regions in the presence of v_j(t). Therefore, latent signals s(t) in M regions at time t is a bilinear function of modulatory inputs v_j(t). and its previous state s(t−1). w(t). is an M × 1 state noise vector whose distribution is assumed to be Gaussian distributed with covariance matrix Q(w(t) ~ N(0,Q)). Additionally, state noise vector at time instances 1,2,….,T (w(1), w(2)… w(T) ) are assumed to be identical and independently distributed (iid). The latent dynamics modeled in equation (1) and equation (2) give rise to observed fMRI time series represented by Equation (3).

We model the fMRI-BOLD time series in region m as a linear convolution of HRF and latent signal s_m(t) in that region. To represent this linear convolution model as an inner product of two vectors, the past L values of s_m(t) are stored as a L × 1 vector x_m(t) in equation (2).

In equation (3), y_m(t) is the observed BOLD signal at time t of m-th region. Φ is a p × L matrix whose rows contain bases for HRF. b_m is a 1 × p coefficient vector representing the weights for each basis function in explaining the observed BOLD signal y_m(t). Therefore, the HRF in m-th region is represented by the product b_mΦ The BOLD response in this region is obtained by convolving HRF (b_mΦ) with the L past values of the region’s latent signal (x_m(t)) and is represented mathematically by the vector inner product b_mΦ x_m(t). Uncorrelated observation noise e_m(t) with zero mean and variance ${\sigma }_m^2$ is then added to generate the observed signal y_m(t). e_m(t) is also assumed to be uncorrelated with w(τ), at all t and τ .Therefore, equation (3) represents the linear convolution between the embedded latent signal x_m(t) and the basis vectors for HRF. Here, we use the canonical HRF and its time derivative as bases, as is common in most fMRI studies.

Equations (1–3) together represent a state-space model for estimating the causal interactions in latent signals based on observed multivariate fMRI time series. Crucially, MDS also takes into account variations in HRF as well as the influences of modulatory stimuli in estimating causal interactions between the brain regions.

Estimating causal interactions between M regions specified in the model is equivalent to estimating the parameters C_j,j = 1,2..J. In order to estimate C_j’s, the other unknown parameters Q, ${\left\{b_m\right\}}_{m=1}^M$ and ${\left\{{\sigma }_m^2\right\}}_{m=1}^M$ and the latent signal ${\{{\mathit{s}}^s(t)\}}_{t=1}^T$ based on the observations ${\{y_m^s(t)\}}_{m=1,s=1}^{M,S}$, t = 1,2..T, where T is the total number of time samples and S is the number of subjects, needs to be estimated. We use a variational Bayes approach (VB) for estimating the posterior probabilities of the unknown parameters of the MDS model given fMRI time series observations for S number of subjects (Ryali et al., 2011). In this analysis we set J = 1 corresponding to one condition in our simulated data sets. We use the same non-informative hyperparameters as in our previous study (Ryali et al., 2011). We assume a Gaussian prior distribution on each element of C_j(m,n) with mean 0 and precision Λ_j (m,n) We assume that each precision parameter Λ_j (m,n) follows a Gamma distribution with hyper-parameters c_o and d_o, which are set to uninformative values of 10⁻³ each. We also use a Gamma distribution for each diagonal element of the noise precision Q⁻¹ in Equation (1) with hyper-parameters a_o and b_o set to non informative values of 10⁻³ each. We use similar prior distributions for the parameters b_m and e_m(t) in the output Equation (3). The details of VB estimation of these parameters are provided in our previous study (Ryali et al., 2011). We initialized the MDS algorithm using the same procedures described therein.

The fMRI time time series for each region m and subject s, $y_m^s(t)$, is linearly de-trended, its temporal mean removed and normalized by its standard deviation prior to applying MDS.

Granger causal analysis (GCA)

We benchmarked MDS against Granger causal analysis (GCA), a commonly used method for estimating causal interactions in fMRI data (Deshpande et al., 2009a; Roebroeck et al., 2005; Seth, 2010). In this study, we use the Matlab implementation of GCA published by Seth and colleagues (Seth, 2010). We provide a brief description of GCA framework in the Supplementary Materials.

Statistical Inference and performance metrics

We examined the performance of MDS on simulated datasets in estimating causal networks on various datasets by computing the receiver operating characteristics (ROC), which is a plot of FPR on the x-axis and sensitivity on the y-axis at various FPR thresholds. These quantities are defined as:

$$\mathit{\text{Sensitivity}}=\frac{\mathit{\text{TP}}}{\mathit{\text{TP}}+\mathit{\text{FN}}}$$ (4)

$$\mathit{\text{False Positive Rate}}=\frac{\mathit{\text{FP}}}{\mathit{\text{TN}}+\mathit{\text{FP}}}$$ (5)

where TP is the number of true positives, TN is the number of true negatives, FN is the number of false negatives and FP is the number of false positives. These quantities are estimated for simulated datasets at the group level using the random effects analysis as suggested in (Stephan et al., 2010). The statistical significance of a causal connection between a pair of nodes is determined as follows:

1. Apply MDS or GCA on each subject

2. Apply one-sample t-test on the estimated causal link from node j to i (A(i,j)) in the case of MDS or doi(i,j) in the case of GCA), on every subject and assess at a given p-value.

3. Compute sensitivity and FPR using the ground truth of each network.

4. Plot the ROC curve by computing sensitivity and FPR at different p-values.

We examined the performance of MDS on individual simulated datasets by computing the area under the curve (AUC) of the ROC. At chance level performance, AUC will be close to 0.5 and a better performing method will have AUC close to 1. AUC criteria were used to compare the relative performance of MDS and GCA. The performance of MDS and GCA on simulated datasets are also illustrated using a threshold of p = 0.05 with Bonferroni correction for multiple comparisons.

Stability analysis of causal interactions within a fronto-cingulate-parietal network in HCP data

Here we investigate causal interactions in a fronto-cingulate-parietal network constructed using core nodes of the SN and CEN as identified by an independent component analysis (ICA) of resting-state fMRI data (Supekar and Menon, 2012). The detailed procedures are described in (Supekar and Menon, 2012). From the right SN ICA map, ROIs in the AI, ACC and VLPFC were identified. From the right CEN ICA map, ROIs in the right DLPFC and PPC were identified. Figure 4A shows the MNI coordinates of these ROIs (Supekar and Menon, 2012).

Figure 4.

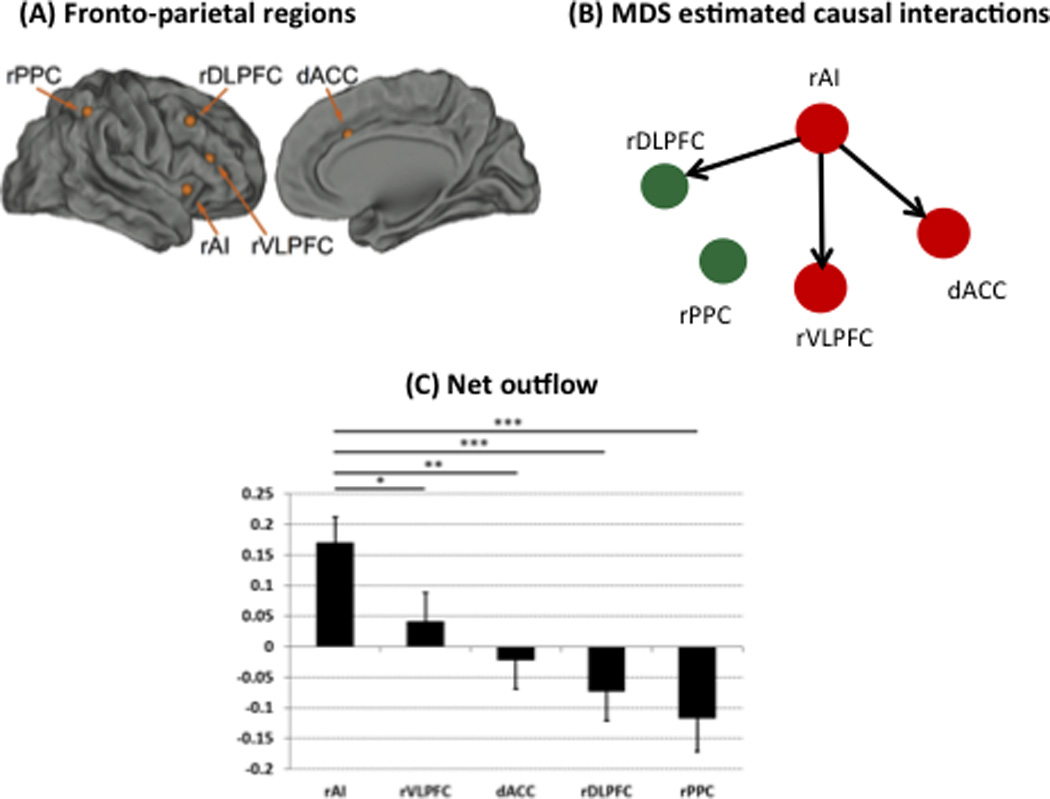
(A) Fronto-cingulate-parietal regions used in analysis of working memory task data from the human connectome project Include of the anterior cingulate cortex (ACC); ventrolateral prefrontal cortex (VLPFC); dorsolateral prefrontal cortex (DLPFC); posterior parietal cortex (PPC). (B) Stable dynamic causal interactions estimated using MDS and stability analysis. Each link of the causal network has a stability of 80% or more that is stable across 5000 bootstrap replications of data from 25 participants, selected from 63 participants without replacement. (C) Right anterior insula (rAI) is a causal hub with significantly greater net outflow of causal interactions than all other nodes of the fronto-cingulate-parietal network.

We determined causal interactions between the fronto-cingulate-parietal network illustrated in Figure 4A using the following procedures:

1. Randomly select 25 from 63 participants without replacement.

2. Estimate dynamic causal interactions by applying MDS on the selected 25 subjects.

3. Apply one-sample t-test on each causal link between nodes.

4. Determine significant interactions at p = 0.05 (FDR correction for multiple comparisons).

5. Repeat steps (1)-(4) 5000 times.

6. Determine stable causal interactions between network nodes that were reliably identified at least 80% percent of the time.

Network graph-theoretical analysis

To further characterize the causal outflow pattern uncovered by MDS on the HCP working memory data, we examined the net outflow in each node in the network. Net outflow of a node is defined as its out-strength minus its in-strength. Out-strength is the strength of causal outflow connections from a node in the network to any other node, and similarly in-strength is the strength of causal inflow connections from any other nodes to the node of interest. A Wilcoxon signed-rank test was then applied on this metric of net outflow to identify those nodes whose network metrics were significantly different from the other nodes.

Results and Discussion

Dataset 1: DCM forward model

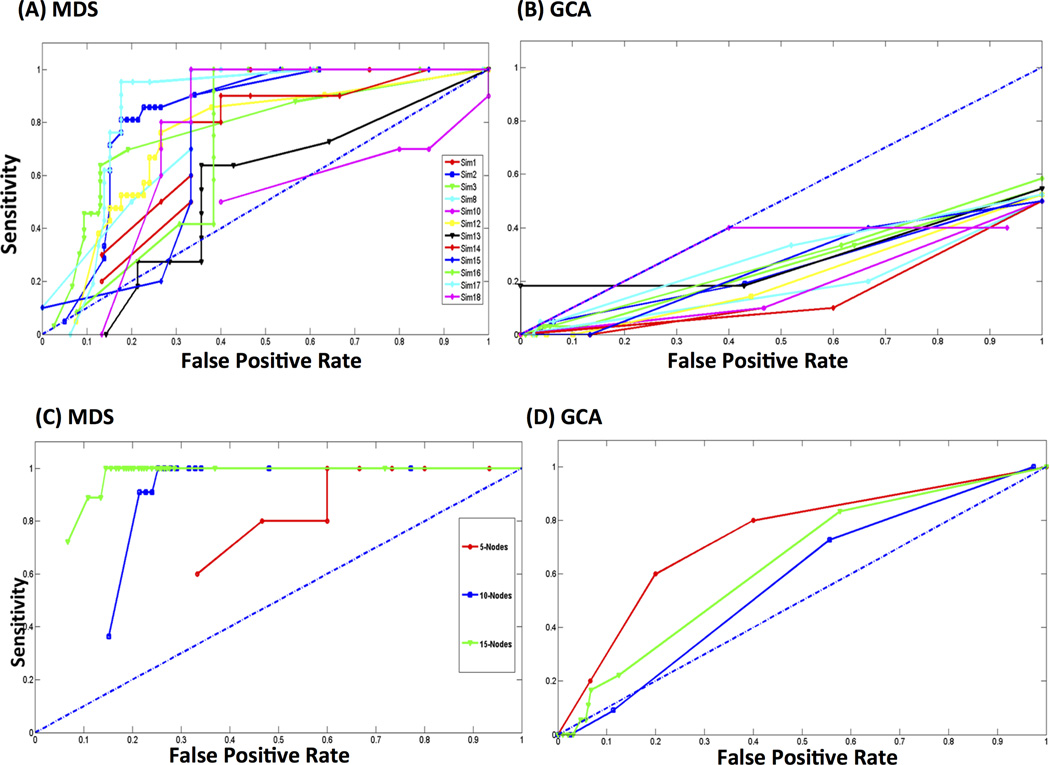
Figures 3A and 3B show ROC curves for MDS and GCA respectively on 12 DCM simulated datasets used in this study (see (Smith et al., 2011) for details of each simulated dataset). The ROC curves for MDS are above chance level performance as shown by the diagonal dotted line in blue in Figure 3A for all the datasets except for the simulated dataset Sim10. On the other hand, ROC curves for GCA lie below the chance level for all the datasets as shown in Figure 3B. Table 1 shows the AUC of ROCs for MDS and GCA on all the 12 datasets. AUCs are below the chance level of 0.5 for GCA while AUCs for MDS are above 0.7 except for Sim10 and Sim13, suggesting that MDS is more effective in estimating the underlying causal networks from the data at group level when compared to GCA. Below we examine the performance of MDS on the 12 simulated datasets in detail, and contrast it with GCA.

Figure 3.

Receiver Operating Characteristic (ROC) curves for (A) MDS and (B) GCA on benchmark datasets. ROC curves obtained by MDS indicate performance significantly above chance level (blue dotted diagonal line), for all simulations excepting Sim10. ROC curves using GCA are well below the chance level. Area under the Curves (AUCs) obtained by MDS for most of simulated datasets are well above 0.7 while those using GCA are below the chance level of 0.5 (Table 1). Receiver Operating Characteristic (ROC) curves for (C) MDS and (D) GCA on datasets simulated using stochastic neurophysiological models. ROC curves obtained by MDS are well above chance level (blue dotted diagonal line), for simulations Sim1, Sim2 and Sim3. ROC curves using GCA are well below that obtained by MDS. Areas under the Curves (AUCs) determined by MDS are close to 1 while those determined using GCA are below 0.7 (Table 3).

Table 1.

Performance of MDS and GCA on benchmark datasets simulated using the deterministic model in terms of AUC (area under the curve of receiver operating characteristics).

Sim No.	MDS	GCA
Sim1	0.74	0.18
Sim2	0.82	0.25
Sim3	0.76	0.25
Sim8	0.8	0.18
Sim10	0.39	0.18
Sim12	0.75	0.21
Sim13	0.55	0.29
Sim14	0.71	0.15
Sim15	0.72	0.26
Sim16	0.7	0.28
Sim17	0.84	0.29
Sim18	0.76	0.29

(a) Baseline simulations

Sim1, Sim2 and Sim3 are the baseline simulations (Smith et al., 2011) consisting of 5, 10 and 15 nodes respectively with 50 simulated datasets. AUC values of MDS are well above the chance level of 0.5 while that of GCA are below chance as shown in Table 1. As an illustration, Figures 1C, 1D and 1E show the estimated causal networks from these datasets at group level by MDS at a p-value of 0.05 with Bonferroni correction for multiple comparisons. MDS resulted in sensitivity of 1 and FPR of 0.27 for Sim1; sensitivity of 0.91 and FPR of 0.06 for Sim2 and sensitivity of 0.56 with FPR of 0.01 for Sim3 as shown in Table 2. The sensitivity and FPR of MDS decreased with increasing network size. A decrease in sensitivity is expected because of the overly-conservative Bonferroni correction. The sensitivity of discovering causal networks can be further improved by using less conservative approaches for multiple comparisons such as FDR but at the expense of increased FPR. In contrast, GCA was not able to identify any causal links from these three datasets resulting in fully disconnected networks with sensitivity of 0 and FPR of 0.

Table 2.

Performance of MDS on benchmark datasets simulated using the deterministic model in terms of sensitivity and false positive rate (FPR) at p = 0.05 (Bonferroni corrected).

Sim No.	Sensitivity	FPR
Sim1	1	0.27
Sim2	0.91	0.06
Sim3	0.56	0.01
Sim8	1	0.27
Sim10	0.8	0.87
Sim12	0.91	0.08
Sim13	0.5	0.07
Sim14	0.8	0.13
Sim15	1	0.27
Sim16	0.71	0.23
Sim17	0.73	0.03
Sim18	0.8	0.27

(b) Effect of shared inputs

Sim8 was specifically designed to investigate the effects of shared inputs on the performance of causal estimation methods. In the case of datasets Sim1, Sim2 and Sim3, independent external or sensory inputs drive each node in the network. However, in real fMRI datasets, some of the nodes could be driven by the same sensory input. Sim8 data are from a 5 node network that simulates a scenario where a sensory input could drive more than one node, reflecting the case of “shared inputs”. MDS resulted in AUC of 0.8 while that of GCA was only 0.18 as shown in Table 1. The sensitivity of MDS in estimating the causal network from this dataset is 1 with FPR of 0.27 (Table 2). The performance of MDS on this dataset is the same as that on Sim1 despite reduction in the strength of an external stimulus driving the network nodes from 1 in Sim1 to 0.3 in Sim8. Note that in (Smith et al., 2011) nodes are driven by the external inputs, thus the power in the time series is dependent only on the external drive; in contrast, our model is driven both by random noise and external input. Similar to the baseline simulations described in the previous section, GCA resulted in disconnected networks.

(c) Effect of global additive confound

Simulated dataset Sim10 with 5 nodes investigates the effects of global confounds in causal estimation. In this case, both MDS and GCA performed poorly with AUCs of 0.39 and 0.18 respectively which are below the chance level of 0.5 (Table 1). At a p-value of 0.05 with Bonferroni correction, the sensitivity of MDS is high at 0.8 but with high FPR of 0.87 as shown in Table 2. Like in previous datasets, GCA resulted in disconnected networks. The addition of global confounds adversely effected the performance of MDS. We re-examined the performance of these two methods by regressing out the average time series computed from 5 nodes of the network. However, the performance of MDS and GCA did not improve (data not shown). Further research is needed to extensively evaluate the performance of causal estimation methods in the presence of confounding global signals.

(d) Effect of inaccurate Regions of Interest (ROI)

In real fMRI studies, the time series for a network node is usually derived by averaging the time series of voxels in a given ROI. This average time series for a node is not a perfect representative if the ROI does not match the actual functional boundaries. The effect of such inaccurate ROIs was simulated in a 10 node network of Sim12. On this simulation, MDS resulted in AUC of 0.75 (Table 1) sensitivity of 0.91 and FPR of 0.08 at a p-value of 0.05 with Bonferroni correction (Table 2). This performance, which is similar to that of the baseline data Sim2, suggests that the specification of inaccurate ROIs did not influence MDS. GCA, however, resulted in disconnected networks with this criterion and with AUC of 0.21 (Table 1).

(e) Effect of backwards connections

The simulation Sim13 models the effect of having both forward and backward connections between network nodes in estimating causal interactions. To investigate this scenario (Smith et al., 2011) chose half of the forward connections randomly and added backward connections with almost equal negative connections reflecting the scenario that some of the connections could be of opposite signs. On these simulations, MDS resulted in AUC of only 0.55 (Table 1), sensitivity of 0.5 and FPR of 0.07 at a p-value of 0.05 with Bonferroni correction (Table 2). The performance of MDS is just above the chance level on this dataset. These findings are similar to previous reports (Smith et al., 2011) where the performance of various network estimation methods performed poorly at single subject level. As in the case of previous data sets, GCA failed to discover any network connections at a p-value of 0.05 with Bonferroni correction and with AUC of only 0.29 (Table 1).

(f) Effect of cyclic connections

In simulation Sim14, the directed connection from 1 to 5 was reversed in the 5 node network shown in Figure 1A in order to simulate data from a network consisting of cyclic connections. Methods similar to Bayes networks used in studies such as (Ramsey et al., 2011; Ramsey et al., 2009) cannot be used in this case because these methods assume that the underlying network is acyclic. However, the causal estimation methods used here (MDS and GCA) do not have such restrictions. On this simulation, the value of AUC was 0.71 (Table 1); sensitivity was 0.8 with FPR of 0.13 at a p-value of 0.05 with Bonferroni correction (Table 2) using MDS. The performance of MDS is comparable to the baseline simulation Sim1. As in the other simulations, GCA resulted in a disconnected network at this criterion with poor AUC of 0.15 (Table 1)

(g) Effect of stronger connections

In simulation Sim15, the connection strengths between the nodes were increased from the mean value of 0.4 to 0.9 (Smith et al., 2011). The performance of MDS is the same as that of the baseline simulation, Sim1, with AUC of 0.72 (Table 1), sensitivity of 1 with FPR of 0.27 at a p-value of 0.05 with Bonferroni correction (Table 2). Increasing the strengths of the connections did not improve the performance of GCA. In this case also, GCA is not able to discover any network connections at a p-value of 0.05 with Bonferroni correction and AUC of 0.26 that is much below the chance value of 0.5.

(h) Effect of increased number of connections

The effect of increased number of connections on causal estimation was investigated in simulation Sim16 using additional connections to the 5 node network shown in Figure 1A (Smith et al., 2011). In this case, the sensitivity of MDS decreased to 0.71 from 1 as compared to the baseline simulation with FPR of 0.23 at a p-value of 0.05 with Bonferroni correction (Table 4) and AUC value of 0.7 (Table 1) at group level. In contrast with our finding, (Smith et al., 2011) reported that the performance of network estimation methods used in that study were similar to that of baseline simulation Sim1 at single subject level. However, it should be noted that the performance metrics used in our study are different from that used in (Smith et al., 2011). GCA resulted in disconnected networks at a p-value of 0.05 with Bonferroni correction and below chance level with AUC value of 0.28 (Table 2).

Table 4.

Performance of MDS on datasets simulated using the neurophysiological model in terms of sensitivity and false positive rate (FPR) at p = 0.05 (Bonferroni corrected).

Network Size	Sensitivity	FPR
5 Nodes	1	0.27
10 Nodes	0.91	0.18
15 Nodes	0.78	0.07

(i) Effect of HRF variability

Using data simulated from a DCM forward model Smith and colleagues (Smith et al., 2011) reported that lag-based methods such as GCA were not effective in discovering causal networks at a single-subject level. One of the criticisms of lag-based methods such as GCA is that these methods explicitly do not account for HRF variability at various nodes of the network. To further investigate this issue, they removed the HRF variability in the simulation Sim18 and assessed the performance of these methods. They found that even in these simulations, the performance of lag-based methods did not improve when compared to the baseline simulation (Sim1). Our results for GCA at group level corroborate the findings at single subject level reported in (Smith et al., 2011). In the case of MDS, the performance of MDS is comparable (AUC = 0.76, Table 1, sensitivity = 0.8) (FPR = 0.27 at p-value of 0.05, Table 2, Bonferroni corrected) to the baseline simulation Sim1.

In summary, the performance of MDS is superior to GCA in terms of AUC, sensitivity and FPR at a p-value of 0.05 with Bonferroni corrections.

Dataset 2: Neurophysiological model

To further evaluate the performance of MDS and GCA, we used a neurophysiological model to simulate BOLD-fMRI time series. In contrast to the deterministic DCM model described above, this model uses multivariate nonlinear stochastic differential equations to generate neuronal dynamics and incorporates realistic conduction delays and saturation effects that are generally present in real datasets. Figures 3C and 3D respectively show ROC curves underlying the performance of MDS and GCA from three datasets consisting of 5, 10 and 15 node networks that are generated from the neuronal mass model. The ROC curves in Figure 3C suggest that the performance of MDS is well above the chance level shown by the diagonal line while the performance of GCA is close to the chance level as shown in Figure 3D. The AUC of ROC curves for MDS and GCA are shown in Table 3 for all the three networks. AUCs for MDS are close to 1 and are better than those obtained by GCA.

Table 3.

Performance of MDS and GCA on datasets simulated using the stochastic neurophysiological model in terms of AUC (area under the curve of receiver operating characteristics).

Network Size	MDS	GCA
5 Nodes	0.93	0.74
10 Nodes	0.92	0.54
15 Nodes	0.99	0.63

Figures 1G, 1H and 1I show the MDS-estimated 5, 10 and 15 node networks respectively at p = 0.05, Bonferroni corrected. Table 4 shows the sensitivity and FPRs of these estimated networks. MDS recovered underlying causal links with sensitivity of 1, 0.91 and 0.78 for 5, 10 and 15 network nodes respectively as shown in Table 4 with respective FPRs of 0.27, 0.18 and 0.07. As expected, the sensitivity of MDS decreased while the number of false positives decreased with the increase in the network size. On the three datasets, GCA resulted in disconnected networks at a p-value of 0.05 with Bonferroni correction. We repeated these analyses with datasets generated with TR of 3 s, as used in the previous DCM simulations (Smith et al., 2011). Here again, we found that MDS accurately recovered dynamic causal networks, whereas GCA resulted in disconnected networks with significantly lower AUC values compared to those resulting from MDS (data not shown). In summary, MDS performed better than GCA on two simulated datasets that were generated independent of the models used for the estimation of causal interactions.

Simulation with Deterministic and Stochastic Neurophysiological Models

We investigated the performance of MDS and GCA on two different simulation models. The first simulation model uses a deterministic DCM model for simulating neuronal dynamics of network nodes. This model uses a linear differential equation to model linear causal interactions without a noise component in the neuronal signals. The neurophysiological model proposed in (Holcman and Tsodyks, 2006; Testa-Silva et al., 2012) is a neuronal mass model to simulate complex dynamics for neuronal signals. This model uses a multivariate nonlinear stochastic differential equation with delays that model causal interactions between several nodes in the network. Stochastic noise is a key component of the model, consistent with properties of real biological systems. We use a similar set of parameters (Supplementary Table S2) that are suggested for simulating fMRI datasets using deterministic DCM models (Smith et al., 2011). Our results suggest that that the performance of MDS in terms of ROC curves (Figure 3C) and AUCs (Table 3) on these datasets are, in fact, much better than those obtained using DCM datasets (Figure 3A and Table 1). Moreover, both sensitivity and specificity of the estimated networks are much better for datasets simulated using the neurophysiological model (Table 4) when compared to the performance on DCM simulated datasets (Table 2) (Smith et al., 2011). This difference in performance may be attributed to the stochastic dynamics used in the neurophysiological model. The deterministic DCM model was initially proposed for estimating causal interactions from fMRI datasets (Friston et al., 2003) but is not designed to simulate complex dynamics of neuronal signals. In the DCM model, signals are driven solely by the external stimuli to the network nodes with no stochastic noise component. The neurophysiological model in our study, on the other hand, uses a multivariate nonlinear stochastic differential equation to generate neuronal dynamics in which signals are driven by both external stimuli as well as stochastic noise. Although the performance of GCA on the two simulated datasets used in this study was generally poor, this does not necessarily preclude its use in the estimation of causal interactions in experimental fMRI studies because of potential un-modelled effects in small-scale brain data simulation (Wen et al., 2012). Further work is needed to validate causal estimation methods such as MDS, GCA, DCM and other related methods (Smith et al., 2009) using more realistic datasets generated from large-scale brain network models (Deco et al., 2013; Jirsa and Stefanescu, 2011; Sanz Leon et al., 2013; Stefanescu and Jirsa, 2008).

Finally, the neurophysiological model used in this study can also be more easily extended to investigate brain and neurodevelopmental disorders because model parameters for pathological neuronal and synaptic activity have been characterized in experiments using the stochastic dynamic models used in our study (Testa-Silva et al., 2012). Simulation datasets generated using this model will be available at http://cosyne.stanford.edu upon publication to facilitate further research, with relevance to both cognitive function and dysfunction.

Autoregressive versus state space models

Our results suggest that the performance of MDS is superior to that of GCA across all the datasets tested. MDS uses state-space models and estimates causality in latent states while explicitly modeling the effects of HRF variations across brain regions. GCA uses a multivariate vector autoregressive model (VAR) that directly estimates causality from the BOLD observations without explicitly accounting for HRF variations. We believe that the one of the reasons for the poor performance of GCA is that it does not take into account regional variations in HRF. Previous studies have shown that time-to-peak of the HRF can vary from approximately 2.5 to 6.5 s across subjects and brain regions (Aguirre et al., 1998; Baldwin and LeBlanc, 1992) (Chang et al., 2008). Such HRF variations are known to confound dynamic causal analysis in BOLD fMRI data (Friston et al., 2003; Ryali et al., 2011; Seth et al., 2013; Smith et al., 2009). Previous studies have shown that GCA can estimate causal interactions only (a) when neuronal delays between brain regions are on the order of hundreds of milliseconds, and (b) these delays are greater than time-to-peak variations in hemodynamic responses across brain regions (Deshpande et al., 2009b; Seth et al., 2013). However, neither of these assumptions is biologically valid (Friston et al., 2003; Ryali et al., 2011; Seth et al., 2013; Smith et al., 2009). In this study, we show that MDS is effective in estimating the underlying causal interactions for short neuronal delays in the presence of hemodynamic variations between brain regions.

Another possible explanation for the advantages of state space over VAR models has been suggested by Barnett and colleagues (Barnett and Seth, 2015). The “Granger” causality in general can be implemented using autoregressive moving average (ARMA) models. ARMA models can be equivalently represented using vector autoregressive models (VAR) if their model order is sufficiently large. However, in fMRI applications, GCA is realized using finite order VAR models (Roebroeck et al., 2005; Seth, 2010) and the optimal model order as estimated by information criteria such as Akaike information or Bayesian information criterion is typically about 2 to 3 (Supekar and Menon, 2012). Therefore, a second or third order VAR models may not adequately represent equivalent ARMA models. If the moving average component of the ARMA model is not adequately modeled by the VAR model, then GCA will not be able to accurately model the underlying causal interactions (Barnett and Seth, 2015). Barnett and Seth suggest using state space models (Barnett and Seth, 2015) to solve this problem because state space models are equivalent to ARMA models. Moreover, state space models, unlike ARMA models, do not require assumptions of linearity and wide-sense stationarity. Like DCM, MDS uses state space models (equation 1–equation 3) with the additional feature of estimating causal interactions that are specific to the underlying experimental condition (for example, C_j in equation 1 corresponds to causal interactions in j-th experimental condition) in task fMRI. Further studies are needed to validate task condition-specific causal interactions. In sum, our results on the simulated datasets suggest that the state-space models used in MDS are effective in estimating the causal interactions between brain areas.

Stability of causal interactions in working memory fMRI data within a fronto-cingulate-parietal network

Neuroimaging studies have consistently demonstrated that the prefrontal and parietal cortices play a critical role in working memory (Owen et al., 2005; Rottschy et al., 2012). Furthermore, it has been hypothesized that working memory is an emergent property of the interaction between different brain areas (D’Esposito, 2007; Feredoes et al., 2011; Lee and D’Esposito, 2012; Palva et al., 2010a; Palva et al., 2010b). Here we investigated dynamic causal interactions in a frontal-cingulate-parietal network which has been consistently implicated in working memory (Nee et al., 2013; Owen et al., 2005; Wager and Smith, 2003) using MDS. This network comprised 5 nodes of the SN and CEN: rAI, rVLPFC and dACC, which are key nodes of the salience network, and rDLPFC and rPPC, which are key nodes of the central executive network (Figure 4A). We found that the rAI has significant, causal influences on the dACC, rVLPFC, and the rDLPFC (Figure 4B). Although the ground truth here is not known, we were able to use stability analysis to uncover robust and stable patterns of dynamic causal interactions underlying stimulus-driven cognitive control during working memory task performance. Crucially, our approach overcomes a key issue in the interpretation of dynamic causal interactions in human neuroimaging analysis.

The working memory task requires participants to register incoming task-relevant stimuli and compare with targets maintained in working memory. Strong causal interactions within the fronto-cingulate-parietal network are consistent with their putative roles in detecting behaviorally salient information and holding information online, respectively (Chafee and Goldman-Rakic, 1998; Downar et al., 2002; Jonides et al., 1998; Menon and Uddin, 2010; Oliveri et al., 2001). Interestingly, the AI showed strong causal influences with multiple nodes of the frontal-cingulate-parietal network, including the dACC, rVLPFC and rPPC, during the working memory task. Our findings suggests that the AI is a dominant source of causal signaling influencing dorsal fronto-parietal regions and for implementing control processes during working memory. Our findings are convergent with previous studies that also revealed dominant causal influences from the rAI to other nodes in the frontal-cingulate-parietal network during cognitive control and attention, emphasizing the replicability, stability and consistency of MDS-based findings across different experimental paradigms and independent datasets (Cai et al., 2015; Chen et al., 2015; Menon, 2011; Sridharan et al., 2007; Sridharan et al., 2008; Supekar and Menon, 2012).

Finally, to further characterize the critical role of AI within the frontal-cingulate-parietal network, we performed graph-based network analysis on the causal net outflow for each node and for each participant in the working memory task (Cai et al., 2015; Chen et al., 2014; Supekar and Menon, 2012). This analysis revealed that the rAI had the highest net outflow (out-strength – in-strength) among all regions in the network. Notably, the AI had significantly higher causal net outflow than all other nodes (Figure 4C), pointing to its critical role in integrative causal signaling during working memory task performance.

Future Work

In the current study, datasets simulated with artificially constructed networks were used to validate causal estimation methods such as MDS. Specifically, in simulating fMRI time series using DCM, we used deterministic linear differential equations together with a nonlinear balloon model of neurovascular coupling, while in the more realistic neurophysiological models we used non-linear stochastic equations and linear convolution with the HRF. In both cases, the simulated fMRI time series was thus generated using a nonlinear model. The GCA model we employed is based on widely used linear vector autoregressive models for fMRI time series (Deshpande et al., 2009a; Deshpande et al., 2008; Deshpande et al., 2011; Jiao et al., 2011; Roebroeck et al., 2009, 2005; Seth, 2005, 2010; Smith et al., 2011; Sridharan et al., 2008). Recently, GCA has been extended to estimate time resolved partial directed coherence (Anwar et al., 2013) and nonlinear causal relationships between time series using kernel methods (Marinazzo et al., 2008); model free methods based on transfer entropy (Montalto et al., 2014) have also been developed to infer causal relations between time series. In the time resolved partial directed coherence approach, a state space approach was used to estimate the time varying causal interactions between time series and partial directed coherence was used to infer causal relationships on simultaneously recorded fMRI and near infrared spectroscopy (NIRS) datasets (Anwar et al., 2013). Future works needs to investigate, within our simulation framework, whether these GCA models can improve causal estimation in fMRI data. Future work will also need to use more realistic virtual brain models (Deco et al., 2013; Jirsa and Stefanescu, 2011; Sanz Leon et al., 2013; Stefanescu and Jirsa, 2008) that better reflect the structural and functional organization of the human brain. Finally, validating rapid changes in the strength of causal interactions associated with distinct stimuli and task contexts in event-related experimental fMRI data remains an important challenge as the ground truth is typically not known.

Conclusions

We investigated the performance of MDS, a state-space method, on two different simulated datasets at the group level. Critically, simulated data were produced using generative models independent of MDS, thereby eliminating circularity and potential bias. MDS accurately recovered dynamical causal network interactions in both benchmark data (Smith et al., 2011) as well as neurophysiologically realistic data generated using nonlinear stochastic neuronal mass models (Holcman and Tsodyks, 2006; Testa-Silva et al., 2012) with AUC of about 0.7 and above in most cases examined. The performance of MDS was far superior to that of the GCA, with the latter often resulting in disconnected networks. Our findings demonstrate for the first time that MDS can identify stable and replicable patterns of causal interactions in experimental fMRI data. MDS analysis revealed that the right anterior insula functions as a hub driving causal interactions with other nodes of the fronto-cingulate-parietal control network during working memory. Our methods and stability analysis are likely to be useful for identification of stable causal interactions in other functional brain circuits during cognition. There is also great potential for understanding aberrant causal brain networks in psychiatric and neurologic disorders.