Deconvolution of Ensemble Chromatin Interaction Data Reveals the Latent Mixing Structures in Cell Subpopulations

Abstract

Chromosome conformation capture (3C) experiments provide a window into the spatial packing of a genome in three dimensions within the cell. This structure has been shown to be correlated with gene regulation, cancer mutations, and other genomic functions. However, 3C provides mixed measurements on a population of typically millions of cells, each with a different genome structure due to the fluidity of the genome and differing cell states. Here, we present several algorithms to deconvolve these measured 3C matrices into estimations of the contact matrices for each subpopulation of cells and relative densities of each subpopulation. We formulate the problem as that of choosing matrices and densities that minimize the Frobenius distance between the observed 3C matrix and the weighted sum of the estimated subpopulation matrices. Results on HeLa 5C and mouse and bacteria Hi-C data demonstrate the methods' effectiveness. We also show that domain boundaries from deconvolved matrices are often more enriched or depleted for regulatory chromatin markers when compared to boundaries from convolved matrices.

1. Introduction

The spatial organization of the genome as it is packed into the cell is closely linked to its function. Chromatin loops as well as locally clustered topological domains (Dixon et al., 2012) play a role in long-range transcriptional regulation (Gorkin et al., 2014; Ay et al., 2014) and the progression of cancer (Fudenberg et al., 2011). For instance, the impact of the long-range interacting gene clusters in the conformation of HOXA cluster is better understood in the context of the genome's three-dimensional relationships (Rousseau et al., 2014). Loci of mutations that affect expression of genomically far-away genes (eQTLs) are statistically significantly closer in 3D to their regulated genes than expected by a stringent null model (Duggal et al., 2014), indicating that 3D contacts play a widespread role in gene regulation. Measuring and modeling the three-dimensional shape of eukaryotic and prokaryotic genomes is thus essential to obtain a more complete understanding of how genomes function.

A class of recently introduced experimental techniques called chromosome conformation capture (3C) allows for the measurement of pairwise genomic contacts at much higher resolutions than FISH microscopy experiments (Dekker et al., 2013). These techniques cross-link spatially close fragments of the genome within a population of millions of cells and use high-throughput sequencing to determine which fragments were cross-linked together. Since the development of the original 3C method, a number of enhancements to the protocol, such as 3C, 4C, 5C, Hi-C, and TCC, have been introduced (Simonis et al., 2006; Lieberman-Aiden et al., 2009; Kalhor et al., 2012; Duan et al., 2010). Genome-wide interactions from Hi-C experiments, for example, can be analyzed at fragment lengths as low as 10 kb (Jin et al., 2013), though resolutions of 20–40 kb are more common. Here, for simplicity, we refer to all 3C-like techniques as 3C. All of these methods result in a matrix 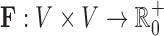where V = {1,2,…,n} is the set of genome fragments and where F_i,j is the number of times genome fragment i was observed in close proximity to fragment j within the assayed population of cells. Under the assumption that these contact events will be more common for spatially close pairs as shown in Tanizawa et al. (2010), the counts can be converted into spatial distances. The count matrix F or its associated distance matrix are then analyzed in the context of long-range gene regulation or used to produce three-dimensional models of the genome.

A challenge with 3C data is that it is collected over a population of cells. The genome structures within these cells vary since (1) they exist at different points in time within a particular phase of the cell cycle, (2) they may be associated with different methylation and therefore heterochromatin formations (Barski et al., 2007), and (3) chromatin itself can fluidly take on different 3D forms. Analysis of the combined matrix F therefore may be misleading.

We tackle the problem of extracting the genome contact map of each subpopulation of cells from the combined, ensemble matrix F. A subpopulation represents cells with similar interaction matrices and can model cells in distinct subphases in the cell cycle (e.g., early G1 vs. late G1), cells that are undergoing different gene expression programs, or cells that are in different stochastic structural states. We present a method to deconvolve the observed F into a collection of biologically plausible, unobserved subpopulation matrices Fⁱ such that

where λ_i are the relative abundances (densities) of cells in each subpopulation (class) i. This is the 3C deconvolution problem (3CDE), which we show to be NP-hard when λ_i is in .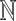

To solve this problem, we assume that the interaction matrix Fⁱ of each class is composed of nonoverlapping topological domains that are highly self-interacting consecutive genomic intervals. Such topological domains (TADs) have been widely observed and are a natural unit of genome structure (Dixon et al., 2012; Bickmore and van Steensel, 2013). We model these domains here using a particular type of quasi-clique, allowing for missing interactions within a densely interacting domain. The algorithm supports the use of prior knowledge of TAD structure as estimated from the ensemble matrix F or through other means that inform the choice of domains that appear in each Fⁱ. We explore two variants of our algorithm: one called 3CDEint, in which the class densities λ_i are required to be integers, and one called 3CDEfrac, in which they are not. The integer case is appropriate when the matrix F contains unnormalized counts, while the real-valued version is appropriate when F has been normalized to account for experiment bias (Yaffe and Tanay, 2011).

Both 3CDEint and 3CDEfrac solve 3CDE in an iterative two-step fashion that alternates between optimizing the matrices Fⁱ (Step 1 in sec. 2.3) and then optimizing the densities λ_i (Step 2 in sec. 2.4). We show that each step can be solved near optimally. These two steps use non-monotone supermodular optimization and SDP relaxations, respectively. For smaller problem instances, we develop optimal methods 3CDEint-opt and 3CDEfrac-opt based on quadratic integer programming that allow us to compare our approximate solutions of 3CDEint and 3CDEfrac to the true optimal solutions. In order to deconvolve very large matrices from high-resolution 3C datasets, we modify 3CDEint and 3CDEfrac to iterative three-step methods that optimize the matrices Fⁱ in two steps rather than a single step.

We show that our estimated deconvoluted matrices and topological domain structures are very similar to those derived from ground truth single cell data (Nagano et al., 2013) as well as domain structures, in particular, cell phases (Naumova et al., 2013). We also show that domain boundaries from deconvolved matrices are often more enriched or depleted for regulatory chromatin markers H3K4me3, H3K36me3, H3K9me3, and CTCF when compared to boundaries from convolved matrices. The deconvolved domain substructures we produce may therefore be more useful in analyses of long-range regulation with respect to chromatin structure, and our methods can be used as a way to simultaneously find domains while determining population substructures.

1.1. Related work

Most existing methods for finding domains within 3C matrices (Filippova et al., 2014; Weinreb and Raphael, 2015; Dixon et al., 2012) and for embedding 3C matrices in 3D space treat 3C interaction data as a single unit ignoring the fact that it is an ensemble over millions of cells. Although none of the existing methods explicitly solve the deconvolution problem, some (Rousseau et al., 2011; Hu et al., 2013; Kalhor et al., 2012; Filippova et al., 2014; Diament and Tuller, 2015) find multiple 3D embeddings or multiple domain decompositions. For example, Rousseau et al. (2011) develop an MCMC sampling technique MCMC5C, and Hu et al. (2013) develop BACHMIX that optimizes likelihood over a mixture model to find multiple embeddings. Neither of these methods considers the additive effects of interactions. Another method discussed in Kalhor et al. (2012) generates a population of structures by restricting the number of times each interaction is involved in a solution, which may mimic the deconvolution to a certain extent but ignores the domain structure of the genome. Recently, Junier et al. (2015) consider similar demultiplexing problems in which they decompose the ensemble matrix in terms of statistical interaction domains by matrix inversion. However, their domains may overlap so demultiplexing identifies simply the mixing ratios of them. Armatus (Filippova et al., 2014) finds multiple optimal and near-optimal domain decompositions at multiple scales by optimizing a density-like objective. None of these methods determine domain substructures or population densities of these substructures.

On the experimental side, two recent Hi-C modifications try to limit the effect of cell-to-cell variations. Nagano et al. (2013) carry out experiments on single cells that come at a higher experimental cost and produce lower-resolution interaction matrices. Another modification measures the interactions at a particular cell phase by arresting the population of cells at that phase by thymidine and nocodazole. However, these chemicals may disrupt the original genome structure (Naumova et al., 2013; Le et al., 2013). Since single cell 3C data (Nagano et al., 2013) is so recent, we provide the first comparison of deconvoluted structures to real single cell matrices.

1.2. The deconvolution problem (3CDE)

We want to estimate the interaction matrices Fⁱ of the subpopulations. Without additional constraints, deconvolution is under-constrained because an infinite number of matrices can explain the ensemble data equally well. However, we can exploit the fact that a 3C interaction matrix is (1) fairly dense around the diagonal due to the abundance of short-range interactions even being sparse overall, and (2) composed of topological domains that are highly self-interacting, nonoverlapping genomic intervals that are the building blocks of genomes (Dixon et al., 2012; Bickmore and van Steensel, 2013).

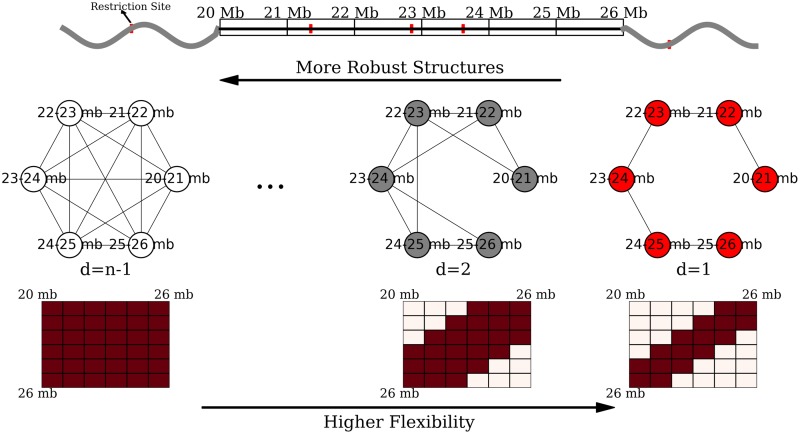
We encode these assumptions by modeling topological domains as bandwidth-quasi-cliques (BQCs) to allow domain structures to be locally dense while not requiring all interactions to exist. A d-BQC is defined by a genomic subrange [s_p, e_p] where there is an interaction between every pair of fragments that are separated by at most d fragments, resulting in a banded pattern of interactions. Figure 1 shows a BQC for a six-loci domain at 1 mb resolution. Let l_min and l_max be minimum and maximum possible domain sizes (l_min ≤ e_p − s_p + 1 ≤ l_max). There are e_p − s_p possible BQCs for a domain p covering the range [s_p, e_p], so total number of BQCs over all domains is 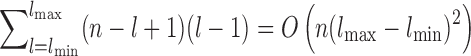, where n is the number of fragments. We know that TADs are megabase-sized structures so l_max = 100 is enough in most of the datasets.

FIG. 1.

The d-bandwidth-quasi-clique (d-BQC).

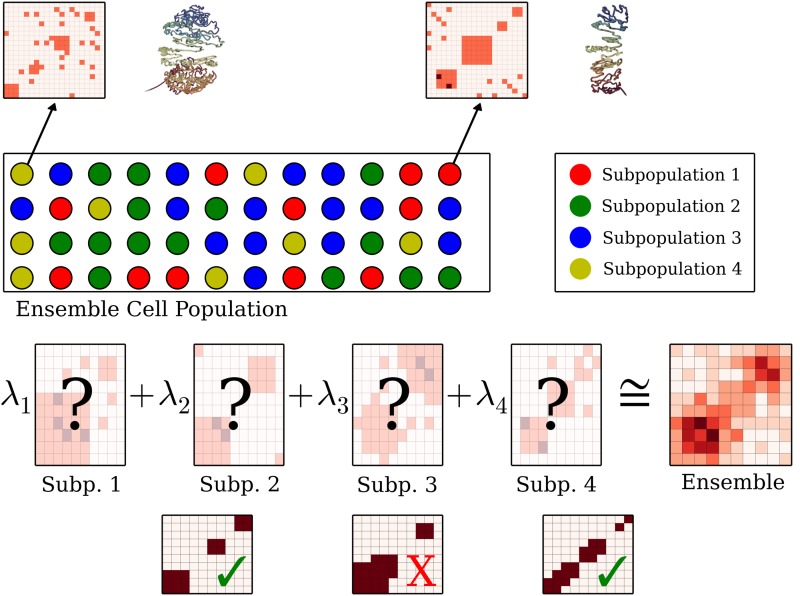
We assume that the observed ensemble matrix F is the sum of binary interaction matrices ({F¹,F²,…,F^k}), each multiplied by their densities (Λ = {λ₁,λ₂,…,λ_k}). We further assume that each Fⁱ is composed of nonoverlapping BQCs. Finally, we assume that the number of classes k is given or it can be easily estimated as each subpopulation is a meaningful distinct unit such as different phases of the cell cycle. Let I = {1,…,k} be the set of class labels. Figure 2 illustrates 3CDE, which is defined formally below:

FIG. 2.

Given the ensemble matrix, we infer the mixing matrices in terms of BQCs and the densities λ's without letting BQCs overlap in each subpopulation.

Problem 1 (3CDE). We are given an ensemble interaction matrix F, a number of classes k, and (optionally) a set of prior domains P_c. For each class i, we want to choose a set of nonoverlapping bandwidth-quasi-cliques and density λ_i such that the squared Frobenius norm of the difference between F and the weighted sum of the matrices Fⁱ derived from the chosen bandwidth-quasi-cliques is minimized.

2. Approximate 3C Deconvolution Methods

2.1. Mathematical formulation and hardness

We formulate the 3CDE problem using a three-part objective that (1) minimizes the squared Frobenius norm of the difference between observed convolved matrix and convolution of the deconvolved matrices, (2) maximizes the quality of domains defined by their BQCs, and (3) maximizes the overlap with a prior set of candidate domains P_c if available. Formally, given minimum and maximum domain sizes l_min and l_max, let P = {[s_p, e_p]∣s_p ∈1,…,n; e_p ∈s_p + l_min − 1,…,min(n, s_p + l_max − 1)} be the set of possible domains, and M : V → 2^P be a function that maps each 3C fragment to the set of domains to which it could belong:

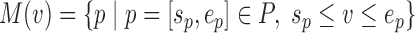Define G_q = (V_q, E_q) to be the BQC intersection graph where

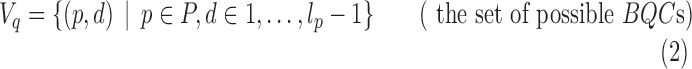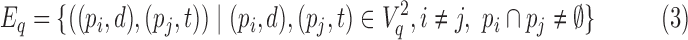A pair (p, d) represents a BQC by its domain and bandwidth d. Let l_p be the number of fragments in domain p. We can express 3CDE as:

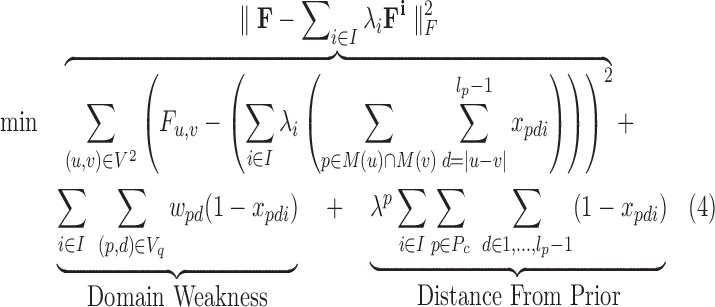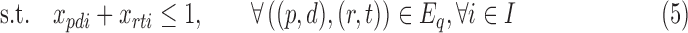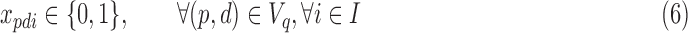where x_pdi = 1 if d-BQC of interval p is assigned to class i. Here, d ranges from |u – v| to l_p − 1 for each entry (u, v) since d-BQC of p correspond to matrix entries up to d away from the diagonal. Equation (5) ensures each Fⁱ is made up of nonoverlapping BQCs. We penalize for selecting less dense (weaker) BQCs where w_pd is the quality of d-BQC of p. We also reward larger overlaps with the prior candidate domains P_c from domain finders, such as Armatus, by minimizing the distance from the prior domains where λ^p is the weight of the prior.

3CDE has two variants depending on the class densities: (1) 3CDEint where λ_i are integers and (2) 3CDEfrac where λ_i can take any nonnegative values (useful for normalized F). 3CDEint is NP-complete as proven in Theorem 1, and 3CDEint can be solved exactly in pseudo-polynomial time by dynamic programming. However, this approach is impractical and prohibitively slow for large n, k, F_max = max{F_i,j}.

Theorem 1. 3CDEint is NP-complete.

2.2. Practical approximate methods

Due to hardness of 3CDE, we design the approximate methods 3CDEfrac and 3CDEint for integer and real-valued class densities respectively. Both methods are similar, so we explain 3CDEint in detail and discuss the differences between 3CDEfrac from 3CDEint in the last subsection. Let S = {0,1,…,F_max} be the set of integer subpopulation densities where F_max = max{F_{i, j}}, and we define y_is = 1 if subpopulation i's density is s. Program (4)–(6) can be expressed as constrained minimization of the biset function Q(X, Y) as in Program (7)–(11):

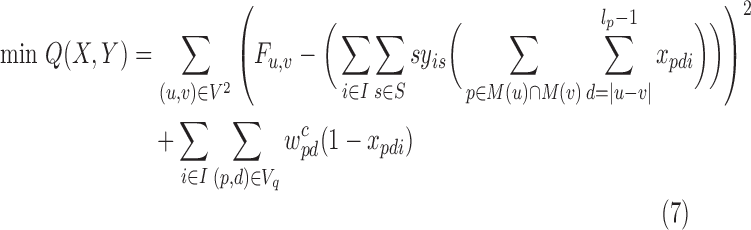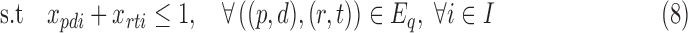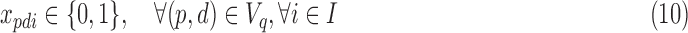where 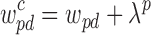is the combined domain prior and robustness weight, and y_is = 1 if class i has density s. The nonoverlapping BQC constraints (8) depend only on X, and (9) ensures a single density assignment for each class. We solve Program (7)–(11) iteratively in two steps starting with unit class densities. We describe these two steps with their approximation guarantees in detail below. Intuitively, the first step tries to find the best BQC assignments X given the class densities Y, while the second step tries to find the best Y given X. These steps are iterated until convergence.

2.3. Step 1: Non-monotone supermodular optimization for estimating mixing matrices

When the class densities Y are given, (9) disappears and the objective is slightly modified as in:

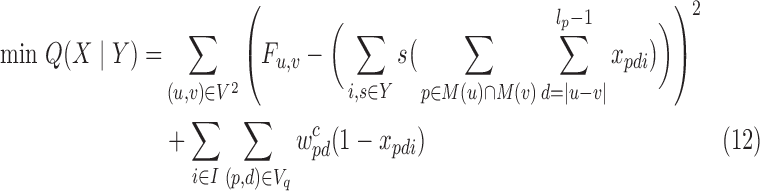This is minimum non-monotone supermodular independent set in the interval graph defined by the BQC intersection graph G_q since objective (12) is non-monotone supermodular. We solve its fractional relaxation optimally, round the fractional solution via (1,e⁻¹)-balanced contention resolution scheme by Feldman et al. (2011) 100 times and return the minimum solution. This scheme gives 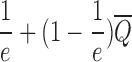approximation guarantee as in Lemma 1 where 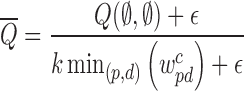for arbitrarily small constant ε > 0. This bound is also preserved up to an additive error for large matrices, for which weights can be estimated by sampling in order to speedup the optimization. Each rounding step is defined as follows: For each class i, we choose a BQC with probability 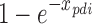to put into the solution R. After sampling, we mark the BQC represented by x_pdi for deletion if there is a different BQC in solution R that intersects the interval p. Assigning priority to earlier added BQC is important to prevent conflicts between BQCs. After removing all marked BQCs from R, we return independent set R as a solution.

Lemma 1. Step 1 can be approximated to a factor .

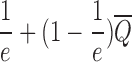2.4. Step 2: SDP relaxation of binary least squares for density assignment

Given BQC assignments X, (8) disappears and the resulting program is a binary quadratic program under the assignment constraints (9). However, the size of this program is linear in terms of F_max, which may be arbitrarily large. To efficiently estimate the class densities, we express the program more compactly by defining a variable for every s ∈S′ = {2^d∣d ∈ 0,1,…,⌊log(F_max)⌋}. This modification also removes (9) without losing any expressiveness since we can express any density up to F_max as a sum of subset of S′. The resulting problem is:

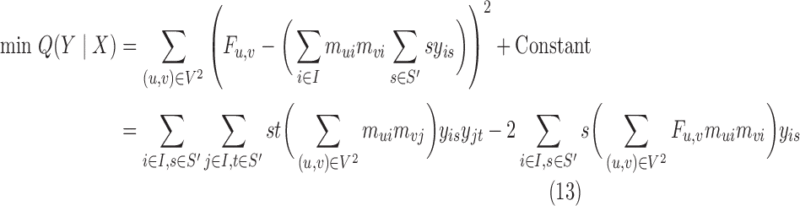where binary y_is = 1 if s is part of class i's density, m_ui is an indicator for whether u is assigned to a BQC in class i that is known from given X, and ∑ _s∈S′ sy_is is the density of class i. Optimizing (13) is NP-hard via reduction from PARTITION (Verdú, 1989). To solve it efficiently, we turn our {0, 1} quadratic program into a homogenous {±1} quadratic program by replacing every y_is with (1 + y′_is)/2 where y′_is ∈{±1}, and then by substituting y′_is = ry′′_is where r ∈{±1}, which turns the objective into homogenous matrix multiplication form. The resulting boolean program can be rewritten as:

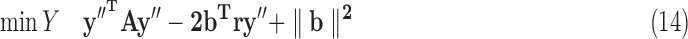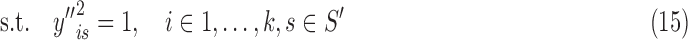where A is the matrix of quadratic coefficients in (13) modified by the transformation above, b is the modified vector of linear coefficients in (13), and y′′ is a k|S′| length vector. We relax this quadratically constrained quadratic program into the following semidefinite program (SDP):

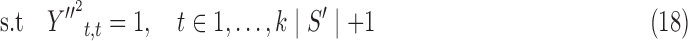where Y′′ = [y^T′′, r]^T[y′′, r] is a positive-semidefinite matrix, and 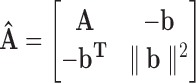. After solving this SDP optimally, we run the following rounding procedure based on Gaussian sampling (Luo et al., 2010): We generate a set of random vectors ξ_l, l ∈ 1,…,L = 100 from multivariate Gaussian distribution 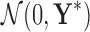, quantize each of them into a binary vector ŷ_l = sign(ξ_l) ∈ {±1}^k|S′|+1, and obtain a solution by 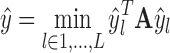. This procedure gives 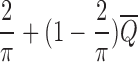approximation guarantee for Step 2 as proven in Lemma 2.

Lemma 2. Step 2 can be approximated to a factor .

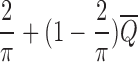2.5. The case of real-valued densities: 3CDEfrac

We modify only Step 2 of 3CDEint for nonnegative, real-valued class densities. Let y_i be the variable for class i's density; 3CDEfrac's second step optimally solves the following convex quadratic program:

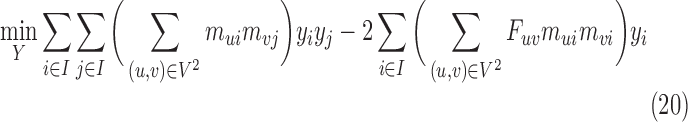3. Exact 3C Deconvolution Methods

For smaller problem instances, we develop optimal methods 3CDEint-opt and 3CDEfrac-opt based on convex quadratic integer programming (QIP). 3CDEint-opt can be expressed as in Program (22)–(27):

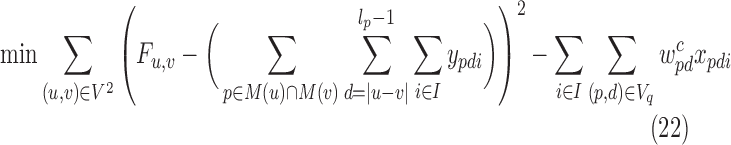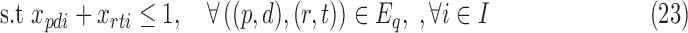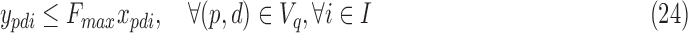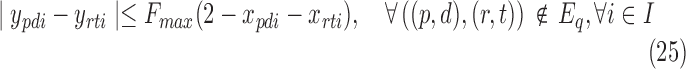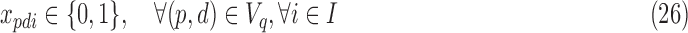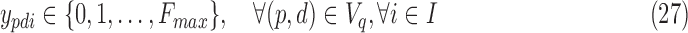where binary x_pdi = 1 if d-BQC of domain p is assigned to class i, and integer y_pdi is its density. Objective (22) is convex, and overlapping BQCs cannot coexist in the same class according to (23). In addition, (24) ensures that density of d-BQC of domain p in class i is 0 if not used in i, and if assigned, its density is at most F_max. Lastly, (25) ensures that all BQCs of the same class have the same density. When the class densities are real-valued, we propose 3CDEfrac-opt by relaxing the integer density constraints (27) in Program (22)–(27), which turns it into a convex mixed integer quadratic program (MIQP).

4. Results

4.1. Implementation

We implemented our methods using CPLEX (ILOG, Inc, 2006) to solve LP, ILP and convex quadratic programs, and SDPT3 (Tütüncü et al., 2003) to solve SDP relaxations. We use the public implementations of Armatus (Filippova et al., 2014) and MCMC5C (Rousseau et al., 2011) for comparison, and implemented the 3C normalization method by Yaffe and Tanay (2011). Codes, datasets, and proofs can be found online. The approximate methods are reasonably fast: 3CDEint and 3CDEfrac can deconvolve CD4⁺ interaction matrices in less than 30 minutes on a laptop with 2.5Ghz processor and 8Gb Ram when l_max = 25. They typically converge in fewer than five iterations. Our methods can also deconvolve larger 20–40 kbp resolution matrices in under 45 minutes by restricting l_max = 50 as TADs are typically less than a few megabases in length.

4.2. Evaluating performance

We evaluate deconvolution methods in the few cases where small, synchronized populations were assayed with 3C methods. Nagano et al. (2013) performed Hi-C on 10 single mouse cells, Naumova et al. (2013) performed Hi-C on several populations of HeLa cells, each synchronized to a specific phase of the cell cycle, and Le et al. (2013) performed Hi-C on populations of Caulobacter cells, also synchronized to various phases of the cell cycle. In each of these experiments, we have more-than-usual confidence that the assayed cells represent a single, unmixed population of structures. To simulate a more typical population of cells with mixture, we sum together the individual matrices from each of these experiments to obtain a synthetic ensemble matrix F that we then attempt to deconvolve into its constituent components (the matrices from the single cell or synchronized experiments).

We measure the agreement between our estimated subpopulation contact matrices and the true contact matrices (single cell or synchronized cell cycle) using two metrics: the normalized mean absolute error (MAE) and the normalized variation of information (NVI). Let T_p and E_p be the set of true and estimated domain partitions respectively, and T and E be the set of associated interaction matrices. To estimate either metric (MAE or VI), we perform a minimum-weight bipartite perfect matching between T and E where the edges are weighted by the value of the metric (VI or MAE), and the value of the agreement between T and E is the average value of the edges in minimum perfect matching. In the case of VI, this metric measures agreement between clusterings (here partitions of fragments into domains and nondomains). Since the true domain partitions are unknown, we use the consensus Armatus domains computed on each known subpopulation as the truth. In both measures, lower score means better performance.

We compare our methods with greedy baseline Armatus_Base and MCMC5C (Rousseau et al., 2011). In Armatus_Base, we add the domains from the top-k Armatus decompositions into a set. For each class, we shuffle the set and iterate through half of the set by assigning a domain from this set unless it intersects with the currently assigned domains. We repeat this procedure 10,000 times to estimate the distribution of the scores. Using domains from Armatus equips Armatus_Base with domains that appear in the convoluted data set, and it is therefore a more conservative comparison to our methods. We present the mean Armatus_Base score, and estimate P-values of our results from this distribution to test for the significance. We also estimate the matrices of k embeddings via inverse frequency-distance mapping in MCMC5C. When estimating the marker distribution, we define a domain boundary as a region extended to the left and right of the exact boundary by half of the resolution since this reflects the uncertainty in its position due to binning. Unless otherwise noted, we use an exponential kernel for BQC quality where quality decreases exponentially with decreasing bandwidth (≈ e^x) and assume no prior domain knowledge.

4.3. Deconvolution of single mouse CD4⁺ interaction matrices

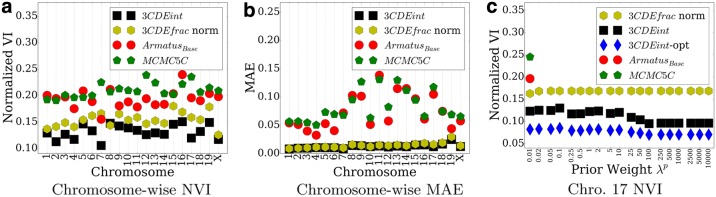
We apply our method and the baseline methods to the CD4⁺ interaction dataset at 250 kbp resolution by providing them with the sum of the matrices from the 10 experiments in which 3C contacts were estimated on single mouse CD4⁺ cells. We compare the estimated subpopulation matrices using this summed matrix as input to the original single cell matrices. Performance is shown in Figure 3a and b.

FIG. 3.

Chromosome-wise deconvolution performance of CD4⁺ dataset in terms of (a) normalized VI (b) mean absolute error (MAE). (c) Performance on the 17th chromosome for various prior weights λ^p.

3CDEint and 3CDEfrac nearly always perform the best in identifying contact matrices that match the single cell matrices. Even though Armatus_Base greedily assigns domains to the classes, mean Armatus_Base performs better than MCMC5C in Figure 3a for most of the chromosomes. 3CDEfrac over normalized data (Yaffe and Tanay, 2011) may perform worse than Armatus_Base because CD4⁺ data is an ensemble over only 10 cells rather than millions of cells as in traditional 3C experiments. We observe similar performance trend in terms of the metric MAE as in Figure 3b. Normalization does not decrease the performance as it did for normalized VI in Figure 3a. 3CDEint performs significantly better than Armatus_Base on all chromosomes (p < 0.05) in terms of both metrics. In general, lower matrix error scores show the quality of the deconvolution in estimating the mixing matrices.

We examine the performance of chromosome 17 as the domain prior weight λ is increased (Fig. 3c). The prior weight seems to have little effect on the overall performance, though 3CDEfrac over normalized data is more robust to different prior weights. Chromosome 17 is small enough that we can use 3CDEint-opt to find the true optimum of our objective (blue diamonds in Fig. 3c). This shows that our heuristics achieve close to the optimum value.

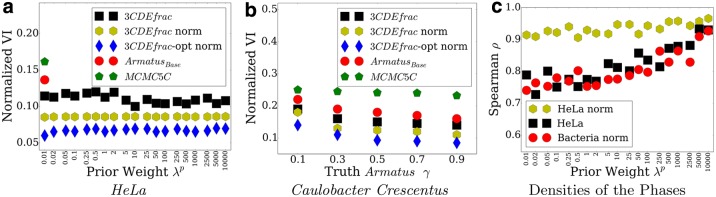
4.4. Temporal deconvolution of interphase populations in HeLa and Caulobacter cells

We deconvolve the sum of measured matrices of the 21st chromosome of HeLa cells at 250 kbp resolution using data from Naumova et al. (2013). Here, each subpopulation represents cells at a particular phase of the cell cycle, and so we are deconvolving along the temporal dimension. Figure 4a shows the performance for several choices of prior. Again, we match the true matrices better than either a greedy approach or sampling approach (MCMC5C). All the methods perform better in HeLa cells than CD4⁺ cells as shown in Figure 3c. Unlike in CD4⁺, normalization improves the deconvolution performance as well as making the performance of both approximate 3CDEfrac and exact 3CDEfrac-opt less dependent on the prior weight. This performance stability shows that we may obtain true domain decompositions without strong reliance on prior data. 3CDEfrac and 3CDEfrac-opt also outperform the competing methods in terms of average error per matrix entry: 3CDEfrac without a domain prior can achieve MAE of 0.004, whereas MCMC5C achieves almost eight-fold more MAE, 0.03.

FIG. 4.

(a) Deconvolution performance on HeLa dataset by increasing prior weight λ^p in terms of NVI. (b) Performance on prokaryotic bacteria dataset vs. Armatus γ in terms of NVI. (c) Performance of 3CDEfrac in estimating the densities of the cell cycle phases on eukaryotic HeLa and prokaryotic Caulobacter datasets in terms of Spearman's correlation ρ by increasing λ^p.

We performed a similar experiment for the bacterium Caulobacter where Le et al. (2013) provided cell-cycle-phase-specific Hi-C matrices. Figure 4b reports these results using the NVI metric as the resolution of the ground truth domains varied. While ground truth matrices are known in these experiments, the true domain decomposition is estimated computationally via a topological domain finder Armatus. This program has a parameter γ that controls the domain sizes, with larger γ corresponding to smaller domains. As γ increases, all methods perform better; however, the ranking of the methods in terms of performance is the same regardless of γ. We observe a similar performance trend on the HeLa dataset as well. This shows both that we can deconvolve bacterial Hi-C experiments and that the performance is robust to the scale at which we define the true domains.

Our methods also estimate the densities of the mixing cell cycle phases quite accurately on HeLa and Caulobacter if densities of the four cell cycle phases (early G1, mid G1, S, M) are assumed to be proportional to their durations. Figure 4c plots the Spearman's ρ correlation between estimated and true densities at 250 kbp for both datasets. We often achieve correlations over 0.75. Existing methods do not provide any estimate of the densities of the subpopulations.

4.5. Results on synthetic interaction data

To understand the practical hardness of the deconvolution problem under different types of class densities and wide range of domain sizes, we also tested our methods on synthetic data. There is no known domain generation procedure that mimics the true domain structure, so we generated the synthetic data as follows: For a given number of classes and matrix sizes in each class, we repeatedly flip an unbiased coin starting from the first bin to generate either domains of size sampled from gaussian distribution 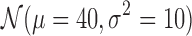or 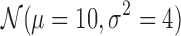, or inter-domain regions of size sampled from 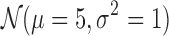until we reach the last bin. Similarly, we sample the class densities from 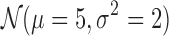by rounding them when the class densities are supposed to be integers. Lastly, we obtain the ensemble matrix by summing up the interaction matrices multiplied by their densities.

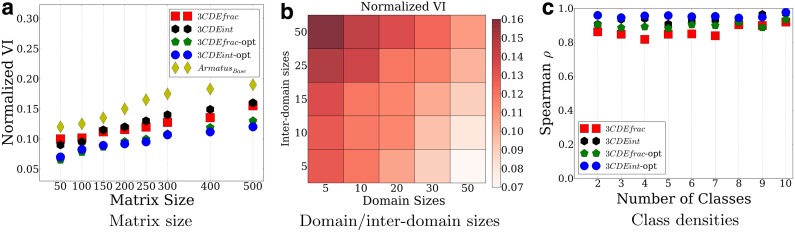
According to Figure 5a, increasing the matrix size by sampling the domain sizes from 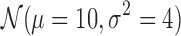and inter-domain sizes from 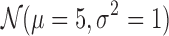decreases the performance similar to the effect of the increasing resolution on real datasets as in Figure 6a and b. Increasing the matrix size also increases the performance difference between our methods and Armatus_Base. The ratio of the domain sizes to inter-domain sizes is the major determinant of the performance as in Heatmap 5b for 3CDEint: Increasing the inter-domain sizes without increasing the domain sizes leads to poorer performance due to increasing numbers of possible optimal solutions. We also observe similar results for other methods. Lastly, our methods can also estimate the mixing class densities quite accurately in terms of Spearman's correlation ρ as in Figure 5c without being affected by the number of classes. Unlike the mixing matrices estimation, exact and approximate methods perform similarly in estimating the densities.

FIG. 5.

Performance of our methods on synthetic datasets versus (a) interaction matrix sizes, (b) domain and inter-domain sizes in terms of normalized VI; and (c) class densities estimation performance in terms of Spearman's correlation ρ.

FIG. 6.

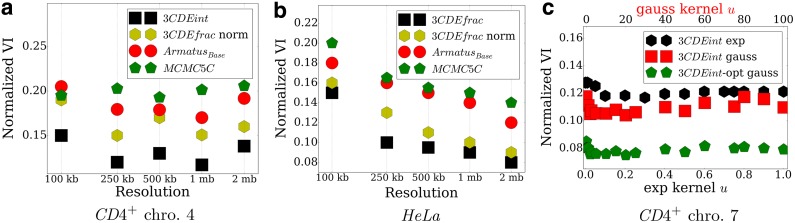
Effect of 3C resolution on the performance in (a) 4th CD4⁺ chromosome, (b) HeLa cells, and the effect of weighting kernel of the robustness prior in (c) CD4⁺ chromosome 7.

4.6. Effect of resolution and robustness prior

The deconvolution methods developed here work well at various 3C resolutions. When we binned the input 3C matrices at decreasing intervals, increasing the resolution leads to larger, more detailed interaction matrices, which usually decreases performance somewhat (Fig. 6a and b). The performance decreases monotonically on the HeLa dataset by increasing resolution, but the score trend is non-monotonic in CD4⁺ cells due to its smaller population size with more influential outliers. However, the 3CDEfrac and 3CDEint methods still outperform the other methods. This is likely due in part to the definition of BQCs, which can properly model long-range, out-of-domain interactions in the higher resolution matrices. The choice of the kernel for the robustness prior also seems to have relatively little effect on performance as shown in Figure 6c or the 7th CD4⁺ chromosome. We obtain similar results for the 21st HeLa chromosome.

4.7 Distribution of epigenetic markers relative to deconvolved domains

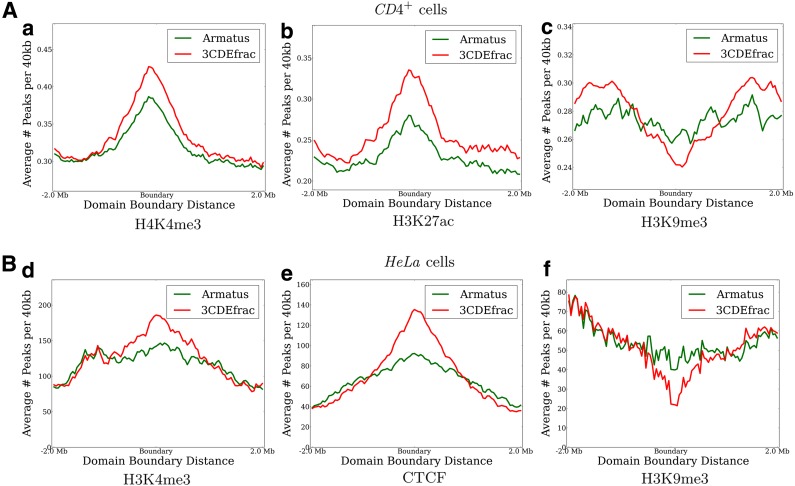
Epigenetic markers are distributed differently in the genome depending on its local conformation, and domain organization of the genome is correlated to a certain extent with their distribution. For instance, H3K4me3 and CTCF binding sites are enriched in the domain boundaries due to their insulator roles. We calculate the distribution of several such markers near the domain boundaries as identified within the subpopulation matrices (Fig. 7). Each subfigure in Figure 7 plots the average number of markers in 40 kb bins for +/−2 Mb from all the estimated domain boundaries that occur within some estimated subpopulation matrix. For the Armatus domain, we estimate the average number of markers over top-k decompositions for multiple γ between 0.1 and 0.9 (k = 4 for HeLa, and k = 10 for CD4⁺). We obtain histone markers from ChIP-Seq experiments (Shen et al., 2012; Deaton et al., 2011) for CD4⁺ cells, from Barski et al. (2007) for HeLa cells, and add CTCF sites from CTCFBSDB (Ziebarth et al., 2013).

FIG. 7.

Distribution of several markers around the domain boundaries in (A) CD4⁺ and (B) HeLa cells. Red and green lines represent 3CDEfrac and Armatus respectively in all plots.

Overall, the relationship between histone markers and our domain boundaries are consistent with the experimentally characterized different roles of the epigenetic markers (Barski et al., 2007; Sefer and Kingsford, 2015). Barrier-like histones H3K4me3, H3K27ac, and CTCF are more enriched in the deconvolved domain boundaries than Armatus boundaries in both species, whereas non-promoter-associated represssor H3K9me3 is more depleted in the deconvolved domain boundaries. This greater enrichment and depletion of the appropriate histone markers near the deconvolved domain boundaries, in accordance with the experimental results, shows the improvement in extracting biologically plausible domains from the ensemble data achieved by deconvolution.

To better interpret these scores, we estimate the significance of these coverage scores with respect to the random positioning of the same domains in terms of both enrichment and depletion by shuffling the domains 10,000 times and keeping the markers fixed. We estimate the resulting p-value by combining the multiple p-values from different CD4⁺ chromosomes by Fisher's method. Consistent with the previous results, H3K4me3, H3K27ac, and CTCF with insulator roles are significantly enriched in the domain boundaries, whereas non-promoter-associated trimethylations H3K9me3 and H3K27me3 are depleted in the boundaries. Enrichments in CD4⁺ cells do not mainly depend on whether we use the prior domain data, but the prior Armatus domains make the enrichment differences more pronounced in HeLa cells since CD4⁺ results are average over all chromosomes representing the whole genome, whereas the HeLa data is composed of a single chromosome. We may use our methods as alternative domain finders returning multiple domain decompositions in the ensemble as suggested by the significance of the above results.

5. Conclusion

We formulate the novel 3C deconvolution problem to estimate classes of contact matrices and their densities in the ensemble chromatin interaction data. We prove its hardness and design optimal and near-optimal methods that are practical on real data. Experimental results on mouse, HeLa, and bacterial datasets demonstrate that our methods outperform related methods in unmixing convoluted interaction matrices of prokaryotes and eukaryotes as well as in estimating the mixing densities without any biological prior. Our methods solve the previously unsolved problem of 3C experiments efficiently, and they return biologically meaningful domains supporting their alternative use as domain finders.

Acknowledgments

This research is funded in part by the Gordon and Betty Moore Foundations Data-Driven Discovery Initiative through Grant GBMF4554 to Carl Kingsford. It is partially funded by the U.S. National Science Foundation (CCF-1256087, CCF-1319998) and the U.S. National Institutes of Health (R21HG006913, R01HG007104). C.K. received support as an Alfred P. Sloan Research Fellow. A preliminary version of this article appeared in RECOMB 2015 (Sefer et al., 2015).

Author Disclosure Statement

The authors declare that no competing financial interests exist.