Linking ice accretion and crown structure: towards a model of the effect of freezing rain on tree canopies

Abstract

Background and Aims Despite a longstanding interest in variation in tree species vulnerability to ice storm damage, quantitative analyses of the influence of crown structure on within-crown variation in ice accretion are rare. In particular, the effect of prior interception by higher branches on lower branch accumulation remains unstudied. The aim of this study was to test the hypothesis that intra-crown ice accretion can be predicted by a measure of the degree of sheltering by neighbouring branches.

Methods Freezing rain was artificially applied to Acer platanoides L., and in situ branch-ice thickness was measured directly and from LiDAR point clouds. Two models of freezing rain interception were developed: ‘IceCube’, which uses point clouds to relate ice accretion to a voxel-based index (sheltering factor; SF) of the sheltering effect of branch elements above a measurement point; and ‘IceTree’, a simulation model for in silico evaluation of the interception pattern of freezing rain in virtual tree crowns.

Key Results Intra-crown radial ice accretion varied strongly, declining from the tips to the bases of branches and from the top to the base of the crown. SF for branches varied strongly within the crown, and differences among branches were consistent for a range of model parameters. Intra-crown variation in ice accretion on branches was related to SF (R² = 0·46), with in silico results from IceTree supporting empirical relationships from IceCube.

Conclusions Empirical results and simulations confirmed a key role for crown architecture in determining intra-crown patterns of ice accretion. As suspected, the concentration of freezing rain droplets is attenuated by passage through the upper crown, and thus higher branches accumulate more ice than lower branches. This is the first step in developing a model that can provide a quantitative basis for investigating intra-crown and inter-specific variation in freezing rain damage.

INTRODUCTION

Ice storms are important disturbance events that strongly impact eastern North American forests (Irland, 2000). Developing when warm, moist (tropical) air passes over a colder ground-level air mass (Lemon, 1961), raindrops cool as they pass through the colder air below and turn to ice as they strike branches that are at or below freezing. When ice loads surpass the mechanical strength of branches, the resulting damage to trees may strongly influence forest dynamics, and leads to large losses in wood production (Lemon, 1961; Proulx and Greene, 2001; Greene et al., 2007). Furthermore, the frequency and severity of ice storms may increase in the future as conditions favouring freezing rain, such as warmer winter temperatures, become more common due to climate change (Cheng et al., 2007; Costes et al., 2008).

In early qualitative studies, crown damage or mortality from ice accumulation was merely descriptive (Harshberger, 1904; Illick, 1916; Deuber, 1940). In subsequent studies, assessments of tree-level damage to an event were used as a basis for developing ordinal schemes for damage classes by species or tree size (Croxton, 1939; Siccama et al., 1976; Whitney and Johnson, 1984; Nicholas and Zedaker, 1989; Seischab et al., 1993; Rebertus et al., 1997; Warrillow and Mou, 1999). In general, studies that applied more quantitative approaches such as examining the number of fallen branches (Melancon and Lechowicz, 1987) or the volume of woody litter have been rare (Bruederle and Stearns, 1985; Proulx and Greene, 2001; Rustad and Campbell, 2012). Often, investigators have measured fallen branches on the ground rather than the causative ice loading simply because the ice quickly melts, well before the investigator arrives at a stand, as the warm front passes through the area (e.g. Proulx and Greene 2001; but see Ackley and Itagaki, 1970).

In one approach, percentage canopy damage was related to reported spatial variation in radial ice accretion from a broad network of horizontal cylinders (Proulx and Greene, 2001). However, extrapolating this measure to ice accretion on branch elements arranged in a tree crown assumes equivalent radial ice accretion along branches and at all positions within a crown (Proulx and Greene, 2001; Greene et al., 2007). Similarly, related research on natural snow loading on branches has also ignored along-branch variation (Cannell and Morgan, 1989) or vertical variation within a crown (Makkonen, 2000).

In a recent paper, an experimental approach to studying the effects of freezing rain was tested (Rustad and Campbell, 2012). Trees in two plots in a hardwood forest were treated by artificially applying freezing rain, resulting in 7–12 mm radial ice thickness. However, efforts were focused on measurements that could be made from the ground: litter fall and changes in canopy openness (Rustad and Campbell, 2012). Greene et al. (2007) called for an experimental approach to determine how ice accretes on branches, i.e. is the radial thickness independent of diameter, so that loading of branches and their biomechanical limits could be estimated (Greene et al., 2007). Recently, by experimentally applying freezing rain and capturing the resulting crown structure and ice distribution on branches using terrestrial LiDAR scanning (TLS), substantial intra-crown variation was revealed (Nock et al., 2013c). Understanding the drivers of such variation is important for understanding variation in the damage both within a crown and, in turn, among neighbouring trees of different species or sizes.

Makkonen (2000) speculated that variation in ice loading by position within a crown would occur, with lower branches presumably receiving less accretion due to interception by branches above. That is, the probability of a raindrop being intercepted by a canopy element can be expected to increase vertically with the cumulative sum of branch area index (m² m^–2, analogous to leaf area index). This conceptual model of ice accretion, or attenuation, by tree crowns resembles the Beer–Lambert law (i.e. a negative exponential relationship), which is frequently applied in forests to describe the attenuation of light through the canopy (Sampson and Smith, 1993; Brown and Parker, 1994; Lieffers et al., 1999).

Ideally, point cloud representations of branch or crown structure from TLS measurements could be converted into a geometric model that accurately describes the attributes of the measured tree (Nock et al., 2013b; Delagrange et al., 2014). However, for large trees that have complex structure, this modelling process requires supervision or assistance and is therefore often time consuming (Delagrange et al., 2014). In addition, without a quality reconstruction it may be difficult to capture variables such as branch diameters or ice diameter on branches accurately. An alternative approach for extracting structural information from point clouds, but which does not require a supervised geometrical modelling process, is based on converting point clouds to a collection of voxels. Voxels (the term derived by combining volume and pixel) represent a value on a grid in 3-D space. Methods for the analysis of vegetation structure based on voxels have received increasing attention in recent years (Durrieu et al., 2008; Côté et al., 2009; Hosoi and Omasa, 2009; Van der Zande et al., 2010; Béland et al., 2014).

To test our hypothesis that variation in ice accretion on branches at different positions in a tree crown can be predicted by an index analogous to the amount of branch area index in a superior position (z) above a given point, we developed two novel complementary modelling tools for the study of freezing rain accretion in tree crowns. The first model, IceCube, is empirically derived and relates discrete in situ branch ice radius measurements to the superior crown structure using voxels. The second, IceTree, is derived from a light simulator developed for functional–structural plant modelling (Dauzat et al., 2001, 2008), and is used to validate our findings for the influence of crown structure on ice accumulation variation from IceCube on simulated trees in silico and provide a foundation for future investigations on the vulnerability of trees to freezing rain in relation to their architecture.

MATERIALS AND METHODS

Experimental simulation of freezing rain

We conducted the experimental icing in the city of Montreal, Quebec, on 22 February 2011. Weather conditions were deemed to be suitable for the experiment when the wind speed was low, because strong winds would influence patterns of ice accretion both vertically and horizontally. On the day of the experiment, there was a gentle breeze (average wind speed 3–5 m s^–1) and daytime temperature ranged from a low of –15 °C to a high of –6 °C.

For this experiment, we utilized the European tree species Acer platanoides L. because it is the most common urban tree in eastern North America (Nock et al., 2013a). Tree age was determined from ring counts to be 43 years, diameter at breast height was 35 cm, height was about 9 m and the crown diameter was approx. 5 m. The tree grew on a flat site with wide spacing (approx. 6 m) between neighbouring trees and, due to the lack of competition for light, the lower crown was much more fully developed than for a forest tree.

Water from a hydrant approx. 30 m away was pumped to the site via a fire hose, where a reducer fitting was used to connect it to plastic polyvinyl piping and then to an oscillating sprinkler perched atop a scaffolding tower above the tree. Estimated water output of the sprinkler was 17 L min^–1 which, given the area covered (approx. 160 m²), converts to 6·15 mm h^–1. The experimental irrigation began at 0930 h with a single sprinkler. From approx. 1200 h to 1600 h, a second sprinkler was added, thus the estimated precipitation rate for during the afternoon is estimated to be as large as about 12 mm h^–1, although the degree of overlap of the spray of the two sprinklers could not be accurately quantified.

Measurement of crown structure, branches and variation in accreted ice

The studied tree was scanned both prior to icing and throughout the experiment using a Z+F terrestrial laser scanner (Z+F 5006h, Z+F USA Inc., Bridgeville, USA) from three positions separated by approx. 120°, each at a distance comprised between 12 and 17 m. Point clouds were acquired with settings allowing a beam size of 5 mm at 10 m and a distance of 0·34 mm between points at 10 m (Nock et al., 2013c). We used the high resolution setting, which required approx. 3 min per scan.

In the laboratory, scans acquired from the three positions for each of the scanning intervals (pre- and post-icing) were registered in the Z+F software using stationary targets (Z+F LaserControl, Z+F USA Inc.). In some cases, targets were obscured due to safety fencing and so additional fixed points (e.g. on the scaffolding towers flanking the tree) were used for scan registration in the software Pointstream (Arius3d Corp, Mississauga, Canada). Registration quality was assessed from the alignment of immovable objects in the scans such as the scaffolding, slices of large diameter branches and the main stem.

Measurements of branch diameter prior to icing and during icing were obtained from PypeTree, an open source Python and VTK-based software tool for the reconstruction and modelling of 3-D tree architecture from point cloud data (Delagrange et al., 2014). Based on the PypeTree model for a given branch, measurement markers (i.e. spheres with a position and radius) were automatically generated at generally evenly spaced intervals (approx. 30 cm, an interval originally selected to match field-based validation data). Marker radius was subsequently adjusted if a deviation from the boundary of the branch point cloud was readily apparent (Nock et al., 2013c). In this way, ‘virtual’ radial ice thickness measurements were collected after validation with field-based validation data (Nock et al., 2013c). Equivalent radial ice thickness (determined by measuring the volume of melted ice from branch samples of known diameter and length) did not significantly differ from caliper-based measurements of radial ice thickness (the average of two measurements separated by 90°) because the shape of accreted ice on branches was generally cylindrical; incipient icicles occurred but were rare (Nock et al., 2013c).

Modelling ice accretion

Two complementary modelling approaches were developed. The first one, IceCube, takes the point clouds generated by TLS as input data but without 3-D tree structure reconstruction. IceCube allows the effects of experimental icing in the field for individual trees or for whole stands to be studied and interpreted. An advantage is that realism is high, but since experimental icing is difficult, the potential to repeat the experiment in order to examine factors of interest is constrained (species, architecture).

The second modelling effort, IceTree, is a ‘structural’ approach, which utilizes virtual trees with fully quantifiable tree structure. While simulated trees may differ from actual trees, development of a model which captures the essential processes of ice accretion opens up the possibility to analyse the architectural features involved in tree vulnerability to freezing rain without needing to conduct challenging field studies involving experimental freezing rain.

Assumptions common to both models include: (1) the rain interception by a branch segment is proportional to its projected area perpendicularly to the rain direction; (2) several rain directions can be accounted for during freezing rain episodes; (3) there is no loss of intercepted rain by splashing, stem flow or dripping; and (iv) the ice accumulation is evenly layered all around any stem or branch segment.

To relate either the field-based measurements of ice accretion or the simulated ice accretion to output from the IceCube model or from the IceTree model, respectively, we fit an exponential extinction model similar to the Beer–Lambert’s law (Nilson, 1971; Ross, 2012):

$$I_x{}_{,y,z}=I_0\times {\text{e}}^{–\text{SF}\left(x,y,z\right)\times a}$$

where I₀ is the rainfall in mm of water (integrated over the rain storm duration), I_x,y,z is the rainfall at a given location inside the canopy, SF (x,y,z) is the average number of non-empty voxels above the given location, and a is an attenuation coefficient analogous to the extinction coefficient K of the Beer–Lambert law for light. Both I₀ and a were calibrated on the data by least square optimization (optimization procedure using the Nelder–Mead’s method on R 3.1.2).

IceCube: a voxel-based description of freezing rain attenuation by canopies

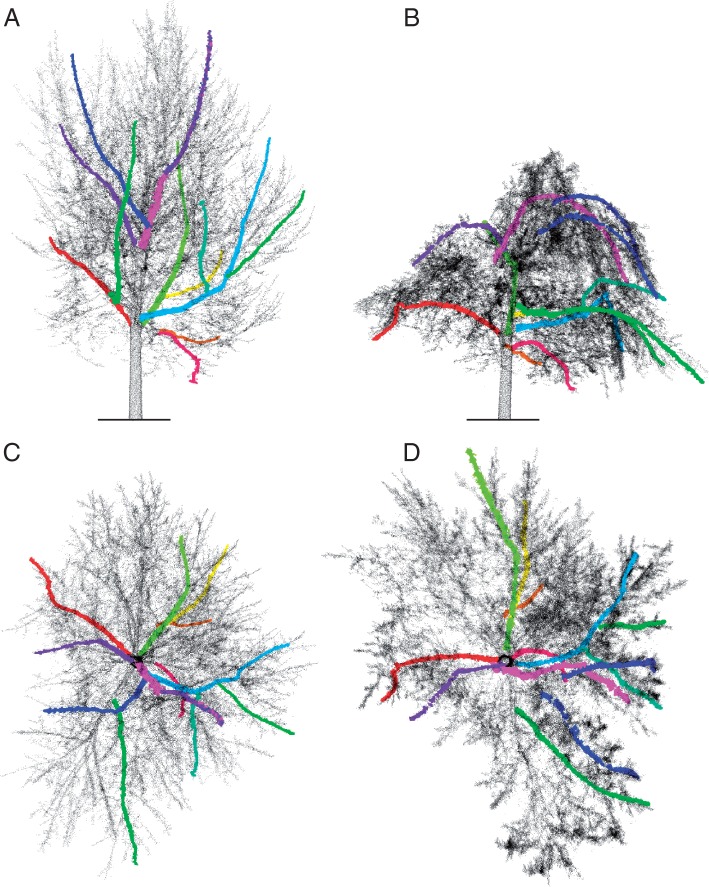
To test our hypothesis that variation in ice accretion on branches at different positions in a tree crown can be predicted by an index analogous to the branch area index above a given point, IceCube takes as input: a point cloud for the entire sample tree (tree point cloud; Fig. 1), and one or a set of point clouds for ‘target’ objects (here each individual branch; Fig. 1).

Fig. 1.

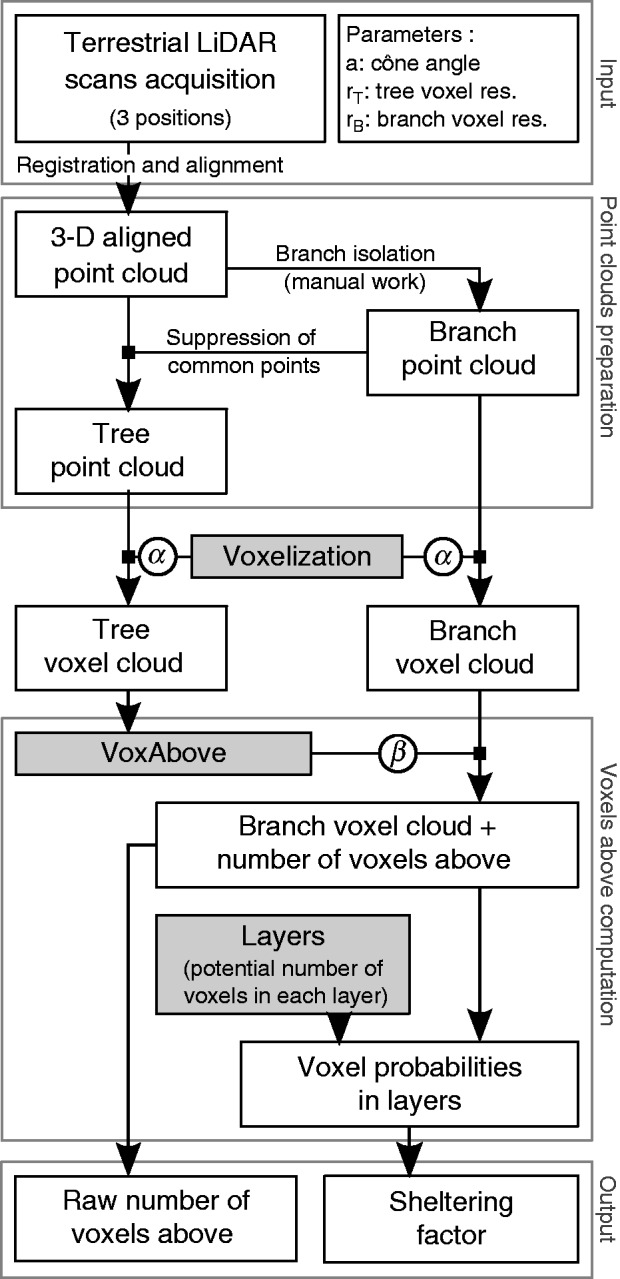
Conceptual diagram of the complete method of analysis of ice accretion from TLS point clouds to modelling in IceCube. White boxes correspond to different data sets, grey boxes to algorithmic procedures and circles to the parameters used for algorithmic procedures. Square arrows indicate a transformation applied to a data set.

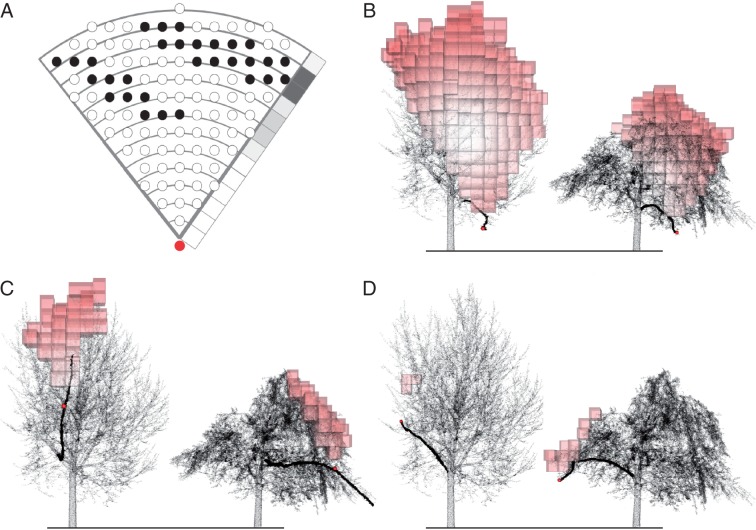
Assuming for simplicity that rain falls primarily from the zenith, IceCube basically sums for a point on a target branch the number of voxels of the sample tree that are found within an inverted cone above the point (Fig. 2). As voxels can be viewed as a portion of space explored by the tree, the voxel cloud, and, subsequently, the voxels located within the inverted cone are assumed to be representatives of non-empty portions of the 3-D space above the target point. Consequently voxels are portions of the 3-D space that variably attenuate precipitation.

Fig. 3.

Distribution of branches throughout the crown viewed from the side (A, B), and above (C, D). Branches were sampled from the beginning of the experiment prior to freezing rain exposure (A, C), and after several hours of icing (B, D).

Fig. 2.

(A) Schematic illustration of a sheltering factor (SF), developed to quantify the influence of crown structure on ice accretion from TLS point clouds. SF is calculated as the sum of filled voxels (black dots) above a measurement point (within a user-defined cone). Thus, higher SF values correspond to a higher chance of a raindrop being intercepted before reaching the measurement point (grey-scale showing layers with many branch voxels). (B–D) Three-dimensional visualizations of the voxels (red cubes) influencing SF for different target branches at an early stage (left) and at a late stage (right) during icing. All examples are given with α equal to 40 cm and β equal to 30°.

The Beer–Lambert law assumes (1) a one-dimensional variable (i.e. the distance that droplets must travel trough the tree structure) and (2) the homogeneity of the resistance along the fall. The absolute number of voxels (i.e. the number of voxels present within the inverted cone) located above a target point was then transformed into a ‘sheltering factor’ (hereafter SF) according to the following assumptions: first, that water droplets trajectories are all equivalent in terms of intensity; and, secondly, that branches (i.e. voxels) closer to the target point have a stronger occluding effect than those farther away. This normalization was done using a probabilistic approach that aims to quantify the proportion of resistant space (i.e. non-empty voxels) in discrete layers based on voxel distance from the target point (layer thickness was set equal to voxel size, Fig. 2A):

$$SF=\sum _{l=1}^n\left(\frac{V_l}{N_l}\right)$$ (1)

where V is the number of non-empty voxels in the l layer and N is the total number of voxels (N = non-empty + empty voxels) in a layer. SF is thus the average number of voxels that water droplets must pass through before they reach the target point and can be easily transformed into distance by multiplying SF by α. Thus, SF increases with the number of voxels above a target branch and also with increasing proximity of voxels to the target.

Because the choice of voxel size (cm) should be based on the distribution of branch diameters, it is defined by the user (parameter α). Furthermore, the angle of the inverted cone in degrees (parameter β) is also user-defined in order to take into account the fact that water droplets may have slightly varying trajectories even with very low turbulence. We tested iteratively all combinations of α (ranging from 5 to 40 cm) and β (ranging from 10 to 40°) and conserved the combination offering the best predictions. Generally α had little effect on the change in SF with increasing distance from the branch tip (Supplementary Data Fig. S1). Similarly, differences among branches were consistent across β values ranging from 20 to 40° (Supplementary Data, Fig. S1).

The SF and manual ice radius measurements were paired based on their respective distance from the branch tip: for each manual ice radius measurement, the nearest calculated SF value was attributed using a dedicated function. The function to compute SF is available in the R-package VoxR which was created for the analysis of TLS point clouds (Lecigne et al., 2014).

A significant problem in modelling freezing rain accretion is that branches deflect downward under the increasing load of the ice, especially in the top of the crown. Thus, crown structure is expected to vary with ice accretion and with time. Here we describe our first attempt to address this challenge and capture this complex process. Assuming that the pattern of ice accretion is driven by crown structure, which in turn can be described using voxels, the ice radius at the end of the icing period is probably the aggregated effect of the continual changes in structure. We assume one can approximate the continual change from ‘mixing’ crown structures at discrete time points. Specifically, given the data for crown structure as well as measured ice accretion for discrete times 0 (ice free; t₀) and time 1 (t₁; here defined as 6·5 h of freezing rain, approx. 30 mm of ice on upper branches) we related SF and measured ice in the following combinations: SF_t0 vs. ice_t1, SF_t1 vs. ice_t1, as well as a weighted combination of crown structure at two time points [x × SF_t0 + (1 – x) × SF_t1] vs. ice_t1, where the subscript t₀ or t₁ indicates the time during the experiment and x ranged from 0 to 1 (Supplementary Data Fig. S2).

A simulation model for predicting freezing rain attenuation by canopies

The IceTree model is a novel approach to studying canopy–precipitation interaction, which is capable of tracking the attenuation of freezing rain passing through 3-D virtual plant canopies. The core of IceTree is adapted from previous work on modelling canopy–light interactions and is based on the calculation of Z-buffer images of 3-D stands from discrete directions (Dauzat et al., 2008; Griffon and de Coligny, 2014). The interception of incident light from a given point of view is obtained straightforwardly by analysing the visible (i.e. intercepting) parts of plant components that are visible from this given point of view. Consequently the quantity of direct radiation intercepted by each component of a tree crown can be evaluated by counting its number of pixels on the image (and applying a weighting factor corresponding to the energy associated with one pixel for the direction of incident light). The same principle is used here for simulating the interception of droplets falling from one or several directions.

The Z-buffering technique was implemented in software in the present study because it allows specific treatments such as a virtual duplication of plants for simulating an infinite canopy without border effects, as well as integration with the AMAPstudio software suite dedicated to plant architecture modelling (Griffon and de Coligny, 2014).

The IceTree model makes full use of the AMAPstudio suite and its multiscale representations of plants including their topological structure (that defines how plant components are connected together through a tree graph), their geometry (dimensions and orientation of plant components) and various attributes associated with plant components at different scales. These features are essential for integrating the results of simulation (quantity of intercepted rain) from the scale of elementary plant components (e.g. internodes) to the scale of small and larger branches (corresponding to different branching order). By doing so, one can assess the load of ice throughout the tree crown and ultimately evaluate the risks of branch breakage. Finally, the XPlo application of AMAPstudio was used for extracting and analysing the ice accretion according to the size, orientation and topological position of branch elements within the crown. Thus, the ice load can be easily calculated at any location in the stem and branches with XPlo.

The following model assumptions were made: (1) the trajectory of a droplet is a straight line, an assumption which could be modified for varying directions to account for the variability of droplet direction due to wind shifts; (2) the size of droplets is not accounted for (droplets are assumed to be infinitesimally small); and (3) there is no loss of intercepted rain by splashing, stem flow or dripping from branches.

AmapSim was used to produce a virtual tree with architecture (Barczi et al., 2008) resembling a vigorous 20-year-old fir tree (Abies). The simulated freezing rain corresponds to a total of 35 mm of rain falling primarily from the zenith (50 %), but which also varied slightly (Supplementary Data Table S1). The output of IceTree is the radial ice accretion (in mm, but not accounting for the greater density of ice than water) on each of the 40 454 internodes of the virtual tree.

Having performed the following two analyses: (1) an empirical analysis of the experimental tree using IceCube, and (2) a simulation experiment using a virtual tree in IceTree, we also link the IceCube and IceTree analyses using a third analysis, by (3) performing a simulation of voxel occupancy on the virtual tree.

To this aim, we selected 3-D co-ordinates of branch elements (internodes) and generated a point cloud. The resulting resolution of about 1 cm was comparable with TLS acquisitions. Parameter β was set to 10° in IceCube for consistency with selected rain angles in IceTree. The same Beer–Lambert model was used for fitting the simulated ice radius with the SF output at the internode scale.

RESULTS

Within-crown variation in SF values

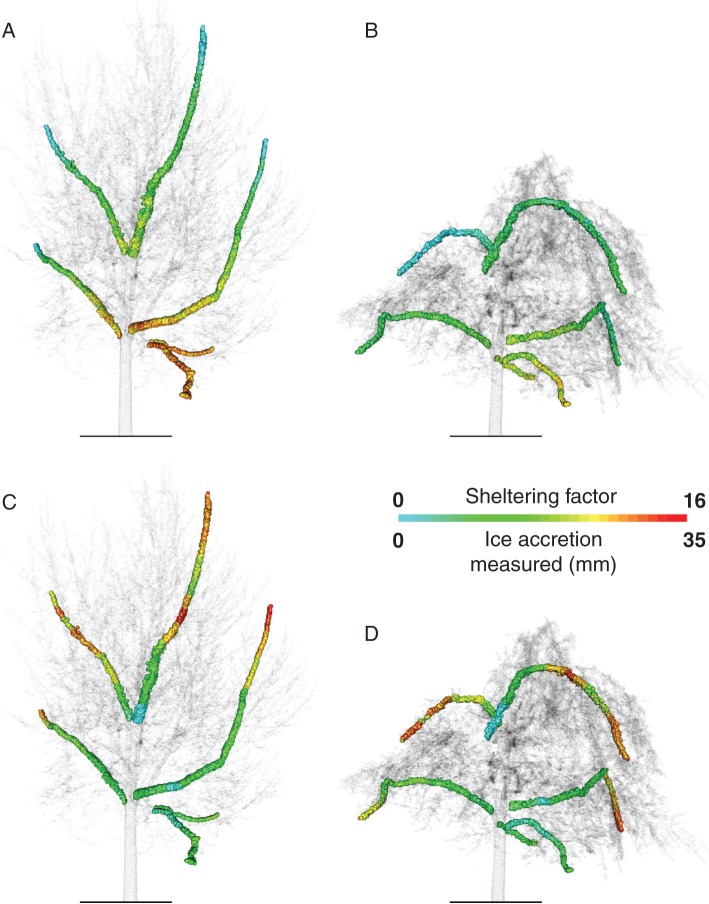
As hypothesized, values for SF varied with woody material height and central vs. external position within the tree crown. For example, small plagiotropic branches located in the lower part of the crown had much greater values than branches in the upper portion of the crown (Fig. 4). Further, as hypothesized, SF increased with distance from the terminal tips of branches toward the interior of the crown (Fig. 4A). This pattern was clearest prior to any changes in the crown structure due to ice accretion (Fig. 4A vs. B), with branches exhibiting a general trend of increasing SF towards the bases of branches from the tips (cool to warm colours; Fig. 4A).

Fig. 4.

Target branches (see Fig. 4) showing covariation between the modelled sheltering factor (SF; A, B) and ice accretion (C, D). Target branches are shown for both an early stage (left) and at a late stage of icing (right).

Relationship between SF index and ice accretion from the field experiment

Comparing SF with ice accretion qualitatively, one can see an inverse relationship, with low values for SF associated with high values for ice accretion (Fig. 4).

Measured ice accretion for the branches sampled was strongly related to SF (Fig. 5). As expected, the strongest relationship (R² = 0·46) was found for the combination of the measured ice radius at time 1 predicted by the combination (0·3 × t₀, 0·7 × t₁) of normalized voxels calculated at t₀ and t₁ (Fig. 5B), although this was not very different from the combination of measured ice radius at t₁ and the SF at t₁. Further, small differences in the weighting produced similar values for the R² of the relationship (Supplementary Data Fig. S2).

Fig. 5.

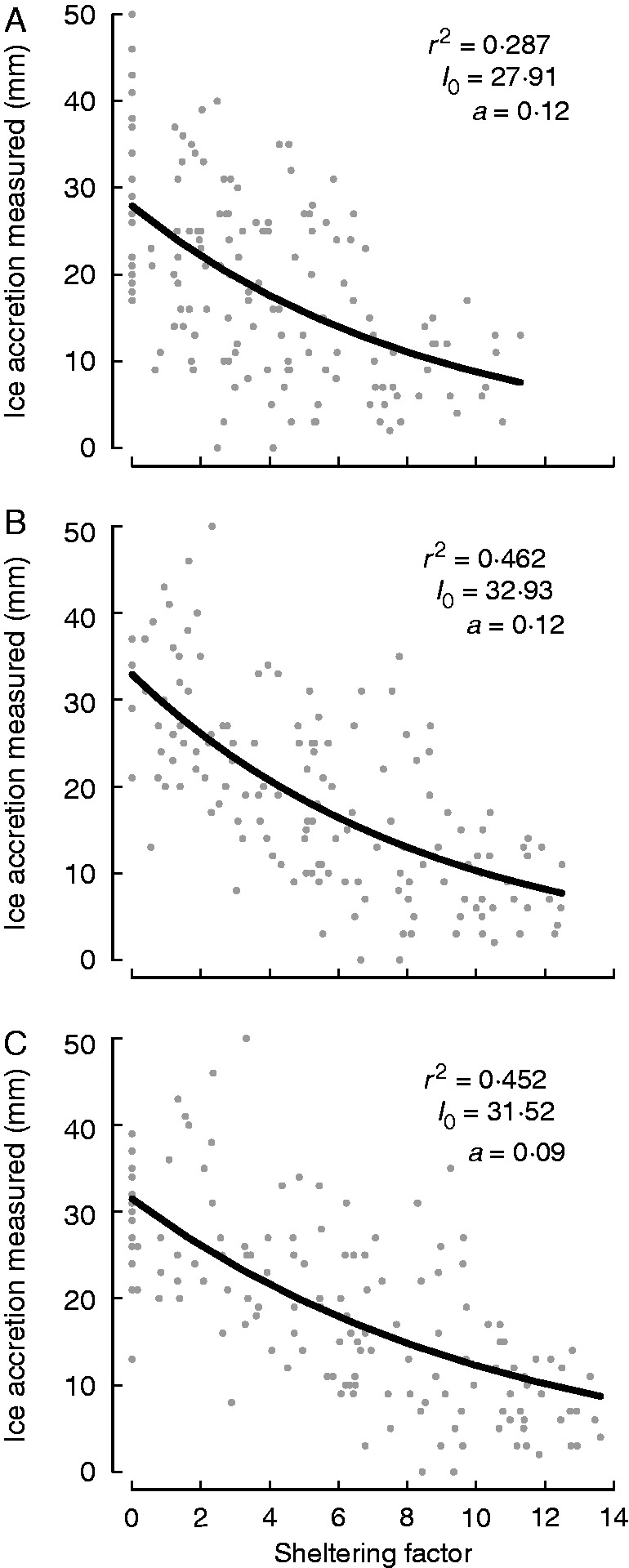
Relationship between measured ice radius (always for t₁; 6·5 h of icing) on branch segments and SF calculated for the tree point cloud at different times: (A) SF calculated for t₀ (pre-icing), (B) weighted SF (proportions: 0·3 for t₀ and 0·7 for t₁) for t₀ and t₁, and (c) SF at t₁. The black line corresponds to the modelled relationship based on the Beer–Lambert extinction model (see the Materials and Methods; I₀ and a are obtained by calibration).

Relationship between SF index and ice accretion simulated with IceTree

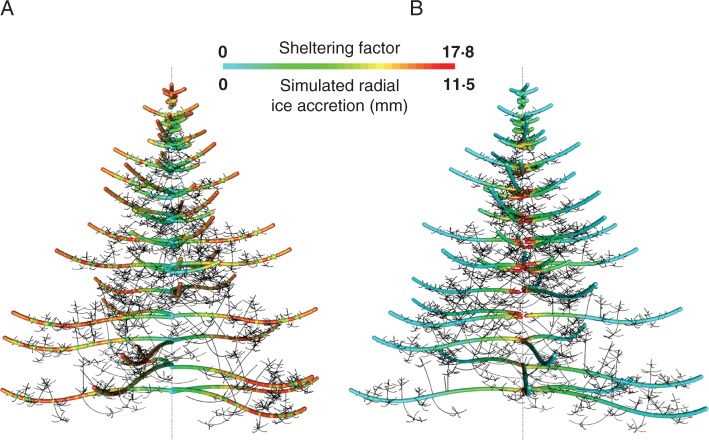
Results from IceTree for the simulated freezing rain event showed qualitatively similar patterns to those observed from the real experiment (Fig. 6). For example, ice accretion declined in a similar fashion with increasing distance from branch tips towards the centre of the crown (Fig. 6).

Fig. 6.

Simulated tree from a functional–structural modelling suite. Using the freezing rain simulation tool IceTree, we have simulated a freezing rain event. Simulated ice accretion on branches of secondary branching order of the simulated tree showing covariation between SF (α = 10 cm, β = 10°) and ice accretion. Colour gradients (scale on the figure) show: (A) the simulated radial ice accretion (mm), and (B) SF.

Matching simulated ice accretion with IceCube output for the virtual tree presented a similar pattern to the real data with an inverse relationship between ice accretion and SF (Fig. 7). A Beer–Lambert extinction model was fit to the data. The calibrated model appears to be very reliable, with an R² as high as 0·87; moreover the calibrated I₀, 10·6 mm, is very close to 11·1 mm – the expected uniform radial accretion of the precipitation on branches for 35 mm precipitation in the IceTree simulation (ignoring the small effect of volume change from water to ice, 35 mm/π = 11·1 mm; Fig. 7). Accounting for the ice–water density difference, the comparison becomes 10·6 mm vs. 12·2 mm.

Fig. 7.

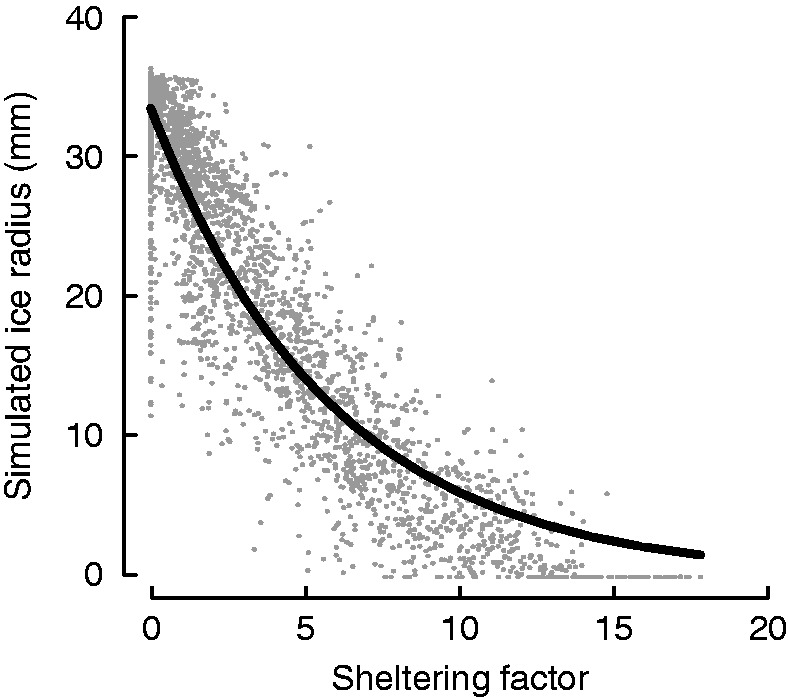
Relationship between simulated ice radius on second ramification order branch internodes and SF (α = 10 cm, β = 10°) calculated for the simulated tree point cloud. The black line corresponds to the modelled relationship based on the Beer–Lambert extinction model (see the Materials and Methods) (I₀ = 10·6 mm; a= 0·17; R² = 0·87).

DISCUSSION

Freezing rain leads to substantial reductions in forest productivity in the eastern half of North America; however, direct observation of ice loading and crown damage has been precluded by two challenges: (1) the fact that the warm front which produces the precipitation often quickly advances over the damaged area, leading to warming temperatures and the melting of the ice (Proulx and Greene, 2001), and (2) difficulties in travelling and thus acessing study sites even if ice persists due to colder weather. One solution to this problem is to load trees experimentally (e.g. Rustad and Campbell, 2012; Nock et al., 2013c). The second problem – how to measure ice within the crown – has been satisfactorily resolved as shown here by the use of TLS.

We previously hypothesized that variation in ice accretion in tree crowns probably arises when raindrops are intercepted by branch elements higher up in the crown, with the probability of a raindrop being intercepted by a canopy element increasing with the accumulation of branch area index (m² m^–2, analogous to leaf area index) along a predominantly vertical path through the canopy (Nock et al., 2013c). Here, we developed a novel model to link field-derived empirical measurements of ice accretion with voxel descriptions of canopy structure in order to better understand the variation in ice accretion patterns in tree crowns. Our model captured the influence of crown structure on the patterns of ice accretion in a tree crown and performed quite well, expressing about half the variation in loading (R² = 0·46).

A particular challenge is that tree crowns represent a very dynamic system whose initial structure not only determines ice accretion, but also changes as a result of ice accretions, for example as branches bend and eventually break. This requires modelling not only the pattern of ice accretion but also the biomechanical consequences of the ice loading for the complete network of branches. Although examples have been illustrated theoretically using single, isolated branches (Greene et al., 2007), we are not aware of any studies which have attempted to address these issues at the crown level using models or empirical data. In the present study, we approached this challenging problem in a simple way. Assuming that the pattern of ice accretion is driven by crown structure, which in turn can be described using voxels, we proposed that the ice radius at the end of the icing period should reflect the continual changes in structure and that these changes could be discretized and approximate the continual change. We found that the strongest relationship for ice radius and SF was for the combination of a small influence of the pre-loading structure and a larger influence closer to the time of ice radius measurement (Fig. 6; Supplementray Data Fig. S1). This is due to the rapid bending of branches as ice accumulates.

Although our experiment was limited to one individual and a population of sample branches, our method could be extended to explore how pruning (or virtual pruning of the tree point cloud) might influence the quantity and spatial pattern of intercepted freezing rain, with the intent of reducing the risks of branch breakage in urban areas. Similarly, one could also explore species-specific differences based on their contrasting architectural patterns of crown development (cf. Hallé and Oldeman, 1970). That is to say, comparing contrasting phyllotaxy, and branching patterns on crown sensitivity with ice load and breakage (e.g. species with characteristically slender branches such as Betula vs. thicker branched species such as Fraxinus using terrestrial laser scans). It may also be possible to scale up results collected at a smaller scale, working with digitized or laser-scanned branch samples in a facility with the ability to generate freezing rain. A recent meta-analysis examined trends in damage by grouping species according to Grimes CSR classification of species life history strategies (Grime, 1974), finding that C species were more damaged than stress-tolerating species. In future work it may be insightful to try to understand these group differences through quantitative traits related to ice accretion such as branching intensity and terminal branch diameter as well as biomechanics (e.g. wood density, limb junctions; Wonkka et al., 2013).

In the present study, we used a simple method of voxel analysis to represent branch radius and tested the sensitivity of our results to the voxel resolution (Supplementary Data Fig. S1). However, it is important to note that there are more advanced methods for translating TLS point cloud data into more geometrically accurate representations of tree structure (e.g. Béland et al., 2014). Employing such methods would provide a more accurate description of crown structure and increase the strength of the relationship between ice radius and voxelized canopy structure. We also note that in the present study we did not adapt IceCube to allow for freezing rain from angles other than the zenith, although making the changes to the model to relax the zenithal assumption is feasible. It is thus possible that some of the unexplained variation may have been related to the zenithal assumption not entirely reflecting reality; wind speed was not 0 and, due to the oscillating sprinkler, non-zenithal rain was likely.

Occlusion is a constant possibility when working with TLS. By scanning from the ground, occlusion may be a problem for small branches at the top of the crown since penetration of laser beams is stopped by large branches at the bottom. While there were no obvious problems with our tree point clouds, occlusion of some amount of branch material could have influenced our results, particularly in the later stages as branches bent.

Wind speed was a gentle breeze (3–5 m s^–1), similar to the mean winter wind speed at 10 m height at nearby Trudeau airport. At these wind speeds, there may have been some small effect of branch motion during scans that could have affected alignment of small diameter branches, and this swaying could have had slight effects on the scatter observed for the relationship between SF and ice accretion.

Towards a simulation model for freezing rain accretion in tree crowns

Sophisticated models have been developed during the last 20 years which can capture important variation in tree architecture. Furthermore, some models have been incorporating biomechanics into their structural sub-models (Costes et al., 2008; DeJong et al., 2011). Thus, the essential components for a simulator which can examine the influence of different architectural features of sympatric tree species (branching coarseness, crown depth) on ice accretion – while holding other variables constant such as crown exposure or ontogeny – are already present. Here, we took some first steps with the development of IceTree, a freezing rain simulation tool. By converting the structure of the virtual tree to a point cloud, which was subsequently modelled with IceCube (generating data for SF), we were able to relate the simulated ice accretion with SF. The resulting strong relationship (Figs 6 and 7) demonstrated the consistency of the two approaches with our conceptual model for freezing rain accretion in tree crowns. The indirect validation of IceTree opens up new perspectives for evaluating the risks of branch breakage depending on the architecture of tree species. If the ice accretion is correctly simulated on virtual trees, it is then easy to calculate the corresponding gravitational force applying at every location within the tree crown. However, realistic calculations must account for the branch bending resulting from increasing ice loads (e.g. Cannell and Morgan, 1989). Biomechanical models have already been developed for simulating the branches’ curvature (Guillon et al., 2012) and the deformation of tree crowns enduring wind stresses (Sellier et al., 2008; Sellier and Fourcaud, 2009). Such models could be adapted for simulating the branches deflection as ice load increases and ultimately for evaluating their risk of breakage.

Of course, for both ecologists and foresters, ice accumulation is only interesting insofar as it leads to rupture. Thus, the final step in the research programme initiated by Nock et al. (2013c) is to couple biomechanical models of branch breakage (e.g. Greene et al., 2007) with models of ice accumulation (e.g. Jones, 1998). At that point, one should be able to relate the probability of breakage with branch size and crown position, wind speed and species-specific factors such as breaking stress. One complication that must be dealt with is the effect of falling branches. Undoubtedly, the heavily loaded upper branches will, if broken, fall on the more lightly loaded lower branches, breaking them in turn.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. Table S1: zenith and azimuth angles for the simulated freezing rain experiment with the virtual tree in AMAPstudio. Figure S1: effects of parameter variation on the sheltering factor (SF) for individual branches. Figure S2: model R² values for the relationship between measured ice radius and SF as a function of x, a parameter that sets the weighted average between scanning times.