A field-to-desktop toolchain for X-ray CT densitometry enables tree ring analysis

Abstract

Background and Aims Disentangling tree growth requires more than ring width data only. Densitometry is considered a valuable proxy, yet laborious wood sample preparation and lack of dedicated software limit the widespread use of density profiling for tree ring analysis. An X-ray computed tomography-based toolchain of tree increment cores is presented, which results in profile data sets suitable for visual exploration as well as density-based pattern matching.

Methods Two temperate (Quercus petraea, Fagus sylvatica) and one tropical species (Terminalia superba) were used for density profiling using an X-ray computed tomography facility with custom-made sample holders and dedicated processing software.

Key Results Density-based pattern matching is developed and able to detect anomalies in ring series that can be corrected via interactive software.

Conclusions A digital workflow allows generation of structure-corrected profiles of large sets of cores in a short time span that provide sufficient intra-annual density information for tree ring analysis. Furthermore, visual exploration of such data sets is of high value. The dated profiles can be used for high-resolution chronologies and also offer opportunities for fast screening of lesser studied tropical tree species.

INTRODUCTION

Quantifying the response of terrestrial vegetation to a globally changing environment is essential to predict future forest distribution and diversity as well as to assess their role in the carbon balance (Lewis et al., 2009; Martin and Thomas 2011). The combined action of intrinsic and environmental factors is responsible for the unique structure of wood, which makes tree rings important natural archives (Vaganov et al., 2006). There is an urgent need for more knowledge to increase our understanding of wood formation under changing environments (Worbes, 2002; De Micco et al., 2012) which requires methodological improvements (Fonti et al., 2010). In addition to ring width, wood density is a promising indicator. It is determined by anatomical and chemical traits (Lachenbruch and McCulloh, 2014) and is a key descriptor of wood (Chave et al., 2009). Wood density is defined as its mass divided by its volume, and can be seen as a proxy for carbon allocation per unit of volume (Müller-Landau, 2004; Plourde et al., 2015), as it reflects past climate conditions (Hughes, 2002; Büntgen et al., 2010) and is an important property for life history strategies (Preston et al., 2006; Swenson and Enquist, 2007; Poorter et al., 2010; Zanne et al., 2010).

Densitometry is used to quantify density variations that reach the intra-ring level (Fritts, 1976). X-ray densitometry by means of radiographies was developed by Polge (1966) and is, together with other systems such as SilviScan (Evans, 1994), widely used as a basic technique for density profiling of tree increment cores. Derived parameters such as maximum latewood density (MXD) have proven to be more sensitive to climate than tree ring width in high northern latitudes (Briffa et al., 1998). Features such as intra-annual density fluctuations can be detected with densitometry (Gonzalez-Benecke et al., 2015) and are vital for monitoring response to short-term climatic changes (Pilcher et al., 1990; Wimmer, 2002; Battipaglia et al., 2014), yet can be masked by averaging over the entire tree ring width (Rossi and Deslauriers, 2007). Such density profiles can be used to match within and between individuals, similar to matching ring width series, i.e. cross-dating. Density might even be more important than ring width itself in the matching process (Polge, 1966, 1970; Allen et al., 2012; Drew et al., 2013). Traditionally, cross-dating is a fundamental principle of dendrochronology where ring width series are matched and anomalies are detected in order to assign every ring to an exact calendar year (Fritts, 1976). Next to several existing software packages such as COFECHA (Holmes, 1983; Grissino-Mayer, 2001), the eventual cross-dating is often dependent on personal judgement (Pilcher et al., 1990) and is non-trivial in many regions (e.g. tropical and sub-tropical latitudes) and often difficult to reproduce (Wils et al., 2009) and to formalize. Density profiles thus offer a clear opportunity for improvement in this respect.

Throughout the years, the original idea postulated by Polge (1966), i.e. cross-dating using original density profiles, was only possible on a visual basis and on a limited number of samples. Furthermore, despite the potential high resolution, the classic technique is costly, time-consuming and still labour-intensive, hampering fast data acquisition and thus the possibility for high-throughput automated tree ring analysis, although semi-automated density-based delineations of ring width (Mothe et al., 1998) and density parameters (Koubaa et al., 2002) exist. Furthermore, due to increasing demand for incorporating other sources of information to disentangle tree growth, often involving destructive analyses such as isotope measurements (Schollaen et al., 2014) or elemental analysis (Hietz et al., 2015), there is a need for digitally archiving structural data before further analysis. There is an ongoing interest in developing new methods for determining wood density in a more detailed and less time-consuming way (Mannes et al., 2007) and less dependent on physical manipulations. Recent techniques specifically reducing labour and time costs are high-frequency densitometry (Schinker et al., 2003; Wassenberg et al., 2014) and medical X-ray computed tomography (X-ray CT) (Steffenrem et al., 2014). Blue intensity measurements based on optical images are also being developed as a more cost-effective method for MXD in conifers (Rydval et al., 2014). However, an integrative approach of high-throughput density profiling combined with the application of software to apply full densitometry information for objective cross-dating is still lacking. In this study, the Nanowood X-ray CT scanner developed at UGCT (Dierick et al., 2014) is used for high-throughput 3-D scanning of increment cores to obtain density profiles from pith to bark. De Ridder et al. (2011) and Van den Bulcke et al. (2014) elaborated on this technique for temperate and tropical species to demonstrate the possibility for tree ring analysis, taking into account ring and grain directions to obtain structure-corrected density profiles.

The aim of this study was to establish an X-ray CT-based field-to-desktop toolchain for large sets of increment cores, with accompanying software routines that allow: (1) screening and archiving of 3-D digital wood samples before any further physical treatment, followed by batch processing of calibrated re-interpolated density profiles with minimum labour-input; and (2) automating the process of tree ring registration and formalizing cross-dating through density-based pattern matching of the profiles archived in (1), in order to detect anomalies and explore data sets via built-in graph functions.

We demonstrate the approach by explaining the toolchain for two long-lived deciduous temperate species: sessile oak (Quercus petraea) and common beech (Fagus sylvatica), as well as a tropical brevi-deciduous tree species limba (Terminalia superba).

MATERIALS AND METHODS

Quercus petraea, Fagus sylvatica and Terminalia superba increment cores (5 mm), drilled at breast height, were used for density profiling and tree ring analysis. A total of 46 cores from Q. petraea and 46 cores from F. sylvatica were sampled (two cores per tree) in the winter of 2014 at different locations in the South of Belgium. Forty-six T. superba cores (on average three cores per tree) were sampled at the end of the growing season in 2014 in the Luki Reserve, located in a semi-deciduous forest that is part of the southernmost edge of the Mayombe forest (Democratic Republic of the Congo). All increment cores were put in paper straws after sampling for ease of storage and labelling, and remained unwrapped throughout the entire X-ray CT toolchain. The samples were dried for 24 h at 103 ± 1 °C and mounted in custom-made cardboard holders for scanning. The current set-up allows storage of up to 33 intact cores of variable length (up to 50 cm) in one holder. A data sheet that links the sample label with position in the holder allows for batch extraction, and metadata (site, co-ordinates, etc.) are included for archiving. The sample holders with cores were scanned at a resolution of 110 μm using the NanoWood CT facility (Dierick et al., 2014), developed in collaboration with XRE (www.XRE.be). A sample holder does not fully fit in the field of view and therefore the top and bottom part were scanned separately, reconstructed (GPU GeForce GPX 770 4 GB) with the Octopus reconstruction software package (Dierick et al., 2004; Vlassenbroeck et al., 2007; licensed by InsideMatters: www.insidematters.eu) and digitally stitched, resulting in a single greyscale volume of the entire sample holder. All routines to process the greyscale volume, as elaborated in the Results, were written in MATLAB^® R2015a and are available as a stand-alone package with a graphical user interface (GUI) and associated graphs.

RESULTS

A flow-chart of the toolchain is given in Supplementary Data Fig. S1. Several steps are executed as batch processes, as such minimizing labour cost and increasing speed of analysis.

Screening and archiving

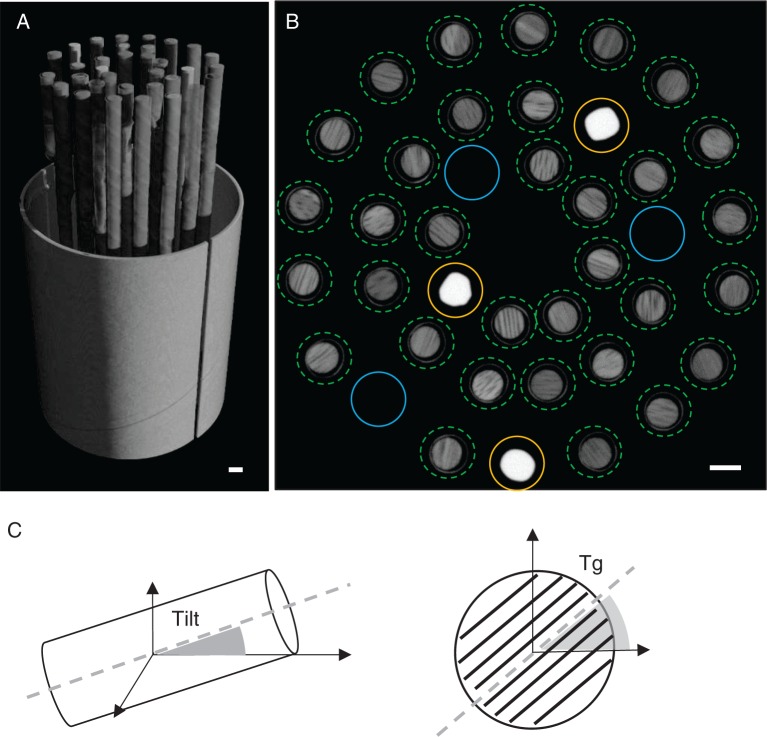
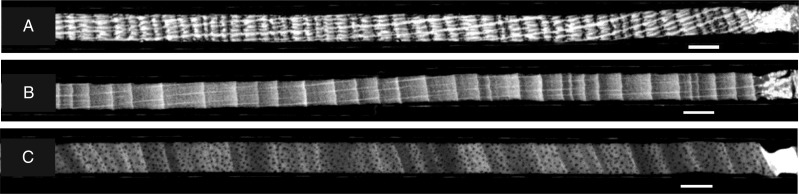
A total of 50 min scanning and 30 min reconstruction time per cylinder are required. The reconstructed greyscale volume of the entire sample holder is loaded in the toolbox; all cores are indicated on a cross-section and labelled automatically based on the data sheet (Fig. 1A). Each labelled core is then extracted from the total greyscale volume and converted to wood density estimates by rescaling using a reference material with known density (1400 kg m^–3) and similar elemental composition to wood (De Ridder et al., 2011), and air (1·2 kg m^–3) (Fig. 1B). Wood density is thus defined as oven dry weight divided by oven dry volume. Each core density volume then needs to be oriented perpendicularly to the grain, which is essential for proper structure direction correction later on. This orientation is automated as a two-step process including tilt and tangential alignment (Fig. 1C), avoiding tedious manual rotation of the object in three dimensions. The former aligns the core axis parallel to the x-axis of the global co-ordinate system. The latter rotates the core in the tangential plane according to the user-indicated grain angle based on display previews through the core. Each core density volume is then stored as a single 16-bit multipage TIFF file. These digital cores can then be loaded in the GUI, an extended version of the structure correction module described in Van den Bulcke et al. (2014), allowing visualization of both the transversal (Fig. 2) and the radial plane. Cores are first assessed visually in order to exclude cores showing, for example, knots, wound reactions or anomalously suppressed growth.

Fig. 1.

(A) 3-D rendering of the sample holder volume containing the tree cores. (B) Cross-section of the volume with indication of the cores (green dotted circles) for batch extraction. Reference material (yellow circles) and air (blue circles) are extracted and used to convert the separate core greyscale values into wood density values. (C) Tilt and tangential alignment of the core volume for further analyses. Scale bar = 5 mm.

Fig. 2.

Visual screening of the X-ray CT images allows fast inspection of the wood surface: transversal view of (A) Quercus petraea, (B) Fagus sylvatica and (C) Terminalia superba core. Scale bar = 5 mm.

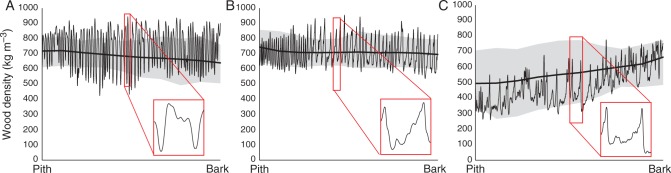
Subsequently, structure direction is corrected for, tackling (1) ring curvature and (2) radial variations in grain direction (Supplementary Data Fig. S2). This can be accomplished by indicating the main structure direction. In classic tree ring analysis, ring angle is accounted for by rotating the sample during tree ring width measurements, while grain deviations in the radial plane are not considered. For coniferous tree species with a clear ring structure, this correction can be performed automatically (for details, see Van den Bulcke et al., 2014). Other tree species with more subtle structures at the tree ring border (e.g. tropical tree species) require manual indications. Once the structure direction is indicated, a re-interpolated density profile is calculated excluding the paper straw and surrounding air using a morphological operator (Supplementary Data Fig. S3). This approach will segment the wood volume from the background, such that no manual cropping of the volume is necessary and all the density profiles are automatically extracted. Re-interpolated density profiles from pith to bark and the average density trend are presented in Fig. 3 for the three wood species studied. For Q. petraea and F. sylvatica, a rather constant density from pith to bark is observed, while for T. superba an increasing density occurs. These profiles can then be used to indicate tree rings automatically or to fine-tune manual indications made in the GUI. This detection is based on a user-specified threshold for minima, maxima or inflection points in the density profile, a decision which should be based on the tree ring boundary type (Worbes 1989): Q. petraea is a ring-porous species with tree ring boundaries defined by minimal density (early-onset wood vessels), while F. sylvatica and T. superba are diffuse-porous characterized by a clear density peak at the ring boundary. The maximum density is caused by a decrease in number of vessels for F. sylvatica, and smaller thick-walled fibres for T. superba. Errors can easily be removed interactively and, if manual indications of the tree-ring boundaries already existed, a fine-tune function can be used to shift the indications to the extrema or inflections of the density profile.

Fig. 3.

Averaged wood density trend (smoothed line, error bands show 1 s.e.) and single density profile from pith to bark for (A) Quercus petraea, (B) Fagus sylvatica and (C) Terminalia superba. The latter shows an increase in density from pith to bark. Magnification of a single ring illustrates the tree ring boundary type.

A smoothing filter can be applied to each density profile in order to reduce high frequency details originating from wood anatomical features such as, for example, abrupt changes between vessels/parenchyma and fibres and crystals. Flatbed images serve as a complementary archive and can easily be coupled to the X-ray images (Supplementary Data Fig. S4).

Tree ring analysis

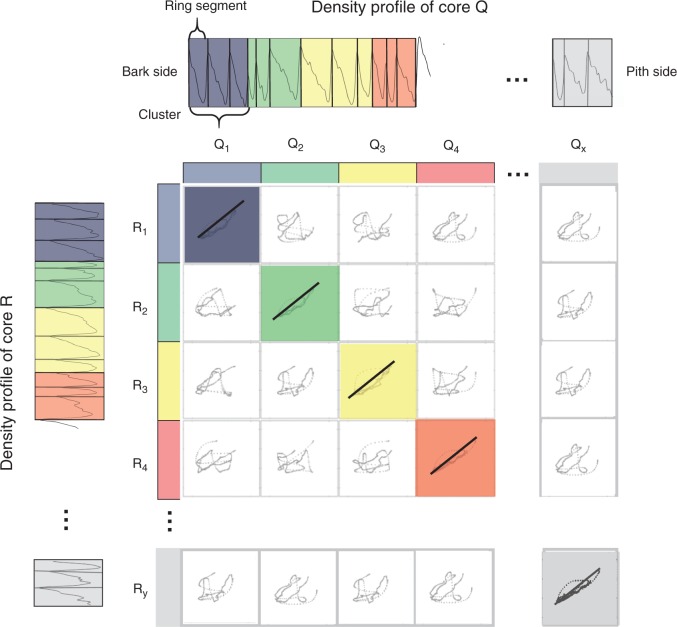
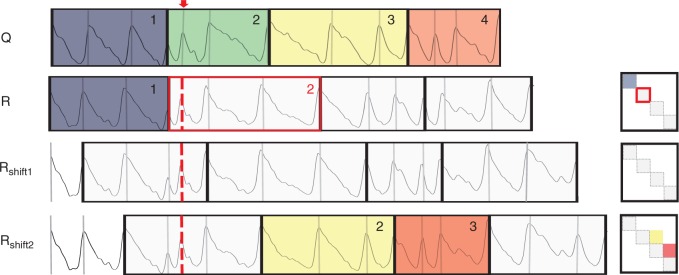
Density-based pattern matching (DBPM) is illustrated for two F. sylvatica core profiles, referred to as R and Q (Fig. 4), but is analogous for comparison of multiple cores. For each core, tree ring boundaries, manually or automatically indicated in the GUI, are used to divide the density profile into separate ring density profiles. Subsequently, these consecutive ring profiles are merged into clusters with a user-specified size. Clustering thus allows the inclusion of sufficient density information in order to reduce the number of false positives while matching. All cluster sequences are correlated using Pearson correlation. This requires resizing of the clusters to equal length and standardizing density, emphasizing relative differences in wood density, rather than absolute differences. The DBPM starts arbitrarily on the bark side. If tree rings are indicated properly, i.e. without any false or missing rings and cross-dated, high correlations will appear on the diagonal of the R–Q correlation matrix, which is a similarity measure reflecting the mutual structural synchronicity along the growth axis. To account for false/missing rings or errors in ring indications (further referred to as anomalies), a method is proposed where ring segments are shifted and re-clustered, followed by a recalculation of the correlation matrix. Figure 5 illustrates the procedure for the same two cores as in Fig. 4, with a missing indication in the second cluster of core R. The initial situation, without any shifts, will only cause matching of the first cluster of Q and R. All further clusters from Q and R cannot be matched due to the anomaly. The maximum shift is cluster size 1 because the initial situation is re-attained when the number of shifts equals the cluster size. After shifting one ring (R_shift1), no clusters are correlated any longer with Q because the positions are moved. Shifting two ring segments (R_shift2) results in a match for the third and the fourth cluster of core Q with the second and third cluster of core R. Evaluating all shifts results in localization of the cluster that contains the error. The approach thus allows the location of all ring indications based on density and leads to actual matching (cross-dating) by tracking the anomalies and removing them using the GUI. False rings or errors in ring indications can be interactively removed. Missing rings are marked and labelled in the GUI and will be accounted for in further analysis. Broken cores, cracks, scars and other artefacts can be labelled in order to exclude these for further processing (Supplementary Data Fig. S5). Different sampling dates are accounted for during the DBPM procedure.

Fig. 4.

Density profiles of Fagus sylvatica core R and Q are segmented based on ring indications. In this example, rings are grouped by three to form resized clusters to assess similarity based on a correlation matrix. High correlations are noted on the diagonal, which is the basis of the similarity measure.

Fig. 5.

Illustration of the shift procedure of the density-based pattern matching (DBPM) for core R and Q with one missing indication (red dotted line) in cluster two of core R (cluster size 3). Clusters are shifted with one ring (R_shift1) and two rings (R_shift2), and ring segments are merged into new clusters and correlation is recalculated. Coloured clusters represent matched zones between the cores.

The software allows DBPM parameters and the associated plots to be verified with classic ring width curves and tree ring descriptive statistics such as the corrected Gleichläufigkeit criterion (Buras and Wilmking, 2015) (Supplementary Data Fig. S6). Simultaneously, core volumes are loaded in the GUI to remove/add rings, depending on the above-mentioned assessment procedure, after which all statistics are updated. Once all cores are cross-dated, a batch operation exports the density profiles, associated ring width series and derived parameters such as mean density per ring or MXD for use in other statistical or tree ring analysis software packages. During the procedure, the user can visually assess multiple profiles simultaneously.

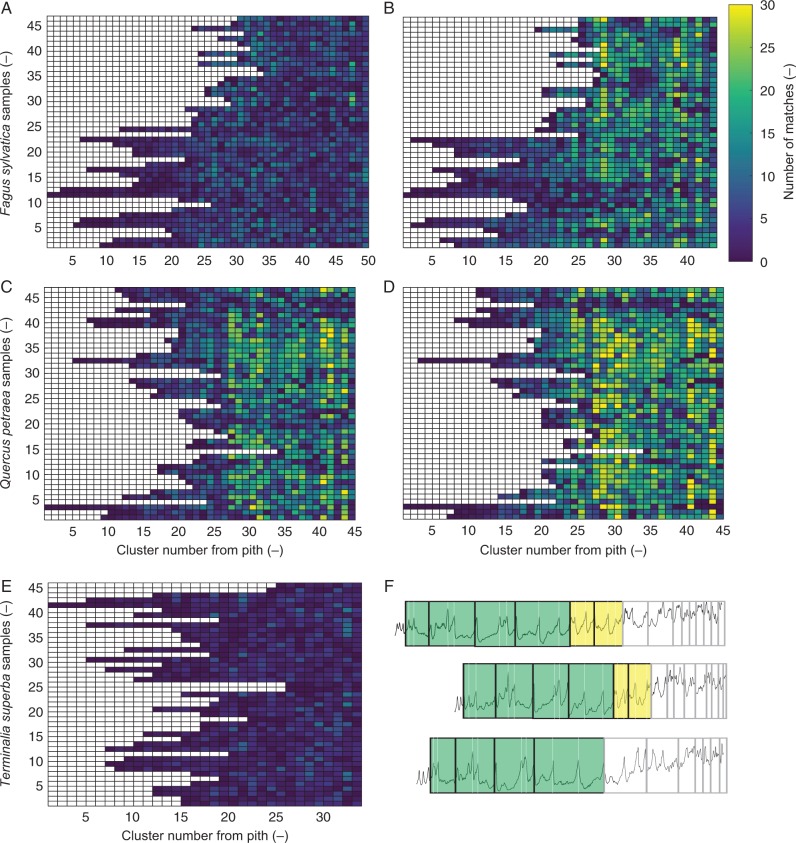
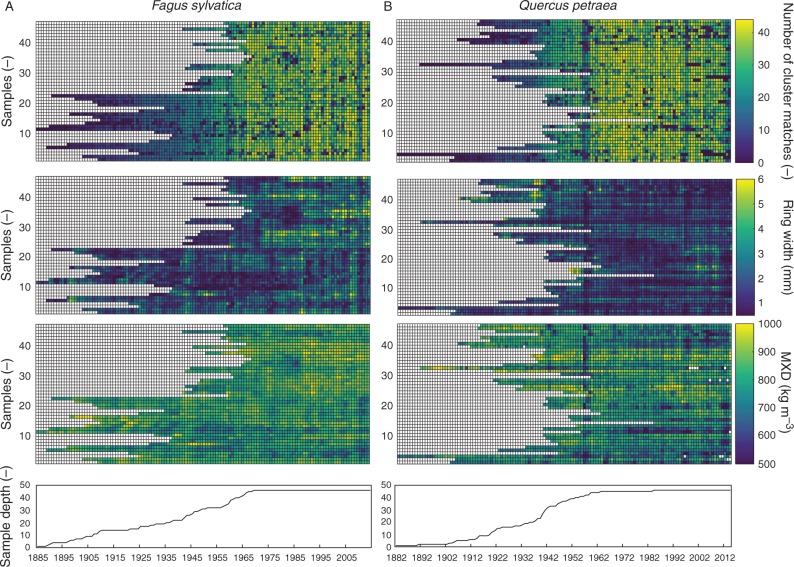
The DBPM was applied on semi-automated ring indications of undated profiles which resulted in effective cross-dating of all density profiles of F. sylvatica and Q. petraea, and was verified with ring width statistics. A matrix output for the two species illustrates the difference in number of cluster matches before (Fig. 6A, C) and after (Fig. 6B, D) cross-dating with cluster size 3. On specific radial positions, a higher number of cluster matches is noted for cross-dated cores of F. sylvatica and Q. petraea. For T. superba, only medium-sized rings provided sufficient density information to be matched between cores. Due to a strong age trend, very small rings occur in the outermost core section, which complicated exact dating of the T. superba profiles (Fig. 6E, F). Subsequently, to interpret the DBPM matching, the matched clusters from Fig. 6 should be assigned to calendar years: the number of density matches per year is plotted for all the samples, allowing assessment of possible common intra-annual density signals (Fig. 7A, B). Additionally, matrix plots of ring width and density parameters of cross-dated cores can serve as data exploration to look for signal patterns.

Fig. 6.

Matrix plots of the number of density-based matched clusters (A) before and (B) after cross-dating of Fagus sylvatica as a function of the sample and the position of the cluster within the sample. (C and D) The same for Quercus petraea. The colour scale of each element represents the number of clusters that it has in common with other profiles in that same cluster number. The same colour scale is used for the three species. After cross-dating, a higher number of clusters is found (cluster size 3). The number of clusters is different before and after cross-dating due to adding/deleting ring indications. (E) For Terminalia superba, few matches are found due to (F) difficult matching of small rings.

Fig. 7.

Matrix plots of the number of matched years based on density-based pattern matching (DBPM), together with output of ring width, maximum density (MXD) of the cross-dated profiles of (A) Fagus sylvatica and (B) Quercus petraea allow exploration of the data set for patterns.

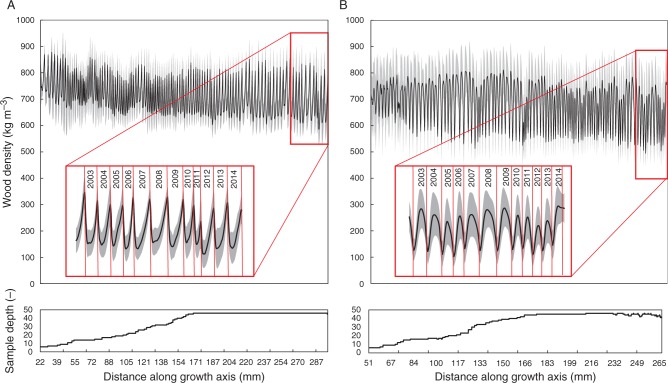
As a combined output of density and ring width, an envelope profile based on all cross-dated cores is shown for Q. petraea and F. sylvatica (Fig. 8A, B). The length of each dated intra-annual density segment is rescaled to the average ring width of that year, illustrating density and ring width variability through time.

Fig. 8.

Envelope profile of (A) Fagus sylvatica and (B) Quercus petraea profiles visualizes ring width and density variation. Error bands show 1 s.e.

DISCUSSION

X-ray CT toolchain allows fast screening and archiving and generates high-resolution density profiles

Physical sample manipulation throughout the toolchain remains limited and is considered as a significant advantage in the processing time of large core sample sets, with several steps performed in batch (Fig. S1), resulting in density profiles in a limited time span. The high-throughput character of the toolchain thus meets the need for efficiently measuring variables along large series of rings to increase sample size (Fonti et al., 2010). X-ray CT scanning is independent of sample thickness and surface (Van den Bulcke et al., 2014), thus 3-D acquisition overcomes several sample preparation steps that occur in classic X-ray densitometry (Polge, 1966; Evans, 1994) as well as high-frequency densitometry (Schinker et al., 2003). The resolution of 110 μm used in this study is a result of a trade-off between processing time and accuracy. The required time to perform all batch operations is obviously dependent on CPU/GPU performance of desktop computers. A flexible set-up allows changing the resolution, in contrast to medical X-ray CT equipment (Steffenrem et al., 2014). Sample holders can be tailored to specific needs, and the number of cores depends on the size of the data set vs. the required resolution. Throughout the toolchain, the only manual operation is performed in the GUI, where structure direction and/or rings need to be indicated. Semi-automated tree ring demarcation on the density profiles (Evans, 1994; Mothe et al., 1998; Van den Bulcke et al., 2014) is implemented, but should always be verified with visual control. 3-D corrections are possible, resulting in a re-interpolated density profile that reduces peak flattening (Van den Bulcke et al., 2014). Complicated analysis due to twisting and rolling of the cores (Allen et al., 2012) is largely overcome here due to software corrections, since several alignments and structure corrections are implemented. Wood density is directly calculated using a reference material and air, allowing accurate values to be obtained (De Ridder et al., 2011) and still avoiding the need for calibration functions as in high-frequency densitometry (Wassenberg et al., 2014). Consequently, reliable trends of wood density can be pictured for many cores in a fast and efficient way (Fig. 3). Extractives and minerals can influence the density profile (Vansteenkiste et al., 2007), although for our study species these problems did not occur due to low extractive contents. Species with an extractive content that affects the density profile (Grabner et al., 2005) can be extracted with solvents before scanning.

Density-based pattern matching as a suitable parameter for cross-dating

This study is innovative in its goal to use intra-annual density profiles to tackle the challenge of cross-dating, instead of evaluating ring averages of derived density parameters (Allen et al., 2012; Drew et al., 2013). The presented DBPM is a formalization of the classic cross-dating procedure, as the matching relies on higher resolution parameters. The approach of shifts to locate dating errors presented herein is comparable with the methodology of shorter segments applied on ring widths in COFECHA (Holmes, 1983; Grissino-Mayer, 2001), yet density profiling allows for shorter series, as more information is available per ring (Fig. 4). This study uses Pearson correlation as a similarity measure, but other similarity measures can also be implemented. Although density and ring width matching are difficult to compare, both parameters are complementary in the final evaluation of cross-dating quality; therefore, classic ring width parameters are also considered.

It is shown that profiles at 110 μm resolution provide sufficient intra-annual density information for screening the studied samples for cross-dating quality. Moreover, the nature of the DBPM method implies that significantly small rings, not visible on the density profile on this resolution, can be detected by means of DBPM shifting, similarly to anomalies, thus reducing the effect of resolution on the matching (Fig. 5). Synchronous density matches (Fig. 6) offer scope for further exploration of the data set. The simultaneous matrix output of density and ring width parameters allows checking for patterns in the data set (Fig. 7).

The limited number of matches for T. superba (Fig. 6E, F) is due to a significant growth trend where ring widths tend to decrease drastically at higher age, which complicates matching due to insufficient intra-annual information. Moreover, due to a dominating proportion of vessels and parenchyma, local density variations in these very narrow rings make them less clear toward the bark side (Schongart et al., 2006). The anatomical pattern of ring boundaries formed during senescent growth can be insufficient for reliable demarcation (Stahle 1999), which is certainly true for T. superba, due to its pioneer character and the large number of senescent trees in the data set. The intrinsic biological nature of the wood structure thus limits the use of the technique (Cherubini et al., 2013). It is unlikely that rings will be better detected at a higher resolution, unless the resolution attains the anatomically resolving threshold, and stem disks should be used to account for wedging rings (Groenendijk et al., 2014). Rejection of large sets of cores is reported in tropical regions (Schongart et al., 2006), mostly after the time-consuming process of cross-dating. DBPM can reject series at an early stage, making tedious dating trials unnecessary. Compared with ring width matching, more series might be withheld based on density parameters (Drew et al., 2013), thus increasing sample size for further analysis of these difficult species.

Many authors do not profoundly discuss the cross-dating process, especially for tropical species, which makes it difficult to assess their work (Wils et al., 2009). The digital X-ray/flatbed image archive together with the ring indications and profiles presented here ensures that all steps in the cross-dating process can easily be checked and re-assessed. Matrix plots are used for data exploration as they are a powerful tool for visually assessing sample quality. Typical output parameters (e.g. ring width and MXD; Fig. 7) can be imported in conventional software packages or in other open source tree ring analysis software (Bunn, 2010) to assess the link with climate. After cross-dating, the user can focus on certain sections containing features such as intra-annual density fluctuations which can, when shown to be synchronous, be considered as characteristic years. Such years can be spotted and, due to the flexible set-up, processed for detailed anatomical studies with dedicated sample holders. A guided approach of additional scans of particular regions of interest is possible with resolution up to 35 μm (Van den Bulcke et al., 2014) and eventually to the anatomically resolvable level (Van den Bulcke et al., 2009) (Supplementary Data Fig. S7).

Conclusion

A non-destructive X-ray CT-based screening procedure is presented, going from field to desktop while reducing sample treatment and analysis time. Many research disciplines are focusing on sampling tree cores for densitometry and/or tree ring analysis, but classic methods are time-consuming, so obtaining data without reducing accuracy is essential. In-house-developed software routines treat all data from input (tree cores) to output (dated density profiles). Several batch processes are implemented in the toolchain, minimizing manual effort. Moreover, wood density is determined by rescaling with a reference material.

In contrast to classic X-ray densitometry or high-frequency densitometry, no physical surface treatment is necessary, and cores can be scanned immediately after drying. The digital approach avoids the time needed to surface or microtome the samples, and allows the screening and selection of large sets of cores. Since many tropical tree species remain poorly studied for their dendrochronological potential, the toolchain allows screening of large sets of cores for such species. It should be noted that not all tropical species might show sufficient density variations at the ring boundaries to be detected with X-ray CT, which will require surface treatment followed by careful examination of the ring boundaries via classic light microscopy.

High-throughput profiling in combination with exploratory tools such as DBPM with associated plots is necessary to establish high-resolution chronologies, which is complementary to other techniques that allow incorporation of detailed anatomical, chemical and isotope information (Fonti et al., 2010; Schollaen et al., 2014; Hietz et al., 2015) within tree ring boundaries. The dated density profiles can be further synchronized at the intra-annual level by means of alignment of intra-annual profiles once all cores are cross-dated (Bender et al., 2012).

The toolchain enables cross-dating entirely based on batch-generated X-ray CT profiles, which is a new approach in dendrochronology. The obtained similarity, i.e. a correlation-based similarity criterion of density information, is a robust and objective method in the decision-making process of cross-dating, which can improve tree ring analysis for species that are more difficult to match and include more cores in the overall analysis.

This study aims at filling a methodological gap concerning the integrative approach of tree ring analysis and more continuous proxies such as density profiles, and illustrates how an X-ray CT-based toolchain with minimal labour input results in a digital archive and data exploration via pattern matching.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. Figure S1: workflow of the X-ray CT toolchain for densitometry and corresponding tree ring analysis. Figure S2: screenshot of ring and grain angle correction on a Terminalia superba core. Figure S3: segmenting the wood volume from background. Figure S4: graphical user interface to include optical images. Figure S5: screenshot with ring indications that are altered, with functions for missing rings and broken cores. Figure S6: density-based pattern matching visualizations together with ring width descriptive statistics. Figure S7: screening (110 μm) of increment cores as a first step for detailed analysis at higher resolution (4 μm).