PReMiuM: An R Package for Profile Regression Mixture Models Using Dirichlet Processes

Abstract

PReMiuM is a recently developed R package for Bayesian clustering using a Dirichlet process mixture model. This model is an alternative to regression models, non-parametrically linking a response vector to covariate data through cluster membership (Molitor, Papathomas, Jerrett, and Richardson 2010). The package allows binary, categorical, count and continuous response, as well as continuous and discrete covariates. Additionally, predictions may be made for the response, and missing values for the covariates are handled. Several samplers and label switching moves are implemented along with diagnostic tools to assess convergence. A number of R functions for post-processing of the output are also provided. In addition to fitting mixtures, it may additionally be of interest to determine which covariates actively drive the mixture components. This is implemented in the package as variable selection.

1. Introduction

Profile regression is an alternative to regression models when one wishes to make inference beyond main effects for datasets with potentially correlated covariates. In particular, profile regression non-parametrically links a response vector to covariate data through cluster membership (Molitor et al. 2010). We have implemented this method in the R (R Core Team 2014) package PReMiuM (Hastie, Liverani, and Richardson 2015).

PReMiuM performs Bayesian clustering using a Dirichlet process mixture model and it allows binary, categorical, count and continuous response, as well as continuous and discrete covariates. Moreover, predictions may be made for the response, and missing values for the covariates are handled. Several samplers and label switching moves are implemented along with diagnostic tools to assess convergence. A number of R functions for post-processing of the output are also provided. In addition to fitting mixtures, it may additionally be of interest to determine which covariates actively drive the mixture components. This is implemented in the package as variable selection.

In order to demonstrate the PReMiuM package, it is helpful to present an overview of the Dirichlet process. We begin this section by re-familiarizing the reader with such a process, introducing notation that we shall call upon throughout the paper. Formally, let (Ω, 𝓕, P) be a probability space comprising a state space Ω with associated σ-field 𝓕 and a probability measure P. We say that a probability measure P follows a Dirichlet process with concentration parameter α and base distribution P_Θ0 parametrized by Θ₀, written P ~ DP(α, P_Θ0) if

$$(P(A_1),P(A_2),\dots ,P(A_r))\sim \text{Dirichlet}(\alpha P_{{\Theta }_0}(A_1),\alpha P_{{\Theta }_0}(A_2),\dots ,\alpha P_{{\Theta }_0}(A_r))$$ (1)

for all A₁, A₂, …, A_r ∈ 𝓕 such that A_i ∩ A_j = Ø for all i ≠ j and ${\displaystyle {\cup }_{j=1}^r{A}_j=\Omega .}$

1.1. The stick-breaking construction

Although Definition 1 is perhaps rather abstract, proof of the existence of such a process has been determined in a variety of ways, using a number of different formulations (Ferguson, 1973 and Blackwell and MacQueen, 1973). In this paper we focus on Dirichlet process mixture models (DPMM), based upon the following simplified constructive definition of the Dirichlet process, due to Sethuraman (1994). If

$$\begin{array}{l}P\hspace{0.17em}=\hspace{0.17em}{\displaystyle \sum _{c=1}^{\infty }{\psi }_c{\delta }_{{\Theta }_c},}\hfill \\ {\Theta }_c\hspace{0.17em}\sim \hspace{0.17em}{P}_{{\Theta }_0}\hspace{0.17em}\text{i.i.d.}\hspace{0.17em}\text{for}\hspace{0.17em}c\in {\mathbb{Z}}^{+},\hfill \\ {\psi }_c\hspace{0.17em}=\hspace{0.17em}{V}_c{\displaystyle \prod _{l<c}(1-V_l)\hspace{0.17em}\text{for}\hspace{0.17em}c\in {\mathbb{Z}}^{+}\backslash \left\{1\right\},}\hfill \\ {\psi }_1\hspace{0.17em}=\hspace{0.17em}{V}_1,\hspace{0.17em}\text{and}\hfill \\ V_c\hspace{0.17em}\sim \hspace{0.17em}\text{Beta}(1,\alpha )\hspace{0.17em}\text{i.i.d.}\hspace{0.17em}\text{for}\hspace{0.17em}c\in {\mathbb{Z}}^{+},\hfill \end{array}$$ (2)

where δ_x denotes the Dirac delta function concentrated at x and Θ_c is independent of V_c for c ∈ ℤ⁺, then P ~ DP(α, P_Θ0). This formulation for V and ψ is known as a stick-breaking distribution. Importantly, the distribution P is discrete, because draws ${\tilde{\Theta }}_1,{\tilde{\Theta }}_2,\dots$ from P can only take the values in the set {Θ_c : c ∈ ℤ⁺}.

As noted by many authors (for example Ishwaran and James, 2001 and Kalli, Griffin, and Walker, 2011) it is possible to extend the above formulation to more general stick-breaking formulations, for example allowing V_c ~ Beta(a_c, b_c) independently, resulting in a generalized Dirichlet process, such as the two parameter Poisson-Dirichlet process (Pitman and Yor 1997). The methods and results that we propose within this paper hold for such generalized processes, but at present the package is only coded to implement the Dirichlet process in Equation 2 and the Poisson-Dirichlet process with V_c ~ Beta(1 − d, α − cd) where d ∈ [0, 1) and α > −d. For d = 0 the Dirichlet process is a special case of the Poisson-Dirichlet process.

Typically, because of the complexity of the models based on the stick-breaking construction, inference is made in a Bayesian framework using Markov chain Monte Carlo (MCMC) methods. Until recently, a perceived difficulty in making inference about this model was the infinite number of parameters within the stick breaking construction. Historically, this obstacle has resulted in the use of algorithms that either explore marginal spaces where some parameters are integrated out or use truncated approximations to the full Dirichlet process mixture model, see for example Neal (2000) and Ishwaran and James (2001).

More recently, two alternative innovative approaches to sampling the full DPMM have been proposed. The first, introduced by Walker (2007), uses a novel slice sampling approach, resulting in full conditionals that may be explored by the use of a Gibbs sampler. The slice sampling method updates the cluster allocations jointly as opposed to the marginal methods which require as many Gibbs steps to update as the number of observations to cluster. The difficulty of the proposed approach is the introduction of constraints that complicate the updates of the mixture component weights, leading to potential mixing issues. To overcome this, Kalli et al. (2011) generalize this sampler, adding further auxiliary variables, and report good convergence results, although the authors note that the algorithm is sensitive to these additional parameters. The second distinct MCMC sampling approach was proposed in parallel by Papaspiliopoulos and Roberts (2008). The proposed sampler again uses a Gibbs sampling approach, but is based upon an idea termed retrospective sampling, allowing a dynamic approach to the determination of the number of components (and their parameters) that adapts as the sampler progresses. The cost of this approach is an ingenious but complex Metropolis-within-Gibbs step, to determine cluster membership.

Despite the apparent differences between the two strategies, Papaspiliopoulos (2008) noted that the two algorithms can be effectively combined to yield an algorithm that improves either of the originals. The resulting sampler was implemented and presented by Yau, Papaspiliopoulos, Roberts, and Holmes (2011), and a similar version was presented by Dunson (2009) for DPMM. The current sampler presented in this paper is our interpretation of these ideas, implemented as an R package. This package, called PReMiuM, is based upon efficient underlying C++ code for general DPMM sampling.

The aims behind the product partition model (PPMx) in Müller, Quintana, and Rosner (2011) and Quintana, Müller, and Papoila (2013) are very similar to ours. Furthermore, both sets of work adopt flexible Bayesian partition models based on the Dirichlet process (DP), although the PPMx approach is adaptable to formulations other than the DP. However, there are significant differences in how the two models are built. For example, the PPMx model is built by considering the likelihood of the partition given the covariates and variable selection parameters, using similarity functions. In contrast, we consider the likelihood of the covariates given the partition and variable selection parameters. The two modeling approaches offer different options for defining the dependence structure between the quantities of interest, and we would argue that it is a matter of personal preference which one should be adopted.

In Section 2 we describe formally the Dirichlet process mixture model implemented in PReMiuM and the blocked MCMC sampler used. In Section 3 we discuss profile regression and its link with the response and covariate models included in the package while in Section 4 we discuss how predictions are computed. In Section 5 we give an overview of the postprocessing tools available in PReMiuM to learn from the rich output produced by our Bayesian model and in Section 6 we discuss diagnostic tools that we propose to investigate the convergence of the MCMC. Finally, in Section 7 we give a brief overview of the structure of the code and show examples of its use in Section 8. We also give an indication of run times.

2. Sampling the Dirichlet process mixture model

2.1. Definition and properties

Perhaps the most common application of the Dirichlet process is in clustering data, where it can be used as the prior distribution for the parameters of an infinite mixture model. Consider again the stick breaking construction in Equation 2. For the DPMM, the (possibly multivariate) observed data D = (D₁, D₂, …, D_n) follow an infinite mixture distribution, where component c of the mixture is a parametric density of the form f_c(·) = f (·|Θ_c, Λ) parametrized by some component specific parameter Θ_c and some global parameter Λ. Defining (latent) parameters ${\tilde{\Theta }}_1,{\tilde{\Theta }}_2,\dots ,{\tilde{\Theta }}_n$ as draws from a probability distribution P following a Dirichlet process DP (α, P_Θ0) and again denoting the Dirac delta function by δ, this system can be written as

$$\begin{array}{l}{D}_i|{\tilde{\Theta }}_i,\Lambda \hspace{0.17em}\sim \hspace{0.17em}f(D_i|{\tilde{\Theta }}_i,\Lambda )\hspace{0.17em}\text{for}\hspace{0.17em}i=1,2,\dots ,n,\hfill \\ {\tilde{\Theta }}_i\hspace{0.17em}\sim \hspace{0.17em}{\displaystyle \sum _{c=1}^{\infty }{\psi }_c{\delta }_{{\Theta }_c}\hspace{0.17em}\text{for}\hspace{0.17em}i=1,2,\dots ,n,}\hfill \\ {\Theta }_c\hspace{0.17em}\sim \hspace{0.17em}{P}_{{\Theta }_0}\hspace{0.17em}\text{i.i.d.}\hspace{0.17em}\text{for}\hspace{0.17em}c\in {\mathbb{Z}}^{+},\hfill \\ {\psi }_c\hspace{0.17em}=\hspace{0.17em}{V}_c{\displaystyle \prod _{l<c}(1-V_l)\hspace{0.17em}\text{for}\hspace{0.17em}c\in {\mathbb{Z}}^{+}\backslash \left\{1\right\},}\hfill \\ {\psi }_1\hspace{0.17em}=\hspace{0.17em}{V}_1,\hspace{0.17em}\text{and}\hfill \\ V_c\hspace{0.17em}\sim \hspace{0.17em}\text{Beta}(1,\alpha )\hspace{0.17em}\text{i.i.d.}\hspace{0.17em}\text{for}\hspace{0.17em}c\in {\mathbb{Z}}^{+}\hfill \end{array}$$ (3)

with Θ_c independent of V_c for c ∈ ℤ⁺.

When making inference using mixture models (either finite or infinite) it is common practice to introduce a vector of latent allocation variables Z. Such variables enable us to explicitly characterize the clustering and additionally facilitate the design of MCMC samplers. Adopting this approach and writing ψ = (ψ₁, ψ₂,…) and Θ = (Θ₁, Θ₂, …), we re-write Equation 3 as

$$\begin{array}{l}{D}_i|\mathit{\text{Z}},\mathbf{\Theta },\Lambda \hspace{0.17em}\sim \hspace{0.17em}f(D_i|{\Theta }_{Z_i},\Lambda )\hspace{0.17em}\text{for}\hspace{0.17em}i=1,2,\dots ,n,\hfill \\ {\Theta }_c\hspace{0.17em}\sim \hspace{0.17em}{P}_{{\Theta }_0}\hspace{0.17em}\text{i.i.d.}\hspace{0.17em}\text{for}\hspace{0.17em}c\in {\mathbb{Z}}^{+},\hfill \\ \mathbb{P}(Z_i=c|\psi )\hspace{0.17em}=\hspace{0.17em}{\psi }_c\hspace{0.17em}\text{for}\hspace{0.17em}c\in {\mathbb{Z}}^{+},\hspace{0.17em}i=\hspace{0.17em}1,2,\dots ,n,\hfill \\ {\psi }_c\hspace{0.17em}=\hspace{0.17em}{V}_c{\displaystyle \prod _{l<c}(1-V_l)\hspace{0.17em}\text{for}\hspace{0.17em}c\in {\mathbb{Z}}^{+}\backslash \left\{1\right\},}\hfill \\ {\psi }_1\hspace{0.17em}=\hspace{0.17em}{V}_1,\hspace{0.17em}\text{and}\hfill \\ V_c\hspace{0.17em}\sim \hspace{0.17em}\text{Beta}(1,\alpha )\hspace{0.17em}\text{i.i.d.}\hspace{0.17em}\text{for}\hspace{0.17em}c\in {\mathbb{Z}}^{+}\hfill \end{array}$$ (4)

with Θ_c independent of V_c for c ∈ ℤ⁺.

The likelihood of D_i associated with the DPMM is simply the first line of Equation 4. Integrating out the latent variable Z_i we obtain the more recognizable mixture likelihood

$$\begin{array}{c}p(D_i|\psi ,\mathbf{\Theta },\Lambda )\hspace{0.17em}=\hspace{0.17em}{\displaystyle \sum _{c=1}^{\infty }p(D_i|Z_i=c,\mathbf{\Theta },\Lambda )p(Z_i=c|\psi )}\\ =\hspace{0.17em}{\displaystyle \sum _{c=1}^{\infty }{\psi }_{c}f(D_i|{\Theta }_c,\Lambda ).}\end{array}$$

The remainder of Equation 4 provides the prior specification for the DPMM, allowing us to write the joint posterior distribution as

$$\begin{array}{c}p(\mathit{\text{Z}},\mathbf{\Theta },\Lambda ,\mathit{\text{V}},\alpha |\mathit{\text{D}})\hspace{0.17em}\propto \hspace{0.17em}p(\mathit{\text{D}}|\mathit{\text{Z}},\mathbf{\Theta },\Lambda )p(\mathit{\text{Z}},\mathit{\text{V}},\alpha ,\mathbf{\Theta },\Lambda |{\Theta }_0)\\ \propto \hspace{0.17em}{\displaystyle \prod _{i=1}^n\{f(D_i|{\Theta }_{Z_i},\Lambda )p(Z_i|\mathit{\text{V}})\}{\displaystyle \prod _{c=1}^{\infty }\{p(V_c|\alpha )p({\Theta }_c|{\Theta }_0)\}p(\Lambda )p(\alpha )}}\\ \propto \hspace{0.17em}{\displaystyle \prod _{i=1}^n\left\{f(D_i|{\Theta }_{Z_i},\Lambda )\left[V_{Z_i}{\displaystyle \prod _{\iota <Z_i}(1-V_l)}\right]\right\}}\\ \times {\displaystyle \prod _{c=1}^{\infty }\{\alpha {(1-V_c)}^{\alpha -1}p({\Theta }_c|{\Theta }_0)\}p(\Lambda )p(\alpha ).}\end{array}$$ (5)

Of course, additional layers of hierarchy could easily be introduced, for example through hyper-priors for Θ₀.

2.2. The MCMC sampler

A common approach to MCMC sampling from the DPMM is to integrate out V and use a Gibbs sampler on the resulting space. Such samplers are commonly referred to as Pólya urn samplers, since they are motivated by the Pólya urn representation of a Dirichlet process introduced by Blackwell and MacQueen (1973). Ishwaran and James (2001) provide a review of this approach and demonstrate that conditionals of the type p(Z_i|Z_−i) can be derived, where Z_−i = (Z₁, …, Z_i−1, Z_i+1, …, Z_n). Many other authors have focused on developing alternative samplers of this nature, including Neal (2000) and Green (2010). However, as noted by many authors, samplers of this nature, where the allocation of a single observation is conditional on the allocations of all other observations, can often suffer from poor mixing. This motivates the need for an alternative class of samplers that sample from the full model in Equation 4.

In the full model, the posterior conditionals for the allocation variables Z depend upon an infinite number of variables V and Θ. One way to bypass this complication is to truncate the definition in Equation 4 to mixtures with C components (of which potentially only a subset will be non-empty). Ishwaran and James (2001) demonstrate that under this model the conditional distributions are standard distributions which can be easily sampled from. This is one of the three samplers implemented in our R package, and we refer to it as truncated. For the truncated sampler we have also implemented the more general Poisson-Dirichlet stick-breaking formulation (Pitman and Yor 1997), constructed by allowing V_c ~ Beta(1−d, α−cd) where d ∈ [0, 1) and α > −d in Equation 2. For this model α and d are fixed parameters.

Although the approach of Ishwaran and James (2001) resolves the challenges of sampling from the full model, if C is not chosen to be sufficiently large, then the posterior may be quite different on the truncated model space compared to the full model space. The authors provide some guidance for choice of C, but more recent work by Walker (2007) and Papaspiliopoulos and Roberts (2008) demonstrate techniques that alleviate the need for such a truncation, whilst retaining many of the sampling properties of the full conditionals.

The first step is to borrow the idea of Walker (2007) and introduce auxiliary variables U = (U₁, U₂, …, U_n) such that the joint posterior can be re-written as

$$p\left(\mathit{U},\mathit{Z},\mathbf{\Theta },\Lambda ,\mathit{V},\alpha |\mathit{D}\right)\propto {\displaystyle \prod _{i=\mathbf{1}}^n\left\{f(D_i|{\Theta }_{Z_i},\Lambda )1_{\{U_i<{\psi }_{Z_i}\}}\right\}}\times {\displaystyle \prod _{c=1}^{\infty }\{\alpha {(1-V_c)}^{\alpha -1}p({\Theta }_c|{\Theta }_0)\}p(\Lambda )p(\alpha )}$$ (6)

$$\propto {\displaystyle \prod _{i=1}^n\left\{f(D_i|{\Theta }_{Z_i},\Lambda ){\mathbf{1}}_{\{U_i<V_{Z_i}{\displaystyle {\prod }_{l<Z_i}(1-V_l)\}}}\right\}}\times {\displaystyle \prod _{c=1}^{\infty }\{\alpha {(1-V_c)}^{\alpha -1}p({\Theta }_c|{\Theta }_0)\}}p(\Lambda )p(\alpha ).$$ (7)

Here, 1_A, is the function that takes the value 1 over the set A and 0 elsewhere. By combining this auxiliary variable approach with the notion of retrospective sampling (i.e., adopting a just-in-time approach to sampling empty mixture component parameters, as introduced in Papaspiliopoulos and Roberts, 2008), it is possible to construct an efficient Gibbs sampler for sampling from the joint posterior in Equation 7. Integrating U out of Equation 7 with respect to the Lebesgue measure yields the DPMM posterior distribution given in Equation 5 meaning that marginalizing samples of the joint distribution over U results in samples from the desired distribution.

Kalli et al. (2011) extend the idea of Walker (2007) to a general class of slice samplers by writing

$$p(\mathit{U},\mathit{Z},\Theta ,\Lambda ,\mathit{V},\alpha |\mathit{D})\propto {\displaystyle \prod _{i=1}^n\left\{f(D_i|{\Theta }_{Z_i},\Lambda ){\mathbf{1}}_{\{U_i<{\xi }_{Z_i}\}}{\xi }_{Z_i}^{-1}{\psi }_{Z_i}\right\}}\times {\displaystyle \prod _{c=1}^{\infty }\{\alpha {(1-V_c)}^{\alpha -1}p({\Theta }_c|{\Theta }_0)\}p(\Lambda )}p(\alpha )$$ (8)

where ξ₁, ξ₂, … is any positive sequence.

When ξ_i = ψ_i, this corresponds to the efficient Gibbs sampler proposed by Papaspiliopoulos (2008) in the context of DPMM using parameter blocking. This is the second of the three samplers implemented in our R package, and we refer to it as slice dependent, in accordance with Kalli et al. (2011).

For the last of the three samplers implemented in our R package, that we refer to as slice independent in accordance with Kalli et al. (2011), we set ξ_i = (κ − 1)κⁱ⁻¹ with κ = 0.8 as proposed by Kalli et al. (2011).

Most importantly, these slice samplers permit the introduction of label switching moves, without which it is very difficult to obtain sufficient mixing. We discuss this in detail in Section 6.

We continue by defining some new notation which is required to present our slice samplers. First, given the allocation variables Z, define

$$Z^{\star }=\underset{1\le i\le n}{\text{max}}\hspace{0.17em}\hspace{0.17em}{Z}_i.$$

Similarly, given the auxiliary variables U and the vector V, define

$$U^{\star }=\underset{1\le i\le n}{\text{min}}\hspace{0.17em}\hspace{0.17em}{U}_i.$$

and

$$\begin{array}{l}{C}^{\star }=\min \left\{c\in {\mathbb{Z}}^{+}:{\displaystyle \sum _{l=1}^c{\psi }_l}>1-U^{\star }\right\}\\ =\min \left\{c\in {\mathbb{Z}}^{+}:{\displaystyle \sum _{l=1}^c\left[V_l{\displaystyle \prod _{r<l}(1-V_r)}\right]}>1-U^{\star }\right\}.\end{array}$$ (9)

It is important to emphasize that these values potentially change at each sweep of the sampler, as the underlying variables change, although for simplicity of exposition we have omitted explicitly labeling the parameters with the sweep. The purpose of the variable C^⋆ is to provide an upper limit on which mixture components need updating at each sweep. Specifically, although there are infinitely many component parameters in the model, since P(Z_i = c|U_i > ψ_c) = 0, we need only concentrate our updating efforts on those components c for which ψ_c > U_i for some i = 1, 2, …, n. By defining C^⋆ as in Equation 9 it can be shown (see Appendix A) that ψ_c < U_i for all c > C^⋆ and all i = 1, 2, …, n. Assuming that the Markov chain is initialized accordingly and is updated using the correct conditionals, it is possible to show Z^⋆ ≤ C^⋆ < ∞ almost surely (details provided in Appendix A).

With these definitions in place we make use of the following sets and vectors (which again will change at each sweep)

$$\begin{array}{c}\begin{array}{ccc}A=\{c\in {\mathbb{Z}}^{+}:c\le Z^{\star }\},& P=\{c\in {\mathbb{Z}}^{+}:Z^{\star }<c\le C^{\star }\},& I=\{c\in {\mathbb{Z}}^{+}:c>C^{\star }\}\end{array}\\ \begin{array}{cc}\hfill V^A=(V_{1,}{V}_2,\dots ,V_{Z^{\star }}),& {\Theta }^A=({\Theta }_1,{\Theta }_2,\dots ,{\Theta }_{Z^{\star }})\hfill \\ V^P=(V_{Z^{\star }+1,}{V}_{Z^{\star }+2},\dots ,V_{C^{\star }}),& {\Theta }^P=({\Theta }_{Z^{\star }+1},{\Theta }_{Z^{\star }+2},\dots ,{\Theta }_{C^{\star }})\hfill \\ \hfill V^I=(V_{C^{\star }+1,}{V}_{C^{\star }+2},\dots ),& {\Theta }^I=({\Theta }_{C^{\star }+1},{\Theta }_{C^{\star }+2},\dots ).\hfill \end{array}\end{array}$$

Here A, P and I are disjoint sets (updated at every sweep of the MCMC algorithm) that partition ℤ⁺, with names chosen to denote Active, Potential and Inactive components respectively. It is possible that P = Ø. By definition, all observations are allocated to a mixture component labeled by one of the indices in A. Components labeled with an index in P or I are necessarily empty (i.e., have no observations allocated to them), the difference being that at the next update of the allocation variables, components with labels in P may potentially become non-empty.

The blocked infinite DPMM algorithm can now be defined using the following blocked Gibbs updates to sample from the relevant conditionals.

DPMM algorithm

Suppose we are at sweep t of the sampler. Update as follows:

Step A. Compute Z^⋆ and the set A.

Step B. Sample $({\mathit{V}}_{t+1}^A,{\mathbf{\Theta }}_{t+1}^A,\tilde{\mathit{Z}},{\mathit{U}}_{t+1})\sim p({\mathit{V}}^A,{\mathbf{\Theta }}^A,\mathit{Z},\mathit{U}|{\mathit{V}}_t^P,{\mathit{V}}_t^I,{\mathbf{\Theta }}_t^P,{\mathbf{\Theta }}_t^I,{\alpha }_t,{\Lambda }_t,{\Theta }_0,\mathit{D}).$

$$\begin{array}{l}\mathit{B}\mathit{.1}\hspace{0.17em}{\tilde{\mathit{V}}}^A\sim p({\mathit{V}}^A|{\mathit{Z}}_t,{\alpha }_t)\\ \mathit{B}\mathit{.2}\hspace{0.17em}{\tilde{\mathbf{\Theta }}}^A\sim p({\mathbf{\Theta }}^A|{\mathit{Z}}_t,{\Lambda }_t,{\Theta }_0,\mathit{D})\\ \mathit{B}\mathit{.3}\hspace{0.17em}({\mathit{V}}_{t+1}^A,{\mathbf{\Theta }}_{t+1}^A,\tilde{\mathit{Z}})\sim p({\mathit{V}}^A,{\mathbf{\Theta }}^A,Z|V_t^P,{\Theta }_t^P,{\alpha }_t,{\Lambda }_t,{\Theta }_0,\mathit{D})\\ \mathit{B}\mathit{.4}\hspace{0.17em}{\mathit{U}}_{t+1}\sim p(\mathit{U}|{\mathit{V}}_{t+1}^A,\tilde{\mathit{Z}})\end{array}$$

Step C. Compute U^⋆. Recompute Z^⋆ and the set A.

Step D. Sample $({\alpha }_{t+1},{\mathit{V}}_{t+1}^P,{\mathit{V}}_{t+1}^I)\sim p(\alpha ,{\mathit{V}}^P,{\mathit{V}}^I|{\mathbf{\Theta }}_{t+1}^P,{\mathit{V}}_{t+1}^A,{\mathbf{\Theta }}_{t+1}^A,{\mathbf{\Theta }}_t^I,{\mathit{U}}_{t+1},\tilde{\mathit{Z}},{\Lambda }_t,{\Theta }_0,\mathit{D}),$ computing C^⋆ and the set P in the process.

$$\begin{array}{l}\mathit{D}\mathit{.1}\hspace{0.17em}{\alpha }_{t+1}\sim p(\alpha |{\mathit{V}}_{t+1}^A,\tilde{\mathit{Z}})\\ \mathit{D}\mathit{.2}\hspace{0.17em}{\mathit{V}}_{t+1}^P\sim p({\mathit{V}}^P|{\alpha }_{t+1},{\mathit{U}}_{t+1},\tilde{\mathit{Z}})\end{array}$$

Step E. Sample $({\mathbf{\Theta }}_{t+1}^P,{\mathbf{\Theta }}_{t+1}^I)\sim p({\mathbf{\Theta }}^P,{\mathbf{\Theta }}^I|{\mathit{V}}_{t+1}^A,{\mathit{V}}_{t+1}^P,{\mathit{V}}_{t+1}^I,{\mathbf{\Theta }}_{t+1}^A,{\mathit{U}}_{t+1},\tilde{\mathit{Z}},{\alpha }_{t+1},{\Lambda }_t,{\mathbf{\Theta }}_0,\mathit{D}).$

$$\mathit{E}\mathit{.1}\hspace{0.17em}{\mathbf{\Theta }}_{t+1}^P\sim p({\mathbf{\Theta }}^P|{\Theta }_0)$$

Step F. Sample ${\Lambda }_{t+1}\sim p(\Lambda |{\mathit{V}}_{t+1}^A,{\mathit{V}}_{t+1}^P,{\mathit{V}}_{t+1}^I,{\mathbf{\Theta }}_{t+1}^A,{\mathbf{\Theta }}_{t+1}^P,{\mathbf{\Theta }}_{t+1}^I,{\mathit{U}}_{t+1},\tilde{\mathit{Z}},{\alpha }_{t+1},{\Theta }_0,\mathit{D}).$

$$\mathit{F}\mathit{.1}\hspace{0.17em}\Lambda \sim p(\Lambda |{\mathbf{\Theta }}_{t+1}^A,\tilde{\mathit{Z}},\mathit{D})$$

Step G. Sample ${\mathit{Z}}_{t+1}\sim p(\mathit{Z}|{\mathit{V}}_{t+1}^A,{\mathit{V}}_{t+1}^P,{\mathit{V}}_{t+1}^I,{\mathbf{\Theta }}_{t+1}^A,{\mathbf{\Theta }}_{t+1}^P,{\mathbf{\Theta }}_{t+1}^I,{\mathit{U}}_{t+1},{\alpha }_{t+1},{\Lambda }_{t+1},{\Theta }_0,\mathit{D}).$

$$G.1\hspace{0.17em}{\mathit{Z}}_{t+1}\sim p(\mathit{Z}|{\mathit{V}}_{t+1}^A,{\mathit{V}}_{t+1}^P,{\mathbf{\Theta }}_{t+1}^A,{\mathbf{\Theta }}_{t+1}^P,{\mathit{U}}_{t+1},{\Lambda }_{t+1},\mathit{D})$$

While this algorithm is somewhat generic, the blocking strategy is clearly highlighted. Further details explaining each of the steps are provided in Appendix B. The key idea is that by doing joint updates, we can marginalize out an infinite number of variables when necessary, to ensure that we are always sampling from conditional distributions that depend only upon a finite number of parameters. In particular, after marginalization, the parameters corresponding to the inactive set I do not contribute to the conditional distributions of the other parameters, so we do not actually need to sample their values. Since these parameters have no contribution to the likelihood, if values are subsequently required they can simply be sampled from the prior retrospectively as necessary. Although the sampler is written as a blocked Gibbs sampler, where it is not possible to sample directly from full conditionals (for example in the update of Θ, depending upon the choices of f and $P_{{\Theta }_0}$) Metropolis-within-Gibbs steps are applied. Depending on the application, the Gibbs updates specified above may comprise several different Gibbs or Metropolis-within-Gibbs steps (for example updating Θ and Λ). Typically, where Metropolis-Hastings updates are required we advocate adopting an adaptive Metropolis-Hastings approach: see Andrieu and Thoms (2008) for a review.

3. Example models

The general sampler of the previous section is applicable for many specific models, depending on the choices of f and $P_{{\Theta }_0}.$ In this section we provide further details for some of the models that are implemented within our software. We detail the prior choices that are made within our implementation, but, of course, alternative priors could be chosen.

3.1. Gaussian mixtures

Perhaps the most common model to be implemented under the DPMM framework is the Gaussian mixture model, where D = X for some covariate data X, and X assumes a mixture of Gaussian distributions. Under this setting for each cluster c, the cluster specific parameters are given by Θ_c = (µ_c, Σ_c), where µ_c is a mean vector and Σ_c is a covariance matrix. There are no additional global parameters Λ. Under this setting

$$p\left(X_i|Z_i,{\Theta }_{Z_i},\Lambda \right)=f\left(X_i|{\mu }_{Z_i},{\Sigma }_{Z_i}\right)={(2\pi )}^{-\frac{J}{2}}|{\Sigma }_{Z_i}{|}^{-\frac{1}{2}}\exp \left\{-\frac{1}{2}{\left(X_i-{\mu }_{Z_i}\right)}^{\top }{\Sigma }_{Z_i}^{-1}\left(X_i-{\mu }_{Z_i}\right)\right\}.$$ (10)

By choosing µ_c ∼ Normal(µ₀, Σ₀) and Σ_c ∼ InvWishart(R₀, κ₀) (for each c) for our prior model $P_{{\Theta }_0}$ we have a conjugate model, permitting Gibbs updates for the parameters µ^A and Σ^A associated with the active clusters, and also those (µ^P and Σ^P) associated with the potential clusters. The choice of values for the hyperparameters Θ₀ = (µ₀, Θ₀, R₀, κ₀) is discussed further in Section 7.

3.2. Discrete mixtures

Clearly the DPMM model applies to mixtures other than the Gaussian one. Consider for example the case where for each individual i, D_i = X_i is a vector of J locally independent discrete categorical random variables, where the number of categories for covariate j = 1, 2, …, J is K_j. Then we can write Θ_c = Φ_c = (Φ_c,1, Φ_c,2 …, Φ_c,J) with ${\Phi }_{c,j}=({\varphi }_{c,j,1},{\varphi }_{c,j,2},\dots ,{\varphi }_{c,j,K_j})$ and

$$p\left(D_i|Z_i,{\Theta }_{Z_i},\Lambda \right)=f\left(D_i|{\Phi }_{Z_i}\right)={\displaystyle \prod _{j=1}^J{\varphi }_{Z_i,j,X_{i,j}.}}$$ (11)

Again, there are no global parameters Λ.

Letting Θ₀ = a = (a₁, a₂, …, a_J), where for $j=1,2,\dots ,J,\hspace{0.17em}{a}_j=(a_{j,1},a_{j,2},\dots ,a_{j,K_j})$ and adopting conjugate Dirichlet priors Φ_c,j ∼ Dirichlet(a_j), each Φ_c can be updated directly using Gibbs updates. For full details of the posterior conditional distribution see Molitor et al. (2010).

3.3. Mixed mixtures

An alternative model is given by a mixture of some continuous and discrete random variables. Following the notation used above for Gaussian and discrete mixtures, for J₁ continuous random variables and J₂ discrete random variables,

$$p\left(D_i|Z_i,{\Theta }_{Z_i},\Lambda \right)=p\left(D_i^1|{\mu }_{Z_i},{\Sigma }_{Z_i}\right)p\left(D_i^2|{\Phi }_{Z_i}\right)$$ (12)

where $D_i^1$ is the subset of the continuous random variables in D_i and $D_i^2$ is the subset of the categorical random variables in D_i. Note that we are assuming independence between continuous and categorical data conditional on the cluster allocations.

3.4. Profile regression

Recently, interest has grown in using DPMM as an alternative to regression models, non-parametrically linking a response vector Y to covariate data X through cluster membership. This idea has been pioneered by several authors including Dunson, Herring, and Siega-Riz (2008), Bigelow and Dunson (2009), Molitor et al. (2010), Papathomas, Molitor, Richardson, Riboli, and Vineis (2011), and Molitor et al. (2011). Our presentation is most similar to the latter three of these articles which refer to this idea as “profile regression”.

For the case of either Gaussian or discrete mixtures, as described above, our implementation permits the joint modeling of a response vector, for various response models which we present below. Formally, the data D = (Y, X) are now extended to contain response data Y_i and covariate data X_i for each individual i, where the contribution of the covariate data to the response may be cluster dependent. There is also the possibility to include additional fixed effects W_i for each individual, which are constrained to only have a global (i.e., non-cluster specific) effect on the response Y_i.

The data D_i are then jointly modeled as the product of a response model and a covariate model, to give the following likelihood:

$$p\left(D_i|Z_i,\Theta ,\Lambda ,W_i\right)=f_Y\left(y_i|{\Theta }_{Z_i},\Lambda ,W_i\right)f_X(x_i|{\Theta }_{Z_i},\Lambda ).$$

The covariate likelihood f_X is of either of the forms presented in Sections 3.1 or 3.2. The likelihood f_Y depends upon the choice of response model.

Binary response

Adopting a binary response model, each parameter vector Θ_c is extended to include an additional parameter θ_c. We also introduce the global parameter vector Λ = β, of the same length L as the fixed effects vector W_i, to capture the contribution of these effects. Then, $f_Y(y_i|{\Theta }_{Z_i,}\Lambda ,W_i)=p(Y_i=1|{\theta }_{Z_i,}\beta ,W_i)$ is given by

$$\text{logit}\left\{p\left(Y_i=1|{\theta }_{Z_i},\beta ,W_i\right)\right\}:={\lambda }_i={\theta }_{Z_i}+{\beta }^{\top }{W}_i.$$

For each cluster c, we adopt a t location-scale distribution for θ_c, with hyperparameters µ_θ and σ_θ with 7 degrees of freedom, as discussed by Molitor et al. (2010). Similarly, for each fixed effect l, we adopt the same prior for β_l, but with hyperparameters µ_β and σ_β.

The components of Θ_c corresponding to the covariate model for X retain the possibility of being updated according to Gibbs samples. However, since conjugacy is not achieved with our prior choice, updating θ_c for each cluster (and β_l for each fixed effect l) requires a Metropolis-within-Gibbs sampler. In our implementation we propose the use of adaptive random-walk-Metropolis moves.

Categorical response

The categorical response model that we use is a simple extension of the binary response model of the previous section. In particular, each parameter vector Θ_c additionally contains an extra parameter vector θ_c = (θ_c,1, θ_c,2, …, θ_c,R−1) of length R − 1, where R is the number of possible categories represented in the response data Y. Treatment of fixed effects is also extended, so that for each response category r = 1, 2, …, R − 1, there is a vector β_r = (β_r,1, β_r,2, …, β_r,L), where β_r,l is the coefficient for each fixed effect l (l = 1, 2, …, L). This gives $f_Y(y_i|{\Theta }_{Z_i},\Lambda ,W_i)=p(Y_i=r|{\theta }_{Z_i,r},\beta ,W_i)$ as

$$\begin{array}{cc}\text{logit}\left\{p\left(Y_i=r|{\theta }_{Z_i},\beta ,W_i\right)\right\}={\theta }_{Z_i,r}+{\beta }_r^{\top }{W}_i,& \text{for}\hspace{0.17em}r=1,2,\mathrm{\dots },R-1\end{array}$$

and $p\left(Y_i=0|{\theta }_{Z_i},\beta ,W_i\right)=1-{\displaystyle {\sum }_{r=1}^{R-1}p(Y_i=r|{\theta }_{Z_i},\beta ,W_i)}.$

In our sampler we use the same priors for each θ_c,r as for θ_c and β_r,l as for β_l in the binary case, with the resulting observation about Metropolis-within-Gibbs updates remaining true. Note that θ_c,r and β_c,r are independent across r.

Count response modeled as Binomial

By providing a number of trials T_i associated with each individual i (in this model an “individual” might correspond to an area or “experiment”) we can extend the binary response model to a Binomial response model. In particular,

$$f_Y\left(y_i|{\Theta }_{Z_i},\Lambda ,W_i\right)=p\left(Y_i|{\theta }_{Z_i},\beta ,W_i\right)=\left(\begin{array}{c}{T}_i\\ Y_i\end{array}\right)p_i^{Y_i}{\left(1-p_i\right)}^{T_i-Y_i},$$

where

$$\text{logit}\left\{p_i\right\}:={\lambda }_i={\theta }_{Z_i}+{\beta }^{\top }{W}_i.$$

Priors used are identical to the binary case. Molitor et al. (2011) provide an example where this model is employed.

Count response modeled as Poisson

For count-type response data, an alternative to the Binomial model is the Poisson model. Under this model, each individual i is associated with an expected offset E_i, and the response is then modeled as

$$f_Y\left(y_i|{\Theta }_{Z_i},\Lambda ,W_i\right)=p\left(Y_i|{\theta }_{Z_i},\beta ,W_i\right)=\frac{{\mu }_i^{Y_i}}{Y_i!}\exp \left\{-{\mu }_i\right\},\hspace{0.17em}$$

where

$$\begin{array}{cc}{\mu }_i=E_i\exp \left\{{\lambda }_i\right\},& \text{for}\hspace{0.17em}{\lambda }_i={\theta }_{Z_i}+{\beta }^{\top }{W}_i.\end{array}$$

Prior models for θ_c and β are as above.

Extra variation in the response

For the binary, Binomial and Poisson models above, it is possible that we may wish to allow for extra variation in the response. In the case of the Poisson model this corresponds to modeling counts with a Negative Binomial distribution. Our sampler is designed to achieve this by alternatively modeling λ_i (as defined in the above response models) by

$$\begin{array}{cc}{\lambda }_i={\theta }_{Z_i}+{\beta }^{\top }{W}_i+{\epsilon }_i,& \text{where}\hspace{0.17em}{\epsilon }_i\sim \text{Normal}\left(0,{\sigma }_{\epsilon }^2\right).\end{array}$$

Prior distributions for θ_c and β are unchanged, but in this model Λ contains an additional parameter, ${\sigma }_{\epsilon }^2,$ for which prior specification is required. For simplicity we work in terms of the precision ${\tau }_{\epsilon }=1/{\sigma }_{\epsilon }^2,$ and adopt a Gamma distribution with shape parameter $s_{{\tau }_{\epsilon }}$ and rate parameter $r_{{\tau }_{\epsilon }}.$ This approach permits a simple Gibbs update of this parameter. In order to make inference about this model, it is also necessary to update the latent variables λ_i at every sweep of the MCMC sampler. These parameters are considered an extension of Λ (as they are not directly associated with a specific cluster) and are therefore updated in Step F of the DPMM algorithm. Updates to these parameters are done using adaptive random-walk-Metropolis steps.

Gaussian response

Our sampler is able to handle continuous response data. As for many of the discrete response models, Θ_c is extended to contain θ_c for each c. As before Λ contains β, but also ${\sigma }_Y^2.$ These parameters allow us to write the response model as:

$$f_Y\left(y_i|{\Theta }_{Z_i},\Lambda ,W_i\right)=p\left(Y_i|{\theta }_{Z_i},\beta ,{\sigma }_Y^2,W_i\right)=\frac{1}{\sqrt{2\pi {\sigma }_Y^2}}\exp \left\{-\frac{1}{2{\sigma }_Y^2}{\left(Y_i-{\lambda }_i\right)}^2\right\},$$

where ${\lambda }_i={\theta }_{Z_i}+{\beta }^{\top }{W}_i.$

We impose the same prior settings as for the discrete response models, with the additional prior on ${\tau }_Y=1/{\sigma }_Y^2$ being Gamma $(s_{{\tau }_Y},r_{{\tau }_Y})$ where $s_{{\tau }_Y}$ and $r_{{\tau }_Y}$ are the shape and rate hyper parameters that extend Θ₀. Adopting this conjugate prior, updates for τ_Y are simple Gibbs updates.

3.5. Variable selection

In addition to fitting mixtures, potentially linking covariates and responses, it may additionally be of interest to determine which covariates actively drive the mixture components, and which share characteristics common to all components. This can be formulated as a question of variable selection. Below we present details of how this idea can be modeled, first in the case of discrete covariates, as considered by Papathomas, Molitor, Hoggart, Hastie, and Richardson (2012), and then in the context of Gaussian covariates, a formulation which, as far as we are aware, has not been reported elsewhere. Relevant to the variable selection formulation we have adopted is the model described in Chung and Dunson (2009). A different modeling approach is presented in Quintana et al. (2013). Quintana et al. (2013) consider the logit of the binary cluster specific selection switches and impose an additional level in the hierarchy using Normal densities and associated hyper-parameters. A normalization step is then required. In contrast, we impose an additional level in the hierarchy considering Bernoulli distributions for the binary switches, without the requirement of a normalization step.

Discrete covariates

Following the approach taken by Papathomas et al. (2012) our sampler implements two types of variable selection. We outline these approaches briefly in this section but for full details the reader is referred to this paper.

The first is a cluster specific variable selection approach, based on a modification of the model in Chung and Dunson (2009). Each mixture component c has an associated vector γ_c = (γ_c,1, γ_c,2, …, γ_c,J), where γ_c,j is a binary random variable that determines whether covariate j is important to mixture component c. Let ϕ_0,,j,k be the observed proportion of covariate j taking the value k throughout the whole covariate dataset X. Define the new composite parameters,

$${\varphi }_{c,j,k}^{*}:={\gamma }_{c,j}{\varphi }_{c,j,k}+\left(1-{\gamma }_{c,j}\right){\varphi }_{0,j,k}={\left({\varphi }_{c,j,k}\right)}^{{\gamma }_{c,j}}{\left({\varphi }_{0,j,k}\right)}^{\left(1-{\gamma }_{c,j}\right)}.$$

The above expression is substituted into Equation 11 in place of ϕ_c,j,k, to provide the likelihood for the covariate model. Under this model, each parameter vector Θ_c is extended by γ_c. We assume that, given ρ_j, the γ_c,j, c = 1, …, C, are independent Bernoulli variables with γ_c,j ~ Bernoulli(ρ_j). We further consider a sparsity inducing prior for ρ_j with an atom at zero, so that

$${\rho }_j\sim 1_{\{w_j=0\}}{\delta }_0\left({\rho }_j\right)+1_{\left\{w_{j=1}\right\}}\text{Beta}\left({\alpha }_{\rho },{\beta }_{\rho }\right),\hspace{0.17em}$$

where w_j ~ Bernoulli(p_w). Therefore, additional parameters ρ_j and w_j are introduced into Λ. Here, α_ρ and β_ρ are fixed, and can be specified by the user. The parameter p_w is set equal to 0.5 by default, but it can also be specified by the user, also allowing for the atom at zero to be removed. The binary nature of γ_c,j means that direct Gibbs updates can be used. This is an approach that allows for local cluster specific covariate selection, considering the γ_c,j parameters, as well as global covariate selection, considering the overall selection probabilities ρ_j.

An alternative approach to the variable selection presented above is a type of soft variable selection, where each covariate j, is associated with a latent variable ζ_j, taking values in [0, 1], which informs whether variable j is important in terms of supporting a mixture distribution. We define the new composite parameters as,

$${\varphi }_{c,j,k}^{*}:={\zeta }_j{\varphi }_{c,j,k}+\left(1-{\zeta }_j\right){\varphi }_{0,j,k}.$$

which, as in the first variable selection model, is substituted into Equation 11 in place of ϕ_c,j,k, to provide the likelihood for the covariate model. Similarly to the first specification, we consider a sparsity inducing prior for ζ_j with an atom at zero, so that

$${\zeta }_j\sim 1_{\left\{v_j=0\right\}}{\delta }_0\left({\zeta }_j\right)+1_{\left\{v_j=1\right\}}\text{Beta}\left({\alpha }_{\zeta },{\beta }_{\zeta }\right),$$

where v_j ~ Bernoulli(p_w). The parameter p_w is set equal to 0.5 by default, but it can also be specified by the user, also allowing for the atom at zero to be removed. Conjugacy for ϕ_c,j is no longer retained, meaning that Metropolis-within-Gibbs updates are necessary. We use adaptive random-walk-Metropolis proposals. The second alternative approach only allows for global variable selection and, in principle, is less likely to encounter mixing problems, compared to the more elaborate first formulation. Nevertheless, we have not yet observed considerable mixing problems when adopting either approach using PReMiuM. For extended details of the conditional posteriors and updating strategy the interested reader is referred to Papathomas et al. (2012).

Gaussian covariates

The two variable selection methods described above can equally be applied to the Gaussian mixture case. Defining $\overline{x}\hspace{0.17em}=\left({\overline{x}}_1,{\overline{x}}_2,\mathrm{\dots },{\overline{x}}_J\right),\hspace{0.17em}\text{where}\hspace{0.17em}{\overline{x}}_j=\frac{1}{n}{\sum }_i{x}_{i,j}$ is the average sample value of covariate j, we can define the vector ${\mu }_c^{*}=\left({\mu }_{c,1}^{*},{\mu }_{c,2}^{*},\mathrm{\dots },{\mu }_{c,J}^{*}\right)$ where either

$${\mu }_{c,j}^{*}={\gamma }_{c,j}{\mu }_{c,j}+(1-{\gamma }_{c,j}){\overline{x}}_j$$

or

$${\mu }_{c,j}^{*}={\zeta }_j{\mu }_{c,j}+(1-{\zeta }_j){\overline{x}}_j$$

depending on which variable selection approach is being adopted. We then replace µ_c,j with ${\mu }_{c,j}^{*}$ in Equation 10. Using identical priors for ζ_j or γ_c,j and ρ_j, these parameters are updated as for the discrete covariate case. The posterior conditional distributions for updating µ_c are shown in Appendix C, whereas those for updating other parameters are as before, with µ_c,j replaced with ${\mu }_{c,j}^{*}$ as appropriate.

4. Predictions

An important feature of our software is the computation of predicted responses for prediction scenarios. Suppose that we wish to understand the role of a particular covariate or group of covariates. We can specify a number of predictive scenarios (or pseudo-profiles), that capture the range of possibilities for the covariates that we are interested in. At each iteration the predictive subjects are assigned to one of the current clusters according to their covariate profiles. Seeing how these pseudo-profiles are allocated allows us to understand the risk associated with these profiles.

The predictive subjects have no impact on the likelihood and so do not determine the clustering or parameters at each iteration and missing values in the predictive scenarios are ignored. At each sweep r of the MCMC sampler we define an additional “allocation” variable, ${\tilde{Z}}_s^r$ corresponding to each predictive scenario s. Our software produces predicted values based on simple allocations or a Rao-Blackwellized estimate of predictions. The predicted values based on a simple allocation of cluster c assign ${\widehat{\theta }}_s^r={\theta }_c^r.$ For the Rao-Blackwellized predictions the probabilities of allocations are used instead of actually performing a random allocation. For each pseudo-profile we compute the posterior probabilities $p({\tilde{Z}}_s^r=c|{\mathit{\text{x}}}_s,{\mathbf{\Theta }}^r,\mathit{\text{y}},{\mathit{\text{x}}}_1,\mathrm{\dots },{\mathit{\text{x}}}_n).$ With these probabilities we construct a cluster-averaged estimate of θ for each particular pseudo-profile at each sweep. Specifically,

$${\widehat{\theta }}_p^r={\displaystyle \sum _{c=1}^{\infty }p\left({\tilde{Z}}_p^r=c|{\mathit{\text{x}}}_p,{\mathbf{\Theta }}^r,\mathit{\text{y}},{\mathit{\text{x}}}_1,\mathrm{\dots },{\mathit{\text{x}}}_n\right)}{\theta }_c^r.$$

Looking at the density of these predictions over MCMC sweeps gives us an estimate of the effect of a particular pseudo-profile, and its comparison to other pseudo profiles, allowing us to derive a better understanding of the role of specific covariates. Moreover, the impact of ignoring missing values in the pseudo-profiles essentially means that the missing value will reflect the covariate patterns present in the main sample. Because of this, the marginal effect of covariates or groups of covariates that is derived has to be interpreted as a population average effect, over a population with similar characteristics to that under study.

If a subject is missing fixed effects, then the mean value or 0 category fixed effect is used in the predictions. In this case, effectively, the fixed effects do not contribute to the predicted response. If the offset or number of trials is missing, this value is taken to be 1 when making predictions.

5. Postprocessing of the MCMC output

The rich posterior output produced can be used to learn about the partition space and its uncertainty. It is useful to show a representative partition, as an effective way to convey the output of the clustering algorithm. Moreover, it is also of interest to assess the uncertainty associated with subgroups of this best partition.

We discuss below the necessary steps. See also Molitor et al. (2010).

• 1.Computation of the dissimilarity matrix. Due to the problem of “label switching”, i.e the labels associated with each cluster change during the MCMC iterations, we can not simply assign each observation to the cluster that maximizes the average posterior probability. Methods that deal with label switching, like the relabeling algorithm of Stephens (2000), require the number of clusters K to be fixed. Using the Dirichlet process mixture models, we allow the number of clusters to vary from one MCMC sample to the next. One possible solution is to choose the partition based on a posterior similarity matrix. At each iteration of the sample, we record pairwise cluster membership and construct a score matrix, with entries equal to 1 for pairs belonging to the same cluster and 0 otherwise. Averaging these matrices over the whole MCMC run leads to a similarity matrix S, which can be then used to identify an optimal partition.
• 2.Identifying the optimal partition. Many methods to identify the optimal partition using the posterior similarity matrix have been proposed in the literature. The similarity matrix computed by PReMiuM can be processed using the R package mcclust (Fritsch and Ickstadt 2009). We have implemented directly in PReMiuM two deterministic clustering procedures to characterize the optimal partition.

  The first finds the best partition by choosing the one which minimizes the least-square distance to the matrix S. This approach is equivalent to the Binder’s loss method (Fritsch and Ickstadt 2009). It is fast, but in our experience it is susceptible to Monte Carlo error.

  The second procedure implemented in the package is partitioning around medoids (PAM) on the dissimilarity matrix 1 − S. PAM is available in R in the package cluster (Maechler, Rousseeuw, Struyf, Hubert, and Hornik 2014) and it robustly assigns individuals to clusters in a way consistent with matrix S. PAM is implemented for each possible number of clusters up to a specified maximum, and for each fixed number of clusters the best PAM partition is selected. A final representative cluster is then chosen by maximizing the average silhouette width across these best PAM partitions.

• 3.Computation of the average risk and profile and the corresponding credible intervals. Given an optimal partition P* obtained as above, we examine the MCMC output to assess whether or not the model consistently clusters individuals in a manner similar to P*.
  For example, for Bernoulli response, we obtain a distribution of the baseline risks for each cluster defined by P*. At each iteration of the sampler we compute the average of baseline risks p_zi, defined in Section 3.4, for all individuals within a particular cluster k of the optimal partition. This average baseline risk for cluster k is computed as follows:

  $${\overline{p}}_k=\frac{1}{n_k}{\displaystyle \sum _{i:z_i^{P*}=k}{p}_{z_i}}$$

  where n_k denotes the number of individuals in cluster k. This provides an empirical sample from the baseline risk associated with cluster k. Consistent clustering leads to narrower credible intervals derived from this distribution. In a similar way we can compute the distribution of cluster parameters for other response and covariates types.

6. Mixing of the MCMC algorithm

The likelihood of the DPMM is invariant to the order of cluster labels but the prior specification of the stick breaking construction is not. Therefore, to ensure adequate mixing across orderings, it is important to include label switching moves. In this package we have implemented the two label switching moves proposed by Papaspiliopoulos and Roberts (2008) as well as a third label switching move proposed by Hastie, Liverani, and Richardson (2014). This latter move updates the cluster weights so that for each cluster being updated, the proposed new weight is the expected value of the weight conditional upon the new allocations, adjusted by the ratio of the existing weight and its expected value conditional upon the existing allocations, with the weights appropriately normalized. See Equation 6 of Hastie et al. (2014) for details of the move, and more generally for a review of the sampler performance.

Even with these label switching moves, convergence may be problematic and the user must address this issue using diagnostic tools. One difficulty in this respect is that there are no parameters in the model that can reliably demonstrate convergence. The parameters of the fixed effects tend to converge very quickly, regardless of the underlying clustering, as they are not cluster specific and therefore are not a good indication of the overall convergence. Plotting functions to assess convergence of the global parameters are included in the package and are discussed in Section 8. The cluster parameters, such as the θ_c’s, cannot be tracked as their number (and their labels) can change from one iteration to the next. The concentration parameter α is not a reliable indicator of convergence either, as discussed in Hastie et al. (2014).

To overcome this challenge, we have implemented the computation of the marginal model posterior p(Z|D) as an additional diagnostic tool. This represents the posterior distribution of the allocations given the data, having marginalized out all the other parameters (Hastie et al. 2014). The marginal model posterior is computed for each run of the MCMC and it has proved very effective for our real examples to compare runs with different initializations and identify runs that were significantly different from others. Our experience suggests that it is harder for the MCMC algorithm to split rather than merge clusters. This means that it is important to initialize the algorithm with a number of cluster which is greater than the number of clusters that the algorithm will convergence to. The marginal model posterior can help to assess what such number is for each specific example.

Finally, while optimal partitions allow visualization of the result of a clustering algorithm, such an approach must be applied with care as we are not aware of any effective method to directly quantify nor visualize clustering uncertainty. For this reason, we advise using predictions as an additional tool to assess convergence and visualize the output of the algorithm, as their posterior distributions can be compared across runs using standard methods. More details of using the package for predictions can be found in Section 8. We have observed that these posterior predictive distributions tend to be more stable than optimal partitions.

7. Software

Our implementation of the DPMM algorithm is available as an R package from the Comprehensive R Archive Network (CRAN) at. http://CRAN.R-project.org/package=PReMiuM. The software is primarily written in C++ and R.

The sampler implements the algorithm exactly as detailed in the current paper, although continued work is in progress to extend the scope of the software to cover additional models.

The program is further customizable through the specification of hyperparameters, providing name-value pairs for the various hyperparameters used within the model being run. If the value is not set for a specific hyperparameter, it takes its default value. Default values can be found within the full documentation that is available as part of the software and an example in provided in Section 8.3.

Moreover, this package can produce predicted values based on random allocations, or a Rao-Blackwellized estimate of predictions, where the probabilities of allocations are used instead of actually performing a random allocation.

8. Examples

8.1. Simulated example

We simulated 1,000 subjects, partitioned into 5 groups in a balanced manner. Ten binary covariates were considered. To demonstrate one of the variable selection approaches within the sampler, only the first eight covariates support a clustering structure. The response is binary. This dataset can be simulated as follows.

R> library("PReMiuM")
R> inputs <- generateSampleDataFile(clusSummaryVarSelectBernoulliDiscrete())

We used the default values for all hyperparameters: Dirichlet conjugate priors with a_j = 1 for the covariates and

$$\begin{array}{l}p(\alpha )\hspace{0.17em}\equiv \hspace{0.17em}\text{Gamma}(2,1)\\ p({\theta }_c)\hspace{0.17em}\equiv \hspace{0.17em}{t}_7(0,2.5)\\ p(\beta )\hspace{0.17em}\equiv \hspace{0.17em}{t}_7(0,2.5)\end{array}$$

where $\text{Gamma}(\alpha ,\beta )\equiv \frac{{\beta }^{\alpha }}{\Gamma (\alpha )}{x}^{\alpha -1}{e}^{-\beta x}$ and

$${\text{t}}_v\left(\mu ,\sigma \right)\equiv \frac{\Gamma \left(\frac{v+1}{2}\right)}{\Gamma \left(\frac{v}{2}\right)\sqrt{\pi v\sigma }}{\left[1+\frac{1}{v}{\left(\frac{x-\mu }{\sigma }\right)}^2\right]}^{-\frac{v+1}{2}}.$$ (13)

We initialized all chains allocating subjects randomly to 20 groups. We ran the chain for 10,000 iterations after a burn-in sample of 20,000 iterations. While ensuring convergence is a complex problem, we have observed good stability in all our runs, with results from independent chains virtually identical.

R> runInfoObj <- profRegr(yModel = inputs$yModel, xModel = inputs$xModel,
+    nSweeps = 10000, nBurn = 20000, data = inputs$inputData,
+    output = "output", covNames = inputs$covNames, nClusInit = 20,
+    run = TRUE)
R> dissimObj <- calcDissimilarityMatrix(runInfoObj) 
R> clusObj <- calcOptimalClustering(dissimObj)
R> riskProfileObj <- calcAvgRiskAndProfile(clusObj)
R> clusterOrderObj <- plotRiskProfile(riskProfileObj, "summary-sim.png")

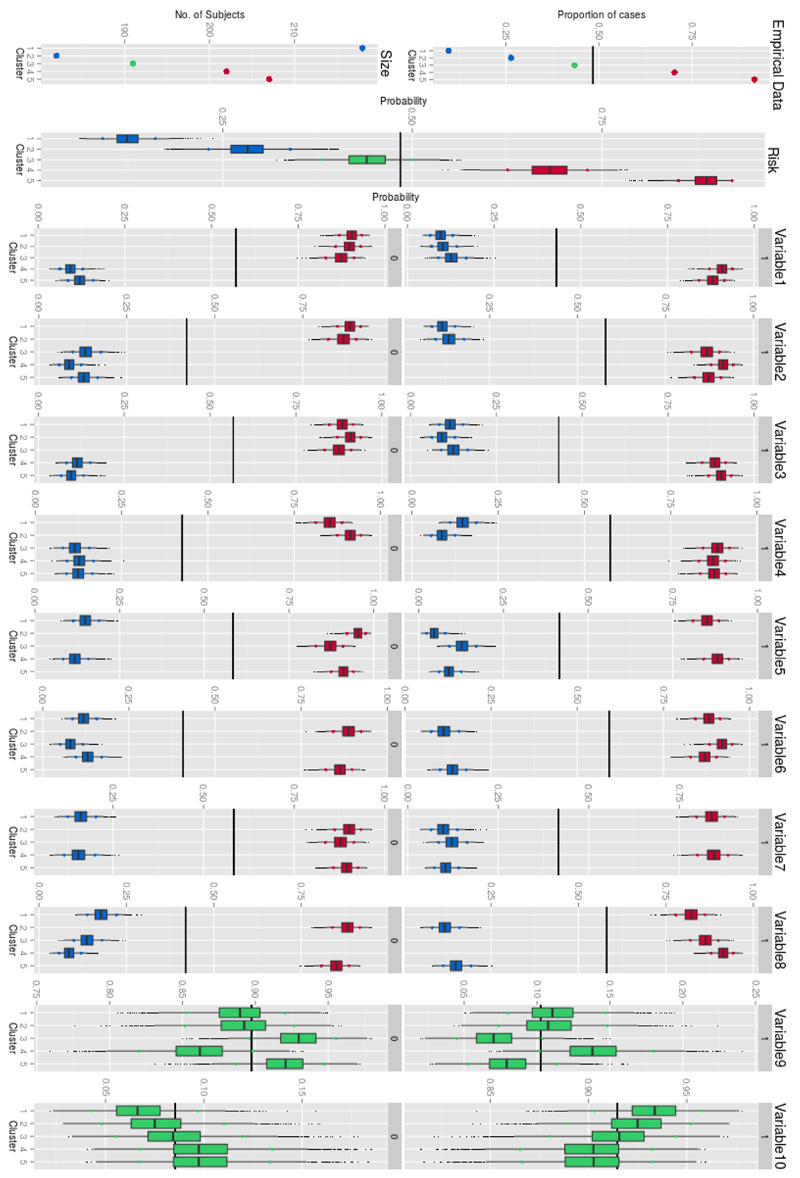
Figure 1 shows a box-plot of the posterior distribution for the probabilities of the response and the covariates for the 5 clusters that form the representative clustering. Additionally, the package includes the function heatDissMat() which produces a heatmap of the dissimilarity matrix, rearranged such that observations with high pairwise cluster membership appear consecutively.

Figure 1.

Posterior distributions of the parameters for binary response and discrete covariates for the representative clustering.

8.2. Predictions

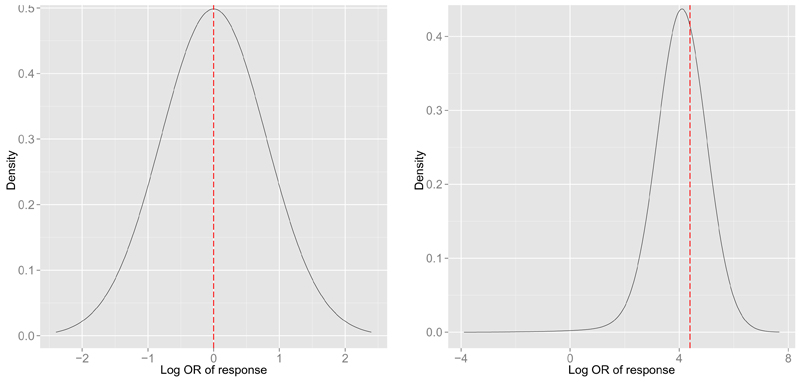
PReMiuM can produce predicted values based on simple allocations (the default), or a Rao-Blackwellized estimate of predictions, where the probabilities of allocations are used instead of actually performing a random allocation. The following code can be used to reproduce the predictive distribution plotted in Figure 2. As discussed in Section 4, the missing values, as in the second prediction scenario given below, are ignored and their marginal effect can be interpreted as a population average effect. The predictions are consistent with the simulated data.

Figure 2.

The predictive distribution of the response for two prediction scenarios. The covariate values for the predictive scenarios are [2, 2, 2, 2] and [0, 0, NA, 0, 0] respectively. ‘NA’ represents a missing value. The dashed lines represent the data generating parameters corresponding to the clusters that we expect these two predictive scenarios to be assigned to.

R> inputs <- generateSampleDataFile(clusSummaryBernoulliDiscrete())
R> preds <- data.frame(matrix(c(2, 2, 2, 2, 2, 0, 0, NA, 0, 0), ncol = 5,
+    byrow = TRUE))
R> colnames(preds) <- names(inputs$inputData)[2:(inputs$nCovariates+1)] 
R> runInfoObj <- profRegr(yModel = inputs$yModel, xModel = inputs$xModel,
+    nSweeps = 1000, nBurn = 1000, data = inputs$inputData,
+    output = "output", covNames = inputs$covNames, predict = preds,
+    fixedEffectsNames = inputs$fixedEffectNames) 
R> dissimObj <- calcDissimilarityMatrix(runInfoObj) 
R> clusObj <- calcOptimalClustering(dissimObj)
R> riskProfileObj <- calcAvgRiskAndProfile(clusObj) 
R> predictions <- calcPredictions(riskProfileObj,
+    fullSweepPredictions = TRUE, fullSweepLogOR = TRUE) 
R> plotPredictions(outfile = "predictiveDensity.pdf",
+    runInfoObj = runInfoObj, predictions = predictions, logOR = TRUE)

8.3. Variable selection

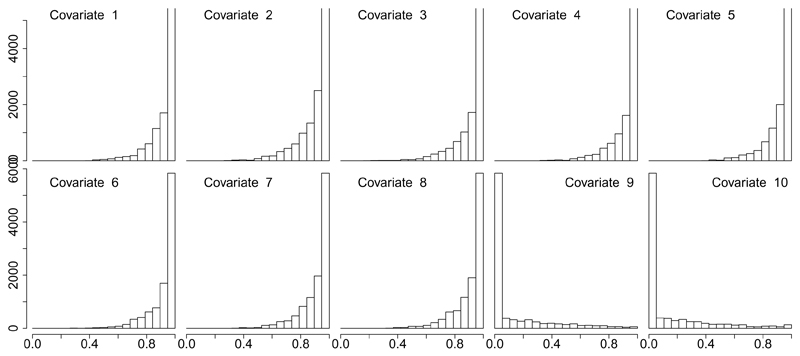
Note that covariates 9 and 10 in Figure 1 have similar profile probabilities for all clusters, as they have been simulated not to affect the clustering. The variable selection approach will identify the covariates that do not contain clustering support and exclude them from affecting the clustering.

We initialized the chains as in the simulated example above, with additional prior specifications given by

$${\rho }_j\sim 1_{\left\{w_j=0\right\}}{\delta }_0\left({\rho }_j\right)+1_{\left\{w_j=1\right\}}\text{Beta}(0.5,0.5),$$

where w_j ~ Bernoulli(0.5). The algorithm consistently sampled values ρ_p in accordance with the simulated data, as shown in Figure 3. This figure can be reproduced as follows.

Figure 3.

The sampled values of the binary variable ρ_j, used for variable selection, for each covariate.

R> inputs <- generateSampleDataFile(clusSummaryVarSelectBernoulliDiscrete())
R> hyp <- setHyperparams(aRho = 0.5, bRho = 0.5, atomRho = 0.5)
R> runInfoObj <- profRegr(yModel = inputs$yModel, xModel = inputs$xModel,
+    nSweeps = 10000, nBurn = 10000, data = inputs$inputData,
+    output = "output", covNames = inputs$covNames,
+    varSelectType = "BinaryCluster", hyper = hyp)
R> rho <- summariseVarSelectRho(runInfoObj)
R> par(mfrow = c(5, 2))
R> for (k in 1:runInfoObj$nCovariates)
+    hist(rho$rho[, k], xlim = c(0, 1), main = "")

8.4. Assessing convergence

There is no method that can assure us that our MCMC chains have converged to the posterior probability distribution but there are several methods that can investigate whether there is evidence against convergence.

We have implemented the function globalParsTrace() which provides a basic diagnostic plot of the trace of some global parameters such as α, β and the number of clusters. For more convergence diagnostics we recommend using the R package coda (Plummer, Best, Cowles, and Vines 2006). coda is an R package to perform convergence diagnostics and statistical and graphical output analysis of the output from an MCMC sampler.

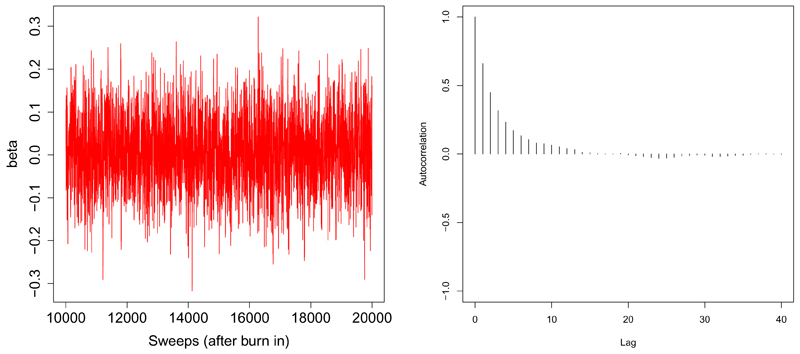
The following code can be used to reproduce the trace plot and autocorrelation plot in Figure 4 for parameter β₁.

Figure 4.

Convergence diagnostics for parameter β1: trace plot and autocorrelation plot done using coda.

R> inputs <- generateSampleDataFile(clusSummaryBernoulliDiscrete())
R> runInfoObj <- profRegr(yModel = inputs$yModel, xModel = inputs$xModel,
+    nSweeps = 10000, nBurn = 10000, data = inputs$inputData,
+    output = "output", covNames = inputs$covNames,
+    fixedEffectsNames = inputs$fixedEffectNames)
R> globalParsTrace(runInfoObj, parameters = "beta", plotBurnIn = FALSE,
+     whichBeta = 1)
R> library("coda")
R> betaChain <- mcmc(read.table("output_beta.txt")[, 1])
R> autocorr.plot(betaChain)

The cluster specific parameters cannot be plotted as easily due to label switching and assessing their convergence is not an easy task. Hastie et al. (2014) introduce the marginal model posterior as a tool to assess convergence for Dirichlet process mixtures. We define the marginal partition posterior as p(Z|D). This quantity represents the posterior distribution of the allocations given the data, having marginalized out all the other parameters.

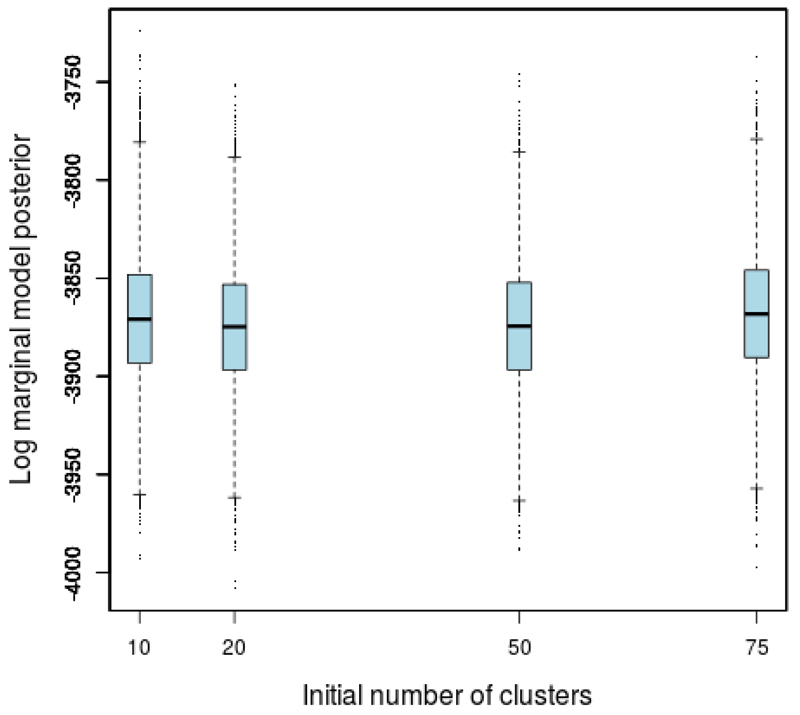
The marginal model posterior can be computed in PReMiuM. The code below computes the marginal model posterior for four different runs of profile regression on the same dataset with different initializations – different number of initial clusters. As seen in Figure 5, plotted using the code below, for the given simulated dataset, all the MCMC runs appear to converge to subsets of the model space with equivalent marginal model posterior. This does not imply convergence, but it is a useful diagnostic tool as it can highlight a lack of convergence in certain circumstances (Hastie et al. 2014). The marginal model posterior can also be plotted using the function globalParsTrace().

Figure 5.

The log marginal model posterior for four runs of profile regression, on the same dataset but with different initializations (i.e., different initial number of clusters).

R> inputs <- generateSampleDataFile(clusSummaryBernoulliDiscrete())
R> nClusInit <- c(10, 20, 50, 75)
R> for (i in 1:length(nClusInit)) {
+    runInfoObj <- profRegr(yModel = inputs$yModel, xModel = inputs$xModel,
+       nSweeps = 10000, nBurn = 10000, data = inputs$inputData,
+       output = paste("init", nClusInit[i], sep = ""),
+       covNames = inputs$covNames, alpha = 1,
+       fixedEffectsNames = inputs$fixedEffectNames,
+       nClusInit = nClusInit[i])
+   margModelPosterior(runInfoObj)
+ }
R> mmp <- list()
R> for (i in 1:length(nClusInit)) {
+    mmp[[i]] <- read.table(paste("init", nClusInit[i], "_margModPost.txt",
+      sep = ""))[, 1]
+ }
R> plot(c(head(nClusInit, n = 1) - 0.5, tail(nClusInit, n = 1) + 0.5),
+    c(min(unlist(mmp)), max(unlist(mmp))), type = "n",
+    ylab = "Log marginal model posterior",
+    xlab = "Initial number of clusters", cex.lab = 1.3, xaxt = "n")
R> axis(1, at = nClusInit, labels = nClusInit)
R> for (i in 1:length(nClusInit)) {
+    boxplot(mmp[[i]], add = TRUE, at = nClusInit[i], pch = ".",
+      boxwex = 5, col = "lightblue")
+ }

8.5. Run times

We have run simulations to test PReMiuM’s speed and how it scales when the number of subjects or covariates increases. The code was run in serial on an Intel Core i7-2600 CPU clocked at 3.40GHz, on a system with 8GB RAM.

9. Conclusions

The structure of PReMiuM objects gives rise to a wider variety of uses than can be described in detail here. Our intention was to provide a tutorial for Dirichlet process clustering and to illustrate the basic features of the sampler and post-processing tools that we have implemented in PReMiuM to demonstrate its utility. Our long-term goal is to continue to develop this package for analysis on complex and high dimensional datasets as well to increase the flexibility with regards to the data types that can be analyzed.

Table 1.

Time required to run 100 iterations of PReMiuM for Bernoulli response and discrete covariates.

	Number of covariates
Number of Subjects	100	1,000	10,000
1,000	7 sec	43 sec	9 min
2,500	10 sec	1 min	18 min
5,000	18 min	2 min	34 min

Table 2.

Time required to run 500 iterations of PReMiuM for continuous response and continuous covariates.

	Number of covariates
Number of Subjects	50	100
3,000	40 sec	3 min
5,000	1 min	7 min

A. Properties of the upper limit of the number of components

We provide the following proposition to support our assertions regarding C^⋆.

Proposition 1. Suppose that we have a model with posterior as given in Equation 7. Suppose Z^⋆, U^⋆ and C^⋆ are defined as in Section 2.2. Then:

• (i)ψ_c < U_i for all i = 1, 2, …, n and all c > C^⋆ almost surely;
• (ii)C^⋆ ≥ Z^⋆ almost surely; and
• (iii)C^⋆ < ∞ almost surely.

Proof. We rely on the fact that if V₁, V_c ~ Beta(1, α), ψ₁ = V₁ and ψ_c = V_c ∏_l<c(1 − V_c) for c = 2, 3, … then ${\displaystyle {\sum }_{c=1}^{\infty }{\psi }_c=1.}$ A proof of this result for the DPMM (in terms of more general conditions) is provided by Ishwaran and James (2001). Then:

• (i)
  By definition, for all i = 1, 2, …, n

  $$U_i\ge U^{\star }>1-{\displaystyle \sum _{c=1}^{C^{\star }}{\psi }_c}={\displaystyle \sum _{c=C^{\star }+1}^{\infty }{\psi }_c\ge {\psi }_{c^{\prime }}}\forall c^{\prime }>C^{\star }.$$
• (ii)
  Let i^⋆ be an individual i such that Z_i = Z^⋆. Again, by definition, $U^{\star }\le U_{i^{\star }}<{\psi }_{Z^{\star }}.$ This implies $1-{\psi }_{Z^{\star }}<1-U^{\star },$ meaning

  $${\displaystyle \sum _{c=1}^{Z^{\star }-1}{\psi }_c<1-{\psi }_{Z^{\star }}<1-U^{\star }}.$$

  By definition of C^⋆, this implies C^⋆ ≥ Z^⋆ almost surely.
• (iii)Since ${\displaystyle {\sum }_{c=1}^{\infty }{\psi }_c=1,}$ this is a convergent series. By definition of a convergent series and because U^⋆ > 0 we have C^⋆ < ∞ almost surely.

B. MCMC scheme and blocking strategy

Below are additional comments to explain the blocking strategy employed in the DPMM algorithm. We use ‘·’ to denote “all other parameters and data”.

• Step A. This step is a straightforward calculation of Z^⋆, which (potentially) changes at each iteration (with the update of Z). The set A is defined immediately conditional on this value.

• Step B. This is a joint update of U and the parameters corresponding to the active components in A, with the inclusion of label switching moves. The principle is to use the identity p(V^A, Θ^A, Z, U|·) = p(V^A, Θ^A, Z|·)p(U|V^A, Θ^A, Z, ·). We proceed by first updating (V^A, Θ^A) ~ p(V^A, Θ^A|Z, ·) = ∫ p(V^A, Θ^A, U|Z, ·)dU. Due to the conditional independence of V and Θ, this can be done in two steps: updating V (B.1) then updating Θ (B.2). The moves are presented as Gibbs updates, but in fact they are Metropolis-Hastings moves, where the variable of interest (for example V^A) is sampled from its full conditional, and the other variables (for example Θ^A and Z) are kept fixed. This results in an acceptance probability of 1, making the Gibbs update equivalent. The updated values are then used as interim values for V and Θ in (Metropolis-Hastings) label switching moves (see Section 6) which are applied in B.3. The moves can change the values of V as well as their order. The resulting sample of V and Θ are the final updated values of these parameters for this sweep. The updated allocation vector Z is used as an interim value throughout the remainder of the steps of the sweep, before the final updated value of Z is sampled in Step G. The final part (B.4) of Step B is to update U conditional upon the updated value of V and Θ and the interim value of Z.

  • B.1 Integrating out U and taking advantage of the conjugacy of the distribution for V inherent in the DPMM, along with the conditional independence structure, each component of vector V^A is updated by sampling $V_c\sim \text{Beta}(1-d+n_c,\alpha +dc+n_c^{+}),$ c ∈ A, where $n_c={\sum }_i{1}_{\{Z_i=c\}}$ and $n_c^{+}={\sum }_i{1}_{\{Z_i>c\}.}$The Dirichlet process is a special case of the Pitman-Yor process for d = 0.

  • B.2 Integrating out U and taking advantage of the conditional independence structure, Θ^A is updated from p(Θ^A|Z, Θ₀, D). The full details of this will depend upon the application and the choice of f and $P_{{\Theta }_0}.$ Examples are given in Section 3.

  • B.3 This step implements the Metropolis-Hastings label switching moves detailed in Section 6. These moves update V^A, Θ^A and Z jointly from their conditional distribution with U integrated out. These moves are conditional upon the values of V^A and Θ^A sampled in steps B.1 and B.2. The third label switching move is proposed and implemented for the Dirichlet process only.

  • B.4 Conditioning on the updated values of V^A, Θ^A and Z from step B.3 , this step samples each U_i, i = 1, …, n, independently according to the full conditional distribution, $U_i\sim \text{Unif}[0,{\psi }_{Z_i}]=\text{Unif}[0,V_{Z_i}{\prod }_{l<Z_i}(1-V_l)],$ as detailed in Walker (2007).

• Step C. To compute U^⋆ is straightforward given the updated value of U from step B.4. The value of Z^⋆ (and with it the set A) can only change from that computed in Step A if the mixture component corresponding to the old Z^⋆ was involved in a label switching move, and then only if the component it was switched with was empty. By design of the label switching moves (see Section 6) this means that Z^⋆ and A can only get smaller, with the consequence that parameters corresponding to a small number of components may be updated twice per MCMC sweep (once in Step B as part of the active components A, and once in Step D and Step E as part of the updated potential components P). This has no ill-effects as long as the most recently updated parameter values are used at each subsequent step.

• Step D. This is a joint update of α, V^P and V^I. The principle is to use the following identity: p(α, V^P, V^I|·) = p(α|·)p(V^P, V^I|α, ·). We proceed by first updating α ~ p(α|·) = ∫ p(α, V^P, V^I|·)dV^PdV^I (step D.1) and then sampling p(V^P, V^I|α, ·) (step D.2). To update V^P, we need to alternate Gibbs samples with checks to evaluate whether the component just updated is C^⋆. In this way the set P is determined on the fly. As mentioned in Section 2.1, no actual sampling is done for the inactive components in set I as these would just be samples from the prior and have no impact on the likelihood or any other conditionals in the MCMC sweep.

  • D.1 Since V^P and V^I both correspond to empty mixture components, the only contribution to the joint posterior conditional is through the prior. This allows us to easily integrate out V^P and V^I. Due to the conditional independence, the resulting posterior from which this step samples is p(α|V^A, Z). Typically this cannot be sampled directly, so we employ a Metropolis-within-Gibbs move to update α, using an adaptive random-walk-Metropolis proposal on the log-scale.

    If the prior for α is a Gamma distribution then it is alternatively possible to sample directly from the conditional with V^A also marginalized (see Walker, 2007 and Escobar and West, 1995 for details). We retain our version as any prior for α can be potentially used, even though only a Gamma prior is available in the code at the moment.

  • D.2 We begin by setting C = Z^⋆. We then repeat the following two steps until the stop condition is reached. First, check if ${\displaystyle {\sum }_{c=1}^C{\psi }_c>1-U^{\star }.}$ Next, if the condition is met we set C^⋆ = C and stop, otherwise we set C = C + 1 and sample V_C ~ Beta(1 − d, α + dC). The Dirichlet process is a special case of the Pitman-Yor process for d = 0.

• Step E. This step updates the parameters Θ^P and Θ^I from the distribution p(Θ^P, Θ^I|·). The set P is fully determined from step D.2. The parameters correspond to empty mixture components, so updated values of Θ^P are sampled directly from the prior. As with other inactive parameter Θ^I play no part in this MCMC sweep and so are not updated.

  • E.1 Taking advantage of the conditional independence structure, in this step we update Θ^P by doing a Gibbs sample from the prior, such that Θ_c ~ p(Θ_c|Θ₀) for each c ∈ P. As Θ_c may be a vector of parameters, this may involve a number of Gibbs updates per component c. The full details depend upon the choice of $P_{{\Theta }_0}.$ See Section 3 for examples.

• Step F. Here, the global (non-cluster specific) likelihood parameters Λ associated with f are updated. There are only a finite number of such parameters so no special updates are needed.

  • F.1 Sample Λ ~ p(Λ|Θ^A, Z, D). Due to the conditional independence structure of the model the update only depends on the current value of the active likelihood parameters Θ^A, the allocations Z, and the data D. Λ may contain multiple parameters, so this stage may contain many Gibbs and / or Metropolis-within-Gibbs steps. Full details will depend upon the choice of f and p(Λ), see Section 3 for examples.

• Step G. The final step of the algorithm is to update the parameter allocations Z, conditional on the newly updated values of the other parameters.

  • G.1 We sample Z ~ p(Z|V^A, V^P, Θ^A, Θ^P, U, Λ, D). Because of the independence of the individuals i, this is a series of Gibbs updates for each i = 1, 2, …, n, sampling Z_i ~ p(Z_i = c|V^A, V^P, Θ^A, Θ^P, U_i, Λ, D_i) where D_i is the data for individual i. For each update, since the conditional p(Z_i = c|·) has no posterior mass for clusters c where U_i > ψ_c, this update depends only on the parameters associated with the finite number of clusters in the sets A and P, making the update a simple multinomial sample according to a finite vector of weights. The full details of the weights will depend upon the choice of f and $P_{{\Theta }_0}.$

C. Posterior conditional distributions for variable selection

In the case of variable selection for continuous covariates, define the J × J matrix Γ_c as

$${\Gamma }_{c,i,j}=\{\begin{array}{l}{\gamma }_{c,j}\hspace{0.17em}i=j;\hspace{0.17em}j=1,2,\dots ,J,\\ 0\text{otherwise,}\end{array}$$

for the first variable selection method, and

$${\Gamma }_{c,i,j}=\{\begin{array}{l}{\zeta }_j\hspace{0.17em}i=j;\hspace{0.17em}j=1,2,\dots ,J,\\ 0\text{otherwise}.\end{array}$$

for the second method as presented in Section 3.5. Let I_J denote the J × J identity matrix, n_c be the number of individuals allocated to cluster c, $\overline{X}$ be as defined in Section 3.5 and ${\overline{X}}_c=\left({\overline{X}}_{c,1},{\overline{X}}_{c,2},\dots ,{\overline{X}}_{c,J}\right)$ such that ${\overline{X}}_{c,j}={\sum }_{i:Z_i=c}{X}_{i,j}/n_c.$ The posterior conditional distributions for updating µ_c for c ∈ A are then given by

$$\mu \sim \text{Normal}(\tilde{\mu },\tilde{\Sigma })$$

where

$$\tilde{\Sigma }={\left({\Sigma }_0^{-1}+n_c\Gamma {\Sigma }_c^{-1}\Gamma \right)}^{-1},$$

and

$$\tilde{\mu }=\tilde{\Sigma }\left[{\Sigma }_0^{-1}{\mu }_0+n_c\Gamma {\Sigma }_c^{-1}({\overline{X}}_c-(I_J-\Gamma )\overline{X})\right].$$