Aggregate Entropy Scoring for Quantifying Activity across Endpoints with Irregular Correlation Structure

Abstract

Robust computational approaches are needed to characterize systems-level responses to chemical perturbations in environmental and clinical toxicology applications. Appropriate characterization of response presents a methodological challenge when dealing with diverse phenotypic endpoints measured using in vivo systems. In this article, we propose an information-theoretic method named Aggregate Entropy (AggE) and apply it to scoring multiplexed, phenotypic endpoints measured in developing zebrafish (Danio rerio) across a broad concentration-response profile for a diverse set of 1,060 chemicals. AggE accurately identified chemicals with significant morphological effects, including single-endpoint effects and multi-endpoint responses that would have been missed by univariate methods, while avoiding putative false-positives that confound traditional methods due to irregular correlation structure. By testing AggE in a variety of high-dimensional real and simulated datasets, we have characterized its performance and suggested implementation parameters that can guide its application across a wide range of experimental scenarios.

1. Introduction

Biological responses in whole animals are the product of coordinated actions (or, in the case of toxic responses, dysregulation) on a systemic level. Accordingly, experimental inquiries into basic biological processes should record multiple phenotypic outcomes when assessing perturbations, from clinical interventions such as drug treatments to environmental stressors such as manufactured chemicals. Innovations in multiplexed endpoint measurement technology and exploratory omics platforms have enabled theoretically comprehensive experiments to be conducted [1]. However, these new, multi-endpoint data present challenges with respect to recapitulating the relevant biological processes: (1) The correlation structure across endpoints is irregular; (2) Individual subjects/samples vary in endpoint presentation; (3) Endpoint measurement methods are imperfect; (4) Experimental questions may depend on subsets and/or recombinations of endpoints. Therefore, analysis methods are needed that can address these challenges while allowing for either focused, a priori analysis or data-wide, empirical analysis.

One such area where comprehensive analysis of systemic response is needed is environmental and clinical toxicology, where adverse responses may manifest anywhere from specific abnormalities to collections of several endpoints that count as toxicity in the aggregate. While there is an ever-increasing number of chemicals in commerce and the environment, comprehensive toxicological knowledge is lacking for all but a handful of compounds mostly pharmaceuticals that have progressed to expensive, late-stage clinical trials. Traditional animal testing is very expensive in terms of labor, time, and money, so high-throughput screening (HTS) is being developed in order to more efficiently assess chemical biocompatibility [2]. Experimental HTS includes both in vitro assays that probe molecular action and in vivo assays that screen for a variety of phenotypic endpoints that cover fundamental developmental, structural, and neurological pathways [3–5].

These HTS in vivo assays provide an ideal workbench for the development and testing of analysis methods for multiple endpoints, in that the data can be generated on a scale that permits evaluation of an analysis method s ability to address the four challenges presented above. In particular, experimental methods for the zebrafish (Danio rerio), a model organism whose fundamental developmental processes are shared across vertebrates and that has high genetic similarity to humans, have exploded in recent years [6,7]. Several endpoints, ranging from specific structural features through outright mortality, have been measured, with a trend toward higher-order assessment of multiple endpoints during embryonic development [8].

Here, we developed an information theory-based method named Aggregate Entropy (“AggE”) to consolidate information into classes across endpoints, then tested this method using both simulated and empirical zebrafish data. We characterized the relationship amongst endpoints to identify the biological processes underlying overall developmental assessments; used simulated data to further validate our method across a range of sample sizes; characterized the irregular correlation structure across endpoints using mutual information and normalized information distance; and used this information to reduce noise by collapsing endpoints with similar phenotypic response patterns. Finally, we parameterized AggE distributions to allow for application to new datasets of varying dimensions from multi-endpoint experiments in any model system.

2. Materials and methods

2.1.Empirical data

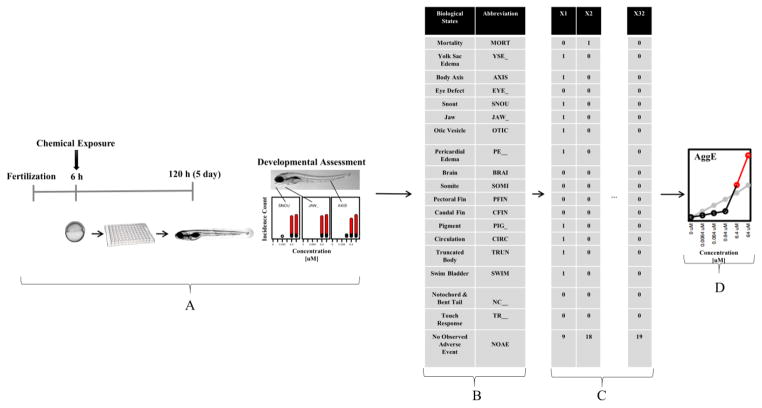
The empirical data were collected as described in Truong et al. 2014 and Noyes et al. 2015. Figure 1 shows the experimental design and data structure. The data include 1,060 unique ToxCast chemicals tested at six concentrations for each chemical (0 μM, 0.0064 μM, 0.064 μM, 0.64 μM, 6.4 μM and 64 μM). There were n=32 replicates (individual embryo wells) at each concentration. At 120 hours post fertilization (hpf), 18 distinct developmental endpoints were evaluated. The data were recorded as binary incidences.

Figure 1.

Experimental Design and Data Structure. A) Chemical exposure started at 6hpf. At 120hpf, 18 distinct developmental assessments were measured. B) 19 biological states (developmental assessments plus NOAE) with their abbreviations. C) Data structure showing three example vectors from n=32 individual wells per concentration-by-chemical. X1 indicates many developmental problems observed; X2 shows mortality; X32 represents no phenotypic consequences recorded. D) Aggregate Entropy, in nats (natural unit of information) on the vertical axis by concentration on the horizontal axis. The black lines connect the concentration-wise AggE for this example chemical, turning red at the point-of-departure concentration, where the line crosses the grey significance threshold.

As in Figure 1(B) and 1(C), we constructed 19 different biological states, including 18 developmental endpoints plus one NOAE (No Observed Adverse Effect) state. Thus, for each embryo per chemical-per concentration, data were shown as 0 and 1 for 18 binary endpoints with NOAE recorded as 19 − Σ(Binary Endpoints). All analysis was performed using R [13].

2.2.Aggregate Entropy

The traditional Shannon s entropy H(X) [14], in nat units, is:

Let X be a discrete random variable with a possible set of realizations x, thus;

$$H(X)=-\sum _{x}p(x){\mathit{log}}_{e}p(x)$$

We define a random variable and its realizations as follows:

For each chemical C at a given concentration, let X_i represent embryo i with i = 1, … ,32 and B_j represent biological state j with j = 1, … ,19. In addition, X_i has realization x_ij with its sample value shown in Figure 1. The probability mass function can be written as:

$$p(B_j\mid C,X_i)=\frac{x_{ij}}{19}$$

The Aggregate Entropy (AggE) for chemical C at a given concentration is summarizing the Shannon s entropy of all tested embryos, which is:

$$\mathit{AggE}=-\sum _{\mathrm{i}=1}^{32}\sum _{\mathrm{j}=1}^{19}p(B_j\mid C,X_i){\text{log}}_{\mathrm{e}}\{p(B_j\mid C,X_i)\}$$

2.3.Threshold determination

We first used a chi square approximation to the distribution of AggE of each concentration as well as the distribution of the pooled concentration [15–16]. We estimated our chi square degree of freedom by using the Newton algorithm to optimize the logarithm of the full likelihood of a chi square probability density function. Let (AggE₁, AggE₂, … AggE_N) be a set of AggE, thus the full likelihood can be written as:

$$f({\mathit{AggE}}_1,{\mathit{AggE}}_2,\dots ,{\mathit{AggE}}_N)={\left(\frac{1}{2^{\frac{k}{2}}\mathit{\Gamma }(k)}\right)}^n{({\mathit{AggE}}_1\ast \dots \ast {\mathit{AggE}}_N)}^{\frac{k}{2}}{e}^{-\frac{{\mathit{AggE}}_1+\cdots +{\mathit{AggE}}_N}{2}}$$

Where k is the degree of freedom of a Chi-square distribution and N is the number of chemicals. Since the maximum likelihood estimator is nonlinear, we first took the negative logarithm of the full likelihood. After that, given a start value, we used Newton iteration to optimize the negative logarithm of the full likelihood such that it gave us the optimal estimate of the degree of freedom of our chi square distribution. Our threshold, which depends on the observed incidences of multiple measurements over many individuals, is the critical value of a one-sided chi square test with the significance level of 0.05.

2.4.Endpoint clustering and sensitivity analysis

We next used pairwise mutual information to characterize the relationship among endpoints. Let E₁ and E₂ represent two endpoints with realization e₁ and e₂ as observed incidence counts per chemical-per concentration, given the Shannon s entropy defined above, the joint Shannon s entropy for E₁ and E₂ is:

$$H(E_1,E_2)=-\sum _{e_1}\sum _{e_2}p(e_1,e_2){\mathit{log}}_{e}p(e_1,e_2)$$

And the conditional entropy can be written as:

$$H(E_1\mid E_2)=-\sum _{e_1}\sum _{e_2}p(e_1,e_2){\mathit{log}}_{e}p(e_1\mid e_2)$$

With all these definitions, the mutual information (MI) is:

$$MI(E_1,E_2)=\sum _{e_1}\sum _{e_2}p(e_1,e_2){\mathit{log}}_e\frac{p(e_1,e_2)}{p(e_1)p(e_2)}=H(E_1)-H(E_1\mid E_2)$$

MI has the following, commutative, property:

$$MI(E_1,E_2)=MI(E_2,E_1)$$

We formed our clusters based on a modified three-step measurement [17]. First, the pairwise mutual information between endpoints, MI (E_i, E_j), i,j = 1, … ,18, is calculated by using R package “infotheo” [18]. Next, the mutual information matrix is transferred to a distance measurement, called normalized information distance [19], which is:

$$d(E_i,E_j)=1-\frac{MI(E_i,E_j)}{H(E_i)+H(E_j)+MI(E_i,E_j)}$$

Finally, hierarchical clustering with normalized information distance and Ward s method was used to characterize the relationship between endpoints.

Our sensitivity analysis followed a three-step procedure. First, based on our clustering analysis, we decided which endpoint or endpoints (super endpoints) we wanted to remove or collapse. Second, we recalculated AggE based on the new set of the endpoints and determined our threshold following the same algorithm defined above. Third, we calculated the concordance (in at least one concentration) between AggE and Fisher s Exact Test for identifying developmental effects.

2.5.Simulation

Given the data structure in Figure 1, for each endpoint, we simulated a series of Bernoulli trials with sample sizes of 8, 16, 32, 64 and 96 per chemical-per concentration with the real frequencies defined as

$$p(x=1)=\frac{{\sum }_{i=1}^{32}{x}_i}{32}\mathit{and}p(x=0)=1-p(x=1)$$

where x_i is the binary incidence for embryo i for the given endpoint.

3. Results

As detailed in Methods, AggE was developed using data collected according to the experimental design presented in Figure 1, where each of the 1,060 unique chemicals were tested at six concentrations, with n=32 replicates (wells each containing an individual embryo) at each concentration (Truong et al. 2014). Chemical exposure began at 6 hours post fertilization (hpf), then all replicates were evaluated for a suite of 18 developmental endpoints at 120 hpf.

3.1. Distribution and threshold across concentration for AggE

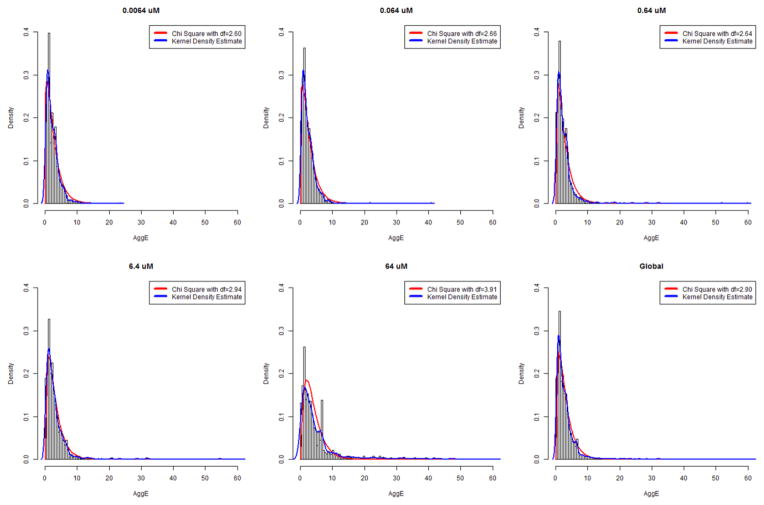
The histograms of AggE across concentrations are shown in Figure 2. Our chi-square approximation is consistent with the kernel density estimate. The distribution shifts to the right as the concentration increases because we generally observed higher incidence rates at higher concentrations. According to our threshold for AggE (versus the univariate Fisher s Exact Test), we found that 24 (versus 10) chemicals significantly affected the development of zebrafish at a concentration of 0.0064 μM; 25 (versus 15) chemicals at 0.064 μM; 49 (versus 34) chemicals at 0.64 μM; 56 (versus 59) chemicals at 6.4 μM and 139 (versus 168) chemicals at 64 μM. The consequences of mortality are evident in the differences between the distributions at 64 μM (highest observed mortality) and the Global threshold, which was less sensitive to suppression of AggE from observed mortality (see discussion of Figure 3, below). Table 1 contains information on thresholds and summary statistics.

Figure 2.

Histogram of AggE across concentrations. The horizontal axis is AggE, and the vertical axis is the density. The blue line is a kernel density estimate, and the red line is a chi square approximation.

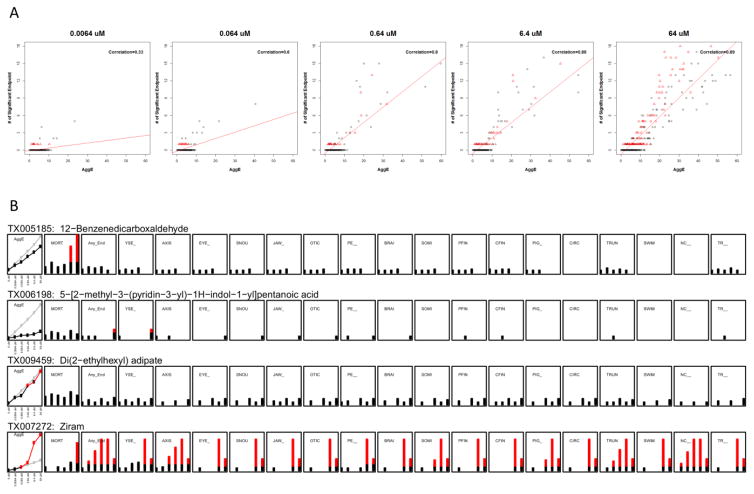
Figure 3.

A) Correlation between the number of chemicals associated with significant endpoints determined by Fisher s Exact Test (vertical axis) by AggE (horizontal axis). From left to the right, the plots show results for concentrations 0.0064 μM, 0.064 μM, 0.64 μM, 6.4 μM and 64 μM, respectively. Red Triangle: Significant mortality and/or other specific endpoint(s); Black Dot: Significant endpoint(s) only (Except Mortality); Red Line: Linear Regression Fit. B) Similarities and dissimilarities between our method and Fisher s Exact Test on each individual endpoint. For the first panel of each chemical (AggE): Gray line is the cumulative summation of the threshold of AggE by concentration; Black line is the cumulative summation of chemical associated AggE by concentration, with points colored red that exceed the threshold. For other panels of each chemical: the dot is incidence counts and for a given concentration, if the count is significant by Fisher s Exact Test, it turns red.

Table 1.

Threshold determination of AggE with multiple evaluations including balanced ROC curve, Balanced F1 Score and Concordance.

Concentration		Degree of Freedom (Chi-square)	Threshold (Q(x>0.05))	# of Significant Chemicals AggE (Univariate Test)	Balanced ROC	Balanced F1 Score	Concordance
0.0064	μM	2.60	7.10	24 (10)	0.56	0.20	0.98
0.064	μM	2.66	7.21	25 (15)	0.70	0.51	0.98
0.64	μM	2.64	7.18	49 (34)	0.73	0.60	0.97
6.4	μM	2.94	7.71	56 (59)	0.88	0.81	0.97
64	μM	3.91	9.35	139 (168)	0.89	0.81	0.95
Global		2.90	7.64

3.2.Evaluation of AggE in predicting individual morphological effects

For each concentration, we also estimated the general agreement between AggE and Fisher s Exact Test on specific endpoints. We did not include mortality in Fisher s Exact Test, because if an embryo was dead, we could not measure any other endpoints, and our method was designed to evaluate the hazard information across endpoints. For our calculations, PP represents tested positive in both tests; NN represents tested negative in both tests; NP represents tested negative in AggE and positive in Fisher s Exact Test and PN represents the opposite case. The balanced ROC (Receiver Operating Characteristic) curve, balanced F1 score measurement $\frac{2\ast PP}{2\ast PP+PN+NP}$ and concordance $\frac{(PP+NN)}{(PP+NN+PN+NP)}$ between the two tests are shown in Table 1. As an overall summary, the 1,060 chemicals are displayed in decreasing order of their maximum-normalized AggE score, summed across all concentrations Supplemental Table 1 (.csv).

3.3.Comparison of AggE with Fisher s Exact test

We next observed a positive relationship between the numbers of significant endpoints of each chemical identified by Fisher s Exact Test and its associated Aggregate Entropy (Figure 3A). We found that AggE is less likely to detect chemicals that cause only mortality, which is expected, given that mortality overwrites all specific endpoints as zero (see Figure 1). 12-Benzenedicarboxaldehyde (6.4 μM; 64 μM) is shown as an example of this particular case (Figure 3B), where no concentration-response is evident in the specific endpoints, and only mortality is observed at higher concentrations. When compared to Fisher s Exact Test for each specific endpoint, our method is less likely to detect chemicals where the incidence rate of that endpoint just reaches the significance threshold, as with 5-[2-methyl-3-(pyridine-3-yl)-1H-indol-1-yl]pentanoic acid (Figure 3B). On the contrary, chemicals having moderate incidence across several endpoints, yet fail to reach the statistical threshold for any single endpoint are identified by AggE. These chemicals have moderate incidence rates across multiple test endpoints and disproportionately affect certain individuals in the population, possibly reflecting genetic variability or experimental difficulty in pathological annotation of several related endpoints. For example, many embryos exhibited developmental endpoints when exposed to Di(2-ethylhexyl) adipate (Figure 3B); however, none of these incidence rates were significant according to univariate criteria, while from an integration perspective, such a profile warrants concern. We also constructed a new endpoint named “Any_End” to contrast with AggE. “Any_End” represents an observable positive response in any of the tested endpoints and should thus behave similarly to the most sensitive specific endpoint. The Ziram example in Figure 3B shows AggE accretion over concentrations displaying several specific endpoint responses.

3.4.Clustering analysis

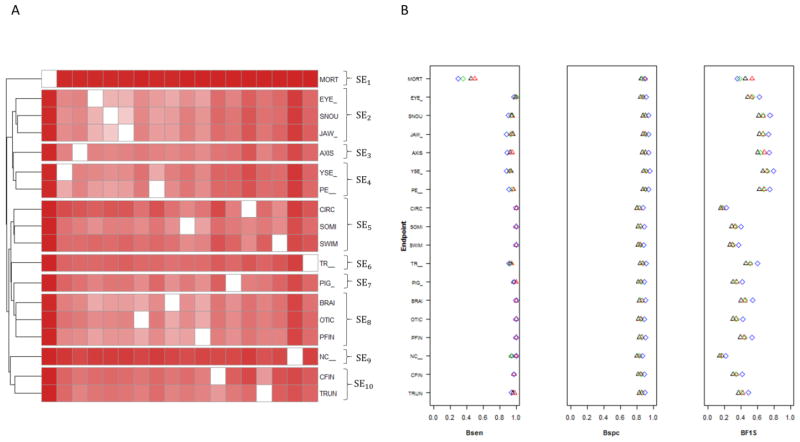
As in Truong et al. a pairwise correlation matrix of the endpoints based on the lowest effect level shows an irregular correlation surface. Here we use an information theory-based approach to identify clusters of the endpoints in order to appropriate handle correlation stemming from individual zebrafish profiles as well as endpoint relatedness. The pairwise mutual information matrix is shown in Supplemental Table 3. We next followed the procedures described in the methods section to find clusters with similar phenotypic responses (Figure 4A). From both the mutual information across endpoints and clustering analysis, notochord distortion (NC), bent body axis (AXIS), touch response (TR), and mortality (MORT) seem to be independent of other endpoints. The other 5 clusters include craniofacial endpoints (Eye, Snout and Jaw), edemas (Yolk Sac Edema and Pericardial Edema), upright body (Swim Bladder, Somite and Circulation), Brain (Brain, Otic Vesicle and Pectoral Fin), and Trunk (Trunk and Caudal Fin).

Figure 4.

A) Heatmap showing hierarchical clustering using normalized information distance with Ward linkage. SE: Super Endpoint. B) Comparison of the predictive power of chemicals that caused significant morphological effect by applying our method on single endpoint with mortality (black triangle); without mortality (green diamond) vs. super endpoint with mortality (red triangle); without mortality (blue diamond). Note that only the super endpoint (red triangle, blue diamond) will be visible for cases of perfect overlap with single endpoints. Bsen: Balanced Sensitivity; Bspc: Balanced Specificity; BF1S: Balanced F1 Score.

We performed a sensitivity analysis by removing one endpoint at a time or a cluster of endpoints (SE: Super Endpoints). After removing one endpoint at a time, we found that we do not lose the power of detecting that particularly removed endpoint due to the high mutual information shared with any other endpoint(s). However, this is not true for removing a single clustered endpoint. For example, the mutual information for two edema endpoints is very high. After removing these two endpoints, we found that we lost the power of detecting chemicals previously associated with edema. However, we increase the power of detecting chemicals that caused other developmental defects because of the reduced noise of the data caused by the irregular correlation structure. This trend continues after the same analysis over other super endpoints. Based on this fact, we carried out an analysis on our 10 super endpoints (Figure 4A), which are the 10 clusters defined above. For any super endpoint that contains more than one single endpoint, if at least one developmental defect was observed within the same super endpoint of that embryo, we recorded that this embryo has this particular defect. For instance, Edema contains two single endpoints (YSE and PE). If one embryo has either one or both, we state that this embryo has an edema problem. We compared the balanced sensitivity, specificity and F1 score of our method on the new super endpoints with the original single endpoint in classifying chemicals that have a significant effect on a specific endpoint based on Fisher s Exact Test (Figure 4B). In general, our method performed better using super endpoints on any measurement and retained high power for detection of hazardous chemicals. Since mortality supersedes recording of specific developmental endpoints, we also performed the same analysis after removing mortality, resulting in 17 single endpoints and 9 super endpoints. In brief, AggE still performed better using super endpoints, and we increased the power of detecting hazardous chemicals that caused significant developmental problems (Figure 4B). This reflects the flexibility of AggE using reduced endpoint sets, or more general annotation of difficult-to-discern specific endpoints (i.e. annotation as “Edema” versus separate YSE or PE entries).

3.5.Simulation

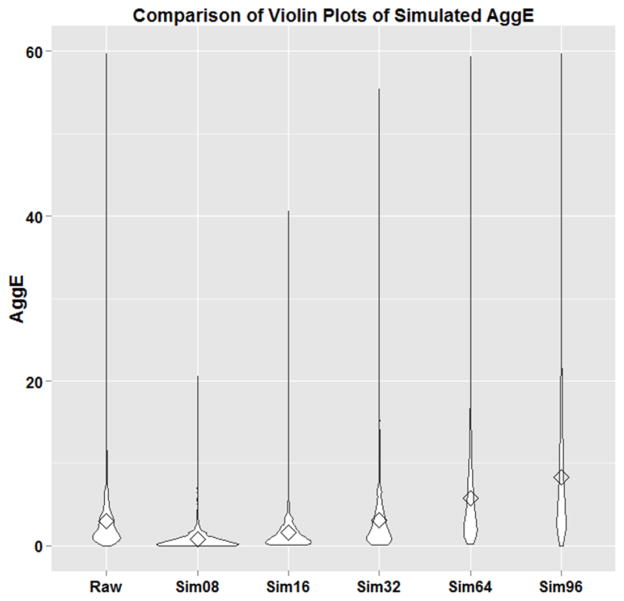
We explored the applicability of our method to different experimental designs by generating simulated data sets with different sample sizes of n=8, 16, 32, 64 and 96. We compared the variation of our simulated AggEs over the pooled concentration by using violin plots (Figure 5). AggE relies on the tested sample size as well as observed incidence rates of multiple measurements. Thus, the degrees of freedom of our chi square approximation to AggE increases with the sample size, because as we attain more embryos, we increase our hazard information (Supplemental table 2). The three measurements, which are balanced ROC curve, F1 score and concordance, all reach to a comparable stationary phase at the sample size of 32 and 64. If the sample size gets too small, balanced ROC curve and concordance become over-representative. Once the sample size gets too big, all three measurements decrease dramatically compared to the raw data measurements in Table 1. In general, we need a big sample size to reduce the bias and get a more accurate estimate. However, in this case, if the sample size gets too big, even a small difference of incidence rate between two experiments can be significant using Fisher s Exact Test, binomial test, or other uncorrected, univariate tests. Thus, these statistical tests on each specific endpoint may not be appropriate, while AggE is still valid regardless of the sample size and can be appropriately parameterized by sample size and observed incidences on multiple measurements.

Figure 5.

Violin plot showing the variation of AggE with different simulated sample sizes over pooled concentrations.

3.6.Validation

We next tested our method based on the results of an external dataset of flame retardant chemicals [9]. The data structure is comparable to what we have shown here, with n=32 and the same set of endpoints. For chemicals that have the same tested concentrations as ours, we used the same threshold concentration-wise in Table 1. For those chemicals that have different tested concentrations (6.4E-6 μM, 6.4E-5 μM, 6.4E-4 μM), we used the global threshold in Table 1. The analysis was redone using Fisher s Exact Test, and the chemicals showing significant morphological effects associated with their effective concentrations are displayed in Table 2. The results also show a strong agreement between our method and Fisher s Exact Test. Our method identified three new chemicals (5-OH-BDE-47, BDE100, and TBP) showing evidence of aggregate developmental hazard. There are three chemicals, DE71 (a mixture of brominated diphenyl ethers) at 64 μM, o-TCP (Tri-o-cresyl phosphate) at 64 μM and TDCPP (Tris(1,3-dichloro-2-propyl) phosphate) at 64 μM, that did not reach our AggE threshold but are significant according to Fisher s Exact Test. o-TCP and TDCPP have a very high mortality rate at 64 μM, and DE71 only univariately significant on body bent axis.

Table 2.

Validation of our method using Noyes et al.(2015)

Chemical Name	Concentration (μM)	Significant Endpoint(s)	Aggregate Entropy
BPDP	64	YSE, AXIS, EYE, SNOU, JAW, PE, PFIN, CFIN	37.91***
mITP	0.64	YSE, AXIS, SNOU, JAW, PE, PFIN, SWIM, TR	31.78***
IPP-1	64	MORT, YSE, AXIS, PE, PFIN, CFIN, TR	23.32***
IPP-3	64	YSE, AXIS, PE, PFIN, CFIN	20.41***
TBBPA	6.4	MORT, AXIS, JAW, CFIN, TRUN, TR	12.23***
IPP-2	64	YSE, AXIS, PE	10.94**
TCP	64	MORT, YSE, AXIS, PE, TR	10.94**
5-OH-BDE-47	0.00064	None	7.28†
BDE100	0.00064	None	6.43†
TBBPA	64	MORT	6.39†
TDCPP	64	MORT, CFIN	5.92
o-TCP	64	MORT	5.73
TBP	0.0064	None	5.66*
DE 71	64	AXIS	3.3

^***Significant at 0.001;

^**Significant at 0.05;

^*Significant at 0.1;

^†Significant at 0.1 using Global Threshold (Concentration does not match)

4. Discussion

We presented a scoring framework called Aggregate Entropy to evaluate the developmental toxicity of chemicals in vivo. In terms of sensitivity, AggE is consistent with Fisher s Exact Test and other contingency-table methods in many scenarios but has advantages when presented with interindividual heterogeneity and endpoint-endpoint correlation. In terms of specificity, AggE reduces potentially false-positive significance calls arising from small numbers in any one cell of a contingency table, rendering AggE more stable in the face of smaller sample sizes and single-endpoints. AggE considers the information of all phenotypic responses of zebrafish after chemical exposure. This aligns with the logic that if a chemical elicits responses in many of the tested endpoints, yet none of these singular endpoints reaches the incidence threshold by Fisher s Exact Test, we should still annotate its potential hazard. Due to our limited knowledge about the underlying biological processes perturbed by most chemicals, and because many of the endpoints share elements of the same Adverse Outcome Pathways (AOPs), these chemicals warrant further scrutiny.

Our clustering analysis and sensitivity analysis indicated that there is a strong, yet not uniform, relationship among many endpoints in these data, which is especially common in developmental studies where a coordinated cascade of biological events must take place. We need to have methods that do not inflate false-positives nor lose power (i.e. inflate false-negatives) when faced with irregular correlation structure. AggE was designed to solve this problem. Across a diverse chemical set, we can capitalize on this correlation structure to hypothesize endpoints related by common perturbations or adverse outcome pathways. In addition, we showed the benefits of removing specific endpoints that shared an especially tight correlation structure with other endpoint(s). The analysis on 10 super endpoints outperformed (measured by detection of previously-identified chemical effects) the results using the full set of original, specific endpoints. This may aid future experimental design by negating the need to annotate difficult-to-separate endpoints into specific bins or enable implementation of fully-automated annotation protocols.

Our method offers several benefits over common statistical methods used in analyzing zebrafish morphological data. First, we were able to detect chemicals having robust effects on specific endpoints based on Fisher s Exact Test, as well as many new chemicals that would be missed by such traditional methods. Second, AggE maintains appropriate detection power when faced with extremely large or small sample sizes, whereas contingency-table methods suffer an inflation of false-positives. Third, AggE does not enforce a global model, whereas simple linear or logistic fit models will not be appropriate in data where the variance of the incidence rate is not constant and residuals differ across concentrations. Fourth, if we simply add all of the observed incidences for each embryo then perform a standard statistical test on the summation, the results can be misleading due to the fact that the same event will be over-counted because of high shared mutual information across endpoints. This is a salient feature of developmental assays, where some key event(s) can trigger many observable phenotypes. Fifth, AggE can be applied to datasets of varying size, complexity, and degree of non-independence, since its threshold is a function of observed incidences over many individuals. We have demonstrated its use in a high-dimensional zebrafish development assay, but this method could be applied to multiplexed measurements in other in vitro or in vivo systems, or even to binarized “hits” from assay suites, gene expression, or pathway enrichment analysis.

5. Conclusions

In summary, we developed a new computational approach to characterize chemical exposure information and applied it scoring multiplexed, phenotypic endpoints measured in zebrafish (Danio rerio) across several concentrations. We were able to elucidate multi-endpoint syndromes across related endpoints as well as identify chemicals that displayed generalized teratogenic effects. As a complement to rank-based [10], curve-fitting [11], and a priori weighting metrics [12], AggE is a flexible approach that is capable of identifying hazardous chemicals from data encompassing a broad parameter space, while avoiding many statistical pitfalls of traditional methods. By testing AggE in a variety of high-dimensional real and simulated datasets, we have characterized its performance and suggested implementation parameters that can guide its application across a wide range of experimental scenarios.

Supplementary Material

1. Supplemental Table 1.

(.csv). All 1,060 ToxCast chemicals are displayed in a decreasing order of their normalized AggE. The list also contains each chemical s name; CAS number; concentration-wise AggE and rank.

2. Supplemental Table 2.

(.pdf). Threshold of AggE with multiple evaluations including balanced ROC curve, Balanced F1 Score and Concordance of 5 different simulated data set.

3. Supplemental Table 3.

(.pdf). Mutual Information amongst endpoints.

Highlights.

• Aggregate Entropy (AggE) is a new approach for scoring multiple phenotypic endpoints.

• AggE elucidated multi-endpoint syndromes across related endpoints in zebrafish.

• AggE also identified chemicals that displayed generalized teratogenic effects.

• AggE is a flexible, statistically robust approach that complements standard methods.

Abbreviations

MORT

Mortality

YSE

Yolk Sac Edema

AXIS

Body Axis

EYE

Eye

SNOU

Snout

JAW

Jaw

OTIC

Otic Vesicle

PE

Pericardial Edema

BRAI

Brain

SOMI

Somite

PFIN

Pectoral Fin

CFIN

Caudal Fin

PIG

Pigment

CIRC

Circulation

TRUN

Truncated Body

SWIM

Swim Bladder

NC

Notochord & Bent Tail

TR

Touch Response

NOAE

No Observed Adverse Effect

AggE

Aggregate Entropy

PP

Positive-Positive

NN

Negative-Negative

NP

Negative-Positive

PN

Positive-Negative

Any_End

Any Endpoint

ROC

Receiver Operating Characteristic

hpf

hours post fertilization

AOP

Adverse Outcome Pathway

HTS

High Throughput Screening

MI

Mutual Information

SE

Super Endpoint