Influence of Glu/Arg, Asp/Arg, and Glu/Lys Salt Bridges on α-Helical Stability and Folding Kinetics

Abstract

Using a combination of ultraviolet circular dichroism, temperature-jump transient-infrared spectroscopy, and molecular dynamics simulations, we investigate the effect of salt bridges between different types of charged amino-acid residue pairs on α-helix folding. We determine the stability and the folding and unfolding rates of 12 alanine-based α-helical peptides, each of which has a nearly identical composition containing three pairs of positively and negatively charged residues (either Glu⁻/Arg⁺, Asp⁻/Arg⁺, or Glu⁻/Lys⁺). Within each set of peptides, the distance and order of the oppositely charged residues in the peptide sequence differ, such that they have different capabilities of forming salt bridges. Our results indicate that stabilizing salt bridges (in which the interacting residues are spaced and ordered such that they favor helix formation) speed up α-helix formation by up to 50% and slow down the unfolding of the α-helix, whereas salt bridges with an unfavorable geometry have the opposite effect. Comparing the peptides with different types of charge pairs, we observe that salt bridges between side chains of Glu⁻ and Arg⁺ are most favorable for the speed of folding, probably because of the larger conformational space of the salt-bridging Glu⁻/Arg⁺ rotamer pairs compared to Asp⁻/Arg⁺ and Glu⁻/Lys⁺. We speculate that the observed impact of salt bridges on the folding kinetics might explain why some proteins contain salt bridges that do not stabilize the final, folded conformation.

Introduction

The well-defined three-dimensional structure of folded proteins and peptides is determined by a large number of relatively weak noncovalent interactions, including hydrophobic effects, Van der Waals forces, hydrogen bonding, and electrostatic interactions (1). The delicate balance between these noncovalent forces determines the overall thermodynamic stability of native protein folds, and their relative contributions to the stability are under ongoing discussion. The influence of electrostatic interactions between oppositely charged residues (salt bridges) on protein stability has proven to be particularly ambiguous (2, 3, 4). This is because the impact of salt bridges on protein structure and stability depends strongly on the relative location of the salt-bridging residues in the primary sequence, the relative orientation and distance between the interacting residues, the effect of neighboring residues, and the degree of solvent accessibility (5, 6, 7). Because the energetically favorable Coulomb interaction between salt-bridging amino-acid residues requires structural reordering and desolvation processes that might be energetically unfavorable (2), the net contribution of a salt bridge to the free-energy balance of proteins can range from highly stabilizing to highly destabilizing (2, 5, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21). The latter type of salt bridges, those that destabilize the folded state, must have a biological function of a different nature. In a previous study, we found evidence that suggests that such apparently nonfunctional salt bridges might have a kinetic rather than a thermodynamic function (22). In particular, we found that Glu⁻/Arg⁺ salt bridges have a strong impact on the kinetics of the helix-coil transition and can speed up as well as slow down the folding rate, depending on their sequence order and distance (22). Here, we investigate how the effect of salt bridges on folding kinetics depends on the residues that form the salt bridge (Glu⁻/Arg⁺, Asp⁻/Arg⁺, or Glu⁻/Lys⁺). We determine the folding and unfolding rates of 12 different alanine-based α-helical peptides (see Table 1), each of which has a nearly identical amino-acid composition with three repeating salt-bridge forming residue pairs (either Glu⁻/Arg⁺, Asp⁻/Arg⁺, or Glu⁻/Lys⁺). Within each set of different salt-bridge combinations, four different sequence patterns were studied that differ only in the relative spacing and order of the oppositely charged residues, such that they have different capabilities of forming salt bridges (Fig. 1). Temporal resolution and structural sensitivity were achieved using transient-infrared (IR) measurements after a laser-induced temperature-jump (T-jump) (23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33) in the amide I′ spectral region, which is a sensitive probe of the backbone conformation (34, 35, 36, 37). Combined analysis of our steady-state ultraviolet circular dichroism (UV CD) and T-jump transient-IR measurements allows a detailed study of the folding and unfolding kinetics. Complementary molecular dynamics (MD) simulations have been carried out to obtain more insight into the correlation between salt-bridge population and α-helical content and how the ability of charged residue pairs to form a salt bridge depends on their order and distance.

Table 1.

Sequences, Folding Transition-State Enthalpy ΔH^‡, and Folding Rates of the Different Peptides at Neutral pH

Sequence	Peptide	pH = 7.0 (Salt Bridges)		pH = 2.5(No Salt Bridges)
$\Delta H_{\text{U}\to \text{F}}^{‡}$ (kJ mol−1)	kU → F,298K (μs−1)a	$\Delta H_{\text{U}\to \text{F}}^{‡}$ (kJ mol−1)	kU → F,298K (μs−1)a
Ac-A(EAAAR)3 A-NH2	(i + 4)ERb	19.1 ± 1.9	4.45 ± 0.15	17.8 ± 1.7	3.13 ± 0.15
Ac-A(AEAAR)3 A-NH2	(i + 3)ERb	15.6 ± 1.1	2.06 ± 0.13	20.0 ± 3.6	1.62 ± 0.21
Ac-A(RAAAE)3 A-NH2	(i + 4)REb	14.3 ± 1.9	1.98 ± 0.12	16.6 ± 3.4	2.55 ± 0.30
Ac-A(ARAAE)3 A-NH2	(i + 3)REb	7.7 ± 1.4 c	0.71 ± 0.22	19.1 ± 3.0	1.26 ± 0.15
Ac-A(DAAAR)3 A-NH2	(i + 4)DR	16.1 ± 2.4	3.88 ± 0.32	21.2 ± 2.1 c	2.04 ± 0.70
Ac-A(ADAAR)3 A-NH2	(i + 3)DR	11.0 ± 1.8 c	1.54 ± 0.24	−	−
Ac-A(RAAAD)3 A-NH2	(i + 4)RD	5.3 ± 1.7 c	1.00 ± 0.15	−	−
Ac-A(ARAAD)3 A-NH2	(i + 3)RD	−	−	−	−
Ac-A(EAAAK)3 A-NH2	(i + 4)EK	21.2 ± 0.9	2.19 ± 0.09	11.4 ± 4.1	1.65 ± 0.21
Ac-A(AEAAK)3 A-NH2	(i + 3)EK	18.6 ± 1.4	1.40 ± 0.07	7.1 ± 4.6	1.65 ± 0.40
Ac-A(KAAAE)3 A-NH2	(i + 4)KE	19.3 ± 2.4	1.22 ± 0.08	9.7 ± 3.7	1.60 ± 0.15
Ac-A(AKAAE)3 A-NH2	(i + 3)KE	11.8 ± 4.2	0.87 ± 0.16	9.4 ± 4.4	1.72 ± 0.21

Sequences, folding transition-state enthalpy $\left(\Delta H_{\text{app}}^{‡}\right)$, and folding rates at 298 K (as determined by interpolating the Arrhenius fit to the data) of the different peptides at neutral pH (salt-bridge formation) and at acidic pH (no salt-bridge effects). Ac, acetyl; A, alanine; E, glutamic acid; R, arginine; D, aspartic acid; K, lysine.

^aThe different peptides were not studied at exactly the same temperatures. For better comparison of the rates, we give the interpolated value at 298 K as obtained from the Arrhenius fit. The uncertainty given is the average of those of the two experimentally determined rates at temperatures closest to 298 K.

^bData from (22).

^cAsymptotic standard errors (80). The error bars on the points of this particular data set were unrealistically large. To obtain realistic estimates for the uncertainties in the parameter values of ΔH^‡ and ΔS^‡ obtained from the fit to these points, we use the deviation of the data points from the fit to estimate the uncertainties in the parameter values (the so-called asymptotic standard errors, see http://arxiv.org/abs/1210.3781).

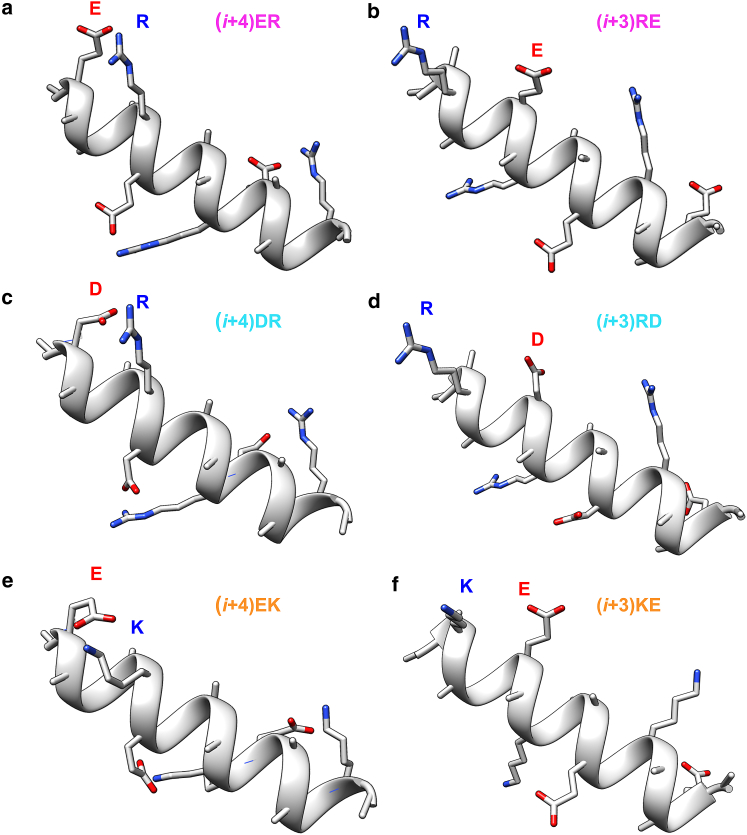
Figure 1.

Schematic representation of the folded conformation of six of the investigated peptides, showing the salt-bridge-forming side groups (a and b) Glu⁻ (E) and Arg⁺ (R), (c and d) Asp⁻ (D) and Arg⁺ (R), and (e and f) Glu⁻ (E) and Lys⁺ (K). (Left column) Salt-bridging side chains are spaced four (i, i + 4) peptide units apart. Shown are peptides (i + 4)ER (top), (i + 4)DR (center), and (i + 4)EK (bottom). (Right column) Salt-bridging side chains are spaced three (i, i + 3) peptide units apart and are in reverse order. Shown are peptides (i + 3)RE (top), (i + 3)RD (center), and (i + 3)KE (bottom). Structures were optimized and rendered with Chimera (38). To see this figure in color, go online.

Materials and Methods

Sample preparation and experimental measurements

The peptides (consisting of the sequences listed in Table 1) were purchased from GL Biochem (Shanghai, China). Peptide purity (≥ 95%) was assessed by reverse-phase high-performance liquid chromatography, and the peptides were lyophilized against a 35% DCl/D₂O solution to remove residual trifuoroacetic acid and to achieve H/D-exchange. Stock solutions of 12–16 mM were prepared by directly dissolving lyophilized solids in 50 mM KD₂PO₄/K₂DPO₄ D₂O buffer (pH^∗ 7.0 or pH^∗ 2.0). For measurements under neutral conditions (pH^∗ 7.0), the pH^∗ of the peptide solutions was adjusted by addition of NaOD solution (the volume added was <1% of the peptide solution). The peptide samples used in the IR measurements were kept at 12–16 mM concentration between 2 mm thick CaF₂ windows separated by a 50 μm Teflon spacer. All CD experiments were performed at peptide concentrations of 40 μM in 20 mM phosphate buffer (pH 6.8 or pH 2.0) using 2 mm quartz cuvettes. A detailed description of the steady-state UV CD and FTIR transient T-jump IR-probe experiments and computational methods has been reported previously (22).

MD simulations

The sequences of peptides were modeled as an ideal α-helix using Chimera (38), and capped with acetate at the N-terminus and methylamide at the C-terminus. Glutamate and aspartate residues were deprotonated and arginine and lysine residues were protonated. These structures were solvated in a periodic dodecahedral box with a distance of at least 1 nm between the box edge and the most extended atom of the peptide, and water was then added. The number of water molecules added ranged from 3136 to 3145. To meet experimental conditions and ensure electrostatic neutrality, 1 Na⁺ ion and 1 Cl⁻ ion were added, representing a concentration of 20 mM NaCl. In total, the number of atoms in the systems ranged from 9643 to 10,264. Interactions between atoms were described by the AMBER99-SB-ILDN force field (39, 40), in combination with the TIP3P water model (41). Long-range electrostatic interactions were treated via the particle-mesh Ewald method (42, 43) with a short-range electrostatic cutoff distance at 1.1 nm. van der Waals interactions were cut off at 1.1 nm. Preparation of the systems consisted of energy minimization and 10 ps of equilibration. Energy minimization was performed using the conjugate gradient method. After energy minimization, the positions of water molecules were equilibrated by a 10 ps MD run at a temperature of 278 K and a pressure of 1 bar, in which the heavy atoms in the protein were position-restrained with a force constant in each direction of 1000 kJ mol⁻¹ nm⁻². We performed seven 300 ns runs for each peptide system. Initial conditions were varied by assigning new random starting velocities, drawn from the Maxwell-Boltzmann distribution at 278 K. In addition, we simulated each peptide for 100 ns with position restraints on each heavy atom of the main chain (atoms N, CA, C, and O), with a force constant of 1000 kJ mol⁻¹ nm⁻² in each direction, thus restraining the peptide in an α-helical conformation. All simulations were performed with GROMACS v.4.5.4 (44) with the leap-frog integration scheme and a time step of 2 fs, using LINCS to constrain bonds in the protein and SETTLE to constrain water bonds. All simulations were performed in the isothermal-isobaric ensemble at a pressure of 1 bar, using the v-rescale thermostat (45) and the Parrinello-Rahman barostat (46).

Frames were stored every 10 ps. Analysis focused on helical hydrogen bonds and salt bridges between side chains, with the first 150 ns of each simulation excluded. Helical hydrogen bonds were defined as hydrogen bonds between the backbone carbonyl oxygen, O, of residue i and the backbone amide nitrogen, N, of residue i + 4. Helical-hydrogen-bond analysis consisted of counting the number of helical hydrogen bonds, indicated as hhb, and calculating the distance between the acceptor (atom O in residue i) and donor (atom N in residue i + 4 in helical hydrogen bond i, indicated as d_O-H. A helical hydrogen bond was counted if the distance between these atoms was <0.35 nm and the angle between the oxygen, nitrogen, and hydrogen was <30°. Salt-bridge analysis consisted of measuring the distance for each possible salt-bridge pair and counting the number of salt bridges occurring within a repeat, indicated as nsb. For each peptide system, three salt bridges can occur between pairs within the same repeat (in-repeat) and six can occur if the pairs are formed across different repeats (out-repeat). Distances are measured between Glu-C_δ/Asp-C_γ, and Arg-C_ζ/Lys-N_ζ atoms. A salt bridge was counted as nsb if it occurred between the glutamate/aspartate and arginine/lysine within the same repeat and with a distance of <0.6 nm between the atom pairs. For the calculation of the salt-bridge fractions, the same criteria were used to determine whether a salt bridge is formed. Probability distributions are calculated for all hhb and nsb distances, with a bin size of 1 for hhb and nsb. Two-dimensional probability plots are contoured at intervals of p = 0.01. Snapshots were visualized with PyMol (47). To determine the orientation of a salt bridge with respect to the main helical axis we calculated for each repeat the angle α between the helical hydrogen bond involving the residue at the end of the repeat and the salt bridge. To this end, we defined the angle α as the angle between two vectors, the first connecting the carbonyl oxygen of residue 2 (7 and 12 for subsequent repeats) and the nitrogen of residue 6 (11 and 16 for subsequent repeats), and the second connecting Glu-C_δ/Asp-C_γ and Arg-C_ζ/Lys-N_ζ. To calculate the probability distributions for α, we selected only those data points that had both an intact hydrogen bond (d_O-H ≤ 0.35) and an intact salt bridge (distance ≤0.6). For the first repeat of KE(i + 4), no data points fullfilled these criteria.

Results and Discussion

Sequence design

The sequences of the investigated alanine-based α-helical peptides (see Table 1) are based on a previously reported design (8, 14). The peptides are 17 residues long and have nearly identical amino-acid compositions with three repeating salt-bridging residue pairs, viz., Glu⁻ (E) and Arg⁺ (R), Asp⁻ (D) and Arg⁺ (R), or Glu⁻ (E) and Lys⁺ (K). Within each set of salt-bridge combinations, the charged residues are positioned either three (i, i + 3) or four (i, i + 4) peptide units apart, and the different acidic (A, either Glu⁻ or Asp⁻) and basic (B, either Arg⁺ or Lys⁺) residues are ordered in the sequence as AB or BA (see Fig. 1). To avoid end-charge effects, the N- and C-terminal ends are capped with acetyl and amide groups, respectively. To specifically examine the helix-stabilizing or destabilizing effect of the salt bridge and its impact on the folding and unfolding kinetics of the α-helix to random-coil transition, each of the peptides was studied under both neutral and acidic pH conditions. At neutral pH, both the acidic and basic side chains are charged, and formation of an AB- or BA-oriented salt bridge is possible, whereas at low pH (≤2.5) the acidic side groups are neutral (isolated Glu and Asp side-group pK_a values are ∼4.4 and 4.0, respectively) (1), preventing salt-bridge formation. We verify that the side chains of the Glu or Asp residues are completely protonated from the IR response of the COO⁻ (Glu⁻ 1565 cm⁻¹, Asp⁻ 1586 cm⁻¹) and COOH (Glu 1705 cm⁻¹, Asp 1713 cm⁻¹) groups (Fig. S4 in the Supporting Material) (35).

Equilibrium properties

Thermodynamic stabilities using UV CD

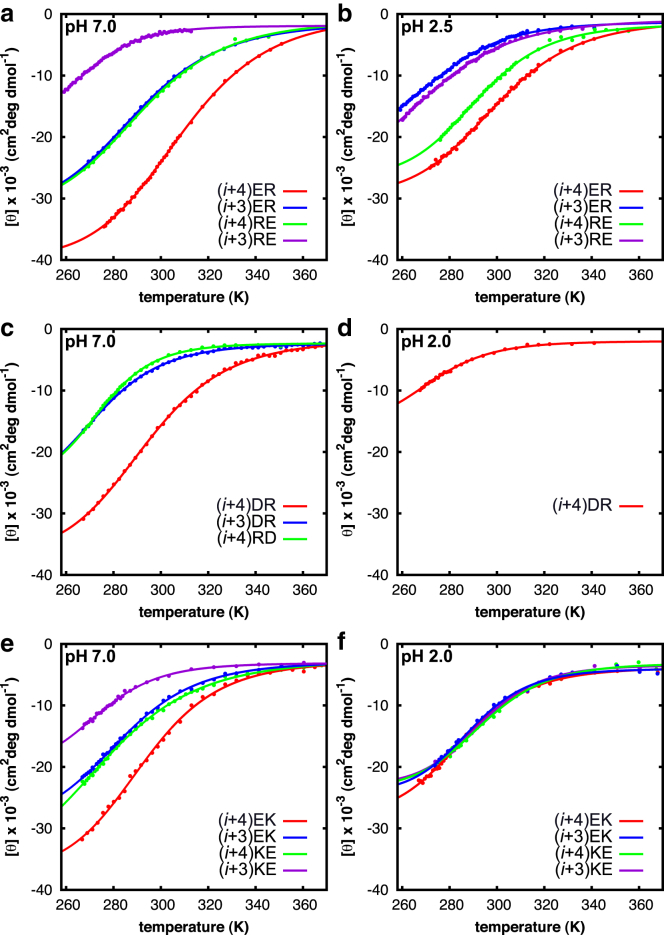
The unfolding transition of the peptides was studied in thermal equilibrium by collecting temperature-dependent UV CD spectra (Fig. S1) under both neutral (salt-bridge effects) and acidic (no salt bridges) pH conditions. Fig. 2 shows the temperature dependence of the mean residue ellipticity detected at 222 nm for each of the peptides at neutral and acidic pH. All melting curves show a sigmoidal transition, reflecting the temperature-induced conformational changes of the peptides in thermal equilibrium. From a singular value decomposition of the temperature-dependent CD spectra and global fitting, we find that the α-helix to random-coil transition can be very well described by a two-state model. We use a least-squares fit of a two-state model (48) to the data to obtain estimates of the melting temperatures (T_m) and the unfolding enthalpy changes (ΔH) (see Table S1 for the results). For some peptides, the low-temperature baseline was difficult to determine because of the low melting point, and this is reflected in the comparatively larger uncertainties in the reported values (this larger uncertainty in the steady-state folding parameters also causes larger uncertainties in the folding and unfolding rate constants; see below). All reported values are the weighted averages of at least three independent measurements.

Figure 2.

Thermal denaturation curves at 222 nm using UV CD of the different E/R peptides (a and b) (22), D/R peptides (c and d), and E/K peptides (e and f), under neutral (a, c, and e) and acidic (b, d, and f) pH conditions. The solid curves represent least-square fits to a two-state unfolding transition (48). The experimental values obtained for ΔH and T_m are listed in Table S1. To see this figure in color, go online.

As has been shown previously (14, 22, 49), the relative helicity and thermodynamic stability of the Glu/Arg peptides at neutral pH follows the trend (i + 4) ER > (i + 3) ER ≈ (i + 4) RE > (i + 3) RE, indicating that an ER-oriented salt bridge with E and R spaced four peptide units apart is most favorable for the folded α-helical conformation (Fig. 2; Table S1). A similar trend is observed for the D/R salt bridges, viz., (i + 4) DR > (i + 3) DR ≈ (i + 4) RD ≫ (i + 3) RD, in agreement with previous results (14, 49). Note that the UV CD spectrum of peptide (i + 3) RD indicates that at neutral pH the random-coil conformation is predominantly populated even at the lowest temperatures (Fig. S1), making a quantitative determination of the thermodynamic parameters impossible. The conformational stability of the peptides containing E/K salt bridges follows a trend analogous to the Arg-based peptides, viz., (i + 4) EK> (i + 3) EK ≈ (i + 4) KE > (i + 3) KE, suggesting that (i + 4) EK is the most favorable Lys-based salt-bridge geometry in an α-helix. Thus, within each particular set of E/R, D/R, and E/K salt bridges, we observe a similar sequence-distance and order dependence, and find that the α-helix-stabilizing effect is largest for AB-oriented salt bridges in which the interacting side chains are spaced four (i, i + 4) peptide units apart, whereas the (i + 3) BA type of salt bridges are less favorable for the α-helical conformation.

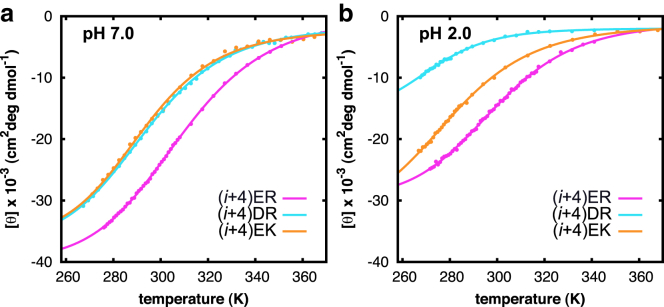
A comparison of helix content and thermodynamic stability between peptides containing different types of salt bridges (either E/R, D/R, or E/K) reveals significant differences (Fig. 3 a). The thermodynamic stability of the α-helices with optimized salt bridges follows the trend (i + 4) ER > (i + 4) DR ≈ (i + 4) EK, suggesting that substitution of the Glu residues with Asp, or Arg residues with Lys, leads to destabilization of the α-helical conformation (Fig. 2; Table S1). The differences in conformational stability between peptides containing different charge pairs possibly arises from the intrinsic helix-forming propensity of the specific amino acids (50). We observe that the Arg-based peptides that contain Asp in all cases have a lower thermodynamic stability than the corresponding peptides with Glu. Furthermore, we find that replacement of Arg with Lys also destabilizes the α-helical conformation of peptides (i + 4) ER and (i + 3) ER. Compared to the guanidinium moiety of the Arg side chain, the single amino group of Lys allows a reduced number of potential interactions with the carboxylate of Glu, resulting in different geometric specificities of Glu-Lys and Glu-Arg salt bridges (51, 52). In contrast, a comparison of the thermodynamic stability of the KE- and RE-oriented peptides indicates that these geometric effects become smaller upon reversing the charge orientation. To obtain more detailed insight into the folded and unfolded conformations and the relative salt-bridge populations of the investigated peptides, we carried out MD simulations (see below).

Figure 3.

Thermal unfolding curves detected at 222 nm using UV CD of the peptides containing different types of geometrically optimized salt bridges at neutral (a) and acidic (b) pH: peptides (i + 4)ER, (i + 4)DR, and (i + 4)ER. The solid curves represent least-square fits to a two-state unfolding transition (48). To see this figure in color, go online.

To determine whether the salt bridges (de)stabilize the α-helical conformation of the different peptides, the salt-bridge interaction was eliminated by protonating the carboxylates of either Glu⁻ or Asp⁻ at acidic pH (Fig. 2, right column). As we reported previously (22), the relative helicity and thermodynamic stability of the Glu/Arg peptides at acidic pH follows the trend (i + 4) ER ≈ (i + 4) RE > (i + 3) ER ≈ (i + 3) RE. For the Asp/Arg peptides, we find that the low-temperature UV CD spectra of peptides (i + 3) DR, (i + 4) RD, and (i + 3) RD exhibit essentially no helicity at acidic pH (Fig. S1), and the thermodynamic parameters for these three peptides could therefore not be reliably determined. However, the relative helicity at neutral pH follows the trend (i + 4) DR > (i + 3) DR ≈ (i + 4) RD > (i + 3) RD, in agreement with previous results (14). The thermodynamic stability of the Glu/Lys peptides in the absence of salt-bridge interactions is (i + 4) EK ≈ (i + 4) KE ≈ (i + 3) KE ≈ (i + 3) EK, indicating no significant positional dependence of the Lys residues at acidic pH. Overall, within each set of salt-bridge combinations we find that the α-helical content and thermodynamic stability of the AB-oriented peptides decreases in the absence of salt-bridge interactions. By contrast, all BA-type peptides (except for peptide (i + 4) RD) show an enhanced helicity and/or stability upon salt-bridge breaking, indicating that the formation of BA-oriented salt bridges at neutral pH destabilizes the folded conformation. As can be seen in Fig. 3 and Table S1, the increase in T_m and in ΔH_{F → U} upon deprotonation (and making salt-bridge formation possible) are much larger for Asp- than for Glu-based (i + 4) AB peptides. This difference can be explained by the significantly higher helix propensity of neutral Glu versus Glu⁻ (53): upon deprotonation the formation of a salt bridge becomes possible, which stabilizes the helix both for Asp and for Glu, but for Glu, deprotonation also decreases the helix propensity, and this partly counteracts the helix-stabilizing effect of the salt bridges; this counteracting effect does not occur for Asp (for which the helix propensity is independent of the protonation) (53), and this explains why the Asp-based (i + 4) AB peptide exhibits a larger increase in T_m and ΔH^‡ upon deprotonation than does the Glu-based peptide.

Analysis of salt-bridge formation using MD simulations

To study the investigated peptides in more detail, we performed seven 300 ns MD simulations for each peptide, starting from a helical structure, with different velocities for each run. As a measure of the stability of the helical conformation, we counted the number of backbone hydrogen bonds between the carbonyl oxygen O in residues i and the N-H group in residues i + 4, indicated as 〈hhb〉. In a perfect helix, this number is 15, including the caps on the termini. Fig. S11 shows the seven time traces of 〈hhb〉 for each peptide. In all systems, loss of helical structure occurs. Some systems, such as (i + 4) ER and (i + 4) EK, show unfolding and refolding within 300 ns. Other systems, such as (i + 3) RE, (i + 3) RD, and (i + 3) KE, have lost all helical structure within the first 150 ns. Therefore, subsequent analysis includes data from the last 150 ns.

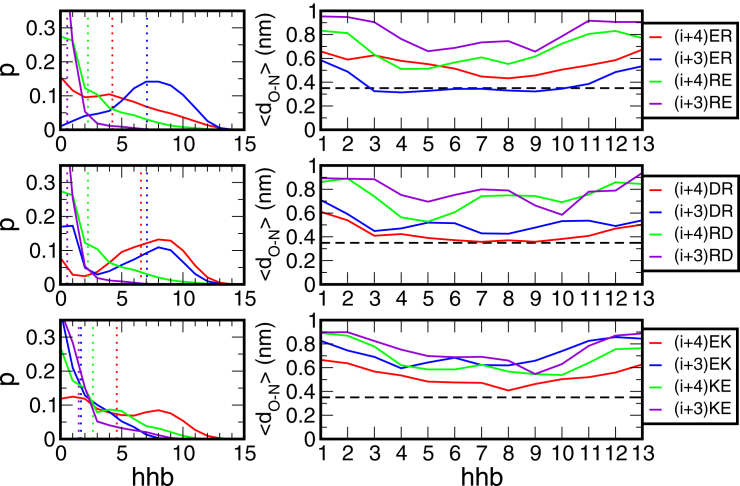
The lefthand column of Fig. 4, shows the probability distribution of the number of helical hydrogen bonds for each peptide, with the means indicated by vertical dotted lines. The distributions of helical hydrogen bonds show two peaks for (i + 4) ER, (i + 4) DR, (i + 3) DR, and (i + 4) EK, one at 〈hhb〉 = 0 and one at higher values up to 8 helical hydrogen bonds. The relative populations of both folded and unfolded cannot be determined accurately from these simulations, as they have not reached equilibrium. With this in mind, we can still observe that overall, the peptides with the negative charge preceding the positive charge in the sequence show the highest values for 〈hhb〉, with (i + 3) ER and (i + 3) DR as the most stable peptide (〈hhb〉 = 7). The BA (i + 3) peptides show the lowest values for 〈hhb〉, with peaks at 〈hhb〉 = 0 for (i + 3) RE, (i + 3) RD, and (i + 3) KE, in agreement with the experimental observations. With the value of 〈hhb〉 indicating the helical stability of the peptide, the order of peptides from most stable to least stable is (i + 3) ER > (i + 4) ER > (i + 4) RE > (i + 3) RE for the Glu-Arg based peptides, (i + 3) DR ≈ (i + 4) DR > (i + 4) RD > (i + 3) RD for the Asp-Arg series, and (i + 4) EK > (i + 4) KE > (i + 3) EK ≈ (i + 3) KE for the Glu-Lys series. In all three series, the peptides with the acidic group positioned at the N-terminal side of the repeat retain more helical structure than the peptides with the basic group positioned first in the repeat. Considering that these simulations have possibly not yet reached equilibrium, these results are in good qualitative agreement with the experimental observations.

Figure 4.

Helical hydrogen bonds in the peptide systems. (Left) Probability distribution (p) of the number of helical hydrogen bonds (hhb) for each peptide, with the means indicated by vertical dotted lines. (Right) Distance between the donor (N) and acceptor (O), d_O-N, averaged over the seven simulations (excluding the first 150 ns) as a function of the residue number of the acceptor. The dashed line at 0.35 nm indicates the distance criterion for forming a hydrogen bond. To see this figure in color, go online.

For each helical hydrogen bond, we calculated the distance between the donor (N) and the acceptor (O), d_O-N. In the righthand column of Fig. 4, d_O-N averaged over the seven simulations (excluding the first 150 ns) is plotted as a function of the residue number of the acceptor. The dashed line at 0.35 nm indicates the distance criterion for forming a hydrogen bond. For all peptides, d_O-N is highest at the ends of the peptide, indicating fraying of the α-helix.

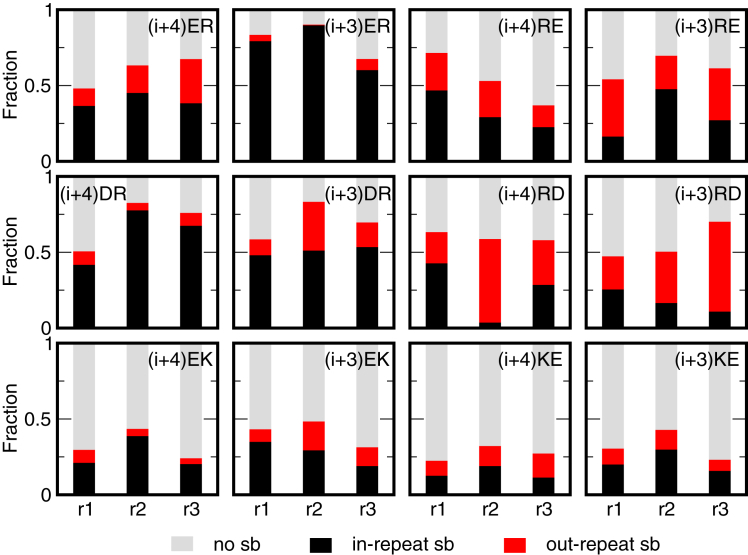
Salt bridges may form within the same repeat, but they also form across repeats. Considering that a salt bridge is formed if the ends are closer than 0.6 nm (see Materials and Methods for details), we calculated the fractions of salt bridges formed within the same repeat and across different repeats, as well as the absence of salt-bridge formation. Fig. 5 shows the fraction of the different types of salt bridges occurring in the simulations. For the Glu-Arg series, the total fraction of formed salt bridges is comparable and ranges from 0.5 to 0.75. Salt bridges formed within the same repeat dominate the total fraction of formed salt bridges in the AB-peptides, whereas the salt bridges formed across repeats and within repeats contribute almost equally in the BA-peptides. This effect is even more pronounced in the Asp-Arg series, where the AB-peptides contain mainly salt bridges formed within the same repeat and the BA-peptides contain mainly salt bridges formed across repeats. The Glu-Lys series does not show a similar trend, as the total fraction of formed salt bridges is significantly lower compared to the Arg-based peptides. These results indicate that the order of charges within the repeats has a much stronger effect on the formation of salt bridges than does the spacing between the charges.

Figure 5.

The fraction of salt bridges shown as bar plots for each repeat, with different colors indicating in-repeat salt bridges, out-repeat salt bridges, and no salt bridge. To see this figure in color, go online.

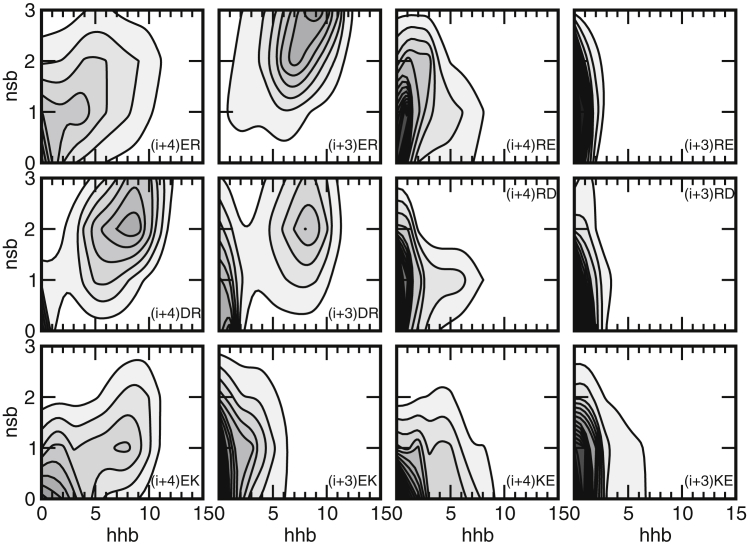
To investigate the effect of the salt bridges on the stability of the helices, we calculated two-dimensional probability distributions for 〈hhb〉 and the number of intact salt bridges formed within the same repeat, nsb. The results are plotted in Fig. 6. In the peptides with the acidic group occurring first in the repeat ((i + 4) ER, (i + 3) ER, (i + 4) DR, (i + 3) DR, (i + 4) EK, and (i + 3) EK), hhb and nsb show a positive correlation. Configurations with high helical content contain two or more in-repeat salt bridges, whereas conformations with little helical structure contain one in-repeat salt bridge at most. This indicates that the formation of salt bridges coincides with higher helical content. In contrast, peptides (i + 4) RE, (i + 4) RD, and (i + 4) KE show a weak negative correlation between hhb and nsb, revealing helical conformations without any salt bridges formed within the same repeat, or salt bridges formed in conformations with very little helical structure. The probability maxima in the profiles of peptides (i + 3) RE, (i + 3) RD, and (i + 3) KE contain little helical structure, and at most one formed salt bridge.

Figure 6.

Probability plots as a function of the number of helical hydrogen bonds, hhb, and the number of in-repeat salt bridges, nsb. Contour lines are drawn at intervals of p = 0.01. To see this figure in color, go online.

There are two possible explanations for the effect of the spacing and charge order of the salt bridges on helical stability: 1) alignment of the electric dipole of the salt bridges with the helical dipole (which would explain why AB sequences, which have a charge order following the helical dipole, form salt bridges more frequently within repeats); and 2) sterical clashes that impose torsional limitations on the bond rotation in the salt-bridge side chains, thus allowing only a limited number of orientations. To investigate whether helix-dipolar effects play a role, we calculated the angle α between a vector connecting the ends of a formed salt bridge and a vector following the helical hydrogen bond formed within the same repeat (see Fig. S12 for the distribution of these angles). The (i, i + 4) AB peptides all have a strong preference for angles around −30°, indicating that the salt bridge has a tilted orientation with respect to the axis of the helix, as shown in Fig. S12. The (i, i + 3) AB peptides favor positive values with α ranging from 0 to 90°, also representing salt bridges with a tilted conformation with respect to the helical hydrogen bond, but in the opposite direction. These differences indicate that the constraints on bond rotation impose different orientations for the intact salt bridge. The (i, i + 4) BA peptides can adopt both orientations. The (i, i + 3) BA peptides show both negative and positive values for α in the Glu-Arg systems. In the Asp-Arg and Glu-Lys systems, the (i, i + 3) BA peptides favor negative α values. These results show that the salt bridges can have two orientations with respect to the helical axis (as represented by the helical hydrogen bond), thus suggesting that aligning the salt-bridge dipole with the helical dipole has little stabilizing effect. We thus conclude that the dependence of the stabilizing effect of the salt bridges on the order and spacing of the salt-bridge residues is mainly due to torsional constraints that allow for only a limited number of salt-bridge configurations within the given charge order and spacing.

Finally, we investigated the effect of the salt-bridge orientation on the frequency of salt-bridge formation by performing 100 ns of molecular dynamics on each peptide, with position restraints on the main-chain atoms. Fig. S13 shows time traces of the number of salt bridges within repeats, nsb, for each peptide. Formation and dissocation of salt bridges occurred multiple times for each system, with the exception of (i, i + 4) RD in which only one transition occurred from having all salt bridges broken (nsb = 0) to having all salt bridges formed (nsb = 3). No salt bridges between side chains in different repeats were formed in any significant number, except in the case of (i, i + 4) RD (data not shown). The observation that salt bridges between repeats occur in the restrained simulation of (i, i + 4) RD may explain the low frequency of salt-bridge formation for this system, as salt bridges first have to be broken before salt bridges within the same repeat can be formed. The peptides containing lysine show the largest number of changes between nsb = 3 and nsb = 0. Within the group of lysine-containing peptides, the (i, i + 4) EK system has the highest probability for having all in-repeat salt bridges formed. The frequency of salt-bridge breaking and formation is much lower for the systems containing arginine, in particular for the peptides with aspartate. The peptides with the negatively charged side chain preceding the positive charge tend to form salt bridges within the same repeat, whereas salt-bridge formation occurs less often for the peptides with opposite charge order, in particular for (i, i + 3) RD. These backbone-restrained simulations indicate that the charge order has a strong effect on the tendency to form salt bridges, further emphasizing the role of torsional constraints in de formation of salt bridges.

Infrared spectra

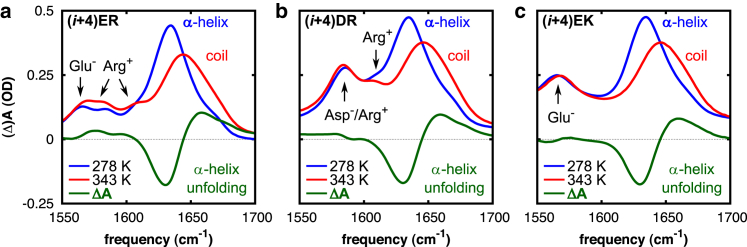
In the kinetic studies of the α-helices, we use the IR response as a probe of conformation. We first probe the α-helix-to-random-coil transition in thermal equilibrium. Temperature-dependent FTIR spectra were collected in the amide I′ spectral region. The amide I′ vibration of proteins and peptides, primarily arising from carbonyl stretch vibrations of the backbone amide residues, is very sensitive to secondary structure and can be directly related to the conformation of the backbone (34). In particular, the IR absorption band of amide residues in an α-helical structure is centered at ∼1635 cm⁻¹, whereas a random backbone conformation absorbs at higher frequencies (∼1645 cm⁻¹) (35, 54). To characterize the temperature-induced absorption changes of the amide I′ mode, equilibrium FTIR spectra were collected between 274 K and 353 K with incremental steps of 5 K. As can be seen in Fig. 7, all low-temperature FTIR spectra (blue) of the (i, i + 4)-spaced and AB-oriented peptides exhibit an amide I′ band centered at 1634 cm⁻¹ arising from the amide carbonyl groups involved in an α-helical conformation. With increasing temperature (Fig. 7, red), the amide I′ absorption maxima are shifted from 1634 cm⁻¹ to 1644 cm⁻¹, indicative of an α-helical-to-random-coil transition. Accordingly, all temperature-difference spectra show a broad negative feature centered at 1630 cm⁻¹ and a positive feature centered at 1658 cm⁻¹ (Fig. 7, green). The negative contribution is characteristic for the loss of α-helical population, whereas the positive feature is attributed to the associated formation of random-coil conformations (25). In addition, the minor components occurring at 1585 and 1607 cm⁻¹ in the FTIR spectra of the Arg-containing peptides (i + 4)ER and (i + 4)DR (Fig. 7, a and b) arise from the symmetric and antisymmetric stretch vibration of the guanidinium group of Arg (35). The small peak at 1565 cm⁻¹ in the spectra of the Glu-based peptides (i + 4)ER and (i + 4)EK (Fig. 7, a and c), originates from side-chain contributions of the carboxylate group of Glu⁻, and shifts to 1705 cm⁻¹ upon protonation under acidic pH conditions (Fig. S4, a and e) (35). As can be seen in Fig. 7 b, the CO-stretching mode of the COO⁻ group of Asp⁻ arises at 1586 cm⁻¹, and shifts to 1713 cm⁻¹ upon protonation (Fig. S4 b) (35). The absence of the COO⁻ peaks in the FTIR spectra obtained at low pH confirms that the carboxylate groups of the Glu and Asp side chains are completely protonated under acidic pH conditions, thereby inhibiting the formation of salt bridges (Fig. S4, b, d, and f).

Figure 7.

Temperature-dependent equilibrium FTIR spectra in the amide I′ spectral region of peptides (a) (i + 4)ER (22), (b) (i + 4)DR, and (c) (i + 4)EK at neutral pH. FTIR difference spectra were generated by subtracting the spectrum measured at 274 K from the spectrum collected at 353 K, and reflect the changes in IR absorption upon thermal unfolding of the α-helices. To see this figure in color, go online.

T-jump relaxation kinetics

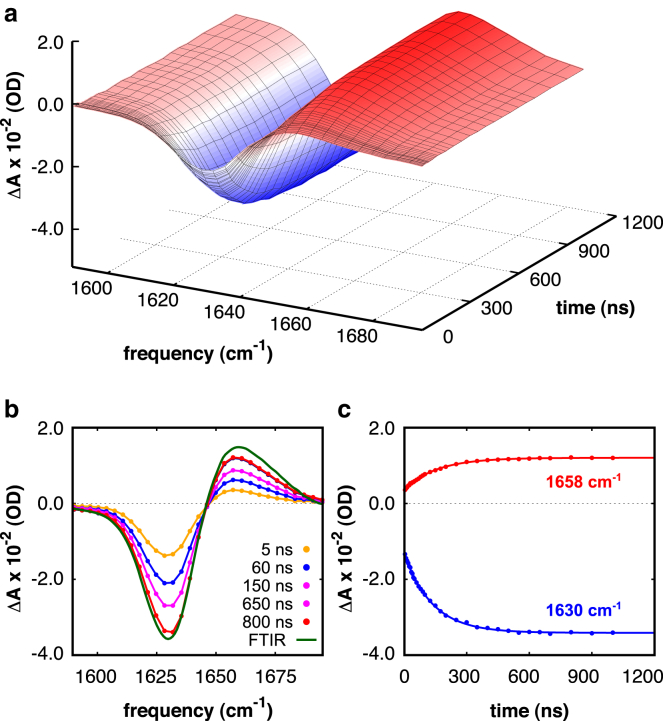
We probed the T-jump-induced relaxation kinetics of each of the investigated α-helices in the amide I′ spectral region starting from various initial temperatures. Fig. 8 a shows a solvent-corrected three-dimensional representation of the relaxation kinetics of peptide (i + 4)EK at neutral pH in response to a T-jump from 293 to 301 K. The time- and frequency-resolved change in IR absorption (ΔA) shows negative (blue) and positive (red) contributions, reflecting the blue shift of the amide I′ mode that arises from the conformational redistribution process of the peptide during reequilibration. As can be seen in Fig. 8 b, the transient spectra at long time delays are essentially identical to the equilibrium FTIR temperature-difference spectrum and exhibit the negative and positive contributions at 1630 and 1658 cm⁻¹ indicative of an α-helix-to-random-coil transition. We find that the T-jump relaxation kinetics probed at these two structure-sensitive frequencies can be well described by a single-exponential function, i.e., with an observed relaxation time constant of τ = 143 ± 4 ns at a final temperature of 301 K (Fig. 8 c). Moreover, for each of the investigated peptides we find that the transients show single-exponential T-jump relaxation kinetics with equal relaxation rates at 1630 cm⁻¹ (decrease of the α-helical population) and 1658 cm⁻¹ (increase of the random-coil population) at all final T-jump temperatures and at all pH values (see Section S4 in the Supporting Material).

Figure 8.

Representative data set probing the T-jump relaxation dynamics of peptide (i + 4)EK in the amide I′ region after a T-jump from 293 to 301 K. (a) Three-dimensional representation of the observed relaxation kinetics corrected for solvent absorption changes. The difference in absorption (ΔA) is presented as a function of frequency and time. (b) Transient spectra for selected delay times compared to the (scaled) FTIR difference spectrum. (c) Time course of the T-jump relaxation monitored at 1630 cm⁻¹ (α-helix) and 1658 cm⁻¹ (random coil). The relaxation kinetics are globally fitted to a single-exponential decay function (solid curve), ΔA(t) = A₀ + A₁exp(−t/τ), with an observed time constant of τ = 143 ± 4 ns. To see this figure in color, go online.

The detection of single-exponential T-jump relaxation kinetics at all final temperatures, IR frequencies, and pH values, indicates that the folding and unfolding of the investigated α-helical peptides can be described by an effective two-state model (55), as already suggested by our static temperature-dependent measurements. Although classifying the conformational population distribution of α-helices into two macroscopically distinct states, viz., α-helix and random coil, might not be rigorously correct, effective two-state folding behavior has been observed previously for a large number of α-helices (56, 57, 58, 59, 60, 61, 62, 63). These experimental observations probably originate from a conformational free-energy profile in which the α-helical and random coil ensembles can be characterized as two broad free-energy minima that are separated by a single main free-energy barrier (57, 58, 59). When the free-energy barrier separating these two conformational macrostates is much higher than the barriers between the microstates within each of them, preequilibration within the microstate populations occurs on timescales much faster than that of the population exchange involving the crossing of the main free-energy barrier (64, 65, 66, 67). If the population distribution of all microstates preequilibrates within the time resolution of the T-jump pulse (∼5 ns), the relative populations in each distribution will remain constant from this point in time, and single-exponential T-jump relaxation kinetics reflecting the crossing of the main free-energy barrier and the conformational redistribution process between the α-helical and random-coil ensembles is observed (66). Accordingly, the detection of a single kinetic timescale indicates that the investigated α-helical peptides fold and unfold effectively as two-state systems, allowing the estimation of the effective folding and unfolding rates (k_F,eff and k_U,eff) involving the crossing of the main free-energy barrier using a combined analysis of the experimentally observed T-jump relaxation rate (k_R) and the folding equilibrium constants (K_eq) obtained from our temperature-dependent CD measurements (because k_R = k_F + k_U and K_eq = k_F/k_U) (55).

Folding and unfolding kinetics

Because all our equilibrium and kinetic data fit a two-state model quantitatively, the effective folding and unfolding rates (k_F,eff and k_U,eff) involving the crossing of the main free-energy barrier at a particular temperature can be estimated. We find that the effective folding and unfolding rates (k_F,eff and k_U,eff) of each of the investigated peptides exhibit Arrhenius temperature dependence (plots of k_R, k_F,eff, and k_U,eff for the individual peptides are shown in Figs. S9–S11). From least-squares fits of the data to the Arrhenius equation, we obtain the apparent enthalpy for the formation of the transition state $\left(\Delta H_{\text{app}}^{‡}\right)$ for the folding (U → F) and unfolding (F → U) transitions (68). The results are listed in Table 1 (folding) and Table S2 (unfolding).

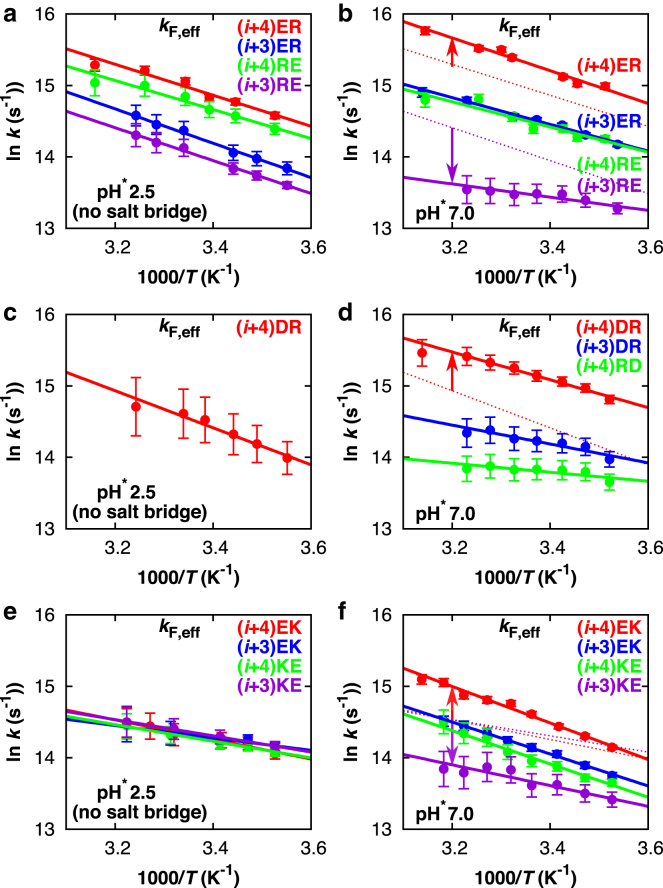
To determine the effect of salt bridges on the (un)folding kinetics, we first compare the effective α-helical folding rates (k_F,eff) of the different E/R, D/R, and E/K peptides in the absence of salt bridges at acidic pH (see Fig. 9, left column). We observe small but measurable differences in the kinetic behavior of the investigated peptides. As we reported in a previous study (22), the effective folding rates at acidic pH of the (i, i + 4) spaced E/R peptides are slightly faster than those of the (i, i + 3) spaced E/R peptides. This dichotomy probably arises from a slight sequence-position dependence of the preferred rotamer conformations (and helix-forming propensity) of Glu⁰ and Arg⁺ with respect to each other (69). For the D/R analogs at acidic pH, only the effective folding rates of peptide (i + 4) DR could be estimated (Fig. 9 c), because the folding equilibrium constants (K_eq) for peptides (i + 3) DR, (i + 4) RD, and (i + 3) RD could not be reliably determined in the absence of salt-bridge effects at acidic pH. Comparison of the effective folding rates of peptides (i + 4) ER and (i + 4) DR shows that replacement of Glu⁰ with Asp⁰ only marginally slows down the folding. Notably, the effective folding rates of the Lys-based peptides at acidic pH are slightly slower compared to the Arg-based variants (Fig. 9 e). In both cases, these effects might arise from differences in the helix-forming propensity of the involved amino-acid residues (50). In contrast to the Arg-based peptides, the Lys-containing sequences do not show any dependence of the kinetics on the position and order of Glu⁰ and Lys⁺ (Fig. 9 e).

Figure 9.

Arrhenius plots of the effective folding rates (k_F,eff) of the different E/R peptides (a and b) (22), D/R peptides (c and d), and E/K peptides (e and f), measured in the absence (left) and presence (right) of salt-bridge effects. The solid lines are least-square linear fits. For better comparison, in the plots of k_F,eff at neutral pH (salt-bridge effects), the fits to k_F,eff at acidic pH (no salt bridges) are shown as dotted lines for peptides (i + 4)ER and (i + 3)RE (b), (i + 4)DR (d), and (i + 4)EK and (i + 3)EK (f). The values for $\Delta H_{(\text{U}\to \text{F})}^{‡}$ obtained from fitting of the data to the Arrhenius equation are summarized in Table 1. To see this figure in color, go online.

Effect of charge spacing and order

Fig. 9 (right column) shows the effective folding rates (k_F,eff) of the different E/R, D/R, and E/K peptides at neutral pH and reveals that the ability to form salt bridges has a significant impact on the folding kinetics of the investigated α-helices. We find that a salt bridge can both speed up and slow down the rate of α-helix formation, depending on the type of charge pairs and their geometry. As we have found previously (22), the rates of α-helix folding of the E/R peptides at neutral pH show the same trend as their structural stability, viz., (i + 4) ER > (i + 3) ER ≈ (i + 4) RE > (i + 3) RE (see Fig. 9 b). In this study, a similar correlation between folding kinetics and thermodynamics is found for the D/R sequence patterns, as the effective folding rates show the trend (i + 4) DR > (i + 3) DR > (i + 4) RD (see Fig. 9 d). The folding rates of peptide (i + 3) RD could not be reliably estimated, as the UV CD measurements did not allow a quantitative determination of the folding equilibrium constant (K_eq). As in the case of the Arg-based peptides, the folding rates of the Lys-containing peptides show the same trend as the thermal stability of the folded structures, viz., (i + 4) EK > (i + 3) EK ≈ (i + 4) KE > (i + 3) KE (see Fig. 9 f). Thus, the effective folding rates within each particular set of E/R, D/R, or E/K salt-bridge combinations show a similar sequence-position dependence of the charged side chains. In all cases, the ability to form an AB-oriented salt bridge spaced at (i, i + 4) speeds up the rate of α-helix formation (Fig. 9, right column, red data points), by >40% in the case of (i, i + 4) ER and by 90% in the case of (i, i + 4) DR. By contrast, a BA-oriented salt bridge spaced at (i, i + 3) slows down α-helical folding (Fig. 9, right column, purple data points). Hence, inhibiting the formation of this unfavorable BA-oriented salt bridge upon protonation of Glu or Asp has an accelerating effect on the folding of the investigated α-helices.

For the unfolding rates, we find exactly the opposite behavior (see the Supporting Material). Fig. S10 shows the Arrhenius plots of the unfolding rates in the absence of salt bridges at acidic pH (left column) and in the presence of salt-bridge effects (right column). We observe that the possibility of forming salt bridges significantly affects the unfolding kinetics of the investigated α-helices. Notably, the rates of unfolding in the presence of geometrically optimized AB-oriented salt bridges at neutral pH (Fig. S10, right column) are distinctly slower compared to their unfolding rates in the absence of salt bridges at acidic pH (Fig. S10, left column). By contrast, the presence of unfavorable BA-oriented salt bridges is reflected in marginally faster unfolding rates. Thus, within each set of E/R, D/R, and E/K salt bridges, the unfolding rates show a trend opposite to that of the folding rates, indicating that the ability to form geometrically optimized salt bridges not only speeds up folding, but can also prevent unfolding.

Effect of the type of salt bridge: E/R, D/R, or E/K

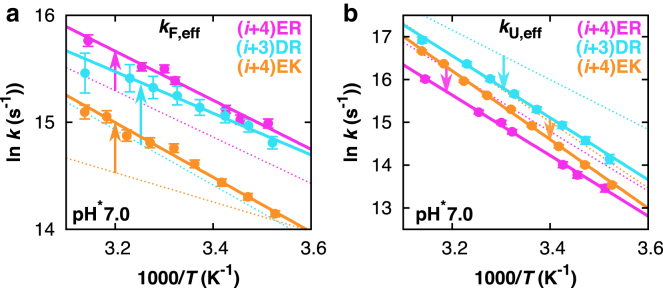
In Fig. 10, we compare the effective α-helical folding and unfolding rates in the absence (acidic pH; Fig. 10, dotted lines) and presence (neutral pH) of different types of geometrically optimized salt bridges. The data indicate significant differences in the folding kinetics of peptides containing different type of charge pairs. We find that the rates of α-helix formation at neutral pH are in the order (i + 4) ER > (i + 4) DR ≫ (i + 4) EK, indicating that an optimized E/R salt bridge is most favorable for the speed of folding and that the Arg-containing peptides fold faster compared to the Lys-based variant (Fig. 10 a). Remarkably, the trend observed for the folding rates of the different E/R, D/R, and E/K peptides deviates from that observed for the conformational stability, viz., (i + 4) ER > (i + 4) DR ≈ (i + 4) EK (see Fig. 3 a). This suggests that the parallel between thermodynamic stability and kinetic behavior as observed within each set of E/R, D/R, and E/K sequence patterns is not necessarily a general effect. The observed differences in folding rates between peptides with different types of optimized E/R, D/R, or E/K salt bridges probably mainly originate from differences in the rotameric accessibility of the charged amino acid residues that allows salt-bridging in the folded state of the peptides (see the MD Simulations section).

Figure 10.

(a) Arrhenius plots of the effective folding rates of peptides (i + 4) ER, (i + 4) DR, and (i + 4) EK measured in the presence of salt-bridge effects at neutral pH. The fits to k_F,eff at acidic pH (no salt bridges) are shown as dotted lines. (b) Arrhenius plots of the effective unfolding rates. To see this figure in color, go online.

Comparing the folding rates of the two Arg-containing peptides (i + 4)ER and (i + 4)DR at neutral pH, we observe that the Glu-containing variants fold slightly faster (Fig. 10 a). However, inhibiting the formation of a geometrically optimized D/R salt bridge by lowering the pH (Fig. 10 a, dotted line) slows down folding more than in the E/R equivalent, suggesting a larger net effect of D/R salt bridges on the folding kinetics. This might originate from the changes in helix propensity of the acidic amino acid residues due to lowering of the pH, as it is known that the change in intrinsic helix propensity upon neutralization is larger for Asp than for Glu (50). However, another plausible explanation for the observed larger net contribution of D/R salt bridges to the speed of folding arises from differences in the probability of the accessible side-chain rotamers and their corresponding free energies (see the MD Simulations section).

The effective unfolding rates in the presence of geometrically optimized E/R, D/R, or E/K salt bridges show the trend (i + 4) DR > (i + 4) EK > (i + 4) ER (Fig. 10 b). In contrast to the tendencies within each set of sequence patterns, the rates of unfolding of the different types of optimized E/R, D/R, or E/K salt bridges do not follow a trend exactly the opposite that of their folding rates. In particular, the rate of folding of the Lys-based peptide deviates from this trend. This deviation may arise from differences in the intrinsic helical propensity of the interacting amino acids and their relatively larger geometric restraints when involved in a salt bridge compared to those for Arg-containing salt bridges (see MD Simulations section). To summarize, α-helix formation is fastest in the presence of geometrically optimized E/R salt bridges. By contrast, the ability to form optimized E/R salt bridges reduces the rate of the unfolding process more effectively compared to that associated with formation of D/R and E/K equivalents.

Potential implications for protein folding

Our results show a correlation between the stability of the native structure (ΔG_FU) and the folding rates of different peptides within the same set of salt-bridge combinations. We find that geometrically (rotamerically) optimized salt bridges, which stabilize the folded conformation, also enhance the ability to fold rapidly, whereas destabilizing salt bridges reduce the folding rate. Comparing the trends of the conformational stability and kinetic behavior of salt bridges formed between different type of charge pairs, we find that the observed correlation between thermodynamic and kinetic effects of salt bridges within each set of sequence patterns is not necessarily a general effect. This observation suggests a potential explanation for the presence of nonstabilizing, evolutionarily conserved salt bridges that exist in many proteins. Many solvent-exposed salt bridges are known to be only marginally stabilizing (13, 21), or even destabilizing (11, 12). The contribution of buried salt bridges to protein stability has been questioned as well, because the free-energy contribution of the salt bridge has to be sufficient to cancel both the high free-energy cost required for desolvation of the charged residues during the folding process (2) and the entropic penalty caused by the restriction of a buried salt bridge to a single rotameric state (70, 71). On the other hand, the hydrophobic protein interior also facilitates stronger electrostatic interactions between the salt-bridging side-chains due to reduced solvent screening (5). A classical example of a stabilizing salt bridge is the Asp-His salt bridge buried in the hydrophobic core of lysozyme that lowers the free energy of the native fold by 10–20 kJ mol⁻¹ (10). By contrast, a buried Glu-Arg salt bridge in the Arc repressor of bacteriophage P22 destabilizes the native structure (16), and the formation of this salt bridge has been proposed to be the rate-limiting step in the folding process (72). Moreover, MD simulations have shown that the formation of the Asp-Arg salt bridge deeply buried in the protein core of human salivary α-amylase is highly destabilizing and increases the free energy of the folded state by as much as 44 kJ mol⁻¹ (73). The question arises as to the possible evolutionary advantages of the conservation of such (highly) structure-destabilizing salt bridges in proteins functioning in the living cell.

In this study, we find that solvent-exposed salt bridges can have a strong impact on the kinetics of folding and unfolding. It is tempting to speculate whether such kinetic effects of salt bridges might be a more general phenomenon, in which the equilibrium effect (stabilizing or destabilizing) of a salt bridge is of secondary importance. It might be possible for a salt bridge to stabilize the transition state and/or a certain folding intermediate, but not necessarily the final, folded state. For several proteins, there exists evidence for such a purely kinetic function of salt bridges. For example, the solvent-exposed salt bridge formed between Glu and Arg in Staphylococcal nuclease has been shown to contribute only marginally to the structural stability of the folded state (2.1 kJ mol⁻¹) (74). However, simulation studies indicate that this salt bridge can create significant kinetic barriers for the unfolding process, thereby “locking” the protein in its native conformation and preventing the protein from unfolding (75, 76). Evidence for a kinetic function of salt bridges has also been observed during the early stages of ATP hydrolysis by myosin, in which a Glu-Arg salt bridge stabilizes the transition state of hydrolysis (77). Finally, experimental evidence shows that the presence of an Arg-Asp salt bridge in triosephosphate isomerase (78) and an Arg-Glu salt bridge in mouse Paneth cell α-defensin cryptidin-4 (79) both play a critical role in efficient and correct folding of the native structures, rather than having a stabilizing impact on the native folds. The impact of salt bridges on the kinetics of α-helix formation observed here might thus explain the evolutionary pressure for the conservation of apparently nonfunctional (destabilizing) salt bridges in many proteins.

Author Contributions

S.W. conceived and designed the experiments. H.M. performed the experiments. J.V. performed the simulations. H.M., J.V., and S.W. wrote the article.

Editor: Jose Faraldo-Gomez.