A Simple Model of Protein Domain Swapping in Crowded Cellular Environments

Abstract

Domain swapping in proteins is an important mechanism of functional and structural innovation. However, despite its ubiquity and importance, the physical mechanisms that lead to domain swapping are poorly understood. Here, we present a simple two-dimensional coarse-grained model of protein domain swapping in the cytoplasm. In our model, two-domain proteins partially unfold and diffuse in continuous space. Monte Carlo multiprotein simulations of the model reveal that domain swapping occurs at intermediate temperatures, whereas folded dimers and folded monomers prevail at low temperatures, and partially unfolded monomers predominate at high temperatures. We use a simplified amino acid alphabet consisting of four residue types, and find that the oligomeric state at a given temperature depends on the sequence of the protein. We also show that hinge strain between domains can promote domain swapping, consistent with experimental observations for real proteins. Domain swapping depends nonmonotonically on the protein concentration, with domain-swapped dimers occurring at intermediate concentrations and nonspecific interactions between partially unfolded proteins occurring at high concentrations. For folded proteins, we recover the result obtained in three-dimensional lattice simulations, i.e., that functional dimerization is most prevalent at intermediate temperatures and nonspecific interactions increase at low temperatures.

Introduction

Many biologically relevant protein-protein interactions require partial unfolding of the protein. Such interactions include aggregation into ordered amyloid structures or disordered aggregates, as well as protein domain swapping, whereby two proteins exchange a structural element such that native-like contacts are formed with the complementary portion of the other protein (1, 2). Although much work in experiment, theory, and simulation has been devoted to understanding the kinetics and thermodynamics of protein folding, the theory of the folding of multiple proteins into aggregates or domain-swapped structures is far less established.

Domain swapping has been shown to have functional relevance (e.g., in proteins involved in DNA cleavage (3) and in receptor binding (4)) and it may play a role in the evolution of functional dimers (5, 6). In addition, domain-swapped oligomers are suspected to be precursors to protein aggregates (1). Although domain swapping sometimes requires nearly complete unfolding of the protein, other domain-swapped structures can be formed by opening of the protein into a partially folded state (7, 8). The domain that is exchanged may range from an entire protein domain to a single β-strand or -helix. The segment of the protein between the two domains is referred to as the hinge loop, signifying its role as a hinge that allows the protein to convert from the closed monomeric state to the open form required for domain swapping. Recent studies showed that mutant forms of the essential metabolic enzyme DHFR oligomerized at elevated temperatures, and that this mutant had a beneficial fitness effect when introduced into the bacterial chromosome, replacing the wild-type protein (9). Since oligomerization is manifest only at the high temperature of 42°C, it is likely that it involves partial unfolding of the protein, suggesting that the observed dimeric form of the protein may be a domain-swapped dimer.

An important factor in protein evolution is the avoidance of nonfunctional interactions between unfolded or partially unfolded proteins, which results in the formation of amyloids or disordered aggregates, and between folded proteins. For instance, highly abundant proteins tend to have less sticky surfaces due to the necessity of avoiding promiscuous interactions (10). How protein sequences and abundances evolve to promote folding and functional interaction in the presence of nonspecific interaction partners has not been fully elucidated (11, 12).

Lattice models of protein folding and protein-protein interactions have provided valuable insights into kinetic and thermodynamic aspects of protein systems (11, 13, 14, 15, 16). In addition, off-lattice coarse-grained models have been used to study protein folding, dimerization, and aggregation (15, 17, 18). Although they are lacking in biophysical detail, such simplified models speed computation and allow for a greater sampling of the accessible conformational space. Many models contain fewer than the natural 20 amino acid types, which further simplifies such models by reducing the allowed sequence space (14, 19, 20). This reduction to a few residue types may have physical validity, since it has been shown that foldable proteins can be constructed from reduced alphabets in vitro (21), and that α-helical bundle proteins tolerate extensive mutations that maintain the binary division into polar and nonpolar regions (22). Minimal lattice models, along with more detailed atomistic models, have been used to study aspects of protein-protein interactions, including protein aggregation and nonfunctional interactions between proteins in the cell cytoplasm (11, 12, 19, 23). A recent theoretical study simulated aggregation in vitro and in vivo in the endoplasmic reticulum using both a simple 3D Monte Carlo model and a mean field kinetic approach (24), although the model did not explicitly account for protein sequence and structure.

Here, we present a simple model of interacting proteins that allows for partial unfolding of the proteins. This four-residue-type, two-dimensional (2D) model is intended to be a minimal model that incorporates protein domain swapping. As such, the model potentially can reproduce the temperature dependence and sequence sensitivity of the domain-swap interaction while allowing for specific and nonspecific interactions between folded and partially unfolded proteins. Although the proteins in their native state have the shape of a 3 × 4 lattice protein, they move in continuous space and partially unfold by rotation of each of the two domains about a hinge, adding complexity beyond that of a 2D lattice model of folded proteins. We apply our model to several protein sequences and find that domain swapping occurs at intermediate temperatures and intermediate concentrations, whereas nonspecific interactions between unfolded proteins occur at high concentrations and intermediate temperatures. We find that a strong domain-domain interaction combined with torsional strain favoring the open conformation promotes domain swapping. For folded proteins, promiscuous interactions are common at low temperatures, whereas strong specific interactions are favored at intermediate temperatures and monomers are favored at high temperatures.

Materials and Methods

Model

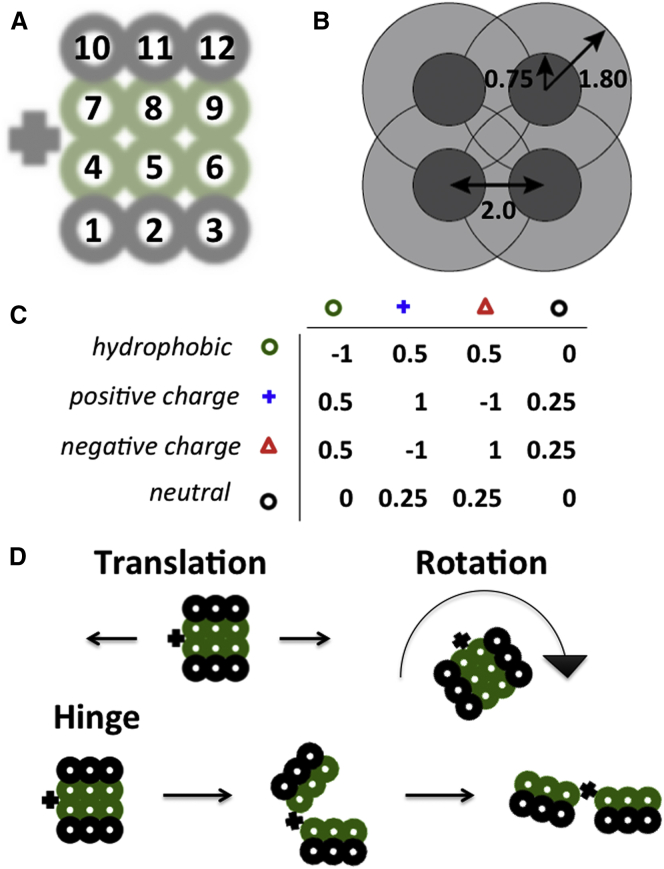
Monte Carlo simulations were performed on model proteins moving in continuous space. The folded structure of a single model protein is shown in Fig. 1 A. The protein consists of two domains (residues 1–6 and 7–12) that can individually rotate about the hinge, denoted by a black +. The functional interface is defined as the four-residue surface opposite the hinge. The interaction potential is a step function centered at each residue, with a hard-sphere radius of 0.75 units and an interaction radius of 1.80 units. The spacing between residues within a protein is chosen so that adjacent and diagonal residues within the protein interact, as shown in Fig. 1 B.

Figure 1.

Simple protein model. (A) Individual protein in the native state. Each residue is represented by a black or green circle and is numbered (residues 1–12). The hinge is represented by a + to the left of the protein and does not contain a residue. (B) Residue interaction radii. The inner (hard sphere) radius is 0.75 units, the outer (interaction) radius is 1.80 units, and the distance between two residues in the native protein is 2.0 units. (C) Matrix showing the energy of interaction between two contacting residues. The residue types are hydrophobic (green circle), positively charged (blue +), negatively charged (red triangle), and neutral (black circle). (D) The three move types in the Monte Carlo move set: translation in any direction, in two dimensions; rotation of the entire protein clockwise or counterclockwise; and rotation of a single domain about the hinge in a clockwise or counterclockwise direction. To see this figure in color, go online.

The interaction energy matrix and the symbols representing each residue type are shown in Fig. 1 C. As shown in the interaction matrix, opposite charges attract, like charges repel, and hydrophobic residues attract. Hydrophobic and neutral residues repel charged residues by an amount smaller than the charge-charge repulsion, reflecting phase separation. Units of energy are defined in our simulations such that the interaction energy of two contacting charged residues is equal to one. Solvent is not explicitly included in this model, although hydrophobic attraction implies the presence of solvent. The electrostatic interaction in this model is short-range, reflective of screening by salt.

An additional energy term is added that biases the two domains toward an open conformation. This term reflects the torsional strain that is present in the residues of the hinge loop in many real domain-swapping proteins. In our simple model, the energy is assumed to be proportional to the angle between the domains, with the maximum negative energy value corresponding to an open protein (180° angle between domains). The open conformation represents a partially unfolded state. Partial unfolding is required for domain swapping to occur.

To mimic a crowded cellular environment containing many interacting proteins, multiple proteins are simulated within a square cell. Periodic boundary conditions are employed. Proteins begin in the folded state, evenly spaced within the cell. The protein concentration is varied by changing the cell size. Proteins interact with one another, using the same cutoff distances and energy function as for intraprotein interactions.

Simulation move set

Three possible moves are allowed: translation of the protein in two dimensions, rotation of the protein in two dimensions, and conformational change by rotation of a domain about the hinge outside of the protein (see Fig. 1 D). In addition, a move is included to allow two contacting proteins to translate or rotate simultaneously (11). The magnitude of each move is chosen according to a Gaussian distribution centered at 0, with standard deviation = 0.5 for translation, 0.3 for rotation, and 0.2 for the hinge move. The probabilities of each move are 0.2 for rotation, 0.6 for the hinge move, and 0.2 for translation. These weights allow for a reasonable sampling of the interaction space over the course of a simulation at a given temperature. If the single-protein translation or rotation move is rejected (i.e., the complex does not dissociate), a two-protein move is attempted with a probability of 0.5. Moves are accepted according to the Metropolis criterion (25):

$$\text{Probability}=\text{min}\left(e^{-\frac{\Delta E}{kT}},1\right),$$ (1)

where a move is rejected if hard-sphere overlap occurs.

States of folding and interaction

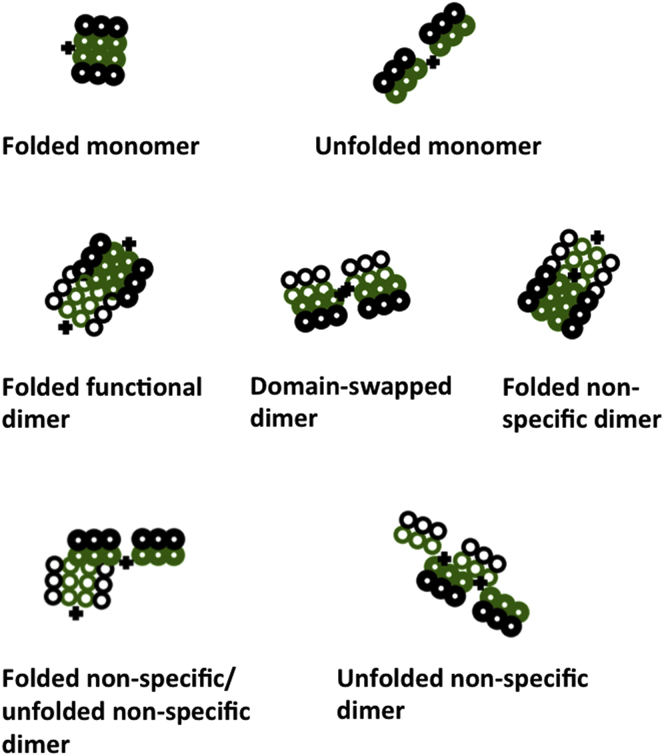
The numbers of folded monomers, unfolded monomers, folded specific or functional dimers, domain-swapped dimers, unfolded proteins involved in nonspecific interactions, and folded proteins involved in nonspecific interactions, were tracked over the course of the simulation. Representative proteins sampling each of these states are depicted in Fig. 2. Referring to the numbering system defined in Fig. 1 A, the folded monomer contains interactions between residues 4 and 7, 5 and 8, and 6 and 9, while the unfolded monomer lacks at least one pair of folded-state interactions. In this work, the terms “unfolded” and “partially unfolded” are used synonymously to refer to this open state of the model protein. The folded functional dimer consists of two proteins in the folded state, with interactions between residue 9 of one protein and residue 6 of the other protein, so that the interfaces opposite the hinge are in contact. The domain-swapped dimer incorporates the same contacts as the folded monomer, but is exchanged between proteins, with residues 4–6 belonging to a different protein than residues 7–9. All six contacts must be present for the protein to be considered domain-swapped. The folded nonspecific dimer, folded nonspecific/unfolded nonspecific dimer, and unfolded nonspecific dimer contain at least four contacts between proteins, but do not fall into the functional dimer or domain-swapped dimer categories.

Figure 2.

States of protein folding and interaction. To see this figure in color, go online.

Because interactions between three or more proteins can occur, the total number of interactions involving folded or unfolded proteins, rather than the total number of dimers of each type, was tabulated. For instance, an interaction between a folded and an unfolded protein would count as one nonspecific folded interaction and one nonspecific unfolded interaction. At each value of temperature and concentration, the most prevalent protein state was determined, along with the average number of molecules in this state, to construct phase diagrams. Separate phase diagrams were constructed for each protein sequence and hinge strength. For each protein state, a smoothing function was applied to the 2D histogram; raw plots are given in the Supporting Material.

Sequence selection

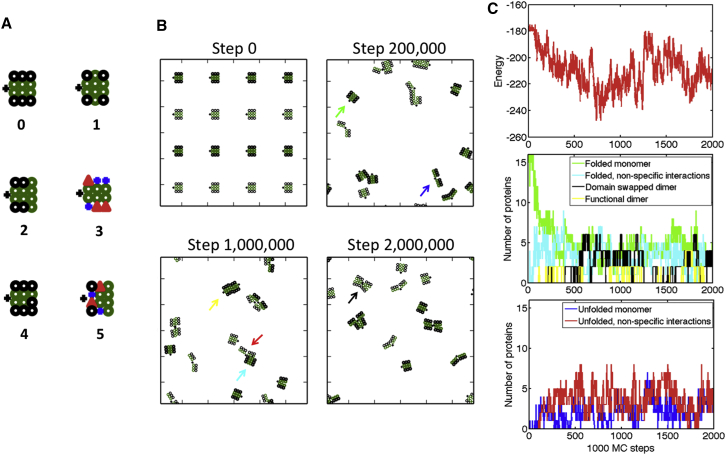
Six sequences were chosen that exhibited different propensities for interaction and/or different folding stabilities (Fig. 3 A). Sequence 0 contains hydrophobic residues at the domain-domain interface and neutral residues at the three-residue surfaces. This leads to a partially hydrophobic protein surface, since some residues of this simplified protein belong to both the surface and the protein interior. Sequence 1 contains hydrophobic residues at the domain-domain interface and a hydrophobic residue at the central position of each three-residue surface of the protein, contributing to hydrophobicity of the protein surface. Sequence 2 contains hydrophobic residues at the domain-domain interface and also along the functional interaction interface opposite the hinge. Sequence 3 contains charged residues along the three-residue surfaces of the protein, allowing for specific interactions between charges in the folded protein. This also weakens the interaction between four-residue surfaces, since residues interact at the diagonal. Sequence 4 is similar to sequence 0, but with a single mutation of a hydrophobic residue to a neutral residue, weakening the domain-domain interaction and surface hydrophobicity. Sequence 5 contains a hydrophobic functional dimerization surface, with charged and neutral residues elsewhere along the protein surface, leading to a destabilized domain-domain interface relative to sequence 0. The interaction energy between domains, which is the energy difference between the folded and partially unfolded states, is −7 for proteins 0, 1, 2, and 4; −5 for protein 3; and −4 for protein 5.

Figure 3.

Protein sequences and sample trajectory. (A) Protein sequences, numbered 0–5. Residue types are defined in Fig. 1 C. (B) Frames from steps 0, 200,000, 1,000,000, and 2,000,000 of a sample trajectory with sequence 0, hinge energy = 2 times the angle between domains, cell length = 113 units, and kT = 0.7. Colored arrows denote a protein in each state, as defined in the legends in (C). (C) Plots of total energy and population of each protein state as a function of the Monte Carlo step. To see this figure in color, go online.

Simulation protocol

The initial simulation frame consisted of a square grid of 16 equally spaced folded proteins. Periodic boundary conditions were employed, and simulations were carried out at a range of concentrations by varying the cell length from 80 to 320 units. We attempted 2,000,000 Monte Carlo steps per run, with statistics averaged over the last 200,000 steps. Temperatures ranged from kT = 0.2 to 2.0, in increments of 0.1. Due to the simplicity of our model, we did not attempt a linear mapping from our temperature units to real temperatures. Simulations were carried out with a hinge energy biasing the protein toward the partially unfolded state, with a magnitude of 2 times the angle between domains, in radians, and with hinge energy equal to zero. Results were averaged over 20 separate runs for each set of parameters.

Energy diagrams

Plots of intraprotein energy versus hinge angle were generated by sampling the angle at increments of 0.01 radians and calculating (energy between domains) + (hinge energy). Plots of folded fraction versus kT were generated by calculating $e^{-E/kT}$ at each point and calculating the sum over folded states divided by the sum over all states.

Code

The complete code for our model can be found on the E.I.S. group’s website (http://faculty.chemistry.harvard.edu/shakhnovich/software).

Additional analysis was carried out in MATLAB (The MathWorks, Natick, MA). A smoothing function was applied to 2D plots for phase diagrams and energies using gridfit.m by John D’Errico (available on the MATLAB Central File Exchange, http://www.mathworks.com/matlabcentral/fileexchange/), with smoothness = 5.

Results

Simulation trajectories

An individual trajectory for sequence 0 is shown in Fig. 3, B and C. Proteins begin in the folded monomeric state. Equilibrium between folded and unfolded monomers is established over the first 500,000 steps. Nonspecific interactions involving folded and partially unfolded proteins appear early in the trajectory, whereas domain-swapped dimers appear later in the trajectory.

Temperature and concentration dependence of oligomeric state

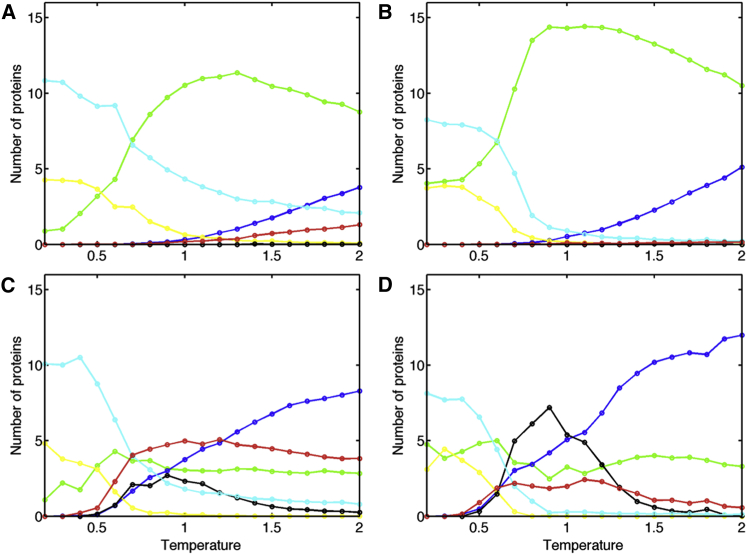
Trajectory statistics were averaged over the final 200,000 Monte Carlo steps and over 20 individual runs. Results as a function of temperature are shown in Fig. 4 for sequence 0. At high concentration (small cell size; Fig. 4 A) and low temperature, most of the protein is in the folded dimeric state. As the temperature increases, dimers dissociate and unfolded proteins begin to accumulate, with some exhibiting nonspecific interactions. A sample frame from simulations at high temperature and high concentration is shown in Fig. S7 A in the Supporting Material. At lower concentration (Fig. 4 B), dimers dissociate more abruptly with increasing temperature, with a transition temperature near kT = 0.7, and protein-protein interactions are not seen at high temperature. The presence of hinge strain causes unfolding to occur at lower temperatures (Fig. 4, C and D), and causes domain swapping to occur at intermediate temperatures between approximately kT = 0.6 and 1.4. The number of nonspecific interactions involving unfolded protein is smaller at lower concentrations. However, there are more domain-swapped interactions at lower concentrations. Domain-swapped interactions exhibit a more rapid fall-off at high temperatures relative to nonspecific unfolded interactions, most likely due to the low entropy of the domain-swapped state relative to the nonspecific unfolded state. The behavior at low temperatures is similar to that observed in simulations with zero hinge energy, since the proteins remained in the folded state.

Figure 4.

Protein state as a function of temperature, for sequence 0: dependence on protein concentration and hinge energy. The population of each protein state is shown as a function of temperature, averaged over the final 200,000 Monte Carlo steps and over 20 separate runs. Line colors are as in Fig. 3C: green for the folded monomer, yellow for functional dimers, black for domain-swapped dimers, cyan for folded proteins engaged in nonspecific interactions, blue for unfolded monomers, and red for unfolded proteins engaged in nonspecific interactions. (A) Cell length = 80, hinge = 0. (B) Cell length = 240, hinge = 0. (C) Cell length = 80, hinge = 2 times the angle between domains. (D) Cell length = 240, hinge = 2 times the angle between domains. To see this figure in color, go online.

Statistics as a function of temperature are shown for all six protein sequences at three concentrations in Figs. S1–S6. The decrease in domain swapping at high concentrations, coinciding with an increase in nonspecific interactions between proteins, is particularly pronounced for proteins with hydrophobic surfaces, such as sequences 1 and 2. Fig. S7 B shows that nonspecific interactions for sequence 1 include a variety of interaction types involving both the protein surface and the domain-domain interface residues. Energy diagrams for isolated proteins (Fig. S8) show that the folded state is energetically favored for sequences 0–2, with hinge energy biasing the protein toward the open state (and for all sequences with hinge energy equal to zero), whereas the unfolded state is more entropically favorable. This causes folded proteins to dominate at low temperatures, whereas unfolding occurs at higher temperatures. For sequences 3–5 with the hinge energy applied, the energy of the folded state is approximately equal to or higher than the energy of the unfolded state, indicating that kinetic factors and/or protein-protein interactions help to stabilize the folded state at low temperatures.

Sequence determines the phase behavior of proteins

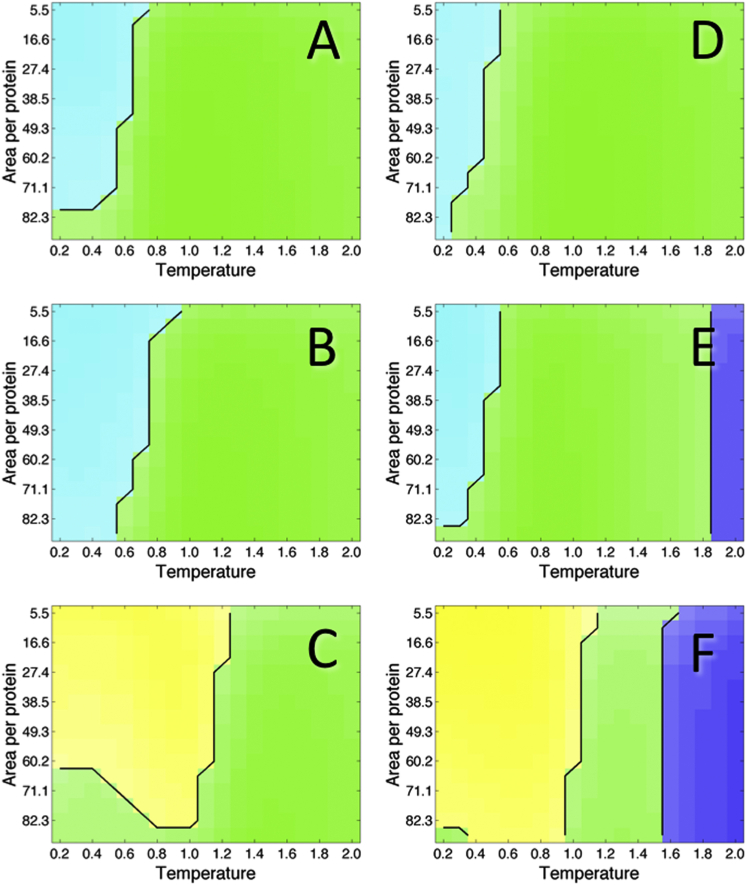
Phase diagrams showing the most prevalent protein species at each temperature and concentration value are shown in Fig. 5 for all six protein sequences with hinge energy set equal to zero. Interactions between proteins are common at low temperatures and high concentrations (upper left region of each plot). Sequences 2 and 5 (Fig. 5, C and F), which contain hydrophobic residues lining the functional dimerization surface, show the greatest propensity for functional dimerization. These functional interactions persist out to higher temperatures than the weaker, nonspecific interactions present in other protein sequences. For sequence 2, the amount of functional dimer is greatest at intermediate temperatures. Fig. S3, C and E, reveal that there is a drop in the number of folded proteins exhibiting nonfunctional interactions coincident with a rise in the number of folded functional interactions, in moving from low to intermediate temperatures. In sequence 3 as well, functional interactions persist out to higher temperatures than nonfunctional interactions at relatively low concentrations (see Fig. S4, C and E), although nonfunctional interactions are more common at low temperatures, since there are more ways to interact nonfunctionally. Sequences 4 and 5, which are less stable than the other sequences, exhibit unfolding at high temperatures, within the temperature range plotted. The melting temperature, at which the number of unfolded proteins becomes equal to the number of folded proteins, is roughly consistent with that predicted based on energy diagrams for individual proteins (Fig. S8 B). For sequence 5, the introduction of charges stabilizes the functional dimer relative to sequence 2 at relatively low temperatures. Among proteins for which nonspecific interactions are common, protein 1, with additional hydrophobic residues on the protein surface, exhibits the most protein-protein interactions. Fig. S9 shows that the lowest energy occurs in the folded dimeric regions of the phase diagram, for all six sequences. Monomeric states, which are higher in energy and entropy, occur at higher temperatures, and unfolded states occur at the highest temperatures.

Figure 5.

Phase diagrams showing the protein state as a function of concentration and temperature, for hinge energy = 0. Temperature is given in simulation units of kT and concentration is given in terms of area per protein, normalized by the length times the width of a single protein (72.96), with cell length ranging from 60 to 320 in simulation units, so that concentration increases along the y axis. Color denotes the most populated protein state (see legend in Fig. 3C), with populations averaged over the final 200,000 Monte Carlo steps and over 20 separate runs, and the shade indicates the population of this state, with darker shades corresponding to a greater number of proteins. Each plot represents a single protein and hinge energy value. (A) Sequence 0. (B) Sequence 1. (C) Sequence 2. (D) Sequence 3. (E) Sequence 4. (F) Sequence 5. To see this figure in color, go online.

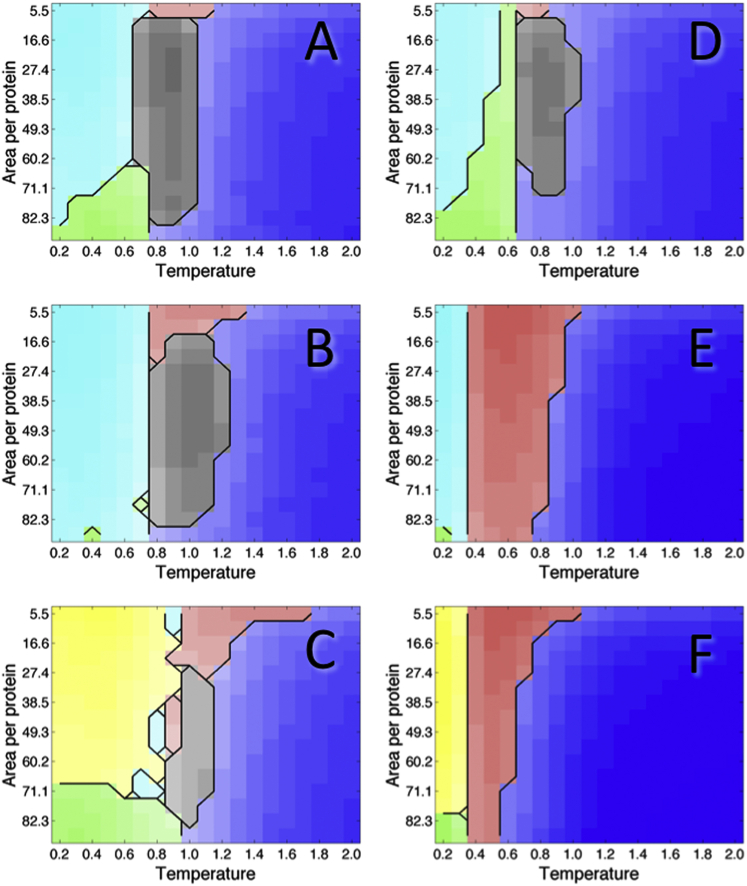
Phase diagrams for each of the six protein sequences with hinge energy equal to 2 times the angle between domains are shown in Fig. 6. For proteins 0–3, domain swapping is present at intermediate temperatures. At low temperatures, proteins exist in the folded state, either as dimers or as monomers, whereas at high temperatures, proteins exist primarily as unfolded monomers. Domain swapping is reduced for sequence 2, which shows folded dimerization out to higher temperatures and a greater number of nonspecific interactions involving unfolded proteins. In sequence 1, domain swapping persists out to higher temperatures than in the other sequences. This is most likely due to the lower energy of the domain-swapped state, since the magnitude of the interaction radius allows for hydrophobic surface residues to contact the domain-swap interface in some forms of the domain-swapped state. In fact, Fig. S8 shows that for sequence 1, the lowest energy occurs in the domain-swapped region of the phase diagram. Domain swapping is greatest at intermediate concentrations, with unfolded monomers and nonspecific unfolded oligomers becoming more common at low and high concentrations, respectively.

Figure 6.

Phase diagrams showing the protein state as a function of concentration and temperature, for hinge energy = 2 times the angle between domains. (A) Sequence 0. (B) Sequence 1. (C) Sequence 2. (D) Sequence 3. (E) Sequence 4. (F) Sequence 5. To see this figure in color, go online.

For sequences 4 and 5, which are destabilized relative to other sequences, nonspecific interactions between unfolded proteins are more common than domain swapping at all temperature and concentration values. Such nonnative interactions occur at intermediate temperatures, whereas folded states are populated at very low temperatures and unfolded monomers are populated at high temperatures. The interaction propensity between unfolded proteins increases with increasing concentration. For sequence 5, the folded functional dimer represents the lowest-energy state (Fig. S10 F). However, Fig. S8 E shows that for sequence 4, the unfolded nonnative interaction region of the phase diagram is actually lower in energy than the folded region, indicating that the folded dimer may occupy a kinetically trapped state, which is populated at low temperature. Fig. S5 shows that the domain-swapped state is populated in sequence 4 at an intermediate temperature, though to a lesser extent than the unfolded nonspecific dimer. Although unfolded proteins emerge at a lower temperature for sequence 4, in comparison with sequences 0 and 3, the temperature at which unfolded monomers become most prevalent is similar, indicating that functional or domain-swapped interactions are traded for nonfunctional ones. Interestingly, the presence of a hydrophobic functional surface (sequences 2 and 5) seems to promote an increased number of nonspecific interactions at high concentrations relative to low concentrations, leading to a curved interface between unfolded monomer and protein interaction states.

Discussion

A key finding of our simulations that is consistent with observations on real proteins is the nonmonotonic temperature dependence of protein dimerization. At the lowest temperatures, the proteins are folded, and many of these folded proteins form intermolecular interactions with one another, particularly proteins with hydrophobic surfaces. In this way, favorable contacts are maximized. At higher temperatures, an increasing number of proteins are found in the unfolded state, which has higher entropy in our model as well as in real proteins. For domain swapping to occur, two proteins must first unfold. Since unfolding is not common at very low temperatures, it is only at intermediate temperatures that the domain-swap interaction is possible. At higher temperatures, unfolded monomers prevail over folded and domain-swapped states, as would be expected in real protein systems, since this state has the highest entropy.

In a recent study from our lab (9), dimers of a mutant DHFR protein formed at elevated temperatures. In our model, upon increasing temperature, domain-swapped dimers or nonspecific dimers between unfolded proteins form, whereas the amount of native-native dimers decreases. Therefore, our model suggests that the dimerization observed in Bershtein et al.’s (9) study is either domain-swapped or a nonnative interaction involving partially unfolded proteins. Interestingly, a DHFR mutant that forms dimers at elevated temperatures also exhibits improved fitness in Escherichia coli. It is possible that domain-swapped dimerization leads to a beneficial fitness effect by stabilizing the protein relative to the wild-type and preventing aggregation. In fact, in our model, domain-swapped dimerization occurs out to temperatures higher than the folded-unfolded melting temperature seen at low concentrations or predicted from single-protein energy diagrams. In general, intertwining of protein chains has been proposed as a mechanism to increase protein stability (26, 27).

It is known that in many proteins, a single site mutation is sufficient to induce the transition from monomer to domain-swapped dimer (28, 29, 30, 31). Torsional strain in the hinge loop, generated through either mutation of loop residues or truncation of the loop, can also affect the propensity for domain-swap dimerization, as can lengthening the hinge loop, since this increases the entropic penalty associated with complete folding (1). In our simple model, we model hinge strain as a term biasing the angle between domains toward the open, domain-swap-prone state. We find that for all six sequences studied, an increase in torsional strain leads to domain swapping, although the extent of domain swapping and the temperature at which it occurs depends on the protein sequence. One might expect that a mutation at the domain-domain interface of some model proteins (e.g., protein 4) could increase the propensity to domain swap at relatively low temperatures. Although this is the case (Fig. S5), the destabilizing mutation also increases the amount of nonspecific interaction between unfolded proteins, to a greater extent than it increases domain swapping. Although the mutation decreases the activation barrier for unfolding, it also decreases the interaction strength between monomers in the domain-swapped state. Thus, our model suggests that modifying the hinge loop while maintaining the primary interface is a more effective strategy to promote domain swapping.

For proteins primarily in folded states (hinge = 0), our model shows that the dimer dissociation temperature is highest for proteins with a large hydrophobic surface (see Fig. 5), and that the drop in dimeric protein with increasing temperature is most abrupt at lower concentrations (see Fig. 4, A and B, for instance). These dependencies can be predicted by considering the partition function accounting for the interaction between two folded proteins at each protein surface. In addition, we see for protein 2, which has both a strong functional interaction interface and the propensity to form nonfunctional interactions, that functional interactions are most prevalent at intermediate temperatures, whereas nonfunctional interactions are increased at low temperatures and monomers dominate at high temperatures. This effect was previously noted for lattice proteins in three dimensions (11).

Another interesting prediction of our model is the concentration dependence of the domain-swap interaction at intermediate temperatures. At low concentrations, monomers become more populated, whereas at high concentrations the number of domain-swapped dimers decreases and the number of nonspecific interactions between proteins increases. The effect does not seem to be due to lower energy of the nonspecific unfolded interaction relative to domain swap interactions, since this region of parameter space is higher in energy (see Fig. S10). We suggest that this observation is an instance of the Flory theorem for polymer chains (32), which states that high-entropy unfolded states become common at high concentrations due to the prevalence of interchain interactions over intrachain ones, while the domain-swapped state is lower in entropy. It will be interesting to test systematically in real protein systems whether domain swapping and/or amyloid formation is decreased relative to amorphous aggregation at high concentrations or in crowded environments.

We observe dimerization at low temperatures for all sequences. High surface area-to-volume ratios for our proteins may contribute to the large interaction strengths at low temperatures. However, we note that the lowest temperatures simulated would be below the physiological range for most proteins. Therefore, our simulations are not at odds with the observation that most domain-swapping proteins do not form folded dimers; rather, they simply set a range of realistic temperatures for our proteins.

A key assumption of our model is that dimerization proceeds through the interaction of partially unfolded states. However, full unfolding of some proteins may be required to enable a domain swap. In the cell, where proteins are generally degraded before they achieve full unfolding (33), the mechanism of domain swapping is likely to be between partially unfolded states. Although our model lacks biophysical detail, it incorporates essential elements of interacting protein systems, including entropically driven unfolding and sequence-specific interactions, and it reproduces general trends involving the temperature and concentration dependence of protein interactions.

Our simple model describes a rich behavior that is directly relevant to real proteins, much of which would currently be out of reach for more realistic models. We predict the nonmonotonic temperature dependence of domain swapping, with domain swaps occurring at intermediate temperatures, for several sequences, and we propose a concentration dependence whereby domain-swapped forms exist at intermediate concentrations and nonspecific interactions between unfolded proteins exist at high concentrations. We also predict that specific interactions between folded proteins occur at intermediate temperatures. Such extensive mapping of oligomeric forms as a function of temperature is possible due to the simplicity, and thus the low computational cost, of our model, but it captures aspects of protein behavior that would not be seen in more basic models. In addition, we reproduce and rationalize the observation that hinge loop modification can often facilitate domain swapping. We expect that further protein engineering insights may be gained from analysis of additional protein sequences using our model.

Future work will include a more complete exploration of sequence space, to reveal how sequence and stability determine the dimerization state. By assigning fitness values to protein states, it will be possible to generate an evolutionary model that allows proteins to evolve through mutations in sequence. Multiple sequences can be simulated within the same periodic cell to explore how proteins evolve specific interactions while avoiding nonspecific interaction partners. In addition, with its simple visualization and concise code, the model can serve as an educational tool to promote a basic understanding of the use of Monte Carlo methods in simulations of proteins.

In general, it will be interesting to explore, computationally and experimentally, which cases of domain swapping result from full unfolding of the protein versus partial unfolding into an open monomer, and to investigate domain swapping in further molecular detail. Domain-swapped structures have been reproduced in simulations using a Go-like model in which native-like contacts are favorable both within the same protein chain and between chains (17, 34, 35). Domain swapping has been investigated computationally in the multidomain protein titin, reproducing experimental results that self-similar domains tend to be more prone to aggregation and predicting several possible domain-swapped structures (36, 37). As another approach, we are currently developing multichain all-atom Monte Carlo simulations utilizing a transferable potential, which can account for native-like and nonnative-like interactions between folded, partially unfolded, and fully unfolded proteins.

Conclusions

We have developed a simple model of protein-protein interaction that combines the simple rigid interaction interfaces of lattice proteins with continuous motion in 2D space and the possibility of partial unfolding by rotation of each domain about a hinge. This is among the simplest possible coarse-grained models that allow for the correct temperature dependence of oligomerization propensity: folded dimers prevail at low temperatures, folded monomers and domain-swapped dimers prevail at intermediate temperatures, and unfolded monomers prevail at high temperatures. In addition, it is straightforward to extend this model to larger proteins and to sample a larger amount of sequence space. Phase diagrams for several sequences indicate that our model contains reasonable complexity and could be useful for addressing biological questions such as how proteins evolve to form specific interactions while avoiding aggregation and other forms of nonfunctional interaction.

Author Contributions

Designed research, E.I.S. and J.C.W.; Performed research, J.C.W.; Contributed code and analytic tools, S.D.; Analyzed data, E.I.S. and J.C.W.; Wrote the manuscript, E.I.S. and J.C.W.

Editor: Amedeo Caflisch.