Mixing Temperatures of Bilayers Not Simply Related to Thickness Differences between L_o and L_d Phases

Abstract

Micron-scale coexisting L_o and L_d liquid phases can appear in lipid bilayers composed of a ternary mixture of a low-melting temperature lipid, a high-melting temperature lipid, and cholesterol. A priori, temperatures at which membranes demix, T_mix, are not simply related to differences in thicknesses, Δh, between L_o and L_d phases. Here, we use fluorescence microscopy to measure T_mix and we use atomic force microscopy at 22°C to measure Δh for a series of bilayers composed of different ratios of the three components. Our data illustrate cases in which a change in T_mix or Δh does not result in a change in the other parameter. The data provide a context in which to evaluate recent reports of a correlation between T_mix and Δh.

Main Text

Model lipid membranes composed of a high-melting temperature (T_melt) lipid, a low-T_melt lipid, and a sterol can phase-separate into liquid-ordered (L_o) and liquid-disordered (L_d) phases (1). Typically, the L_o phase is thicker than the L_d phase (2, 3, 4), and is sometimes referred to as the “raft phase” by researchers who associate membrane phases with the lipid raft hypothesis (5).

Two important parameters characterizing this phase separation are T_mix, the mixing temperature below which L_o and L_d phases appear in the membrane, and Δh, the thickness difference between L_o and L_d phases at a given temperature. Previous studies have shown that a mismatch between L_o and L_d thicknesses affects protein sorting (6), and that bilayer thickness affects protein function (7, 8).

Fig. 1 frames possible relationships between Δh and T_mix: the variables can vary independently (line A or B) or be correlated (curve C). Previous work by García-Sáez et al. (2) reported that T_mix increases with increasing Δh (as in Fig. 1 C) for bilayers at a fixed 40:40:20 mol ratio of low-T_melt lipid/high-T_melt lipid/cholesterol. In their work, the high-T_melt lipid was stearoyl-sphingomyelin. Their low-T_melt lipids were a series of phosphocholines (PCs) with carbon chains that systematically lengthened from 14:1 (largest T_mix and Δh) to 22:1 (smallest T_mix and Δh). They reported T_mix proportional both to Δh² and to line tension.

Figure 1.

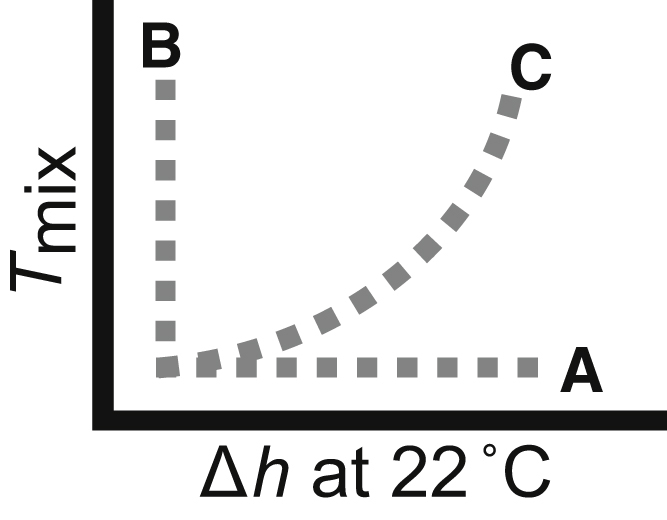
Possible trends between thickness mismatch (Δh) and miscibility temperatures (T_mix) for membranes that demix into L_o and L_d phases. Data as in curve C appear in García-Sáez et al. (2) and may correspond to Fig. S1, a and b. Here we present data as in lines A and B.

The results of García-Sáez et al. (2) have been used to support statements that hydrophobic length mismatch between lipid types promotes their segregation in phase-separated membranes (6) and drives domain formation by increasing line tension (8). However, the quantitative result of García-Sáez et al. (2) holds only for the particular ratio and types of lipids for which it was reported. For a broader class of membrane systems, T_mix is not related to Δh (or to line tension) in a simple way. T_mix is determined by the shape of the phase boundary and depends on the ratio and type of lipids. Consider an analogy of an ant crawling over a bowl placed upside-down on the floor. Specifying the type of bowl (the types of lipids in the membrane) limits the ant’s highest possible elevation (the highest T_mix), but does not specify the ant’s current elevation (the membrane’s T_mix) unless the shape of the bowl and the ant’s latitude and longitude across the floor (the ratio of lipids in the membrane) are known.

Moreover, the highest T_mix can be difficult to predict for a membrane composed of an arbitrary ternary set of lipids (as opposed to the series of García-Sáez et al. (2)). We have found no monotonic relationship between the highest T_mix of a ternary membrane and the estimated thickness difference between the L_o and L_d phases at room temperature (4).

Now imagine two ants crawling over two nested bowls. The bowls may be nonaxisymmetric and their centers may be offset. Even if the bowl depths are simply related (e.g., the highest possible elevation of ant 1 is half that of ant 2), and the ants share the same latitude and longitude with respect to the floor, the difference between the ants’ elevations is nontrivial to find. This scenario corresponds to the nested phase diagrams in Fig. S1 in the Supporting Material. To give concrete examples, here we use data to illustrate cases in which a change in Δh or T_mix does not result in a change in the other parameter, as schematically depicted in Fig. 1, lines A and B.

To gather data as in lines A and B in Fig. 1, we used tactics applicable to any membrane that demixes into L_o and L_d phases. All possible ratios of the three lipid types in a membrane can be plotted in a plane. By definition, a tie-line passes through the overall lipid ratio of any particular membrane. The ends of that tie-line fall at the lipid ratio of that particular membrane’s L_o phase, and of its L_d phase. The length and orientation of the tie-line within the plane varies with temperature (9). Two membranes at the same temperature that have different overall ratios of the same lipid types demix into exactly the same L_o and L_d phases if their overall lipid ratios fall on the same tie-line. Along the line, relative areas of the L_o and L_d phases vary.

To observe the trend in line A of Fig. 1, our goal was to measure Δh for a series of membranes with lipid ratios that follow an isotherm in T_mix. We chose each lipid ratio to fall on a different tie-line. Based on previous work, we hypothesized that membrane compositions that lie on longer tie-lines would produce larger values of Δh (9, 10, 11).

To observe the trend in line B, our goal was to measure T_mix for a series of membranes with lipid ratios that follow a previously determined tie-line at 22°C (9). Because the composition of the L_o and L_d phases are constant along this line, all of these membranes should share the same Δh.

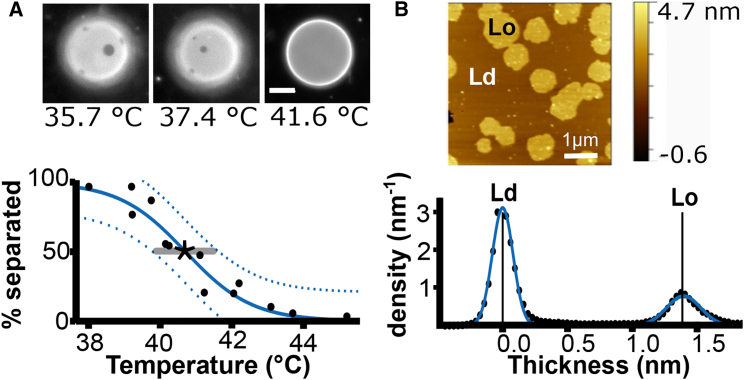
We determined T_mix as the temperature at which 50% of giant unilamellar vesicles (GUVs) demix, as in Fig. 2 A. GUVs were composed of mixtures of DPPC (dipalmitoyl-PC), DiPhyPC (diphytanoyl-PC), and cholesterol. They were labeled with 0.8 mol % Texas Red, which partitions preferentially to the L_d phase. GUVs were electroformed and imaged as previously noted in Veatch and Keller (11). We determined Δh from atomic force microscopy (AFM) measurements of supported bilayers. Small unilamellar vesicles were deposited on mica at 60°C in a solution of 5 mM CaCl₂ (10). The resulting bilayer was rinsed with 18 MΩ-cm water by pipette and scanned in an atomic force microscope at 22°C. AFM images were flattened in Gwyddion (12). Height histograms were exported to MATLAB (The MathWorks, Natick, MA) and fit with Gaussian peaks as in Fig. 2 (4). Further details of Materials and Methods are in the Supporting Material.

Figure 2.

Measured values of T_mix and Δh for 48:32:20 DiPhyPC/DPPC/chol bilayers. (A) Fluorescence micrographs for a single GUV (top) and a graph of percent demixed GUVs versus temperature for a population of GUVs (bottom). The solid blue line is a sigmoidal fit of the black points. Dashed lines bound the 95% confidence interval. The star lies at T_mix, and the bar spans the uncertainty; here T_mix = 40.7 ± 0.3°C. (B) AFM scan of a supported lipid bilayer at 22°C (top) and height histogram of the same scan (bottom). The blue line follows two Gaussian peak fits of the black data points. For a single scan, Δh is reported as the distance between the mean thicknesses of the two peaks, and uncertainty is reported as the standard deviation of the bootstrap fit, here Δh = 1.39 ± 0.02 nm. Values of T_mix and Δh are listed in Table S2 in the Supporting Material. To see this figure in color, go online.

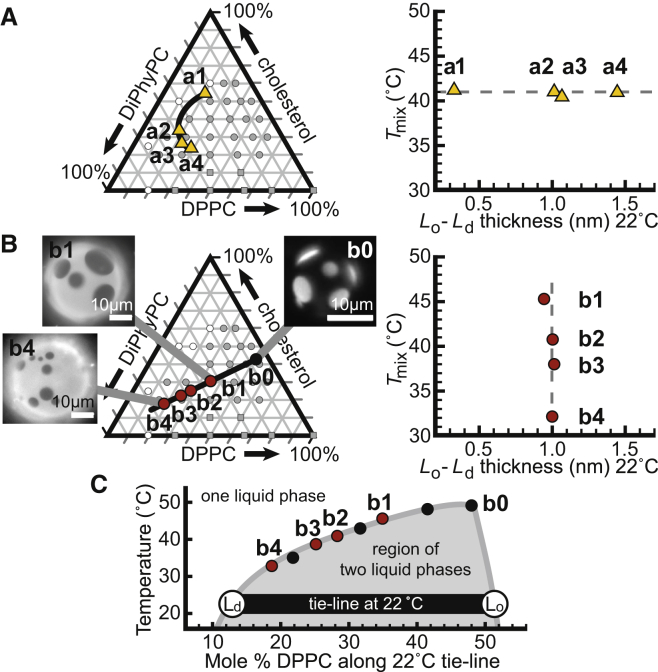
Our central result, namely that T_mix and Δh can vary independently, is shown in Fig. 3. Points a1–a4 in Fig. 3 A lie on an isotherm in T_mix. Points b1–b4 in Fig. 3 B lie on a tie-line. Because our result follows from general attributes of phase diagrams, it applies to any ternary membrane that demixes into L_o and L_d phases.

Figure 3.

Measured values of T_mix versus Δh at 22°C for bilayers of DiPhyPC/DPPC/Chol that fall (A) on a T_mix isotherm and (B) on a tie-line. Ternary phase diagrams at 22°C are from Veatch et al. (9), where shaded circles denote two liquid phases, open circles denote one liquid phase, and squares denote that a gel phase is present. Micrographs show that area fractions of the L_d phase increases from point b0 to b4. Dashed lines are not fits. Tables S2–S9 list values and uncertainties. (C) Phase boundary along the tie-line in (B). Solid points were determined in this study. The underlying shaded curve is not a fit. To see this figure in color, go online.

Our result reveals difficulties inherent in quantifying relationships between T_mix and Δh for membranes made from different lipid species unless full phase diagrams and tie-lines are known. Generalizing from data collected at just one ratio of lipids is meaningful only when phase boundaries for the two systems are related by a simple geometric scaling and are centered at the same ratio of lipids. In addition, either the phase boundary must be hemispherical or the direction of the tie-lines must not change with temperature (see Fig. S1). We know of no two membrane phase diagrams discovered to date that meet these criteria.

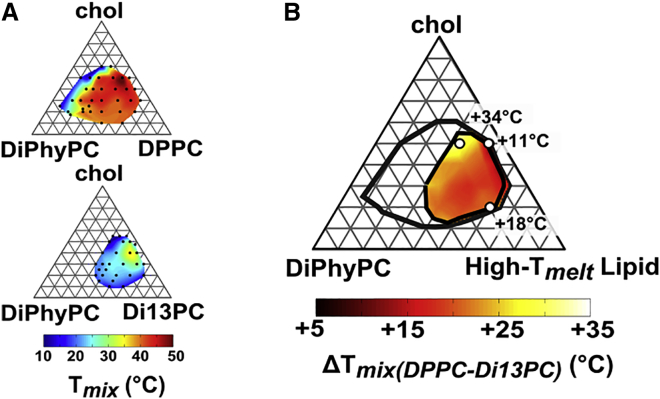
Fig. 4 illustrates this point for two ternary membrane systems for which the high-T_melt lipid species differ in the lengths of their acyl chains. Fig. 4 A plots T_mix values for membranes of DiPhyPC/DPPC/chol and DiPhyPC/Di13:0-PC/chol, where Di13:0-PC has three fewer carbons in each of its two chains than DPPC. The membrane containing DPPC demixes over a broader range of lipid ratios at all temperatures, and its T_mix is higher at any lipid ratio at which both membranes demix. A broader range of ratios means longer tie-lines, which can translate into larger Δh (10). If we arbitrarily choose any ratio of the three membrane components, we would expect some positive correlation between values of T_mix and Δh. However, because the phase boundaries and the tie-lines differ in the two systems, a different choice of this ratio will result in a different quantitative relationship between Δh and T_mix. Inherent in this discussion is the perspective that demixing of membranes into phases of different compositions gives rise to Δh and line tension (with values that vary across the phase diagram), and that the value of Δh or line tension at a single lipid ratio and temperature does not determine the shape of the full phase boundary.

Figure 4.

(A) Phase diagrams for which the high-T_melt lipid is either DPPC (with 16 carbons in its acyl chain, top) or Di13:0-PC (bottom). Black dots are experimental values of T_mix including values from Veatch et al. (9). The top diagram has higher values of T_mix at any lipid ratio and a larger phase boundary at any temperature. (B) Difference in T_mix (denoted ΔT_mix) for GUVs of the two ternary lipid mixtures in (A). To see this figure in color, go online.

Given that Fig. 3 shows how a single ternary membrane can produce a horizontal or vertical line in a graph of T_mix versus Δh, various functional forms relating T_mix and Δh for two ternary membranes are then possible, subject to the choice of lipid ratio. Extending this idea, it is possible to imagine future discoveries of membrane systems that produce a negative slope on a graph of T_mix versus Δh, as in Fig. S1.

Separately, we can test the correlation between domain size and Δh reported by Heberle et al. (13). They used neutron scattering to find that small, 60-nm vesicles with low Δh values had more unmerged domains. They report <2 domains/vesicle for Δh = 0.97 nm and 23 domains/vesicle for Δh = 0.64 nm. These Δh values are in line with AFM values from similar lipid systems (2). In our GUVs, domains of the same liquid phase merge until only one domain of each phase remains, even when Δh is as small as 0.32 nm. Our results imply that a small Δh value alone does not determine the number of stable, liquid domains.

In conclusion, our results demonstrate challenges of quantitatively establishing how Δh relates to T_mix. There is no reason to question the validity of the correlation between Δh and T_mix reported by García-Sáez et al. (2) for the systems they studied. Nevertheless, Fig. 4 illustrates why other groups are likely to find different values if they employ different ratios of lipids. We also illustrate a method that follows directly from known thermodynamic principles to identify lipid ratios for which T_mix and Δh vary independently. We present this method to support future studies of how lipid structure affects T_mix and Δh.

Editor: David Cafiso.