Ensemble View of RNAs and Proteins: Loops, Knots, Territories, and Evolution

Main Text

There is an old joke about a lazy doctor who, instead of looking at each patient individually, requested information about average body temperature of all patients in the hospital. The joke pretends to be funny because an ensemble view of patients is absurd. But in some other cases, including in the life sciences, an ensemble view is not only not absurd, but the right instrument, and Liu and Hyeon (1) in this issue of the Biophysical Journal offer a nice example: not only do they look at ensembles, they compare two different ones—ensemble of proteins and ensemble of RNAs. Their findings are remarkably thought-provoking.

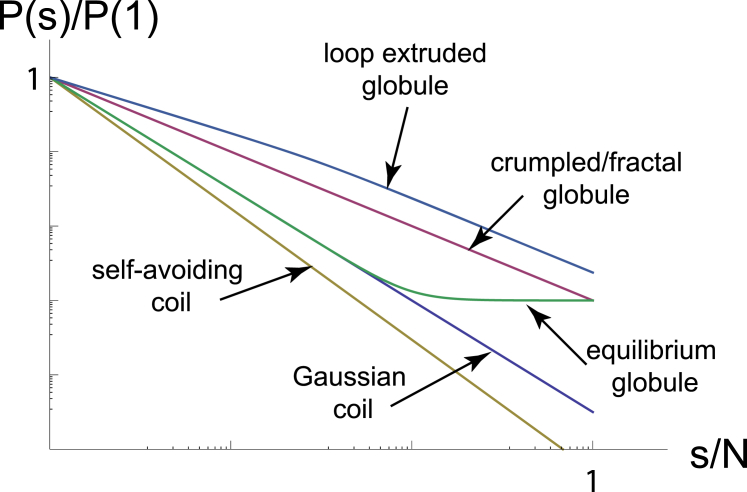
Their main technical tool is the study of contact probability—the probability that two monomers of a specific polymer chain, separated by a contour distance of s monomers, are found in contact in three dimensions (Fig. 1). In polymer physics, a similarly defined quantity P(s) is widely used to distinguish between different phases of a polymer chain. In particular, for various fractal conformations, P(s) decays as a power law $P\left(s\right)\sim s^{-\gamma }$, including Gaussian (random walk) coils with γ = 3/2 (in three dimensions), swollen self-avoiding coils (γ ≈ 1.765), and various crumpled (2), fractal (3), and loopy (4) globules (γ close to unity). In all these cases, P(s) reveals no characteristic scale; by contrast, P(s) for an equilibrium globule has a distinct crossover at s ∼ N^2/3, separating different fractal behaviors with a power-law drop γ ≈ 3/2 at s < N^2/3, and saturation to a constant (γ ≃ 0) at s > N^2/3. Furthermore, in the recently suggested steady but nonequilibrium (energy-consuming) loop extrusion model of chromatin (5, 6, 7), γ ≈ 3/4 < 1 at small s, crossing over to crumpled globule-type γ close to unity at larger s (and possibly further switching to an even faster decay).

Figure 1.

Ideal-world contact probability for various states of a polymer chain. Logarithmic scale. To see this figure in color, go online.

Liu and Hyeon (1) found that, compared to an ensemble of globular proteins, an ensemble of RNAs is much more reminiscent of a crumpled than an equilibrium globule, with γ close to unity. Why is this important?

Slow decay of P(s) for a certain polymer ensemble is usually indicative of several other properties. Firstly, these ensembles are characterized by dramatically lowered incidence of conformations with knots. Indeed, it was recently shown (8) that all known RNAs are unknotted—unlike proteins, some of which do have knots, including sometimes pretty complex and deeply buried ones (9). Secondly, these conformations are typically territorial, in the sense that different parts of the chain tend to avoid overlap, with each of them carving out a piece of territory for itself. This concept of territoriality became known in the context of interphase chromatin (see references in Halverson et al. (10)), but there is evidence that RNAs also exhibit territoriality, as in the case of influenza virus (11, 12).

Although these three properties (i.e., slow fractal decay of P(s), reduced abundance of knots, and territoriality) seem to go hand in hand, it is fair to emphasize that our understanding of such conformations is still incomplete. They were first implicated in the context of rapid collapse of a homopolymer (2), but more recent studies suggest that the process of rapid collapse may be more intricate than initially thought (13). Related conformations are observed in dense systems of unconcatenated rings, but the exact nature of these conformations is still under debate (4, 10); trees, especially annealed ones (14), share many properties with unconcatenated rings, but whether they belong to the same or to a different universality class is not known. In the light of the work by Liu and Hyeon (1), these theoretical questions begin to impinge on the RNA world.

At the end of this comment, we should return to the beginning, to the question of ensemble versus individual approach. When we talk about, say, P(s) behavior for various states of a polymer, we deal with an ensemble in the standard statistical mechanics sense—with the ensemble of microstates of a fluctuating object, a polymer chain in this case. Neither the ensemble of protein conformations from the Protein Data Bank (PDB) nor similar RNA ensembles are like that. First, for both proteins and RNAs, there is an existing ensemble selected by evolution. Second, there is a subensemble of those molecules that are in the PDB, but the selection of proteins and RNAs in the PDB may be statistically biased. It is possible, for instance, that territoriality of a certain macromolecule may be correlated (positively or negatively) with its ability to crystallize. We are presently not aware (at least this writer does not know) of any specific statistical bias of the PDB with respect to P(s) or any related conformational property, but we must remain alert that such bias may exist, even if hidden from the eye.

As an example, consider the question of knot abundance. As mentioned above, we do know of a certain number of knotted proteins (9), but no knotted RNAs (8). As a matter of principle, there are two possibilities as far as protein knots are concerned. First, it is possible that normal proteins should have no knots, and only when a knot is needed for some purpose (e.g., protection against destruction by a protease), then evolution manages to make a knot; in this scenario, the logical question is—what is the functional purpose of every particular knot found in a protein? But there is also a second possibility, that evolution is largely indifferent toward the presence or absence of knots, and then one should expect the knot abundance in protein ensemble to be about the same as in a suitably chosen random one; in this scenario, the main logical question is shifted—what is the right statistical ensemble? Now we should welcome RNA to the club of similar controversies: do RNAs lack knots because knots are bad for something and were eliminated by evolution, or is it that the ensemble of RNA conformations, chosen by evolution for some other reason, is simply not friendly to knots?

In this sense, Liu and Hyeon’s findings (1) illuminate from an unexpected direction the entire landscape of protein and RNA evolution.

Editor: Rohit Pappu.