Abstract
Background:
The Malaria Early Warning System is defined as the use of prognostic variables for predicting the occurrence of malaria epidemics several months in advance. The principal objective of this study was to provide a malaria prediction model by using meteorological variables and historical malaria morbidity data for malaria-endemic areas in south eastern Iran.
Methods:
A total of 2002 locally transmitted microscopically confirmed malaria cases, which occurred in the Minab district of Hormozgan Province in Iran over a period of 6 years from March 2003 to March 2009, were analysed. Meteorological variables (the rainfall, temperature, and relative humidity in this district) were also assessed. Monthly and weekly autocorrelation functions, partial autocorrelation functions, and cross-correlation graphs were examined to explore the relationship between the historical morbidity data and meteorological variables and the number of cases of malaria. Having used univariate auto-regressive integrated moving average or transfer function models, significant predictors among the meteorological variables were selected to predict the number of monthly and weekly malaria cases. Ljung-Box statistics and stationary R-squared were used for model diagnosis and model fit, respectively.
Results:
The weekly model had a better fit (R2= 0.863) than the monthly model (R2= 0.424). However, the Ljung-Box statistic was significant for the weekly model. In addition to autocorrelations, meteorological variables were not significant, except for different orders of maximum and minimum temperatures in the monthly model.
Conclusions:
Time-series models can be used to predict malaria incidence with acceptable accuracy in a malaria early-warning system. The applicability of using routine meteorological data in statistical models is seriously limited.
Keywords: Malaria, Models, Statistical, Time-Series, Iran
Introduction
Successful implementation of programmes to combat malaria has led to a significant decrease in cases in Iran in recent years (Edrissian 2006, Raeisi et al. 2009). Iran is currently in the ‘elimination phase’ in terms of malaria control programmes, and the Malaria Control Office of the Centre for Disease Control of The Ministry of Health and Medical Education has developed a programme toeliminate malaria in Iran by the year 2025 (Raeisi 2009).
The Malaria Early Warning System (MEWS) is defined as the use of prognostic variables for predicting the occurrence of malaria epidemics several months in advance. The three categories of indicators that are used in the system to detect the epidemic at its early stage are (1) indicators of vulnerability, such as immune status, malnutrition and population displacement, (2) transmission risk indicators, such as an abnormal increase of rainfall, and (3) early detection indicators, such as reports of an excessive number of cases (Thomson and Connor 2000). A combination of the above variables can be used to predict epidemics before they occur, with varying accuracy. In fact, there is a balance between the timeliness and accuracy of predictions made with this method. As we get closer to the occurrence of the epidemic, the predictions become more accurate, but there is shorter lead time for taking action (Matola and Magayuka 1987).
The relationship between predictor variables and occurrences of malaria epidemics is very complex, and the connection between some variables, such as meteorological factors, and malaria, has been investigated in some previous studies (Abeku et al. 2002, Abeku et al. 2003, Bouma 2003, Abeku et al. 2004, Teklehaimanot et al. 2004a, Pascual et al. 2006, Medina et al. 2007, Pascual et al. 2008, Haghdoost et al. 2008, Paaijmans et al. 2009, Yamana and Eltahir 2010, Ermert et al. 2011). However, the impact of these variables is also very complex, and they interact with one another. Therefore, using these relationships to predict epidemics is fraught with limitations. Moreover, due to the complexity of the biological, statistical and mathematical models offered for use at a peripheral level, and their limited validity, based on the period and place of data on which they are built, such models cannot be practically used in malaria control programmes (Hay et al. 2002b, Cox and Abeku 2007).
Although these facts have been taken into consideration, efforts to provide an early warning system for malaria epidemics by monitoring meteorological variables have nevertheless been undertaken in recent years (Teklehaimanot et al. 2004b). However, the results have shown that such attempts can lead to unreliable predictions, especially if these systems are used in areas where an association between the disease and climatic conditions has not been established (Hoshen and Morse 2004). Of all the epidemiologic models, time-series models, especially univariate auto-regressive integrated moving average (ARIMA), are currently frequently used for prediction, as well as for the investigation of the relationship between prognostic factors and malaria. These models use the autocorrelation that exists in malaria incidence in consecutive time units, as well as the association between malaria incidence and meteorological variables, to make predictions.
The principal objective of this study was to provide a model to predict the occurrence of malaria by using meteorological variables and cases that have occurred in the past 5 years at district level in the malaria-endemic, south-eastern provinces of Iran.
Materials and Methods
Study area
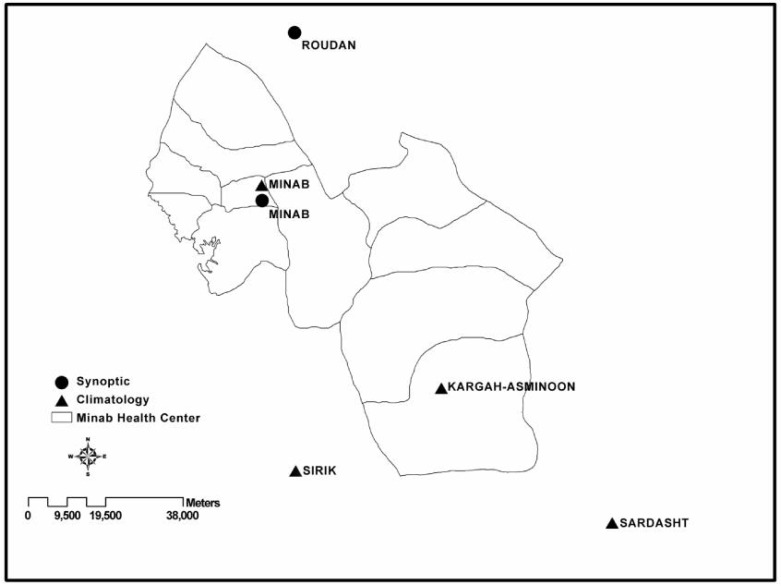
This study was conducted in the Minab District, which is an area of approximately 7500 square km, located in Hormozgan Province in southern Iran. The majority of this district is flat, with a primarily hot and dry climate, and in 2006 its population was approximately 257,000. The public health system, which is responsible for the malaria surveillance system, included two urban and 10 rural health centers. Figure 1 shows a map of the district and its subdivisions.
Fig. 1.
Minab Districts’ Health Centers and Meteorological Stations
Calendar
The Jalali calendar was used in this study. On the basis of this calendar, a year consists of 365 days made up of 12 months, in which the first 6 months are all 31 days in length, the next 5 months each have 30 days, and the 12th month has 29 days, but 30 days once every 4 years. March 21 is the first day of the year in the Jalali calendar.
Malaria data
Malaria surveillance system data covering a 6-year period from 1382 to 1387 (March 21, 2003 to March 20, 2009) were used. Individual records data were used, because the malaria surveillance system was based on paper forms during the study period. Individual records of malaria patients included their demographic characteristics, including their full name and parents’ names, age and gender, epidemiological data, including parasite types (P. vivax, P. falciparum and mixed), surveillance type (passive or active), epidemiological status (local transmission or imported), treatment outcome and the date of diagnosis. All malaria cases had been confirmed microscopically by expert examiners.
Meteorological data
Data from meteorological stations for the period from 2000 to 2009 were received from the Iran Meteorological Organization (http://irimo.ir). The Minab district has a synoptic meteorological station and a climatology meteorological station, both of which are located in the political center (i.e., Minab). Figure 1 shows the name and location of the meteorological stations in the district of Minab. The climatology meteorological station of Kargah-Asminon in the southern part of the district was inactive during the period covered by this study, therefore no data from this station were available.
As shown in Fig. 1, there are also three meteorological stations, a synoptic station and two climatology stations, in the neighborhood. Data used for the analysis are the mean data from all five meteorological stations.
Time-series models
The forecasting menu of IBM SPSS Statistics 19 was used for data analysis. The dependent variable in the analysis was the total cases of local transmission in the desired time period (months or weeks) in the first 5 years of the study, that is, years 1382 to 1386 (2003–2008). The independent variables included the total rainfall (in ml), the minimum mean temperature, the maximum mean temperature, the dry bulb mean temperature, the wet bulb mean temperature (all in °C), the relative humidity (in percent) and the effect of the maximum temperature interaction (as representative of temperature variables) with the relative humidity. Expert modeler was used to build the model. Appropriate date variables were defined for the consideration of seasonal terms in the model by using the define date menu from the data tab in SPSS (for the monthly models), or by using special Syntax (for the weekly models). Outliers in the data were automatically found, and their effects were controlled. In case other independent variables, except in cases of malaria in the past, was remained in the model, ARIMA models with Transfer Function (TF) and otherwise univariate ARIMA model was fitted to the data.
Normalized BIC and stationary R-squared indicators were used to determine the fitness of the model, and the Ljung-Box Q statistic was used to determine its suitability. Models with a significance value of more than 0.05 were considered suitable. The autocorrelation function (ACF) and partial autocorrelation function (PACF) graphs of the residuals were assessed to ensure that they were not correlated. The non-significant independent variables were automatically removed from the model by the expert modeler.
To assess other possible models, the ACF and PACF graphs, as well as cross-correlation function (CCF) graphs between the dependent variable and the predictor variables, and trend analysis and seasonal decomposition charts were initially examined. Suitable ARIMA models, fitting the description of the data, were then created. Finally, the models with the best fit, with respect to the above criteria, were selected.
The files of the selected models were stored as XML data and applied to the year 1387 (almost 2008) data. Minitab 16 Statistical Software and Microsoft Excel 2010 were also used to sketch the graphs.
Results
Malaria data
The total number of malaria cases in the years 1382 (2003) to 1387 (2008) was 2,239. Of these, 2002 were locally transmitted. A total of 98.8% of cases of malaria that occurred in the Minab district during this time were due to P. vivax.
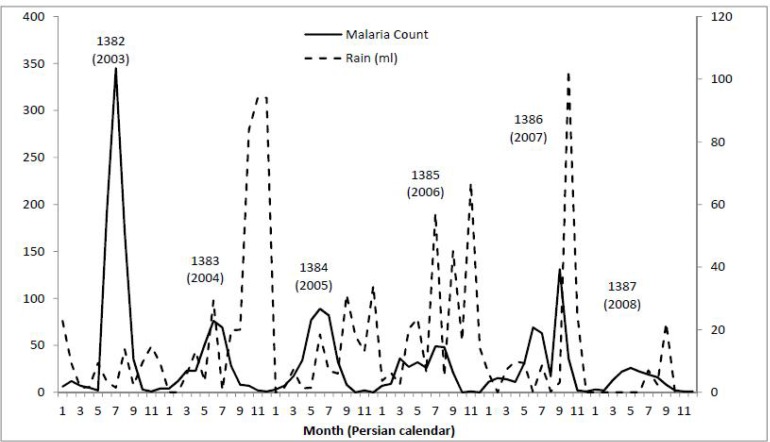
The majority of the malaria cases were observed during the months of September and October (Sahrivar and Mehr in the Jalali calendar). The number of cases in the months of January, February, March and April (Day, Bahman, Esfand and Farvardin in the Jalali calendar) was very low. The increase in the number of cases begins in May. Figure 2 shows the annual temporal distribution of malaria cases in the district of Minab.
Fig. 2.
Monthly malaria case count and rainfall in Minab, years 1382–1387 (2003–2008)
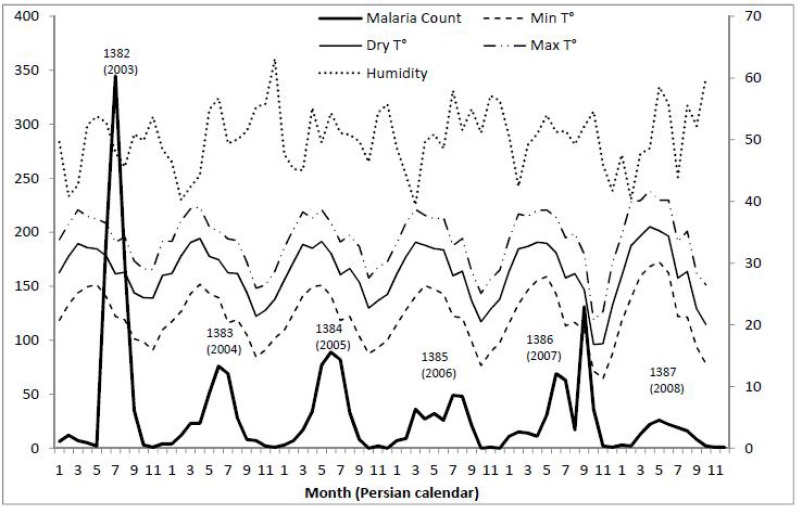
As shown in Fig. 3, temporal distribution was different in different years, and the highest number of cases was recorded in the year 1382 (2003). In the years 1382 (2003) to 1384 (2005), the number of cases peaked once in a year, but during the years 1385 (2006) to 1387 (2008), two peaks per year were observed. A significant increase in the number of cases was shown in December 1386 (2007), which was not observed in the other years studied.
Fig. 3.
Monthly malaria case count and temperature (°C) and relative humidity (%) in Minab, years 1382–1387 (2003–2008)
Meteorological variables
There was a considerable annual variation in rainfall, but a more or less comparable seasonal pattern, with a minimum of 78mm in the year 1387 (2008) and a maximum of 366mm in the year 1383 (2004) (Fig. 2). Changes of temperature and humidity had a seasonal pattern during the year, which was accompanied by an increasing trend during the years of study. As indicated in Fig. 3, the peak average maximum temperature increased over the years. However, the peak average minimum temperature decreased during this time. Change of humidity also followed a seasonal trend. However, unlike the changes in temperature, changes in humidity were not regular. Figure 3 shows the changes that occurred during the study period.
Autocorrelation Analysis
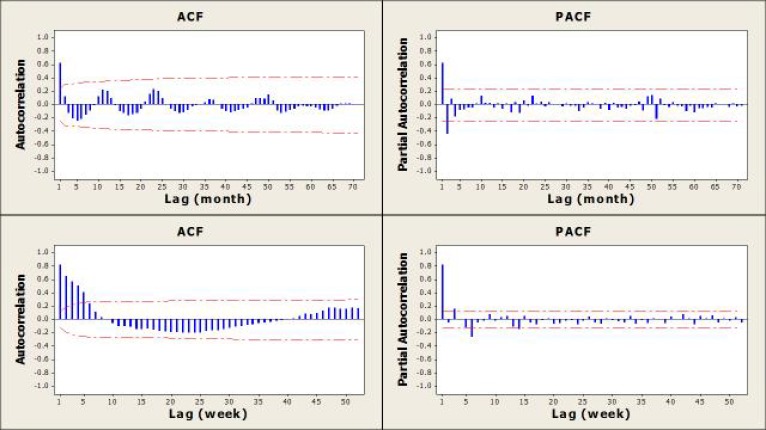
Evaluation of the ACF graphs shows that there was a significant positive correlation between the numbers of monthly malaria cases with those that occurred in the previous 1 month (Fig. 4, top left graph). These positive correlations were for 5 weeks for the weekly data (Fig. 4, bottom left graph). On the basis of the PACF graphs, these correlations were 2 months for the monthly data and up to 6 weeks for the weekly data, after controlling for the effects of other lag times (Fig. 4, top right of the chart (monthly) bottom right (weekly)).
Fig. 4.
ACF graph (left) and PACF graph (Right), monthly (top) and weekly (bottom) number of locally transmitted malaria case count
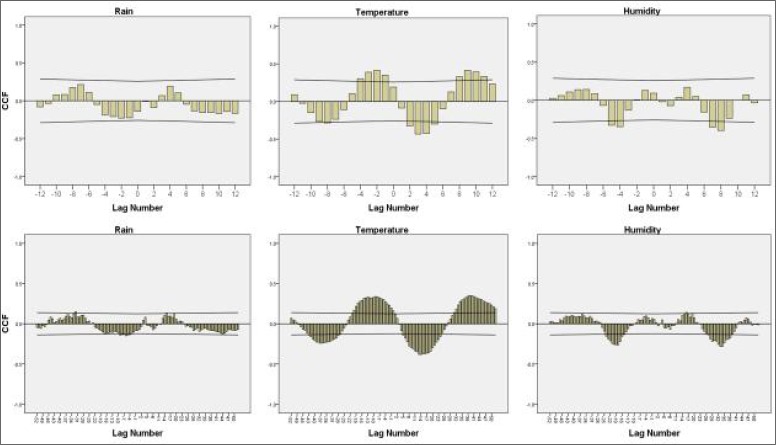
Cross-correlation analysis
Assessment of the monthly meteorological variables data in the cross-correlation graphs in Figure 5 indicated that there was no significant correlation between the total rainfall and the number of malaria cases in the monthly data. Although a lag time of 6 to 10 months, and the maximum correlation at a lag time of 7 months (top left graph), were non-significant positive correlations, significant positive correlations were found between the monthly number of malaria cases and the mean monthly temperature at a lag time of 1 to 4 months (top middle graph), and significant negative correlations were observed for the relative humidity variable at a lag time of 4 and 5 months (top left graph). The weekly graph was similar to the monthly graph in terms of cross-correlation between the number of malaria cases and rainfall, temperature and humidity variables. The contrasting point in the graph corresponds to the rainfall, where a number of positive and negative correlations were significant at different lag times (Fig. 5, bottom graphs).
Fig. 5.
Cross-correlation graphs between monthly (top) and weekly (bottom) malaria case count and rainfall (left), mean dry temperature (middle), and relative humidity (right)
Time series analysis
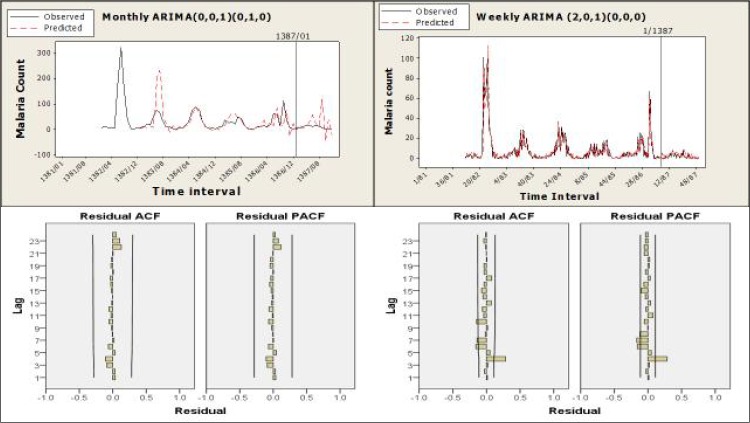
Table 1 shows the details of the monthly and the weekly time. As can be observed, the optimum model [ARIMA (0, 0, 1) (0, 1, 0)] did not fit well for the monthly data, (stationary R2= 0.424). None of the predictor variables remained in the ARIMA model created for monthly data, while the maximum temperature and the minimum temperature were the two significant variables in the weekly data ARIMA model [ARIMA (2,0,1) (0,0,0)]. Although the weekly model gave better predictions than the monthly model (stationary R2= 0.863), the Ljung-Box test for this model was significant.
Table 1.
Comparison of the time-series models of locally transmitted cases in Minab, years 1382–1386 (2003–2007)
| Level (Time Interval) | Model | Predictors (s) | Fit Statistics (s) | Model Statistics | Model Parameter(s) | |||
|---|---|---|---|---|---|---|---|---|
|
(Ljung-Box Q) |
Parameter | Estimate (Sig.) | ||||||
| Statistics | Sig. | |||||||
| District (Monthly) | ARIMA (0,0,1)(0,1,0) | No | Stationary R2: 0.424 Normalized BIC: 7.357 |
2.200 | 1.000 | MA SD |
Lag1 1 |
−0.883 (0.000) |
| District (Weekly) | ARIMA (2,0,1)(0,0,0) | Max. T° | Stationary R2: 0.863 Normalized BIC: 3.752 |
52.906 | 0.000 | AR | Lag2 | 0.751 (0.000) |
| Min. T° | MA | Lag1 | −0.999 (0.000) | |||||
| Max. T° | ||||||||
| Num Lag0 | −0.644 (0.001) | |||||||
| Den Lag2 | −0.518 (0.005) | |||||||
| Min. T° | Num Lag0 | 1.000 (0.000) | ||||||
Figure 6 shows the cases predicted in comparison with the observed cases in the best-fit ARIMA monthly model (top left) and ARIMA weekly model (top right). As seen in the graph of the monthly model, the prediction was not made in the first year (1382–2003), due to the seasonal order in the model. In this model, the predictions made in the second year were in excess of the number of cases actually observed, due to a peak in the first year. The number of cases predicted in the sixth year (1387–2008) was also nowhere near the number that was actually observed.
Fig. 6.
Graphs of the observed and predicted cases for the monthly (top left) and the weekly (top right) prediction models, and ACF and PACF graphs of residuals for the monthly (bottom left) and the weekly (bottom right) models
ACF and PACF charts for the residuals follow white noise pattern in the monthly model (Fig. 6, bottom left), which shows that there was no autocorrelation among the residuals, and therefore that this model was suitable. Although the weekly model could reliably predict the weekly amount, on the basis of what is shown in Figure 6 (top right), the ACF and PACF graphs do not follow the white noise pattern for the weekly model (Fig. 6, bottom right).
Discussion
Meteorological variables
Based on the results of the statistical model used, rainfall is not a reliable predictor for the occurrence of malaria. The cross-correlation graphs show that the 6 and 7 months’ delay in incidence of malaria had an insignificant positive correlation with the monthly total rainfall (Fig. 5). This variable is absent in both of the monthly and weekly models. Below average rainfall in the district and centralisation of rainfall in the months of autumn and winter, in which the average temperature is below the minimum requirement for the development of malaria parasites in the mosquito, decreases the model’s capacity to use this variable as a predictor that is potentially effective in parasite and vector development.
Another important point is that the data on rainfall in the meteorological stations may not be generalised to the entire region in the district. Other variables, such as altitude, slope and soil type, have a considerable effect on the extrapolation of these data. The type and extent of vegetation and cultivation, as well as product types and sources of ground/surface water interact with the effect of rainfall. Conversely, since the possibility of other water sources for the development and breeding of the vectors, in addition to the rainfall, is greater in urban areas, the effect of rainfall could be different in urban and rural populations (Teklehaimanot et al. 2004a).
The fact that the developmental stages of malaria vectors require water cannot be denied. In addition, environmental water contributes to providing relative humidity, and also increases the longevity of adult mosquitoes (Martens et al. 1995). However, this environment is not necessarily provided by the rainfall. Stagnant water from agriculture, drinking water pipes, or even water dripped from air conditioners, can provide the right environment for the breeding of vectors. Conversely, heavy rain can reduce malaria transmission by washing away the breeding sites in the short-term.
Many positive correlations between rainfall and malaria incidence, or epidemics, have been reported (Loevinsohn 1994, Lindblade et al. 1999, Kilian et al. 1999, Gomez-Elipe et al. 2007, Tian et al. 2008), and other studies have also shown a positive correlation between rainfall and vector density (Koenraadt et al. 2004, Koenraadt et al. 2006, Kristan et al. 2008, Yamana and Eltahir 2010). However, due to the complex relationship between the rainfall and entomological variables and malaria incidence, the efforts to build statistical models using rainfall to predict malaria have not been successful in many cases (Abeku et al. 2003, Cox and Abeku 2007, Briet et al. 2008, Haghdoost et al. 2008, Zhang et al. 2010, Loha and Lindtjorn 2010). Effective vector control measures, especially larviciding, after the creation of breeding sites following rainfall, can also reduce the impact of rainfall on the incidence of malaria (Briet et al. 2008). In addition, Minab River (a permanent river in the district) may act as a permanent breeding place for vectors and reduce the effect of rainfall as well as high temperature in transmission.
Another difference between our results and those obtained in other studies is the time interval (lag time) between the rainfall and its effect on the incidence of malaria. In most previous studies, the impact of this variable has been considered with a monthly lag time, but in this study the highest positive correlation between rainfall and malaria can be seen with a lag time of 6 to 7 months. This difference could be associated with the difference between the climate of the Minab district assessed in this study and the climates examined in other studies. The majority of the previous studies were conducted in tropical areas with a high average rainfall throughout the year, while other studies have been conducted in temperate regions, with a higher average and a longer period of rainfall over a year, compared to Minab. The effect of rainfall on the incidence of malaria in areas where it is very hot (like Minab) is shorter than in regions with lower temperatures (due to evaporation of the surface water and drying of breeding sites (Teklehaimanot et al. 2004b), so the effect of rainfall could indirectly be through the increase of the water level of rivers, surface water level, ground water level, and extent of cultivation. This might explain the relatively long delay observed with regard to the effect of rainfall on malaria incidence.
The annual mean of the maximum, the minimum, and the average temperature was negatively correlated with the incidence of malaria in the district studied. Since high temperature is fatal to malaria vectors, to some extent this correlation is biologically justified in areas with very high temperatures. Similar results have also been reported in a previous study (Teklehaimanot et al. 2004a). However, the increase in mean annual temperature (especially at the lowest temperature) can increase incidence by increasing the annual transition period, which is in contrast with the results obtained in this study. Since the transmission peak is at the end of summer in the district of Minab, a temperature rise in this period can cause the delay and shortening of the transmission period, which could be considered as an explanation for this negative correlation.
In this study, the temperature variable with 2 months’ lag time shows the maximum correlation with malaria cases (Fig. 6). This delay is reported as being 1 month in a study which was also conducted in Iran (Haghdoost et al. 2008). Time delay for the effect of temperature on malaria incidence was reported as being 2 months in a study carried out in Tibet (Huang et al. 2011), and as being 1 month in studies conducted in China (Zhang et al. 2010, Bi et al. 2003). Temperature variables (the minimum and the maximum temperature) were also significant in the weekly model.
Despite the undeniable importance of the effect of temperature on the development of parasite and vector, the applicability of using this variable to predict the incidence of malaria is uncertain. Further, a justifiable correlation between malaria cases and temperature was not demonstrated in the present study. Numerous studies have been conducted to examine this correlation and to use it to predict incidence of malaria, and a variety of variables, such as the maximum temperature, the minimum temperature and the mean temperature, or a combination of these variables, was used for prediction. A positive correlation between temperature and malaria, or its successful use in prediction, has been reported in many previous studies (Kiang et al. 2006, Gomez-Elipe et al. 2007, Haghdoost et al. 2008, Zhou et al. 2010, Wangdi et al. 2010). However, in some other studies, use of these variables has not been successful in predicting the incidence of malaria (Loha and Lindtjorn 2010).
Relative humidity in the 4th and the 5th months prior to the current month showed a significant correlation with malaria incidence (Fig. 7). However, this correlation was negative. A negative correlation between humidity and the incidence of malaria was reported in a study, conducted in Kahnouj (Iran) (Haghdoost et al. 2008). Since relative humidity of 50% to 60% is necessary for vector activity, and thereafter the incidence of malaria, the effect of interaction between humidity and temperature could explain this negative correlation. However, in the present study there was no significant correlation between average monthly temperature and humidity. Interaction effect of temperature and humidity variables was entered in time-series models to control this effect. However, this variable was not present in any of the weekly or the monthly models (Table 1).
With the exception of a single study in Iran (Haghdoost et al. 2008), a negative correlation between humidity and malaria has not been reported in any previous studies. A positive correlation has been reported in some studies (Loha and Lindtjorn 2010, Huang et al. 2011), while in others, the correlation between humidity and incidence or epidemic of malaria was not significant (Bi et al. 2003, Zhang et al. 2010). It appears that further epidemiological and entomological studies are required to investigate the causes of the negative correlation that was found in the present study.
In short, meteorological variables do not appear to explain a significant amount of the variation in malaria incidence. Although there is a known biological association between malaria and these variables, it seems that the limitations in measurement are hindering the showing of this relationship in the statistical models. In addition, their use is not of much help in predicting incidence of malaria. Data from meteorological stations are hardly generalizable to areas that are far from the stations with high dispersion. However, a microclimate, with different climatic conditions, has made it possible for the vectors to dwell and reproduce in any climatic condition; therefore the impact of climate variables on the incidence of malaria is more complex. The impact that interactions of climate variables make on each other, and the interaction between other variables affecting the incidence of malaria and the climate variables, is another factor that adds to the complexity of this correlation. Some studies have suggested that additional variables, such as socio-economic factors, should be used in malaria prediction models (Hay et al. 2002b, Small et al. 2003, Abeku et al. 2004, Teklehaimanot et al. 2004a, Craig et al. 2004, Zhou et al. 2004, Gething et al. 2010).
Since the vast majority of cases of malaria in this study are P. vivax malaria, consideration of relapse cases is highly important. Such cases can show the association between meteorological variables and incidence of malaria as being weaker than it actually is. In fact, as explained previously with regard to removing the imported cases from this study, the incidence of relapse cases has no correlation with climate variables and therefore should be excluded. A high relapse rate can create a serious problem in the assessment of the correlation between malaria and meteorological variables. A study reported an annual relapse rate of 16.8% and a biennial relapse rate of 24.5% in Kahnouj, Iran, using epidemiological methods (Haghdoost et al. 2006a). If extended to other parts of the country, including the Minab district, this relapse rate is very significant and therefore a serious obstacle to the approach of using statistical models to predict P. vivax malaria through meteorological variables. However, a serious limitation to the present study is the inability to recognize and delete the relapse cases.
The results of previous studies examining the correlation between malaria incidence and meteorological variables, and the possibility of using this correlation in an early warning system to predict malaria incidence, have shown different, and sometimes conflicting, results. Although the reason for this heterogeneity is not clear, biological, social and economic variables effective in the incidence of malaria could explain these contrasting results (Ostovar et al. 2012). These studies have been conducted in various regions/climatic conditions (tropical, temperate, highlands etc.) and endemicity (stable malaria, unstable malaria). There was also variation in the type of malaria parasite investigated. In most studies, only cases of P. falciparum malaria have been examined, but in some cases, both, or only P. vivax parasites have been assessed. The sources of the climate data and the area across which the data were generalised also varied in different studies. While some studies used ground meteorological station data, others used satellite data.
The number of malaria cases in the past
The past temporal records of the number of malaria cases are the most important variables of the models in this study. These variables were significant in both the monthly and the weekly models, and have had a considerable effect on model fit. In fact, the number of previous malaria cases may reflect the interaction of all the current factors effective in malaria incidence, including meteorological, social and economic variables. However, the results of a study in an unstable malaria region in Ethiopia have shown that previous incidence of malaria cannot alone suitably predict the incidence of malaria now (Abeku et al. 2002).
Based on the ACF and PACF graphs in the present study, the current incidence of malaria shows a significant correlation with the incidence of malaria in the last 2 months. In addition, in the time-series models, one moving average (MA) order in the monthly model, and two MA order with one autoregression (AR) order in the weekly model remain. The results of this study are consistent with those obtained by a number of other studies (Haghdoost et al. 2008, Briet et al. 2008, Loha and Lindtjorn 2010).
Most previous studies were conducted based on monthly data, due to unavailability of weekly data. However, a number of studies have suggested weekly (Githeko and Ndegwa 2001, Teklehaimanot et al. 2004, Abeku et al. 2004, Gomez-Elipe et al. 2007) or decade (10-day interval) (Haghdoost et al. 2008) data. However, the models obtained from the weekly and the monthly data were not compared with each other in any of these studies.
When considering the number of previous malaria cases, since there are positive correlations between the number of malaria cases and 1 or 2 months’ lag time in the monthly models, and 4 to 5 weeks’ lag time in the weekly models, is there sufficient lead time for the MEWS to apply malaria control measures? If the answer is in the negative, as it was in the Huang study (Huang et al. 2011), then there will be serious limitations to the use of these models in practice.
The present study has a number of limitations. First, the data obtained from the surveillance system were not qualitatively and quantitatively adequate for the analysis of further districts, and are therefore limited to Minab. Second, it is doubtful that the data obtained from meteorological stations located in the center of the entire district of Minab can be extended, due to the fact that a large area of the district has a low number of meteorological stations. Finally, the time period allocated to building the model in this study was relatively short. Despite all these limitations, this study can be considered as a step toward clarifying both the relationship between meteorological variables and the incidence of malaria in Iran, and the statistical models to consider for use in prediction.
Conclusion
The statistical models can be used in line with a MEWS to predict malaria incidence, while the time-series models can also be used, due to their acceptable accuracy. It appears that the contribution of the meteorological variables is not significant in explaining the variations in the incidence of malaria, and that the monitoring, recording and use of these data in a malaria surveillance system, in order to predict an early warning of incidence, cannot be of any help in making predictions. However, this study has limitations that make its conclusion uncertain, therefore further entomological and epidemiological studies are required to better understand the relationship between meteorological variables and the incidence of malaria.
Acknowledgements
The authors would like to acknowledge the invaluable contribution by Dr Reza Safari, manager of Disease Control Department of Deputy for Health of Hormozgan University of Medical Sciences, for his help in accessing the data and Mr Gholamreza Khatami for his help in cleaning and preparing meteorological data for analyses. This paper is a part of the PhD thesis in School of Public Health, Tehran University of Medical Sciences. The authors declare that there is no conflict of interests.
References
- Abeku TA, de Vlas SJ, Borsboom G, Teklehaimanot A, Kebede A, Olana D, van Oortmarssen GJ, Habbema JD. (2002) Forecasting malaria incidence from historical morbidity patterns in epidemic-prone areas of Ethiopia: a simple seasonal adjustment method performs best. Trop Med Int Health. 7: 851– 857. [DOI] [PubMed] [Google Scholar]
- Abeku TA, de Vlas SJ, Borsboom GJ, Tadege A, Gebreyesus Y, Gebreyohannes H, Alamirew D, Seifu A, Nagelkerke NJ, Habbema JD. (2004) Effects of meteorological factors on epidemic malaria in Ethiopia: a statistical modelling approach based on theoretical reasoning. Parasitology. 128: 585– 593. [DOI] [PubMed] [Google Scholar]
- Abeku TA, van Oortmarssen GJ, Borsboom G, de Vlas SJ, Habbema JDF. (2003) Spatial and temporal variations of malaria epidemic risk in Ethiopia: Factors involved and implications. Acta Tropica. 87: 331– 340. [DOI] [PubMed] [Google Scholar]
- Bi P, Tong S, Donald K, Parton KA, Ni J. (2003) Climatic variables and transmission of malaria: a 12-year data analysis in Shuchen County, China. Public Health Rep. 118: 65– 71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouma MJ. (2003) Methodological problems and amendments to demonstrate effects of temperature on the epidemiology of malaria. A new perspective on the highland epidemics in Madagascar, 1972–1989. Trans R Soc Trop Med Hyg, 97: 133– 139. [DOI] [PubMed] [Google Scholar]
- Briet OJ, Vounatsou P, Gunawardena DM, Galappaththy GN, Amerasinghe PH. (2008) Models for short term malaria prediction in Sri Lanka. Malar J. 7: 76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox J, Abeku TA. (2007) Early warning systems for malaria in Africa: from blueprint to practice. Trends Parasitol. 23: 243– 246. [DOI] [PubMed] [Google Scholar]
- Craig MH, Kleinschmidt I, Nawn JB, Le Sueur D, Sharp BL. (2004) Exploring 30 years of malaria case data in KwaZulu-Natal, South Africa: part I. The impact of climatic factors. Trop Med Int Health. 9: 1247– 1257. [DOI] [PubMed] [Google Scholar]
- Edrissian G. (2006) Malaria in Iran: Past and Present Situation. Iran J Parasitol. 1: 1– 14. [Google Scholar]
- Ermert V, Fink AH, Jones AE, Morse AP. (2011) Development of a new version of the Liverpool Malaria Model. II. Calibration and validation for West Africa. Malar J. 10: 62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gething PW, Smith DL, Patil AP, Tatem AJ, Snow RW, Hay SI. (2010) Climate change and the global malaria recession. Nature. 465: 342– 345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Githeko A, Ndegwa W. (2001) Predicting Malaria Epidemics in the Kenyan Highlands Using Climate Data: A Tool for Decision Makers. Global Change and Human Health. 2: 54– 63. [Google Scholar]
- Gomez-Elipe A, Otero A, van Herp M, Aguirre-Jaime A. (2007) Forecasting malaria incidence based on monthly case reports and environmental factors in Karuzi, Burundi, 1997–2003. Malar J. 6: 129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haghdoost AA, Alexander N, Cox J. (2008) Modelling of malaria temporal variations in Iran. Trop Med Int Health. 13: 1501– 1508. [DOI] [PubMed] [Google Scholar]
- Haghdoost AA, Mazhari S, Bahaadini K. (2006a) Estimating the relapse risk of Plasmodium vivax in Iran under national chemotherapy scheme using a novel method. J Vector Borne Dis, 43: 168– 172. [PubMed] [Google Scholar]
- Haghdoost AA, Mazhari S, Bahadini K. (2006b) Comparing the results of light microscopy with the results of PCR method in the diagnosis of Plasmodium vivax. J Vector Borne Dis. 43: 53– 57. [PubMed] [Google Scholar]
- Hay SI, Cox J, Rogers DJ, Randolph SE, Stern DI, Shanks GD, Myers MF, Snow RW. (2002a) Climate change and the resurgence of malaria in the East African highlands. Nature. 415: 905– 909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hay SI, Rogers DJ, Randolph SE, Stern DI, Cox J, Shanks GD, Snow RW. (2002b) Hot topic or hot air? Climate change and malaria resurgence in East African highlands. Trends Parasitol. 18: 530– 534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoshen MB, Morse AP. (2004) A weather-driven model of malaria transmission. Malar J. 3: 32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang F, Zhou S, Zhang S, Wang H, Tang L. (2011) Temporal correlation analysis between malaria and meteorological factors in Motuo County, Tibet. Malar J. 10: 54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiang R, Adimi F, Soika V, Nigro J, Singhasivanon P, Sirichaisinthop J, Leemingsawat S, Apiwathnasorn C, Looareesuwan S. (2006) Meteorological, environmental remote sensing and neural network analysis of the epidemiology of malaria transmission in Thailand. Geospat Health. 1: 71– 84. [DOI] [PubMed] [Google Scholar]
- Kilian AH, Langi P, Talisuna A, Kabagambe G. (1999) Rainfall pattern, El Nino and malaria in Uganda. Trans R Soc Trop Med Hyg. 93: 22– 23. [DOI] [PubMed] [Google Scholar]
- Koenraadt CJ, Githeko AK, Takken W. (2004) The effects of rainfall and evapotranspiration on the temporal dynamics of Anopheles gambiae s.s. and Anopheles arabiensis in a Kenyan village. Acta Trop. 90: 141– 153. [DOI] [PubMed] [Google Scholar]
- Koenraadt CJ, Paaijmans KP, Schneider P, Githeko AK, Takken W. (2006) Low larval vector survival explains unstable malaria in the western Kenya highlands. Trop Med Int Health. 11: 1195– 205. [DOI] [PubMed] [Google Scholar]
- Kristan M, Abeku TA, Beard J, Okia M, Rapuoda B, Sang J, Cox J. (2008) Variations in entomological indices in relation to weather patterns and malaria incidence in East African highlands: implications for epidemic prevention and control. Malar J. 7: 231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindblade KA, Walker ED, Onapa AW, Katungu J, Wilson ML. (1999) Highland malaria in Uganda: prospective analysis of an epidemic associated with El Nino. Trans R Soc Trop Med Hyg. 93: 480– 487. [DOI] [PubMed] [Google Scholar]
- Loevinsohn ME. (1994) Climatic warming and increased malaria incidence in Rwanda. Lancet. 343: 714– 718. [DOI] [PubMed] [Google Scholar]
- Loha E, Lindtjorn B. (2010) Model variations in predicting incidence of Plasmodium falciparum malaria using 1998–2007 morbidity and meteorological data from south Ethiopia. Malar J. 9: 166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martens W, Niessen LW, Rotmans J, McMichael AJ. (1995) Potential impacts of global climate change on malaria risk. Environmental Health Perspectives. 103: 458– 464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matola YG, Magayuka SA. (1987) The changed pattern of malaria endemicity and transmission at Amani in the eastern Usambara Mountains, northeastern Tanzania. J Trop Med Hyg. 90: 127– 134. [PubMed] [Google Scholar]
- Medina DC, Findley SE, Guindo B, Doumbia S. (2007) Forecasting non-stationary diarrhoea, acute respiratory infection, and malaria time-series in Nino Mali. PLoS One. 2: e1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostovar A, Raeisi A, Haghdoost AA, Ranjbar M, Rahimi A, Sheikhzadeh K, Majdzadeh R. (2012) Lessons learnt from malaria epidemics in the Islamic Republic of Iran. East Mediterr Health J. 18: 864– 869. [DOI] [PubMed] [Google Scholar]
- Paaijmans KP, Read AF, Thomas MB. (2009) Understanding the link between malaria risk and climate. Proc Natl Acad Sci USA, 106: 13844– 13849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pascual M, Ahumada JA, Chaves LF, Rodo X, Bouma M. (2006) Malaria resurgence in the East African highlands: temperature trends revisited. Proc Natl Acad Sci USA. 103: 5829– 5834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pascual M, Cazelles B, Bouma MJ, Chaves LF, Koelle K. (2008) Shifting patterns: malaria dynamics and rainfall variability in an African highland. Proc Biol Sci. 275: 123– 132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raeisi A. (2009) Malaria Elimination, in I.R. Iran, Horizon 1404. Tehran, Ministry of Health and Medical Education. [Google Scholar]
- Raeisi A, Nikpoor F, Ranjbar Kahkha M, Faraji L. (2009) The trend of Malaria in Iran from 2002 to 2007. Hakim Research Journal. 12: 35– 41. [Google Scholar]
- Small J, Goetz SJ, Hay SI. (2003) Climatic suitability for malaria transmission in Africa, 1911–1995. Proc Natl Acad Sci USA. 100: 15341– 15345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teklehaimanot HD, Lipsitch M, Teklehaimanot A, Schwartz J. (2004) Weather-based prediction of Plasmodium falciparum malaria in epidemic-prone regions of Ethiopia I. Patterns of lagged weather effects reflect biological mechanisms. Malar J. 3: 41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teklehaimanot HD, Schwartz J, Teklehaimanot A, Lipsitch M. (2004a) Alert threshold algorithms and malaria epedemic detection. Emerg Infect Dis 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teklehaimanot HD, Schwartz J, Teklehaimanot A, Lipsitch M. (2004b) Weather-based prediction of Plasmodium falciparum malaria in epidemic-prone regions of Ethiopia II. Weather-based prediction systems perform comparably to early detection systems in identifying times for interventions. Malar J. 3: 44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomson MC, Connor SJ. (2000) Malaria Early Warning System, concepts, indicators and partners Geneva, Switzerland: World Health Organization, Roll Back Malaria. [Google Scholar]
- Tian L, Bi Y, Ho SC, Liu W, Liang S, Goggins WB, Chan EY, Zhou S, Sung JJ. (2008) One-year delayed effect of fog on malaria transmission: a time-series analysis in the rain forest area of Mengla County, south-west China. Malar J. 7: 110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wangdi K, Singhasivanon P, Silawan T, Lawpoolsri S, White NJ, Kaewkungwal J. (2010) Development of temporal modelling for forecasting and prediction of malaria infections using time-series and ARIMAX analyses: a case study in endemic districts of Bhutan. Malar J. 9: 251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamana TK, Eltahir EA. (2010) Early warnings of the potential for malaria transmission in rural Africa using the hydrology, entomology and malaria transmission simulator (HYDREMATS). Malar J. 9: 323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Bi P, Hiller JE. (2010) Meteorological variables and malaria in a Chinese temperate city: A twenty-year time-series data analysis. Environ Int. 36: 439– 445. [DOI] [PubMed] [Google Scholar]
- Zhou G, Minakawa N, Githeko AK, Yan G. (2004) Association between climate variability and malaria epidemics in the East African highlands. Proc Natl Acad Sci USA. 101: 2375– 2380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou SS, Huang F, Wang JJ, Zhang SS, Su YP, Tang LH. (2010) Geographical, meteorological and vectorial factors related to malaria re-emergence in Huang-Huai River of central China. Malar J. 9: 337. [DOI] [PMC free article] [PubMed] [Google Scholar]