The origin of extracellular fields and currents — EEG, ECoG, LFP and spikes

Abstract

Neuronal activity in the brain gives rise to transmembrane currents that can be measured in the extracellular medium. Although the major contributor of the extracellular signal is the synaptic transmembrane current, other sources — including Na⁺ and Ca²⁺ spikes, ionic fluxes through voltage- and ligand-gated channels, and intrinsic membrane oscillations — can substantially shape the extracellular field. High-density recordings of field activity in animals and subdural grid recordings in humans, combined with recently developed data processing tools and computational modelling, can provide insight into the cooperative behaviour of neurons, their average synaptic input and their spiking output, and can increase our understanding of how these processes contribute to the extracellular signal.

Electric current contributions from all active cellular processes within a volume of brain tissue superimpose at a given location in the extracellular medium and generate a potential, V_e (a scalar measured in Volts), with respect to a reference potential. The difference in V_e between two locations gives rise to an electric field (a vector whose amplitude is measured in Volts per distance) that is defined as the negative spatial gradient of V_e. Electric fields can be monitored by extracellularly placed electrodes with submillisecond time resolution and can be used to interpret many facets of neuronal communication and computation (FIG. 1). A major advantage of extracellular field recording techniques is that, in contrast to several other methods used for the investigation of network activity, the biophysics related to these measurements are well understood. This has enabled the development of reliable and quantitative mathematical models to elucidate how transmembrane currents give rise to the recorded electric potential.

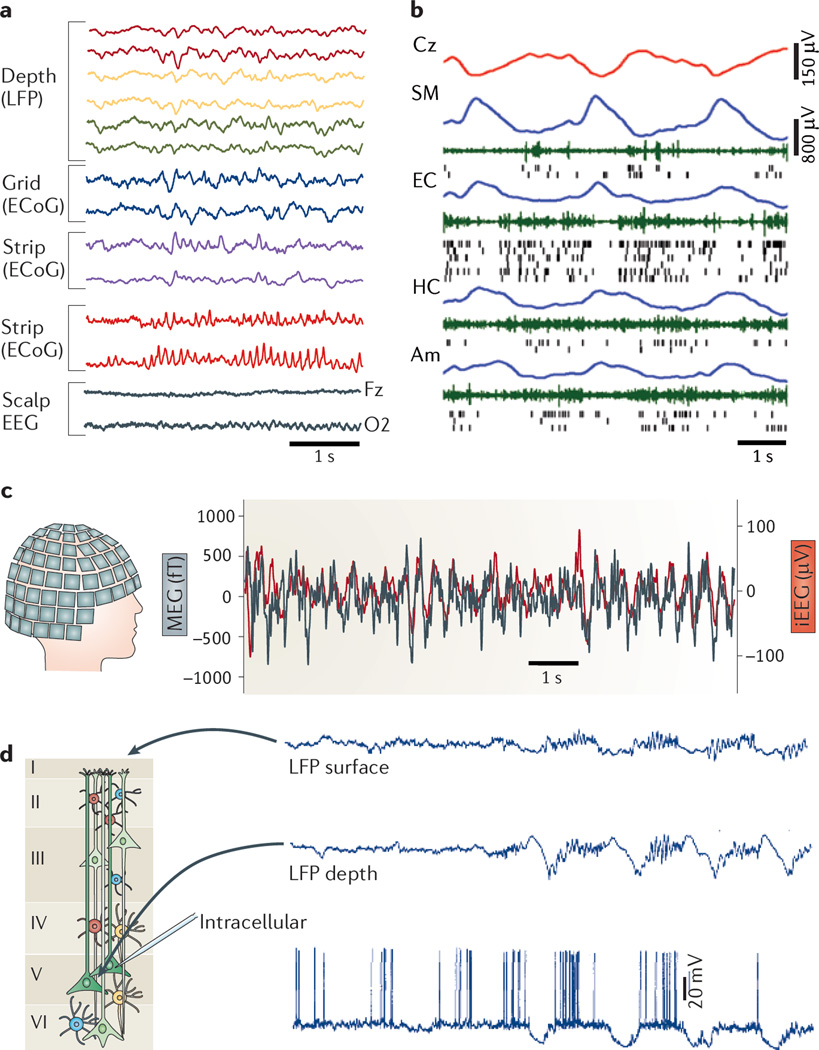
Figure 1. Extracellular traces using different recording methods are fundamentally similar.

a | Simultaneous recordings from three depth electrodes (two selected sites each) in the left amygdala and hippocampus (measuring the local field potential (LFP)); a 3 × 8 subdural grid electrode array placed over the lateral left temporal cortex (measuring the electrocorticogram (ECoG); two four-contact strips placed under the inferior temporal surface (measuring the ECoG); an eight-contact strip placed over the left orbitofrontal surface (measuring the ECoG); and scalp electroencephalography (EEG) over both hemispheres (selected sites are the Fz and O2) in a patient with drug-resistant epilepsy. The amplitude signals are larger and the higher-frequency patterns have greater resolution at the intracerebral (LFP) and ECoG sites compared to scalp EEG. b | A 6 s epoch of slow waves recorded by scalp EEG (Cz, red), and LFP (blue) recorded by depth electrodes placed in the deep layers of the supplementary motor area (SM) and entorhinal cortex (EC), hippocampus (HC) and amygdala (Am). Also shown are multiple-unit activity (green) and spikes of isolated neurons (black ticks). c | Simultaneously recorded magnetoencephalogram (MEG; black) and anterior hippocampus depth EEG (red) from a patient with drug-resistant epilepsy. Note the similar theta oscillations recorded by the depth electrode and the trace calculated by the MEG, without any phase delay. d | Simultaneously recorded LFP traces from the superficial (‘surface’) and deep (‘depth’) layers of the motor cortex in an anaesthetized cat and an intracellular trace from a layer 5 pyramidal neuron. Note the alternation of hyperpolarization and depolarization (slow oscillation) of the layer 5 neuron and the corresponding changes in the LFP. The positive waves in the deep layer (close to the recorded neuron) are also known as delta waves. iEEG, intracranial EEG. Part a courtesy of G. Worrell, Mayo Clinic, Minneapolis, Minnesota, USA, and S. Makeig, University of California at San Diego, USA. Part b is reproduced, with permission, from REF. 157 © (2011) Cell Press. Part c courtesy of S. S. Dalal, University of Konstanz, Germany, and J.-P. Lachaux and L. Garnero, Université de Paris, France. Part d is reproduced, with permission, from REF. 158 © (1995) Society for Neuroscience.

Historically, V_e has been referred to as the electroencephalogram (EEG) when recorded from the scalp, as the electrocorticogram (ECoG) when recorded by subdural grid electrodes on the cortical surface, and as the local field potential (LFP; also known as micro-, depth or intracranial EEG¹) when recorded by a small-size electrode in the brain (BOX 1; FIG. 1). The term ‘local field potential’ (meaning an electric potential (V_e)), is a regrettable malapropism, but we continue to use the term LFP because it is familiar to most neuroscientists. The magnetic field induced by the same activity is referred to as the magnetoencephalogram (MEG)².

Box 1. Recordings methods of extracellular events.

Electroencephalography

Electroencephalography (EEG) is one of the oldest and most widely used methods for the investigation of the electric activity of the brain^10,16. The scalp electroencephalogram, recorded by a single electrode, is a spatiotemporally smoothed version of the local field potential (LFP), integrated over an area of 10 cm² or more. Under most conditions, it has little discernible relationship with the firing patterns of the contributing individual neurons¹⁶, and this is largely due to the distorting and attenuating effects of the soft and hard tissues between the current source and the recording electrode. The recently introduced ‘high-density’ EEG recordings, in combination with source-modelling that can account for the gyri and sulci (as inferred from structural MRI imaging) of the subject, have substantially improved the spatial resolution of EEG^16,146,147.

Magnetoencephalography

Magnetoencephalography (MEG) uses superconducting quantum interference devices (SQUIDs) to measure tiny magnetic fields outside the skull (typically in the 10–1,000 fT range) from currents generated by the neurons². Because MEG is non-invasive and has a relatively high spatiotemporal resolution (~1 ms, and 2–3 mm in principle)², it has become a popular method for monitoring neuronal activity in the human brain. An advantage of MEG is that magnetic signals are much less dependent on the conductivity of the extracellular space than EEG. The scaling properties (that is, the frequency versus power relationship) of EEG and MEG often show differences, typically in the higher-frequency bands. These differences may be partly explained by the capacitive properties of the extracellular medium (such as skin and scalp muscles) that distort the EEG signal but not the MEG signal¹⁴⁸.

Electrocorticography

Electrocorticography (ECoG) is becoming an increasingly popular tool for studying various cortical phenomena in clinical settings¹⁴⁹. It uses subdural platinum–iridium or stainless steel electrodes to record electric activity directly from the surface of the cerebral cortex, thereby bypassing the signal-distorting skull and intermediate tissue. The spatial resolution of the recorded electric field can be substantially improved (<5 mm²)¹⁰² by using flexible, closely spaced subdural grid or strip electrodes (FIG. 1).

Local field potential

EEG, MEG and ECoG mainly sample electrical activity that occurs in the superficial layers of the cortex. Electrical events at deeper locations can be explored by inserting metal or glass electrodes, or silicon probes into the brain to record the LFP (also known as ‘micro-EEG’). Recording the wide-band signal (direct current to 40 kHz) — which contains both action potentials and other membrane potential-derived fluctuations in a small neuronal volume — using a microelectrode yields the most informative signal for studying cortical electrogenesis. Many observation points, with short distances between the recording sites and with minimal impact on brain tissue, are needed to achieve high spatial resolution. In principle, the spiking activity of nearly all or at least a representative fraction of the neuron population in a small volume can be monitored with a sufficiently large density of recording sites. Additional clues about the intracellular dynamics can be deduced from the waveform changes of the extracellular action potentials^99,150. Progress in this field has been accelerated by the availability of micro-machined silicon-based probes with ever-increasing numbers of recording sites^130,151,152.

Voltage-sensitive dye imaging

Voltage changes can also be detected by membrane-bound voltage-sensitive dyes or by genetically expressed voltage-sensitive proteins^153–155. Using the voltage-sensitive dye imaging (VSDI) method, the membrane voltage changes of neurons in a region of interest can be detected optically, using a high-resolution fast-speed digital camera, at the peak excitation wavelength of the dye. A major advantage of VSDI is that it directly measures localized transmembrane voltage changes, as opposed to the extracellular potential. A second advantage is that the provenance of the signal can be identified if a known promoter is used to express the voltage-sensitive protein. Limitations are inherent in all optical probe-based methods¹⁵⁶, and for VSDI these include interference with the physiological functions of the cell membrane, photoxicity, a low signal-to-noise ratio and the fact that it can only measure surface events.

Recent advances in microelectrode technology using silicon-based polytrodes offer new possibilities for estimating input–output transfer functions in vivo, and high-density recordings of electric and magnetic fields of the brain now provide unprecedented spatial coverage and resolution of the elementary processes involved in generating the extracellular field. In addition, novel time-resolved spectral methods provide insights into the functional meaning of the information-rich high-frequency bands of the V_e signal^3,4. These new developments have led to a more in-depth understanding not only of the relationship between network activity and cognitive behaviour⁵ but also of the pathomechanisms in brain diseases⁶.

Several excellent but somewhat dated reviews discuss various aspects of extracellular signals in the brain^2,7–25. Here we provide an overview of our present understanding of the mechanisms that underlie the generation of extracellular currents and fields. Although all nervous structures generate extracellular fields, our focus is the mammalian cerebral cortex, as most of our quantitative knowledge is the result of studies in cortex.

Contributors to extracellular fields

Any excitable membrane — whether it is a spine, dendrite, soma, axon or axon terminal — and any type of transmembrane current contributes to the extracellular field. The field is the superposition of all ionic processes, from fast action potentials to the slowest fluctuations in glia. All currents in the brain superimpose at any given point in space to yield V_e at that location. Thus, any transmembrane current, irrespective of its origin, leads to an intracellular as well as an extracellular (that is, LFP) voltage deflection. The characteristics of the LFP waveform, such as the amplitude and frequency, depend on the proportional contribution of the multiple sources and various properties of the brain tissue. The larger the distance of the recording electrode from the current source, the less informative the measured LFP becomes about the events occurring at the location(s) of the source(s). This is mainly owing to the fact that the V_e amplitude scales with the inverse of the distance r between the source and the recording site, and to the inclusion of other (interfering) signals (leading to ‘spatial averaging’). In addition to the magnitude and sign of the individual current sources, and their spatial density, the temporal coordination of the respective current sources (that is, their synchrony) shapes the extracellular field. Thus, extracellular currents can emerge from multiple sources, and these are described below.

Synaptic activity

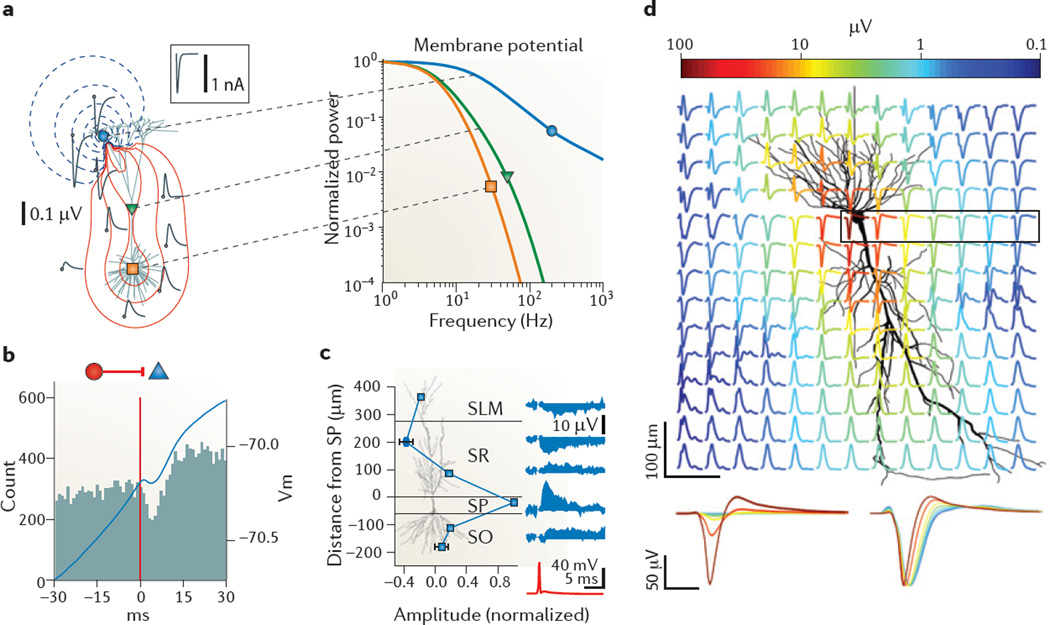
In physiological situations, synaptic activity is often the most important source of extracellular current flow. The idea that synaptic currents contribute to the LFP stems from the recognition that extracellular currents from many individual compartments must overlap in time to induce a measurable signal, and such overlap is most easily achieved for relatively slow events, such as synaptic currents^7,10,23. The dendrites and soma of a neuron form a tree-like structure with an electrically conducting interior that is surrounded by a relatively insulating membrane, with hundreds to tens of thousands of synapses located along it. Neurotransmitters acting on synaptic AMPA and NMDA receptors mediate excitatory currents, involving Na⁺ or Ca²⁺ ions, respectively, which flow inwardly at the synapse. This influx of cations from the extracellular into the intracellular space gives rise to a local extracellular sink. To achieve effective electroneutrality within the time constants of relevance for systems neuroscience, the extracellular sink needs to be ‘balanced’ by an extracellular source, that is, an opposing ionic flux from the intracellular to the extracellular space, along the neuron; this flux is termed passive current or return current. Depending on the location of the sink current(s) and its distance from the source current(s), a dipole or a higher-order n-pole is formed (FIG. 2a). The contribution of a monopole to V_e scales as 1/r, whereas the contribution of a dipole decays faster, as 1/r²; this steeper decay is due to the two opposing charges that comprise the dipole cancelling each other out to first order.

Figure 2. Excitatory and inhibitory postsynaptic currents are the most ubiquitous contributors to V_e.

a | Computer-simulated local field potential (LFP) traces (left panel; grey) in response to an excitatory synaptic current input (a sink, shown by the blue circle) injected into the distal apical dendrite of a purely passive layer 5 pyramidal model neuron. The waveform of the injected current is illustrated in the box. Red and blue contour lines correspond to positive and negative values for the LFP amplitude, respectively. The calculated double logarithmic power spectra of the transmembrane potential are also shown (right panel), following injection of current into the apical dendrite near the injection site (blue trace), mid-apical dendrite (green trace) and soma (orange trace). Note that high-frequency activity decreases with the distance from the active synaptic site (that is, the sink). b | A monosynaptic inhibitory connection between a putative layer 3 entorhinal cortical interneuron (red circle) and intracellularly recorded pyramidal cell (blue triangle). Below it, a cross-correlogram between the spikes of the reference interneuron (at time 0, red line) and the pyramidal cell and, superimposed on it, the spike-triggered average of the membrane potential (Vm) of the pyramidal cell (in blue). Note the small, short-latency hyperpolarization (the dip) superimposed on the rising phase of the intracellular theta oscillation and the corresponding decreased spike discharge of the pyramidal cell. c | Inhibition-induced LFPs. LFPs were generated in the vicinity of a pyramidal neuron (bottom cell) by intracellularly induced action potentials in a nearby basket cell (top cell), and were recorded extracellularly at six sites in multiple layers of the hippocampus. The mean LFP amplitude at each site is shown by the blue squares. Example LFP traces (blue) from six sites and the action potential of the basket cell (red trace) are shown on the right. Note that the largest positive response by inhibition-induced hyperpolarization occurs near the soma. d | Extracellular contribution of an action potential (‘spike’) to the LFP in the vicinity of the spiking pyramidal cell. The magnitude of the spike is normalized. The peak-to-peak voltage range is indicated by the colour of the traces. Note that the spike amplitude decreases rapidly with distance from the soma, without a change in polarity within the pyramidal layer (the approximate area of which is shown by the box), in contrast to the quadrupole (that is, reversed polarity signals both above and below the pyramidal layers) formed along the somatodendritic axis. The distance-dependence of the spike amplitude within the pyramidal layer is shown (bottom left panel) with voltages drawn to scale, using the same colour identity as the traces in the boxed area in d. The same traces are shown normalized to the negative peak (bottom right panel). Note the widening of the spike with distance from the soma, owing to greater contributions from dendritic currents and intrinsic filtering of high-frequency currents by the cell membrane. SLM, stratum lacunosum moleculare; SO, stratum oriens; SP, stratum pyramidale; SR, stratum radiatum. Part a is reproduced, with permission, from REF. 83 © (2010) Springer. Part b is reproduced, with permission, from REF. 137 © (2010) Society for Neuroscience. Part c is reproduced from REF. 29 © (2009) Macmillan Publishers Ltd. All rights reserved. Part d courtesy of E. W. Schomburg, California Institute of Technology, USA.

Notably, GABA subtype A (GABA_A) receptor-mediated inhibitory currents are typically assumed to add very little to the extracellular field as the Cl⁻ equilibrium potential is close to the resting membrane potential^26,27. However, in actively spiking neurons the membrane is depolarized, and therefore inhibitory (and often hyperpolarizing) currents can generate substantial transmembrane currents^28–30 (FIG. 2b,c).

Fast action potentials

Fast (Na⁺) action potentials generate the strongest currents across the neuronal membrane and can be detected as ‘unit’ or ‘spike’ activity in the extracellular medium²⁷. Although Na⁺ spikes generate large-amplitude V_e deflections near the soma (FIG. 2d), until recently they were thought not to contribute substantially to the traditionally considered LFP band (<100 Hz) or to the scalp-recorded EEG^10,16, because the strongest fields they generate are of short duration (<2 ms) and nearby neurons rarely fire synchronously in such short time windows under physiological conditions³¹. However, synchronous action potentials from many neurons can contribute substantially to high-frequency components of the LFP. Therefore, with appropriate methods, valuable information can be extracted from the LFP about the temporal structure of spiking neuronal populations (see below).

Calcium spikes

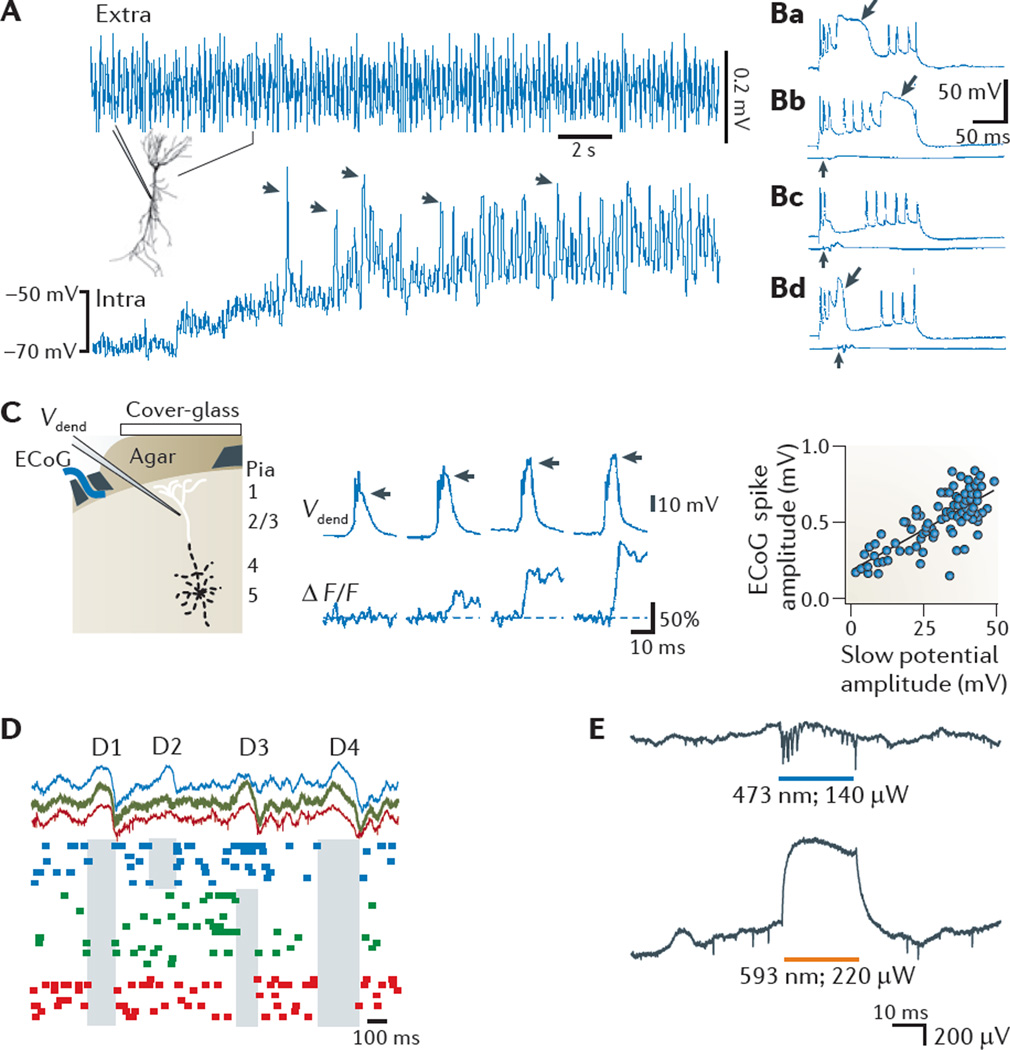
Other non-synaptic events that can contribute prominently to the extracellular field are the long-lasting (10–100 ms) Ca²⁺-mediated spikes³². Because voltage-dependent regenerative Ca²⁺ spikes are often triggered by NMDA receptor-mediated excitatory postsynaptic potentials (EPSPs)^33–36, separating them from EPSPs in extracellular recordings is not straightforward. A potential differentiating factor is that, in contrast to EPSPs, Ca²⁺ spikes can actively propagate within the cell and can therefore generate fields across the laminar boundaries of afferent inputs. Ca²⁺ spikes can also be triggered by back-propagating somatic action potentials³⁷, in which case they are independent of synaptic activity. Because dendritic Ca²⁺ spikes are large (10–50 mV) and long lasting^37–39, their share in the measured extracellular events can be substantial under certain circumstances (FIG. 3). Unfortunately, very little is known about Ca²⁺ spikes in vivo⁴⁰.

Figure 3. Non-synaptic contributions to the LFP.

Ca²⁺ spikes, disfacilitation and disinhibition contribute to the local field potential (LFP). A | Voltage-dependence of a theta-frequency oscillation in a hippocampal pyramidal cell dendrite in vivo. A continuous recording of extracellular (extra) and intradendritic (intra) activity in a hippocampal CA1 pyramidal cell is shown. The holding potential was manually shifted to progressively more depolarized levels by intradendritic current injection. The recording electrode contained QX-314 to block Na⁺ spikes. Note the large increase in the amplitude of the intradendritic theta oscillation upon depolarization. Arrows, putative high-threshold Ca²⁺ spikes phase-locked to the LFP theta oscillation. Ba | Dendritic Ca²⁺ spikes (shown by an arrow) have a large amplitude and are long-lasting in vivo. Bb–Bd | The response of a CA1 pyramidal cell to ventral hippocampal commissural stimulation (vertical arrows) paired with dendritic depolarization. Such inhibition can delay (Bb), prevent (Bc) or abort (Bd) the dendritic Ca²⁺ spike. LFPs recorded from a nearby electrode in the pyramidal layer show the timing and magnitude of the stimulation (lower traces in Bb–Bd). Note that the number of Na²⁺ spikes remains approximately the same, irrespective of the presence or absence of the Ca²⁺ spike. C | Whisker stimulation-evoked dendritic Ca²⁺ spikes correlate with surface cortical LFP changes. The setup for recording the electrocorticogram (ECoG), intradendritic potential (V_dend) and Ca²⁺ fluorescence is shown in the left panel. The relationship between the intradendritic potential amplitude (horizontal arrows) and simultaneously measured Ca²⁺ influx (ΔF/F) is shown in the middle panel. The ECoG response as a function of the Ca²⁺ spike (‘slow potential’) amplitude is shown in the right panel. D | ‘Down’ states in cortical pyramidal cells during sleep produce extracellular LFP ‘delta’ waves. Shown are simultaneously recorded LFP (top) and unit activity (bottom) at three layer 5 intracortical locations (spaced approximately 1 mm apart; indicated by different colours). Note that down states (shaded areas), reflected as positive waves (delta waves) in the LFP, can be either strongly localized (in D2 and D3) or more widespread (in D1 and D4). E | Generation of extracellular potentials by depolarization or hyperpolarization of a limited number of CA1 neurons that express both channelrhodopsin 2 (ChR2) and halorhodopsin, in response to blue (top) and yellow (bottom) light in vivo. Note the depolarization-induced negative LFP (top) and the hyperpolarization-induced positive LFP (bottom) in the pyramidal layer. Part A is reproduced, with permission, from REF. 159 © (1998) Wiley. Part B is reproduced, with permission, from REF. 160 © (1996) National Academy of Sciences. Part C is reproduced from REF. 161 © (1999) Macmillan Publishers Ltd. All rights reserved. Part D is reproduced, with permission, from REF. 56 © (2005) Cambridge Journals. Part E courtesy of E. Stark, New York University, Langone Medical Center, USA.

Intrinsic currents and resonances

I_h currents and I_T currents are prominent examples of intrinsic, voltage-dependent membrane responses³⁹. Although synaptically induced voltage changes are a prerequisite for the activation of voltage-dependent hyperpolarization-activated cyclic nucleotide (HCN)-gated and T-type calcium channels, the large membrane and extracellular currents that these channels generate are not synaptic events. These and other voltage-gated currents contribute to intrinsic resonance and oscillation of the membrane potential. Several neuron types possess resonant properties; that is, they respond more effectively to inputs of a particular frequency range³⁹. When intracellular depolarization is sufficiently strong, the resonant property of the membrane can give way to a self-sustained oscillation of the voltage. Voltage-dependent resonance and oscillations at theta frequency have been described in principal neurons of several cortical regions^39,41–44. By contrast, perisomatic inhibitory interneurons have a preferred resonance in the gamma frequency (30–90 Hz) range^45,46. Because resonance is both voltage- and frequency-dependent^39,41, its impact on the magnitude of the extracellular field can vary in a complex manner. To contribute substantially to the LFP, resonant membrane potential fluctuations must occur synchronously in nearby neurons, a feature that most often occurs in inhibitory interneurons.

Spike afterhyperpolarizations and ‘down’ states

Elevation of the intracellular concentration of a certain ion may trigger influx of other ions through activation of ligand-gated channels, and this will in turn contribute to V_e. For example, bursts of fast spikes and associated dendritic Ca²⁺ spikes are often followed by hyperpolarization of the membrane, owing to activation of a Ca²⁺-mediated increase of K⁺ conductance in the somatic region⁴⁷. As the amplitude and duration of such burst-induced afterhyperpolarizations (AHPs) can be as large (and last as long as) synaptic events, AHPs also contribute to the extracellular field⁴⁸, particularly when bursting of nearby neurons occurs in a temporally coordinated fashion: for example, following hippocampal sharp-wave events⁴⁹. In the intact brain, responses to unexpected stimuli or movement initiation are often associated with relatively long-lasting (0.5–2 s) LFP shifts, which might be mediated by synchronized AHPs. This slow LFP is often referred to as Bereitschaftspotential⁵⁰, readiness potential or contingent negative variation⁵¹.

During non-rapid eye movement (non-REM) sleep, the membrane potential of cortical neurons periodically shifts (0.5–1.5 Hz) between a hyperpolarized ‘down’ state and a more depolarized ‘up’ (that is, spiking) state⁵² (FIGS 1d,3D). At least part of the cessation of spiking during the down states can be explained by AHPs of the synchronously bursting pyramidal cells in the up state^48,53. The temporally coordinated silent down state of nearby neurons is associated with a positive V_e in infragranular layers and a negative V_e in the supragranular layers (these down states are also known as delta waves^48,54–56). Various mechanisms contribute to these state transitions, including a gradual decrease in extracellular Ca²⁺ concentration and a corresponding decrease in synaptic transmission, inactivation of I_h channels^53,57, and other network effects⁵². As the largest-amplitude up–down shifts of the membrane voltage occur in large layer 5 pyramidal neurons^53,58, it has been suggested that the large voltage shifts in the somata of the synchronously active– silent neurons induce the formation of an extracellular dipole between deep (infragranular) and superficial (supragranular) layers^48,58. Neither interneurons nor the thalamocortical inputs are active during the down state, so that the down state (characterized by delta waves) is a disfacilitatory, non-synaptic event that can be mimicked by synchronous hyperpolarization of nearby pyramidal neurons (FIG. 3E).

Gap junctions and neuron–glia interactions

Direct electric communication between neurons through gap junctions (also known as electrical ‘synapses’)^59–61 can enhance neuronal synchrony^49,62,63. Although gap junctions allow ionic movement across neurons and, therefore, do not involve any extracellular current flow, they can affect neuronal excitability and contribute indirectly to the extracellular field.

Membrane potential changes in non-neuronal cells, such as glia, may also give rise to V_e. Recent studies on neuron–glia interactions have indicated that the glial syncytium may contribute to slow and infraslow (<0.1 Hz) field patterns^1,64,65. These slow LFPs may arise from glia, glia–neuron interactions or from vascular events^66–68.

Ephaptic effects

Neurons are surrounded by a conducting medium — the extracellular space — and can therefore ‘sense’ the electric gradients they generate during neuronal processing. In fact, the effect of gradients brought about by synchronous population activity along cable-like dendrites can be mimicked by appropriate intracellular current injections^69,70. This raises the question of whether the spatiotemporal field fluctuations in the brain are merely an epiphenomenon of coordinated cellular activity or whether they also have a functional ‘feedback’ (or even amplification) role by affecting the discharge properties of neurons⁷¹. That is, do they serve any function for the organism or are they like the heartbeat, a useful diagnostic epiphenomenon? Given the resistivity of the extracellular medium in the mammalian brain and the highly transient nature of spikes, it is unlikely that spikes from individual neurons greatly affect the excitability of nearby neurons through ephaptic coupling. However, the situation is very different when many neurons are simultaneously active, as such synchrony can generate strong spatial gradients in the extracellular voltage. Experiments have shown that small-amplitude, slow-frequency application of extracranial currents (trans-cranial electrical stimulation) has a detectable effect on neuronal activity⁷² and cognitive function⁷³; the small but effective voltage gradients brought about in brain tissue by such external fields are comparable to the voltage gradients produced by population patterns in vivo under physiological conditions^70,74–76. Ephaptic coupling has been shown to affect population activity during hypersynchronous epileptic discharges^77,78. Furthermore, ephaptic feedback may enhance spike– field coherence and bias the preferred spiking phases with respect to the LFP also under physiological conditions^{75,76,79–81}; for example, during hippocampal sharp waves or theta waves^70,76,77.

Neuronal geometry and architecture

All neuron types contribute to the extracellular field, but their relative contribution depends in part on the shape of the cell. Pyramidal cells are the most populous cell type. They have long, thick apical dendrites that can generate strong dipoles along the somatodendritic axis. Such dipoles give rise to an open field, as there is considerable spatial separation of the active sink (or the source) from the return currents. This induces substantial ionic flow in the extracellular medium (FIG. 2). Therefore, neurons that generate open fields, such as pyramidal cells, make a sizeable contribution to the extracellular field. By contrast, spherically symmetric neurons — such as thalamocortical cells — that emanate dendrites of relatively equal size in all directions, can give rise to a closed field⁸². However, a strictly closed field only occurs when several dendrites are simultaneously activated. As this is rarely the case, depolarization of a single dendrite generates a small dipole even in spherically symmetric cells⁸³.

Assuming a homogeneous medium, the two most important determinants of the extracellular field strength are the spatial alignment of neurons and the temporal synchrony (discussed in the next section) of the dipole moments they generate^13,22,84. In cytoarchitecturally regular structures, such as the cortex, the apical dendrites of pyramidal neurons lie parallel to each other and the afferent inputs run perpendicular to the dendritic axis. This geometry is ideal for the superposition of synchronously active dipoles and is the primary reason why LFPs are largest in cortex. In the rodent hippocampus, the somata of pyramidal cells occupy only a few rows. By contrast, in the human hippocampus the cell bodies are vertically shifted relative to each other and form a wider somatic layer⁸⁵. As a result, the source currents from the soma flow in the opposite direction to the sink currents from the dendrites of neighbouring neurons, effectively cancelling each other. This partly explains why the amplitude of the LFP decreases from rat to cat, and from cat to primate^86,87. Another reason why brain size affects the magnitude of the extracellular current is that mammals with smaller brains have smaller pyramidal neurons, which are therefore more densely packed compared to mammals with larger brains⁸⁸, leading to a smaller conductivity σ. Indeed, all LFP patterns have larger amplitude in the mouse brain than in the rat brain⁸⁹.

Another important geometric factor that affects the magnitude of the extracellular current flow is the highly folded nature of the cortex in higher mammals¹⁰. When the cortical sheet bends to form a gyrus, the apical dendrites are pushed closer to each other on the concave side, and current density becomes higher compared to when the apical dendrites occupy the convex side of the curve¹⁶. The influence of tissue curving on the LFP is particularly striking in the dentate gyrus–hippocampus–subiculum axis, where concave and convex bends alternate⁹⁰. In subcortical structures, spatial regularity of neurons and afferents is much less prominent. Nevertheless, afferent fibres from one source may have some asymmetric distribution on spherically symmetric neurons (for example, cortical afferents to the medium spiny neurons of the striatum⁹¹), whose temporally synchronous activity can generate spatially distinct sinks and sources.

Temporal scaling properties

Geometric factors alone cannot fully explain the magnitude of the extracellular current. For example, the cerebellum is a perfectly ordered structure with stratified inputs and a single layer of giant Purkinje neurons, but it generates very small extracellular fields⁹². This is because cerebellar computation is mainly local and therefore does not require the cooperation of large numbers of neurons. However, when synchrony is imposed on the cerebellar cortex from the outside, large-amplitude LFP signals can emerge from cerebellar circuits⁹³. Thus, in addition to cytoarchitecture, a second critical factor in determining the magnitude of the extracellular current is the temporally synchronous fluctuations of the membrane potential in large neuronal aggregates. Synchrony, which is often brought about through network oscillations, explains why different brain states are associated with dramatically different magnitudes of LFP^9–14. A consistent quantitative feature of the LFP is that the magnitude of LFP power (that is, the square of the Fourier amplitude) is inversely related to temporal frequency f, that is, there is 1/fⁿ scaling with n = 1–2 (the exact value of n depends on various factors)^94,95. These features have given rise to much speculation regarding the relationship between network features of the brain and the extracellular signal (see below), although a strict power law behaviour of the LFP is still being debated^94,96–98.

The 1/fⁿ scaling of the LFP power can be primarily attributed to the low-pass frequency filtering property of dendrites^83,99,100. Simulations have shown that in layer 5 pyramidal neurons (FIG. 2a) the effect of a high-frequency local input (100 Hz) to the distal dendrite can be detected extracellularly near the distal dendritic segment, whereas the signal is attenuated approximately 100-fold near the soma. Slower signals (for example, 1 Hz) are attenuated much less. The low-pass filtering effect of a purely passive neuron depends on the distance between the soma and the location of the input, and on the membrane time constant²⁷. This suggests that dendritic morphology is an important factor in frequency filtering and that pyramidal cells, with their long dendrites, are particularly effective low-pass filters. However, as the electrotonic length and input resistance of neurons can be effectively altered by synaptically induced excitatory and inhibitory conductance changes^26,101, the frequency filtering performance of neurons depends not only on the geometric characteristics of the neurons but also on their physiological state. Another frequently cited cause of high-frequency attenuation of the LFP is the capacitive nature of the extracellular medium itself^96,102, although the capacitive and inductive properties of the brain tissue remain a subject of debate^16,24,103.

Network mechanisms also contribute to the 1/fⁿ feature of the power spectrum. In a brief time window, only a limited number of neurons can be recruited in a given volume, whereas in longer time windows the activity of many more neurons can contribute to the LFP, therefore generating larger amplitude LFP at slower frequencies. This frequency dependence is also reflected in the phase coherence–distance relationship, with lower-frequency signals having higher coherence compared to high-frequency signals. Provided that neuronal recruitment occurs within the time constant of an integrating mechanism (for example, NMDA or GABA_B receptors have a slow time constant, whereas AMPA or GABA_A receptors have a fast time constant), the amplitude of low-frequency LFP components will be larger than the amplitude of high-frequency LFP components. Finally, the different network oscillations generated in the cerebral cortex show a hierarchical relationship^5,104,105, often expressed by cross-frequency coupling between the various rhythms^106–111. As the phase of the slower oscillations modulates the power of higher-frequency events (a phenomenon known as phase–amplitude coupling), the duration of the faster events is limited by the ‘allowable’ phase of the slower event. In summary, multiple mechanisms can contribute to the 1/fⁿ power scaling.

Although the phenomenological 1/fⁿ relationship may capture various statistical aspects of brain dynamics at longer timescales, it should be emphasized that most neuronal computation takes place in short time windows (from tens to hundreds of milliseconds). The spectral properties of such short time windows strongly deviate from the scale-free frequency–power distribution and are often dominated by oscillations or sensory input-triggered ‘evoked’ or ‘induced’ events. These stimulus-driven, transient LFP events are the physiologically relevant time windows from which one aims to infer neuronal computation from the mean field behaviour of neuronal populations¹³.

The role of volume conduction in V_e

The electric field specifies the forces acting upon a charged particle. The field is defined at every point of space from which one can measure a force ‘felt’ by an electric charge, and it can be transmitted through volume (for example, through brain tissue); a phenomenon known as volume conduction. The origin of the volume-conducted field is the return currents of the dipoles^18,22,83. The extent of volume conduction depends on the intricate relationships between the current dipole and the features of the conductive medium^84,112. Consequently, some LFP patterns can be recorded far away from the source, whereas others remain relatively local. The most robust demonstration of the importance and extent of volume conduction is that return currents from active dipoles in brain tissue can be measured on the scalp by electric recording methods (BOX 1).

Assuming that conductivity in the brain is purely ohmic, the V_e induced by a current dipole depends on the magnitude and location of the current source, and on the conductivity of the extracellular medium. In turn, conductivity in the medium depends on the degree of isotropy and homogeneity of the medium and is therefore a function of a number of factors, including the geometry of the extracellular space. The relationship between V_e and the current source density (CSD) J (measured in A m⁻²) at a particular point of brain tissue is given by Maxwell’s equations of electromagnetism, that in their simplified form (that is, when the magnetic contributions can be neglected) dictate ∇(σ⃗V_e) = −∇ J⃗, where σ⃗ (amplitude measured in S m⁻¹) is the extracellular conductivity tensor. The properties of σ⃗ crucially affect the waveform and functionality of the spatiotemporal V_e deflections. Assuming that the extracellular milieu can be satisfactorily described by a purely homogeneous and isotropic ohmic conductivity σ, V_e is governed by Laplace’s equation ∇²V_e = 0, with the boundary condition along a cable-like source described by σ V_e = J (with J as the transmembrane current density). For a single point source in an unbounded isotropic volume conductor, the solution is V_e = I/4πσr, in which I (unit, A) is the current amplitude of the point source and r (unit, m) is the distance from the source to the measurement. Multiple current sinks and sources then combine linearly by the superposition principle. Conceptually, the point-source equation is key to computing the extracellular potential in response to any transmembrane current. It also follows that the transmembrane voltage, often used in intracellular versus extracellular comparisons, is a relatively poor estimator of the LFP, whereas the transmembrane current is a more reliable estimator⁹⁹. The above calculations assume that the extracellular medium is homogeneous and isotropic (that is, a constant σ). Measurements of the extracellular medium in the relevant frequency range (<10 kHz) have not yet fully resolved this issue, with some experiments concluding that the extracellular medium is anisotropic and homogeneous^24,113, and others suggesting that it is strongly anisotropic, inhomogeneous^68,103,114 and may even possess capacitive features^91,96,97.

Striking examples of volume-conducted events have been described in hemispherectomized patients over the missing hemisphere¹¹⁵. Furthermore, auditory-evoked brain stem responses recorded over the scalp are a clinically used diagnostic tool that is based on volume conduction¹¹⁶. Volume conduction clearly poses problems for the interpretation of the functional meaning of the relationship between signals recorded from different brain locations. For example, two nearby dipoles with different orientations can produce volume-conducted fields at distant sites. When the coherence between signals recorded at these distant sites increases (for example, as a function of behaviour), this may be falsely interpreted to reflect some ‘dynamic’ or ‘functional coupling’ between the circuits residing at the sites of the recording electrodes, even though the coherence increase was brought about by the temporal shifts between the two close dipoles¹¹⁷. For these reasons, verification of the local nature of the signal always requires the demonstration of a correlation between the LFP and local neuronal firing.

The inverse problem of LFP

Extracellular signals provide information about the collective behaviour of aggregates of neurons, particularly with regard to the temporal scales of their activity. However, the same macroscopic extracellular signal can be generated by diverse cellular events. Thus, a seemingly similar theta oscillation in the hippocampus and neocortex may be brought about by different elementary mechanisms. A common obstacle in interpreting the ‘mean field signal’ is the ‘inverse problem’^16,118. The inverse problem arises when attempting to infer the microscopic variables from the macroscopic ones — in this case, inferring the characteristics of the primary current dipoles from the spatiotemporal profile of the volume-conducted field. The inverse problem is commonly dealt with by first solving the ‘forward problem’ — deriving macroscopic variables from their elementary, causal constituents — and then using the established relationships between microscopic and macroscopic variables to gain insight into the microscopic events from the macroscopic patterns. The first step in this process is to identify the contribution of the suspected synaptic and non-synaptic mechanisms of the LFP by correlating the macroscopic events (that is, the LFP) and the microscopic events^119,120,122. The second step is to experimentally recreate the LFP from its primary constituents, such as synaptic currents and the spiking patterns of various neuron types. The technical means required to create such LFP patterns are now available (FIG. 3E). Alternatively, synthetic mean fields can be generated in network models of neurons in which events in the different domains of the neurons are timed on the basis of experimentally observed temporal patterns.

Localizing the current sinks and sources: CSD analysis

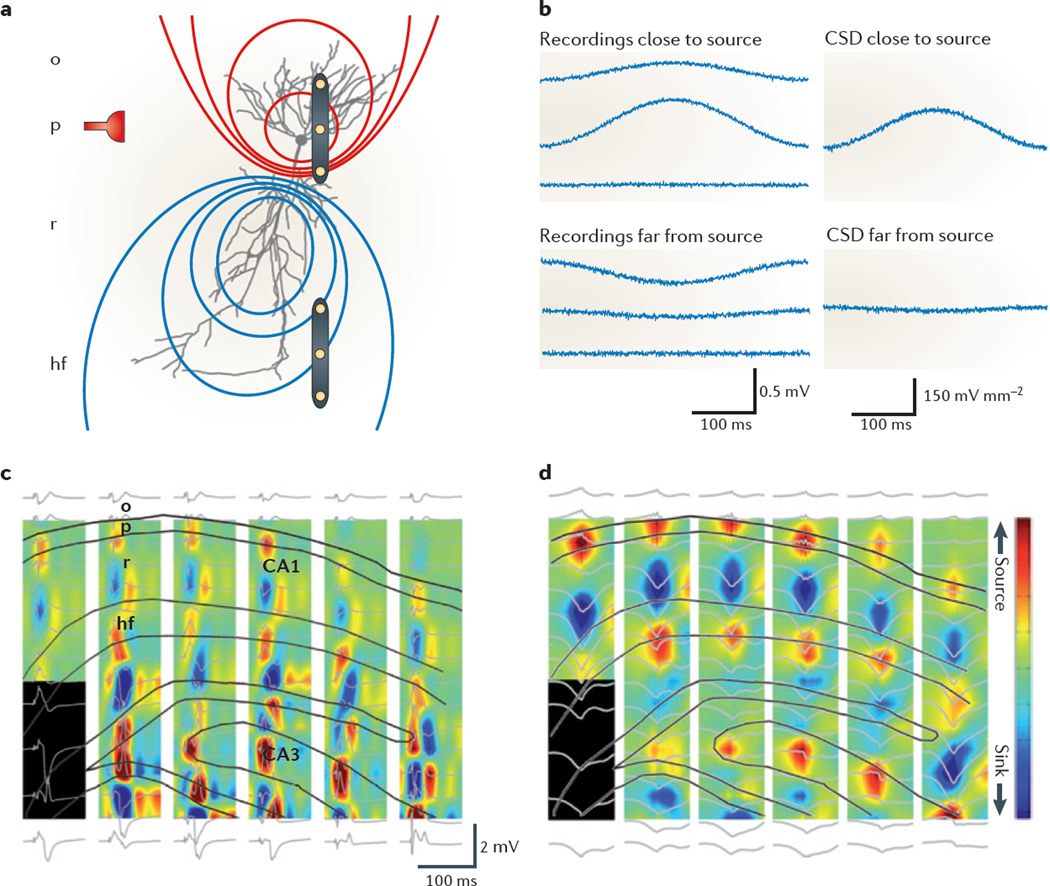
In deciphering the location of the current sources (that is, cations flowing from the intracellular space to the extracellular space) and sinks (that is, cations flowing into the cell) that give rise to the LFP, the concept of CSD is useful. CSD is a quantity that represents the volume density of the net current entering or leaving the extracellular space^113,121. Consider a distant current source relative to three linearly and equally spaced recording sites in a homogenous volume (FIG. 4). Each electrode will measure some contribution to the field from the distant source, and the voltage difference between the middle and side electrodes will be small. As a consequence, the difference between the ‘voltage differences per distance’ (that is, the second spatial derivative of V_e, a vector with units of V m⁻²) between the middle and side electrodes is small; an indication that the field can be attributed to a distant source. By contrast, if the three electrodes span the location of the current-generating synapse or neuron group, the voltage at the three recording sites will be unequal and the difference magnitude of this derivative will be large; an indication of the local origin of the current. The current flow between two recording sites can be calculated from the voltage difference and resistivity using Ohm’s law, provided that information about the conductance (which is inversely proportional to resistivity) of the tissue is available (0.15–0.35 Ω m in brain tissue^68,103,113). The conductance is a factor of both conductivity and the specific geometry of volume. Using high-density recording probes to monitor the LFP, it is possible to precisely determine the maximum CSD and therefore the exact location of the current sink (or source).

Figure 4. Identifying current sources.

a | A current source–sink dipole, embedded in a homogeneous and isotropic conductive medium, that is induced by barrage-like inhibitory input (shown by the red symbol) impinging on the perisomatic region. Lines show the iso-potentials (red, positive; blue, negative). A triplet of linearly and equally spaced recording electrodes (shown in yellow) is located near the soma (top), that is, close to the current source, and another is located far from the current source. b | V_e traces (left panels) measured at the three equally spaced locations relative to an ideal infinite (reference) site. The middle trace in the top panel is from the electrode positioned closest to the soma. The voltage contribution induced by the active dipole decays in the medium as the inverse square of the distance (compare with FIG. 2a). The current source density (CSD) traces (right panels) are calculated from the voltage traces. Although dipole-induced V_e can be measured far from the source, CSD is spatially confined and can therefore help to identify the anatomical location of the dipole. c | Simultaneous recordings from 96 sites (six shanks (represented by columns in the figure) with 16 recording sites each (LFP traces shown in grey)) in a behaving rat. Simultaneously recorded evoked field responses in the CA1–dentate gyrus axis of the rat hippocampus (black lines show the outline of the layers) in response to electrical stimulation of entorhinal afferents are shown. Such trisynaptic activation of CA1 pyramidal cells is reflected as negative LFP (and sink, blue) in the apical dendritic layer (stratum radiatum, r). The black rectangle indicates missing channels. d | A CSD map of average spontaneously occurring sharp waves. Note the nearly identical distribution of sinks and sources in CA1 during the evoked responses and sharp waves, supporting the idea that sharp waves reflect CA3-induced depolarization of the apical dendrites of CA1 neurons. Selective activation of known afferents thus can be used to ‘calibrate’ the locations of sinks and sources, and relate them to the CSD distribution of spontaneously occurring LFP events. hf, stratum lacunosum-moleculare; o, stratum oriens; p, pyramidal layer. Parts c and d courtesy of J. Csicsvari, Institute of Science and Technology, Austria, and D. Sullivan, New York University, Langone Medical Center, USA.

Interpreting current density

Unfortunately, it is not possible to conclude using CSD measurement alone whether, for example, an outward current close to the cell body layer is due to active inhibitory synaptic currents or reflects the passive return current of active excitatory currents impinging along the dendritic arbor. The missing information may be obtained by selectively stimulating the various anatomically identified inputs to the recorded circuit (FIG. 4). This process helps to attribute the sinks (and sources) to the known sources of synaptic inputs^106,122. In addition to anatomical knowledge, simultaneous intracellular recordings from representative neurons within the population responsible for the generation of the LFP may be required. Alternatively, it is possible to record extracellularly from identified pyramidal cells and inhibitory interneurons in the same volume of tissue and use the spike–field correlations to determine whether, for example, a local current is an active hyperpolarizing current or a passive return current from a more distant depolarizing event. Unfortunately, ambiguity may still remain if the sinks and sources are generated by a non-synaptic mechanism rather than by a synaptic mechanism.

Somatic hyperpolarization brought about by the activity of perisomatic basket neurons^44,123 also generates a voltage gradient between the soma and dendrites (inhibitory dipole; FIGS 2b,c,4a,b). As dendritic excitation and somatic inhibition result in the same direction of current flow, the excitatory and inhibitory return currents will superimpose in the extracellular space, resulting in large-amplitude LFPs. Although strong somatic inhibition can enhance the magnitude of the LFP, it may at the same time ‘veto’ the occurrence of action potentials in pyramidal cells. This complex relationship is the reason why large-amplitude extracellular current flow may be associated with strong spiking, moderate spiking or no spike output at all from the pyramidal neurons. As a result, the measured correlation between LFP and spiking activity can vary substantially even within a small volume. Such variable coupling between LFP and unit firing may be one of the sources of the controversy regarding the contribution of LFP versus spikes to the functional MRI (blood oxygen level-dependent (BOLD)) signal because often there is a strong correlation between LFP power in the gamma-frequency band and spiking activity^23,124.

The CSD method described above is, in principle, applicable to any other a priori identified rhythmic or transient LFP event. However, it is important to emphasize that conventional one-dimensional (typically along the somatodendritic axis) estimation of CSD is possible only in a situation in which the LFP varies little in the lateral direction, that is, within the same layer. The assumption is often not satisfied when the layers curve. In this case, two-dimensional estimation of the CSD, using equally spaced high-density electrodes in both vertical and horizontal directions, is required^113,125. Further complications arise when several dipoles are involved in the generation of LFP patterns, particularly when these dipoles are temporally disparate, as is the case in the generation of most cortical patterns^48,126,127. Nevertheless, the above strategies have been successfully used in the identification of evoked and spontaneous LFP patterns in multiple brain regions^{121,122,128,129}. The ever-increasing density of recording sites on silicon-based recording probes¹³⁰ in combination with optogenetic tools¹³¹ will help us to disentangle the contribution of multiple dipoles.

Spike contribution to the LFP

As noted above, any transmembrane current contributes to the LFP, including currents that are generated by action potentials. The action potential includes not only the ‘spike’ itself but also spike-induced AHPs, which have durations and magnitudes that vary for different neuron types and that can change as a function of brain state¹³². The spike contribution to the LFP has important implications. First, increased spiking generates a broad-frequency spectrum with a power distribution that depends on the composition of the active cell types^{95,98,111,133,134}. Second, both increased spike frequency and synchrony increase spectral power, particularly in the higher-frequency (>100 Hz) bands^135,136 (FIG. 5). However, when spike AHPs are also considered, the contribution of action potentials may be substantial in the lower-frequency range as well, even in the absence of synaptic transmission¹¹⁹. Thus, increased power in the higher-frequency bands can be regarded as an index of spiking synchrony. Third, high-frequency power has a restricted spatial component: it increases in layers with a high density of cell bodies^111,137 and axon terminals. Fourth, high-frequency power, which largely reflects spiking activity, co-varies with LFP components that emanate from postsynaptic potentials and other non-spike-related membrane voltage fluctuations^{18,22,23,86,98,100–112,133,136}. Fifth, the high-frequency power can be phase-locked to lower-frequency oscillations; this occurs because it is largely the phase-locked spiking neurons that generate the rhythmic extracellular currents^{22,23,86,111,112,133,136}. Last, the high-frequency power of extracellular LFP provides indirect access to the spike outputs of neurons^{4,111,124,138}. Together, these aspects show that spike ‘contamination’ of the LFP should be regarded as good news, in that high-frequency LFP power can provide a ‘proxy’ for the assessment of neuronal outputs. The ‘mesoscopic’ information provided by the high-frequency band of the LFP is therefore an important link between the macroscopic-level EEG and the microscopic-level spiking activity of neuronal assemblies.

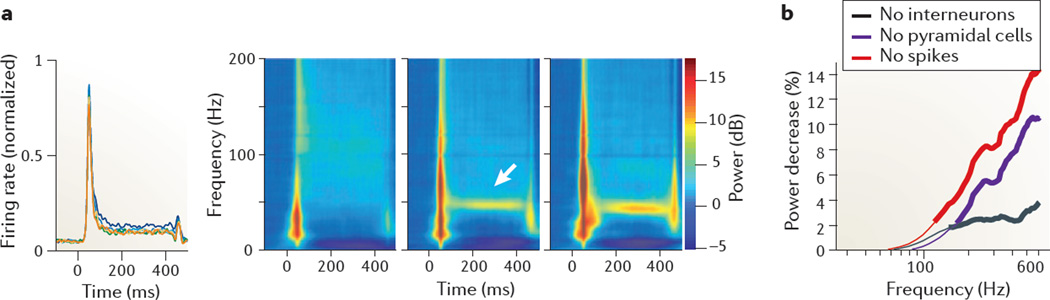
Figure 5. Spike contribution to the LFP.

a | Average multiunit recording of the visual cortex of a monkey during presentation of a static grating (0 to 400 ms) at six different sizes, shown in different colours (left panel). Also shown are time–frequency–power difference plots demonstrating the difference between baseline power (in dB) and power in response to increasing size stimuli (right panel). Note the increase in wide-band power (at ~50 ms) with increased firing and synchrony of units after stimulus onset. The arrow indicates sustained gamma frequency oscillation. b | The effect of local field potential (LFP) ‘de-spiking’ on spectral power. The figure shows the percentage change of power at different frequencies after de-spiking the LFP. Thick lines indicate the frequencies at which there was a significant difference between the original LFP power and the power of the LFP after removing interneuron spikes (No interneurons), pyramidal cell spikes (No pyramidal cells) or all spikes (No spikes). Part a is reproduced from REF. 162. Part b is reproduced, with permission, from REF. 111 © (2012) Society for Neuroscience.

Conclusions and future directions

Electric currents from all excitable membranes contribute to the extracellular voltage. These currents emerge mainly from synaptic activity but often with substantial contributions from Ca²⁺ spikes and other voltage-dependent intrinsic events, as well as from action potentials and spike afterpotentials. The two most important factors contributing to the LFP are the cellular-synaptic architectural organization of the network and synchrony of the current sources. The extracellular potential can be reconstructed from simultaneous monitoring of several current source generators across the neuronal membrane, provided that sufficient details are known about the contributing sources and the extracellular milieu. This forward reconstruction is theoretically possible because the physical processes underlying the generation of V_e are mostly understood. The forward reconstruction of the LFP is accelerated by advancements in microelectrode technology and other new methods, and developments in computational modelling. Reconstruction of the LFP signal from the measured current sources and sinks can, in turn, provide insights into resolving the inverse problem, that is, the deduction of the microscopic processes from the macroscopic LFP measurements.

A practically important application of the forward–inverse relationship would be the reconstruction of cell assembly sequences from the constellation of the LFP. Cell assemblies can be defined as a temporal coalition of neurons — typically within gamma cycles — the collective action of which can lead to the discharge of a downstream ‘reader’ neuron¹³⁹. Such assemblies (or ‘neural letters’) are organized into assembly sequences (or ‘neural words’) by the slower rhythms. Although the temporal organization of neuronal dynamics can be effectively inferred from the cross-frequency coupling of the various brain rhythms, additional steps are required to reveal the spiking content of the LFP patterns. In the intact brain, spiking neurons are embedded in interconnected networks and may be influenced by the local electric field through ephaptic effects. Therefore, the output spikes of the cell assemblies within and across networks are transformed into spatially distributed transmembrane events through synaptic activity (‘synapsembles’)¹³⁹. Of course, these transmembane events are responsible for the LFP. We suggest that as the composition of spiking assemblies varies over time, the spike patterns induce unique patterns of LFPs, which vary from moment to moment (for example, from one gamma cycle to the next). Recording the LFP from a sufficiently large and representative neuronal volume with sufficiently high spatial density may therefore provide access to the time-evolving synaptic currents brought about by the spiking assemblies (FIG. 6; Supplementary information S1 and S2 (movies)). Such synapsembles¹³⁹, reflected indirectly by the LFP vectors, can be as informative about the encoded information as the spiking cell assemblies themselves^140–142. In support of this idea, it has been shown that during cognitive tasks, the spatial distribution of spectral power varies in a task-relevant manner^{98,134,143–145}. We foresee that the spatially resolved, wide-band LFP signal, which contains information about both afferent patterns and assembly outputs, may turn out to be the most useful signal for understanding neuronal computations^11,13,135.

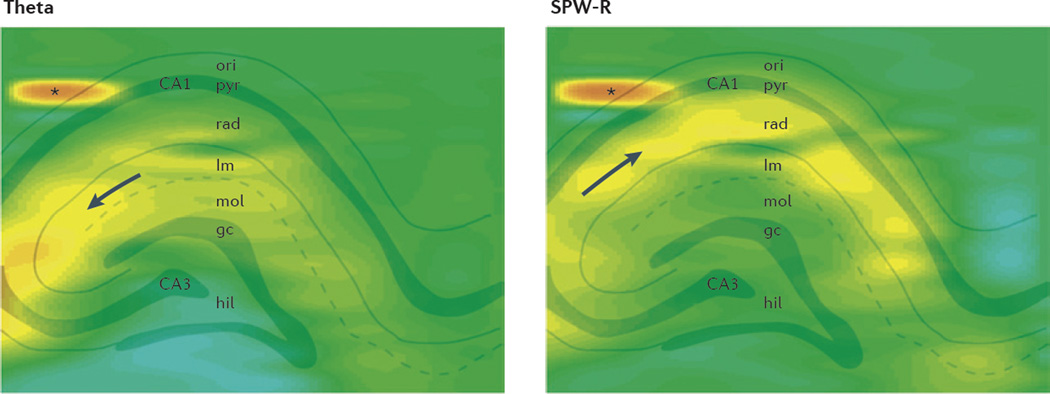
Figure 6. Spikes are embedded in unique synapsembles and spatially distributed LFP.

Spike-triggered averages of the local field potential (LFP) in the hippocampus during exploration (left panel) and sleep (right panel). During exploration, spikes were sampled while the rat ran on a linear track for a water reward; during sleep, spikes were sampled during sharp wave-ripples (SPW-R). Recordings were made by an eight-shank (300 µm intershank distance), 256-site silicon prove (32 recording sites on each shank, linerarly spaced 50 µm apart). The LFP was smoothed both within and across shanks. The LFP was triggered by the spikes of a fast-firing putative interneuron in CA1 stratum oriens (ori; shown by a star). Both panels show a 100 µs snapshot of the LFP map at the time of the spike occurrence. Note that during exploration (left panel), the spike is associated with synaptic activity (negative wave, hot colours) mainly in the stratum lacunosum-moleculare (lm; shown by an arrow) and the dentate molecular layer (mol), indicating entorhinal cortex activation. During sleep (right panel), activity arises in CA3 and invades the CA1 stratum radiatum (rad; shown by an arrow). We propose that such LFP ‘snapshots’ reflect unique constellations of cell assemblies responsible for the discharge of the neuron. The LFP map changes characteristically with time (see Supplementary information S1 and S2 (movies)). We suggest that the time-evolving constellation of the LFP map or vector reflects a unique distribution of postsynaptic potentials (that is, synapsembles¹³⁹) brought about by the evolving spike assemblies within and upstream of the hippocampus. Sufficiently high-density LFP recordings can therefore be informative of the evolving cell assemblies that bring about the LFP changes. gc, granule cell layer; hil, hilus; pyr, pyramidal layer. Figure courtesy of A. Berényi and Z. Somogyvári, New York University, Langone Medical Center, USA.

Glossary

Sink

By convention, a site on the neuronal membrane where positive charges enter the neuron.

Electroneutrality

The phenomenon that, owing to charge conservation, at any given point in time the total charge entering and leaving the cell across all of its membrane equals zero.

Sources

Locations along the neuronal membrane where positive charge flows out of the neuron. For negative charge, the location of sinks and sources is inverted.

Return current

A loop current that flows in the opposite direction to an active sink or source.

Dipole

An ideal electric dipole is defined by two charges of opposite polarity with infinitely small separation, such that the product of the charge times the distance r separating them remains finite. The electric potential of a dipole falls off as 1/r².

Equilibrium potential

The voltage difference between intracellular and extracellular space of a neuron when the net ionic flux across the membrane equals zero.

I_h currents

Currents flowing through hyperpolarization deinactivated cyclic nucleotide-gated channels.

I_T currents

Low-threshold (hyperpolarization-induced) transient Ca²⁺ currents, which often lead to burst firing.

Resonance

A property of the neuronal membrane to respond to some input frequencies more strongly than others. At the resonant frequency, even weak periodic driving can produce large-amplitude oscillations.

Silicon probes

Multiple-site recording electrodes for high spatial density monitoring of the extracellular field. The recordings sites can record Ve along one, two or even three orthogonal axes.

Ephaptic coupling

The effect of the extracellular field on the transmembrane potential of a neuron.

Open field

When the sink (or the source) is substantially spatially separated from the return currents of the dipole.

Closed field

When the sink (or the source) is minimally spatially separated from the return currents of the dipole.

Power law (of LFP)

The power law of LFP describes a relationship between the amplitude of the extracellular signal and its temporal frequency. A descending straight line on the log–log plot (power versus frequency) would be an indication of a power law that scales as 1/fⁿ.

Low-pass frequency filtering

A process by which the frequency components of a signal beyond a cutoff frequency are increasingly attenuated, typically owing to a serial capacitance (for example, the bi-lipid membrane).

Phase–amplitude coupling

The power of a faster oscillation is phase-modulated by a slower oscillation.

Ohmic

Electrical current flow through a purely resistive milieu. The extracellular cytoplasm is primarily ohmic in the 1–10,000 kHz frequency range.

Current source density

(CSD). The current source density reflects the rate of current flow in a given direction through the unit surface (unit, A m⁻²) or volume (unit, A m⁻³).

Anisotropic

Ansiotropic tissue can conduct electricity in a direction-dependent manner.