Joint detection of copy number variations in parent-offspring trios

Abstract

Motivation: Whole genome sequencing (WGS) of parent-offspring trios is a powerful approach for identifying disease-associated genes via detecting copy number variations (CNVs). Existing approaches, which detect CNVs for each individual in a trio independently, usually yield low-detection accuracy. Joint modeling approaches leveraging Mendelian transmission within the parent-offspring trio can be an efficient strategy to improve CNV detection accuracy.

Results: In this study, we developed TrioCNV, a novel approach for jointly detecting CNVs in parent-offspring trios from WGS data. Using negative binomial regression, we modeled the read depth signal while considering both GC content bias and mappability bias. Moreover, we incorporated the family relationship and used a hidden Markov model to jointly infer CNVs for three samples of a parent-offspring trio. Through application to both simulated data and a trio from 1000 Genomes Project, we showed that TrioCNV achieved superior performance than existing approaches.

Availability and implementation: The software TrioCNV implemented using a combination of Java and R is freely available from the website at https://github.com/yongzhuang/TrioCNV.

Contact: ydwang@hit.edu.cn

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Copy number variations (CNVs) are defined as changes in the copy number (gain or loss) of large genomic segments, which can be transmitted from parents or arise de novo. CNVs have been shown to play an important role in human morbidities, including neuropsychiatric disorders (Cook and Scherer, 2008; Gilissen et al., 2014; Levy et al., 2011) and cancers (Beroukhim et al., 2010).

CNVs have been traditionally detected using fluorescent in situ hybridization, array comparative genomic hybridization and SNP microarray (Alkan et al., 2011). Recently, next generation sequencing (NGS), especially whole genome sequencing (WGS), has become extremely powerful in detecting CNVs comprehensively, being able to identify CNVs that are often missed by array-based assays. On the other hand, NGS-based approaches present substantial challenges for CNV calling. They usually work by mapping sequencing reads to the reference genome and subsequently identifying discordant mapping signatures putatively caused by CNVs. As summarized in Alkan et al. (2011) and Medvedev et al. (2009), there have been four main categories of mapping signatures that can be leveraged to detect CNVs from WGS data: (i) read depth (RD), (ii) paired-end mapping (PEM), (iii) split read (SR) and (iv) a combination of the above. In addition, CNVs can be detected by using the de novo assembly approach, which first reconstructs contigs from short sequencing reads and then compares the assembled contigs with the reference genome sequence to identify the regions with discordant copy numbers (Iqbal et al., 2012).

Most existing CNV detection approaches focus on one single sample (individually) or multiple samples without considering the inter-sample relatedness (Handsaker et al., 2011; Hormozdiari et al., 2011). Naturally, when genetic relatedness is known for multiple individuals, effective utilization of this information could potentially improve CNV detection accuracy. A common relevant study design with known inter-individual relationships is sequencing parent-offspring trios. Indeed, the parent-offspring trio design has been shown to be powerful in identifying disease-associated genetic variants for both common and rare diseases (Samocha et al., 2014; Zhu et al., 2015). For trio-based NGS data, a joint modeling approach leveraging the parent-offspring relationship can potentially improve detection accuracy for CNVs, as the same principle has been successfully applied to improve detection accuracy for inherited and de novo single nucleotide variants and INDELs from NGS data (Chen et al., 2013; Li et al., 2012; Liu et al., 2014; Peng et al., 2013; Ramu et al., 2013; Wei et al., 2014) as well as that for CNVs from SNP array data (Chu et al., 2013; Wang et al., 2008). Importantly, the joint modeling approach allows for an explicit identification of de novo mutations that have been increasingly recognized to play critical roles in many human diseases (Malhotra et al., 2011; Sebat et al., 2007; Xu et al., 2008). To our knowledge, there have been no approaches for calling CNVs from trio WGS data in a trio-aware manner. Due to the popularity of trio sequencing in both research and clinical settings, such a tool is urgently needed.

In this study, we presented TrioCNV to fulfill this purpose. First, we modeled read depth signal with negative binomial regression to accommodate over-dispersion and considered GC content and mappability bias. Second, we leveraged parent-offspring relationship to apply Mendelian inheritance constraint while allowing for the rare incidence of de novo events. Third, we used a hidden Markov model (HMM) by combining the two aforementioned models to jointly perform CNV segmentation for the trio. We applied TrioCNV to a simulated trio and a WGS trio from 1000 Genomes Project (1000GP) to demonstrate its performance and strength over existing approaches.

2 Methods

2.1 Workflow

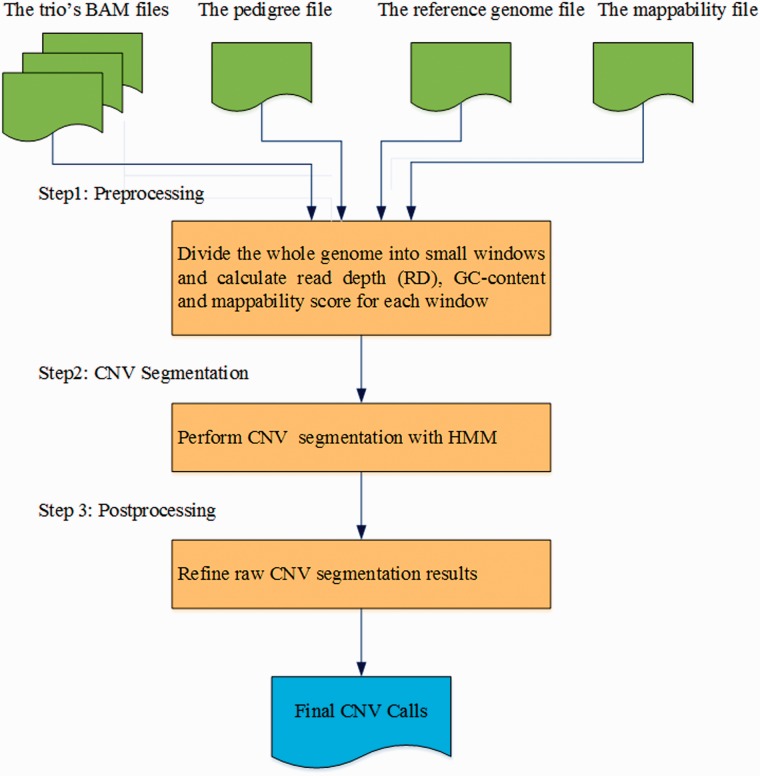
The workflow of TrioCNV is illustrated in Figure 1. There are three main steps. The preprocessing step extracts the information needed for building the model from trio WGS data. The CNV segmentation step performs raw CNV inference using an HMM. The postprocessing step refines raw segmentation results and outputs final CNV calls.

Fig. 1.

. The workflow of TrioCNV. TrioCNV takes three BAM files of a trio (one for each individual), a pedigree file, a reference genome file (FASTA format) and a mappability file (BigWig format) as input, and generates a tab-delimited file containing final CNV calls

2.2 Data preprocessing

We split whole genome into non-overlapping, contiguous windows with a predefined size (default 200 bp), and then obtained RD, GC content and mappability score for each window for all three samples of the trio. RD was computed by counting the number of mapped reads (a minimum read mapping quality can be specified) that start within the window. GC content was computed as the fraction of G+C nucleotides within the window in the reference genome sequence. Mappability score was computed as the average of all positions’ mappability scores within the window. The mappability file used in this study was obtained from http://hgdownload.cse.ucsc.edu/goldenPath/hg19/encodeDCC/wgEncodeMapability/wgEncodeCrgMapabilityAlign100mer.bigWig. The k-mer length for the mappability file is recommended to be approximately equal to the length of the sequencing reads. Mappability files for different k-mer lengths can be downloaded from UCSC Genome Browser or calculated by specific tools (Derrien et al., 2012; Koehler et al., 2011; Lee and Schatz, 2012).

2.3 HMM for CNV segmentation

We used a HMM to simultaneously segment the three genomes of a trio into regions of different copy number statuses. A triplet of RD, GC content and mappability score for each window of the three samples was used as the input for this step. For each sample, we defined five discrete copy number states for each window, representing two-copy deletion, one-copy deletion, normal, one-copy duplication and multiple-copy duplication, respectively. To jointly model the three samples, each hidden Markov state was associated with a set of possible copy number states at the window, for all three samples, resulting in a total of 125 possible copy number state combinations as hidden Markov states.

2.3.1 Emission probability

We interpreted RD as HMM’s emission. Theoretically, RD follows a Poisson distribution with the mean proportional to the copy number in the absence of systematic bias. However, the Poisson assumption fails in real sequencing data due to various biases, among which GC content and mappability are particularly important (Teo et al., 2012). There is a nonlinear correlation between RD and GC content, and an approximately linear correlation between RD and mappability score. To accommodate over-dispersion and account for both the GC content and mappability biases, we used the more dispersed negative binomial regression to model the emission probability distribution, in a different way from existing negative binomial emission models (Backenroth et al., 2014; Mccallum and Wang, 2013; Szatkiewicz et al., 2013). We first grouped all windows into 101 bins (GC = 0, 1, …, 100%) by GC content, and then used the negative binomial regression to model the relationship between RD and mappability score in each bin (see Equations 1 and 2).

$$p(o_t|z_t=i,g_t=j)\sim NB({\mu }_{i,j},{\theta }_{i,j}),$$ (1)

$${\mu }_{i,j}=\exp ({\alpha }_{i,j}+{\beta }_{i,j}{m}_t),$$ (2)

where o_t denotes RD, z_t copy number state, g_t GC content, m_t mappability score in tth window, µ_i,j RD’s mean, α_i,j and β_i,j the regression coefficients and θ_i,j the over-dispersion parameter given copy number i in the jth GC bin.

We estimated the parameters for each GC bin of a sample separately. Since presumably only a small portion of an individual human genome harbors CNVs, most windows for a given sample should have the normal state. After removing windows with outlier RDs, those windows containing CNVs or strong noises were very likely to have been excluded, and the remaining windows can be used to estimate all unknown parameters at the normal state. In this step, GC bins with extremely low (i.e. <0.3) or high (i.e. >0.7) GC content were ignored, because these GC bins having extremely variable RDs can affect accuracy of parameter estimation. In addition, we ignored those GC bins with insufficient data, which similarly can have an adverse effect. Finally, we used the maximum likelihood approach implemented in the R package MASS to estimate the unknown parameters α_2,j, β_2,j, and θ_2,j; then μ_2,j can be solved from α_2,j, β_2,j and m_t.

After estimating the unknown parameters at normal state, the unknown parameters for the other four copy number states can be calculated according to the parameters of the normal state, as shown in Equations (3) and (4), where ε is a tuning parameter (ε is set to 0.1 in this study).

$${\theta }_{i,j}=\{\begin{array}{l}\frac{i}{2}{\theta }_{2,j}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}i\ne 0\\ \epsilon {\theta }_{2,j}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}i=0\end{array}$$ (3)

$${\mu }_{i,j}=\{\begin{array}{l}\frac{i}{2}{\mu }_{2,j}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}i\ne 0\\ \epsilon {\mu }_{2,j}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}i=0\end{array}$$ (4)

Thus, given RD, GC content and mappability score at one window, the probability of observing a particular RD can be calculated by Equation (5).

$$p(o_t|z_t=i,g_t=j,m_t=m)={\left(\frac{{\theta }_{i,j}}{{\theta }_{i,j}+{\mu }_{i,j}}\right)}^{{\theta }_{i,j}}\frac{\Gamma \left(o_t+{\theta }_{i,j}\right)}{\Gamma (o_t+1)\Gamma ({\theta }_{i,j})}{\left(\frac{{\mu }_{i,j}}{{\theta }_{i,j}+{\mu }_{i,j}}\right)}^{O_t}$$ (5)

Overall, the HMM’s emission probability at one window can be defined as Equation (6).

$$p(o_{t,f},o_{t,m},o_{t,o}|z_{t,f},z_{t,m},z_{t,o},g_t,m_t)={\displaystyle \prod _{k\in \{f,m,o\}}p(o_{t,k}|z_{t,k},g_t,m_t)}$$ (6)

2.3.2 Transition probability

For a trio, we assume that each parent’s copy number state transition is independent of other two samples (assuming unrelated parents). Intuitively, adjacent windows are likely to share the same copy number state. Therefore, for each parent, the copy number state transition probability was chosen such that a lower probability was assigned to the transition to a different state and a higher probability to the transition to itself (i.e. no change). Thus, the copy number state transition matrix A = (a_i,j), A∈$\mathbb{R}$^5 × 5 from the t − 1th window to the tth window can be specified as Equation (7). The specification of p is very robust, and a smaller value can be assigned to p for low-coverage data and a larger value for high-coverage data.

$$a_{i,j}=\{\begin{array}{l}p \text{if\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}}i\ne j\\ 1-4p\text{\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}if\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}}i=j\end{array}$$ (7)

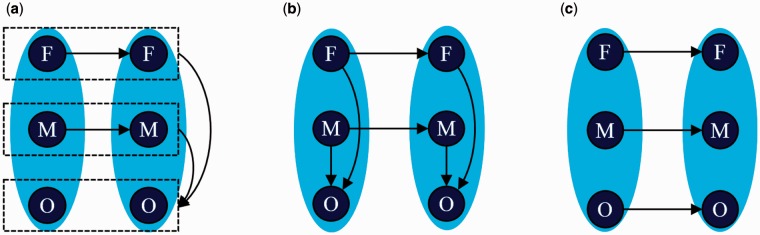
The offspring’s copy number state either follows Mendelian inheritance pattern or, more rarely, is consistent with a de novo event. We considered four different combinations of inheritance patterns at two consecutive windows separately (Fig. 2).

Fig. 2.

. Schematic transition diagrams of the HMM used in TrioCNV. (a) Represents the copy number state transitions between two consecutive windows that follow Mendelian inheritance and the transitions are able to happen; (b) represents the copy number state transitions between one window that follow Mendelian inheritance and one window that is de novo event; (c) represents the copy number state transitions between two groups of windows that are de novo events, or the copy number state transitions between two groups of windows that follow Mendelian inheritance but the transitions are impossible to happen

If the copy number states at two consecutive windows both follow Mendelian inheritance pattern, then the offspring’s copy number state transition depends on the parents’ copy number state transitions. To model this relationship, we introduced two-marker copy number inheritance matrix B = (b_{f,f ′,m,m′,o,o′}), B∈$\mathbb{R}$^{5 × 5×5 × 5×5 × 5} proposed in Wang et al. (2008), representing the conditional probability of observing the offspring’ transition from o to o′ given the father’s transition from f to f ′ and the mother’s transition from m to m′. Therefore, the final transition probability of HMM at tth group of windows can be calculated as Equation (8).

$$p(z_{t,f}=f\prime ,z_{t,m}=m\prime ,z_{t,o}=o\prime |z_{t-1,f}=f,z_{t-1,m}=m,z_{t-1,o}=o)=a_{f,f\prime }{a}_{m,m\prime }{b}_{f,f\prime ,m,m\prime ,o,o\prime }$$ (8)

If the copy number state at one window is consistent with de novo event and the copy number state at the other window follows Mendelian inheritance pattern, these two windows are treated independently. To model this relationship, we introduced single-marker inheritance probability matrix C = (c_f,m,o), C∈$\mathbb{R}$^{5 × 5×5} proposed in Chu et al. (2013) that extends the one in Wang et al. (2008) by incorporating an additional parameter representing the probability of a de novo mutation. This matrix gives conditional probabilities of the total copy number of the offspring given the total copy numbers of the father and the mother. Therefore, the final transition probability of HMM at tth group of windows can be calculated as Equation (9).

$$p(z_{t,f}=f\prime ,z_{t,m}=m\prime ,z_{t,o}=o\prime |z_{t-1,f}=f,z_{t-1,m}=m,z_{t-1,o}=o)=a_{f,f\prime }{a}_{m,m\prime }{c}_{f,m,o}{c}_{f\prime ,m\prime ,o\prime }$$ (9)

If the copy number states at two consecutive windows are both consistent with de novo events or two consecutive windows both follow Mendelian inheritance pattern, but not all copy number state transitions are possible to happen between the two, the offspring’s copy number state transition is independent of the parents’ copy number state transitions, and the offspring’s transition probability can be calculated as the parents’. The final transition probability of HMM at tth group of windows can be calculated as Equation (10).

$$p(z_{t,f}=f\prime ,z_{t,m}=m\prime ,z_{t,o}=o\prime |z_{t-1,f}=f,z_{t-1,m}=m,z_{t-1,o}=o)=a_{f,f\prime }{a}_{m,m\prime }{a}_{o,o\prime }$$ (10)

2.3.3 CNV segmentation

The reference genome sequence has a lot of gaps (the long sequence of “N” bases); sequencing reads cannot be mapped to these gapped regions, generating non-contiguous contigs with mapped reads in each chromosome. We considered each contig separately and used HMM Viterbi algorithm to infer the most likely sequence of hidden Markov sates. In this step, we ignored those windows in GC bins with extremely low or high GC content and windows with insufficient data; hence, copy number states of these windows depend on their adjacent windows. Finally, only windows with at least one non-normal copy number state were retained and joined together as output.

2.4 Data postprocessing

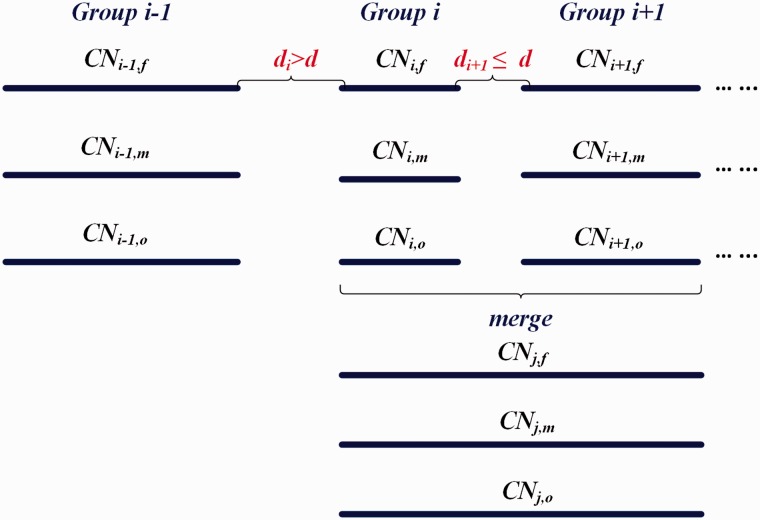
The variability of RD at a window arises not only from true CNVs, GC content bias and mappability bias, but also from other sources of noise, which can result in miscalls in the raw CNV segmentation result. A strategy for merging adjacent CNVs with the same or ambiguous copy number states is required to obtain accurate CNV calls. We included CNV calls of the trio at one region as a group. Our CNV merging strategy is illustrated in Figure 3. Before merging, the two-copy deletion and one-copy deletion states were classified as a unified deletion state; the one-copy duplication and multiple-copy duplication states were classified as a unified duplication state. If two consecutive groups of CNV calls share at least one same kind of CNVs and the distance between them was less than or equal to a specified threshold, then these two consecutive groups were merged into one group. For the merged group, each sample’s copy number state was determined by the copy number state with the maximum sum of length in original groups. In addition, since sequencing reads cannot be confidently mapped to the reference genome in regions with extremely low mappability scores, CNVs cannot be confidently detected in these regions. Therefore, removing CNV calls in these regions can significantly reduce false positive rate with a slight sacrifice in sensitivity.

Fig. 3.

. Schematic illustration of CNV merging strategy used in TrioCNV. Each group has at least one CNV (deletion, duplication or both). d is the specified distance threshold to determine if two adjacent groups can be merged. In addition to the distance constraint, if two adjacent groups are merged, they must share at least one same type of CNV

2.5 Software availability

We developed TrioCNV based on the approaches described above. TrioCNV was implemented using a combination of Java and R and available at https://github.com/yongzhuang/TrioCNV.

3 Results

3.1 Simulation data analysis

To evaluate TrioCNV’s performance and compare it with existing approaches, we simulated WGS data for a hypothetical trio. We first generated two haploid genome sequences of chromosome 1 for each parent by randomly sampling non-overlapping CNVs (≥200 bp in size) from the Database of Genomic Variants (MacDonald et al., 2014), and then used RSVSim (Bartenhagen and Dugas, 2013) to introduce sampled CNVs into the reference genome sequence. Duplications have at most three copies. Then two haploid sequences were paired together to form each parent’s diploid sequence. Having two parents’ diploid sequences, we generated the offspring’s diploid sequence by randomly sampling one of the two haploid sequences from each parent and pairing them together. The numbers of simulated CNVs for father, mother and offspring were 196 (100 deletions and 96 duplications), 190 (97 deletions and 93 duplications) and 193 (100 deletions and 93 duplications), respectively. For each individual, we used the ART Illumina read simulator (Huang et al., 2012) to generate 100-bp paired-end sequencing reads at 40× coverage (20× coverage for each haploid sequence) with an insert size from a Gaussian with mean of 400 bp and standard deviation of 40 bp. We used BWA-MEM (Li, 2013) with default parameters to map all simulated reads to the 1000GP Phase II reference genome.

Since there are no CNV callers for NGS data considering familial relatedness, we compared TrioCNV with CNVnator (version 0.3) (Abyzov et al., 2011), an RD-based single-sample CNV caller and also one of the most sensitive approaches (Mills et al., 2011). We specified the same window size of 200 bp for both CNVnator and TrioCNV. For each method, sensitivity was calculated as the number of true CNVs detected divided by the total number of true CNVs, and false discovery rate (FDR) was calculated as the number of false CNVs detected divided by the total number of CNVs detected. We used a 1-bp reciprocal overlap to determine whether two CNVs are the same or not.

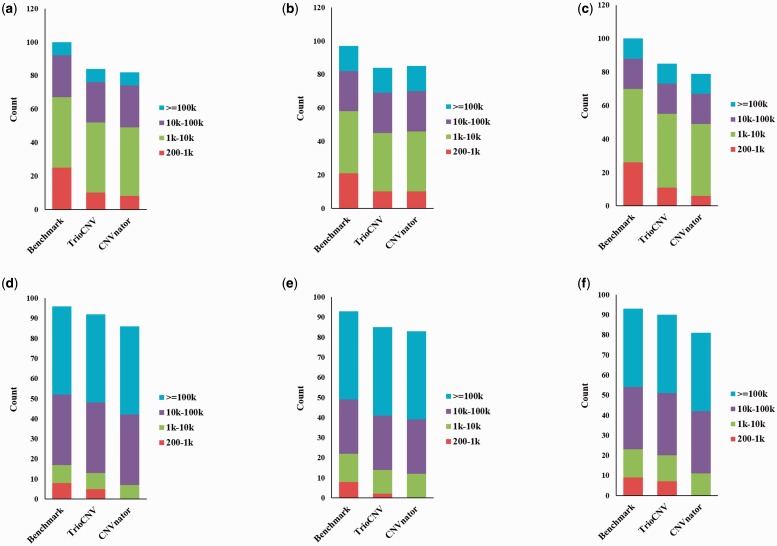
The performance of TrioCNV and CNVnator on the simulated trio is summarized in Table 1 (see raw results in Supplementary Table S1). TrioCNV shows a better sensitivity than CNVnator while maintaining a similar FDR. Figure 4 shows the size distributions of simulated CNVs that are detected by TrioCNV and CNVnator. For large CNVs (≥1000 bp), both TrioCNV and CNVnator are very sensitive, whereas for small CNVs (<1000 bp), TrioCNV is more sensitive than CNVnator. Overall, both TrioCNV and CNVnator have lower sensitivities for small CNVs than for large CNVs, in accordance with the observation that RD-based approaches are more suitable for detecting large CNVs (Medvedev et al., 2009).

Table 1.

. CNV detection performance of TrioCNV and CNVnator for the simulated dataset

Program	Sample	Deletions			Duplications
		Count	Sensitivity (%)	FDR (%)	Count	Sensitivity (%)	FDR (%)
TrioCNV	Father	262	84.0	68.3	103	95.8	8.7
	Mother	217	86.6	61.3	88	91.4	1.1
	Offspring	279	85.0	69.9	96	96.8	5.2
CNVnator	Father	241	82.0	66.0	97	89.6	9.3
	Mother	233	87.6	63.5	86	89.2	1.2
	Offspring	251	79.0	68.5	89	87.1	5.6

Fig. 4.

. Size distributions of simulated CNVs detected by TrioCNV and CNVnator. (a) Deletions in father; (b) deletions in mother; (c) deletions in offspring; (d) duplications in father; (e) duplications in mother sample; (f) duplications in offspring

3.2 Real data analysis

To further evaluate the performance and make a comparison, we ran TrioCNV and CNVnator on a real WGS trio.

In addition, we also ran three other representative CNV callers, BreakDancer (version 1.4.4) (Chen et al., 2009), Pindel (version 0.2.5) (Ye et al., 2009) and DELLY (Rausch et al., 2012). BreakDancer is a PEM-based caller. Pindel is an SR-based caller. DELLY is an integrated PEM and SR caller. For BreakDancer, we used BreakDancerMax designed for detecting large structural variation. For DELLY, only CNVs that passed the filter were kept in the output. All three callers were ran with default parameters. The real dataset is the high coverage (>75×) Illumina Hiseq WGS data of one CEU (Utah residents with ancestry from northern and western Europe) trio (father NA12891, mother NA12892 and the female offspring NA12878) from the 1000GP, sequenced and preprocessed at the Broad Institute (the data can be downloaded from ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/technical/working/20120117_ceu_trio_b37_decoy/). The alignment (.bam) files were generated as follows: all reads were aligned to 1000 Genomes Phase II reference genome using BWA (Li and Durbin, 2009); PCR duplicates were marked using Picard (http://picard.sourceforge.net); recalibration of base quality scores and local realignment around INDELs were performed using GATK (DePristo et al., 2011). We used the same reciprocal overlap criterion and the same definitions for sensitivity and FDR as we used for simulation data analysis.

To evaluate sensitivity, we obtained the gold standard call set from the 1000 Genome Structural Variant discovery study for the offspring of this trio (NA12878) (Mills et al., 2011). There were 610 autosomal deletions and 261 autosomal duplications successfully converted from NCBI36 to NCBI37 using liftOver (https://genome.ucsc.edu/cgi-bin/hgLiftOver). Furthermore, we examined Mendelian inconsistency for CNVs detected. Because of the extremely low de novo mutation rate, although true de novo CNVs can be present, most of the Mendelian inconsistent CNV calls should be false positives. Therefore, Mendelian inconsistency rate can indicate the overall performance of CNV detection for a trio, especially in the absence of true CNV call sets. In this study, we required a Mendelian consistent call be detected in the offspring and overlap (1-bp reciprocal) with a CNV of the same copy number in at least one parent, and all the remaining calls were treated as Mendelian inconsistent.

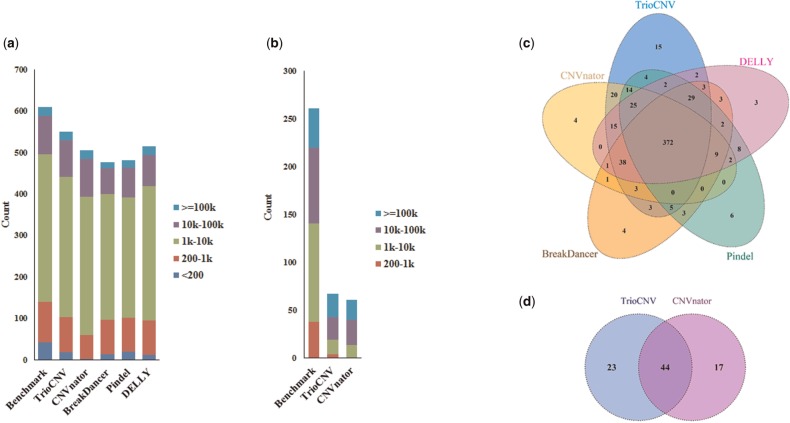
The performance of TrioCNV, CNVnator, BreakDancer, Pindel and DELLY on the 1000GP CEU trio is summarized in Table 2 (see raw results in Supplementary Table S2). For both deletions and duplications, TrioCNV achieved the highest sensitivity and at the same time the lowest Mendelian inconsistency rate. Figure 5a and b shows the size distributions of CNVs in the gold standard call set that were detected by the five methods. TrioCNV is more sensitive than all other four methods for large (≥200 bp) CNVs. For small (<200 bp) CNVs, CNVnator is less sensitive than other four approaches, especially for CNVs smaller than 200 bp. TrioCNV also showed lower sensitivity for small CNVs than for large CNVs. This can be partially explained by the default 200 bp window size we have specified for both TrioCNV and CNVnator, so there would be no windows entirely covered by CNVs smaller than 200 bp. In other words, under the 200-bp window size, the RD signal is insufficient for detecting CNVs smaller than 200 bp. Figure 5c and d shows the concordance among CNVs in the gold standard call set that were detected by the above four approaches. There is 61.0% (372/610) concordance among deletions detected by TrioCNV, CNVnator, BreakDancer, Pindel and DELLY and there is 16.9% (44/261) concordance among duplication detected by TrioCNV and CNVnator. Each approach reports some unique CNVs, and moreover, 17 deletions cannot be detected by any of approaches and 177 duplications cannot be detected by either TrioCNV or CNVnator.

Table 2.

. CNV detection performance of TrioCNV, CNVnator, BreakDancer, Pindel, and DELLY on the 1000GP CEU trio

Program	Deletions		Duplications
	Sensitivity (%)	Mendelian inconsistency rate (%)	Sensitivity (%)	Mendelian inconsistency rate (%)
TrioCNV	90.3	0.6	25.7	1.5
CNVnator	82.8	65.6	23.4	13.1
BreakDancer	78.2	28.3	–	–
Pindel	79.2	11.5	–	–
DELLY	84.4	45.0	–	–

Sensitivity was calculated according to the gold standard CNV call set from the sample NA12878. Since all gold standard CNVs are larger than 50 bp in size, we only kept CNV calls larger than 50 bp for BreakDancer, Pindel and DELLY. BreakDancer cannot detect duplications, and Pindel and DELLY cannot detect interspersed duplications, so these three methods were ignored when evaluating duplications

Fig. 5.

. CNVs in the gold standard call set that are detected by TrioCNV, CNVnator, BreakDancer and Pindel. (a, b) Show the size distributions of gold standard CNVs detected by different approaches, (a) for deletions and (b) for duplications; (c, d) Show the concordance among gold standard CNVs detected by four approaches, (c) for deletions and (d) for duplications

In addition, we compared the autosomal deletions called by the above five methods to another two truth sets, one containing 3376 deletions and the other 4095 deletions, both used by Layer et al. (2014). Since these two truth sets contain many small deletions, we specified a smaller window size (100 bp) for RD-based CNVnator and TrioCNV to capture small deletions. For the 1-bp reciprocal overlap criterion used above, the results are summarized in Supplementary Table S4. TrioCNV achieved the lowest Mendelian inconsistency rate among the five methods and is consistently more sensitive than CNVnator and DELLY. Since BreakDancer, Pindel and CNVnator were used to generate the two truth sets, these truth sets should be both biased toward these three methods (Layer et al., 2014). This might explain TrioCNV’s lower sensitivity than BreakDancer and Pindel. Furthermore, we calculated the sensitivity across different reciprocal overlap (RO) criteria from 1-bp to 50% (see Supplementary Figs S1 and S2). TrioCNV is more sensitive than CNVnator and DELLY for some ROs <50%, but less sensitive than BreakDancer and Pindel perhaps due to the biased true sets. Theoretically, RD-based methods usually define fixed-sized window (from hundreds to thousands of base pairs), so they can only provide window-sized resolution. In contrast, SR-based, PEM-based and de novo assembly methods can provide single-nucleotide resolution. Consequently, it is understandable that RD-based methods are less sensitive when large ROs are used for evaluation, especially for small CNVs. Similarly, we calculated the Mendelian inconsistency rate across different RO criteria from 1-bp to 50% (see Supplementary Fig. S3). Since TrioCNV performs joint segmentation and models the family relationship explicitly, it achieved an extremely low Mendelian inconsistency rate, while the other four methods all showed higher error rates.

4 Discussion

In summary, we introduced TrioCNV, a novel approach to jointly detecting CNVs from WGS data in parent-offspring trios. First, we modeled read depth by the negative binomial regression to accommodate over-dispersion and account for GC content bias and mappability bias. Second, we incorporated parent-offspring relation-ship into our model to leverage Mendelian inheritance constraint while allowing the rare incidence of de novo mutations. Third, we used an HMM to jointly make CNV segmentation of the parent-offspring trio. To our knowledge, this is the first CNV detection method developed specifically to handle trio sequencing data. To evaluate the performance of TrioCNV and compare it with existing approaches, we applied TrioCNV to a simulated trio and a sequenced trio from 1000GP. Our results illustrate that TrioCNV achieves a better performance compared with existing approaches in the trio setting.

Our approach may be further enhanced in several ways. For example, we only modeled the RD signal for emission probability, while not all CNVs are assessable by RD. Therefore, other types of mapping signals such as read pairs and split reads can be incorporated to detect CNVs that are not easily assessable by RD. Similar to other RD-based CNV detection methods, TrioCNV reports lower (i.e. window-based) breakpoint resolution than SR-, PEM- and de novo assembly-based methods, and these three kinds of signals can help refine breakpoints. In addition, our approach is now limited to WGS data, but it can be potentially adapted to support whole exome sequencing data.

Funding

Natural Science Foundation of China [No: 61173085] and the National High-Tech Research and Development Program (863) of China [Nos: 2012AA020404, 2012AA02A602, 2012AA02A604 and 2014AA021505] and the National Institute of Health grant 1R01HG006857-01A1 (to B.L.).

Conflict of interest: None declared.