Abstract
Motivation: Illustrating how HIV-1 is transmitted and how it evolves in the following weeks is an important step for developing effective vaccination and prevention strategies. It is currently possible through DNA sequencing to account for the diverse array of viral strains within an infected individual. This provides an unprecedented opportunity to pinpoint when each patient was infected and which viruses were transmitted.
Results: Here we develop a mathematical tool for early HIV-1 evolution within a subject whose infection originates either from a single or multiple viral variants. The shifted Poisson mixture model (SPMM) provides a quantitative guideline for segregating viral lineages, which in turn enables us to assess when a subject was infected. The infection duration estimated by SPMM showed a statistically significant linear relationship with that by Fiebig laboratory staging (P = 0.00059) among 37 acutely infected subjects. Our tool provides a functional approach to understanding early genetic diversity, one of the most important parameters for deciphering HIV-1 transmission and predicting the rate of disease progression.
Availability and implementation: SPMM, webserver, is available at http://www.hayounlee.org/web-tools.html.
Contact: hayoun@usc.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
A genetic bottleneck during HIV-1 transmission has been reported in a number of studies comparing sequence variants among transmission partners (Learn et al., 2002; Long et al., 2000; Wolinsky et al., 1992). The HIV-1 transmission bottleneck has been recently linked to a fitness bottleneck, preferentially transmitting high-fitness viruses (Carlson et al., 2014). Whereas a single-strain infection is prevalent in heterosexuals, intravenous drug users (IDUs) show a higher chance of being productively infected by more than one virus (Abrahams et al., 2009; Bar et al., 2010; Keele et al., 2008; Li et al., 2010). Even within the same risk category, additional clinical variables may create a significantly different transmission landscape, which can in turn affect the frequency of multiple-founder infections. For example, the presence of a genital infection may lead to a more permissive environment for multiple-founder infections (Haaland et al., 2009).
Early genetic diversity, typically associated with the number of transmitted strains, has been shown as a significant indicator of HIV-1 disease progression. Greater diversity among the infecting virus population was correlated with an increased risk of death, a higher steady-state level of HIV-1 viremia, and a faster CD4+ T cell decline (James et al. 2011; Sagar et al., 2003). Multiplicity of infection has been linked to increased transmission risk (Abrahams et al., 2009; Carlson et al., 2014). Therefore, addressing the diversity of viral variants at transmission is an important task that may help evaluate viral evolution and predict clinical outcomes.
Recent advances in sequencing technology provide an accurate representation of the HIV-1 sequence population within an infected individual (Palmer et al., 2005; Salazar-Gonzalez et al., 2008). Early HIV-1 evolution has been quantitatively addressed, accomplishing tasks such as identifying transmitted/founder viruses (Keele et al., 2008), estimating infection duration (Keele et al., 2008; Lee et al., 2009), and calculating the rate and timing of the viral escape from the first T cell responses (Goonetilleke et al., 2009). However, success has been limited because current tools have been specifically designed for the analysis of infections originating from a single transmitted virus (Keele et al., 2008; Lee et al., 2009). Early viral diversity arising from multiple founder lineages should be interpreted with caution because viral diversity due to early, random evolution is intertwined with sequence heterogeneity caused by distinct founder viruses. Tree-based methods have been useful for segregating viral sequences into multivariant founder lineages (Abrahams et al., 2009; Bar et al., 2010; Keele et al., 2008). Here we develop an alternative framework to systematically estimate the duration of infection originating from multiple founders based on the characteristics of HIV-1 transmission and early evolution. We use this tool, called shifted Poisson mixture model (SPMM), to characterize early HIV-1 evolution within acutely infected subjects (Abrahams et al., 2009; Bar et al., 2010; Keele et al., 2008).
2 Materials and methods
2.1 Model of multiple variant transmissions and evolution
We develop a model for early HIV-1 evolution to analyze infections originating from multiple viruses. We formulate the SPMM by extending a previously developed acute sequence evolution model (Keele et al., 2008; Lee et al., 2009) to the case of an HIV-1 infection that starts with multiple founder viruses. Our primary goal is to devise a tool for assessing the duration of infection by segregating different founder lineages. In the SPMM, we assume that each descendant population evolves and replicates independently without any recombination. Due to this assumption, putative recombinant strains are removed prior to our model analysis. Assuming no preferential selection of a particular founder lineage, which is a reasonable assumption to make within the first weeks since infection due to a delay in host immune response, the rate of viral diversification of each lineage is governed by the same set of model parameters, including the single cycle error rate of viral reverse transcriptase (Mansky and Temin, 1995), the viral generation time (Markowitz et al., 2003; Perelson et al., 1996), and the basic reproductive ratio (Ribeiro et al., 2010; Stafford et al., 2000). Each founder lineage behaves like a single infection wherein the pairwise nucleotide base differences, Hamming distances (HD), between HIV-1 gene sequences conform to a Poisson distribution (Keele et al., 2008; Lee et al., 2009).
Let be the sequences of the distinct founder strains in a systemic HIV-1 infection with pairwise Hamming distances among these founder strains, Let be the total number of sampled sequences and be a partition function that assigns each of the sampled descendants to one of the founder strains; for example, if and then the th sequence and the th sequence originated from two different founders, and . From the partition , the number of sequences in each of the lineages is determined, with . Two randomly-chosen sequences, and , which evolved independently from distinct ancestors and , are assumed to have a HD at least as great as the distance between their founders, . The HD distribution between the sequences, and , is given by the sum of the probability of each possible pair of mutations in si and sj away from their respective founders:
| (1) |
where is the average number of mutations away from the founder virus in the HIV-1 genome when sequences are sampled at time post infection. This describes a shifted-Poisson distribution with mean and shift . The Poisson parameter has a linear relationship with the time since the beginning of the infection, , which is given by the following equation when the infection is assumed to occur in discrete generations,
| (2) |
where is the rate of base substitution by HIV-1 reverse transcriptase, is the number of bases of the sequence, and is viral generation time (Lee et al., 2009).
By collecting the probability distributions of HDs within lineages and those among lineages, we obtain the pairwise HD distribution for the entire sample when an infection starts with founder viruses,
| (3) |
where if and 0 otherwise, denoting that the founder distances must be at least as small as current distances (see Supplementary back-mutation correction section). When viruses are transmitted, the number of peaks of the HD distribution should be given by , consisting of one peak from within-lineage pairs and peaks from pairs across different lineages when the distances between each pair of founder lineages are not equal. These distinct peaks of the HD distribution indicate early stages of infection, as increased accumulation of mutations would flatten the peaks at chronic stages (Park et al., 2011).
2.2 Parameter estimation: number of founder viruses and duration of infection
Using the method of conditional maximization (Schervish, 1995), we estimated the set of model parameters consisting of the Poisson parameter, , the number of initial founder strains, , the pairwise Hamming distances (HDs) between all possible pairs of founder strains, , and the partition of sampled descendants into each group, . The approximate likelihood is calculated as the product of the individual HD distributions as in references (Giorgi et al., 2010; Lee et al., 2009). It is an approximation because the intersequence HDs are not independent. When a sequence pair and belongs to the same group, we set . Using a Poisson distribution for the number of accumulated mutations, the approximate likelihood is
| (4) |
where is the intersequence HD between strains and . The approximate log-likelihood function is given by the log of Equation (4) and is simplified to be numerically maximized. For the shifted Poisson mixture it is given by,
| (5) |
Given a set of intersequence HDs, the values of the parameters , , and which maximize Equation (5) are the approximate maximum likelihood estimates of the parameters. The vector, and the permutation function, depend on the value of , and it is difficult to estimate at the same time as the other parameters. Therefore, for a range of likely values of , we fix the value of and estimate , and . In addition, the minimum intersequence distance between any founder sequences is set as 6. We then compare the fit of the model to the HD distribution for each value of and choose the best-fitting parameters.
We employ a one-dimensional, deterministic optimization method to estimate the parameters that maximize the approximate log-likelihood function, Equation (5). We start with a clustering algorithm, Partitioning Around Medoids (PAM) to partition the sampled sequences into groups (Kaufman and Rousseeuw, 2005; Theodoridis and Koutroumbas, 2008). For each parameter in the model, the approximate maximum likelihood value is calculated, conditional on the current values of the other parameters in the model. This method is guaranteed to find one of the local maxima in the approximate likelihood. One way to increase the odds of finding the global maximum is by starting the algorithm at a likely point, close to the global maximum, which is why we start with the PAM partition. For a full discussion of the convergence of generalized maximization algorithms, see references (Boyles, 1983; Dempster et al., 1977). With the high-dimensional, discrete nature of the parameter space, our method is one of the most computationally feasible ones. The parameter space of this model contains the set of partitions of objects in groups, which grows exponentially with . For a limited number of examples, we implement a complete search of the approximate likelihood space. For three example subjects with 15, 28, and 49 sampled sequences, conditional maximization yields the same estimates as does exhaustive maximization.
The estimated number of founder virus strains is the smallest k such that the model has the smallest sum of squared errors (SSE) or Akaike Information Criteria (AIC) among the values of k fit to the data. Here we measure the SSE with the normalized HD distribution. The AIC is a
| (6) |
measure of the fit of the data to the likelihood penalized by the number of parameters (Akaike, 1974). The AIC for the SPMM is given by where the degrees of freedom come from the number of estimated parameters, one , founder distances, and indicators of the partition.
The estimated is evaluated by the goodness of fit χ2 test to examine whether the data significantly diverges from the fitted SPMM (Chernoff and Lehmann, 1954; Giorgi et al., 2010; Lee et al., 2009). This test requires that the observations be independent, which is not the case for intersequence Hamming distances. Therefore, instead of fitting the inter-sequence HDs, we calculate the within-lineage distances from each lineage’s consensus sequence and define the χ2 statistic as follows: where is the observed pooled frequency of the distance from the lineage consensus sequences and is the expected frequency if the distribution were to follow a Poisson with mean , where is the parameter estimated through the SPMM model. The factor comes from the fact that we are testing the consensus distances instead of the inter-sequence distances.
2.3 Sequence data sources
The sequence clones were collected from the published data set in references (Abrahams et al., 2009; Bar et al., 2010; Keele et al., 2008). Geographic locations of the cohorts were US, Trinidad, South Africa, Malawi, and Canada. A total of 182 subjects with acute, very early HIV-1 subtype B and C infections were re-grouped according to the routes of exposure: 92 heterosexual transmissions, 16 MSM subjects, 12 IDU subjects, and 62 patients of unknown risk group.
2.4 Sequence preparation: recombination and hypermutation
Prior to fitting the SPMM model, all samples were aligned and checked for instances of recombination and hypermutation. Retroviral recombinant DNA sequences are synthesized by HIV-1 reverse transcriptase which switches between distinct RNA templates when a single target cell is infected by virions with heterozygous RNAs (Hu and Temin, 1990; Robertson et al., 1995a, 1995b). The SPMM will generally designate recombinant strains as separate lineages because of large sequence differences from each of their parent lineages. Recombinant sequences may therefore result in inaccurate estimates of the number of founder viruses. Thus, the proper usage of the SPMM requires pre-screening for recombinant sequences. All alignments were checked for recombination using a combination of the Recombination Detection Program version 3 (RDP3) (Martin et al. 2010; Martin et al., 2005) and the beta version of our in house Recombination Analysis Program (RAP, http://www.hiv.lanl.gov) in tandem with manual inspections. All recombinants were removed prior to our model analysis, as in Supplementary Table S1 and Supplementary Data and Supplementary Data.
Similarly, APOBEC3G/F-mediated hypermutation (Simon et al., 2005) affects the outcome of our model because mutations with APOBEC3G/F signatures occur at a higher rate than the background mutation rate. Therefore, hypermutated sequences and general enrichment for hypermutation were checked in all alignments using the LANL tool Hypermut (http://www.hiv.lanl.gov/content/sequence/HYPERMUT/hypermut.html) and either hypermutated sequences (when found significantly enriched with a P-value < 0.1) or hypermutated positions (when the whole sample was found to be enriched with a P-value < 0.1) were removed, as in Supplementary Table S2 and Supplementary Data.
2.5 Analysis of maximum likelihood trees
Sequences were converted into the PHYLIP format. Maximum likelihood trees were then generated using the PHYML program (http://www.atgc-montpellier.fr/download/papers/phyml_2003.pdf). The program was set up to read the DNA sequences in a sequential format. A single dataset was analyzed at a time, without bootstrap analysis. The general time-reversible model was used, with the ‘ML’ option selected for base frequency estimates. Invariable sites were estimated, with twelve substitution rate categories. The gamma distribution parameter was estimated, the tree was generated by the BIONJ option, and tree topology was optimized. We produced images of these trees using FigTree (http://tree.bio.ed.ac.uk/software/figtree/).
3 Results
3.1 Approximate likelihood-based inference of SPMM
We use our model to assess the number of founder viruses and the duration of infection for 182 acutely infected subjects whose HIV-1 full envelope gene sequences were previously published (Abrahams et al., 2009; Bar et al., 2010; Keele et al., 2008). Figure 1 shows four representative examples of the model’s fit to the pairwise HD distribution of envelope gene sequences obtained from each acutely infected subject. Here the best fitting model parameters are obtained using the conditional maximization method (Schervish, 1995). When an infection is estimated to originate from a single viral genome, we observe a single peak of the HD distribution (Fig. 1A). Multiple founder transmissions are marked by multiple peaks in the HD distribution (Fig. 1B–D). The two peaks of subject 9076-08’s HD distribution, shown in Figure 1B, indicate an infection originating from two founder variants; the first peak near HD = 0 represents sequence pairs within each of two founder lineages and the second peak near HD = 28 denotes sequence pairs between the two founder lineages. The SPMM estimated the duration of infection in subject 9076-08 as 13.5 days with a 95% C.I. of (8.1, 18.9) (goodness-of-fit P = 0.74).
Fig 1.
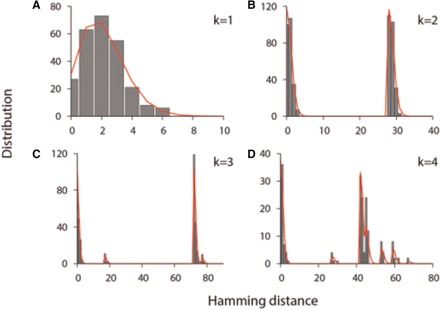
Best fits of the shifted Poisson mixture model to the intersequence HD distributions. (A) The pairwise HD distribution of HIV-1 envelope sequences sampled from patient 705010026 in reference (Abrahams et al., 2009) (gray bars). The shifted Poisson mixture model estimates the number of founder variants as 1 and the duration of infection as 38.3 [27.5–49.1] (goodness of fit P = 0.54). The best fit of the model is presented by the red curve (B) The pairwise HD distribution from patient 9076-08 in reference (Keele et al., 2008). The model estimates the number of founder strains as 2 and the duration of infection as 13.5 (8.1, 18.9) days (P = 0.74). The number of nucleotide base differences between the two founders is estimated as 28. (C) The pairwise HD distribution from subject 62615-13 in reference (Keele et al., 2008) with the best fit of the shifted Poisson mixture model (red line). The estimated number of founder sequences is 3, the time since infection is 9.3 (4.6, 14.0) days (P = 0.36), and the number of base substitutions among pairs of the three founder stains are 17, 72, and 77. (D) The pairwise HD distribution from subject CAP222 in reference (Abrahams et al., 2009) with the best fit of the SPMM. The estimated number of founder variants is 4 and the estimated time post infection is 14.0 (7.2, 20.8) days (P = 0.071). The pairwise estimated HDs among the founders are 53, 45, 42, 67, 27, and 59
The SPMM can complement tree-based lineage classification methods. Here we provide a side-to-side comparison between the SPMM analysis and a phylogenetic tree method. As shown in Figure 2A, the SPMM estimates two founder lineages from the sequence sample of subject CAP8 in reference (Abrahams et al., 2009); the two peaks of the HD distribution conform to the fit of the SPMM with two founder variants. Indeed, the fit of two founder variants shows both a smaller sum of squared errors (SSE) and Akaike Information Criteria (AIC) than the single founder fit (0.031 versus 0.0032 (SSE) and 803.2 versus 612.6 (AIC)). On the other hand, the analysis of the maximum likelihood tree does not conclusively determine whether the infection originated from a single lineage or multiple lineages; the three strains colored in red in Figure 2B can be grouped with the other 15 strains (colored in black) or considered as a separate lineage. As presented in the highlighter plot in Figure 2C, the three sequences of the second lineage show aligned mutations from the consensus sequence of the first lineage, resulting in the second peak in the HD distribution (Fig. 2A). By taking into account that the sequences of subject CAP8 were sampled in Fiebig stage V, we may consider the second lineage as an escape mutant lineage rather than a transmitted/founder lineage. Supplementary Figures S4 and Supplementary Data show additional side-to-side comparisons between the SPMM and phylogenetic analyses. This side-to-side comparison highlights that the SPMM provides a quantitative guideline for lineage classification based on the fine signatures of the sequence difference distribution of an HIV-1 infected individual.
Fig. 2.
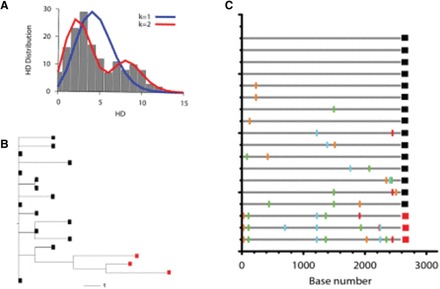
Comparison of SPMM and a maximum likelihood tree model. (A) The pairwise HD distribution of the envelope sequences sampled from subject CAP8 in reference (Abrahams et al., 2009) is represented by gray boxes. The fit of the SPMM with one founder variant (blue line) is compared with that of two founder variants (red line). (B) The maximum likelihood tree for subject CAP8. Two lineages classified by the SPMM are separately marked by black and red squares. (C) The highlighter plot of the envelope sequences of subject CAP8. The three HIV envelope sequences marked in red are classified as a separate lineage by the SPMM from the 15 sequences marked in black
3.2 Risk group and multiple variant transmissions
Viral diversity at transmission has been known to be associated with the exposure route and the risk behavior of infected individuals (Powers et al., 2008). Heterosexual transmission involves a significant genetic bottleneck, as around 80% of these transmissions originate from just one founder variant (Haaland et al., 2009; Keele et al., 2008). The rate of multivariant transmission is approximately doubled among HIV-1-infected men who have sex with men (MSM) (Li et al., 2010). Infections originating from multiple founder viruses are more common than those from a single founder within injection drug users (IDUs) (Bar et al., 2010). Here we systematically address the differences in the number of founder viruses among different exposure routes of infection using the published data in references (Abrahams et al., 2009; Bar et al. 2010; Keele et al., 2008).
The SPMM identifies a total of 20 cases of multivariant transmissions out of 92 heterosexual transmissions. Subject SC42 is excluded from our analysis to avoid small sample size artifacts because the number of sequences of the subject’ most prevalent lineage is less than 5. Table 1 lists the SPMM fit results of the remaining 19 subjects with multivariant heterosexual transmissions; the number of founder viruses is estimated to range from 2 to 7, with a mean of 2.8 (±1.2, standard deviation). We find 44% of the MSM group (7 out of 16 subjects) to have multivariant infections. Excluding subject Z10, for the same reason as for subject SC42, the number of founder variants of 6 multivariant MSM subjects ranges from 2 to 5 with a mean of 3.2 (±1.3) (Table 1). About three-quarters of the IDU group (9 out of 12) are estimated to be infected by multiple viral variants. The IDU group shows a much higher multiplicity of founder variants; on average, multivariant transmissions in IDUs involve 5.5 (±2.6) distinct strains and the maximum number of founder viruses estimated is 9. Subject ACTDM580208 of the IDU group and Subject Z29 of the unknown risk group are excluded from the SPMM analysis for the same reason as for the other two exclusions. Table 1 shows the SPMM estimates with full envelope gene sequences (HXB2 6225-8795) of the 41 multiple founder cases. Supplementary Table S3 examines the sequence length parameter by applying the SPMM to 2000, 1000 and 500 base long HIV-1 envelope gene segments (HXB 6596-8596, HXB2 6596-7596 and HXB2 6596-7096) from each of the 41 subjects. The estimates for k and infection duration are not significantly different for 2000 or 1000 base long segments. However, 500 base long gene segments averaged 1.10 lower k (P = 0.034) and 44.30 longer infection duration (P = 0.009).
Table 1.
SPMM estimates
| Subject ID | K | Days post infection with 95% CI | P # | SSE |
|---|---|---|---|---|
| Heterosexual | ||||
| SC33 | 2 | 22.4 [14.8–30.1] | 0.040 | 0.0049 (1053.2) |
| TT27P | 3 | 10.8 [6.4–15.2] | 0.33 | 0.0020 (1538.3) |
| CAP8a | 2 (1) | 49.1 [35.4–62.9] | 0.18 | 0.0032 (612.6) |
| CAP224 | 2 | 20.2 [11.7–28.8] | 0.57 | 0.0091 (510.7) |
| 703010228 | 2 | 21.3 [13.9–28.7] | 0.89 | 0.0010 (1040.4) |
| SC31a | 2 (1) | 24.2 [17.4–31.1] | 0.095 | 0.019 (2104.2) |
| CAP222a | 4 (3) | 14.0 [7.2–20.8] | 0.071 | 0.0063 (564.9) |
| 0478a | 2 (3) | 54.2 [40.3–68.2] | 0.021 | 0.011 (721.7) |
| 703010010 | 3 | 11.9 [5.8–18.0] | <0.0001 | 0.039 (631.0) |
| CAP136 | 2 | 36.7 [23.2–50.2] | 0.33 | 0.0085 (327.1) |
| CAP260 | 2 | 28.3 [14.9–41.7] | 0.45 | 0.018 (186.1) |
| Z30 | 2 | 64.0 [50.2–77.9] | 0.15 | 0.0062 (1040.1) |
| CAP37 | 3 | 46.1 [33.3–58.9] | 0.55 | 0.024 (839.6) |
| 0114 | 3 | 32.3 [22.5–42.0] | 0.82 | 0.0012 (861.7) |
| 703010200a | 4 (3) | 42.0 [28.6–54.6] | 0.89 | 0.013 (497.5) |
| 1335 | 3 | 28.4 [18.4–38.4] | 0.32 | 0.012 (617.8) |
| 706010151a | 3 (2) | 49.2 [31.8–66.6] | 0.044 | 0.023 (257.5) |
| CAP69a | 7 (5) | 4.8 [0.095–9.41] | 0.85 | 0.0074 (205.4) |
| 1196 | 3 | 49.5 [36.9–62.1] | 0.40 | 0.017 (884.2) |
| MSM | ||||
| Z35 | 2 | 19.3 [11.1–27.5] | 0.20 | 0.050 (571.9) |
| CAAN5342a | 2 (>2) | 30.2 [22.0–38.5] | 0.49 | 0.017 (1547.5) |
| Z16a | 4 (5) | 65.7 [49.4–82.0] | 0.97 | 0.0038 (575.9) |
| BORI0637 | 5 | 17.2 [10.1–24.3] | 0.84 | 0.0055 (698.3) |
| Z18a | 4 (3) | 33.2 [24.2–42.2] | 0.039 | 0.024 (1425.1) |
| Z03a | 2 (3) | 102.3 [83.1–121.6] | 0.39 | 0.034 (859.9) |
| IDU | ||||
| HDNDRPI029a | 2 (1) | 56.0 [44.5–67.6] | <0.0001 | 0.012 (1820.7) |
| HDNDRPI032 | 3 | 53.4 [39.6–67.2] | 0.87 | 0.0098 (682.2) |
| HTM319a | 8 (3) | 50.1 [36.4–63.9] | 0.00019 | 0.0047 (662.7) |
| PSL024 | 4 | 50.5 [33.5–67.5] | <0.0001 | 0.029 (303.5) |
| HDNDRPI001a | 4 (5) | 67.3 [49.6–84.9] | 0.0047 | 0.0090 (480.4) |
| I034-3 | 8 | 123.2 [113.6–132.7] | <0.0001 | 0.014 (28068.0) |
| 700010019a | 6 (>3) | 15.0 [7.3–22. 7] | 0.62 | 0.018 (417.5) |
| HDNDRPI034a | 9 (16) | 30.0 [23.6–36.3] | 0.08 | 0.0064 (4163.5) |
| Risk g roup u nknown | ||||
| 9076-08 | 2 | 13.5 [8.1–18.9] | 0.74 | 0.0040 (1153.4) |
| 62615-03 | 3 | 9.3 [4.6–14.0] | 0.36 | 0.0042 (809.7) |
| 9026-07 | 2 | 14.0 [6.0–22.0] | 0.97 | 0.011 (275.1) |
| 12008-09 | 2 | 8.0 [3.5–12.5] | 0.61 | 0.0079 (751.7) |
| PRB957-06a | 3 (4) | 52.5 [42.0–63.0] | <0.0001 | 0.047 (2355.0) |
| 63068-05 | 2 | 13.3 [6.3–20.2] | 0.34 | 0.030 (441.8) |
| 701010016 | 2 | 49.4 [35.6–63.2] | 0.14 | 0.0095 (622.2) |
| 1051-12a | 3 (4) | 29.9 [23.5–36.4] | <0.0001 | 0.015 (4530.4) |
aSubjects who were estimated to have a different number of founder strains using phylogenetic methods (Previously-published, phylogenetic tree-based estimates for the number of founder viruses are presented in parenthesis).
#Less than 0.05 implies statistically significant deviation from the SPMM.
3.3 SPMM estimates of infection duration and Fiebig staging
The SPMM analysis is cross-checked by an independent Fiebig laboratory staging of infection duration (Fiebig et al., 2003, 2005). Figure 3 shows the times since infection for a group of 37 heterogeneous subjects out of the 41 presented in Table 1 for whom Fiebig staging was available (Abrahams et al., 2009; Bar et al., 2010; Keele et al., 2008). While Fiebig staging provides a rough approximation of the time since infection, the SPMM and Fiebig estimates are nonetheless significantly correlated (Spearman’s r = 0.54, P = 0.00059). In a linear regression model, the slope of the linear fit is 0.55 (P < 0.0001), indicating that the infection duration estimated by the SPMM is on average lower than the laboratory staging estimate. When we exclude patients’ samples at the late acute stage of approximately 101 days following infection (Fiebig V), the two estimates show a weaker correlation among 24 subjects (Spearman r = 0.27, P = 0.20). However, the SPMM estimates become more comparable to the Fiebig estimates, with a linear regression slope of 1.02 (P < 0.0001). Therefore, the SPMM shows consistency in assessing infection duration with Fiebig staging, in particular, during early acute infection up to Fiebig stage IV.
Fig. 3.
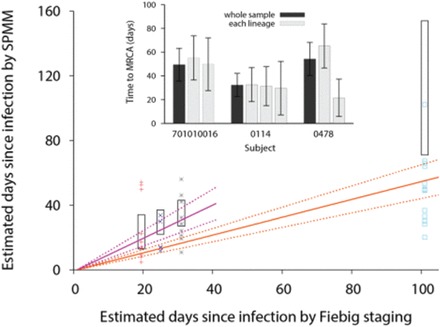
Comparison between SPMM estimates of infection duration and Fiebig staging and comparison of time to MRCA among different lineages. Our estimates of the duration of infections by the SPMM are compared with estimated times post infection by Fiebig staging for 37 acutely infected individuals whose infections originated from multiple founder viruses. The Fiebig stages I/II, III, IV, and V were colored as red, blue, gray, and sky blue, respectively. Here Fiebig stages I and II are grouped together because subjects in reference (Abrahams et al., 2009) were staged as I or II. The average estimated time post infection for each Fiebig stage was taken from references (Fiebig et al., 2003; Keele et al., 2008; Lee et al., 2009) and the stage I/II value is presented by averaging over the two stages. The 95% confidence interval for days post infection for each Fiebig stage is presented by the black box. The orange solid line with the slope of 0.55 shows a linear relationship between the Fiebig staging and SPMM estimate and the correlation is statistically significant (Spearman’s r = 0.54, P = 0.00059). The 95% confidence intervals of the fit are presented by orange dotted lines. Excluding patients’ samples at Fiebig stage V, the two estimates show a weaker correlation (Spearman r = 0.27, P = 0.20) but the SPMM estimates become more comparable to the Fiebig staging, with a linear regression slope of 1.02 (purple lines). Inset Time to the MRCA of a whole sequence sample (black bar) is compared with that of each mutant lineage (gray bar) from three HIV-1 infected subjects. The 95% CIs are presented as black line
3.4 Recombinant analysis
Recombination strains are detected within a considerable portion of subjects whose infection originated from multiple variants, as shown in Supplementary Table S1 and Supplementary Data and Supplementary Data. In the 41 multiple transmission cases listed in Table 1, 26 subjects show a recombination signature. On average, 17.4% of strains obtained from each of these subjects are designated as recombinants, ranging from 2.0% to 42.4%. Without each patient’s inferred recombinant strains, the duration of infection is decreased by a median of 19.3% in 15 subjects and increased by a median of 5.6% in 11 subjects. The number of founder viruses is decreased by a median of 3 in 22 subjects, ranging from 1 to 14. Our sensitivity analysis shows that the addition of up to 20 artificial recombinant sequences to subject 9076-08’s 32 sequences does not change the original estimate by more than one day, though the SPMM groups those as a separate lineage (Supplementary Fig. S6). The proper usage of the SPMM requires pre-screening for recombinant sequences.
3.5 Validity of model assumptions
The SPMM assumes that each founder population evolves at the same rate. We examine this aspect by comparing the times to the most recent common ancestor (MRCA) of the lineages within an infected individual. Figure 3 inset shows representative examples of comparing the time to the MRCA of a whole sequence sample with that of each mutant lineage. Two founder lineages are identified in subject 701010016 in reference (Keele et al., 2008) and the two lineages’ evolution time is estimated to be comparable to each other while also matching the evolution time of the whole sample, corroborating our model assumption. The difference in the time to the MRCA among the three lineages of subject 0114 in reference (Abrahams et al., 2009) is also negligible. On the other hand, there is a marked difference in time to the MRCA between the two lineages in subject 0478 in reference (Abrahams et al., 2009), violating the model assumption.
We systematically quantify the difference in the time to the MRCA across lineages within 10 cases from a total of 41 identified multivariant transmissions in Table 1. Samples are excluded from this analysis when the prevalence of a minor lineage is less than 17% to avoid small sample size artifacts. The absolute difference in the time to the MRCA across lineages ranges from 1.3 to 43.7 days, with a median of 11.8 days. Times to the MRCA significantly differ among lineages in one subject, 0478; the 95% confidence intervals of the subject’s two lineages’ times to the MRCA do not overlap each other (Fig. 3). The SPMM estimates of time since infection should be interpreted with caution when an individual’s within-lineage times to the MRCA differ considerably from each other. In addition, the supplementary back-mutation correction section discusses the SPMM’s assumption that mutations always increase the distances between sequence pairs of different founder lineages.
4 Discussion
We have formulated the SPMM to assess the infection duration along with the number of founder strains initiating a productive HIV-1 infection. The SPMM enables us to assess the time since infection even for multiple variant transmission cases by objectively classifying the transmitted lineages in the host. One of the advantages of our approach is the rigorous quantitative criteria it provides for the classification of lineages. Our method focuses on the fine structure of the pairwise sequence differences and quantitatively evaluates the models with different numbers of lineages to find the one with the best fit to the available data.
Proper segregation of viral clones into distinct multivariant founder lineages leads to a rational assessment of the duration of early infection. For the 37 subjects at Fiebig stages I-V who were classified as multiple-variant transmissions, our estimates of the time since infection were 34.5 (±21.4) days on average, which lies within the range of the Fiebig estimates. Furthermore, there existed a significant linear relationship (P = 0.00059) between the Fiebig staging and the SPMM estimates. However, the remaining discrepancies between our model estimates and Fiebig staging can be attributed to the following factors. First, the Fiebig estimate itself is subject to uncertainty, mainly due to variability in antibody dynamics across individuals. Second, one or more of the SPMM’s assumptions could be violated. Indeed, we observed variations in the time to MRCA among different lineages within an individual, which might contribute to the inaccuracy of SPMM estimates. As shown in Table 1, lineage prevalence differs considerably in some individuals, suggesting the potential for preferential selection of a particular founder lineage. The SPMM assumes that viral populations evolve in the absence of selection. While this is true early after infection, the HIV-1 gene population eventually evolves under heavy immune pressure (Liao et al., 2013; McMichael et al., 2010; Richman et al., 2003) and depending upon when the sequence samples were taken this may affect the precision of SPMM estimates. For instance, when we treated subject PRB957-06’s putative escape lineage from immune selection as a separate lineage, the fit of the SPMM with 4 founder variants better conformed to the subject’s HD distribution (goodness of fit P = 0.18) than the original fit with 3 founders (goodness of fit P < 0.0001, Supplementary Fig. S7). Third, model parameters may differ among individuals, resulting in inaccurate infection duration estimates. For example, the viral generation time was estimated to range from 1.76 days to 4.2 days among 22 subjects who were administered the same antiretroviral regimen (Kilby et al., 2008) though the precision of the viral generation time estimates is complicated by our lack of knowledge of in vivo drug efficacy.
When a lineage’s evolution time is considerably different from that of another lineage, this might be indicative of an HIV-1 superinfection in which an individual with an established infection acquires a second virus. The incidence rate of HIV-1 superinfection has been reported to range from 0% to 7.7% per year (Redd et al., 2013), with some vulnerable populations reporting a rate as high as 57% of the primary HIV-1 incidence rate (Piantadosi et al., 2007; Redd et al., 2012). Subject 0478 in reference (Abrahams et al., 2009) shows a considerable difference between the subject’s two lineages’ time to the MRCA, 65.2 [46.6–83.8] days versus 21.5 [5.8–37.2] days. Thus, this subject’s sequence sample might be interpreted as the outcome of a superinfection. However, other scenarios such as varying evolutionary rates among different lineages cannot be ruled out as possible explanations for the inconsistency between the lineages’ times to the MRCA. This example suggests our model could be used for detecting HIV-1 superinfection and determining the timing of primary infection and superinfection, although further testing is needed.
The enumeration of the number of founder variants using the SPMM can be influenced by many factors such as selection signatures, hypermutation signatures, the presence of closely related founder sequences and recombinant strain designation. The SPMM requires removal of recombinants; however, if recombinants were generated in the donor, the SPMM could underestimate the number of founder lineages as these excluded recombinants would indeed be additional founders. In addition, when the number of sampled sequences from an individual is small, the fit of SPMM can considerably deviate from a patient’s intersequence HD distribution, particularly when the number of sequences for each lineage is very small and the number of lineages is as large as that in most IDU samples. Therefore the SPMM’s estimates on the number of founder variants should be interpreted with caution in the context of these complications.
A mathematical description of early HIV-1 infections provides a quantitative guideline for systematically estimating the number of founder viruses and the duration of infection. The ability to molecularly date HIV-1 infections from multiple founder viruses widens the scope and applicability of HIV genomic incidence assays (Park et al., 2011, 2014). Our study offers novel insights into interpreting early genetic diversity, which is a key parameter not only for deciphering HIV-1 transmission events but also for predicting the rate of disease progression.
Supplementary Material
Acknowledgements
We thank Dr. Sally Thurston, Nolan Goeken and Casey Ren for stimulating discussions and reviewing this manuscript.
Funding
This work has been supported by NIH grants R01-AI083115 and R01-AI095066 (HYL). Portions of this work were done under the auspices of the US Department of Energy under contract DE-AC52-06NA25396 and supported by NIH grants R01-AI028433, R01-OD011095 and UM1-AI100645 (ASP).
Conflict of Interest: none declared.
References
- Abrahams M.R. et al. (2009) Quantitating the multiplicity of infection with human immunodeficiency virus type 1 subtype C reveals a non-Poisson distribution of transmitted variants. J. Virol., 83, 3556–3567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akaike H. (1974) A new look at the statistical model identification. IEEE Trans. Automatic Control AC, 19, 716–723. [Google Scholar]
- Bar K.J. et al. (2010) Wide variation in the multiplicity of HIV-1 infection among injection drug users. J. Virol., 84, 6241–6247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyles R.A. (1983) On the convergence of the EM Algorithm. J. R. Stat. Soc. Ser. B, 45, 47–50. [Google Scholar]
- Carlson J.M. et al. (2014) HIV transmission. Selection bias at the heterosexual HIV-1 transmission bottleneck. Science, 345, 1254031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chernoff H., Lehmann E.L. (1954) The use of maximum likelihood estimates in X tests for goodness-of-fit. Ann. Math. Stat., 25, 579–586. [Google Scholar]
- Dempster A.P. et al. (1977) Maximum likelihood estimation from incomplete data via the EM algorithm (with discussion). J. R. Stat. Soc. Ser. B, 39, 1–38. [Google Scholar]
- Fiebig E.W. et al. (2005) Intermittent low-level viremia in very early primary HIV-1 infection. J. Acquir. Immune Defic. Syndr., 39, 133–137. [PubMed] [Google Scholar]
- Fiebig E.W. et al. (2003) Dynamics of HIV viremia and antibody seroconversion in plasma donors: implications for diagnosis and staging of primary HIV infection. Aids, 17, 1871–1879. [DOI] [PubMed] [Google Scholar]
- Giorgi E.E. et al. (2010) Estimating time since infection in early homogeneous HIV-1 samples using a Poisson model. BMC Bioinformatics, 11, 532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goonetilleke N. et al. (2009) The first T cell response to transmitted/founder virus contributes to the control of acute viremia in HIV-1 infection. J. Exp. Med., 206, 1253–1272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haaland R.E. et al. (2009) Inflammatory genital infections mitigate a severe genetic bottleneck in heterosexual transmission of subtype A and C HIV-1. PLoS Pathog., 5, e1000274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu W.S., Temin H.M. (1990) Genetic consequences of packaging two RNA genomes in one retroviral particle: pseudodiploidy and high rate of genetic recombination. Proc. Natl. Acad. Sci. USA., 87, 1556–1560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James M.M. et al. (2011) Association of HIV diversity and survival in HIV-infected Ugandan infants. PLoS One, 6, e18642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufman L., Rousseeuw P.J. (2005) Finding Groups in Data: An Introduction to Cluster Analysis. Wiley-Interscience, Hoboken, NJ. [Google Scholar]
- Keele B.F. et al. (2008) Identification and characterization of transmitted and early founder virus envelopes in primary HIV-1 infection. Proc. Natl. Acad. Sci. USA, 105, 7552–7557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilby J.M. et al. (2008) Treatment response in acute/early infection versus advanced AIDS: equivalent first and second phases of HIV RNA decline. Aids, 22, 957–962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Learn G.H. et al. (2002) Virus population homogenization following acute human immunodeficiency virus type 1 infection. J. Virol., 76, 11953–11959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee H.Y. et al. (2009) Modeling sequence evolution in acute HIV-1 infection. J. Theor. Biol., 261, 341–360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H. et al. (2010) High multiplicity infection by HIV-1 in men who have sex with men. PLoS Pathog, 6, e1000890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao H.X. et al. (2013) Co-evolution of a broadly neutralizing HIV-1 antibody and founder virus. Nature, 496, 469–476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long E.M. et al. (2000) Gender differences in HIV-1 diversity at time of infection. Nat. Med., 6, 71–75. [DOI] [PubMed] [Google Scholar]
- Mansky L.M., Temin H.M. (1995) Lower in vivo mutation rate of human immunodeficiency virus type 1 than that predicted from the fidelity of purified reverse transcriptase. J. Virol., 69, 5087–5094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markowitz M. et al. (2003) A novel antiviral intervention results in more accurate assessment of human immunodeficiency virus type 1 replication dynamics and T-cell decay in vivo. J. Virol., 77, 5037–5038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin D.P. et al. (2010) RDP3: A flexible and fast computer program for analysing recombination, Bioinformatics, 6, 2462–2463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin D.P. et al. (2005) RDP2: recombination detection and analysis from sequence alignments. Bioinformatics, 21, 260–262. [DOI] [PubMed] [Google Scholar]
- McMichael A.J. et al. (2010) The immune response during acute HIV-1 infection: clues for vaccine development. Nat. Rev. Immunol., 10, 11–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer S. et al. (2005) Multiple, linked human immunodeficiency virus type 1 drug resistance mutations in treatment-experienced patients are missed by standard genotype analysis. J. Clin. Microbiol., 43, 406–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park S.Y. et al. (2014) Developing high-throughput HIV incidence assay with pyrosequencing platform. J. Virol., 88, 2977–2990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park S.Y. et al. (2011) Designing a genome-based HIV incidence assay with high sensitivity and specificity. Aids, 25, F13–F19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perelson A.S. et al. (1996) HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science, 271, 1582–1586. [DOI] [PubMed] [Google Scholar]
- Piantadosi A. et al. (2007) Chronic HIV-1 infection frequently fails to protect against superinfection. PLoS Pathog., 3, e177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powers K.A. et al. (2008) Rethinking the heterosexual infectivity of HIV-1: a systematic review and meta-analysis. Lancet Infect. Dis., 8, 553–563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Redd A.D. et al. (2012) The rates of HIV superinfection and primary HIV incidence in a general population in Rakai, Uganda. J. Infect. Dis., 206, 267–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Redd A.D. et al. (2013) Frequency and implications of HIV superinfection. Lancet Infect. Dis., 13, 622–628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ribeiro R.M. et al. (2010) Estimation of the initial viral growth rate and basic reproductive number during acute HIV-1 infection. J. Virol., 84, 6096–6102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richman D.D. et al. (2003) Rapid evolution of the neutralizing antibody response to HIV type 1 infection. Proc. Natl. Acad. Sci. U. S. A., 100, 4144–4149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robertson D.L. et al. (1995a) Recombination in AIDS viruses. J. Mol. Evol., 40, 249–259. [DOI] [PubMed] [Google Scholar]
- Robertson D.L. et al. (1995b) Recombination in HIV-1. Nature, 374, 124–126. [DOI] [PubMed] [Google Scholar]
- Sagar M. et al. (2003) Infection with multiple human immunodeficiency virus type 1 variants is associated with faster disease progression. J. Virol., 77, 12921–12926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salazar-Gonzalez J.F. et al. (2008) Deciphering human immunodeficiency virus type 1 transmission and early envelope diversification by single-genome amplification and sequencing. J. Virol., 82, 3952–3970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schervish M.J. (1995) Theory of Statistics. Springer-Verlag, New York. [Google Scholar]
- Simon V. et al. (2005) Natural variation in Vif: differential impact on APOBEC3G/3F and a potential role in HIV-1 diversification. PLoS Pathog., 1, 0020–0028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stafford M.A. et al. (2000) Modeling plasma virus concentration during primary HIV infection. J. Theor. Biol., 203, 285–301. [DOI] [PubMed] [Google Scholar]
- Theodoridis S., Koutroumbas K. (2008) Pattern Recognition. Academic Press, Burlington. [Google Scholar]
- Wolinsky S.M. et al. (1992) Selective transmission of human immunodeficiency virus type-1 variants from mothers to infants. Science, 255, 1134–1137. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


