Ethnic Inequality

Abstract

This study explores the consequences and origins of between-ethnicity economic inequality across countries. First, combining satellite images of nighttime luminosity with the historical homelands of ethnolinguistic groups we construct measures of ethnic inequality for a large sample of countries. We also compile proxies of overall spatial inequality and regional inequality across administrative units. Second, we uncover a strong negative association between ethnic inequality and contemporary comparative development; the correlation is also present when we condition on regional inequality, which is itself related to under-development. Third, we investigate the roots of ethnic inequality and establish that differences in geographic endowments across ethnic homelands explain a sizable fraction of the observed variation in economic disparities across groups. Fourth, we show that ethnic-specific inequality in geographic endowments is also linked to under-development.

1 Introduction

Ethnic diversity has costs and benefits. On the one hand, diversity in skills, education, and endowments can enhance productivity by promoting innovation. On the other hand, diversity is often associated with poor and ethnically targeted policies, inefficient provision of public goods, and ethnic-based hatred and conflict. In fact, a large literature finds a negative impact of ethnolinguistic fragmentation on various aspects of economic performance, with the possible exception of wealthy economies (see Alesina and Ferrara (2005) for a review). Income inequality may also have both positive and negative effects on development. On the negative side, a higher degree of income inequality may lead to conflict and crime, prevent the poor from acquiring education, and/or lead to expropriation and lofty taxation discouraging investment. On the positive side, income inequality may spur innovation and entrepreneurship by motivating individuals and by providing the necessary pools of capital for capital-intensive modes of production. Further complicating the relationship between the two, a positive correlation between inequality and development may reflect Simon Kuznetz’s conjecture that industrialization translates into higher levels of inequality at the early stages of development; while at later stages, the association becomes negative. Given the theoretical ambiguities (and data issues), perhaps it comes at no surprise that it has been very hard to detect empirically a robust association between inequality and development (see Benabou (2005) and Galor (2011) for surveys).

This paper puts forward and tests an alternative conjecture that focuses on the intersection of ethnic diversity and inequality. Our thesis is that what matters most for comparative development are economic differences between ethnic groups coexisting in the same country, rather than the degree of fractionalization per se or income inequality conventionally measured (i.e., independent of ethnicity).¹

The first contribution of this study is to provide measures of within-country differences in well-being across ethnic groups, defined as “ethnic inequality.” To overcome the sparsity of income data along ethnic lines and in order to construct country-level indicators of ethnic inequality for the largest possible set of states, we combine ethnographic and linguistic maps on the location of groups with satellite images of light density at night which are available at a fine grid. Recent studies have shown that luminosity is a strong proxy of development (e.g., Henderson, Storeygard, and Weil (2012)). The cross-ethnic group inequality index is weakly correlated with the commonly employed –and notoriously poorly measured– income inequality measures at the country level and is modestly correlated with ethnic fractionalization. To isolate the cross-ethnic component of inequality from the overall regional inequality, we also construct proxies of spatial inequality and measures capturing regional differences in well-being across first and second-level administrative units.

Second, we document a strong negative association between ethnic inequality and real GDP per capita across countries. This correlation holds even when we control for the overall degree of spatial inequality and inequality across administrative regions. The latter is also inversely related to a country’s economic performance, a novel finding in itself. We also uncover that the negative correlation between ethnolinguistic fragmentation and development weakens considerably (and becomes statistically indistinguishable from zero) when we account for ethnic inequality; this suggests that it is the unequal concentration of wealth across ethnic lines that correlates with development rather than diversity per se.

Third, in an effort to shed light on the roots of ethnic inequality, we explore its geographic underpinnings. In particular, motivated by recent work showing that linguistic groups tend to reside in distinct land endowments, see Michalopoulos (2012), we construct Gini coefficients reflecting differences in various geographic attributes across ethnic homelands and show that the latter is a strong predictor of ethnic inequality. On the contrary, there is no link between contemporary ethnic inequality and often-used historical variables capturing the type of colonization and legal origin among others.

Fourth, we show that contemporary development at the country level is also inversely related to inequality in geographic endowments across ethnic homelands. Yet, once we condition on between-group income inequality, differences in geographic endowments are no longer a significant correlate of underdevelopment. These results suggest that geographic differences across ethnic homelands influence comparative development mostly via shaping economic inequality across groups.

Mechanisms and Related Works

Income disparities along ethnic lines are likely to lead to political inequality based on ethnic affiliation, increase between-group animosity, and lead to discriminatory policies of one (or more) groups against the others. In line with this idea, in recent work Huber and Suryanarayan (2013) document that party ethnification in India is more pronounced in states with a high degree of inequality across sub-castes.² Furthermore, differences in preferences along both ethnic and income lines may lead to inadequate public goods provision, as groups’ ideal allocations of resources will be quite distant. Baldwin and Huber (2010) provide empirical evidence linking between-group inequality to the under-provision of public goods for 46 democracies. In Alesina, Michalopoulos, and Papaioannou (2014), we show that there is a strong inverse link between ethnic inequality and public goods within 18 Sub-Saharan African countries (and that this effect partly stems from political inequality and ethnic-based discrimination).³ Ethnic inequality may also impede institutional development and the consolidation of democracy (Robinson (2001)). In line with this conjecture, Kyriacou (2013) exploits survey data from 29 developing countries and shows that socioeconomic ethnic-group inequalities reduce government quality.

Chua (2003) presents case-study evidence arguing that the presence of an economically dominant ethnic minority may lower support for democracy and free-market institutions, as the majority of the population usually feels that the benefits of capitalism go to just a handful of ethnic groups. She discusses, among others, the influence of Chinese minorities in the Philippines, Indonesia, Malaysia, and other Eastern Asian countries; the dominant role of (small) Lebanese communities in Western Africa; and the similarly strong influence of Indian societies in Eastern Africa. Other examples, include the I(g)bo in Nigeria and the Kikuyu in Kenya. Finally, to the extent that ethnic inequality implies that well-being depends on one’s ethnic identity, then it is more likely to generate envy and perceptions that the system is “unfair,” and reduce interpersonal trust, more so than the conventionally measured economic inequality, since the latter can be more easily thought of as the result of ability or effort. Consistent with the view that ethnic inequality is detrimental to the formation of social ties across groups, Tesei (2014) finds that greater racial inequality across US metropolitan areas is associated with low levels of social capital.

Organization

The paper is organized as follows. In section 2, we describe the construction of the ethnic (and regional) inequality measures and present summary statistics and the basic correlations. In section 3, we report the results of our analysis associating income per capita with ethnic inequality across 173 countries. Besides reporting various sensitivity checks, we also examine the link between development and inequality across administrative regions. In section 4, we explore the geographic origins of contemporary differences in economic performance across groups. In section 5, we report estimates associating contemporary development with inequality in geographic endowments across ethnic homelands. In the last section, we summarize our findings and discuss avenues for future research.

2 Data

To construct proxies of ethnic inequality for the largest set of countries, we combine information from ethnographic/linguistic maps on the location of groups with satellite images of light density at night that are available at a fine grid. In this section, we discuss the construction of the cross-country measures reflecting inequality in development (as captured by luminosity per capita) across ethnic homelands within 173 countries. We also describe in detail the construction of the other measures of spatial inequality and discuss the main patterns.

2.1 Ethnic Inequality Measures

2.1.1 Location of Ethnic Groups

We identify the location of ethnic groups employing two data sets/maps.⁴ First, we use the Georeferencing of Ethnic Groups (GREG), which is the digitized version of the Soviet Atlas Narodov Mira (Weidmann, Rod, and Cederman (2010)). GREG portrays the homelands of 928 ethnic groups around the world. The information pertains to the early 1960s, so for many countries, in Africa in particular and to a lesser extent in South-East Asia, it corresponds to the time of independence.⁵ The data set uses the political boundaries of 1964 to allocate groups to different countries. We thus project the ethnic homelands to the political boundaries of the 2000 Digital Chart of the World; this results in 2,129 ethnic homelands within contemporary countries. Most areas (1,637) are coded as pertaining to a single group, whereas in the remaining 492 homelands, there can be up to three overlapping groups. For example, in Northeast India over an area of 4,380 km², the Assamese, the Oriyas and the Santals overlap. The luminosity of a region where multiple groups reside contributes to the average luminosity of each group. The size of ethnic homelands varies considerably. The smallest polygon occupies an area of 1.09 km² (French in Monaco), and the largest extends over 7,335,476 km² (American English in the US). The median (mean) group size is 4,183 (61,213) km². The median (mean) country in our sample has 8 (11.5) ethnicities with the most diverse being Indonesia with 95 groups.

Our second source is the 15th edition of the Ethnologue (Gordon (2005)) that maps 7,581 language-country groups worldwide in the mid/late 1990s, using the political boundaries of 2000. In spite of the comprehensive linguistic mapping, Ethnologue’s coverage of the Americas and Australia is rather limited while for others (i.e., Africa and Asia), it is very detailed. Each polygon delineates a traditional linguistic region; populations away from their homelands (in cities, refugee camps) are not mapped. Groups of unknown location, as well as widespread and extinct languages are not mapped either, the only exception is the English in the United States. Ethnologue also records areas where languages overlap. Ethnologue provides a more refined linguistic aggregation compared to the GREG. As a result the median (mean) homeland extends to 726 (12,676) km². The smallest language is the Domari in Israel which covers 1.18 km² and the largest group is the English in the US covering 7,330,520 km². The median (mean) country has 9 (42.3) groups with Papua New Guinea being the most diverse with 809 linguistic groups.

GREG attempts to map major immigrant groups whereas Ethnologue generally does not. This is important for countries in the New World. For example, in Argentina GREG reports 16 groups, among them Germans, Italians, and Chileans, whereas Ethnologue reports 20 purely indigenous groups (e.g., the Toba and the Quechua). For Canada, Ethnologue lists 77 mostly indigenous groups, like the Blackfoot and the Chipewyan with only English and French being non-indigenous; in contrast, GREG lists 23 groups featuring many non-indigenous ones, such as Swedes, Russians, Norwegians, and Germans. Hence, the two ethnolinguistic mappings capture different cleavages, at least in some continents. Though we have performed various sensitivity checks, for our benchmark results we are including all groups without attempting to make a distinction as to which cleavage is more salient.⁶

It is important to note that the underlying maps do include regions where groups overlap and we take that into account in our measure, as we show below. However, both maps do not capture relatively recent within-country migrations towards the urban centers, for example. The reason is that the original sources attempt to trace the historical homeland of each group. Hence, actual ethnic mixing is likely higher than what the ethnographic maps reflect. This will induce measurement error to our proxies of ethnic inequality. Nevertheless, under the assumption that in a given urban center the respective indigenous group is relatively more populous than recent migrant ones, then assigning the observed luminosity per capita to this group is not entirely ad hoc. Moreover, there is a large literature documenting that migrant workers channel systematically a fraction of their earnings back to their homelands. This would imply that although we do not observe migrant workers in our dataset to the extent that they send remittances to their families and influence their livelihoods, this will be reflected in the luminosity per capita of the ancestral homelands which we directly measure. Moreover, to at least partially account for this issue, we have constructed all inequality measures also excluding the regions where capitals fall.

2.1.2 Data on Luminosity and Population

Comparable data on income per capita at the ethnicity level are scarce. Hence, following Henderson, Storeygard, and Weil (2012) and subsequent studies (e.g., Chen and Nordhaus (2011), Pinkovskiy (2013), Pinkovskiy and Sala-i-Martin (2014), Hodler and Raschky (2014), Michalopoulos and Papaioannou (2013) Michalopoulos and Papaioannou (2014), we use satellite image data on light density at night as a proxy. These –and other works– show that luminosity is a strong correlate of development at various levels of aggregation (countries, regions, ethnic homelands). The luminosity data come from the Defense Meteorological Satellite Program’s Operational Linescan System that reports images of the earth at night (from 20:30 till 22:00). The six-bit number that ranges from 0 to 63 is available approximately at every square kilometer since 1992.

To construct luminosity at the desired level of aggregation, we average all observations falling within the boundaries of an ethnic group and then divide by the population of each area using data from the Gridded Population of the World that reports georeferenced pixel-level population estimates for 1990 and 2000.⁷

2.1.3 New Ethnic Inequality Measures

We proxy the level of economic development in ethnic homeland i with mean luminosity per capita, y_i; and we then construct an ethnic Gini coefficient for each country that reflects inequality across ethnolinguistic regions. Specifically, the Gini coefficient for a country’s population consisting of n groups with values of luminosity per capita for the historical homeland of group i, y_i, where i = 1 to n are indexed in non-decreasing order (y_i ≤ y_i+1), is calculated as follows:

$$G=\frac{1}{n}\left(n+1-2\frac{{\displaystyle {\sum }_{i=1}^n\left(n+1-i\right)y_i}}{{\displaystyle {\sum }_{i=1}^n{y}_i}}\right)$$

The ethnic Gini index captures differences in mean income –as captured by luminosity per capita at the ethnic homeland– across groups. For each of the two different ethnic-linguistic maps (Atlas Narodov Mira and Ethnologue) we construct Gini coefficients for the maximum sample of countries using cross-ethnic-homeland data in 1992, 2000, and 2012. For each mapping we construct three ethnic Ginis. First, for our baseline estimates we use information from all groups. Second, we construct the Gini coefficient dropping the capital cities. This allows us to account both for extreme values in luminosity and also for population mixing which is naturally higher in capitals. Third, we compile measures excluding small ethnicities, defined as those representing less than 1% of the 2000 population in a country.⁸

2.2 Measures of Spatial Inequality

Since we use ethnic homelands (rather than individual-level) data to measure between-group inequality, the ethnic inequality measures also reflect regional disparities in income and/or public goods provision that may not be related to ethnicity per se. To isolate the between-ethnicity component of inequality from the regional one, we also construct Gini coefficients reflecting (i) the overall degree of spatial inequality and (ii) inequality across (first and second level) administrative units for each country. Moreover, in an attempt to assess the accuracy of the underlying groups’ mappings, we perturbed the original homelands and compiled Gini coefficients based on these altered ethnic homelands.

2.2.1 Overall Spatial Inequality Index

Our baseline index reflecting the overall degree of spatial inequality is based on aggregating (via the Gini coefficient formula) luminosity per capita across roughly equally-sized pixels in each country. We first generate a global grid of 2.5 × 2.5 decimal degrees (that extends from −180 to 180 degrees longitude and from 75 degrees latitude to −65 degrees latitude). Second, we intersect the resulting grid with the 2000 Digital Chart of the World that portrays contemporary national borders. This results in 4,865 pixels across the globe falling within country boundaries. The median (mean) box extends to 22,438 (27,622) km², being comparable to the size of ethnic homelands in the GREG dataset, when we exclude small groups. Note that boxes intersected by the coastline and national boundaries are smaller. Third, for each box we compute luminosity per capita in 1992, 2000, and 2012. Fourth, we aggregate the data at the country level estimating a Gini coefficient that captures the overall degree of spatial inequality. The cross-country mean (median) number of pixels used for the estimation of the spatial Ginis is 24.9 (8); so these Ginis are quite comparable to the ethnic inequality measures.

2.2.2 Inequality across Administrative Regions

We also compiled inequality measures across administrative units, using data from the GADM Global Administrative Areas database on the boundaries of administrative regions. Following a similar procedure to the derivation of the ethnic inequality and the overall spatial inequality indexes, we construct measures reflecting inequality (in lights per capita) across first-level and second-level administrative units. In our sample of 173 countries, the median (mean) number of first-level administrative units is 13 (17). A median (mean) first-level administrative unit spans roughly 7,197 (44,050) square kilometers, which is somewhat larger than the median size (4,578) for groups in the Atlas Narodov Mira. The cross-country median (mean) size of second-level administrative units is 110 (301) km². So, these units are much smaller than the Ethnologue or the Atlas Narodov Mira homelands.

2.2.3 Inequality across Perturbed Ethnic Regions

We have also created ethnic Gini coefficients using perturbed ethnic regions. Using as inputs the centroids of ethnic-linguistic homelands, we generate Thiessen polygons that have the unique property that each polygon contains only one input point and that any location within a polygon is closer to its associated point than to a point within any other polygon. Thiessen polygons have the exact same centroids as the actual linguistic and ethnic homelands in the Ethnologue and GREG databases, respectively; the key difference being that the actual homelands have idiosyncratic shapes.⁹ We then construct a spatial Gini coefficient that reflects inequality in lights per capita across these sets of Thiessen polygons. The mean size of the Thiessen polygons based on the Ethnologue (GREG) database is 11,862 (58,784) km², very similar to the mean size of homelands in the Ethnologue (GREG) −12,676 (61,213) km².

Comment

All three proxies of the spatial inequality also reflect inequality across ethnic homelands, since (i) there is clearly some degree of measurement error on the exact boundaries of ethnic regions, (ii) population mixing is likely higher than the one we observe in the data. Moreover, in several countries, administrative boundaries follow ethnic lines, while in the case of large groups, the spatial Gini coefficients may also (partially) capture within-ethnic-group inequality.¹⁰

2.3 Example

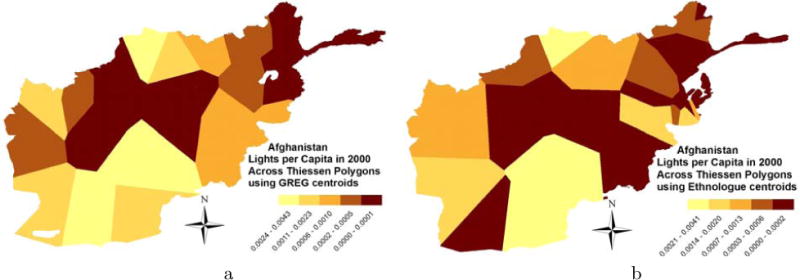
Figures 1 and 2 provide an illustration of the construction of the ethnic inequality measures for Afghanistan. The Atlas Narodov Mira (GREG) maps 31 ethnicities (Figure 1a) whereas the Ethnologue reports 39 languages (Figure 2a). According to GREG, the Afghan (Pashtuns) is the largest group residing in the southern and central-southern regions. This group makes up 51% of the population in 2000. The second largest group are the Tajik people, who compose 22% of the population and are located in the north-eastern regions and in scattered pockets in the western part of the country. There are 8 territories in which groups overlap.

Figure 1.

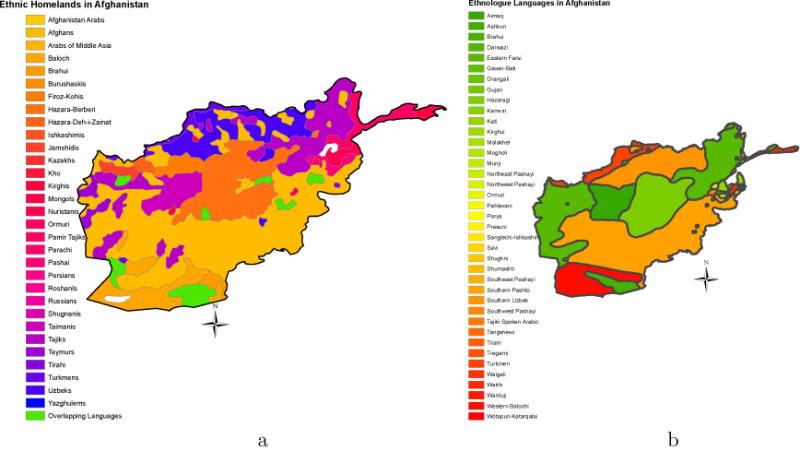
Figure 2.

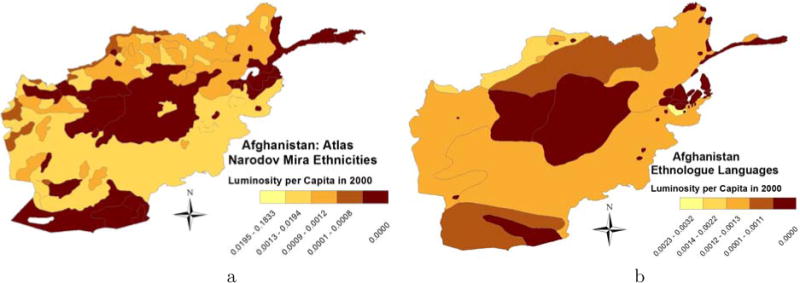
Figures 1b and 2b portray the distribution of lights per capita for each group with lighter colors indicating more brightly-lit homelands. The center of the country, where the Hazara-Berberi reside, is poor; the same applies to the eastern provinces, where the Nuristani, the Pamir Tajiks, the Pashai, and the Kyrgyz groups are located. Luminosity is higher in the Pashtun/Pathans homelands and to some lesser extent in the Tajik regions. Second, using lights per capita across all homelands, we estimate the Gini coefficient in 1992, in 2000, and in 2012. In 2000 the Gini coefficient estimated from GREG (Ethnologue) is 0.95 (0.90).¹¹ We also estimated the ethnic inequality measures excluding the ethnic homeland where the capital, Kabul, falls. In this case the ethnic Ginis are similar (0.95 with GREG and 0.91 with Ethnologue). For robustness, we also estimated Gini coefficients of ethnic inequality excluding groups constituting less than 1% of the country’s population. In this case the Gini coefficient with the GREG mapping is based on just 4 groups, while the Ethnologue-based Gini is based on 7 ethnic homelands.

Figure 3 illustrates the construction of the overall spatial inequality. When we divide the globe into boxes of 2.5 × 2.5 decimal-degree boxes, we get 24 areas in Afghanistan. The estimated Gini index capturing the overall degree of spatial inequality in Afghanistan is 0.73. For consistency we also estimated the overall spatial inequality (Gini) index excluding the pixel where the capital city falls or those boxes where less than 1% of the country’s population lived in 2000. Figures 4a and 4b illustrate the construction of inequality measures across administrative regions using both the first-level and second-level units. There are 32 provinces (velayat) that constitute the first-level administrative units and there are 328 second-level administrative units (wuleswali). After estimating average luminosity per capita for each unit, we construct Gini indexes capturing inequality in development across administrative regions. Again, we construct these inequality measures using all regions, dropping the capital, and also excluding those units with less than one percent of total population. In our example, the first-level administrative unit Gini index is 0.76 and the second-level administrative unit Gini coefficient is 0.93. Figures 5a and 5b illustrate the derivation of the perturbed ethnic homelands Gini index for Afghanistan based on the Atlas Narodov Mira and the Ethnologue, respectively. There are 31 and 39 Thiessen polygons, as many as the number of ethnic and linguistic groups. The centroids of the Thiessen polygons are identical to the ones of the actual homelands, the only difference being that the actual homelands have rather peculiar shapes.

Figure 3.

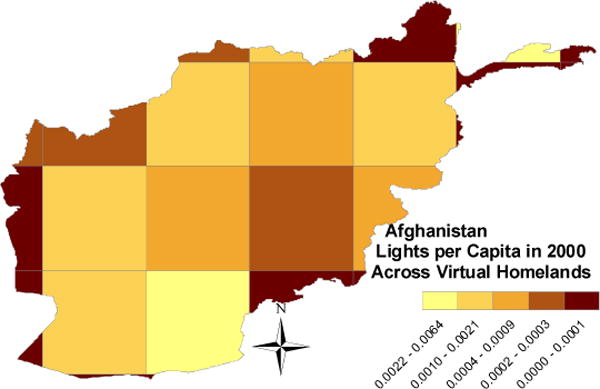
Figure 4.

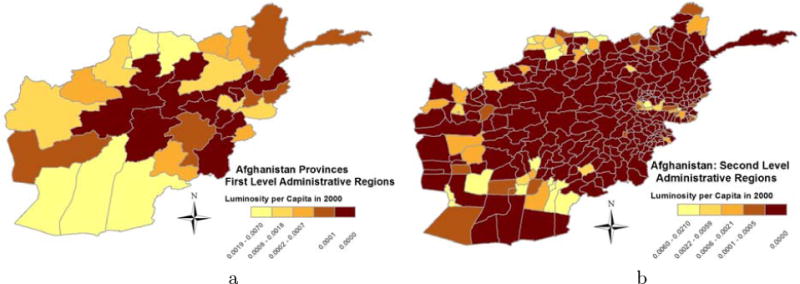
Figure 5.

2.4 Descriptive Evidence

2.4.1 Ethnic Inequality around the World

Table 1 reports summary statistics for the baseline ethnic inequality measures and the proxies of the overall degree of spatial inequality and regional inequality across administrative units. The average and median values of the ethnic Gini coefficients are quite similar with both mappings in each year (around 0.42 – 0.49 in 2000). The average (median) value of the overall spatial Gini coefficient in 2000 is similar, 0.42 (0.43). The Gini coefficients based on administrative regions are on average smaller when estimated across first-level units (mean 0.37) and larger when estimated at the finer second-level (mean 0.57). Moreover, regional inequality seems to be slightly trending downward, as all Gini coefficients are smaller in 2012 (and in 2000). This may be driven by the expansion of electrification (and regional convergence) in many underdeveloped and developing countries (mostly in Africa and South Asia).

Table 1.

Summary Statistics – Cross-Country Inequality Measures

	Obs.	mean	st. dev.	min	p25	median	p75	max
	Panel A: Atlas Narodov Mira (GREG)
Number of Ethnic Homelands (GREG)	173	10.994	13.579	1	3	8	12	94
Ethnic Gini in 2012 (GREG)	173	0.406	0.248	0.00	0.21	0.44	0.57	0.96
Ethnic Gini in 2000 (GREG)	173	0.424	0.260	0.00	0.20	0.48	0.63	0.97
Ethnic Gini in 1992 (GREG)	173	0.473	0.280	0.00	0.27	0.54	0.70	0.96
	Panel B: Ethnologue
Number of Linguistic Homelands (ETHNOLOGUE)	173	38.619	94.029	1	3	8	35	753
Ethno-Linguistic Gini in 2012 (ETHNOLOGUE)	173	0.439	0.325	0.00	0.13	0.44	0.74	0.98
Ethno-Linguistic Gini in 2000 (ETHNOLOGUE)	173	0.446	0.333	0.00	0.12	0.49	0.77	0.98
Ethno-Linguistic Gini in 1992 (ETHNOLOGUE)	173	0.487	0.346	0.00	0.14	0.54	0.80	0.99
	Panel C: Pixels
Number of Pixels	173	19.572	36.838	1.00	4.00	8.00	20	292
Spatial Gini in 2012, Pixels	173	0.411	0.270	0.00	0.18	0.42	0.60	0.98
Spatial Gini in 2000, Pixels	173	0.421	0.269	0.00	0.18	0.43	0.64	0.97
Spatial Gini in 1992, Pixels	173	0.463	0.271	0.00	0.21	0.49	0.70	0.96
	Panel D: First-level Administrative Units
Number of 1st-Level Administrative Units	173	16.873	14.962	1.00	8.00	12.00	20	88
Administrative Unit (1st-level) Gini in 2012	173	0.353	0.202	0.00	0.20	0.30	0.45	0.93
Administrative Unit (1st-level) Gini in 2000	173	0.368	0.215	0.00	0.21	0.31	0.48	0.94
Administrative Unit (1st-level) Gini in 1992	173	0.422	0.241	0.00	0.21	0.38	0.59	0.94
	Panel E: Second-level Administrative Units
Number of 2nd-Level Administrative Units	135	290.104	626.285	11.00	48.00	99.00	248	5478
Administrative Unit (2nd-level) Gini in 2012	135	0.562	0.237	0.14	0.35	0.56	0.78	0.95
Administrative Unit (2nd-level) Gini in 2000	135	0.572	0.250	0.15	0.36	0.55	0.83	0.96
Administrative Unit (2nd-level) Gini in 1992	135	0.639	0.249	0.13	0.43	0.68	0.87	0.98

The table reports summary statistics for the main ethnic inequality, overall spatial inequality and administrative unit inequality measures employed in the cross-country analysis. Section 2 and the Data Appendix gives details on the construction of the ethnic inequality measures (Gini Coefficients). All Gini coefficients are estimated using luminosity per capita across ethnic homelands (in Panel A), across linguistic homelands (in Panel B), pixels/boxes of roughly same size (in Panel C), first-level administrative units (in Panel D), and second-level administrative units (in Panel E).

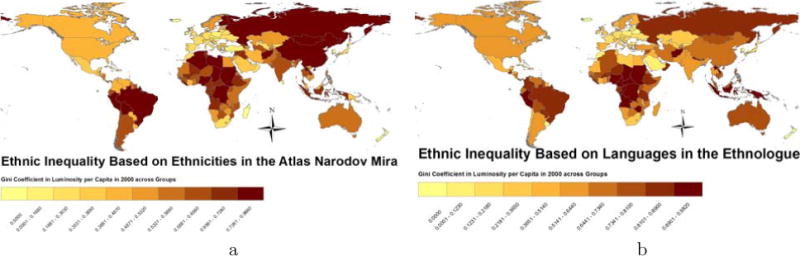
Figures 6a and 6b illustrate the global distribution of ethnic inequality with the GREG and Ethnologue mapping, respectively. Sub-Saharan Africa and East and South Asia host the most ethnically unequal countries. For example, with the Ethnologue mapping the mean (median) of the baseline ethnic inequality index for Sub-Saharan African countries is 0.63 (0.728), while for South and East Asian countries the corresponding mean (and median) value of the ethnic Gini index is 0.59 (0.69).¹² In contrast, Western Europe is the region with the lowest level of ethnic inequality (mean and median values of ethnic Gini around 0.24). According to the Atlas Narodov Mira, the five most ethnically unequal countries are Sudan, Afghanistan, Mongolia, Zambia, and Central African Republic with an average Gini coefficient in luminosity across ethnic homelands of 0.91. According to the Ethnologue’s more detailed mapping of language groups, the countries with the highest cross-ethnic-group inequality (where Gini exceeds 0.95) are: Democratic Republic of Congo, Papua New Guinea, Sudan, Ethiopia, and Chad.

Figure 6.

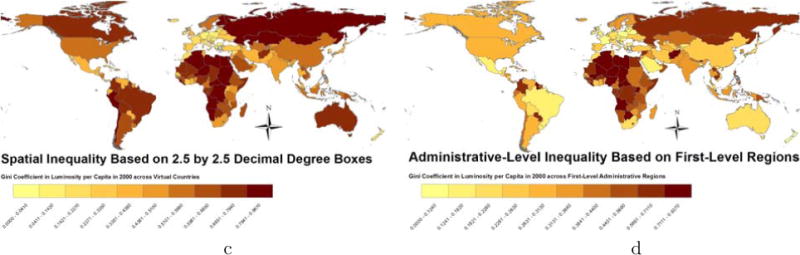
Figures 6c and 6d plot the world distribution of the overall degree of spatial inequality and regional inequality across first-level administrative units, respectively. As it is evident, spatial and regional inequality is much higher in Asia and Africa as compared to Western Europe and Latin America. The countries with the highest overall spatial inequality according to the measure based on the 2.5 × 2.5 decimal degree boxes are Russia, Mongolia, Sudan, Peru, and Egypt; in all these countries the spatial Gini coefficient exceeds 0.90. The countries with the highest regional inequality across first-level administrative units are Libya, Chad, and Guinea (Gini around 0.90). We should stress that in some countries first-level administrative units cover large territories (in terms of both population and land area). Hence, inequality measured across these units may not adequately capture existing regional inequalities. To partly account for this, we have also constructed Gini coefficients using second-level administrative regions that in many countries are numerous. However, an important caveat to keep in mind throughout the analysis is that in several countries regional inequalities and, more importantly, ethnic disparities in income may occur at much finer levels of aggregation (e.g., neighborhoods) than what our ancestral-ethnic-homeland approach allows for.¹³

Appendix Table 1 reports the correlation structure of the ethnic Gini coefficients between the two global maps at different points in time. A couple of interesting patterns emerge. First, the correlation of the Gini coefficients across the two alternative mappings is strong, but not overwhelming. The correlation with the baseline measures that uses all ethnic areas is around 0.75, but when we drop small groups or/and capitals the correlation falls to 0.65. In line with our discussion above, these correlations suggest that the two maps capture somewhat different aspects of ethnic-linguistic cleavages. Second, in the 20-year period where luminosity data are available (1992–2012), ethnic inequality appears very persistent, as the correlations of the Gini coefficients over time exceed 0.90. Given the high inertia, in our empirical analysis below we will exploit cross-country variation. Third, not surprisingly, the correlation between ethnic inequality and the Gini coefficient capturing the overall degree of spatial inequality and regional inequality across (first-level) administrative units is positive, but again far from perfect. In particular, the correlation of the ethnic Gini with the overall spatial Gini (based on artificial boxes) ranges between 0.55 and 0.70, while the correlation of the ethnic Gini coefficients with the administrative unit Ginis is lower, around 0.50.

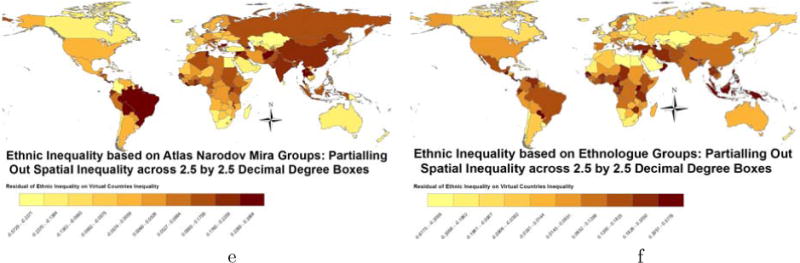
Since we are primarily interested in documenting the explanatory power of ethnic inequality beyond the overall spatial inequality in most specifications, we control for the latter. Figures 6e and 6f portray the global distribution of ethnic inequality partialling out the effect of the overall spatial inequality.

2.4.2 Basic Correlations

Ethnic Diversity

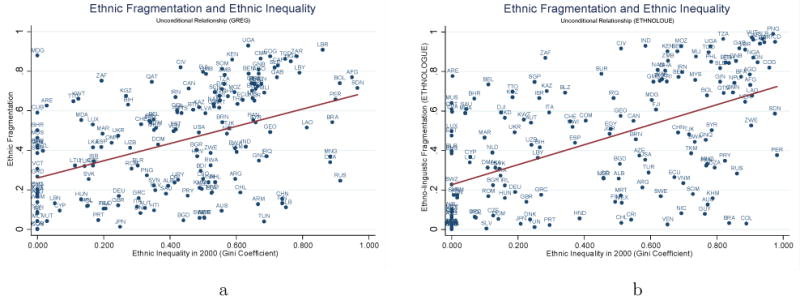
Appendix Table 2 – Panel A reports the correlation structure between the various ethnic inequality and spatial inequality measures and the widely-used ethnolinguistic fragmentation indexes. We observe a positive correlation between ethnic inequality and linguistic-ethnic fractionalization (0.35 – 0.45). Figures 7a and 7b provide a graphical illustration of the association between the two proxies of ethnic inequality and the ethnic and linguistic fragmentation measures of Alesina, Devleeschauwer, Easterly, Kurlat, and Wacziarg (2003) and Desmet, Ortuño-Ortín, and Wacziarg (2012), respectively. The correlation between ethnic inequality and the segregation measures compiled by Alesina and Zhuravskaya (2011) is also positive (0.20–0.45). Ethnic inequality tends to go in tandem with segregation. This is reasonable since economic differences between groups are more likely to persist when groups are also geographically separated. We also examine the association between ethnic inequality and spatial inequality with the ethnic polarization indicators of Montalvo and Reynal-Querol (2005), failing to detect a systematic association. These patterns suggest that the ethnic inequality measure captures a dimension distinct from already-proposed aspects of a country’s ethnic composition.

Figure 7.

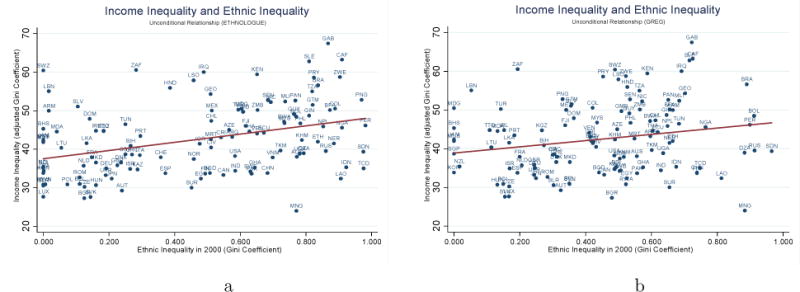
Income Inequality

We then examined the association between ethnic inequality and income inequality, as reflected in the standard Gini coefficient (Appendix Table 2 – Panel B). The income Gini coefficient is taken from Easterly (2007), who using survey and census data compiled by the WIDER (UN’s World Institute for Development Economics Research) constructs adjusted cross-country Gini coefficients for more than a hundred countries over the period 1965 – 2000. Figures 8a and 8b illustrate this association using the GREG and the Ethnologue mapping, respectively. The correlation between ethnic inequality and economic inequality is moderate, around 0.25–0.30. Yet this correlation weakens considerably and becomes statistically insignificant once we simply condition on continental constants.

Figure 8.

3 Ethnic Inequality and Development

3.1 Baseline Estimates

In Table 2 we report cross-country least squares estimates (OLS), relating the log of per capita GDP in 2000 with ethnic inequality. In Panel A we use the ethnic inequality measure based on the Atlas Narodov Mira mapping, while in Panel B we use the measures derived from Ethnologue’s mapping. In all specifications we include region-specific constants (following the World Bank’s classification) to account for continental differences in ethnic inequality and comparative economic development.

Table 2.

A – Baseline Estimates: Ethnic Inequality and Economic Development (in 2000), Atlas Narodov Mira (GREG)
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
Ethnic Inequality [Gini Coeff., GREG]	−1.3911*** (0.2588)		−1.3900*** (0.3416)		−0.9518** (0.3953)	−0.9276* (0.4845)	−1.3449*** (0.4943)	−1.1032** (0.5188)	−1.1172** (0.5492)
Spatial Inequality [Gini Coeff.,]		−0.9973*** (0.2774)	−0.0015 (0.3510)			−0.0315 (0.3568)	−0.0046 (0.3539)	0.0104 (0.3591)	−0.5592 (0.4749)
Log Number of Ethnicitie [GREG]				−0.3136*** (0.0612)	−0.1429 (0.0908)	−0.1433 (0.0917)		−0.2174* (0.1277)	−0.1863 (0.1440)
Ethnic Inequality in Population [Gini Coeff., GREG]							0.6517 (1.1500)	1.1554 (1.1554)	1.0858 (1.2546)
Ethnic Inequality in Size (Area) [Gini Coeff., GREG]							−0.7933 (1.1732)	−0.7949 (1.1060)	−0.8276 (1.2297)
Log Land Area									0.1442 (0.0879)
Log Population (in 2000)									−0.1368 (0.0829)
Adjusted R-squared	0.654	0.623	0.652	0.646	0.657	0.655	0.65	0.656	0.662
Observations	173	173	173	173	173	173	173	173	173
Region Fixed Effects	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes

B – Baseline Estimates: Ethnic Inequality and Economic Development (in 2000), Ethnologue
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
Ethnic Inequality [Gini Coeff., ETHNO]	−1.1603*** (0.2328)		−1.0745*** (0.2652)		−1.1688*** (0.3587)	−1.0636** (0.4241)	−1.3452*** (0.3469)	−1.2368*** (0.4377)	−1.7186*** (0.4549)
Spatial Inequality [Gini Coeff., Pixels]		−0.9973*** (0.2774)	−0.1549 (0.3021)			−0.1564 (0.3136)	−0.1760 (0.3010)	−0.1992 (0.3165)	−0.5351 (0.4235)
Log Number of Languages [ETHNO]				−0.1921*** (0.0466)	0.0021 (0.0688)	−0.0025 (0.0711)		−0.0378 (0.0826)	0.0726 (0.0967)
Ethnic Inequality in Population [Gini Coeff., ETHNO]							0.8012 (0.9324)	0.8460 (0.9387)	0.8453 (0.9144)
Ethnic Inequality in Size (Area) [Gini Coeff., ETHNO]							−0.4898 (0.8948)	−0.4574 (0.9045)	−0.2958 (0.8853)
Log Land Area									0.1366* (0.0808)
Log Population									−0.2105** (0.0840)
Adjusted R-squared	0.654	0.623	0.652	0.632	0.652	0.65	0.651	0.649	0.665
Observations	173	173	173	173	173	173	173	173	173
Region Fixed Effects	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes

The table reports cross-country OLS estimates. The dependent variable is the log of real GDP per capita in 2000. The ethnic Gini coefficients reflect inequality in lights per capita across ethnic-linguistic homelands. In Table 2A we use the digitized version of the Atlas Narodov Mira (GREG) to aggregate lights per capita across ethnic homelands. In Table 2B we use the digitized version of the Ethnologue database to aggregate lights per capita across linguistic homelands. The overall spatial inequality index (Gini coefficient) captures the degree of spatial inequality across 2.5 by 2.5 decimal degree boxes/pixels in each country (boxes intersected by national boundaries are of smaller size). Section 2 gives details on the construction of the ethnic inequality and spatial inequality (Gini) indexes. The log number of ethnicities in columns (4)–(6), (8), and (9) denotes the logarithm of the number of ethnic and linguistic groups in each country according to the Atlas Narodov Mira (in Table 2A) and the Ehnologue (in Table 2B). Columns (7), (8), and (9) include as controls a Gini index capturing inequality in population across ethnic (linguistic) homelands and a Gini index capturing inequality in land area across ethnic (linguistic) homelands. Column (9 includes the log of country’s land area and the log of population in 2000. All specifications include regional fixed effects (constants not reported). The Data Appendix gives detailed variable definitions and data sources. Robust (heteroskedasticity—adjusted) standard errors are reported in parentheses below the estimates.

***, **, and *indicate statistical significance at the 1%, 5%, and 10% level, respectively.

The coefficient of the ethnic inequality index in column (1) is negative and significant at the 1% level. Figures 9a – 9b illustrate the unconditional and the conditional on regional fixed effects association. Specification (2) also reveals a negative association between economic development and the overall degree of spatial inequality, as reflected on the Gini coefficient based on pixels of 2.5 × 2.5 degrees. This suggests that underdevelopment goes in tandem with regional inequalities. In column (3) we include both the ethnic inequality Gini index and the spatial Gini coefficient. The estimate on the ethnic inequality Gini is stable with both the GREG and the Ethnologue mapping. In contrast, the coefficient on the overall spatial inequality measure drops considerably and becomes statistically indistinguishable from zero in both models. This suggests that the ethnic component of spatial inequality is the relatively stronger negative correlate of development.

Figure 9.

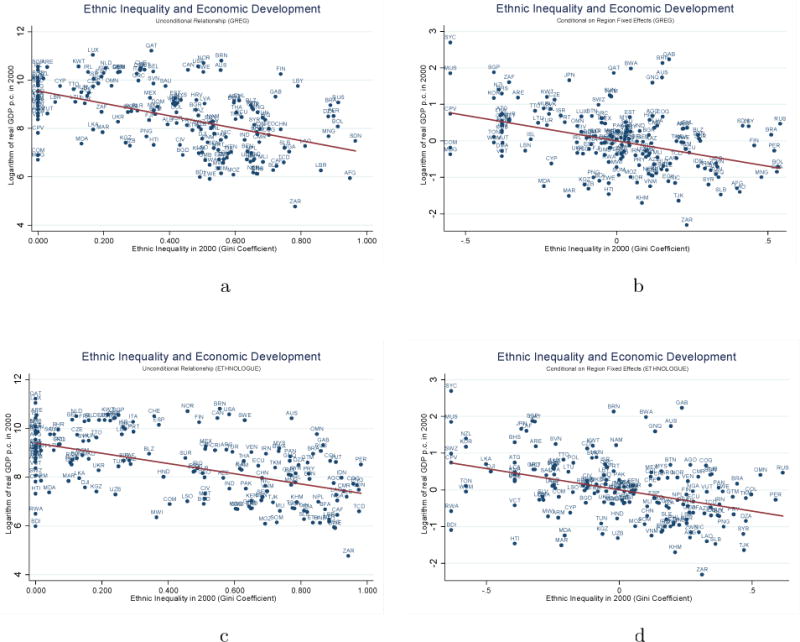
In column (4) we associate the log of per capita GDP with the log number of ethnic/linguistic groups. In line with previous works, income per capita is significantly lower in countries with many ethnic (Panel A) and linguistic (Panel B) groups; yet the estimates in column (5), where we jointly include in the empirical model the proxies of ethnic inequality and fractionalization, show that it is income differences along ethnic lines rather than ethnolinguistic heterogeneity per se that correlates with underdevelopment. The results are similar when we jointly include in the specification the ethnic Gini index, the overall spatial inequality measure, and the fractionalization measure in column (6). Although due to the small number of observations and multi-collinearity (see Appendix Table 1), these results should be interpreted with caution, only the ethnic inequality measure enters with a statistically significant estimate.

In columns (7)–(8) we examine whether the significantly negative association between ethnic inequality and income per capita is driven by an unequal clustering of population across ethnic homelands or by the skewness in the size of ethnic homelands; to do so we construct Gini coefficients of population and land area that capture inequality in the size of ethnic homelands. The ethnic inequality Gini index retains its economic and statistical significance, while both the population and the homeland size ethnic Ginis enter with statistically indistinguishable from zero estimates. This suggests that the association between ethnic inequality and underdevelopment is not driven by inequality in the size of ethnic homelands captured either by the population of each group or the area of each homeland. In column (9) we also control for a country’s size including in the empirical model the log of population in 2000 and log of land area, as ethnic heterogeneity, ethnic inequality, and the overall degree of spatial inequality are likely to be increasing in size. Doing so has little effect on our results. Ethnic inequality remains a systematic correlate of underdevelopment.

The estimate on the ethnic inequality index with the Atlas Narodov Mira mapping in Panel A (column 9) implies that a reduction in the ethnic Gini coefficient by 0.25 (one standard deviation, from the level of Nigeria where the ethnic Gini is 0.76 to the level of Namibia where the ethnic Gini is 0.53) is associated with a 28% (0.25 log points) increase in per capita GDP (these countries have very similar overall spatial Ginis of around 0.8). The standardized beta coefficient of the ethnic inequality index is around 0.20 – 0.30, quite similar to the works on the role of institutions on development (e.g., Acemoglu, Johnson, and Robinson (2001)).

Other Aspects of the Ethnic Composition

In Table 3 we investigate whether other dimensions of the distribution of the population across groups, related to fractionalization, polarization, and genetic diversity, rather than income inequality across ethnic lines, influence comparative development. In columns (1) and (6) we augment the specification with the Alesina, Devleeschauwer, Easterly, Kurlat, and Wacziarg (2003) and Desmet, Ortuño-Ortín, and Wacziarg (2012) ethnic and linguistic fractionalization measures, respectively. Doing so has no effect on the coefficient on ethnic inequality that retains its economic and statistical significance. Moreover, the fractionalization indicators enter with unstable and statistically insignificant estimates, suggesting that it is differences in well-being across ethnic lines that explain underdevelopment rather than fragmentation per se.¹⁴ In columns (2) and (7) we experiment with Fearon’s (2003) cultural fragmentation index that adjusts the fractionalization index for linguistic distances among ethnic groups. Cultural fractionalization enters with a statistically insignificant estimate, while the ethnic inequality Gini index retains its economic and statistical significance.

Table 3.

Ethnic Inequality and Economic Development Ethnic Inequality and Other Features of Ethnolinguistic Fragmentation, Polarization, and Diversity

	Atlas Narodov Mira (GREG)					Ethnologue
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
Ethnic Inequality [Gini Coeff.]	−1.3911*** (0.3511)	−1.6116*** (0.3876)	−1.3987*** (0.3478)	−1.4369*** (0.5274)	−1.3684*** (0.3551)	−1.0716*** (0.2932)	−0.9620*** (0.2942)	−1.0893*** (0.2619)	−1.0477* (0.5808)	−1.0108*** (0.2901)
Ethnic/Linguistic Fragmentation	0.0055 (0.3549)					−0.0061 (0.2943)
Cultural Fragmentation		−0.3721 (0.3486)					0.0108 (0.3637)
Ethno-linguistic Polarization			0.4442 (1.0061)					0.6216 (1.0004)
Ethnic/Linguistic Segregation				−1.3294* (0.7294)					−0.1890 (0.8974)
Genetic Diversit					183.0360** (84.5187)					195.3181** (81.1672)
Genetic Diversity Squar					−130.1618** (60.2510)					−140.5393** (58.3610)
Spatial Inequality [Gini Coeff.]	−0.0021 (0.3541)	0.2096 (0.3717)	−0.0335 (0.3540)	0.2086 (0.4144)	0.0615 (0.3407)	−0.1557 (0.3046)	−0.1692 (0.3086)	−0.1878 (0.3072)	0.1651 (0.4348)	−0.1015 (0.3038)
Adjusted R-square	0.650	0.684	0.646	0.731	0.678	0.650	0.669	0.646	0.674	0.675
Observations	173	150	172	96	157	173	150	172	92	157
Region Fixed Effect	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes

The table reports cross-country OLS estimates. The dependent variable is the log of real GDP per capita in 2000. The ethnic Gini coefficients reflect inequality in lights per capita across ethnic homelands, based on the digitized version of the Atlas Narodov Mira (GREG) in columns (1)–(5) and based on the Ethnologue in columns (6)–(10). The overall spatial inequality index (Gini coefficient) captures the degree of spatial inequality across 2.5 by 2.5 decimal degree boxes/pixels in each country (boxes intersected by national boundaries and the coastline are of smaller size). Section 2 gives details on the construction of the ethnic inequality and spatial inequality (Gini) indexes. In columns (1) and (6) we control for ethnic and linguistic fragmentation using indicators that reflect the likelihood that two randomly chosen individuals in one country will not be members of the same group (the ethnic fragmentation index in (1) comes from Alesina et al. (2003) and the linguistic fragmentation index in (6) comes from Desmet et al. (2013)). In columns (2) and (7) we control for cultural (linguistic) fragmentation using an index (from Fearon, 2003) that accounts for linguistic distances among groups. In columns (3) and (8) we control for ethnic polarization, using the Montalvo and Reynal-Querol (2005) index. In columns (4) and (9) we control for ethnic and linguistic segregation, respectively, using the measures of Alesina and Zhuravskaya (2011). In columns (5) and (10) we control for the genetic diversity index of Ashraf and Galor (2013). All specifications include regional fixed effects (constants not reported). The Data Appendix gives detailed variable definitions and data sources. Robust standard errors are reported in parentheses below the estimates.

***, **, and * indicate statistical significance at the 1%, 5%, and 10% level, respectively.

Motivated by recent works highlighting the importance of polarization (Montalvo and Reynal-Querol (2005) and Esteban, Mayoral, and Ray (2012)), in columns (3) and (8) we condition on an index of ethnic polarization. Ethnic inequality correlates strongly with development, while the polarization measures enter with insignificant estimates.¹⁵

Building on the recent work of Alesina and Zhuravskaya (2011) showing that countries with a high degree of ethnolinguistic segregation tend to have low quality national institutions and inefficient bureaucracies, in columns (4) and (9) we include in the specifications their measures of ethnic and linguistic segregation, respectively. The sample falls considerably, as these measures are available for approximately 90 countries. While there is some evidence that ethnic segregation is a feature of underdevelopment, the coefficient on the ethnic inequality proxy continues to be quite stable and significant at standard confidence levels.

In columns (5) and (10) we condition on a proxy of within-country genetic diversity, based on migratory distance of each country’s capital from Ethiopia. Since Ashraf and Galor (2013) argue that the effect of genetic diversity on development is non-linear, we enter the latter in a quadratic fashion (though this has no effect on our results). In all permutations the ethnic inequality proxy enters with a stable (around −1) and highly significant estimate.

Overall the results in Table 3 show that the strong negative association between ethnic inequality and income across countries is not mediated by differences in the societies’ ethnic or genetic composition.¹⁶

Alternative Measures of Ethnic Inequality and Geographic Controls

In Table 4 we augment the main specification with an array of geographic traits and experiment with alternative measures of ethnic inequality. In columns (1) and (4) we use the baseline ethnic inequality measures based on all homelands. In columns (2) and (5) we use ethnic Ginis that exclude from the estimation regions where capitals fall. Note that the sample drops as in these models we do not consider mono-ethnic and mono-linguistic countries. In columns (3) and (6) we introduce ethnic Ginis that exclude groups with less than 1% of a country’s population. Note that a priori there is no reason to exclude small groups, since ethnic hatred may be directed to minorities that, nevertheless, control a significant portion of the economy (Chua (2003)). Moreover, by dropping these groups, the sample of ethnic homelands used to estimate the ethnic Ginis drops considerably.¹⁷ To avoid concerns of self-selecting the conditioning set, we follow the baseline specification of Nunn and Puga (2012) and include (on top of log population and log land area) an index of terrain ruggedness, distance to the coast, an index of gem quality, the percentage of each country with fertile soil and the percentage of tropical land (the Data Appendix gives variable definitions). To isolate the role of ethnic inequality on development from regional inequalities and ethnic fragmentation, in all specifications we control for the overall degree of spatial inequality in lights per capita and ethnic-linguistic fractionalization.

Table 4.

Ethnic Inequality and Economic Development (in 2000) Additional Controls and Alternative Measures of Ethnic Inequality

	Atlas Narodov Mira (GREG)			Ethnologue
	All Ethnic Areas	Excl. Capitals	Excl. Small Groups	All Ethnic Areas	Excl. Capitals	Excl. Small Groups
	(1)	(2)	(3)	(4)	(5)	(6)
Ethnic Inequality [Gini Coeff.]	−0.9172*** (0.3287)	−0.6367* (0.3266)	−0.9835** (0.4503)	−0.7692*** (0.2902)	−0.6262** (0.2909)	−0.9356** (0.3955)
Spatial Inequality [Gini Coeff.]	−0.5698 (0.3686)	−1.2035*** (0.3700)	−1.1254* (0.6237)	−0.6952* (0.3825)	−1.3366*** (0.3535)	−1.0495* (0.6105)
Ethnic/Linguistic Fragmentation	0.1409 (0.3145)	0.3185 (0.3009)	0.3793 (0.3444)	0.1075 (0.2671)	−0.0597 (0.2696)	0.1411 (0.2525)
Adjusted R-squared	0.724	0.760	0.736	0.723	0.759	0.734
Observations	173	155	173	173	147	173
Region Fixed Effects	Yes	Yes	Yes	Yes	Yes	Yes
Simple Controls	Yes	Yes	Yes	Yes	Yes	Yes
Geographic Conrols	Yes	Yes	Yes	Yes	Yes	Yes

The table reports cross-country OLS estimates. The dependent variable is the log of real GDP per capita in 2000. The ethnic Gini coefficients reflect inequality in lights per capita across ethnic homelands, based on the digitized version of the Atlas Narodov Mira (GREG) in columns (1)–(3) and on the Ethnologue in columns (4)–(6). The overall spatial inequality index (Gini coefficient) captures the degree of spatial inequality across 2.5 by 2.5 decimal degree boxes/pixels in each country (boxes intersected by national boundaries and the coastline are of smaller size). For the construction of the ethnic and the spatial inequality measures (Gini coefficients) in columns (1) and (4) we use all ethnic (linguistic) homelands (and pixels); in columns (2) and (5) we exclude ethnic areas (and pixels) where capital cities fall; in columns (3) and (6) we exclude polygons (linguistic, ethnic, boxes) with less than one percent of a country’s population. Section 2 gives details on the construction of the ethnic inequality and spatial inequality (Gini) indexes. In all specifications we control for ethnic/linguistic fragmentation using indicators reflecting the likelihood that two randomly chosen individuals in one country will not be members of the same group (the ethnic fragmentation index in (1)–(3) comes from Alesina et al. (2003) and the linguistic fragmentation index in (4)–(6) comes from Desmet et al. (2013)). In all specifications we include as controls log land area and log population in 2000 (simple set of controls), a measure of terrain ruggedness, the percentage of each country with fertile soil, the percentage of each country with tropical climate, average distance to nearest ice-free coast, and an index of gem-quality diamond extraction (geographic set of controls). All specifications include regional fixed effects (constants not reported). The Data Appendix gives detailed variable definitions and data sources. Robust standard errors are reported in parentheses below the estimates.

***, **, and * indicate statistical significance at the 1%, 5%, and 10% level, respectively.

The negative correlation between ethnic inequality and income per capita remains strong. This applies to all proxies of ethnic inequality. While compared to the unconditional specifications, the estimate on ethnic Gini declines somewhat, it retains significance at standard confidence levels. Thus, while still an unobserved or omitted country-wide factor may jointly affect development and ethnic inequality, the estimates clearly point out that the correlation does not reflect (observable) mean differences in commonly-employed geographical characteristics.

3.2 Inequality across Administrative Units, Ethnic Inequality, and Development

We now examine the relationship between ethnic inequality and comparative development, accounting for regional disparities across administrative units. In this regard, as described in Section 2, we have constructed Gini coefficients reflecting inequality in lights per capita across first- and second-level administrative units. This variable is quite useful in many ways. First, as administrative units are well-defined, the regional Ginis are easily interpretable. Second, examining the link between spatial inequality across administrative regions and development is interesting by itself. A vast literature that goes back at least to the work of Williamson (1965) has studied theoretically and empirically the inter-linkages between development and spatial (regional) inequality. (See the reviews of Kanbur and Venables (2008) and Kim (2009) for recent works). Third, since in some countries ethnic boundaries have formed the basis for the delineation of administrative units, we can directly test whether the strong cross-country correlation between inequality across ethnic homelands and GDP per capita reflects an inverse relationship between inequality across politically defined regions and comparative development.

Table 5 reports the results. Let us start with Panel A where we use Gini coefficients of regional inequality estimated across first-level administrative units. On average there are 18 first-level administrative units in each country. Examples of first-unit regions include the German lander (16), the US (50), Brazilian (27), and Indian (35) states, the Swiss cantons (26), and the Chinese provinces and autonomous regions (32). The coefficient on the administrative unit Gini index in the unconditional specification (in [1]) is negative and highly significant (−1.60). This suggests that underdevelopment is characterized by large regional differences in well-being (or public goods provision). This is in accord with our earlier results (e.g., Table 2, column [2]) showing a similar pattern when using the overall spatial inequality Gini. In columns (2) and (6) we include both the administrative unit and the ethnic inequality Ginis (using the Atlas Narodov Mira and Ethnologue mapping, respectively). Both inequality measures enter with negative and significant estimates (magnitude around −1). In columns (3) and (7) we control for ethnic and linguistic fractionalization (using the Alesina, Devleeschauwer, Easterly, Kurlat, and Wacziarg (2003) and Desmet, Ortuño-Ortín, and Wacziarg (2012) measures, respectively). In line with our previous estimates, once we account for inequalities across ethnic (and now also across administrative) regions, there is no systematic link between ethnolinguistic fragmentation and development. In columns (4), (5), (8), and (9) we control for country size (log population and log land area) and the rich set of geographic features. The results remain intact. Across all permutations both the ethnic inequality measure and the Gini index capturing inequality across first-level administrative units enter with negative and highly significant coefficients. The “standardized” beta coefficients that summarize in terms of standard deviations the change in the outcome variable (log of per capita GDP) induced by a one-standard-deviation change in the independent variables are comparable for the two inequality measures, around 0.20.

Table 5.

Ethnic Inequality, Administrative Unit Inequality and Economic Development

Panel A: Inequality across Administrative Units (1st-level)
	Unconditional	Atlas Narodov Mira (GREG)				Ethnologue
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
Admin Unit Inequality [Gini Coeff.]	−1.6717*** (0.4004)	−1.0139** (0.4188)	−1.0185** (0.4230)	−1.5074*** (0.4096)	−1.2651*** (0.4307)	−1.0080** (0.4446)	−1.0150** (0.4486)	−1.5177*** (0.4333)	−1.2752*** (0.4494)
Ethnic Inequality [Gini Coeff.]		−1.0252*** (0.2611)	−1.0401*** (0.2765)	−1.0478*** (0.3557)	−0.8087** (0.3197)	−0.8527*** (0.2487)	−0.8280*** (0.2856)	−0.7952** (0.3158)	−0.6096** (0.2941)
Ethnic/Linguistic Fragmentation			0.0584 (0.3479)	−0.0206 (0.3387)	0.1337 (0.3062)		−0.0548 (0.2783)	−0.1103 (0.2736)	0.0239 (0.2572)
Adjusted R-squared	0.642	0.667	0.665	0.686	0.741	0.667	0.665	0.686	0.738
Observations	173	173	173	173	173	173	173	173	173
Region Fixed Effects	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Simple Controls	No	No	No	Yes	Yes	No	No	Yes	Yes
Geographic Conrols	No	No	No	No	Yes	No	No	No	Yes

Panel B: Inequality across Administrative Units (2nd-level)
	Unconditional	Atlas Narodov Mira (GREG)				Ethnologue
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
Admin Unit Inequality [Gini Coeff.]	−0.6095* (0.3391)	−0.1579 (0.3421)	−0.1713 (0.3409)	−1.0886*** (0.3572)	−0.6976* (0.3675)	−0.2834 (0.3518)	−0.3099 (0.3535)	−1.1967*** (0.3627)	−0.7995** (0.3482)
Ethnic Inequality [Gini Coeff.]		−1.1068*** (0.3315)	−1.0495*** (0.3346)	−1.0863*** (0.3812)	−0.7882** (0.3445)	−0.7086** (0.2974)	−0.6176* (0.3323)	−0.8881*** (0.3389)	−0.6873** (0.3415)
Ethnic/Linguistic Fragmentation			−0.2237 (0.4018)	−0.5142 (0.3772)	0.025 (0.3514)		−0.1827 (0.3207)	−0.2027 (0.2937)	0.0599 (0.2557)
Adjusted R-squared	0.677	0.698	0.696	0.726	0.773	0.692	0.690	0.723	0.773
Observations	135	135	135	135	135	135	135	135	135
Region Fixed Effects	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Simple Controls	No	No	No	Yes	Yes	No	No	Yes	Yes
Geographic Conrols	No	No	No	No	Yes	No	No	No	Yes

The table (both panels A and B) reports cross-country OLS estimates. The dependent variable is the log of real GDP per capita in 2000. The ethnic Gini coefficients reflect inequality in lights per capita across ethnic homelands, based on the digitized version of the Atlas Narodov Mira (GREG) in columns (2)–(5) and on the Ethnologue in columns (6)–(9). The administrative unit Gini index reflects inequality in lights per capita across administrative regions. In Panel A we use first-level administrative units. In Pane B we use second-level administrative units. Section 2 gives details on the construction of the ethnic inequality and spatial inequality (Gini) indexes. In specifications (3)–(5) and (7)–(9) we control for ethnic/linguistic fragmentation using indicators reflecting the likelihood that two randomly chosen individuals in one country will not be members of the same group (the ethnic fragmentation index in (3)–(5) comes from Alesina et al. (2003) and the linguistic fragmentation index in (7)–(9) comes from Desmet et al. (2013)). Specifications (4), (5), (8), and (9) include as controls log land area and log population in 2000 (simple set of controls). Specifications (5) and (10) include as controls a measure of terrain ruggedness, the percentage of each country with fertile soil, the percentage of each country with tropical climate, average distance to nearest ice-free coast, and an index of gem-quality diamond extraction (geographic set of controls). All specifications include regional fixed effects (constants not reported). The Data Appendix gives detailed variable definitions and data sources. Robust standard errors are reported in parentheses below the estimates.

***, **, and * indicate statistical significance at the 1%, 5%, and 10% level, respectively.

Table 5 – Panel B reports similar specifications where administrative-level inequality is estimated across second-level units. The GADM database does not report second-level administrative units for all countries, hence the sample drops to 135 (we mostly lose small countries, such as Singapore, Jamaica, and Swaziland). The results are similar if we assign to these countries the first-level administrative unit Gini coefficients. As the median (mean) number of such units is 110 (301), the respective Ginis are estimated using a very fine aggregation. Examples include the German (regierungsbezirk) government regions (40), the French département (96), and the Brazilian municipalities (5503). The coefficient on the administrative region Gini index in column (1) is negative and significant at the 90% level; yet its magnitude is considerably smaller than the analogous one with the first-level administrative Gini index (−0.61). (The implied “beta” coefficient is −0.10). The coefficient on the administrative region Gini drops considerably and loses its statistical significance once we include the ethnic inequality proxy (columns [2] and [5]) and condition on ethnolinguistic fragmentation (columns [3] and [6]). In contrast, the ethnic inequality measure retains its statistical and economic significance. The coefficient on the ethnic Gini is unaffected when we condition on size and geography (in [4], [5], [8], and [9]).

The evidence in Table 5 reveals two important findings. First, in a large cross-section of countries there is a clear negative association between economic performance and regional inequalities across first-level administrative units. This new (to the best of our knowledge) finding adds to the literature in urban economics and economic geography that studies the relationship between regional economic disparities and the process of development.¹⁸ Second, and more important given our focus, the strong cross-country link between ethnic inequality and underdevelopment does not capture the similarly negative association between GDP per capita and economic differences across politically defined spatial units.

3.3 Perturbing Ethnic Homelands

We now explore whether the pattern uncovered so far survives a horse race between ethnic inequality constructed using the original mappings and ethnic inequality based on slightly modified ethnic homelands.¹⁹ Showing that our original ethnic inequality measures dominate the Gini index based on perturbed ethnic homelands would suggest that not only are the centroids of the groups correctly identified in the original maps, but that also the specific boundaries delineated are more precise than the Thiessen based ones. Effectively, this sensitivity check investigates how precisely drawn the groups’ boundaries are in the underlying datasets.

Table 6 reports the results of the “horse race” regressions, examining the link between the log of per capita GDP and ethnic inequality, conditional on the perturbed ethnic homelands Gini index. Across all specifications the ethnic Gini index enters with a negative and significant estimate that is quite similar (around −0.9) to the more parsimonious specifications in Tables 2 – 4. In contrast, the Gini index based on the perturbed ethnic areas (Thiessen polygons) enters with an unstable and statistically indistinguishable from zero estimate. It is perhaps instructive to point out that the perturbed linguistic homelands of Ethnologue seem to have little predictive power on GDP per capita beyond the role of ethnic inequality based on the Ethnologue homelands themselves, whereas for the case of GREG the perturbed ethnic inequality index enters with a (consistent) negative sign and is of moderate magnitude. This pattern is in line with the idea that the Ethnologue compared to GREG’s mapping may have less measurement error since the former draws from a wealth of resources that are up-to-date and more precisely documented, unlike GREG which derives from maps of the 1960s.

Table 6.

Ethnic Inequality and Development Conditioning on Perturbed Ethnic Homelands

	Atlas Narodov Mira (GREG)				Ethnologue
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Ethnic Inequality [Gini Coeff.]	−0.9510* (0.5004)	−0.9566* (0.5074)	−0.8652* (0.5174)	−0.9276** (0.4383)	−1.4389*** (0.4075)	−1.4365*** (0.4115)	−1.2413*** (0.4159)	−0.8063* (0.4166)
Perturbed Ethnic Inequality [Gini Coeff.]	−0.5371 (0.5258)	−0.5457 (0.5262)	−0.8223 (0.5469)	−0.2645 (0.4829)	0.3302 (0.4640)	0.3376 (0.4718)	0.0259 (0.4950)	−0.1845 (0.4410)
Ethnic/Linguistic Fragmentation		0.0446 (0.3521)	−0.0107 (0.3498)	0.1614 (0.3159)		−0.0213 (0.2962)	−0.0147 (0.2962)	0.1510 (0.2656)
Adjusted R-squared	0.654	0.652	0.662	0.721	0.653	0.650	0.657	0.718
Observations	173	173	173	173	173	173	173	173
Region Fixed Effects	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Simple Controls	No	No	Yes	Yes	No	No	Yes	Yes
Geographic Conrols	No	No	No	Yes	No	No	No	Yes

The table reports cross-country OLS estimates. The dependent variable is the log of real GDP per capita in 2000. The ethnic Gini coefficients reflect inequality in lights per capita across ethnic homelands, based on the digitized version of the Atlas Narodov Mira (GREG) in columns (1)–(4) and on the Ethnologue in columns (5)–(8). The perturbed ethnic inequality measures (Gini coefficients) capture the degree of spatial inequality across Thiessen polygons in each country that use as input points the centroids of the ethnic-linguistic homelands according to the Atlas Narodov Mira (in columns (1)–(4)) and to the Ethnologue (in columns (5)–(8)). Thiessen polygons have the unique property that each polygon contains only one input point, and any location within a polygon is closer to its associated point than to a point of any other polygon. In specifications (2)–(4) and (6)–(8) we control for ethnic/linguistic fragmentation using indicators reflecting the likelihood that two randomly chosen individuals in one country will not be members of the same group (the ethnic fragmentation index in (2)–(4) comes from Alesina et al. (2003) and the linguistic fragmentation index in (6)–(8) comes from Desmet et al. (2013)). Specifications (3), (4), (7), and (8) include as controls log land area and log population in 2000 (simple set of controls). Specifications (4) and (8) include as controls an index of terrain ruggedness, the percentage of each country with fertile soil, the percentage of each country with tropical climate, average distance to nearest ice-free coast, and an index of gem-quality diamond extraction (geographic set of controls). All specifications include regional fixed effects (constants not reported). The Data Appendix gives detailed variable definitions and data sources. Robust standard errors are reported in parentheses below the estimates.

***, **, and * indicate statistical significance at the 1%, 5%, and 10% level, respectively.

3.4 Further Robustness Checks

We have performed numerous sensitivity checks to investigate the robustness of the strong cross-country association between ethnic inequality and under-development. We report and discuss in detail these robustness checks in the on-line Supplementary Appendix. Specifically, we show that the results are similar when: (i) we do not include region fixed effects; (ii) we estimate ethnic Ginis without taking into account observations neither from capitals nor from small groups; (iii) we drop from the estimation (typically small) countries with just one ethnic or linguistic group; (iv) we use radiance-calibrated luminosity data to construct all inequality measures (so as to account for top-coding in the lights data that occurs at the major urban centers); (v) we account for the resolution of population estimates at the grid level that are used to compile the inequality measures; (vi) we use non-standardized by population inequality measures (based on lights) and control for inequality in the distribution of population across ethnic areas; (vii) we perform the analysis at various nodes of Ethnologue’s linguistic tree (this approach follows Desmet, Ortuño-Ortín, and Wacziarg (2012) who show that the impact of ethnic fractionalization on growth, public goods, and conflict depends on the level of linguistic aggregation); (viii) we try accounting for measurement error of the underlying mapping of groups estimating two-stage-least-squares models that extract the common component of ethnic inequality from both Ethnologue and the Atlas Narodov Mira; (ix) on top of the rich set of geographic variables, we also condition on various historical controls; (x) we drop iteratively from the estimation a different continent/region and focus within each region separately. The regional analysis reveals that the development-ethnic inequality nexus is non-existent for countries in Western Europe and North America and weak in Latin America. On the contrary, the association is especially strong within East and South Asia as well as for countries in the Middle East and North Africa.

4 On the Origins of Ethnic Inequality

Given the strong correlation between ethnic inequality and underdevelopment, we have investigated the roots of inequality across ethnic lines.

4.1 Historical (Colonial) Origins

We started by examining the association between ethnic inequality and commonly used historical correlates of contemporary development. There is little evidence linking contemporary differences in well-being across ethnic groups to the legal tradition (La Porta, Lopez-de-Silanes, Shleifer, and Vishny (1998)), the conditions that European settlers faced at the time of colonization, as captured by settler mortality (Acemoglu, Johnson, and Robinson (2001)) or pre-colonial population densities (Acemoglu, Johnson, and Robinson (2002)), the share of Europeans in the population (Hall and Jones (1999) and Putterman and Weil (2010)), and border design and state artificiality (Alesina, Easterly, and Matuszeski (2011)); for brevity, we report these results in the online Supplementary Appendix.²⁰ These insignificant associations suggest that the strong negative correlation between ethnic inequality and development does not reflect the aforementioned aspects of history.

4.2 Geographic Origins

Motivated by the insight of Michalopoulos (2012) that differences in land endowments gave rise to location-specific human capital, leading to the formation of ethnolinguistic groups, we investigated whether differences in geographic and ecological attributes play a role in explaining contemporary income disparities across ethnic lines. To the extent that land endowments shape ethnic human capital and affect the diffusion and adoption of technology and innovation (e.g., Diamond (1997)), then ethnic-specific inequality in the distribution of geographic features would manifest itself in contemporary differences in well-being across groups.²¹

To construct proxies of geographic inequality, we obtained georeferenced data on elevation, land suitability for agriculture, distance to the coast, precipitation, and temperature and calculated for each ethnic area the mean value.²² We then derived Gini coefficients at the country level that reflect group-specific inequality in each of these (five) dimensions. We also estimated measures of the overall degree of inequality in geographic endowments, constructing for each of the five geographic traits spatial Gini coefficients across boxes of 2.5 × 2.5 decimal degrees and across administrative units.

Preliminary Evidence

In Table 7 we explore the association between ethnic inequality (in lights per capita) and these measures of inequality in geographic endowments across ethnic homelands. Specifications (1) and (5) simply condition on region fixed effects. To isolate the ethnic-specific component, in columns (2) and (6) we include in the empirical model Gini coefficients capturing the overall degree of spatial inequality across each of these five traits, while in columns (3) and (7) we include Gini coefficients of inequality in the same five geographic features across first-level administrative units. In specifications (4) and (8) we include as controls the country averages of each of the five variables. In almost all permutations, all five ethnic Ginis enter with positive estimates; this suggests that ethnic-specific differences in geo-ecological endowments translate into larger disparities in ethnic contemporary development. Depending on the specification details –GREG or Ethnologue mapping, whether we condition on the level of each geographical trait and regional inequality in each of the five geographic features– different Gini coefficients of geographic inequality enter with significant estimates. For example, in the specifications using the GREG mapping, the Ginis capturing inequality in elevation and proximity to the coast enter with significant estimates, while in the Ethnologue-based models the Gini indicators reflecting inequality in land quality for agriculture and temperature are the key correlates of ethnic inequality. Moreover, the controls capturing inequality across random pixels or administrative regions all enter with statistically insignificant estimates (coefficients not shown). Thus, while we cannot precisely identify which geographic feature(s) matter most, the message from Table 7 is that differences in geography across ethnic regions translate into differences in contemporary ethnic inequality.

Table 7.

On the Origins of Contemporary Ethnic Inequality Inequality in Geographic Endowments across Ethnic Homelands and Contemporary Ethnic Inequality

	Atlas Narodov Mira (GREG)				Ethnologue
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Land Quality [Gini Coeff.]	0.3035** (0.1348)	−0.0077 (0.2191)	−0.0918 (0.1864)	0.184 (0.1414)	0.4042*** (0.1132)	0.1913 (0.1784)	0.4271** (0.1924)	0.3930*** (0.1230)
Temperature [Gini Coeff.]	1.651 (7.2462)	−9.1956 (11.1686)	7.3784 (10.7068)	3.0874 (8.0507)	19.5600*** (6.8608)	47.6529*** (12.3794)	39.7024*** (10.6988)	36.8859*** (10.1117)
Precipitation [Gini Coeff.]	0.3421* (0.2034)	0.7845* (0.4227)	0.7969** (0.3445)	0.2916 (0.2259)	0.1884 (0.2636)	0.5606 (0.4862)	0.3762 (0.4119)	0.2878 (0.2620)
Distance to the Coast [Gini Coeff.]	0.2852** (0.1123)	0.3954** (0.1801)	0.1589 (0.1631)	0.4640*** (0.1458)	0.1433 (0.1388)	0.1819 (0.1659)	0.0012 (0.1994)	0.3462** (0.1332)
Elevation [Gini Coeff.]	0.5002* (0.2674)	0.6844** (0.3255)	0.9012*** (0.3064)	0.3019 (0.2772)	0.4413*** (0.1584)	0.3449 (0.2232)	0.6396*** (0.2013)	−0.0356 (0.1601)
Adjusted R-square	0.450	0.467	0.493	0.491	0.583	0.611	0.617	0.667
Observations	164	164	164	164	164	164	164	164
Region Fixed Effect	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Controls	No	Spatial	Admin Unit	Levels	No	Spatial	Admin Unit	Levels

The table reports cross-country OLS estimates, associating contemporary ethnic inequality with inequality in geographic endowments across ethnic homelands. The dependent variable is the ethnic Gini coefficient that reflects inequality in lights per capita across ethnic-linguistic homelands, using the digitized version of Atlas Narodov Mira (GREG) in (1)–(4) and Ethnologue in (5)–(8). To construct the inequality measures in geographic endowments across ethnic homelands we first estimate the distance from the centroid of each ethnic homeland to the closest sea coast, average elevation, precipitation, temperature, and land quality for agriculture and then construct Gini coefficients capturing inequality across ethnic homelands in each of these geographic features for each country. In columns (2) and (6) we control for the overall degree of spatial inequality in geographic endowments using the Gini coefficient of each of these features (distance to the closest sea-coast, elevation, precipitation, temperature and land quality for agriculture) estimated across 2.5 by 2.5 decimal degree boxes/pixels in each country (boxes intersected by national boundaries and the coastline are of smaller size). In columns (3) and (7) we control for the regional inequality across administrative units in geographic endowments using the Gini coefficient of each of these features (distance to the coast, elevation, precipitation, temperature and land quality for agriculture) estimated across first-level administrative units in each country. Columns (4) and (8) include as controls the mean values (for each country) of distance to sea coast, elevation, precipitation, temperature, and land quality for agriculture. All specifications include regional fixed effects (constants not reported). The Data Appendix gives detailed variable definitions and data sources. Robust standard errors are reported in parentheses below the estimates.

***, **, and * indicate statistical significance at the 1%, 5%, and 10% level, respectively.

A Composite Index of Inequality in Geographic Endowments

We thus aggregate the five Gini indexes of ethnic inequality in geographic endowments via principal components. The use of factor-analysis techniques is appropriate in our context because we have many variables (Gini coefficients) that aim at capturing a similar concept (with some degree of noise), namely inequality in ethnic-specific geographic attributes. Moreover, we are not sure about which aspects of geographic inequality should matter the most. Table 8 reports the results of the principal component analysis. The first principal component explains approximately 60% of the common variance of the five measures of inequality in geographic endowments across ethnic homelands and close to 50% when we estimate Gini coefficients across pixels of (roughly) the same size and across first-level administrative units. The second principal component explains around 20% of the total variance, while jointly the other principal components explain a bit less than a fourth of the total variance. All five inequality measures load positively on the first principal component. This applies to all inequality measures (across ethnic and linguistic homelands, administrative regions, and boxes). The eigenvalue of the first principal component is greater than two in all permutations (one being the rule of thumb), while the eigenvalues of the other principal components are close to and less than one. We thus focus on the first principal component, which given the significant positive loadings of all Gini coefficients, we label as “inequality in geographic endowments across ethnic homelands.”

Table 8.

Principal Component Analysis. Inequality in Geographic Endowments

	Eigenvalue	Variance Explained	Variable	Factor Loadings
				1st PC	2nd PC	3rd PC	4th PC	5th PC
Panel A: Gini Coefficient GREG – All Groups
1st Principal Comp	2.982	0.596	Gini Land Quality	0.460	−0.133	−0.572	0.647	−0.159
2nd Principal Comp	0.844	0.169	Gini Temperature	0.482	−0.358	0.388	0.097	0.693
3rd Principal Comp	0.746	0.149	Gini Precipitation	0.485	0.025	−0.463	−0.741	0.038
4th Principal Comp	0.251	0.050	Gini Sea Distance	0.297	0.918	0.143	0.145	0.167
5th Principal Comp	0.177	0.035	Gini Elevation	0.482	−0.106	0.536	−0.058	−0.682
Panel B: Gini Coefficient ETHNOLOGUE – All Groups
1st Principal Comp	2.942	0.588	Gini Land Quality	0.432	−0.423	0.585	0.496	−0.215
2nd Principal Comp	1.062	0.213	Gini Temperature	0.448	−0.305	−0.688	0.319	0.362
3rd Principal Comp	0.551	0.110	Gini Precipitation	0.505	−0.250	0.183	−0.781	0.201
4th Principal Comp	0.260	0.052	Gini Sea Distance	0.353	0.710	0.274	0.196	0.509
5th Principal Comp	0.184	0.037	Gini Elevation	0.484	0.403	−0.275	−0.067	−0.724
Panel C: Gini Coefficient – Spatial Inequality Index
1st Principal Comp	2.711	0.542	Gini Land Qualit	0.482	−0.444	0.259	0.118	0.700
2nd Principal Comp	1.149	0.230	Gini Temperatur	0.476	−0.060	−0.678	0.519	−0.203
3rd Principal Comp	0.629	0.126	Gini Precipitatio	0.497	−0.350	0.360	−0.281	−0.650
4th Principal Comp	0.313	0.063	Gini Sea Distance	0.306	0.677	0.504	0.439	−0.042
5th Principal Comp	0.199	0.040	Gini Elevatio	0.448	0.468	−0.301	−0.667	0.212
Panel D: Gini Coefficient – Administrative Unit Inequality
1st Principal Comp	2.314	0.463	Gini Land Qualit	0.484	−0.414	0.428	−0.084	0.637
2nd Principal Comp	1.270	0.254	Gini Temperature	0.482	−0.063	−0.640	0.586	0.100
3rd Principal Comp	0.771	0.154	Gini Precipitation	0.574	−0.200	0.253	−0.089	−0.748
4th Principal Comp	0.403	0.081	Gini Sea Distance	0.181	0.717	0.492	0.455	0.059
5th Principal Comp	0.242	0.048	Gini Elevation	0.415	0.520	−0.318	−0.659	0.150

The table reports the results of the principal component analysis that is based on five measures (Gini coefficients) reflecting inequality in geographic endowments in distance to the coast, elevation, precipitation, temperature, and land quality for agriculture across ethnic/linguistic homelands (Panels A and B), pixels of 2.5 × 2.5 decimal degrees (in Panel C), and first-level administrative regions (in Panel D). Column (1) reports the eigenvalue of each principal component and column (2) gives the percentage of the total variance explained by each principal component. The other columns give the factor loadings for each of the five principal components.

Inequality in Geography across Ethnic Homelands and Ethnic Inequality

In Figures 10a and 10b we plot the baseline index of ethnic inequality (based on lights per capita) against the first principal component of inequality in ethnic-specific geographic endowments. There is a strong positive correlation for both mappings (around 0.55), suggesting that differences in geography explain a sizable portion of contemporary differences in development across ethnic homelands.

Figure 10.

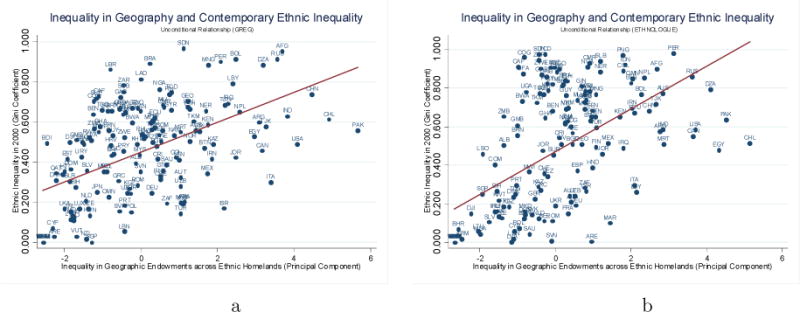
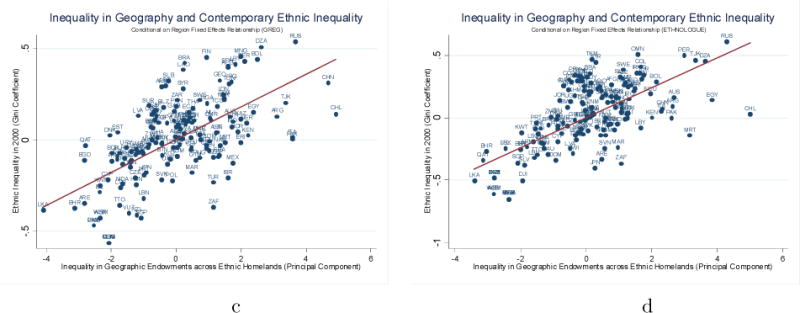
In Table 9 we formally assess the role of ethnic-specific geographic inequality, as captured by the composite index of inequality in geographic endowments across ethnic-linguistic homelands, on contemporary ethnic inequality.²³ Columns (1) and (5) show that the strong correlation illustrated in the figures is not driven by continent-wide differences. In columns (2) and (6) we control for the overall degree of spatial inequality in geographic endowments augmenting the specifications with the first-principal component of the Gini coefficients in geography using pixels of 2.5 × 2.5 decimal degrees. Likewise, in specifications (3) and (7) we add the first principal component of the geographic inequality measures across first-unit administrative regions. This has little effect on the coefficient of the ethnic inequality in geographic endowments that retains its economic and statistical significance (at the 99% level). Moreover, the two proxies of the overall degree of spatial inequality in geography enter with small coefficients that also have the “wrong sign” and are not always statistically significant. In columns (4) and (8) we control for the level effects of geography, augmenting the specification with the country average values of elevation, precipitation, temperature, distance to the coast, and land suitability for agriculture. The composite index reflecting differences in geographic endowments across ethnic homelands continues entering with a positive and significant coefficient. The estimate with the Ethnologue mapping (0.12) implies that a one-standard-deviation increase in the inequality in geography across ethnic homelands index (1.74 points, from Zambia to Ethiopia) translates into a 20-percentage-point increase in the ethnic inequality index (exactly as the difference in ethnic inequality between Zambia and Ethiopia; somewhat more than half a standard deviation; see Table 1).

Table 9.

On the Origins of Contemporary Ethnic Inequality Inequality in Geographic Endowments across Ethnic Homelands and Contemporary Ethnic Inequality

	Atlas Narodov Mira (GREG)				Ethnologue
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Inequality in Geography across Ethnic Homelands (PC) bootstrap s.e.	0.0902*** (0.0101) [0.0102]	0.1053*** (0.0195) [0.0192]	0.1077*** (0.0190) [0.0196]	0.0898*** (0.0107) [0.0108]	0.1210*** (0.0124) [0.0118]	0.1458*** (0.0198) [0.0200]	0.1595*** (0.0186) [0.0192]	0.1181*** (0.0123) [0.0124]
Spatial Inequality in Geography (PC) bootstrap s.e.		−0.0195 (0.0201) [0.0200]				−0.0332* (0.0195) [0.01984]
Inequality in Geography across Administrative Units (PC) bootstrap s.e.			−0.0251 (0.0210) [0.0214]				−0.0569*** (0.0185) [0.0195]
Adjusted R-squared	0.452	0.453	0.456	0.483	0.587	0.594	0.608	0.656
Observations	164	164	164	164	164	164	164	164
Region Fixed Effects	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Additional Controls	No	No	No	Levels	No	No	No	Levels

The table reports cross-country OLS estimates, associating contemporary ethnic inequality with inequality in geographic endowments across ethnic homelands. The dependent variable is the ethnic Gini coefficient that reflects inequality in lights per capita across ethnic/linguistic homelands, using the digitized version of Atlas Narodov Mira (GREG) in (1)–(4) and Ethnologue in (5)–(8). The composite index of inequality in geographic endowments is the first principal component of five inequality measures (Gini coefficients) measuring inequality across ethnic/linguistic homelands in distance to the coast, elevation, precipitation, temperature, and land quality for agriculture. The mapping of ethnic homelands follows the digitized version of Atlas Narodov Mira (GREG) in columns (1)–(4) and of Ethnologue in columns (5)–(8). Columns (2) and (6) include a composite index reflecting the overall degree of spatial inequality in geographic endowments. The composite index aggregates (via principal components) Gini coefficients across 2.5 by 2.5 decimal degree boxes/pixels in each country (boxes/pixels intersected by national boundaries and the coastline are of smaller size) of distance to the coast, elevation, precipitation, temperature, and land quality for agriculture. Columns (3) and (7) include a composite index reflecting regional inequality in geographic endowments across administrative units. The composite index aggregates (via principal components) Gini coefficients across first-level administrative units in distance to the coast, elevation, precipitation, temperature, and land quality for agriculture. Columns (4) and (8) include as controls the mean values (for each country) of distance to sea coast, elevation, precipitation, temperature, and land quality for agriculture. All specifications include regional fixed effects (constants not reported). The Data Appendix gives detailed variable definitions and data sources. Robust standard errors are reported in parentheses in the first-row below the estimates. In the second-row below the estimates we also report bootstrap standard errors that account for the use of a generated (principal component) regressor.

***, **, and * indicate statistical significance at the 1%, 5%, and 10% level, respectively.

In the online Supplementary Appendix, we show that the link between ethnic inequality and inequality in geographic endowments across ethnic homelands prevails: (i) when we compile cross-country composite indicators of inequality in geographic endowments across ethnic lines using a richer set of geographic variables; (ii) when we condition on contemporary differences in development across space or administrative unions; and (iii) when we iteratively drop different regions from the estimation.

5 Geographic Inequality and Development

5.1 Inequality in Geographic Endowments across Ethnic Homelands and Economic Development

Given the strong positive association between ethnic inequality and inequality in geographic endowments, it is interesting to examine whether contemporary development is systematically linked to the unequal distribution of geographic endowments across ethnic homelands. We thus estimated LS specifications associating the log of real GDP p.c. in 2000 with the composite index of ethnic-specific inequality in geography (across the five geographic dimensions). While omitted-variables concerns cannot be eliminated, examining the role of inequality in geographic endowments across ethnic homelands on comparative development assuages concerns that the estimates in Tables 2 – 4 are driven by reverse causation. Moreover, geographic inequality can be thought of as an alternative “primitive” measure of economic differences across linguistic homelands (compared to the ethnic inequality index based on luminosity).

Table 10 reports the results. The coefficient on the proxy of ethnic inequality in geographic endowments in (1) and (5) is negative (around −0.13) and significant at the 99% confidence level. This suggests that countries with sizable inequalities in geographic endowments across ethnic homelands are –on average– less developed. In columns (2) and (6) we condition on the overall degree of inequality in geography with the spatial Gini index based on boxes, while in columns (3) and (7) we control for inequality in the geography across first-level administrative units. This allows examining whether the negative association between development and geographic disparities across ethnic homelands –revealed in (1) and (5)– capture the role of overall spatial geographic inequalities, unrelated to ethnicity. The composite measures capturing geographic inequalities across space and across administrative regions enter with statistically indistinguishable from zero estimates (that have also the “opposite sign”). In contrast, the composite index capturing inequality in geographic endowments across ethnic homelands retains its statistical and economic significance. These results further show that it is inequality across ethnic lines (in geography in this case) rather than across space or administrative regions that correlates with underdevelopment. The same applies when we control for the mean values of the five geographic variables (in [4] and [8]). The most conservative estimate implies that a one-standard-deviation increase in geographic inequality across ethnic homelands (1.7 points) decreases income per capita by approximately 25% (0.22 log points).

Table 10.

Inequality in Geographic Endowments across Ethnic Homelands and Contemporary Development

	Atlas Narodov Mira (GREG)				Ethnologue
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Inequality in Geography across Ethnic Homelands (PC) bootstrap s.e.	0.1347*** (0.0383) [0.0387]	−0.2087*** (0.0754) [0.0758]	−0.1610** (0.0695) [0.0709]	−0.0993*** (0.0367) [0.0389]	−0.1293*** (0.0432) [0.0432]	−0.1687** (0.0708) [0.0717]	−0.1324** (0.0659) [0.0675]	−0.1119*** (0.0364) [0.0379]
Spatial Inequality in Geography (PC) bootstrap s.e.		0.0954 (0.0854) [0.0855]				0.0527 (0.0737) [0.0749]
Inequality in Geography across Administrative Units (PC) bootstrap s.e.			0.0375 (0.0903) [0.0907]				0.0045 (0.0764) [0.0776]
Adjusted R-squared	0.635	0.636	0.633	0.691	0.633	0.632	0.630	0.696
Observations	164	164	164	164	164	164	164	164
Region Fixed Effects	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Additional Controls	No	No	No	Levels	No	No	No	Levels

The table reports cross-country OLS estimates, associating contemporary development with inequality in geographic endowments across ethnic homelands. The dependent variable is the log of real GDP per capita in 2000. The composite index of inequality in geographic endowments is the first principal component of five inequality measures (Gini coefficients) measuring inequality across ethnic/linguistic homelands in distance to the coast, elevation, precipitation, temperature, and land quality for agriculture. The mapping of ethnic homelands follows the digitized version of Atlas Narodov Mira (GREG) in columns (1)–(4) and of Ethnologue in columns (5)–(8). Columns (2) and (6) include a composite index reflecting the overall degree of spatial inequality in geographic endowments. The composite index aggregates (via principal components) Gini coefficients across 2.5 by 2.5 decimal degree boxes/pixels in each country (boxes/pixels intersected by national boundaries and the coastline are of smaller size) of distance to the coast, elevation, precipitation, temperature, and land quality for agriculture. Columns (3) and (7) include a composite index reflecting regional inequality in geographic endowments across administrative units. The composite index aggregates (via principal components) Gini coefficients across first-level administrative units in distance to the coast, elevation, precipitation, temperature, and land quality for agriculture. Columns (4) and (8) include as controls the mean values (for each country) of distance to the coast, elevation, precipitation, temperature, and land quality for agriculture. All specifications include regional fixed effects (constants not reported). The Data Appendix gives detailed variable definitions and data sources. Robust standard errors are reported in parentheses in the first-row below the estimates. In the second-row below the estimates we also report bootstrap standard errors that account for the use of a generated (principal component) regressor.

***, **, and * indicate statistical significance at the 1%, 5%, and 10% level, respectively.

In the online Supplementary Appendix, we show that the negative association between the log income per capita and inequality in geographic endowments across ethnic lines is present also when (i) we drop iteratively a different region; (ii) we control for contemporary differences in spatial development or inequality in lights per capita across administrative regions.

5.2 Geographic Inequality across Ethnic Homelands, Ethnic Inequality, and Economic Development

Given the strong negative correlation between development and ethnic inequality both when the latter is proxied by differences in geographic endowments (Table 10) or in disparities in luminosity per capita (Tables 2 – 6), in Table 11 we report specifications linking development to both measures. The results reveal that once we condition on contemporary ethnic income inequality differences in geography across groups lose their power in explaining cross-country variation in development. While some peculiar type of measurement error may explain this finding, it indicates that ethnic-specific inequality in geographic endowments relates to contemporary development primarily via its influence on ethnic inequality.

Table 11.

Inequality in Geographic Endowments across Ethnic Homelands, Ethnic Inequality, and Contemporary Development

	Atlas Narodov Mira (GREG)				Ethnologue
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Ethnic Inequality (Development) bootstrap s.e.	−1.2984*** (0.3685) [0.3732]	−1.2673*** (0.3601) [0.3646]	−1.2959*** (0.3650) [0.3730]	−1.0602*** (0.3440) [0.3491]	−1.1603*** (0.3326) [0.3342]	−1.1505*** (0.3320) [0.3363]	−1.2258*** (0.3391) [0.3444]	−0.7805** (0.3294) [0.3387]
Inequality in Geography across Ethnic Homelands (PC) bootstrap s.e.	−0.0177 (0.0495) [0.0502]	−0.0753 (0.0719) [0.0735]	−0.0214 (0.0661) [0.0694]	−0.0041 (0.0455) [0.0470]	0.011 (0.0560) [0.0562]	−0.001 (0.0752) [0.0769]	0.0632 (0.0737) [0.0770]	−0.0197 (0.0552) [0.0563]
Spatial Inequality in Geography (PC) bootstrap s.e.		0.0707 (0.0803) [0.0812]				0.0145 (0.0665) [0.0688]
Inequality in Geography across Admininstrative Units (PC) bootstrap s.e.			0.005 (0.0804) [0.0822]				−0.0653 (0.0694) [0.0719]
Adjusted R-squared	0.663	0.662	0.660	0.707	0.662	0.660	0.661	0.705
Observations	164	164	164	164	164	164	164	164
Region Fixed Effects	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Additional Controls	No	No	No	Levels	No	No	No	Levels

The table reports cross-country OLS estimates, associating contemporary development with ethnic inequality and inequality in geographic endowments across ethnic homelands. The dependent variable is the log of real GDP per capita in 2000. The ethnic Gini coefficients reflect inequality in lights per capita across ethnic homelands, based on the digitized version of the Atlas Narodov Mira (GREG) in columns (1)–(4) and based on the Ethnologue in columns (5)–(8). The composite index of inequality in geographic endowments is the first principal component of five inequality measures (Gini coefficients) measuring inequality across ethnic/linguistic homelands in distance to the coast, elevation, precipitation, temperature, and land quality for agriculture. The mapping of ethnic homelands follows the digitized version of Atlas Narodov Mira (GREG) in columns (1)–(4) and of Ethnologue in columns (5)–(8). Columns (2) and (6) include a composite index reflecting the overall degree of spatial inequality in geographic endowments. The composite index aggregates (via principal components) Gini coefficients across 2.5 by 2.5 decimal degree boxes/pixels in each country (boxes/pixels intersected by national boundaries and the coastline are of smaller size) in distance to the coast, elevation, precipitation, temperature, and land quality for agriculture. Columns (3) and (7) include a composite index reflecting regional inequality in geographic endowments across administrative units. The composite index aggregates (via principal components) Gini coefficients across first-level administrative units in distance to the coast, elevation, precipitation, temperature, and land quality for agriculture. Columns (4) and (8) include as controls the mean values (for each country) of distance to the coast, elevation, precipitation, temperature, and land quality for agriculture. All specifications include regional fixed effects (constants not reported). The Data Appendix gives detailed variable definitions and data sources. Robust standard errors are reported in parentheses in the first-row below the estimates. In the second-row below the estimates we also report bootstrap standard errors that account for the use of a generated (principal component) regressor.

***, **, and * indicate statistical significance at the 1%, 5%, and 10% level, respectively.

Since geographic inequality across ethnic lines does not seem to exert an independent influence on GDP once we account for ethnic differences in well-being, we also estimated two-stage-least-squares estimates associating geographic inequality across ethnic homelands to ethnic inequality in lights per capita in the first stage and the component of ethnic inequality explained by geographic disparities with the log per capita GDP in 2000 in the second stage. While the 2SLS estimates do not identify causal effects, they account for measurement error in the proxy measure of development (lights per capita) and also isolate the geography-driven component of ethnic inequality. The 2SLS results (reported in the online Supplementary Appendix Table 23) reveal that the part of ethnic inequality that reflects geographic differences across ethnic homelands is a significant correlate of development.

Remark

These results should not be interpreted as showing that unequal geography across ethnic lines necessarily “causes” ethnic inequality (and under-development). It is possible that certain groups for a plethora of reasons (e.g., higher early development, superior military technology) conquered better-quality territories. In this regard the correlation between inequality in geographic endowments across ethnic lines and ethnic inequality (captured by lights per capita) indicates the sizable persistence of inequality. Hence, one might view an unequal ethnic geography as a manifestation of deeper ethnic differences. Nevertheless, even in this case, it is the presence of an inherently unequal geography that partially allows these primordial ethnic differences to become salient (otherwise there would be no “better land” for stronger groups to conquer and every group would have the same land endowment).

6 Conclusion

This study shows that ethnic differences in economic performance rather than the degree of ethnic diversity or the overall level of inequality are negatively correlated with economic development. While a large literature has examined (a) the interplay between inequality and development and (b) the effects of various aspects of the ethnic composition (such as fragmentation, polarization, segregation) on economic performance, there is little work studying the linkages between ethnicity, inequality, and cross-country comparative development. This paper is a first effort to fill this gap.

First, combining linguistic maps on the spatial distribution of ethnic groups within countries with satellite images of light density at night, we construct Gini coefficients reflecting inequality in well-being across ethnic lines for a large number of countries. Ethnic inequality is weakly correlated with the standard measures of income inequality and modestly correlated with ethnolinguistic fractionalization, polarization, and segregation. Second, we show that the newly constructed proxy of ethnic inequality is negatively related to per capita GDP. The association retains its economic and statistical significance when we condition on inequality across administrative units, which is also inversely related to development. Including in the empirical specification both the ethnic inequality index and the widely-used ethnolinguistic fragmentation indicators, the latter loses significance, suggesting that it is inequality across ethnic lines that is correlated with poor economic performance rather than fractionalization per se. Third, we conduct a preliminary exploration of the roots of contemporary differences in well-being across ethnic groups. In this regard, we construct indicators of ethnic inequality in various geographic endowments and show that contemporary differences in development across ethnic homelands have a significant geographic component. Fourth, we show that geographic inequality across ethnic lines is also inversely related to contemporary development and that this correlation seems to operate via ethnic inequality.

Our study calls for future work both on the empirical and the theoretical front. One could employ our cross-country data and approach to examine the role of specific policies, such as trade openness and democratization, in shaping inequality across ethnic lines (and even administrative regions) over time. Furthermore, building on the literature on institutions (e.g., Acemoglu, Johnson, and Robinson (2005)) and state formation (e.g., Besley and Persson (2011)), one could explore the role of initial –at independence– differences in standards of living across ethnic groups on the subsequent path of economic and political modernization. Future works should also employ within-country approaches that are more suitable for identifying the mechanisms at play. For instance, it is of great interest to understand the channels via which ethnic differences in income shape development. Does the link operate via the provision of public goods, via spurring conflict and animosity, or by shaping trust and beliefs? For example, in ongoing work (Alesina, Michalopoulos, and Papaioannou (2014)) we use a plethora of micro-level data from Africa to assess the role of between-group and within-ethnic group inequality on public-goods provision, trust, and civic and political participation within (rather than across) countries. Moreover, given the large literature on inequality, fragmentation, and conflict, future work should explore in detail the role of ethnic-level income differences on conflict (as Mitra and Ray (2014) do so in the case of Hindu-Muslim conflict in India). Another avenue of future research is to compile between-group inequality measures over time using detailed data from censuses, surveys, or tax records that are available for some developed countries, in the spirit of Atkinson, Piketty, and Saez (2011).

7 Maps & Figures

Figures 1 and 2 provide an illustration of the construction of the ethnic inequality measures for Afghanistan. The Atlas Narodov Mira (GREG) maps 31 ethnicities (Figure 1a) whereas the Ethnologue reports 39 languages (Figure 1b).

Figures 2a and 2b portray the distribution of lights per capita for each group based on GREG and Ethnologue mapping with lighter colors indicating more brightly lit areas.

Figure 3 illustrates the construction of the overall spatial inequality. When we divide the globe into boxes of 2.5 × 2.5 decimal-degree boxes, we get 24 areas in Afghanistan.

Figures 4a and 4b illustrate the construction of inequality measures across administrative regions using both the first-level and second-level units.

Figures 5a and 5b illustrate the perturbed ethnic homelands for Afghanistan based on the Atlas Narodov Mira and the Ethnologue, respectively.

Figures 6a and 6b illustrate the global distribution of ethnic inequality with the GREG and the Ethnologue mapping.

Figures 6c and 6d plot the world distribution of the overall degree of spatial inequality and regional inequality across first-level administrative units.

Figures 6e and 6f portray the global distribution of ethnic inequality partialling out the effect of the overall spatial inequality.

Figures 7a and 7b provide a graphical illustration of the association between the two proxies of ethnic inequality and the ethnic and linguistic fragmentation measures of Alesina, Devleeschauwer, Easterly, Kurlat, and Wacziarg (2003) and Desmet, Ortuño-Ortín, and Wacziarg (2012), respectively.

Figures 8a and 8b illustrate this association between income inequality and ethnic inequality using the Ethnologue and GREG mapping of group’s homelands.

Figures 9a–9d illustrate the unconditional and the conditional on regional fixed effects association between ethnic inequality and GDP per capita across countries.

In Figures 10a and 10b we plot the baseline index of ethnic inequality (based on lights per capita) against the first principal component of inequality in ethnic-specific geographic endowments. Figures 10c and 10d plot the conditional on regional fixed effects association.

8 Data Appendix

8.1 Country-Level Data

Income level

Log of real per capita GDP at PPP (Chain Index) in 2000. Source: Penn World Tables, Edition 7. Source: Heston, Summers, and Aten (2011).

Population

Log population in 2000. Source: Penn World Tables, Edition 7. Source: Heston, Summers, and Aten (2011).

Land Area

Log surface area. Source: Nunn and Puga (2012).

Income Inequality

Adjusted Gini coefficient index averaged over the period 1965–1998. Source: Easterly (2007); based on the United Nations World Institute for Development Economics Research Data.

Ethnic/Linguistic Fractionalization

Index of ethnic/linguistic heterogeneity. It reflects the probability that two randomly selected individuals belong to different ethnolinguistic/religious groups. For completeness we use two measures, one from Alesina et al. (2003), which in turn is based on CIA Factbook and Encyclopedia Britannica and one from Desmet et al. (2012), which is based on Ethnologue (level 15). Source: Alesina, Devleeschauwer, Easterly, Kurlat, and Wacziarg (2003) and Desmet, Ortuño-Ortín, and Wacziarg (2012).

Ethnic/Linguistic Segregation

Index ranging from zero to one capturing ethnic/linguistic segregation (clustering) within countries. If each region is comprised of a separate group, then the index is equal to 1, and this is the case of complete segregation. If every region has the same fraction of each group as the country as a whole, the index is equal to 0; this is the case of no segregation. The index is increasing in the square deviation of regional-level fractions of groups relative to the national average. The index gives higher weight to the deviation of group composition from the national average in bigger regions than in smaller regions. Source: Alesina and Zhuravskaya (2011).

Ethnolinguistic Polarization

Index of ethnolinguistic polarization that achieves its maximum score when a country consists of two groups of equal size. Source: Montalvo and Reynal-Querol (2005).

Cultural Fragmentation

Index of ethnolinguistic fractionalization that accounts for the degree of similarity between linguistic groups using the Ethnologue linguistic tree. Source: Fearon (2003).

Genetic Diversity

The expected heterozygosity (genetic diversity) of a country’s contemporary population. The index is based on distances from East Africa to the year 1500 locations of the ancestral populations of the country’s component ethnic groups in 2000 and on the pairwise migratory distances among these ancestral populations. The source countries of the ancestral populations are identified from the World Migration Matrix (Putterman and Weil, 2010), and the modern capital cities of these countries are used to compute the aforementioned migratory distances. The measure of genetic diversity is then computed by applying (i) the coefficients obtained from regressing expected heterozygosity on migratory distance from East Africa at the ethnic group level, using a worldwide sample of 53 ethnic groups comprising the Human Genome Diversity Cell Line Panel, compiled by the Human Genome Diversity Project (HGDP) and the Centre d’Étude du Polymorphisme Humain (CEPH); (ii) the coefficients obtained from regressing pairwise genetic distance on pairwise migratory distance in a sample of 1,378 HGDP-CEPH ethnic group pairs, and (iii) the ancestry weights representing the fractions of the year 2000 national population that can trace their ancestral origins to different source countries in the year 1500. Source: Ashraf and Galor (2013).

Soil Quality

Percentage of each country with fertile soil. Source: Nunn and Puga (2012).

Ruggedness

The terrain ruggedness index quantifies topographic heterogeneity. The index is the average across all grid cells in the country not covered by water. The units for the terrain ruggedness index correspond to the units used to measure elevation differences. Ruggedness is measured in hundreds of metres of elevation difference for grid points 30 arc-seconds (926 metres on the equator or any meridian) apart. Source: Nunn and Puga (2012).

Tropical

The percentage of the land surface of each country with tropical climate. Source: Nunn and Puga (2012).

Gem-Quality Diamond Extraction

Carats of gem-quality diamond extraction between 1958 and 2000, normalized by land area. Source: Nunn and Puga (2012).

Common Law

Indicator variable that identifies countries that have a common law legal system. Source: La Porta, Lopez-de-Silanes, Shleifer, and Vishny (1999) and Nunn and Puga (2012).

European Descent

The variable, calculated from version 1.1 of the migration matrix of Putterman and Weil (2010), estimates the percentage of the year 2000 population in every country that is descended from people who resided in Europe in 1500. Source: Nunn and Puga (2012).

Settler Mortality

Log of mortality rates faced by European colonizers in late 19th century. Source: Acemoglu, Johnson, and Robinson (2001).

Population Density before Colonization

Log of population density around 1500 CE. Source: Acemoglu, Johnson, and Robinson (2002) and Nunn and Puga (2012).

Border Straightness Index

The 0 – 1 index reflects how straight –and thus likely to be non-organic– national borders are. Source: Alesina, Easterly, and Matuszeski (2011).

Neolithic Transition

The logarithm of the number of thousand years elapsed (as of the year 2000) since the majority of the population residing within a countries modern national borders began practicing sedentary agriculture as the primary mode of subsistence. This measure, reported by Putterman (2008), is compiled using a wide variety of both region- and country-specific archaeological studies as well as more general encyclopedic works on the transition from hunting and gathering to agriculture during the Neolithic Revolution Source: Ashraf and Galor (2013) and Putterman and Weil (2010).

Ethnic Partitioning

Percentage of the population of a country that belongs to partitioned ethnic groups. Source: Alesina, Easterly, and Matuszeski (2011).

Regional Fixed Effects

The region constants correspond to: South-East Asia and the Pacific, Latin America and the Caribbean, North America, Western Europe, Eastern Europe and Central Asia, the Middle East and Northern Africa, and Sub-Saharan Africa. The classification follows World Bank’s World Development Indicators Database.

8.2 Group-Level Data

Light Density at Night per Capita

Light density is calculated by averaging luminosity observations across pixels that fall within each territory (ethnic/linguistic homelands, boxes of 2.5 × 2.5 decimal degrees, administrative units, and Thiessen polygons) and then dividing by population density. Source: National Oceanic and Atmospheric Administration, National Geophysical Data Center. http://ngdc.noaa.gov/eog/dmsp/downloadV4composites.html.

Population Density

Average number of people per square kilometer for 1990 and 2000. Source: Center for International Earth Science Information Network (CIESIN), Columbia University, and Centro Internacional de Agricultura Tropical (CIAT), 2005. Gridded Population of the World Version 3 (GPWv3): Population Density Grids. Palisades, NY: Socioeconomic Data and Applications Center (SEDAC), Columbia University. http://sedac.ciesin.columbia.edu/gpw.

Area

Total area (in square kilometers) of each territory (ethnic/linguistic homelands, boxes of 2.5 × 2.5 decimal degrees, administrative units, and Thiessen polygons).

Elevation

Average elevation above country minimum value in meters. Source: World-Clim – Global Climate Data. Data were originally collected by NASA-JPL SRTM. http://www.worldclim.org/current.

Land Suitability for Agriculture

Average land quality for cultivation within each country. The index is the product of two components capturing the climatic and soil suitability for farming. Source: Michalopoulos (2012); Original Source: Atlas of the Biosphere. http://www.sage.wisc.edu/iamdata/grid_data_sel.php.

Distance to the Sea Coast

The geodesic distance from the centroid of each country to the nearest coastline, measured in 1000s of kilometers. Source: Global Mapping International, Colorado Springs, Colorado, USA. Series name: Global Ministry Mapping System. Series issue: Version 3.0

Average Annual Precipitation

Average annual precipitation (mm) for the approximate 1950 – 2000 time frame within the respective territory (ethnic/linguistic homelands, boxes of 2.5 × 2.5 decimal degrees, administrative units, and Thiessen polygons). Source: WorldClim-Global Climate Data. http://www.worldclim.org/bioclim.

Average Annual Temperature

Average annual temperature for the approximate 1950–2000 time frame within the respective territory (ethnic/linguistic homelands, boxes of 2.5 × 2.5 decimal degrees, administrative units, and Thiessen polygons). Source: WorldClim – Global Climate Data. http://www.worldclim.org/bioclim.

Precipitation Seasonality

Coefficient of variation of annual precipitation for the approximate 1950 – 2000 time frame within the respective territory (ethnic/linguistic homelands, boxes of 2.5 × 2.5 decimal degrees, administrative units, and Thiessen polygons). Source: World-Clim – Global Climate Data. http://www.worldclim.org/bioclim.

Temperature Range

Range (estimated as the difference of the maximum value of the warmest month minus the minimum value of the coldest month) of annual temperature for approximately the period 1950 – 2000 within the respective territory (ethnic/linguistic homelands, boxes of 2.5 × 2.5 decimal degrees, administrative units, and Thiessen polygons). Source: World-Clim – Global Climate Data. http://www.worldclim.org/bioclim.