The Ambient-Potential Composite Ewald Method for Ab Initio QM/MM Molecular Dynamics Simulation

Abstract

A new approach for performing Particle Mesh Ewald in ab initio QM/MM simulations with extended atomic orbital basis sets is presented. The new approach, the Ambient-Potential Composite Ewald Method (CEw), does not perform the QM/MM interaction with Mulliken charges nor electrostatically fit charges. Instead the nuclei and electron density interact directly with the MM environment, but in a manner that avoids the use of dense Fourier transform grids. By performing the electrostatics with the underlying QM density, the CEw method avoids self-consistent field instabilities that have been encountered with simple charge mapping procedures. Potential of mean force (PMF) profiles of the p-nitrophenyl phosphate dissociation reaction in explicit solvent are computed from PBE0/6-31G* QM/MM molecular dynamics simulations with various electrostatic protocols. The CEw profiles are shown to be stable with respect to real-space Ewald cutoff, whereas the PMFs computed from truncated and switched electrostatics produce artifacts. PBE0/6-311G**, AM1/d-PhoT, and DFTB2 QM/MM simulations are performed to generate two-dimensional PMF profiles of the phosphoryl transesterification reactions with ethoxide and phenoxide leaving groups. The semiempirical models incorrectly produce a concerted ethoxide mechanism, whereas PBE0 correctly produces a stepwise mechanism. The ab initio reaction barriers agree more closely to experiment than the semiempirical models. The failure of Mulliken-charge QM/MM-Ewald is analyzed.

TOC images

1 Introduction

The rigorous treatment of long-ranged electrostatics is essential for a proper modeling of biological processes in solution.^1–5 One technique for including long-range electrostatics is Ewald’s method,⁶ which replicates a primary unit cell composed of Gaussian charges to form an infinite periodic lattice. The periodic Gaussian charge density is resolved in a plane-wave basis, whence the electrostatic potential is readily calculated. The plane-wave potential is then modified with short-ranged corrections to account for the Gaussian charge penetration and thus recover the electrostatic potential of the point charge system. The computational performance of Ewald’s method was greatly improved with the advent of the Particle Mesh Ewald^7–10 (PME) method, which has become the de facto standard for molecular mechanical (MM) force field molecular dynamics (MD) simulations. Although the PME method was originally formulated for point charges, it has been extended throughout the years to handle Cartesian^11–16 and solid harmonic^17,18 multipoles for its application with the AMOEBA polarizable force field¹⁹ and the modified Divide-and-Conquer (mDC) quantum mechanical force field^20–22 (QMFF). Before the widespread adoption of PME, electrostatic force truncation, switching, and shifting were frequently used.^23,24 Electrostatic cutoff methods were later found to produce artifacts in the properties of water^25–28 and the structural stability of large biomolecules.^29–31 Consequently it has been suggested that new models not be parametrized using cutoff electrostatics.²⁶

The treatment of electrostatics within quantum mechanical/molecular mechanical (QM/MM) models³² has followed one of two general prescriptions: electrostatic embedding and mechanical embedding.^33,34 Mechanical embedding is a “subtractive” paradigm, whereby the quantum mechanical (QM) region is represented by a MM-analogue, the electrostatics are computed entirely with MM charges, and the QM region is introduced by removing the MM-analogue self-energy and replacing it with the gas-phase QM energy. In this sense mechanical embedding can be viewed as a type of ONIOM method.^35–37 Although mechanical embedding is simple to implement, it suffers from the major drawback that the QM charge density does not directly polarize to the MM environment; therefore, the electrostatic embedding method is instead often used. Electrostatic embedding decomposes the total energy into MM/MM, QM/QM, and QM/MM “additive” components. The QM/MM interaction explicitly includes the electrostatics between the QM charge density and the MM point charges – among other interactions, including van der Waals (vdW) forces – thereby polarizing the QM electron density.

Combined QM/MM MD applications have been dominated by the use of semiempirical Hamiltonians; for example, AM1/d-PhoT,³⁸ DFTB2,^39,40 and related models,^41–43 because the high cost of ab initio wavefunction methods has often precluded their ability to obtain the amount of statistical sampling necessary for making a meaningful comparison with experiment.⁴⁴ Nevertheless ab initio QM/MM methods⁴⁵ have found applications⁴⁶ through the calculation of single point energies,⁴⁷ NMR chemical shifts,⁴⁸ geometry optimizations,⁴⁹ adiabatic potential energy surfaces,⁵⁰ nudge elastic band pathways,⁵¹ finite temperature string methods,^52–54 multiple time step simulations,⁵⁵ and to correct potential of mean force (PMF) free energy surfaces obtained from semiempirical QM/MM calculations.^56–59

Applications of semiempirical QM/MM methods routinely employed electrostatic embedding with truncated QM/MM electrostatic cutoffs^60–62 until the development of the semiempirical QM/MM Ewald presented by Nam,⁶³ which was independently reported by Riccardi;⁶⁴ both of which were influenced by the method presented several years prior by Gao.⁶⁵ More recently these methods have been adapted for use with PME⁶⁶ and semiempirical X-Pol models.⁶⁷ The use of explicit lattice summations can also be found in the literature.⁶⁸

Considering that Ewald methods have traditionally been implemented for point-charge distributions, the semiempirical QM/MM-Ewald methods have chosen to use a Mulliken charge representation of the QM region to perform the long-range interactions. When this approach was applied to ab initio QM/MM, it was found that the use of Mulliken or Löwdin charges caused self-consistent field (SCF) convergence problems when non-minimal atomic orbital (AO) basis sets were used.^69,70 This has motivated the use of ChElPG⁷¹ or other electrostatic potential charge fitting procedures to produce stable ab initio QM/MM-Ewald trajectories.^{69,70,72–76} However, applications of ab initio QM/MM often still forego the use Ewald summations, preferring instead to model the long-range electrostatic with a reaction field method^77,78 or perform real-space electrostatic truncation, shifting, or smoothing.^{52–54,79–84} Recent work has advocated a 22 Å real-space switched electrostatic cutoff method using the minimum image convention.⁸⁵ Regrettably we’ve noticed that many authors have failed to report the size of the QM/MM nonbond cutoff that they’ve used, and other details defining how the electrostatics were performed.

Ab initio QM/MM methods will become frequently used in the near future as QMFFs^80,86–88 and free energy correction methods mature and as hardware technology continues to improve. To this end, we question if the effort placed into the evaluation of the underlying ab initio calculation isn’t somewhat wasted by performing the QM/MM interaction with QM atomic partial charges rather than the nuclei and ab initio electron density. Choosing the partial charges to model the QM electrostatic potential certainly helps to alleviate this concern to the extent that those charges indeed reproduce the potential, but the effort required to perform the fit could instead have been spent on a method that avoids charge fitting altogether. After all, the reason why the community is resorting to partial charge fitting is because a tractable alternative for evaluating the Ewald sum in ab initio QM/MM simulations has yet to be realized. The principle complication encountered in a direct adaptation of the Ewald or PME methods is borne from the electron density’s rapid changes near the nuclei, which requires an unacceptably large number of plane waves to resolve. Even if one could perform Ewald’s method using no more plane waves than what is found to be acceptable in a purely MM application, the analytic evaluation of each AO product’s Fourier coefficients would still be very costly. The computational effort would be further amplified by having to re-evaluate the Ewald potential at each step of the SCF procedure. A wholly new approach is needed.^84,89

In this work, we present a new ab initio QM/MM-Ewald method called the Ambient-Potential Composite Ewald Method, or Composite Ewald Method (CEw) for short. The new method does not require more plane waves than what is typically used within pure-MM applications. The analytic evaluation of AO-product Fourier coefficients are avoided by numerically integrating the Ewald reciprocal-space potential on the molecular quadrature grid normally used to compute the density functional theory (DFT) exchange-correlation functional. The long-range interactions between the QM region and its periodic replicas are computed from a truncated Taylor series that is expanded about a MM point-charge representation of the QM region. This approximation does not affect the interaction between the QM and MM regions; it only affects the interaction of the QM region with its own periodic images. As a consequence of this approximation, the Ewald contribution to the QM Fock matrix does not change during the SCF procedure, and the evaluation of the plane-wave Ewald potential becomes analogous to a one-time evaluation of a local density approximation (LDA) exchange-correlation functional.

We compare the new Ewald method to several other electrostatic protocols by performing umbrella window simulations to compute the PMF profiles of the p-nitrophenyl phosphate dissociation reaction. We show how various electrostatic protocols affect the MM-water solvation around charged QM regions. We extend and elaborate on the analysis first discussed by Holden et al.^69,70 to elucidate the failure of Nam’s semiempirical QM/MM-Ewald method⁶³ when it is applied to non-minimal basis set ab initio methods. We compare the computational cost of the new method to electrostatic embedding as a function of the number of QM atoms. Finally, we compute two-dimensional PMF profiles for phosphoryl transesterification reactions involving ethoxide and phenoxide leaving groups to compare the pathways produced by AM1/d-PhoT,³⁸ DFTB2,^39,40 and the PBE0/6-311G** hybrid functional DFT method.^90,91

2 Methods

2.1 The QM/MM energy

In this work, we consider a QM/MM system that contains a localized QM region; for example, a small solute QM molecule in MM solvent, or a QM active site within a large biomolecule. Furthermore, we suppose that the calculation is performed under periodic boundary conditions, whose real- and reciprocal-space lattice vectors are a₁, a₂, a₃ and ${\mathbf{a}}_1^{\ast }$, ${\mathbf{a}}_2^{\ast }$, ${\mathbf{a}}_3^{\ast }$, respectively. The total potential energy of the QM/MM system is

$$\begin{array}{l}E(\mathbf{R},\mathbf{P})=E_{\text{bonded}}(\mathbf{R})+E_{\text{LJ}}(\mathbf{R})+E_{\text{elec}}(\mathbf{R},\mathbf{P})\\ -E_{\text{bonded-elec}}(\mathbf{R})+E_{\text{kin}}(\mathbf{R},\mathbf{P})\\ +E_{\text{xc}}(\mathbf{R},\mathbf{P})+E_{\text{ex}}(\mathbf{R},\mathbf{P})\end{array}$$ (1)

where R is the set of atomic coordinates and P is the single-particle density matrix (see eq. 11). The various components of the energy are defined below.

The bonded energy E_bonded, is the collection of MM terms describing the bonds, angles, and torsions between covalently linked MM atoms and those combinations of MM and QM atoms which contain at least one MM atom.

$$\begin{array}{l}{E}_{\text{bonded}}(\mathbf{R})=E_{\text{bond}}(\mathbf{R})+E_{\text{angle}}(\mathbf{R})+E_{\text{torsion}}(\mathbf{R})\\ ={\displaystyle \sum _{ab\in \text{bonds}}{k}_{\mathit{ab}}{(R_{\mathit{ab}}-R_{\text{eq},ab})}^2}\\ +{\displaystyle \sum _{\mathit{abc}\in \text{angles}}{k}_{\mathit{abc}}{({\theta }_{\mathit{abc}}-{\theta }_{\text{eq},ab})}^2}\\ +{\displaystyle \sum _{\mathit{abcd}\in \text{torsions}}{\displaystyle \sum _n\frac{k_{\mathit{abcd},n}}{2}}}\\ \times [1+\cos (n{\varphi }_{\mathit{abcd}}-{\varphi }_{0,\mathit{abcd}})]\end{array}$$ (2)

The k values are force constants, and R_ab, θ_abc, and ϕ_abcd are bond lengths, angles, and torsion angles, respectively. The Lennard-Jones (LJ) energy E_LJ, is explicitly evaluated for all pairs of nonbonded atoms within a cutoff R_cut, and a long-range correction is applied to account for the dispersion beyond the nonbond cutoff,

$$\begin{array}{l}{E}_{\text{LJ}}(\mathbf{R})={\displaystyle \sum _{\begin{array}{l}b>a\\ ab\notin \text{bonded}\\ R_{\mathit{ab}}<R_{\text{cut}}\end{array}}\ast \frac{C_{12,ab}}{R_{\mathit{ab}}^{12}}-\frac{C_{6,ab}}{R_{\mathit{ab}}^6}}\\ -{\displaystyle \sum _{u,v}^{N_{\text{atom types}}}\frac{2\pi }{V}{N}_u{N}_v{\displaystyle {\int }_{R_{\text{cut}}}^{\infty }\frac{C_{6,uv}}{r^6}{r}^{2}dr}}\end{array}$$ (3)

where u,v index atom types and N_u is the number of atoms of type u. The asterisk excludes pairs where a and b are both QM, R_ab is assumed to be the “minimum image” distance between atoms a and b, and V = a₁ · a₂ × a₃ is the unit cell volume. The periodic electrostatic energy E_elec, is

$$\begin{array}{l}{E}_{\text{elec}}(\mathbf{R},\mathbf{P})=E_{\text{elec}}[q]\\ =\frac{1}{2}{\displaystyle \sum _{\mathrm{n}}{\displaystyle \int {\displaystyle \int \frac{q(\mathbf{r})q(\mathbf{r}\mathbf{\prime }+\mathbf{n})}{|\mathbf{r}-\mathbf{r}\mathbf{\prime }|}{d}^{3}r{d}^{3}r\prime }}}\end{array}$$ (4)

where n = n₁a₁ + n₂a₂ + n₃a₃ is a lattice translation and q(r) is the total charge density (see eq. 5). The MM atom charge density is a collection of static point charges (see eq. 6), and the QM charge density consists of the atomic nuclei and electrons (see eq. 7). The notation for the electrostatic energy shown in eq. 4 presumes the standard convention of excluding the infinite Coulomb self-energy of the point charges whenever those terms may appear.

Total charge density:

$$q(\mathbf{r})=q_{\text{mm}}(\mathbf{r})+q_{\text{qm}}(\mathbf{r})$$ (5)

MM charge density:

$$q_{\text{mm}}(\mathbf{r})={\displaystyle \sum _{a\in \text{mm}}{q}_a\delta (\mathbf{r}-{\mathbf{R}}_a)}$$ (6)

QM charge density:

$$\begin{array}{l}{q}_{\text{qm}}(\mathbf{r})={\displaystyle \sum _{a\in \text{qm}}{Z}_a\delta (\mathbf{r}-{\mathbf{R}}_a)-\rho (\mathbf{r})}\\ ={\displaystyle \sum _{a\in \text{qm}}{Z}_a\delta (\mathbf{r}-{\mathbf{R}}_a)}\\ -{\displaystyle \sum _{\mu v}{P}_{\mu v}{\chi }_{\mu }(\mathbf{r}-{\mathbf{R}}_{\mu }){\chi }_v(\mathbf{r}-{\mathbf{R}}_v)}\end{array}$$ (7)

Total electron (number) density:

$$\rho (\mathbf{r})={\rho }_{\alpha }(\mathbf{r})+{\rho }_{\beta }(\mathbf{r})$$ (8)

Spin-resolved (number) density:

$${\rho }_{\sigma }(\mathbf{r})={\displaystyle \sum _i{n}_i^{\sigma }{\varphi }_i^{\sigma }(\mathbf{r}){\varphi }_i^{\sigma }(\mathbf{r})}$$ (9)

Spin-resolved molecular orbital (MO):

$${\varphi }_i^{\sigma }(\mathbf{r})={\displaystyle \sum _{\mu }{C}_{\mu i}^{\sigma }{\chi }_{\mu }(\mathbf{r}-{\mathbf{R}}_{\mu })}$$ (10)

Atomic orbital (AO) representation of the single-particle density matrix:

$$P_{\mu v}=P_{\mu v}^{\alpha }+P_{\mu v}^{\beta }$$ (11)

Spin-resolved density matrix:

$$P_{\mu v}^{\sigma }={\displaystyle \sum _i{n}_i^{\sigma }{C}_{\mu i}^{\sigma }{C}_{vi}^{\sigma }}$$ (12)

where Z_a is a nuclear charge, χ(r) is an AO basis function, and n^σ and C^σ are the spin-resolved occupation numbers and MO coefficients, respectively. The densities and MOs defined by eqs. 7–10 have been written as a function of r; however, we emphasize that these terms also depend on the atomic positions through the use of atom-centered basis functions, and this dependence must be considered when evaluating the atomic forces.

The parameters within E_bonded are chosen to implicitly account for the electrostatic interactions between the bonded atoms, but those interactions are explicitly included in eq. 4 for notational convenience. Therefore, E_bonded-elec denotes a correction that removes the explicit electrostatic interactions between the pairs of MM atoms appearing within E_bonded,

$$E_{\text{bonded-elec}}(\mathbf{R})={\displaystyle \sum _{\begin{array}{l}ab\in \text{bonded}\\ ab\in \text{mm}\end{array}}\frac{q_a{q}_b}{R_{ab}}}$$ (13)

The remaining energy terms in eq. 1 are the electron interactions that do not directly couple to the MM environment.

The noninteracting electron kinetic energy:

$$E_{\text{kin}}(\mathbf{R},\mathbf{P})={\displaystyle \sum _{\mu v}{P}_{\mu v}{T}_{\mu v}}$$ (14)

$$T_{\mu v}=-\frac{1}{2}{\displaystyle \int {\chi }_{\mu }(\mathbf{r}-{\mathbf{R}}_{\mu }){\nabla }_{\mathrm{r}}^2{\chi }_v(\mathbf{r}-{\mathbf{R}}_v)d^{3}r}$$ (15)

The Hartree-Fock exchange energy:

$$E_{\text{ex}}(\mathbf{R},\mathbf{P})=-\frac{c_{\text{HF/x}}}{2}{\displaystyle \sum _{\sigma \in \alpha ,\beta }{\displaystyle \sum _{\begin{array}{l}\mu v\\ \mu \prime v\prime \end{array}}{P}_{\mu v}^{\sigma }{P}_{\mu \prime v\prime }^{\sigma }(\mu v\prime |\mu \prime v)}}$$ (16)

Electron repulsion integral (ERI):

$$\begin{array}{l}(\mu v|\mu \prime v\prime )={\displaystyle \int {\displaystyle \int d^{3}r{d}^{3}r\prime {|\mathbf{r}-\mathbf{r}\mathbf{\prime }|}^{-1}}}\\ \times {\chi }_{\mu }(\mathbf{r}-{\mathbf{R}}_{\mu }){\chi }_v(\mathbf{r}-{\mathbf{R}}_v)\\ \times {\chi }_{\mu \prime }(\mathbf{r}\mathbf{\prime }-{\mathbf{R}}_{\mu \prime }){\chi }_{v\prime }(\mathbf{r}\mathbf{\prime }-{\mathbf{R}}_{v\prime })\end{array}$$ (17)

The density functional theory (DFT) exchange-correlation energy:

$$\begin{array}{l}{E}_{\text{xc}}(\mathbf{R},\mathbf{P})={\displaystyle \int e_{\text{xc}}(\mathbf{r};{\rho }_{\alpha },{\rho }_{\beta },{\gamma }_{\alpha \alpha },{\gamma }_{\alpha \beta },{\gamma }_{\beta \beta })d^{3}r}\\ ={\displaystyle \sum _{\begin{array}{l}a\in \text{qm}\\ i\in a\end{array}}{w}_i{e}_{\text{xc}}({\mathbf{r}}_i;{\rho }_{\alpha },{\rho }_{\beta },{\gamma }_{\alpha \alpha },{\gamma }_{\alpha \beta },{\gamma }_{\beta \beta })}\end{array}$$ (18)

where ${\gamma }_{\sigma \sigma \prime }=\nabla {\rho }_{\sigma }(\mathbf{r})\cdot \nabla {\rho }_{\sigma \prime }(\mathbf{r})$, w_i is a molecular quadrature weight, and e_xc is a linear combination of exchange and correlation functional integrands,

$$e_{\text{xc}}(\mathbf{r})=c_{\text{DFT/x}}{e}_{\mathrm{x}}(\mathbf{r})+c_{\text{DFT/c}}{e}_{\mathrm{c}}(\mathbf{r})$$ (19)

where we have simplified the e_xc notation for brevity. The results shown in the present work are evaluated with PBE0/6-31G* or PBE0/6-311G**. PBE0 is the Perdew-Burke-Ernzerhof hybrid functional,^90,91 which uses the generalized gradient approximation functional described in Ref. 92. The PBE0 coefficients are c_DFT/x = 0.75, c_DFT/c = 1, and c_HF/x = 0.25.

The summation appearing in eq. 18 is a numerical integration of the DFT functional performed on a molecular quadrature grid. The molecular quadrature grid is a union of atomic quadrature grids, and an atomic grid is a series of concentric discretized spheres. That is, each atomic quadrature point i is an element within a set of angular points $\left\{{\widehat{\mathbf{r}}}_{\mathrm{\Omega }}\right\}$ that form a spherical shell of radius R_rad which is tethered to atom a. The atomic grid point locations and weights are ${\mathbf{r}}_{i\in a}={\mathbf{R}}_a+R_{\text{rad,}i}{\widehat{\mathbf{r}}}_{\mathrm{\Omega },i}$ and w_atomic,i = w_rad,iwΩ,i, respectively, where the notation i ∈ a denotes the grid point i within the set of points tethered to atom a. Many types of radial quadrature rules have been developed, including those based on Gauss-Chebyshev, Gauss-Legendre, Euler-Maclauren schemes.^93–96 In the present work, we use Gauss-Laguerre and Lebedev⁹⁷ rules for the radial and angular quadratures to form atomic grids consisting of 5580 points per heavy atom and 4296 points per hydrogen. In principle, each atomic grid integrates all-space; however, each atomic grid only samples the integrand adequately near their respective centers. Therefore, the molecular quadrature weights w_i ≡ w(r_i∈a,R) = Γ_a(r_i,R)w_atomic,i, introduce a “spatial partition function” Γ_a, to avoid an over-counting of the integrand when two-or-more atomic grids sample the same spatial area. Specifically, we use the “fuzzy Voronoi” partitioning scheme proposed by Becke,⁹⁸ which is summarized by eqs. 20–26. The relative size of the Voronoi are biased according to the atom’s Bragg-Slater radius, R_BS,a.

$${\mathrm{\Gamma }}_a({\mathbf{r}}_{i\in a},\mathbf{R})=\frac{P_a({\mathbf{r}}_i,\mathbf{R})}{{\sum }_b{P}_b({\mathbf{r}}_i,\mathbf{R})}$$ (20)

$$P_a({\mathbf{r}}_i,\mathbf{R})={\displaystyle \prod _{b\ne a}\frac{1}{2}[1-p(p(p(v_{\mathit{iab}})))]}$$ (21)

$$p(x)=\frac{3}{2}x-\frac{1}{2}{x}^3$$ (22)

$$v_{\mathit{iab}}({\mathbf{r}}_i,\mathbf{R})={\mu }_{\mathit{iab}}+a_{ab}(1-{\mu }_{\mathit{iab}}^2)$$ (23)

$$a_{ab}=\frac{u_{ab}}{u_{ab}^2-1}$$ (24)

$$u_{ab}=\frac{(R_{\text{BS},a}/R_{\text{BS},b})-1}{(R_{\text{BS},a}/R_{\text{BS},b})+1}$$ (25)

$${\mu }_{\mathit{iab}}({\mathbf{r}}_i,\mathbf{R})=\frac{R_{ia}-R_{ib}}{R_{ab}}$$ (26)

Formally, one would need to notationally account for periodicity within eqs. 15–18. If the electron density extends no more than half the box length, then one can evaluate these energy terms as written while assuming a minimum image convention. This is typically implemented by translating the QM region to the center of the simulation box, and then wrapping the MM atoms around it.

For a given set of coordinates, one must nonlinearly minimize the energy with respect to the MO coefficients in a SCF procedure, under the constraint that the MOs remain orthonormal to each other,

$$\begin{array}{l}{\displaystyle \int {\varphi }_i^{\sigma }(\mathbf{r}){\varphi }_j^{\sigma }(\mathbf{r})d^{3}r={\delta }_{ij}}\\ {\mathbf{C}}^{\sigma ,T}\cdot \mathbf{S}\cdot {\mathbf{C}}^{\sigma }=\mathbf{I}\end{array}$$ (27)

where S is the AO overlap matrix,

$$S_{\mu v}={\displaystyle \int {\chi }_{\mu }(\mathbf{r}-{\mathbf{R}}_{\mu }){\chi }_v(\mathbf{r}-{\mathbf{R}}_v)d^{3}r}$$ (28)

and I_ij = δ_ij is the identity matrix. Under these constraints, the optimal set MO coefficients can be shown to obey the Roothaan-Hall equation,

$${\mathbf{F}}^{\sigma }\cdot {\mathbf{C}}^{\sigma }=\mathbf{S}\cdot {\mathbf{C}}^{\sigma }\cdot {\mathbf{E}}^{\sigma }$$ (29)

where E^σ are the spin-resolved orbital eigenvalues and F^σ is the AO representation of the spin-resolved Fock matrix,

$$F_{\mu v}^{\sigma }={\frac{\partial E}{\partial P_{\mu v}^{\sigma }}|}_{\mathbf{R}}$$ (30)

Equation 29 is a generalized eigenvalue problem, which can be reduced to standard form by introducing a transformation matrix,

$$\mathbf{X}=\mathbf{U}\cdot {\mathbf{s}}^{-\frac{1}{2}}$$ (31)

where U and s are the eigenvectors and eigenvalues of the overlap matrix, respectively; S = U · s · U^T. It follows that X^T · S · X = I, and

$${\mathbf{F}}^{\sigma ,\text{OAO}}\cdot {\mathbf{C}}^{\sigma ,\text{OAO}}={\mathbf{C}}^{\sigma ,\text{OAO}}\cdot {\mathbf{E}}^{\sigma }$$ (32)

where F^σ,OAO is the orthonormal atomic orbital (OAO) basis representation of the Fock matrix,

$${\mathbf{F}}^{\sigma ,\text{OAO}}={\mathbf{X}}^T\cdot {\mathbf{F}}^{\sigma }\cdot \mathbf{X}$$ (33)

and C^σ,OAO are the corresponding MO coefficients,

$${\mathbf{C}}^{\sigma }=\mathbf{X}\cdot {\mathbf{C}}^{\sigma ,\text{OAO}}$$ (34)

for the OAO basis defined by the transformation:

$${\chi }_v^{\text{OAO}}(\mathbf{r})={\displaystyle \sum _{\mu }{X}_{\mu v}{\chi }_{\mu }(\mathbf{r}-{\mathbf{R}}_{\mu })}.$$ (35)

The AO Fock matrix elements are the partial derivatives shown in eq. 30 applied to eq. 1:

$$\begin{array}{l}{F}_{\mu v}^{\sigma }=T_{ij}-{\displaystyle \sum _{\mu \prime v\prime }{P}_{\mu \prime v\prime }^{\sigma }(\mu v\prime |\mu \prime v)+{\frac{\partial E_{\text{elec}}}{\partial P_{\mu v}}|}_{\mathbf{R}}}\\ +{\displaystyle \sum _{\begin{array}{l}a\in \text{qm}\\ i\in a\end{array}}{w}_i{\chi }_{\mu }({\mathbf{r}}_i-{\mathbf{R}}_{\mu }){\chi }_v({\mathbf{r}}_i-{\mathbf{R}}_v)\frac{\partial e_{\text{xc}}}{\partial {\rho }_{\sigma }({\mathbf{r}}_i)}}\\ +{\displaystyle \sum _{\begin{array}{l}a\in \text{qm}\\ i\in a\end{array}}{w}_i{\nabla }_{\mathrm{r}}\left({\chi }_{\mu }({\mathbf{r}}_i-{\mathbf{R}}_{\mu }){\chi }_v({\mathbf{r}}_i-{\mathbf{R}}_{\mu })\right)}\\ \cdot \left(2\frac{\partial e_{\text{xc}}}{\partial {\gamma }_{\sigma \sigma }({\mathbf{r}}_i)}{\nabla }_{\mathrm{r}}{\rho }_{\sigma }({\mathbf{r}}_i)+\frac{\partial e_{\text{xc}}}{\partial {\gamma }_{\sigma \sigma \prime }({\mathbf{r}}_i)}{\nabla }_{\mathrm{r}}{\rho }_{\sigma \prime }({\mathbf{r}}_i)\right)\end{array}$$ (36)

where σ^′ denotes the spin that is antiparallel to σ.

Upon reaching SCF convergence, the atomic gradients ∂/∂X_a, are readily obtained from elementary chain-rule differentiation of the energy.

MM atom gradients (a ∈ mm):

$$\frac{\partial E}{\partial X_a}=\frac{\partial E_{\text{bonded}}}{\partial X_a}+\frac{\partial E_{\text{LJ}}}{\partial X_a}+\frac{\partial E_{\text{elec}}}{\partial X_a}-\frac{\partial E_{\text{bonded-elec}}}{\partial X_a}$$ (37)

QM atom gradients (a ∈ qm):

$$\begin{array}{l}\frac{\partial E}{\partial X_a}={\frac{\partial E}{\partial X_a}|}_{\mathbf{P}}+{\displaystyle \sum _{\mu v}{\frac{\partial E}{\partial P_{\mu v}^{\sigma }}|}_{\mathbf{R}}\frac{\partial P_{\mu v}^{\sigma }}{\partial X_a}}\\ {=\frac{\partial E_{\text{bonded}}}{\partial X_a}+\frac{\partial E_{\text{LJ}}}{\partial X_a}+\frac{\partial E_{\text{elec}}}{\partial X_a}|}_{\mathbf{P}}\\ {+{\displaystyle \sum _{\mu v}{P}_{\mu v}\frac{\partial T_{\mu v}}{\partial X_a}+\frac{\partial E_{\text{xc}}}{\partial X_a}}|}_{\mathbf{P}}\\ -\frac{c_{\text{HF/x}}}{2}{\displaystyle \sum _{\begin{array}{l}\sigma \in \alpha ,\beta \\ \mu v,\mu \prime v\prime \end{array}}{P}_{\mu v}^{\sigma }{P}_{\mu \prime v\prime }^{\sigma }\frac{\partial }{\partial X_a}(\mu v\prime |\mu \prime v)}\\ -{\displaystyle \sum _{\mu v}\frac{\partial S_{\mu v}}{\partial X_a}{\displaystyle \sum _{\begin{array}{c}\sigma \in \alpha ,\beta \\ i\end{array}}{n}_i^{\sigma }{E}_{\mathit{ii}}^{\sigma }{C}_{\mu i}^{\sigma }{C}_{\mathit{vi}}^{\sigma }}}\end{array}$$ (38)

Gradient of the exchange-correlation energy:

$$\begin{array}{l}{\frac{\partial E_{\text{xc}}}{\partial X_a}|}_{\mathbf{P}}={\displaystyle \sum _{i,\sigma }{w}_i\frac{\delta E_{\text{xc}}}{\delta {\rho }_{\sigma }({\mathbf{r}}_i)}\left({\frac{\partial {\rho }_{\sigma }}{\partial X_a}|}_{{\mathbf{r}}_i}+{\frac{\partial {\rho }_{\sigma }}{\partial x_i}|}_{\mathbf{R}}\frac{\partial x_i}{\partial X_a}\right)}\\ +{\displaystyle \sum _i{e}_{\text{xc}}({\mathbf{r}}_i)\frac{\partial w_i}{\partial X_a}}\end{array}$$ (39)

The ∂x_i/∂X_a derivative has a value of one only if the quadrature point i is tethered to atom a. Furthermore, the density is a linear combination of AO products, whose gradients satisfy ∇_rχ(r − R) = −∇_Rχ(r − R); therefore, the last term on the first line of eq. 7 reduces to:

$${\frac{\partial {\rho }_{\sigma }}{\partial x_i}|}_{\mathbf{R}}\frac{\partial x_i}{\partial X_a}=\{\begin{array}{ll}{-{\sum }_b\frac{\partial {\rho }_{\sigma }}{\partial X_b}|}_{{\mathbf{r}}_i}\hfill & \text{if }i\in a\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (40)

For brevity, we refer the reader to Ref. 99 for additional simplifications of eq. 39. The appendix of Ref. 99 also contains explicit expressions for the quadrature weight derivative, ∂w/∂X_a. Algorithms for computing the ERIs and ERI gradients are found in Refs. 100 and 101, and the one electron Gaussian integrals can be found in the seminal work by Obara and Saika.¹⁰²

When the QM/MM boundary severs a covalent bond, we use the link atom approach described in Ref. 66. In brief, “dangling bonds” are capped with a hydrogen QM atom. The link atom bond length is fixed, and its orientation is colinear with the severed QM/MM bond. The atomic forces of the link atom are propagated to the real QM and MM atoms via elementary chain rule derivatives. For completeness, we note that other treatments of the QM/MM boundary can be found in the literature, including the Generalized Hybrid Orbital method,^103–106 Effective Fragment Potential method,^107–109 and Local Self-Consistent Field method^110–112 to name just a few.¹¹³

2.2 The Ambient-Potential Composite Ewald Method

It is worthwhile to begin with some clarifying remarks regarding eq. 4 which may cause confusion for some readers because the lattice translation n, occurs in one (but not both) of the charge densities. In other words, one might have expected the Coulomb self-energy of a periodic density Σ_nq(r + n), to be

$$\frac{1}{2}{\displaystyle \sum _{\mathbf{n}}{\displaystyle \int q(\mathbf{r}+\mathbf{n}){\displaystyle \sum _{\mathbf{n}\mathbf{\prime }}{\displaystyle \int \frac{q(\mathbf{r}\mathbf{\prime }+\mathbf{n}\mathbf{\prime })}{|\mathbf{r}-\mathbf{r}\mathbf{\prime }|}{d}^{3}r\prime d^{3}r}}}}$$ (41)

because the Coulomb self-energy of an aperiodic density q(r), is

$$\frac{1}{2}{\displaystyle \int q(\mathbf{r}){\displaystyle \int \frac{q(\mathbf{r}\mathbf{\prime })}{|\mathbf{r}-\mathbf{r}\mathbf{\prime }|}{d}^{3}r\prime d^{3}r}}$$ (42)

However, eq. 41 is formally infinite if q(r) is anywhere nonzero¹¹⁴ because each cell then contains some amount of self-energy and there are an infinite number of cells in the lattice. When performing an inner-product of two functions that are each periodic (the density and the electrostatic potential are both periodic in eq. 41), the desired quantity is actually the inner-product’s average per unit cell. All cells in the lattice are identical, so the calculation of the average energy per unit cell merely requires one to change the range of integration in eq. 41 from “all space” to “the volume of one cell”.

$$E_{\text{elec}}[q]=\frac{1}{2}{\displaystyle \sum _{\mathbf{n}}{\displaystyle {\int }_{V}q(\mathbf{r}+\mathbf{n}){\displaystyle \sum _{\mathbf{n}\mathbf{\prime }}{\displaystyle \int \frac{q(\mathbf{r}\mathbf{\prime }+\mathbf{n}\mathbf{\prime })}{|\mathbf{r}-\mathbf{r}\mathbf{\prime }|}{d}^{3}r\prime d^{3}r}}}}$$ (43)

Equation 4 is recovered from eq. 43 by exploiting the periodicity of the electrostatic potential. Although the aperiodic density is not necessarily confined within a unit cell, the combined effluence of density produced from the construction of Σ_nq(r + n) causes each cell within the lattice to contain one instance of q(r) that appears to have been “wrapped” to the cell boundary. Equation 4 differs from eq. 43 only by “unwrapping” the density and making a corresponding adjustment to the integration limits.

Another possible source of confusion may arise from the prevalence of expressions in the literature that place lattice translations in the denominator rather than the numerator; that is,

$$E_{\text{elec}}[q]=\frac{1}{2}{\displaystyle \int q(\mathbf{r}){\displaystyle \sum _{\mathbf{n}}{\displaystyle \int \frac{q(\mathbf{r}\mathbf{\prime })}{|\mathbf{r}-\mathbf{r}\mathbf{\prime }+\mathbf{n}|}{d}^{3}r\prime d^{3}r}}}$$ (44)

Equations 4 and 44 are equivalent. Equation 4 is recovered from eq. 44 by performing a u-substitution that replaces r^′ → u + n and d³r^′ → d³u within eq. 44 and then changing the dummy integration variable from u to r^′. One could also write eq. 44 with a denominator of |r − r^′ − n|⁻¹, because the lattice summation considers all unique cell translations.

Our description of the Ambient-Potential Composite Ewald Method makes frequent use of Dirac notation, which is now summarized. A function is written as a “ket”, f(r) = 〈r|f〉. A complex conjugate is a “bra”, f^∗(r) = 〈f|r〉. An inner-product is a “braket”, ∫ f ^∗(r)g(r)d³r = 〈f|g〉. If both functions are periodic, then the inner-product’s integration is performed over the unit cell volume, ∫_Vd³r. From these definitions, one can immediately write the aperiodic (or “primary”) charge density:

$$\begin{array}{l}q(\mathbf{r})=\langle \mathbf{r}|q\rangle \\ =\langle \mathbf{r}|q_{\text{qm}}\rangle +\langle \mathbf{r}|q_{\text{mm}}\rangle \end{array}$$ (45)

and the periodic charge density:

$${\displaystyle \sum _{\mathbf{n}}q(\mathbf{r}+\mathbf{n})=}{\displaystyle \sum _{\mathbf{n}}\langle \mathbf{r}+\mathbf{n}|q\rangle }$$ (46)

One can further define an “ambient charge density”:

$$\begin{array}{l}{\displaystyle \sum _{\mathbf{n}\ne 0}q(\mathbf{r}+\mathbf{n})}={\displaystyle \sum _{\mathbf{n}\ne 0}\langle \mathbf{r}+\mathbf{n}|q\rangle }\\ ={\displaystyle \sum _{\mathbf{n}}\langle \mathbf{r}+\mathbf{n}|q\rangle -\langle \mathbf{r}|q\rangle }\end{array}$$ (47)

which consists of all translated copies of the density enclosing the primary image.

The act of producing the various forms of the density described above is aided through the use of specialized electrostatic operators. Let us define the “primary electrostatic operator”:

$$\langle \mathbf{r}|\widehat{J}|\mathbf{r}\mathbf{\prime }\rangle ={|\mathbf{r}-\mathbf{r}\mathbf{\prime }|}^{-1}$$ (48)

the “periodic electrostatic operator”:

$$\langle \mathbf{r}|\widehat{J\mathbf{n}}|\mathbf{r}\mathbf{\prime }\rangle ={\displaystyle \sum _{\mathbf{n}}{|\mathbf{r}-\mathbf{r}\mathbf{\prime }+\mathbf{n}|}^{-1}}$$ (49)

and the “ambient electrostatic operator”:

$$\langle \mathbf{r}|\widehat{J\mathrm{\Delta }}|\mathbf{r}\mathbf{\prime }\rangle ={\displaystyle \sum _{\mathbf{n}\ne 0}{|\mathbf{r}-\mathbf{r}\mathbf{\prime }+\mathbf{n}|}^{-1}}$$ (50)

These operators act upon an aperiodic charge density to produce the “primary electrostatic potential” (the electrostatic potential of the aperiodic density):

$$\langle \mathbf{r}|\widehat{J}|q\rangle ={\displaystyle \int \frac{q(\mathbf{r}\mathbf{\prime })}{|\mathbf{r}-\mathbf{r}\mathbf{\prime }|}{d}^{3}r\prime }$$ (51)

the “periodic electrostatic potential” (the electrostatic potential of the periodic density):

$$\langle \mathbf{r}|\widehat{J\mathbf{n}}|q\rangle ={\displaystyle \sum _{\mathbf{n}}{\displaystyle \int \frac{q(\mathbf{r}\mathbf{\prime }+\mathbf{n})}{|\mathbf{r}-\mathbf{r}\mathbf{\prime }|}{d}^{3}r\prime }}$$ (52)

and the “ambient electrostatic potential”:

$$\begin{array}{l}\langle \mathbf{r}|\widehat{J\mathrm{\Delta }}|q\rangle ={\displaystyle \sum _{\mathbf{n}\ne 0}{\displaystyle \int \frac{q(\mathbf{r}\mathbf{\prime }+\mathbf{n})}{|\mathbf{r}-\mathbf{r}\mathbf{\prime }|}{d}^{3}r\prime }}\\ =\langle \mathbf{r}|\widehat{J\mathbf{n}}|q\rangle -\langle \mathbf{r}|\widehat{J}|q\rangle \end{array}$$ (53)

The ambient electrostatic potential is produced solely from the periodic surroundings. That is, it is how the electrostatic potential is altered upon introducing periodicity to the system.

The electrostatic energy of the periodic system (eq. 4) can be decomposed into QM/QM, MM/MM, and QM/MM interactions as follows:

$$\begin{array}{l}{E}_{\text{elec}}[q]=\frac{1}{2}\langle q|\widehat{J\mathbf{n}}|q\rangle \\ =\frac{1}{2}\langle q_{\text{mm}}|\widehat{J\mathbf{n}}|q_{\text{mm}}\rangle +\langle q_{\text{qm}}|\widehat{J\mathbf{n}}|q_{\text{mm}}\rangle \\ +\frac{1}{2}\langle q_{\text{qm}}|\widehat{J\mathbf{n}}|q_{\text{qm}}\rangle \\ =\frac{1}{2}\langle q_{\text{mm}}|\widehat{J\mathbf{n}}|q_{\text{mm}}\rangle +\langle q_{\text{qm}}|\widehat{J\mathbf{n}}|q_{\text{mm}}\rangle \\ +\frac{1}{2}\langle q_{\text{mm}}|\widehat{J}|q_{\text{mm}}\rangle +\frac{1}{2}\langle q_{\text{qm}}|\widehat{J\mathrm{\Delta }}|q_{\text{mm}}\rangle \end{array}$$ (54)

The last term in eq. 54 is the “QM ambient energy”. It is the Coulomb interaction between the primary image’s QM region with the QM regions located in the periodic surrounding. The QM ambient energy is inconvenient to evaluate because the character of the QM ambient potential changes at each SCF step. We shall introduce an approximation that avoids this inconvenience. To begin, note that the QM region’s ambient energy can be expressed as a Taylor series expansion about a reference charge density, $q_{\text{qm}}^{\text{ref}}(\mathbf{r})$.

QM charge density evaluated about the reference:

$$q_{\text{qm}}(\mathbf{r})=q_{\text{qm}}^{\text{ref}}(\mathbf{r})+(q_{\text{qm}}(\mathbf{r})-q_{\text{qm}}^{\text{ref}}(\mathbf{r}))$$ (55)

QM ambient energy evaluated about the reference:

$$\begin{array}{l}\frac{1}{2}\langle q_{\text{qm}}|\widehat{J\mathrm{\Delta }}|q_{\text{qm}}\rangle =\frac{1}{2}\langle q_{\text{qm}}^{\text{ref}}|\widehat{J\mathrm{\Delta }}|q_{\text{qm}}^{\text{ref}}\rangle \\ +\langle q_{\text{qm}}-q_{\text{qm}}^{\text{ref}}|\widehat{J\mathrm{\Delta }}|q_{\text{qm}}^{\text{ref}}\rangle \\ +\frac{1}{2}\langle q_{\text{qm}}-q_{\text{qm}}^{\text{ref}}|\widehat{J\mathrm{\Delta }}|q_{\text{qm}}-q_{\text{qm}}^{\text{ref}}\rangle \end{array}$$ (56)

where $\langle \mathbf{r}|q_{\text{qm}}-q_{\text{qm}}^{\text{ref}}\rangle \equiv \langle \mathbf{r}|q_{\text{qm}}\rangle -\langle \mathbf{r}|q_{\text{qm}}^{\text{ref}}\rangle$.

Obviously, if $q_{\text{qm}}(\mathbf{r})\approx q_{\text{qm}}^{\text{ref}}(\mathbf{r})$, then the last term in eq. 56 is small. More importantly, the ambient electrostatic operator only interacts the QM region with those located in different periodic cells. If the unit cell was larger than the sphere which circumscribes the QM charge density, then this energy could, in principle, be performed via multipole moment expansions of q_qm(r). In other words, the last term in eq. 56 is also negligible when the multipole moments of $q_{\text{qm}}^{\text{ref}}(\mathbf{r})$ reasonably approximate those of q_qm(r). Therefore, an appropriate choice of $q_{\text{qm}}^{\text{ref}}(\mathbf{r})$ is one which satisfies

$${\displaystyle \int q_{\text{qm}}^{\text{ref}}(\mathbf{r})C_{l\mu }(\mathbf{r})d^{3}r\approx {\displaystyle \int q_{\text{qm}}(\mathbf{r})C_{l\mu }(\mathbf{r})d^{3}r}}$$ (57)

where C_lμ(r) is a regular solid harmonic.¹¹⁵ There are many potential choices which could satisfy this condition; however, considering that force fields have already developed their partial charges to reasonably model the electrostatics, the most convenient choice would be to reuse the underlying MM atomic charges for $q_{\text{qm}}^{\text{ref}}(\mathbf{r})$. Complicating the form of $q_{\text{qm}}^{\text{ref}}(\mathbf{r})$ by using, for example, atomic multipoles or diffuse auxiliary basis functions, would only increase the accuracy of the method insofar as those complications could improve the overall description of the QM region’s multipole moments. Alternatively, one could improve the multipole moments by simply adjusting the underlying MM partial charges if it was found to be necessary, thus rendering additional complications moot. Following this logic, the approach taken in the present work is to use a set of static point charges to approximate the ambient QM charge density,

$$q_{\text{qm}}^{\text{ref}}(\mathbf{r})={\displaystyle \sum _{a\in \text{qm}}{q}_a\delta (\mathbf{r}-{\mathbf{R}}_a)}$$ (58)

and then truncate the Taylor series to first-order,

$$\frac{1}{2}\langle q_{\text{qm}}-q_{\text{qm}}^{\text{ref}}|\widehat{J\mathrm{\Delta }}|q_{\text{qm}}-q_{\text{qm}}^{\text{ref}}\rangle \approx 0$$ (59)

$$\frac{1}{2}\langle q_{\text{qm}}|\widehat{J\mathrm{\Delta }}|q_{\text{qm}}\rangle \approx \langle q_{\text{qm}}|\widehat{J\mathrm{\Delta }}|q_{\text{qm}}^{\text{ref}}\rangle -\frac{1}{2}\langle q_{\text{qm}}^{\text{ref}}|\widehat{J\mathrm{\Delta }}|q_{\text{qm}}^{\text{ref}}\rangle$$ (60)

such that the ambient QM energy becomes a composite interaction between q_qm(r) with $q_{\text{qm}}^{\text{ref}}(\mathbf{r})$, and $q_{\text{qm}}^{\text{ref}}(\mathbf{r})$ with itself. After simplification, the energy becomes E_CEw[q] ≈ E_elec[q],

$$\begin{array}{l}{E}_{\text{CEw}}[q]=\frac{1}{2}\langle q_{\text{mm}}|\widehat{J\mathbf{n}}|q_{\text{mm}}\rangle +\frac{1}{2}\langle q_{\text{qm}}|\widehat{J}|q_{\text{qm}}\rangle \\ +\langle q_{\text{qm}}|\widehat{J\mathbf{n}}|q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}\rangle -\langle q_{\text{qm}}|\widehat{J}|q_{\text{qm}}^{\text{ref}}\rangle \\ -\frac{1}{2}\langle q_{\text{qm}}^{\text{ref}}|\widehat{J\mathbf{n}}|q_{\text{qm}}^{\text{ref}}\rangle +\frac{1}{2}\langle q_{\text{qm}}^{\text{ref}}|\widehat{J}|q_{\text{qm}}^{\text{ref}}\rangle \end{array}$$ (61)

In this manner, the periodic potentials only involve static point charge distributions, which can be computed once before the SCF procedure begins.

Equation 61 is an approximation, but our formulation was designed to reduce the error’s magnitude for typical QM/MM applications. It should be pointed out that the truncated Taylor series expansion only effects the interaction of the QM region with its images; it does not approximate the interaction between the QM and MM regions nor the MM region with itself. Nevertheless, if the interaction between the QM region with its periodic images was such that the Taylor series could not reasonably be truncated, then one could directly evaluate the QM ambient energy in eq. 54 by evaluating the multipole moments of q_qm(r) at each SCF step and then use the point-multipole particle mesh Ewald (PME) method described in Ref. 17; however, the small size of – and, therefore, intercellular distance between – QM regions should make this added layer of complexity unnecessary in most applications.

The periodic electrostatic potential of the point charge distributions appearing in eq. 61 can be computed with either the Ewald or PME methods. A detailed theoretical development of these methods can be found in Ref. 17, whose notation we adopt henceforth. Specifically, we reserve

$$\mathbf{k}=2\pi \left(k_1{\mathbf{a}}_1^{\ast }+k_2{\mathbf{a}}_2^{\ast }+k_3{\mathbf{a}}_3^{\ast }\right)$$ (62)

to index the angular wave numbers of a plane wave basis:

$$\langle \mathbf{r}|\mathbf{k}\rangle =e^{i{\mathbf{k}}^T\cdot \mathbf{r}}$$ (63)

Furthermore, we shall refer to B-spline weights,

$$\theta (\mathbf{r}-{\mathbf{R}}_a)={\displaystyle \prod _{d=1}^3{M}_n\left(N_d{\left(\mathbf{r}-{\mathbf{R}}_a\right)}^T\cdot {\mathbf{a}}_d^{\ast }+\frac{n}{2}\right)}$$ (64)

that are constructed from order–n Cardinal B-spline functions,

$$M_n(u)=\frac{1}{(n-1)!}{\displaystyle \sum _{k=0}^n{\left(-1\right)}^k\left(\begin{array}{l}n\\ k\end{array}\right){\left[max(u-k,0)\right]}^{n-1}}$$ (65)

and whose discrete Fourier transform coefficients,

$${\theta }_{\mathbf{k}}={\displaystyle \sum _{\mathbf{t}}\langle \mathbf{k}|{\mathbf{R}}_{\mathbf{t}}\rangle \langle {\mathbf{R}}_{\mathbf{t}}|\theta \rangle }$$ (66)

are evaluated from a uniformly spaced grid. The grid consists of N = N₁N₂N₃ points that are indexed by t = (t₁,t₂,t₃) and positioned at R_t.

$${\mathbf{R}}_{\mathbf{t}}={\displaystyle \sum _{d=1}^3\frac{t_d-1}{N_d}{\mathbf{a}}_d}$$ (67)

We will continue by summarizing the necessary equations for PME, written below for a generic point charge distribution, q_pt(r).

$$q_{\text{pt}}(\mathbf{r})={\displaystyle \sum _{a\in \text{pt}}{q}_a\delta (\mathbf{r}-{\mathbf{R}}_a)}$$ (68)

In brief, the PME method computes the periodic potential of a model Gaussian density

$${\displaystyle \sum _{a\in \text{pt}}{q}_a{\left(\frac{{\beta }^2}{\pi }\right)}^{3/2}{e}^{-{\beta }^2{|\mathbf{r}-{\mathbf{R}}_a|}^2}}$$ (69)

and then corrects for the short-range difference between the point and Gaussian potentials. The electrostatic potential of the periodic Gaussian density is performed analytically upon fitting it to a plane wave basis. Therefore, the PME potential (see eq. 70) decomposes into a plane-wave potential (see eq. 75), a short-range correction that removes the Gaussian potential (see eq. 73), a corresponding short-range “near-field” potential that reintroduces the point-charges (see eq. 71), and, for charged systems, a uniform background potential (see eq. 76). Several of these potentials can be grouped together, when convenient, into “far-field” (see eq. 72), “real-space” (see eq. 74), and “reciprocal-space” (see eq. 77) potentials. The difference between the Gaussian and point-charge electrostatic potentials is negligible at large distances, so one need only evaluate the near-field and Gaussian potentials within a real-space Ewald cutoff R_cut around r while assuming a minimum image convention. When applied to eq. 61, one must evaluate the potential at all r values where q_qm(r) is non-negligible. In other words, the near-field and Gaussian potentials must be evaluated for all imaged point charges within R_cut of q_qm(r).

PME potential:

$$\begin{array}{l}\langle \mathbf{r}|\widehat{J\mathbf{n}}|q_{\text{pt}}\rangle =\langle \mathbf{r}|\widehat{J\le }|q_{\text{pt}}\rangle -\langle \mathbf{r}|\widehat{J\cap }|q_{\text{pt}}\rangle +\langle \mathbf{r}|\widehat{J\approx }|q_{\text{pt}}\rangle +\langle \mathbf{r}|\widehat{J-}|q_{\text{pt}}\rangle \\ =\langle \mathbf{r}|\widehat{J\le }|q_{\text{pt}}\rangle -\langle \mathbf{r}|\widehat{J\cap }|q_{\text{pt}}\rangle +\langle \mathbf{r}|\widehat{J\%}|q_{\text{pt}}\rangle \\ =\langle \mathbf{r}|\widehat{J\le }|q_{\text{pt}}\rangle +\langle \mathbf{r}|\widehat{J>}|q_{\text{pt}}\rangle \\ =\langle \mathbf{r}|\widehat{J\times }|q_{\text{pt}}\rangle +\langle \mathbf{r}|\widehat{J\%}|q_{\text{pt}}\rangle \end{array}$$ (70)

Near-field potential; that is, the potential caused by everything within the real-space Ewald cutoff R_cut around r:

$$\langle \mathbf{r}|\widehat{J\le }|q_{\text{pt}}\rangle =\{\begin{array}{ll}{\displaystyle \sum _{a\in \text{pt}}\frac{q_a}{|\mathbf{r}-{\mathbf{R}}_a|}}\hfill & 0<|\mathbf{r}-{\mathbf{R}}_a|\le R_{\text{cut}}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (71)

Far-field potential; that is, the potential caused by everything outside R_cut:

$$\begin{array}{l}\langle \mathbf{r}|\widehat{J>}|q_{\text{pt}}\rangle =\langle \mathbf{r}|\widehat{J\approx }|q_{\text{pt}}\rangle -\langle \mathbf{r}|\widehat{J\cap }|q_{\text{pt}}\rangle +\langle \mathbf{r}|\widehat{J-}|q_{\text{pt}}\rangle \\ =\langle \mathbf{r}|\widehat{J\%}|q_{\text{pt}}\rangle -\langle \mathbf{r}|\widehat{J\cap }|q_{\text{pt}}\rangle \end{array}$$ (72)

Gaussian potential:

$$\langle \mathbf{r}|\widehat{J\cap }|q_{\text{pt}}\rangle =\{\begin{array}{ll}{\displaystyle \sum _{a\in \text{pt}}{q}_a\frac{\text{erf}(\beta |\mathbf{r}-{\mathbf{R}}_a|)}{|\mathbf{r}-{\mathbf{R}}_a|}}\hfill & |\mathbf{r}-{\mathbf{R}}_a|\le R_{\text{cut}}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (73)

Real-space potential:

$$\begin{array}{l}\langle \mathbf{r}|\widehat{J\times }|q_{\text{pt}}\rangle =\langle \mathbf{r}|\widehat{J\le }|q_{\text{pt}}\rangle -\langle \mathbf{r}|\widehat{J\cap }|q_{\text{pt}}\rangle \\ ={\displaystyle \sum _{a\in \text{pt}}{q}_a\times \{\begin{array}{ll}\frac{\text{erfc(}\beta \text{|}\mathbf{r}-{\mathbf{R}}_a\text{|)}}{\text{|}\mathbf{r}-{\mathbf{R}}_a\text{|}}\hfill & 0<\text{|}\mathbf{r}-{\mathbf{R}}_a\text{|}\le R_{\text{cut}}\hfill \\ -\frac{2\beta }{\sqrt{\pi }}\hfill & \text{|}\mathbf{r}-{\mathbf{R}}_a\text{|}=0\hfill \\ 0\hfill & \text{|}\mathbf{r}-{\mathbf{R}}_a\text{|}>R_{\text{cut}}\hfill \end{array}}\end{array}$$ (74)

Plane-wave potential (interpolated from a regular grid):

$$\langle \mathbf{r}|\widehat{J\approx }|q_{\text{pt}}\rangle ={\displaystyle \sum _{\mathbf{t}}\langle \theta |\mathbf{r}-{\mathbf{R}}_{\mathbf{t}}\rangle \langle {\mathbf{R}}_{\mathbf{t}}|{\varphi }_{\text{pt}}\rangle }$$ (75)

Uniform background potential:

$$\langle \mathbf{r}|\widehat{J-}|q_{\text{pt}}\rangle =\frac{\pi }{V{\beta }^2}{\displaystyle \sum _{a\in \text{pt}}{q}_a,\forall \mathbf{r}}$$ (76)

Reciprocal-space potential:

$$\langle \mathbf{r}|\widehat{J\%}|q_{\text{pt}}\rangle =\langle \mathbf{r}|\widehat{J\approx }|q_{\text{pt}}\rangle +\langle \mathbf{r}|\widehat{J-}|q_{\text{pt}}\rangle$$ (77)

PME potential interpolation control points:

$$\langle {\mathbf{R}}_{\mathbf{t}}|{\varphi }_{\text{pt}}\rangle =\mathrm{Re}{\displaystyle \sum _{\mathbf{k}\ne 0}\langle {\mathbf{R}}_{\mathbf{t}}|\mathbf{k}\rangle \frac{4\pi e^{-\frac{k^2}{4{\beta }^2}}}{V{k}^2{|{\theta }_{\mathbf{k}}|}^2}{S}_{\mathbf{k}}^{\text{pt}}}$$ (78)

PME structure factor; that is, the forward discrete Fourier transform coefficients of the B-spline interpolated point charges:

$$S_{\mathbf{k}}^{\text{pt}}={\displaystyle \sum _{\mathbf{t}}\langle \mathbf{k}|{\mathbf{R}}_{\mathbf{t}}\rangle {\displaystyle \sum _{a\in \text{pt}}{q}_a\theta ({\mathbf{R}}_{\mathbf{t}}-{\mathbf{R}}_a)}}$$ (79)

Having now introduced the near and far-field potentials, we show how they are used to simplify the second line in eq. 61,

$$\begin{array}{l}\langle q_{\text{qm}}|\widehat{J\mathbf{n}}|q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}\rangle -\langle q_{\text{qm}}|\widehat{J}|q_{\text{qm}}^{\text{ref}}\rangle \\ =\langle q_{\text{qm}}|\widehat{J\le }|q_{\text{mm}}\rangle +\langle q_{\text{qm}}|\widehat{J\le }|q_{\text{qm}}^{\text{ref}}\rangle \\ +\langle q_{\text{qm}}|\widehat{J>}|q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}\rangle -\langle q_{\text{qm}}|\widehat{J}|q_{\text{qm}}^{\text{ref}}\rangle \\ =\langle q_{\text{qm}}|\widehat{J\le }|q_{\text{mm}}\rangle +\langle q_{\text{qm}}|\widehat{J>}|q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}\rangle \end{array}$$ (80)

through the cancellation of terms,

$$\langle q_{\text{qm}}|\widehat{J\le }|q_{\text{qm}}^{\text{ref}}\rangle -\langle q_{\text{qm}}|\widehat{J}|q_{\text{qm}}^{\text{ref}}\rangle =0$$

which are equivalent because $q_{\text{qm}}^{\text{ref}}(\mathbf{r})$ is necessarily within R_cut of q_qm(r). For the same reason, the last line of eq. 61 merely removes of the QM reference density’s near-field energy, assuming that the QM region’s size is less than half the box length.

$$-\frac{1}{2}\langle q_{\text{qm}}^{\text{ref}}|\widehat{J\mathbf{n}}|q_{\text{qm}}^{\text{ref}}\rangle +\frac{1}{2}\langle q_{\text{qm}}^{\text{ref}}|\widehat{J}|q_{\text{q m}}^{\text{ref}}\rangle =-\frac{1}{2}\langle q_{\text{qm}}^{\text{ref}}|\widehat{J>}|q_{\text{qm}}^{\text{ref}}\rangle$$ (81)

The energy expression for the Ambient-Potential Composite Ewald method (see eq. 83) is obtained upon replacing the second and third lines of eq. 61 with the last line of eq. 80 and eq. 81, respectively,

$$\begin{array}{l}{E}_{\text{CEw}}[q]=\frac{1}{2}\langle q_{\text{mm}}|\widehat{J\mathbf{n}}|q_{\text{mm}}\rangle +\frac{1}{2}\langle q_{\text{qm}}|\widehat{J}|q_{\text{qm}}\rangle +\langle q_{\text{qm}}|\widehat{J\le }|q_{\text{mm}}\rangle \\ +\langle q_{\text{qm}}|\widehat{J>}|q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}\rangle -\frac{1}{2}\langle q_{\text{qm}}^{\text{ref}}|\widehat{J>}|+q_{\text{qm}}^{\text{ref}}\rangle \end{array}$$ (82)

and then expanding the far field potentials using the second line of eq. 72.

$$\begin{array}{l}{E}_{\text{CEw}}[q]=\frac{1}{2}\langle q_{\text{mm}}|\widehat{J\mathbf{n}}|q_{\text{mm}}\rangle +\frac{1}{2}\langle q_{\text{qm}}|\widehat{J}|q_{\text{qm}}\rangle +\langle q_{\text{qm}}|\widehat{J\le }|q_{\text{mm}}\rangle \\ +\langle q_{\text{qm}}|\widehat{J\%}|q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}\rangle -\langle q_{\text{qm}}|\widehat{J\cap }|q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}\rangle \\ -\frac{1}{2}\langle q_{\text{qm}}^{\text{ref}}|\widehat{J\%}|q_{\text{qm}}^{\text{ref}}\rangle +\frac{1}{2}\langle q_{\text{qm}}^{\text{ref}}|\widehat{J\cap }|q_{\text{qm}}^{\text{ref}}\rangle \end{array}$$ (83)

Explicit expressions for the energy terms appearing in eq. 83 are summarized by eqs. 84–96.

$$\frac{1}{2}\langle q_{\text{qm}}|\widehat{J\mathbf{n}}|q_{\text{mm}}\rangle =\frac{1}{2}{\displaystyle \sum _{a\in \text{mm}}{q}_a\langle {\mathbf{R}}_a|\widehat{J\mathbf{n}}|q_{\text{mm}}\rangle }$$ (84)

$$\frac{1}{2}\langle q_{\text{qm}}^{\text{ref}}|\widehat{J\%}|q_{\text{qm}}^{\text{ref}}\rangle =\frac{1}{2}{\displaystyle \sum _{a\in \text{qm}}{q}_a^{\text{ref}}\langle {\mathbf{R}}_a|\widehat{J\%}|q_{\text{qm}}^{\text{ref}}\rangle }$$ (85)

$$\frac{1}{2}\langle q_{\text{qm}}^{\text{ref}}|\widehat{J\cap }|q_{\text{qm}}^{\text{ref}}\rangle =\frac{1}{2}{\displaystyle \sum _{a\in \text{qm}}{q}_a^{\text{ref}}\langle {\mathbf{R}}_a|\widehat{J\cap }|q_{\text{qm}}^{\text{ref}}\rangle }$$ (86)

$$\begin{array}{l}\langle q_{\text{qm}}|\widehat{J\%}|q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}\rangle \\ ={\displaystyle \sum _{a\in \text{qm}}{Z}_a\langle {\mathbf{R}}_a|\widehat{J\%}|q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}\rangle +{\displaystyle \sum _{\mu v}{P}_{\mu v}{V}_{\mu v}^{\%}}}\end{array}$$ (87)

$$\begin{array}{l}{V}_{\mu v}^{\%}={\displaystyle \sum _{i=1}^{N_{\text{quad}}}{w}_i{\chi }_{\mu }({\mathbf{r}}_i-{\mathbf{R}}_{\mu }){\chi }_v({\mathbf{r}}_i-{\mathbf{R}}_v)}\\ \times (-\langle {\mathbf{r}}_i|\widehat{J\%}|q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}\rangle )\end{array}$$ (88)

$$\begin{array}{l}\langle q_{\text{qm}}|\widehat{J\cap }|q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}\rangle \\ ={\displaystyle \sum _{a\in \text{qm}}{Z}_a\langle {\mathbf{R}}_a|\widehat{J\cap }|q_{\text{qm}}+q_{\text{qm}}^{\text{ref}}\rangle +{\displaystyle \sum _{\mu v}{P}_{\mu v}{V}_{\mu v}^{\cap }}}\end{array}$$ (89)

$$V_{\mu v}^{\cap }=-{\displaystyle \sum _{a\in \text{qm}}{q}_a^{\text{ref}}{V}_{\mu v,a}^{\cap }-}{\displaystyle \sum _{a\in \text{mm}}{q}_a{V}_{\mu v,a}^{\cap }}$$ (90)

$$\begin{array}{l}{V}_{\mu v,a}^{\cap }={\left(\frac{{\beta }^2}{\pi }\right)}^{3/2}{\displaystyle \int {\displaystyle \int {|\mathbf{r}-\mathbf{r}\mathbf{\prime }|}^{-1}{e}^{-{\beta }^2{|\mathbf{r}\mathbf{\prime }-{\mathbf{R}}_a|}^2}}}\\ \times {\chi }_{\mu }(\mathbf{r}-{\mathbf{R}}_{\mu }){\chi }_v(\mathbf{r}-{\mathbf{R}}_v)d^{3}r{d}^{3}r\prime \end{array}$$ (91)

$$\langle q_{\text{qm}}|\widehat{J\le }|q_{\text{mm}}\rangle ={\displaystyle \sum _{a\in \text{mm}}{Z}_a\langle {\mathbf{R}}_a|\widehat{J\le }|q_{\text{mm}}\rangle +{\displaystyle \sum _{\mu v}{P}_{\mu v}{V}_{\mu v}^{\le }}}$$ (92)

$$V_{\mu v}^{\le }=-{\displaystyle \sum _{a\in \text{mm}}{q}_a{\displaystyle \int \frac{{\chi }_{\mu }(\mathbf{r}-{\mathbf{R}}_{\mu }){\chi }_v(\mathbf{r}-{\mathbf{R}}_v)}{|\mathbf{r}-{\mathbf{R}}_a|}{d}^{3}r}}$$ (93)

$$\begin{array}{l}\frac{1}{2}\langle q_{\text{qm}}|\widehat{J}|q_{\text{qm}}\rangle ={\displaystyle \sum _{\begin{array}{l}a\in \text{qm}\\ b>a\end{array}}\frac{Z_a{Z}_b}{R_{ab}}+{\displaystyle \sum _{\mu v}{P}_{\mu v}{V}_{\mu v}^Z}}\\ +\frac{1}{2}{\displaystyle \sum _{\begin{array}{l}\mu v\\ \mu \prime v\prime \end{array}}{P}_{\mu v}{P}_{\mu \prime v\prime }(\mu v|\mu \prime v\prime )}\end{array}$$ (94)

$$V_{\mu v}^Z=-{\displaystyle \sum _{a\in \text{qm}}{Z}_a{\displaystyle \int \frac{{\chi }_{\mu }(\mathbf{r}-{\mathbf{R}}_{\mu }){\chi }_v(\mathbf{r}-{\mathbf{R}}_v)}{|\mathbf{r}-{\mathbf{R}}_a|}{d}^{3}r}}$$ (95)

$$\begin{array}{l}(\mu v|\mu \prime v\prime )={\displaystyle \int {\displaystyle \int {|\mathbf{r}-\mathbf{r}\mathbf{\prime }|}^{-1}}}\\ \times {\chi }_{\mu }(\mathbf{r}-{\mathbf{R}}_{\mu }){\chi }_v(\mathbf{r}-{\mathbf{R}}_v)\\ \times {\chi }_{\mu \prime }(\mathbf{r}\mathbf{\prime }-{\mathbf{R}}_{\mu \prime }){\chi }_{v\prime }(\mathbf{r}\mathbf{\prime }-{\mathbf{R}}_{v\prime })d^{3}r{d}^{3}r\prime \end{array}$$ (96)

Equation 88 is performed numerically using a molecular quadrature grid consisting of quadrature points r_i and partitioned quadrature weights w_i. In other words, one integrates $\langle \mathbf{r}|\widehat{J\%}|q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}\rangle$ in a manner analogous to a LDA exchange-correlation potential. Specifically, the reciprocal-space potential is computed at the FFT grid points, and the B-splines are used to interpolate the potential onto the molecular quadrature grid. If β (see eq. 69) was large, then the numerical integration of the reciprocal space potential shown in eq. 88 would be inaccurate unless additional atomic quadrature grids were also placed around the near-field MM atoms; that is, the reciprocal space potential has “lumps” at the atomic positions, and those lumps look increasingly like q/r as β → ∞. In practice, the β values used in typical QM/MM simulations are sufficiently small that the use of “MM quadrature centers” is unnecessary. For the sake of argument, even if this were an issue, one would eliminate the lumps by numerically integrating eq. 90 along with the reciprocal-space potential, rather than introducing additional quadrature centers.

The contribution of E_CEw to the QM spin-resolved Fock matrix is the derivative with respect to the density matrix:

$${\frac{\partial E_{\text{CEw}}}{\partial P_{\mu v}^{\sigma }}|}_{\mathbf{R}}=V_{\mu v}^Z+{\displaystyle \sum _{\mu \prime v\prime }{P}_{\mu \prime v\prime }(\mu v|\mu \prime v\prime )+V_{\mu v}^{\le }+V_{\mu v}^{\%}-V_{\mu v}^{\cap }}$$ (97)

Similarly, the electrostatic energy contribution to the atomic gradients is the derivative ∂E/∂X_a|_P. Most of the gradient terms reduce to expressions involving standard nuclear-nuclear, electron-nuclear, and electron-repulsion integrals; for brevity, eqs. 98–101 summarizes only those expressions which involve the plane wave basis and/or numerical quadrature grid.

$$\begin{array}{l}\frac{\partial }{\partial X_a}\frac{1}{2}\langle q_{\text{mm}}|\widehat{J\mathbf{n}}|q_{\text{mm}}\rangle ={\displaystyle \sum _{\mathbf{t}}{q}_a\frac{\partial \theta ({\mathbf{R}}_a-{\mathbf{R}}_{\mathbf{t}})}{\partial X_a}\langle {\mathbf{R}}_{\mathbf{t}}|{\varphi }_{\text{mm}}\rangle }\\ -{\displaystyle \sum _{\begin{array}{c}b\in \text{mm}\\ b\ne a\\ R_{ab}<R_{\mathit{cut}}\end{array}}\frac{q_a{q}_b}{2}\frac{X_{ab}}{R_{ab}}\left(\frac{2\beta }{\sqrt{\pi }}\frac{e^{-{\beta }^2{R}_{ab}^2}}{R_{ab}}+\frac{\text{erfc(}\beta R_{ab}\text{)}}{R_{ab}^2}\right)}\end{array}$$ (98)

$$\frac{\partial }{\partial X_a}\frac{1}{2}\langle q_{\text{qm}}^{\text{ref}}|\widehat{J\%}|q_{\text{qm}}^{\text{ref}}\rangle ={\displaystyle \sum _{\mathbf{t}}{q}_a^{\text{ref}}\frac{\partial \theta ({\mathbf{R}}_a-{\mathbf{R}}_{\mathbf{t}})}{\partial X_a}\langle {\mathbf{R}}_{\mathbf{t}}|{\varphi }_{\text{qm}}^{\text{ref}}\rangle }$$ (99)

$$\begin{array}{l}\frac{\partial }{\partial X_a}\langle q_{\text{qm}}|\widehat{J\%}|q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}\rangle =\\ {\displaystyle \sum _{\mathbf{t}}{Z}_a\langle {\mathbf{R}}_{\mathbf{t}}|\widehat{J\%}|q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}\rangle \frac{\partial \theta ({\mathbf{R}}_a-{\mathbf{R}}_{\mathbf{t}})}{\partial X_a}}\\ -{\displaystyle {\displaystyle \sum }_{i=1}^{N_{\mathit{quad}}}{\displaystyle \sum _{\mathbf{t}}\rho ({\mathbf{r}}_i)\theta ({\mathbf{r}}_i-{\mathbf{R}}_{\mathbf{t}})\langle {\mathbf{R}}_{\mathbf{t}}|\widehat{J\%}|q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}\rangle }}\\ \times \left(\frac{\partial w_i}{\partial X_a}\right)\\ -{\displaystyle \sum _{i=1}^{N_{\text{quad}}}{\displaystyle \sum _{\mathbf{t}}{w}_i\theta ({\mathbf{r}}_i-{\mathbf{R}}_{\mathbf{t}})\langle {\mathbf{R}}_{\mathbf{t}}|\widehat{J\%}|q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}\rangle }}\\ \times ({\frac{\partial \rho ({\mathbf{r}}_i)}{\partial X_a}|}_{{\mathbf{r}}_i}+{\frac{\partial \rho ({\mathbf{r}}_i)}{\partial x_i}|}_{\mathbf{R}}\frac{\partial x_i}{\partial X_a})\\ -{\displaystyle \sum _{i=1}^{N_{\text{quad}}}{\displaystyle \sum _{\mathbf{t}}{w}_i\rho ({\mathbf{r}}_i)\langle {\mathbf{R}}_{\mathbf{t}}|\widehat{J\%}|q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}\rangle }}\\ \times \left(\frac{\partial \theta ({\mathbf{r}}_i-{\mathbf{R}}_{\mathbf{t}})}{\partial x_i}\frac{\partial x_i}{\partial X_a}\right)\\ +{\displaystyle \sum _{\mathbf{t}}{q}_a\frac{\partial \theta ({\mathbf{R}}_{\mathbf{t}}-{\mathbf{R}}_a)}{\partial X_a}}\\ \times \mathrm{Re}{\displaystyle \sum _{\mathbf{k}\ne 0}\langle {\mathbf{R}}_{\mathbf{t}}|\mathbf{k}\rangle \frac{4\pi e^{-\frac{k^2}{4{\beta }^2}}}{V{k}^2{|{\theta }_{\mathbf{k}}|}^2}{S}_{\mathbf{k}}^{\text{qm}}}\end{array}$$ (100)

where

$$\begin{array}{l}{S}_{\mathbf{k}}^{\text{qm}}={\displaystyle \sum _{\mathbf{t}}\langle \mathbf{k}|{\mathbf{R}}_{\mathbf{t}}\rangle ({\displaystyle \sum _{a\in \text{qm}}{Z}_a\theta ({\mathbf{R}}_a-{\mathbf{R}}_{\mathbf{t}})}}\\ -{\displaystyle \sum _{i=1}^{N_{\text{quad}}}{w}_i\rho ({\mathbf{r}}_i)\theta ({\mathbf{r}}_i-{\mathbf{R}}_{\mathbf{t}})})\end{array}$$ (101)

Equation 101 requires the evaluation of the QM electron density on the molecular quadrature grid. Each quadrature grid point density is then B-spline interpolated onto the FFT grid. The FFT-grid representation of the QM charge density then undergoes a forward FFT to produce a set of structure factors. Equation 101 does not introduce a new approximation; it naturally arises from standard chain-rule differentiation of the energy. The numerical integration of the reciprocal-space potential avoids the explicit evaluation of the AO-product Fourier coefficients.

2.3 Other QM/MM electrostatic protocols

The Ambient-Potential Composite Ewald method (denoted by “CEw”, see eq. 83) will be compared to three other electrostatic models:

1. Electrostatic embedding with truncated electrostatics for both the MM/MM and QM/MM interactions (denoted by “cut”, see eq. 102).

2. The QM/MM Mulliken charge Ewald method introduced by Nam⁶³ (denoted by “Ewq”, see eq. 104).

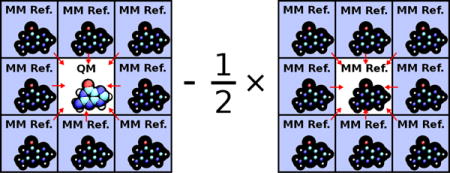
3. A model-MM Ewald energy with a smooth, short-range QM/MM correction (denoted by “MMEw”, see eq. 108). The MMEw model is a mixture of mechanical and electrostatic embedding. We define a nonbond cutoff radius around the QM region, outside of which the QM/MM interactions occur with mechanical embedding (including the long-range Ewald interaction), and inside of which the interactions are performed with electrostatic embedding. This approach is generalized in the MMEw method by introducing a switch that smoothly transitions between the two limits to yield a continuous potential energy. In the limit that the switching width becomes zero, the transition occurs discontinuously.

Cutoff-based electrostatics (E_cut[q] ≈ E_elec[q]):

$$\begin{array}{l}{E}_{\text{cut}}[\rho ]=\langle q_{\text{qm}}|\widehat{J}|q_{\text{qm}}\rangle +{\displaystyle \sum _{\begin{array}{l}a\in \text{mm}\\ b\in \text{mm}\\ b>a\\ R_{\mathit{ab}}<R_{\text{cut}}\end{array}}\frac{q_a{q}_b}{R_{\mathit{ab}}}}\\ +{\displaystyle \sum _{\begin{array}{l}a\in \text{qm}\\ b\in \text{mm}\\ R_{\ast b}<R_{\text{cut}}\end{array}}\frac{Z_a{q}_b}{R_{\mathit{ab}}}-{\displaystyle \sum _{\begin{array}{l}\mu v\\ b\in \text{mm}\\ R_{\ast b}<R_{\text{cut}}\end{array}}{P}_{\mu v}{q}_b}}\\ \times {\displaystyle \int \frac{{\chi }_{\mu }(\mathbf{r}-{\mathbf{R}}_{\mu }){\chi }_v(\mathbf{r}-{\mathbf{R}}_v)}{|\mathbf{r}-{\mathbf{R}}_b|}}{d}^{3}r\end{array}$$ (102)

E_cut contribution to the Fock matrix:

$$\begin{array}{l}{\frac{\partial E_{\text{cut}}}{\partial P_{\mu v}^{\sigma }}|}_{\mathbf{R}}=V_{\mu v}^Z+{\displaystyle \sum _{\mu \prime v\prime }{P}_{\mu \prime v\prime }(\mu v|\mu \prime v\prime )}\\ -{\displaystyle \sum _{\begin{array}{l}b\in \text{mm}\\ R_{\ast b}<R_{\text{cut}}\end{array}}{q}_b{\displaystyle \int \frac{{\chi }_{\mu }(\mathbf{r}-{\mathbf{R}}_{\mu }){\chi }_v(\mathbf{r}-{\mathbf{R}}_v)}{|\mathbf{r}-{\mathbf{R}}_b|}{d}^{3}r}}\end{array}$$ (103)

Mulliken charge QM/MM Ewald method (E_Ewq[q] ≈ E_elec[q]):

$$\begin{array}{l}{E}_{\text{Ewq}}[\rho ]=\langle q_{\text{mm}}+q_{\text{qm}}^{\text{mul}}|\widehat{J\mathbf{n}}|q_{\text{mm}}+q_{\text{qm}}^{\text{mul}}\rangle \\ -\langle q_{\text{qm}}^{\text{mul}}|\widehat{J}|q_{\text{qm}}^{\text{mul}}\rangle +\langle q_{\text{qm}}|\widehat{J}|q_{\text{qm}}\rangle \end{array}$$ (104)

$$q_{\text{qm}}^{\text{mul}}(\mathbf{r})={\displaystyle \sum _{a\in \text{qm}}{q}_a^{\text{mul}}\delta (\mathbf{r}-{\mathbf{R}}_a)}$$ (105)

Mulliken charge:

$$q_{\text{qm}}^{\text{mul}}=Z_a-{\displaystyle \sum _{\begin{array}{l}\mu \in a\\ v\in a\end{array}}{P}_{\mu v}{S}_{\mu v}-\frac{1}{2}{\displaystyle \sum _{\begin{array}{l}\mu \in a,v\notin a\\ \mu \notin a,v\in a\end{array}}{P}_{\mu v}{S}_{\mu v}}}$$ (106)

E_Ewq contribution to the Fock matrix:

$$\begin{array}{l}{\frac{\partial E_{\text{Ewq}}}{\partial P_{\mu v}^{\sigma }}|}_{\mathbf{R}}={\frac{\partial E_{\text{Ewq}}}{\partial P_{\mu v}^{\sigma }}|}_{\mathbf{R},{\mathbf{q}}^{\text{mul}}}+{\displaystyle \sum _{a\in \text{qm}}{\frac{\partial E_{\text{Ewq}}}{\partial q_a^{\text{mul}}}|}_{\mathbf{R}}{\frac{\partial q_a^{\text{mul}}}{\partial P_{\mu v}^{\sigma }}|}_{\mathbf{R}}}\\ =V_{\mu v}^Z+{\displaystyle \sum _{\mu \prime v\prime }{P}_{\mu \prime v\prime }(\mu v|\mu \prime v\prime )}\\ -\frac{S_{\mu v}}{2}({\frac{\partial E_{\text{Ewq}}}{\partial q_{a∍\mu }^{\text{mul}}}|}_{\mathbf{R}}+{\frac{\partial E_{\text{Ewq}}}{\partial q_{b∍v}^{\text{mul}}}|}_{\mathbf{R}})\end{array}$$ (107)

Model-MM Ewald energy with a short-range QM/MM correction (E_MMEw[q] ≈ E_elec[q]):

$$\begin{array}{l}{E}_{\text{MMEw}}[\rho ]=\frac{1}{2}\langle q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}|\widehat{J\mathbf{n}}|q_{\text{mm}}+q_{\text{qm}}^{\text{ref}}\rangle \\ +\langle q_{\text{qm}}|\widehat{J\downarrow }|q_{\text{mm}}\rangle -\langle q_{\text{qm}}^{\text{ref}}|\widehat{J\downarrow }|q_{\text{mm}}\rangle \\ +\frac{1}{2}\langle q_{\text{qm}}|\widehat{J}|q_{\text{mm}}\rangle -\frac{1}{2}\langle q_{\text{qm}}^{\text{ref}}|\widehat{J}|q_{\text{qm}}^{\text{ref}}\rangle \end{array}$$ (108)

The smooth, short-range incorporation of the QM/MM interactions:

$$\begin{array}{l}\langle q_{\text{qm}}|\widehat{J\downarrow }|q_{\text{qm}}\rangle ={\displaystyle \sum _{\begin{array}{l}a\in \text{qm}\\ b\in \text{mm}\end{array}}{S}_{\downarrow }(R_{\ast b};R_{\text{cut}},w_{\text{sw}})\frac{Z_a{q}_b}{R_{ab}}}\\ -{\displaystyle \sum _{\begin{array}{l}\mu v\\ b\in \text{mm}\end{array}}{S}_{\downarrow }(R_{\ast b};R_{\text{cut}},w_{\text{sw}})P_{\mu v}{q}_b}\\ \times {\displaystyle \int \frac{{\chi }_{\mu }(\mathbf{r}-{\mathbf{R}}_{\mu }){\chi }_v(\mathbf{r}-{\mathbf{R}}_v)}{|\mathbf{r}-{\mathbf{R}}_b|}{d}^{3}r}\end{array}$$ (109)

The switched, short-range model-MM interactions:

$$\langle q_{\text{qm}}^{\text{ref}}|\widehat{J\downarrow }|q_{\text{mm}}\rangle ={\displaystyle \sum _{\begin{array}{l}a\in \text{qm}\\ b\in \text{mm}\end{array}}{\displaystyle \sum _{ab}{S}_{\downarrow }(R_{\ast b};R_{\text{cut}},w_{\text{sw}})\frac{q_a^{\text{ref}}{q}_b}{R_{ab}}}}$$ (110)

The “switch off” function:

$$\begin{array}{l}{S}_{\downarrow }(R;R_{\text{cut}},w_{\text{sw}})=\{\begin{array}{l}0,R\ge R_{\text{cut}}\\ 1,R\le R_{\text{cut}}-w_{\text{sw}}\\ 10x^3-15x^4+6x^5,\\ \text{otherwise}\end{array}\\ x=\frac{R_{\text{cut}}-R}{w_{\text{sw}}}\end{array}$$ (111)

The distance between MM atom b and the nearest QM atom:

$$R_{\ast b}=min\{R_{1b},\dots ,R_{N_{\text{qm}}b}\}$$ (112)

E_MMEw contribution to the Fock matrix:

$$\begin{array}{l}{\frac{\partial E_{\text{MMEw}}}{\partial P_{\mu v}^{\sigma }}|}_{\mathbf{R}}=V_{\mu v}^Z+{\displaystyle \sum _{\mu \prime v\prime }{P}_{\mu \prime v\prime }(\mu v|\mu \prime v\prime )}\\ -{\displaystyle \sum _{b\in \text{mm}}{S}_{\downarrow }(R_{\ast b};R_{\text{cut}},w_{\text{sw}})q_b}\\ \times {\displaystyle \int \frac{{\chi }_{\mu }(\mathbf{r}-{\mathbf{R}}_{\mu }){\chi }_v(\mathbf{r}-{\mathbf{R}}_v)}{|\mathbf{r}-{\mathbf{R}}_b|}}{d}^{3}r\end{array}$$ (113)

The expression for the Lennard Jones energy (eq. 3) and the E_CEw (eq. 83), E_cut (eq. 102), E_Ewq (eq. 104), and E_MMEw (eq. 108) electrostatic methods all employ the symbol “R_cut”. In all cases, this distance is the “nonbond cutoff” radius used by the MM program to generate neighbor lists. We proceed by summarizing how the nonbond cutoff is used within different methods. In doing so, we use the phrases “real-space Ewald cutoff”, “electrostatic cutoff”, and “switched cutoff” to aid the reader’s ability to recall how the various methods behave at the nonbond cutoff. If an atom is inside the nonbond cutoff, then the pairwise Lennard-Jones energy is computed; whereas, if it is outside the nonbond cutoff, then its interaction is modeled through a long-range tail correction. The electrostatic methods use a single neighbor list for the QM region, as a whole, which is constructed from the union of the individual QM atom neighbor lists. Therefore, an MM atom is within the nonbond cutoff if its distance to any QM atom is less than R_cut. The R_cut appearing in the E_CEw and E_Ewq methods are “real-space Ewald cutoffs”, which merely denotes the distance where the point charge and PME Gaussian potentials are sufficiently similar that additional real-space corrections would have a negligible effect. The R_cut appearing in the E_cut method is an “electrostatic cutoff” that marks the distance outside of which the electrostatic interactions are strictly (and discontinuously) ignored. The R_cut appearing in the E_MMEw method is the outer edge of a “switched cutoff” that extends from R_cut − w_sw to R_cut. Inside the switching region (R ≤ R_cut − w_sw), the QM/MM electrostatic interaction explicitly involve the atomic nuclei and AO products. Outside of the switched cutoff (R ≥ R_cut), the QM/MM electrostatic interaction (including the long-range Ewald-component of the energy) is performed using a static, MM point charge representation of the QM atoms. The E_MMEw switching region (R_cut −w_sw > R > R_cut) smoothly transitions between these two limits. Therefore, the E_MMEw QM atom forces are influenced by the Ewald potential, but the QM electron density explicitly polarizes only to the nearby MM atoms within the switched cutoff.

It has previously been noted^69,70 that the use of Mulliken charges within E_Ewq can result in SCF convergence instability when applied to standard, all-electron AO basis sets. In order to improve the SCF stability, our implementation of E_Ewq holds the Mulliken charges within the current MD step fixed to the SCF converged Mulliken charges from the previous MD step. In other words, the $\partial E_{\text{Ewq}}/\partial q_a^{\text{mul}}$ charge derivatives appearing in eq. 107 are computed once at the beginning of the SCF procedure.

2.4 Computational details

The ab initio code and all electrostatic methods described in the previous sections were implemented from scratch within a development version of AmberTools 15 and interfaced to the Sander MD program, which was used to perform all simulations described below.¹¹⁶

The notation E_{cut R}, E_{MMEw RwD}, E_{CEw R}, E_{Ewq R} is used to distinguish the electrostatic protocols described in the previous sections and their associated nonbond cutoffs. For example, E_{cut 14} denotes the use of eq. 102 with R_cut = 14 Å, and E_{MMEw 14w4} is eq. 108 with R_cut = 14 Å and w_sw = 4 Å. Similarly, E_{CEw 14} and E_{Ewq 14} refer to eq. 83 and eq. 104, respectively, with R_cut = 14 Å.

All Ewald reciprocal-space calculations are performed using a 1 Å⁻³ grid density, and the Ewald coefficient was chosen from the value of R_cut to reproduce a direct sum tolerance of 10⁻⁶ au.

Figures 1–6 display simulation results for a system composed of a p-nitrophenyl phosphate (pNPP) QM region in a truncated octahedron filled with 4563 TIP4P/Ew water molecules. Salt ions were not added to the system. The total charge of the system is 2-. The Ewald methods use a neutralizing uniform background potential (eq. 76) to account for the net charge. The pNPP Lennard-Jones and q^ref parameters were obtained from the Antechamber program included in AmberTools 15, which chose the LJ parameters and charges from the GAFF force field and AM1-BCC protocol, respectively.^116–119 The system volume was equilibrated using the DFTB2 semiempirical Hamiltonian and the QM/MM Ewald method described in Ref. 63 in the isothermal-isobaric ensemble (NPT) for 100 ps (1 fs/step) at 298 K and 1 atm. The Berendsen barostat was used to control the pressure with a relaxation time of 2 ps, and the Langevin thermostat controlled the temperature with a collision frequency of 5 ps⁻¹. The simulation cell’s equilibrated real-space lattice vectors are 56.42 Å. The equilibrated volume and coordinates were then used for the microcanonical (NVE) and canonical (NVT) ensemble simulations described below.

Figure 1.

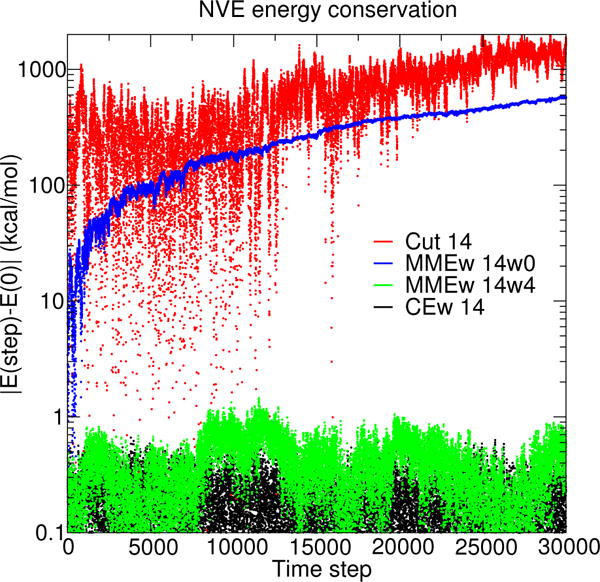
NVE simulation energy conservation as a function of time step (0.001 ps/step) using various electrostatic protocols. The system is a pNPP solute computed with PBE0/6-31G* in a truncated octahedron of TIP4P/Ew waters. See the text in Computational Details for a description of the notation used to distinguish the various electrostatic protocols.

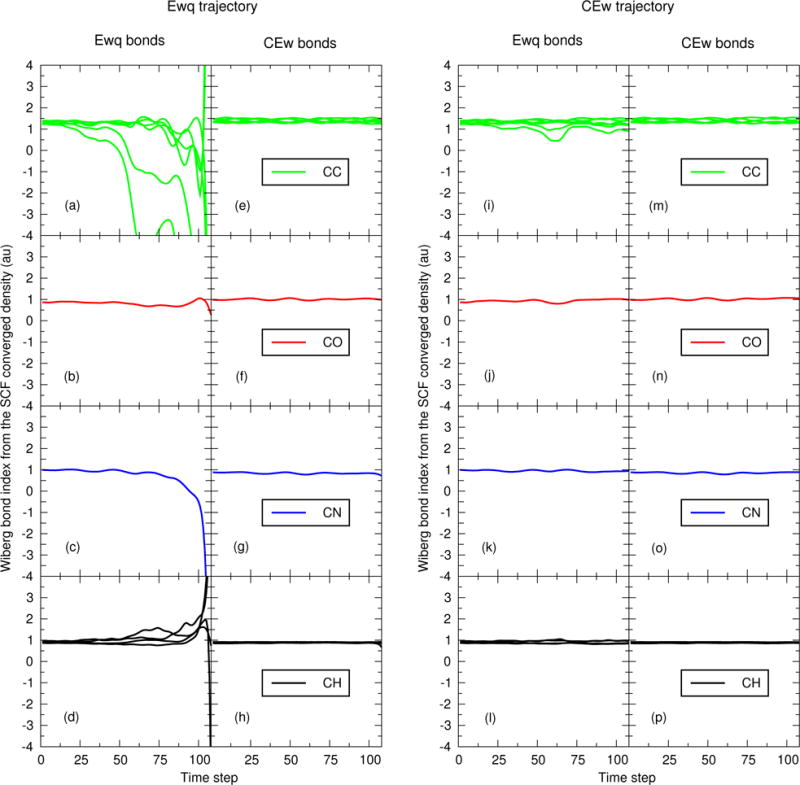
Figure 6.

Wiberg bond order indices of the E_{Ewq 14} and E_{CEw 14} SCF converged electron densities as a function of time step. The two left-most columns are evaluated at the atomic positions generated by the E_{Ewq 14} trajectory. The two right-most columns are evaluated at the atomic positions generated by the E_{CEw 14} trajectory. The E_{Ewq 14} and E_{CEw 14} trajectories as those shown in Figure 4.

Figure 1 shows the PBE0/6-31G* QM/MM simulation total energy, relative to the first step, for a series of NVE simulations that differ only by their choice of electrostatic protocol. Each simulation was run for 30 ps (30 000 steps), and they started from the same initial conditions.

Figure 2 displays PBE0/6-31G* QM/MM potential of mean force (PMF) profiles of the pNPP dissociation reaction: ${\left[{\text{NO}}_2{\mathrm{C}}_6{\mathrm{H}}_6{\text{O-PO}}_3\right]}^{2-}\to {\text{NO}}_2{\mathrm{C}}_6{\mathrm{H}}_6{\mathrm{O}}^{-}+{\text{PO}}_3^{-}$, where the reaction coordinate is the P-O distance. Each PMF was generated from 96 umbrella window NVT simulations that spanned from R_PO = 1.4 Å to 6.1 Å in steps of 0.1 Å. The umbrella harmonic potentials used a force constant of 50 kcal mol⁻¹ Å⁻². The PMFs were generated from the distribution of R_PO values using the variational free energy profile (vFEP) method.¹²⁰ Each NVT simulation was performed at 298 K for 12 ps (Fig. 2a), 24 ps (Fig. 2b and Fig. 2c), or 36 ps (Fig. 2d). The total amount of sampling for each curve was chosen to achieve aesthetically pleasing figures; that is, the PMFs shown in Fig. 2d are all sufficiently similar to one another that additional sampling was added to remove small numerical noise in the region where the PMF is relatively “flat”, so that the curves could be more easily distinguished. Alternatively, the PMFs appearing in Fig. 2a are identifiably different such that sampling beyond 12 ps was not considered to be a prudent use of resources. We note that the E_{MMEw 14w1} PMF appearing in Fig. 2b is terminated at R_PO ≈ 4 Å because many of the E_{MMEw 14w1} simulation windows beyond R_PO > 4 fail to complete due to large velocity warnings. This is expected because the switching width in this case is so small that any waters within the switching layer experience a large force, because the potential energy approaches a discontinuity as the width nears zero. The dashed, horizontal lines in Fig. 2a–2d mark the experimental barrier in solution¹²¹ (29.6 kcal/mol).

Figure 2.

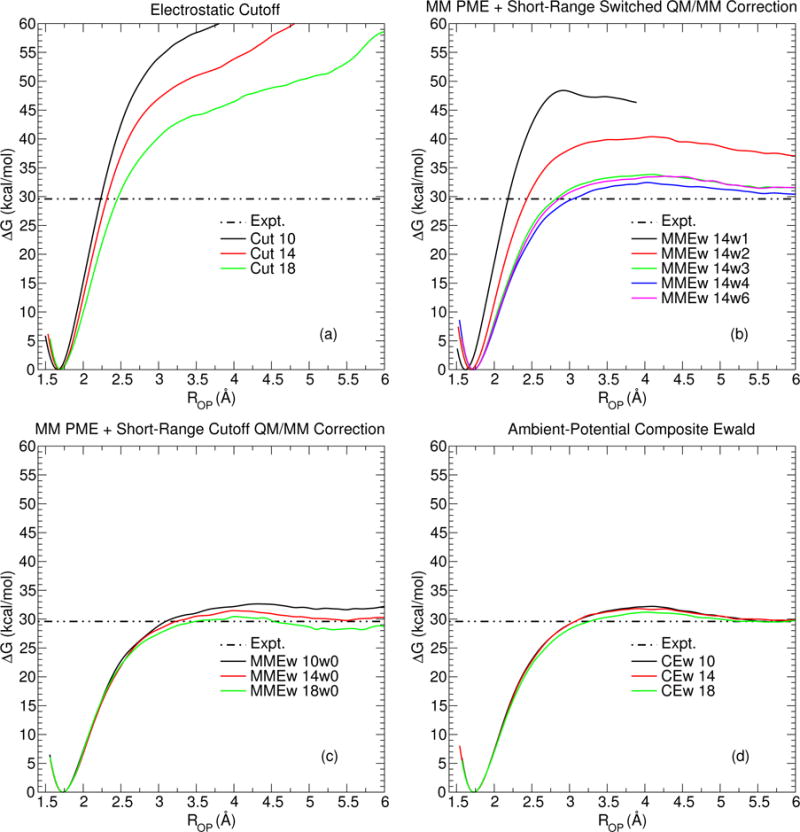
The effect of various electrostatic protocols on the potential of mean force profiles of the pNPP dissociative reaction.

Figure 3 compares radial distribution functions (RDFs) between the phosphorous and water-oxygens observed within PBE0/6-31G* QM/MM pNPP simulations performed using several electrostatic protocols. Figures 3a and 3b are RDFs obtained from simulations whose umbrella potential is centered about R_PO = 1.7 Å (the approximate minimum of the PMF), and Figs. 3c and 3d were obtained using an umbrella window centered about R_PO = 4.0 Å (the approximate transition state of the PMF). Figures 3b and 3d are zoomed areas of 3a and 3c, respectively, as marked by the black boxes. The RDFs were generated from 500 ps of NVT simulations at 298 K, whose trajectory was written every 50 steps.

Figure 3.

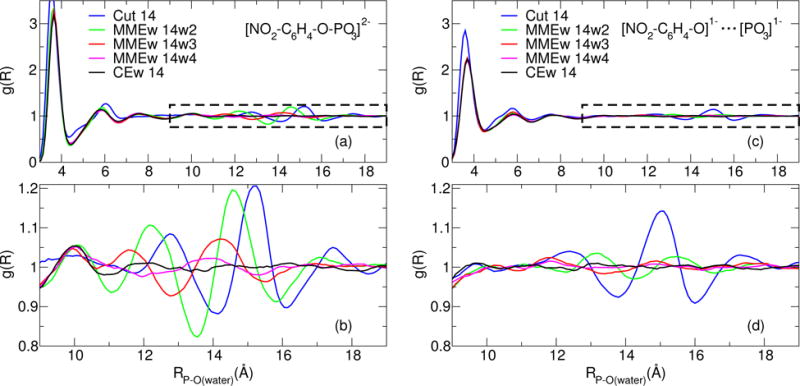
The pairwise radial distribution function between phosphorous and the water-oxygens. The metaphosphate R_PO separation in panes (a) and (c) are 1.70 Å and 4.00 Å, respectively. Panes (b) and (d) are zoomed areas of (a) and (c), as indicated by the dashed boxes.

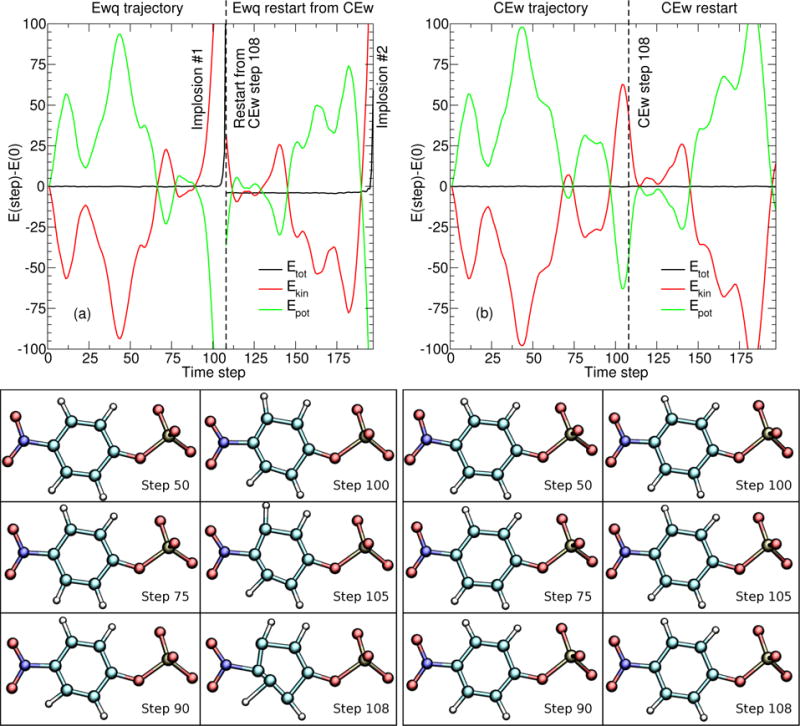
Figure 4 shows the potential, kinetic, and total energies from PBE0/6-31G* QM/MM NVE simulations of pNPP performed using the E_{Ewq 14} (Fig. 4a) and E_{CEw 14} (Fig. 4b) electrostatic protocols as a function of time step (1 fs/step). Both trajectories start from the same coordinates and initial velocities, and an umbrella potential at R_PO = 1.7 Å is applied. The E_{Ewq 14} trajectory fails to SCF converge after step 108. Therefore, the E_{Ewq 14} trajectory is restarted at step 108 from the coordinates and velocities produced by the E_{CEw 14} trajectory at step 108. The E_{Ewq 14} trajectory again fails to SCF converge after step 197. The E_{Ewq 14} SCF failures are marked in Fig. 4a by “Implosion #1” and “Implosion #2.” Several snapshots of the pNPP solute from the E_{Ewq 14} and E_{CEw 14} trajectories are shown immediately below their respective energy profiles.

Figure 4.

QM/MM NVE simulations of the pNPP molecule (near the minimum of the PMF; that is, the R_PO = 1.7Å window) using the E_{Ewq 14} (left) and E_{CEw 14} (right) methods. The plots (top) decompose the total simulation energy into kinetic (red) and potential (green) energy contributions, relative to the initial condition. Both simulations start from the same initial condition. The molecules beneath each plot are snapshots of the QM solute along their respective trajectory. Each time step is 0.001 ps.

Figures 5 and 6 re-analyze the PBE0/6-31G* Mulliken charges and Wiberg bond orders of the first 108 steps from each trajectory shown in Fig. 4. Specifically, Figs. 5a–5d are the SCF converged Mulliken charges produced by the E_{Ewq 14} method using the atomic coordinates from the first 108 steps of Fig. 4a. Figures 5e–5h are the SCF converged Mulliken charges produced by the E_{CEw 14} method using the atomic coordinates from the first 108 steps of Fig. 4a. Similarly, Figs. 5i–5l and 5m–5p are the E_{Ewq 14} and E_{CEw 14} Mulliken charges, respectively, evaluated from the first 108 steps of Fig. 4b. The format of Fig. 6 is analogous; it differs from Fig. 5 only by displaying the Wiberg bond orders rather than Mulliken charges. For clarity, the Mulliken charges and Wiberg bond orders are evaluated using the coordinates of the entire QM/MM system.

Figure 5.

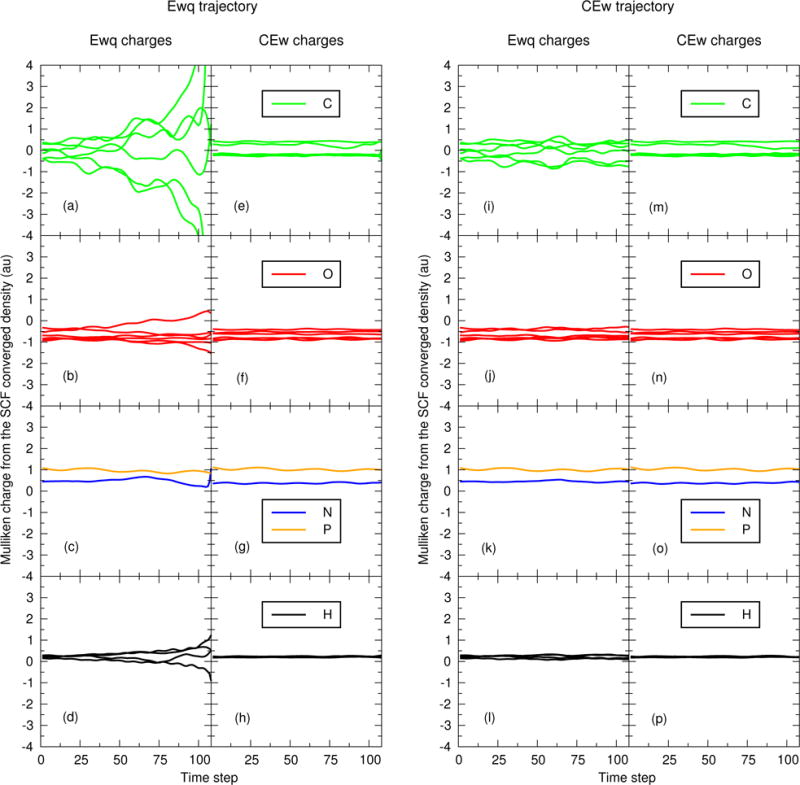
Mulliken charge analysis of the E_{Ewq 14} and E_{CEw 14} SCF converged electron densities as a function of time step. The two left-most columns are evaluated at the atomic positions generated by the E_{Ewq 14} trajectory. The two right-most columns are evaluated at the atomic positions generated by the E_{CEw 14} trajectory. The E_{Ewq 14} and E_{CEw 14} trajectories as those shown in Figure 4.

Table 1 compares the QM/MM simulation rates acheived using E_{CEw 14} and E_{MMEw 14w4} when applied to the solvated 72 atom alanine chain shown in Fig. 7. The alanine chain is enclosed within a truncated octohedron containing 5083 TIP4P/Ew waters. The timings are listed as the average simulation rate (ps/day) reported by Sander after 1 ps (1000 steps) of PBE0/6-31G* NVT simulation at 298 K. The simulation rates are reported as a function of central processing unit (CPU) core count and QM system size, including link atoms. The QM region consists of all atoms to the left of the cuts shown in Fig. 7 and the hydrogen link-atoms crossing the boundaries. The timings were performed on the stampede supercomputing cluster at the Texas Advanced Computing Center. Each node contains two Intel Xeon E5-2680 processors (8 cores/processor), and the nodes are interconnected with Mellanox FDR InfiniBand technology. Although Intel Phi coprocessors and/or Nvidia graphics cards were available on the compute nodes, our code currently only runs on the CPU.

Table 1.

Simulation rates (ps/day; 1 fs/step) using E_{CEw 14} and E_{MMEw 14w4} as a function of CPU core-count (N_core) and QM region size (N_qm, the number of QM atoms) for the solvated alanine chain shown in Fig. 7.

Ncore	Nqm, ECEw 14							Nqm, EMMEw 14w4
	12	22	32	42	52	62	72	12	22	32	42	52	62	72
1	7.4	1.6	0.66	0.36	0.23	0.16	0.12	8.3	1.7	0.71	0.38	0.24	0.17	0.12
2	14.4	3.0	1.3	0.71	0.45	0.30	0.22	16.5	3.3	1.4	0.76	0.48	0.31	0.23
4	27.3	5.7	2.4	1.3	0.84	0.56	0.41	31.1	6.2	2.6	1.4	0.88	0.60	0.42
8	51.2	10.6	4.3	2.4	1.5	0.99	0.72	59.6	11.6	4.6	2.5	1.6	1.0	0.75
16	92.4	19.8	8.1	4.5	2.8	1.9	1.3	110.3	21.8	8.6	4.7	3.0	2.0	1.4
32	157.3	35.3	14.6	7.8	4.9	3.3	2.4	187.9	38.0	15.3	8.2	5.1	3.5	2.5
64	237.4	59.4	24.4	13.3	8.3	5.5	3.9	289.0	64.0	25.4	13.8	8.6	5.7	4.1
128	337.5	90.4	37.3	19.9	12.6	8.3	5.8	418.5	97.7	39.1	20.8	13.0	8.6	6.0
256	428.4	122.7	51.9	28.1	17.0	11.0	7.9	536.4	135.1	54.5	28.5	17.4	11.4	8.1
512	493.0	152.4	62.2	34.5	20.8	13.4	9.4	622.5	167.1	66.0	34.7	21.1	13.7	9.6

Figure 7.

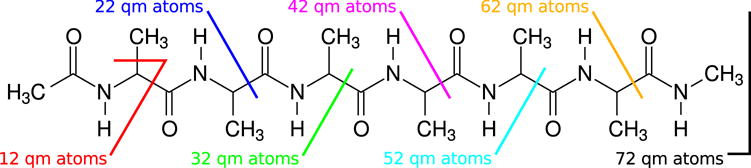
The QM/MM simulation rates are performed using a 72 atom alanine chain solvated by 5083 TIP4P/Ew waters in a truncated octahedron simulation cell. The timings were performed with different QM regions, which correspond to the various cuts in the covalent bonds shown in the figure. The severed bonds are capped with hydrogen link atoms, which are included in the count for the number of QM atoms.

Figure 8 is a schematic of the transesterification of hydroxyalkyl phosphate esters. Of particular interest in this work are the reactions involving ethoxide (EtO) or phenoxide (PhO), which are representative of “poor” and “enhanced” leaving groups, respectively. The “R₁” and “R₂” bond labels appearing in Fig. 8 are reaction coordinates used to perform the two-dimensional (2D) umbrella window simulations shown in Fig. 9. Figures 9a–9c are 2D PMFs of the EtO phosphoryl transesterification and Figs. 9d–9f are 2D PMFs of the PhO phosphoryl transesterification. Figures 9a and 9d were performed with AM1/d-PhoT (abbreviated as AM1/d); Figs. 9b and 9e were performed with DFTB2; and Figs. 9b and 9e were performed with PBE0/6-311G**. The EtO simulations consisted of 134 windows that form a grid from (R₁,R₂) = (1.4 Å,1.4 Å) to (5.6 Å,2.2 Å) and from (1.4 Å,2.1 Å) to (2.4 Å,3.0 Å) using a 0.2 Å spacing in either direction. The PhO simulations consisted of 109 windows from (R₁,R₂) = (1.4 Å,1.4 Å) to (5.6 Å,2.2 Å). The umbrella windows had a force constant of 85 kcal mol⁻¹ Å⁻², and the QM solute was enclosed within an truncated octohedron containing 4204 (EtO) or 5183 (PhO) TIP4P/Ew waters. The density of the system was equilibrated with DFTB2 in a NPT simulation in a manner analogous to the pNPP equilibration protocol described above, and production was performed in the NVT ensemble at 298 K. The AM1/d-PhoT and DFTB2 semiempirial models were sampled and analyzed for 100 ps/window, whereas the PBE0/6-311G** simulations were run for 30 ps/window. Analysis of the first 20 ps changes the PBE0/6-311G** barriers by less than 0.2 kcal/mol; therefore, sampling was suspended at 30 ps. The vFEP method was used to generate the 2D PMFs from the distributions of R₁ and R₂ values observed in the simulations.¹²⁰ The circle and X marks appearing in Fig. 9 are minima and transition states of the 2D surfaces, and the colored lines connecting the stationary points are a nudge elastic band minimum free energy path.^122,123 The 1D PMFs appearing in Fig. 9 are the free energy profiles along the minimum free energy path.

Figure 8.

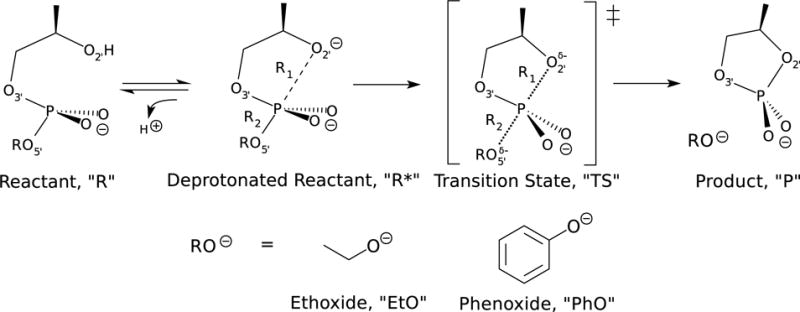
Schematic of the phosphoryl transfer (model RNA transesterification) reactions with ethoxide and phenoxide leaving groups.

Figure 9.

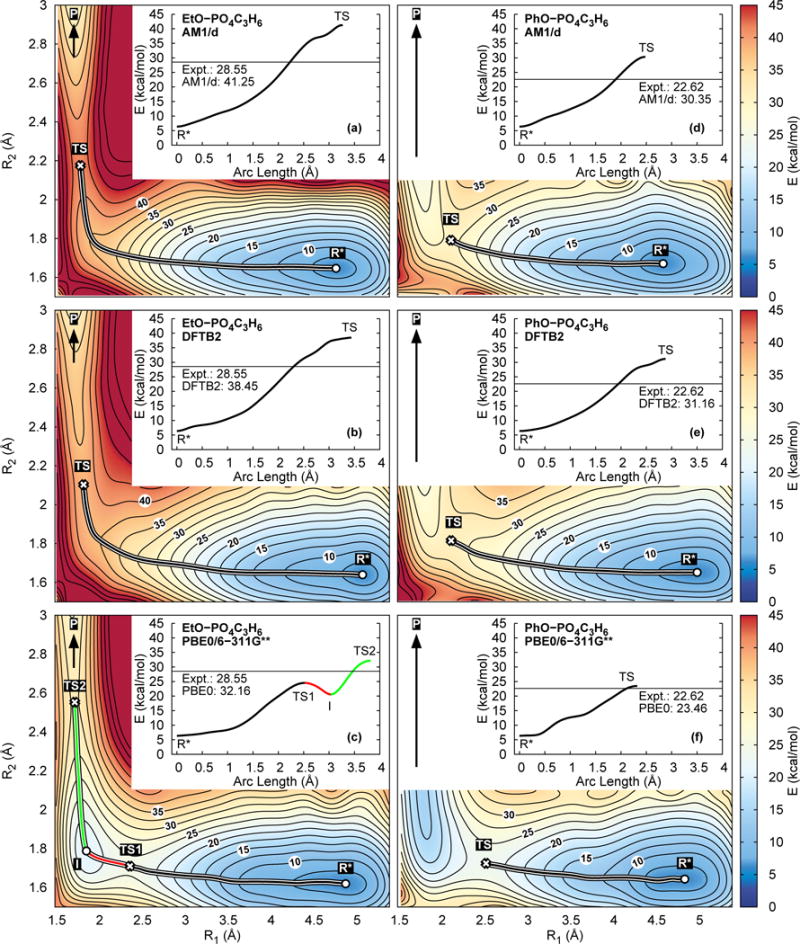
Free energy profiles of the transesterification reactions shown in Fig. 8. Ethoxide leaving group: (a)–(c). Phenoxide leaving group: (d)–(f). The inset, one-dimensional plots are the free energies along the nudge elastic band path connecting the minimum to the rate-limiting transition state. The horizontal line in the inset plots mark the experimental barrier.

Our QM/MM simulations assume that the 2′-O has already been deprotonated. That is, we explicitly model the reaction barrier from R* to TS (see Fig. 8), whereas the experimental barrier corresponds to the reaction from R to TS. Therefore, our calculated free energies are corrected to account for the free energy difference between R and R*. The rate of the reaction shown in Fig. 8 was experimentally determined to be k = 1.57×10⁷ and 7.40×10¹⁰ mol⁻¹s⁻¹ for the EtO and PhO leaving groups, respectively, at 80 C in a pH 8 buffer solution.¹²⁴ The transition state free energies at standard state concentration are computed from the Eyring equation, ΔG^‡ = −RT ln(kh/k_BT), where h and k_B are Planck’s constant and Boltmann’s constant, respectively. Thus the experimental barriers for EtO and PhO are 28.55 and 22.62 kcal/mol, respectively. To correct our free energies, we must consider the pK_a of 2′-OH at pH 8. Experimental measurements of the 2′-OH pK_a in small molecule models of RNA have ranged between 12.35–13.9, depending on the structure and experimental technique.^125–128 Of the available experimental pK_a data, the model most closely resembling those shown in Fig. 8 is the adenosine 3′-ethyl phosphate used in Ref. 127, whose 2′-OH pK_a was found to be 12.68 ± 0.06. Assuming a pK_a of 12.68, the free energy of the deprotonated 2′-O at pH 8 and 298 K is estimated to be ΔG_R→R* = −2.303RT(pH − pK_a) = 6.38 kcal/mol. Therefore, 6.38 kcal/mol have been added to all computed free energies shown in Fig. 9.

3 Results

3.1 Comparison of electrostatic protocols

Energy conservation

The drift in total energy observed within NVE simulations of pNPP are shown in Figure 1. The E_{cut 14} and E_{MMEw 14w0} methods produce strong energy drifts because their potential energy surfaces contain discontinuities. The E_{cut 14} energy drift is larger than E_{MMEw 14w0} because the E_{cut 14} method excludes the long-range interactions entirely. The E_{MMEw 14w4} and E_{CEw 14} methods conserve the total energy. Both models have continuous potential energies and model the long-range interactions, albeit in different manners. The E_Ewq electrostatic method first developed by Nam et al.⁶³ is not shown in Fig. 1 because the QM solute “implodes” after 100 steps. The instability of E_Ewq trajectories will be discussed in detail below. In brief, the E_Ewq simulations do conserve the total energy for the length of time that they can be run.

The conservation of total energy is important for maintaining a stable simulation temperature.¹²⁹ Although the temperature can be corrected through velocity rescaling, the lack of total energy conservation can, over time, manifest itself by dampening high-frequency motion and transforming it to low-frequency motions.¹³⁰ Furthermore, the treatment of long-range forces has also been shown to dramatically affect the structural stability of proteins³⁰ even when switching functions are introduced.¹³¹ The simulations performed in the remainder of this manuscript are not performed on a time scale that is long enough to directly observe these previously observed artifacts.

pNPP free energy profiles

Simulations of reactions involving charged species are ubiquitous in biology. Among the most important are phosphoryl transfer reactions, which are vital for many celluler processes; for example, gene regulation, cell signalling, and energy conversion.^132–134 Phosphoryl transfer reactions have been studied extensively by computational methods,¹³⁵ and mechanistic insights have been gained by studying model systems that provide an interpretation of linear free-energy relations¹³⁶ and kinetic isotope effects.¹³⁷ In this section, we examine how various electrostatic protocols affect the the phosphoryl transfer reaction barrier of pNPP (see Figure 2).

In the vicinity of R_OP ≈ 1.7 Å, the metaphosphate is covalently bound to nitrophenyl such that it is a single molecule with a −2 charge. At a separation of R_OP ≳ 4 Å, the solute is better described as two polyatomic monoanions. One can gain insight into the role of solvation in these two situations by refering to a Born ion model which, for water, approximately translates to: ΔG_solv ≈ −Q²/R, where R is the radius of the ion. In other words, there is a greater degree of solvent stabilization near the PMF minimum than there is near the transition state. Although various electrostatic methods appear to increase the barrier, the differences are related to the solvent stabilization near the PMF minimum, which has been chosen to define the zero of free energy in all cases. Had the system consisted of a pair of counter ions, such as the ${\text{NH}}_4^{+}\dots {\text{Cl}}^{-}$ or ${\text{NH}}_4^{+}\dots {\text{PO}}_3^{-}$ systems examined in Ref. 63, then the solvent stability of the QM region would be enhanced as the ions were separated, because the separation of ions produces an increasing dipole moment.

The series of E_cut profiles shown in Fig. 2a differ strikingly from the other electrostatic protocols. The PMFs continually increase as the metaphosphate dissociates. The truncated electrostatic forces cause the waters to become structured at the QM/MM electrostatic cutoff (see Fig. 3), which acts to create an artificial solvation shell. As one decreases the electrostatic cutoff from 18 Å to 10 Å, the artificial solvation shell forms closer to the solute and thus increases the stability of the PMF minimum. The profiles do not contain a transition state below R_OP < 6 Å for two reasons:

1. The length of the electrostatic cutoff prevents the solvation shells of each fragement from dissociating from each other in this range.

2. The water around phosphorous continues to display an artifically structured RDF even when the metaphosphate is separated (see Figs. 3c–3d), so the radius of the “effective Born ion” increases as the metaphosphate dissociates.

The E_MMEw method’s treatment of the long-range QM/MM electrostatics is fundamentally different from E_cut, and this difference causes the E_MMEw PMFs to exhibit transition states (see Fig. 2b). As the width of the switching region is reduced, the dissociation barrier increases. This observation appears to be related to how the switching width affects the solvent structure in the vicinity of the switching region. Figures 3a–3b and 3c–3d illustrate the solvent structure of E_{MMEw 14w2}, EMMEw _14w3, and E_{MMEw 14w4} at R_OP = 1.70 Å and R_OP = 4.00 Å, respectively. As the switching width becomes smaller, the transition between the QM/MM and MM-analogue/MM interactions occurs more abruptly, and the waters experience a greater force in the switching region. The degree of water structure at the switching region is greater at R_OP = 1.70 Å because the solute more closely resembles a dianion. Unlike the E_cut method, the artificial solvation shell dissipates as the metaphosphate dissociates. The series of E_MMEw profiles shown in Fig. 2c use a switching width of zero. Thus, the width is too small for the waters to experience a force associated with the transition, and the difference between MM-analogue/MM and QM/MM interactions is too subtle to cause a dramatic difference in the transition state barrier. Increasing the real-space Ewald cutoff from 10 to 18 Å lowers the barrier from 32.4 (E_{MMEw 10w0}) to 30.2 (E_{MMEw 18w0}) kcal/mol. Relative to Figs. 2a–2b, the E_{MMEw Rw0} profiles shown in Fig. 2c are relatively stable and agree with experiment much more closely; however, the reader should take note that the electrostatic protocols shown in Fig. 2c do not conserve the total energy in NVE simulations.

The series of E_CEw profiles shown in Fig. 2d exhibit the greatest degree of similarity as a function of nonbond cutoff. The barriers are: 32.2 kcal/mol (E_{CEw 10}), 31.8 kcal/mol (E_{CEw 14}), 31.2 kcal/mol (E_{CEw 18}). Unlike the other electrostatic protocols appearing in Fig. 2a–2c, the E_CEw method allows the QM Hamiltonian to explicitly polarize to both the short- and long-range electrostatics. As a consequence, E_{CEw 14} does not induce an artificially structured solvation shell, as can be seen in Fig. 3.

Electronic polarization

Figures 4–6 are used to discuss the symptoms which arise when attempting to use the semiempirical-style QM/MM-Ewald method⁶³ with an ab initio Hamiltonian. To analyze the behavior of E_{Ewq 14} and E_{CEw 14}, we construct NVE trajectories of each (Fig. 4a and 4b, respectively), starting from the same initial conditions. The E_{Ewq 14} total energy is conserved until step 106, at which point the atom velocities are too large to adequately propagate with a 1 fs time step. Furthermore, we are unable to SCF converge the E_{Ewq 14} QM region after step 108. The solute exhibits unusual changes in the hydrogen covalent angles after the first 75 steps, a dramatic deformation of the phenyl ring after the first 90 steps, and wildly nonphysical bond lengths in the last few steps – at which point, the solute can only be described as having undergone an “implosion”. The E_{CEw 14} trajectory (Fig. 4b) does not encounter any of these symptoms. To demonstrate that the E_{Ewq 14} implosion is not a fluke, we restarted the E_{Ewq 14} simulation from the coordinates taken from step 108 of the E_{CEw 14} trajectory. The E_{Ewq 14} trajectory again implodes after an additional 80 steps.

The instability of E_Ewq trajectories has previously been described by Holden et al.,^69,70 which motivated them to concoct a point-charge representation of the QM charge density using a ChElPG charge-fitting procedure.⁷¹ The E_CEw method described in the present work interacts the QM region with its surroundings without resorting to an auxiliary representation. Nevertheless, we agree with Holden et al. that the underlying reason for the instability of E_Ewq trajectories arises from the manner in which the Mulliken potentials contribute to the Fock matrix. In other words, the E_{Ewq 14} trajectory in Fig. 4a becomes nonphysical because the electrostatic protocol spuriously polarizes the density matrix to the environment.

Figures 5–6 compare how the E_{Ewq 14} and E_{CEw 14} protocols affect the polarization of the QM electron density by monitoring the Mulliken charges and Wiberg bond orders at each step of the trajectories. Figure 5a shows the E_{Ewq 14} carbon Mulliken charges evaluated using the first 108 steps of the E_{Ewq 14} trajectory. The carbon charges diverge as the trajectory reaches the first implosion. At first glance, a reader might be tempted to flippantly dismiss Fig. 5a because Mulliken charges are known to exhibit a sensitivity to basis set.^138,139 However, the E_{CEw 14} carbon Mulliken charges shown in Fig. 5e are evaluated at the same coordinates as those used in Fig. 5a, and yet the E_{CEw 14} charges are remarkably stable – even as the solute implodes. The carbon charges are recomputed along the E_{CEw 14} trajectory in Figs. 5m and Fig. 5i. Again, the E_{Ewq 14} charges (Fig. 5i) are more sensitive, but they do not diverge because the E_{CEw 14} trajectory does not implode. The E_{Ewq 14} Mulliken charges of the other atoms (O,N,P,H) are relatively stable in comparison to carbon. What we conclude from Fig. 5 is:

1. The E_{Ewq 14} Mulliken charges of carbon are particularly sensitive to geometry, and

2. The E_{Ewq 14} electrostatics must be polarizing the underlying density matrix in a suspicious manner, because the E_{CEw 14} Mulliken charges are stable when evaluated with the same coordinates.

The C-C, C-O, C-N, and C-H Wiberg bond indices shown in Fig. 6 are a second means for analyzing the electron polarization. The C-C bond orders in Fig. 6a, 6e, 6i, and 6m should be about 1.5 because of the conjugation within the phenyl ring. However, some of the C-C bonds in Fig. 6a show strong antibonding behavior. The spurious E_{Ewq 14} C-C bonding pattern significantly alters carbon’s bonding to the other atoms as one approaches the implosion.

The E_Ewq method’s polarization is sensitive because:

1. There is a large amount of C-C AO overlap, and

2. The Mulliken potentials produce multiple, inconsistent views of the external environment’s electronic chemical potential.

There is a large amount of C-C AO overlap because the “C3s” function – that is, the primitive s-function in 6-31G* – has a small Gaussian exponent $(0.1687144a_0^{-2})$ and there are 6 carbons in close proximity to each other. To be more precise, there is a large amount of C3s-C3s AO overlap. The strong C3s AO overlap produces a near-linear dependence and a correspondingly small AO overlap matrix eigenvalue. Consequently, the first column (assuming the eigenvalues are sorted) of X (eq. 31) is a series of numbers that are large in magnitude, oscillate in sign, and are dominated by C3s-character. Alternatively stated, the C3s AOs are transformed in the OAO basis (eq. 35) to become oscillatory and delocalized across the phenyl ring. The near-linear dependence that we’ve just described is expected and routine. Most applications of ab initio methods with small molecules encounter far smaller AO overlap eigenvalues than what is found here. The degree of near-linear dependence in the present example only becomes a problem once the chemical potential is inconsistently viewed. The electronic chemical potential produced by the external environment (the MM atoms and long-range electrostatics) is

$${\mu }_{\text{ext}}(\mathbf{r})=\frac{\delta E_{\text{ext}}}{\delta \rho (\mathbf{r})}$$ (114)

and it polarizes the electron density through its contribution to the Fock matrix.

$$\mathrm{\Delta }{F}_{\mu v}^{\sigma }={\displaystyle \int {\mu }_{\text{ext}}(\mathbf{r}){\chi }_{\mu }(\mathbf{r}){\chi }_v(\mathbf{r})d^{3}r}$$ (115)

By performing the interaction through Mulliken charges, the E_Ewq method produces different chemical potentials for each AO product.

$${\mu }_{\text{ext}}(\mathbf{r})\to {\mu }_{\text{Ewq},\mu v}(\mathbf{r})=-\frac{1}{2}\left(\frac{\partial E_{\text{Ewq}}}{\partial q_{a∍\mu }}+\frac{\partial E_{\text{Ewq}}}{\partial q_{b∍v}}\right)$$ (116)

Each of these chemical potentials is a constant throughout space, but every AO-pair experiences a different constant. When eq. 115 is transformed into the OAO basis, the spatial inconsistencies of μ_Ewq,µν(r) and the multicenter delocalization of eq. 35 malforms the chemical potential relative to the other OAO basis functions to produce irregularities in the electron polarization. The E_CEw method presented in this work does not produce errant polarizations because it uses a single, consistent view of the external environment’s chemical potential.

Computational efficiency

The E_CEw method is more expensive than E_MMEw because E_CEw polarizes the QM region to both the short- and long-range interactions. Specifically, E_CEw integrates the Ewald Gaussian potential via molecular quadrature, and the E_CEw gradients (eq. 100) require a forward Fourier transform of the QM charge density from the molecular quadrature grid. As shown in Table 1, this additional layer of computation slows the E_CEw simulations by only a small amount because the dominant effort continues to involve the calculation of standard Gaussian integrals required by the underlying ab initio Hamiltonian. For a 52 atom QM region, the difference in timings between E_CEw and E_MMEw is 1% to 4%, depending on how many CPU cores are used.

The choice of real-space Ewald cutoff affects the relative cost between the real- and reciprocal-space evaluations, and it thus could be tuned to optimize the overall cost. Specifically, reducing the size of the real-space Ewald cutoff necessitates the use of larger Ewald coefficients which in turn requires a larger number of plane waves to resolve. The optimal choice is obtained from empirical observation. The strategy used in Amber, which we have adopted in this work, is to use a 1 point/ų FFT grid density, and then choose the Ewald coefficient such that erf(βR_cut) = εR_cut, where ε is a “direct sum tolerance”. One could argue that larger values of R_cut may be necessary when using ab initio methods because the electron density extends several Ångstroms beyond the nucleus. By employing a 14 Å real-space Ewald cutoff, we are attempting to pre-emptively diffuse that argument. Having said that, we have not yet encountered a scenerio where a 10 Å real-space Ewald cutoff produces a questionable result. In practice, the pNPP simulations employing a 14 Å real-space Ewald cutoff slowed the calculation by 7 to 8% relative to the 10 Å real-space Ewald cutoff.

3.2 Comparison between ab initio and semiempirical free energy profiles

Semiempirical theory has seen widespread use for generating potential of mean force free energy profiles from QM/MM simulations. Considering that semiempirical models are approximately 100 times faster than many ab initio methods, one may verily question whether the accuracy of ab initio approaches is worth their added effort. Figure 9 compares the AM1/d-PhoT and DFTB2 semiempirical model PMFs with those produced by PBE0/6-311G** for the transesterification reaction shown in Fig. 8. The most striking difference occurs with the EtO leaving group (Figs. 9a–9c). The semiempirical models predict a single, late transition state, whereas PBE0 produces two transition states (the late transition state is rate controlling) and an intermediate. In other words, the AM1/d-PhoT and DFTB2 semiempirical models predict a “concerted” mechanism, and PBE0 predicts a “stepwise” mechanism. The experimental rates of this reaction do not provide insight into whether or not an intermediate exists; however, we have used the Gaussian program¹⁴⁰ to perform geometry optimizations and transition state searches using PBE0/6-31G*, PBE0/6-311G**, B3LYP/6-31G*, and B3LYP/6-311G** with polarized continuum model (PCM) implicit solvent.¹⁴¹ All of the PCM calculations that we performed predict the existence of an intermediate and two transition states, in agreement with our PBE0 explicit solvent QM/MM PMF. Previous studies of transesterification reactions with various leaving groups have found that poor (EtO) and enhanced (PhO) leaving groups generally follow a stepwise and concerted mechanisms, respectively.¹³⁶ Indeed, the transesterification reaction PMFs involving the PhO leaving group (Figs. 9d–9f) are predicted to undergo a concerted mechanism for all 3 methods.

The PBE0/6-311G** reaction barriers agree more closely to experiment than either AM1/d-PhoT or DFTB2. The semiempirical methods predict EtO barriers that are 10 kcal/mol larger than experiment, whereas PBE0 is only 3.6 kcal/mol larger. Similarly, the semiempirical models produce PhO barriers that are 8 kcal/mol larger than experiment, and PBE0 differs from experiment by only 0.8 kcal/mol.

4 Conclusion

In this work, we presented a new, composite Ewald method (CEw) for QM/MM simulations. Unlike the semiempirical-QM/MM Ewald method introduced by Nam,⁶³ the new method produces stable MD trajectories when evaluated with non-minimal Gaussian AO basis sets. The CEw method differs from the recently described QM/MM-LREC approach⁸⁵ by polarizing the QM region to the long-range electrostatics using an Ewald summation. It further differs from the approach described by Holden et al.^69,70 by interacting the QM region with the external environment directly through the QM charge density, as opposed to resorting to a point-charge auxiliary representation.

We compared how various electrostatic protocols affect the PMF of the p-nitrophenyl phosphate dissociation reaction. It was shown that the CEw PMFs are less sensitive to the division of short- and long-range interactions than the other methods that we compared to. For example, the difference in free energy barriers between using a real-space Ewald cutoff of 10 Å and 18 Å was found to be 1 kcal/mol when using the composite Ewald method. We compared CEw to a subtractive Ewald scheme (MMEw) and found that CEw avoided the structural artifacts associated with switching the QM/MM interaction between electrostatic and mechanical embedding.

We examined the computational cost of the new method and found that the incorporation of Ewald sums into the QM calculation only slowed the simulation rate by 1% to 4% for a 52 atom QM region.

We confirmed Holden’s explanation^69,70 for the instability encountered with Mulliken charge-based QM/MM Ewald methods.⁶³ The use of Mulliken charges produces inconsistent representations of the electronic chemical potential which, in the orthogonalized atomic orbital representation of the Fock matrix, become deformed and thus errantly polarizes the QM electron density. The new CEw method polarizes the QM density to a globally-consistent representation of the chemical potential.

We performed two-dimensional PMFs of phosphoryl transesterification reactions with ethoxide and phenoxide leaving groups to compare PBE0/6-311G** with the AM1/d-PhoT and DFTB2 semiempirical models. We found that the semiempirical models produced concerted reaction mechanisms for the ethoxide leaving group, whereas PBE0 simulations produced a stepwise mechanism, in agreement with implicit solvation calculations and previous work.^136,137 Furthermore, the PBE0/6-311G** reaction barriers were found to more closely match experiment than the semiempirical methods by 6 to 7 kcal/mol for both leaving groups.