Patient-Specific Oscillometric Blood Pressure Measurement

Abstract

Objective

Most automatic cuff blood pressure (BP) measurement devices are based on oscillometry. These devices estimate BP from the envelopes of the cuff pressure oscillations using fixed ratios. The values of the fixed ratios represent population averages, so the devices may only be accurate in subjects with normal BP levels. The objective was to develop and demonstrate the validity of a patient-specific oscillometric BP measurement method.

Methods

The idea of the developed method was to represent the cuff pressure oscillation envelopes with a physiologic model and then estimate the patient-specific parameters of the model, which includes BP levels, by optimally fitting it to the envelopes. The method was investigated against gold standard reference BP measurements from 57 patients with widely varying pulse pressures. A portion of the data was used to optimize the patient-specific method and a fixed-ratio method, while the remaining data were used to test these methods and a current office device.

Results

The patient-specific method yielded BP root-mean-square-errors ranging from 6.0 to 9.3 mmHg. On average, these errors were nearly 40% lower than the errors of each existing method.

Conclusion

The patient-specific method may improve automatic cuff BP measurement accuracy.

Significance

A patient-specific oscillometric BP measurement method was proposed and shown to be more accurate than the conventional method and a current device.

I. INTRODUCTION

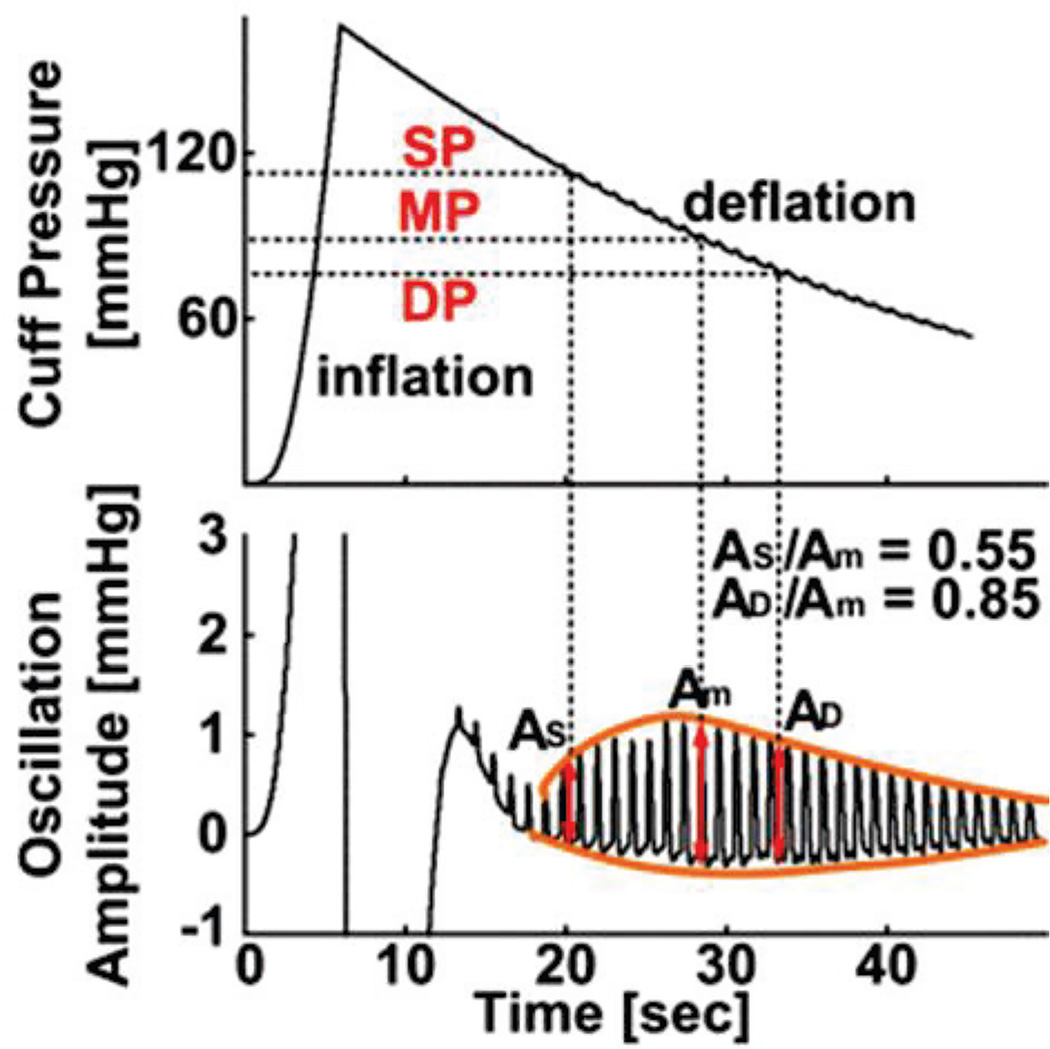
OSCILLOMETRY is a widely used approach for automatic cuff blood pressure (BP) measurement [1]–[3]. In this approach, a cuff placed on the upper arm is inflated and then deflated while the pressure inside the cuff is measured. As shown in Figure 1, the resulting cuff pressure not only rises and falls but also shows small oscillations indicating the pulsatile blood volume within the brachial artery underneath the cuff. The amplitude of these oscillations changes with the applied cuff pressure, as the brachial artery compliance varies with transmural pressure (i.e., BP - cuff pressure). BP is then estimated from the oscillation amplitudes and cuff pressure.

Fig. 1.

Conventional fixed-ratio method for estimating mean blood pressure (MP) and then systolic and diastolic blood pressure (SP and DP) from the oscillometric cuff pressure waveform. The fixed-ratio values (i.e., 0.55 and 0.85) represent population averages.

The BP estimation is conventionally performed via fixed ratios [1], [2], [4]. As shown in Figure 1, first, mean BP (MP) is estimated as the cuff pressure at which the oscillation amplitude is maximal, since the brachial artery compliance peaks near zero transmural pressure. Then, systolic and diastolic BP (SP and DP) are each estimated as the cuff pressure at which the oscillation amplitude is some fixed ratio of the maximal value. While current devices do not disclose their exact methods for estimating BP, they are believed to employ the fixed-ratio method or some variant thereof [1], [2], [5]. Since such methods are based on population averages, the devices may only work well in subjects with normal BP levels. Indeed, the accuracy of the devices is known to be compromised in subjects with large artery stiffening and thus high pulse pressure (PP = SP − DP) [2], [5] – a common condition that occurs with aging and disease.

In this study, we developed a patient-specific method to estimate BP from the oscillometric cuff pressure waveform. The basic idea is to represent the oscillation amplitudes and cuff pressure with a physiologic model and then estimate the patient-specific parameters of the model, which includes BP levels, by optimally fitting it to the measured data. We tested the method against gold standard reference BP measurements in patients referred for diagnostic cardiac catheterization – a population with widely varying PP. Our results indicate that the patient-specific method can afford greater BP estimation accuracy than the fixed-ratio method and a current device used for hypertension management in the office. A preliminary version of this study has been reported in abbreviated form [6].

II. PATIENT-SPECIFIC OSCILLOMETRIC BLOOD PRESSURE MEASUREMENT METHOD

The proposed method was inspired by Drzewiecki et al. who established a model to explain oscillometry [7]. Similar to available methods, a standard oscillometric cuff pressure waveform is obtained; the difference in the upper and lower envelopes of the oscillations (i.e., the high-pass filtered or AC waveform) as a function of the cuff pressure (i.e., the un-filtered waveform) is computed during the inflation or deflation period (whichever is longer); and BP is estimated from this oscillation amplitude versus cuff pressure function. However, in contrast to available methods, the BP estimation is based on a physiologic model and is thus patient-specific.

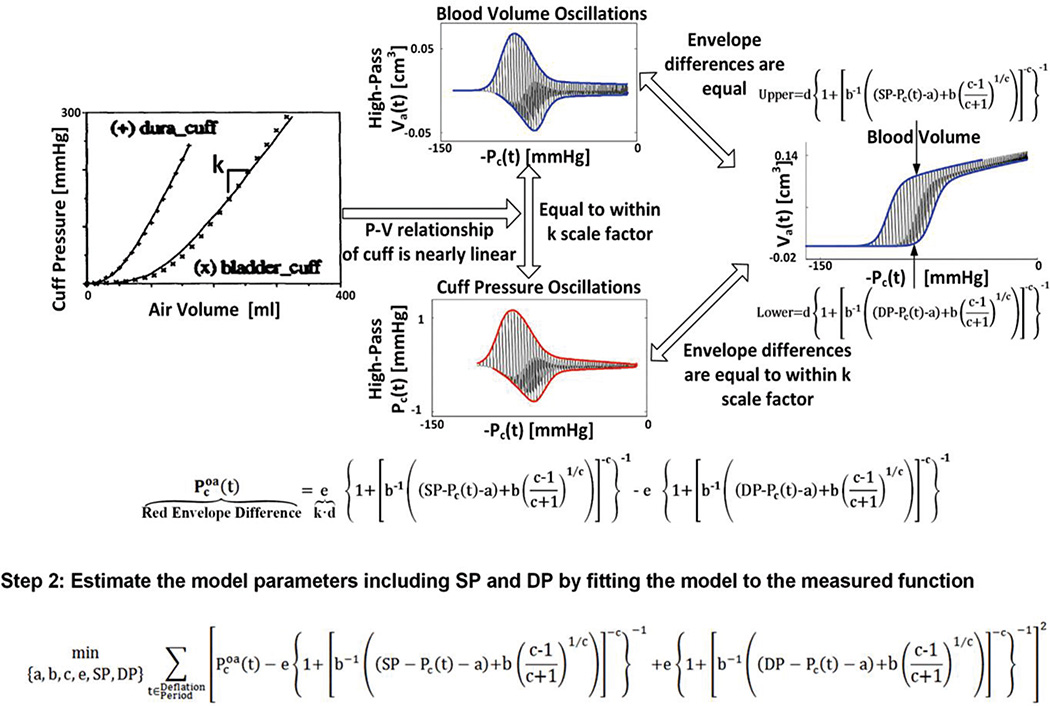
This novel BP estimation is implemented in four steps. First, the oscillation amplitude versus cuff pressure function is represented using a parametric model of the nonlinear brachial artery blood volume-transmural pressure relationship. Second, the model is optimally fitted to the measured function to estimate its unknown parameters including SP and DP. Third, the blood volume waveform is constructed using the parameter estimates and cuff pressure oscillations. Fourth, the BP waveform is derived by applying the blood volume and cuff pressure waveforms to the patient-specific brachial artery blood volume-transmural pressure relationship, and MP is computed from the derived waveform. These steps are fully summarized in Figures 2 and 3 and further described below.

Fig. 2.

Proposed patient-specific method for estimating blood pressure (BP) from the oscillometric cuff pressure waveform. The first two steps of the method yield estimates for SP and DP as well as the parameters, a, b, c, and e, which characterize the underlying model of the brachial artery blood volume-transmural pressure relationship.

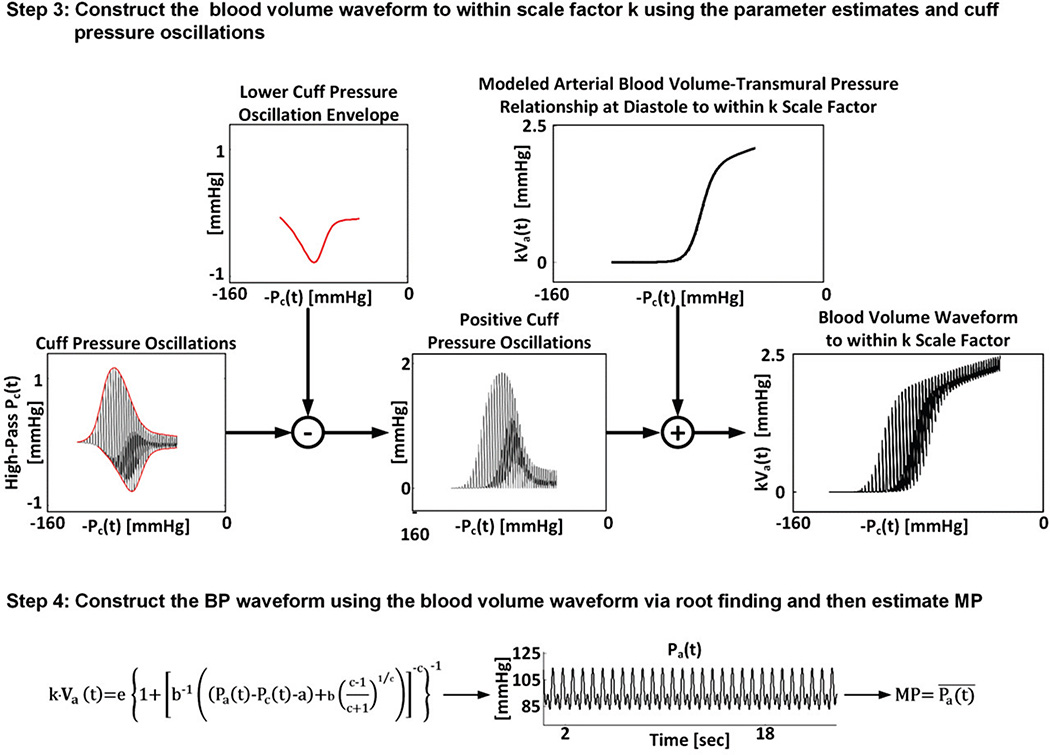
Fig. 3.

Proposed patient-specific method for estimating BP from the oscillometric cuff pressure waveform (cont.). The last two steps of the method use the parameter estimates from the first two steps to ultimately yield an estimate for MP. The left-most plot here and the three right-most plots in Figure 2 were simulated by a mathematical model of oscillometry [7] for illustrative purposes.

In the first step (see Figure 2), the oscillation amplitude versus cuff pressure function is represented using a parametric model of the nonlinear brachial artery blood volume-transmural pressure relationship. This model assumes a sigmoidal relationship as justified by experimental data [7], [8] and is, in particular, based on a left-shifted, Fisk cumulative probability distribution function [9] as follows:

$${\mathrm{V}}_{\mathrm{a}}(\mathrm{t})=\mathrm{d}{\{1+{\left[{\mathrm{b}}^{-1}\right(({\mathrm{P}}_{\mathrm{a}}(\mathrm{t})-{\mathrm{P}}_{\mathrm{c}}(\mathrm{t})-\mathrm{a})+\mathrm{b}{\left(\frac{\mathrm{c}-1}{\mathrm{c}+1}\right)}^{\frac{1}{\mathrm{c}}}\left)\right]}^{-\mathrm{c}}\}}^{-1}$$ (1)

Here, t is time; V_a(t) is the blood volume waveform; P_a(t) is the BP waveform; P_c(t) is the un-filtered cuff pressure waveform; and a, b, c, and d characterize brachial artery mechanics. In terms of the brachial artery compliance curve, which is simply the derivative of Eq. (1) with respect to transmural pressure [P_a(t) − P_c(t)], a (units of mmHg) denotes the transmural pressure at which the curve is maximal; b (units of mmHg) and c (unitless) reflect the width of the curve and the degree of asymmetry about its maximum; and d (units of cm³) determines the amplitude of the curve. Note that Eq. (1) is only valid over the range specified by (P_a(t)−P_c(t) −a)+b((c−1)/(c+1))^1/c> 0.

This model can directly represent a blood volume versus cuff pressure function. That is, the upper and lower envelopes of the blood volume waveform as a function of cuff pressure may be represented with the above model by setting P_a(t) to SP and DP, respectively (see right plot in Figure 2 where the abscissae are specifically given by the negative of the un-filtered cuff pressure waveform). However, the blood volume waveform is not measured.

In order to apply the model to the measured cuff pressure waveform, two approximations are made. First, the difference in the upper and lower envelopes of the blood volume waveform as a function of negative cuff pressure is essentially equivalent to the difference in the upper and lower envelopes of the blood volume oscillations (i.e., the high-pass filtered blood volume waveform) as a function of negative cuff pressure (compare right and upper plots in Figure 2). Second, the cuff pressure-air volume relationship of actual cuffs is nearly linear over a wide range (see left plot in Figure 2) [7]. So, the unmeasured blood volume oscillations may be proportional to the measured cuff pressure oscillations (see upper and lower plots in Figure 2) with a proportionality constant equal to k, which indicates the reciprocal of the compliance of the cuff. Note that these oscillations do not include the x-intercept of the cuff pressure-air volume relationship, as they are derived via high-pass filtering.

Putting the above model and approximations together, the measured oscillation amplitude versus cuff pressure function is precisely represented with the model as follows:

$${\mathrm{P}}_{\mathrm{c}}^{\mathrm{o}\mathrm{a}}(\mathrm{t})=\mathrm{e}{\{1+{\left[{\mathrm{b}}^{-1}\right((\mathrm{S}\mathrm{P}-{\mathrm{P}}_{\mathrm{c}}(\mathrm{t})-\mathrm{a})+\mathrm{b}{\left(\frac{\mathrm{c}-1}{\mathrm{c}+1}\right)}^{\frac{1}{\mathrm{c}}}\left)\right]}^{-\mathrm{c}}\}}^{-1}-\mathrm{e}{\{1+{\left[{\mathrm{b}}^{-1}\right((\mathrm{D}\mathrm{P}-{\mathrm{P}}_{\mathrm{c}}(\mathrm{t})-\mathrm{a})+\mathrm{b}{\left(\frac{\mathrm{c}-1}{\mathrm{c}+1}\right)}^{\frac{1}{\mathrm{c}}}\left)\right]}^{-\mathrm{c}}\}}^{-1}$$ (2)

where P_c^oa(t) is the cuff pressure oscillation amplitude waveform and e = k·d (units of mmHg). P_c^oa(t) and P_c(t) are derived from the measured oscillometric cuff pressure waveform and thus known, whereas a, b, c, e, SP, and DP are patient-specific parameters and thus unknown.

In the second step (see Figure 2), the unknown parameters are estimated by optimally matching both sides of Eq. (2) to each other in the least squares sense. In particular, the following optimization problem is solved:

$$\underset{\{\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{e},\mathrm{S}\mathrm{P},\mathrm{D}\mathrm{P}\}}{\text{min}}\sum _{\mathrm{t}\in \text{Deflation Period}}{[{\mathrm{P}}_{\mathrm{c}}^{\mathrm{o}\mathrm{a}}(\mathrm{t})-\mathrm{e}{\{1+{\left[{\mathrm{b}}^{-1}\right((\mathrm{S}\mathrm{P}-{\mathrm{P}}_{\mathrm{c}}(\mathrm{t})-\mathrm{a})+\mathrm{b}{\left(\frac{\mathrm{c}-1}{\mathrm{c}+1}\right)}^{\frac{1}{\mathrm{c}}}\left)\right]}^{-\mathrm{c}}\}}^{-1}+\mathrm{e}{\{1+{\left[{\mathrm{b}}^{-1}\right((\mathrm{D}\mathrm{P}-{\mathrm{P}}_{\mathrm{c}}(\mathrm{t})-\mathrm{a})+\mathrm{b}{\left(\frac{\mathrm{c}-1}{\mathrm{c}+1}\right)}^{\frac{1}{\mathrm{c}}}\left)\right]}^{-\mathrm{c}}\}}^{-1}]}^2$$ (3)

Hence, the first two steps produce estimates for SP and DP. The last two steps yield an estimate for MP as follows.

In the third step (see Figure 3), a scaled blood volume waveform [k·V_a(t)] is constructed using the parameter estimates. The idea is to construct (to within a scale factor) the right-most plot in Figure 2, which indicates the blood volume waveform, by adding the cuff pressure oscillations to the lower envelope in this plot, which may be derived from the parameter estimates. More specifically and referring back to Figure 3, the lower envelope of the cuff pressure oscillations as a function of negative cuff pressure (second plot from left) is subtracted from the cuff pressure oscillations as a function of negative cuff pressure (left-most plot). The resulting positive amplitude oscillations as a function of negative cuff pressure (middle plot) are then summed to a function defined by the model of Eq. (1) scaled by k with the parameter estimates for a, b, c, and e and P_a(t) set to the DP estimate (second plot from right). The ordinates of the function resulting from these simple operations specify the scaled blood volume waveform (right-most plot; compare to rightmost plot in Figure 2). Note that the scaled blood volume waveform may also be analogously obtained from the upper envelope.

In the fourth step (see Figure 3), the BP waveform is derived using the scaled blood volume waveform according to the model of Eq. (1) scaled by k. In particular, for each t, all quantities in this equation are known, except for P_a(t). Hence, BP is derived at each time instance by finding the root of the equation. Finally, the time average of the constructed BP waveform is computed so as to yield an estimate for MP.

III. MATERIAL AND METHODS

The patient-specific oscillometric BP measurement method was investigated using data comprising the oscillometric cuff pressure waveforms for analysis and gold standard reference BP measurements from human subjects covering a wide PP range. These data were divided into distinct training and testing sets. While the proposed method is patient-specific, a training dataset was still needed to define its detailed aspects including the values of its user-selected variables. The training dataset was also utilized to establish a conventional fixed-ratio method. The testing dataset was utilized to assess the accuracy of the patient-specific method and to compare its performance to the fixed-ratio method as well as a current device. Details follow.

A. Patient data

Patients admitted to the Taipei Veterans General Hospital (Taiwan) were studied under IRB approval and with adherence to the principles of the Declaration of Helsinki. The patient characteristics and study procedures are described in detail elsewhere [10], [11]. Information relevant to the present study is briefly described below.

Sixty patients referred for diagnostic cardiac catheterization were included. These patients (63 ± 14 years, 77% males) had clinical diagnoses of mainly hypertension (68% of the patients), coronary artery disease (65%), dyslipidemia (44%), and/or diabetes (33%) and were on various medications. All patients had normal sinus rhythm, and none of the patients showed an inter-arm BP difference of more than 3 mmHg.

A micromanometer-tipped catheter (SPC-320, Millar Instruments, USA) was placed in a brachial artery to measure the gold standard reference BP waveform. An oscillometric BP cuff (WatchBP Office, Microlife AG, Switzerland or VP-1000, Omron Colin, Japan) was placed over the opposite brachial artery to measure the oscillometric cuff pressure waveform for analysis as well as to document the SP, MP, and DP estimates of the Microlife or Omron device. The waveforms were simultaneously recorded at a sampling rate of 250 Hz. In many of the patients, the measurements were likewise recorded after administration of sublingual nitroglyercin to reduce BP.

B. Data analysis

The data for study were divided into a training set comprising 40 of the patient records and a testing set consisting of the remaining 20 patient records. The patient records in each dataset were randomly selected. All oscillometric cuff pressure waveforms in the two datasets were essentially artifact-free based on visual inspection. However, the fidelity of the reference BP waveforms in three of the patient records in the training dataset was questionable. These patient records were excluded from further analysis yielding a total of 57 patient records for analysis.

The training dataset was first analyzed. More specifically, the patient-specific method was fully defined by minimization of the average of the root-mean-square-error (RMSE) between the SP estimate and reference SP and the RMSE between the DP estimate and reference DP in this dataset. The method that resulted was actually slightly sub-optimal but potentially more robust. This method was implemented as follows. First, the upper and lower envelopes of the oscillations as a function of cuff pressure were identified by detecting the maximum and minimum of each beat, applying a median filter to the maxima and minima to remove respiratory contamination, and linearly interpolating between the filtered maxima and minima. Then, the difference between these envelopes, which is the oscillation amplitude versus cuff pressure function, was represented with the physiologic model of Eq. (2). Next, the unknown model parameters were estimated by solving the optimization problem of Eq. (3) but with constraints on the parameters. The parameter constraints included imposing the valid range of Eq. (1) and setting a, which denotes the peak position of the brachial artery compliance curve, to near 0 mmHg and fixing the value of b for each value of c such that the curve is right-skewed by 35% about its peak. Note that the peak position of the compliance curve is not an identifiable parameter but may be near zero transmural pressure anyhow and that the compliance curve may indeed be typically right-skewed due to differences in collapsed and distended artery mechanics [7]. Also note that fixing the c and d parameters in addition to the a and b parameters degraded the BP estimation accuracy, thereby suggesting that a patient-specific brachial artery blood volume-transmural pressure relationship was necessary. The four-parameter constrained optimization problem was specifically solved using sequential quadratic programming [12] to yield estimates for SP, DP, and the other parameters. The parameter estimates were generally unique as ascertained via multiple initial seeds. Finally, MP was estimated as outlined in detail in Section 2.

A fixed-ratio method was also established using the training dataset. That is, after estimating MP via the cuff pressure at which the oscillation amplitude is maximal, values of fixed ratios for SP and DP were defined by minimizing the RMSE between the SP and DP estimates and their reference values. The optimal values that resulted were 0.55 for SP and 0.78 for DP, which are consistent with previous reports [2], [4], [7].

The testing dataset was then analyzed. First, the patient-specific and fixed-ratio methods were applied to the ocillometric cuff pressure waveforms. Then, the SP, MP, DP, and PP estimates of these methods as well as the Microlife or Omron device were assessed against their reference values via the standard bias error (i.e., mean of the errors) [μ] and precision error (i.e., standard deviation of the errors) [σ] as well as the RMSE (i.e., total magnitude of the errors) [=√(μ²+σ²)]. Finally, the bias and precision errors of the patient-specific method were compared to those of the existing methods using the paired t-test and Pitman-Morgan test [13], respectively. Similar results from the training dataset were also obtained excluding the statistical comparisons with the current device, which, unlike the other two methods, was not optimized with respect to this dataset.

In both datasets, reference SP and DP were specifically computed by detecting the maximum and minimum of each beat of the simultaneously recorded invasive BP waveform during the cuff deflation period (typically about 20 s) and then averaging the respective values over the beats. Reference MP was computed as the time average of the invasive BP waveform during the same period.

IV. RESULT

Table I shows the average, standard deviation, and range of reference SP, MP, DP, and PP before and after nitroglycerin administration in the combined training and testing datasets. These BP statistics were similar between the two datasets. The average of baseline SP was close to hypertensive levels, whereas the average of baseline DP was at normotensive levels. Hence, the average of baseline PP was high. Nitroglycerin reduced the average of SP, which impacted the averages of MP and PP. The standard deviations of PP and SP were highest and near 20 mmHg. PP and SP ranged from normal to high levels, so a number of the patients may not have had large artery stiffening.

Table I.

Reference Blood Pressure (BP) Levels in the Combined Training and Testing Datasets

Condition	SP [mmHg]	MP [mmHg]	DP [mmHg]	PP [mmHg]
Baseline	137±19 (96–182)	95±11 (68–126)	68±10 (44–88)	68±19 (36–110)
Nitroglycerin	126±19 (95–164)	88±11 (68–118)	67±9 (44–90)	59±17 (30–95)

Values are average±standard deviation (range). SP, MP, and DP are systolic, mean, and diastolic BP, respectively, and PP is pulse pressure.

Table II shows the SP, MP, DP, and PP bias and precision errors for the patient-specific and fixed-ratio methods as well as the Microlife device in the training dataset. The patient-specific method produced small bias errors and precision errors of 5.0 to 8.1 mmHg. The fixed-ratio method yielded similar bias errors but higher precision errors of 7.5 to 13.2 mmHg (p < 0.05). Although it may not be fair to compare the Microlife device to these two methods in the training dataset, it is noted that the device did show higher bias and precision errors than the patient-specific method. If the opposite were true, then the current device would be clearly superior.

Table II.

BP Error Metrics for the Patient-Specific Method and Existing Methods in the Training Dataset

Method	SP Error [mmHg]		MP Error [mmHg]		DP Error [mmHg]		PP Error [mmHg]
	Bias	Precision	Bias	Precision	Bias	Precision	Bias	Precision
Patient-Specific	−0.6	5.0	2.0	5.7	−0.5	5.2	−0.1	8.1
Fixed-Ratios	−0.7	8.4*	3.5	10.0*	0.5*	7.5*	−1.2*	13.2*
Microlife	−5.8	7.4	−4.8	8.4	6.9	7.1	−12.7	9.8

^*denotes p<0.05 compared with patient-specific method. The Microlife device was not statistically compared to the patient-specific method.

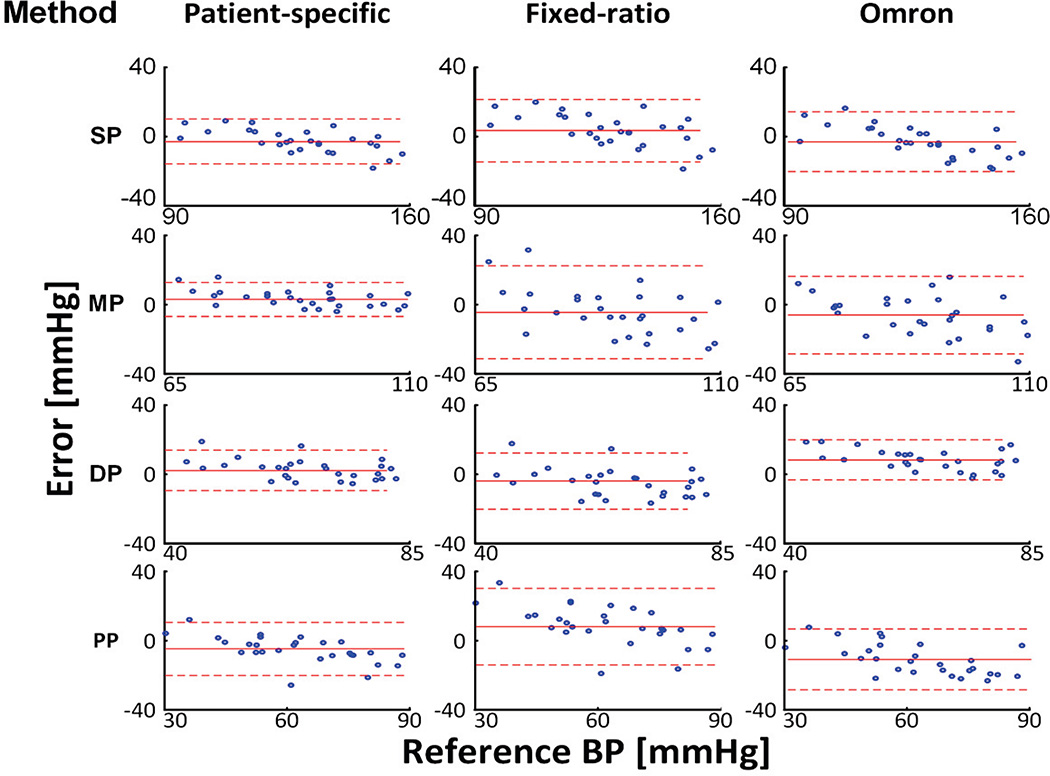
Table III shows the same quantitative BP error metrics for the two methods and the Omron device in the testing dataset, while Figure 4 shows the Bland-Altman plots of these three methods in this dataset so that their accuracy can be visually assessed and compared. The patient-specific method achieved bias errors of 2.6 to 5.3 mmHg in magnitude and precision errors of 5.0 to 7.7 mmHg. The fixed-ratio method showed significantly different bias errors (p < 0.05) with higher magnitudes of 3.8 to 8.6 mmHg and larger precision errors of 8.4 to 14.0 mmHg (p < 0.05). The Omron device yielded larger bias error magnitudes of 6.0 to 11.0 for MP, DP, and PP than the patient-specific method (p < 0.05) and larger precision errors of 8.9 and 11.5 mmHg for SP and MP than this method (p < 0.10 or p < 0.05). These two methods showed precision errors for PP that did not statistically differ. However, the patient-specific method produced two large absolute errors for PP (see Figure 4), which substantially compromised its precision error. Indeed, after removing the bias component, the percent of PP errors >5 and >10 mmHg were 40% and 11% for the patient-specific method but 75% and 25% for the Omron device. In this quantitative sense, the PP precision accuracy of the patient-specific method was superior to the current device. Overall, the average RMSE of the patient-specific method was 7.3 mmHg, which was about 40% smaller than the corresponding RMSE of each existing method. The improved accuracy afforded by the patient-specific method was significant for all four BP estimates. In addition, the patient-specific method showed BP errors that were least correlated with the reference BP values.

Table III.

BP Error Metrics for the Patient-Specific Method and Existing Methods in the Testing Dataset

Method	SP Error [mmHg]		MP Error [mmHg]		DP Error [mmHg]		PP Error [mmHg]
	Bias	Precision	Bias	Precision	Bias	Precision	Bias	Precision
Patient-Specific	−2.6	6.7	3.5	5.0	2.7	6.0	−5.3	7.7
Fixed-Ratios	3.8*	9.4*	−4.0*	14.0*	−4.8*	8.4*	8.6*	11.2*
Omron	−2.9	8.9#	−6.0*	11.5*	8.1*	5.9	−11.0*	8.9

* and # denote p<0.05 and p<0.10 compared with patient-specific method, respectively.

Fig. 4.

Bland-Altman plots (mean±1.96·SD) for the patient-specific method and existing methods in the testing dataset.

Over the combined training and testing datasets, the patient-specific method yielded model parameter estimates that were distributed (mean±SD) as follows: a = 2.5 mmHg, b = 73.3±30.0 mmHg, c = 5.5±0.9 unitless, and e = 8.2±1.5 mmHg. The c and e parameters were 5.2±0.6 unitless and 8.3±1.4 mmHg before nitroglycerin administration and 5.9±1.0 unitless and 8.9±1.5 mmHg after nitroglycerin administration, respectively (p < 0.05 via paired t-tests). These significant c and e increases following nitroglycerin administration correspond to enhanced brachial artery compliance. So, the patient-specific method predicted vascular changes consistent with the known effect of the drug. The BP estimation accuracy of the method was therefore not impacted by nitroglycerin administration but neither was the accuracy of the existing methods (results not shown).

V. DISCUSSION

In summary, we conceived a method to estimate BP from the oscillometric cuff pressure waveform. While current methods may perform the BP estimation based on population averages (see Figure 1), the proposed method leverages a physiologic model in combination with optimization to achieve patient-specific BP estimation (see Figures 2 and 3). In this way, automatic cuff BP measurement accuracy may potentially be maintained over a wide range of BP levels.

We investigated the patient-specific method against gold standard reference BP measurements via a high-fidelity brachial artery catheter from 57 patients whose PP and SP ranged from normal to very high levels (see Table I). We used 65% of the data to develop or train the method and the remaining 35% of the data to test it.

The patient-specific method yielded SP, MP, DP, and PP estimates with bias error magnitudes between 2.6 and 5.3 mmHg and precision errors between 5.0 and 7.7 mmHg for an overall average RMSE of 7.3 mmHg in the testing dataset (see Table III and Figure 4). The corresponding RMSE of the method in the training dataset was 1.2 mmHg lower (see Table II). The accuracy of the method in the testing dataset was well within the AAMI limits of 5 and 8 mmHg bias and precision errors for SP, MP, and DP and close to these limits for PP; however, these results were not obtained with an AAMI data collection protocol [14].

There are several potential sources of the BP estimation error of the method. Firstly, the underlying physiologic model ignores arm tissue compressibility and brachial artery wall viscoelasticity. However, compressibility of tissue around zero transmural pressure, which is most crucial in oscillometry and typically amounts to an applied cuff pressure of about 100 mmHg, may not be that significant, as it is largely compressed already. Furthermore, the wall viscosity of the muscular, but medium-sized, brachial artery may not be that significant compared to its elasticity as argued elsewhere [15]. Secondly, the oscillometric cuff pressure waveforms that were available for analysis were either converted from volts to mmHg with inexact calibration information in the case of the training dataset (Microlife device) or did not include a high resolution (low quantization error) AC component in the case of the testing dataset (Omron device). Hence, if the waveforms were of higher quality, the method could possibly have yielded lower errors. Finally, the method assumes that cuff pressure oscillations are proportional to blood volume oscillations and thus neglects nonlinearity of the arm cuff pressure-volume relationship. However, cuff nonlinearity is greatest at low cuff pressures (see left plot of Figure 2), and the patients for study were not hypotensive (see Table I). So, unlike the other potential error sources, we do not believe that cuff nonlinearity was a major contributor to the error.

For comparison, we also investigated the conventional fixed-ratio method (see Figure 1) by establishing the fixed ratio values using the training dataset and assessing the method in the testing dataset. The overall average RMSE of the method was 9.9 mmHg in the training dataset and 12.1 mmHg in testing dataset (see Tables 2 and 3 and Figure 4). Hence, the patient-specific method reduced the BP estimation error of the conventional method by about 40% in each dataset. The error reduction was achieved mainly via lower precision errors for all four BP estimates. This comparison was apples-to-apples. That is, not only were the analyzed oscillometric cuff pressure waveforms and training and testing datasets the same but also the oscillation amplitude versus cuff pressure functions from which BP was estimated.

In addition, we included the BP estimates of a device designed for hypertension management in the office rather than for home monitoring of normal subjects (Microlife or Omron). The overall average RMSE of the device was 11.3 mmHg in the training dataset (see Microlife in Table II) and 11.6 mmHg in the testing dataset (see Omron in Table III and Figure 4). Hence, the patient-specific method reduced the BP estimation error of a current device by 37% in the more meaningful testing dataset. The error reduction was achieved via lower bias errors for MP, DP, and PP and lower precision errors for SP and MP. Also, though not reflected in these error metrics, the patient-specific method achieved substantially better precision accuracy for PP, which is a more powerful predictor of cardiovascular outcomes in the elderly than SP [16]. However, this comparison was not exactly apples-to-apples. In particular, the oscillometric cuff pressure waveforms analyzed by the Microlife and Omron devices were surely well calibrated and of high resolution. So, the device benefitted from higher quality waveforms for analysis than the other two methods. The device also must have derived different oscillation amplitude versus cuff pressure functions to estimate BP. We suspect that the device performs this initial step, which can also impact the accuracy, quite well.

We utilized the most accurate reference BP measurement method available, namely micromanometer-tipped brachial artery catheterization. For practical reasons, invasive BP has not been assessed as a predictor of risk for stroke and heart disease. Rather, non-invasive BP via auscultation (i.e., manual cuff BP measurement using a stethoscope and mercury manometer) is the proven cardiovascular risk factor [17]. However, auscultation is not as accurate as invasive BP due to various factors including operator error and the well-known auscultatory gap [18]. It may thus be reasonable to assume that invasive BP would constitute a superior predictor of stroke and heart disease. In this sense, the improved accuracy of the patient-specific method shown here may be particularly significant.

Nevertheless, because non-invasive BP via auscultation is the proven cardiovascular risk factor and for practical reasons, most, if not all, BP estimation methods of current office and home devices are built from data using auscultation as the reference [3], [19]. The Microlife and Omron devices studied herein were likely built to predict auscultation BP. There are systematic differences between invasive SP and auscultation SP as well as invasive DP and auscultation DP [14]. These differences could at least partly explain the higher bias error magnitudes of the current device (see Tables 2 and 3). However, even if the bias errors were ignored altogether, the patient-specific method still attained precision errors that were 25% lower for SP and 57% lower for MP than the current device while reducing PP errors >5 and 10 mmHg by 52% compared to this device.

We believe that inclusion of 57 patients for study is not insignificant. Furthermore, even after dividing the patient records into training and testing sets, the improved accuracy of the patient-specific method over the competing methods was statistically significant. Still, the main limitation of this study is the 20 patient sample size of the testing dataset. Future studies are needed in a larger cohort of subjects to fully assess the accuracy of the proposed method relative to existing methods.

VI. CONCLUSION

Most automatic cuff BP measurement devices estimate BP from an oscillometric cuff pressure waveform using population average methods. Hence, these devices may only be accurate over the normal BP range. In this study, we developed a patient-specific method to estimate BP from the same oscillometric cuff pressure waveform. The underlying idea is to represent the waveform with a physiologic model and to then estimate the patient-specific model parameters by optimally fitting the model to the waveform. We demonstrated that this method can appreciably improve the accuracy over the state-of-the-art in patients with widely varying PP using gold standard invasive BP as a reference. Future studies may be worthwhile in a larger and more diverse cohort of subjects to fully assess the capabilities and limitations of the method relative to existing methods. With further successful testing, the patient-specific method could possibly improve automatic cuff BP measurement and thereby facilitate hypertension management in both low and high resource settings.

Biographies

Jiankun Liu received B.S degree in physics from Nanjing University, Nanjing, China, in 2006. He is currently a PhD candidate in the Department of Electrical and Computer Engineering, Michigan State University, East Lansing, USA. His research interests include biomedical computation and modeling as well as their application on patient monitoring and therapeutics. More specifically, his current research focuses on ubiquitous vital sign monitoring and ventricular arterial coupling with utilization of multiscale modeling approach.

Hao-min Cheng received the medical degree in Faculty of Medicine from National Yang-Ming University, Taipei, Taiwan, in 2000 and the Ph.D. degrees in Faculty of Medicine, The University of Adelaide, Australia in 2013. He is a cardiologist in Taipei Veterans General Hospital with the sub-specialty of interventional cardiology and echocardiography. He is currently with National Yang-Ming University, Taipei, Taiwan, where he is an Assistant Professor in Faculty of Medicine, and joint appointed Assistant Professor in Institute of Public Health. Dr. Cheng was a recipient of an International Postgraduate Research Scholarship from Australian Government and Young Investigator Award from Taiwan Society of Cardiology in 2013. He is an Associate Editor of the BMC Cardiovascular Disorders. His research interests include cardiovascular hemodynamics, blood pressure measurements, hypertension management, and evidence-based health care.

Chen-Huan Chen received the MD degree from the Faculty of Medicine, National Yang-Ming University, Taiwan, in 1982. He was a clinical research fellow at the Johns Hopkins Hospital, Division of Cardiology, BA, from 1995–1997. He has been on the faculty of the Department of Medicine since 1989, where he is currently a Professor. He completed internal medicine residency training and cardiology fellowship training at Taipei Veterans General Hospital in 1990, where he is currently an attending physician. His research interests focus on cardiovascular epidemiology, hemodynamics, vascular aging, arterial stiffness, wave reflections, heart failure, and development of new methods for noninvasive assessment of cardiac and vascular functions. His research works have contributed significantly to the understanding and utilization of the generalized transfer function concept and the optimal clinical assessment of the wave reflections.

Shih-Hsien Sung received the MD and PhD degrees from National Yang-Ming University, Taiwan, in 2001 and 2014, respectively. He has been on the faculty of the Department of Medicine since 2007, where he is currently an Assistant Professor. He completed internal medicine residency training and cardiology fellowship training at Taipei Veterans General Hospital in 2009, where he is currently an attending physician. His research interests focus on cardiovascular epidemiology, hemodynamics, vascular aging, heart failure, and pulmonary artery hypertension.

Mohsen Moslehpour received both B.S. and M.S. degrees in electrical engineering from AmirKabir University of Technology, Tehran, Iran, in 2004 and 2007, respectively. He is currently a PhD candidate in the Department of Electrical and Computer Engineering, Michigan State University, East Lansing, USA. His current research interests include biomedical signal processing and system identification and their applications in patient monitoring and cardiovascular system modeling.

Jin-Oh Hahn (M’08) received BS and MS degrees in mechanical engineering from Seoul National University, Seoul, Korea, in 1997 and 1999, and PhD degree in mechanical engineering from Massachusetts Institute of Technology, Cambridge, MA, USA, in 2008. He is currently with the University of Maryland, College Park, MA, USA, where he is an Assistant Professor in the Department of Mechanical Engineering. Dr. Hahn is a recipient of the Young Investigator Program Award from the Office of Naval Research in 2014, and the Young Investigator Grant Award from the Korean-American Scientists and Engineers Association in 2013. His current research interests include systems and controls approach to health monitoring, diagnostics and maintenance of dynamic systems.

Ramakrishna Mukkamala (M'02) received the B.S.E. degree in Biomedical/Electrical Engineering from Duke University, Durham, NC, in 1993 and the S.M. and Ph.D. degrees in Electrical Engineering and Computer Science from the Massachusetts Institute of Technology, Cambridge, MA, in 1995 and 2000, respectively. He was a Postdoctoral Fellow/Research Engineer at the Harvard-MIT Division of Health Sciences and Technology, Cambridge, MA, from 2000 to 2002. Since then, he has been on the faculty of the Department of Electrical and Computer Engineering at Michigan State University, East Lansing, MI, where he is currently a Professor. His research interests include biomedical signal processing and identification, modeling of physiologic systems, cardiovascular physiology, and patient monitoring. Dr. Mukkamala was a recipient of an AHA Scientist Development Grant, an NSF CAREER Award, and an MSU Teacher-Scholar Award. He is an Associate Editor of the IEEE Transactions on Biomedical Engineering, the Editor of the Cardiovascular and Respiratory Systems Engineering Theme of the IEEE EMBS Conference Proceedings, and a member of the IEEE EMBS Technical Committee on Cardiopulmonary Systems.