Mechanisms of in vivo muscle fatigue in humans: investigating age‐related fatigue resistance with a computational model

Abstract

Key points

• Muscle fatigue can be defined as the transient decrease in maximal force that occurs in response to muscle use. Fatigue develops because of a complex set of changes within the neuromuscular system that are difficult to evaluate simultaneously in humans.

• The skeletal muscle of older adults fatigues less than that of young adults during static contractions. The potential sources of this difference are multiple and intertwined.

• To evaluate the individual mechanisms of fatigue, we developed an integrative computational model based on neural, biochemical, morphological and physiological properties of human skeletal muscle.

• Our results indicate first that the model provides accurate predictions of fatigue and second that the age‐related resistance to fatigue is due largely to a lower reliance on glycolytic metabolism during contraction.

• This model should prove useful for generating hypotheses for future experimental studies into the mechanisms of muscle fatigue.

Abstract

During repeated or sustained muscle activation, force‐generating capacity becomes limited in a process referred to as fatigue. Multiple factors, including motor unit activation patterns, muscle fibre contractile properties and bioenergetic function, can impact force‐generating capacity and thus the potential to resist fatigue. Given that neuromuscular fatigue depends on interrelated factors, quantifying their independent effects on force‐generating capacity is not possible in vivo. Computational models can provide insight into complex systems in which multiple inputs determine discrete outputs. However, few computational models to date have investigated neuromuscular fatigue by incorporating the multiple levels of neuromuscular function known to impact human in vivo function. To address this limitation, we present a computational model that predicts neural activation, biomechanical forces, intracellular metabolic perturbations and, ultimately, fatigue during repeated isometric contractions. This model was compared with metabolic and contractile responses to repeated activation using values reported in the literature. Once validated in this way, the model was modified to reflect age‐related changes in neuromuscular function. Comparisons between initial and age‐modified simulations indicated that the age‐modified model predicted less fatigue during repeated isometric contractions, consistent with reports in the literature. Together, our simulations suggest that reduced glycolytic flux is the greatest contributor to the phenomenon of age‐related fatigue resistance. In contrast, oxidative resynthesis of phosphocreatine between intermittent contractions and inherent buffering capacity had minimal impact on predicted fatigue during isometric contractions. The insights gained from these simulations cannot be achieved through traditional in vivo or in vitro experimentation alone.

Key points

• Muscle fatigue can be defined as the transient decrease in maximal force that occurs in response to muscle use. Fatigue develops because of a complex set of changes within the neuromuscular system that are difficult to evaluate simultaneously in humans.

• The skeletal muscle of older adults fatigues less than that of young adults during static contractions. The potential sources of this difference are multiple and intertwined.

• To evaluate the individual mechanisms of fatigue, we developed an integrative computational model based on neural, biochemical, morphological and physiological properties of human skeletal muscle.

• Our results indicate first that the model provides accurate predictions of fatigue and second that the age‐related resistance to fatigue is due largely to a lower reliance on glycolytic metabolism during contraction.

• This model should prove useful for generating hypotheses for future experimental studies into the mechanisms of muscle fatigue.

Abbreviations

F_max

maximal force‐generating capacity

L_ceo

optimal contractile element length

MM

muscle model

MN

motor neuron

MVC

maximal voluntary contraction

PCr

phosphocreatine

P_i

inorganic phosphate

V_max

maximal shortening velocity

Introduction

The mechanisms of muscle fatigue, defined here as the acute decline in force‐generating capacity that accompanies repeated or sustained muscle contraction, are not completely understood because of the interrelated nature of the processes that influence this phenomenon. These processes are typically segregated as central or peripheral in nature. The term ‘central fatigue’ is used to describe a range of neural responses that ultimately reduce the ability to excite skeletal muscle voluntarily (Taylor et al. 2000). Inhibition of α‐motor neurons may result in decreased discharge rate or derecruitment of motor units, starting with the largest, highest‐threshold motor units (Kamen et al. 1995). Peripheral fatigue mechanisms are those located distal to the central nervous system and include reduced excitability at the motor endplate, smaller cytosolic Ca²⁺ transients, reduced Ca²⁺ sensitivity and inhibited actin–myosin force generation (Fitts & Balog, 1996; Galea, 2001). The byproducts of bioenergetic processes that maintain [ATP] in the face of changing energetic demands have been implicated for some time in the development of fatigue during repeated or prolonged contractions (Hill, 1929). Through multiple mechanisms, increased intracellular concentrations of inorganic phosphate (P_i) and H⁺ alter the contractile behaviour of skeletal muscle. Their combined effects ultimately lower force (Debold et al. 2013), rates of relaxation and, possibly, shortening velocity (Fitts & Balog, 1996). Data from in vitro studies suggest that P_i and H⁺ also reduce force‐generating capacity at the level of the cross‐bridge (Debold et al. 2012, 2013), but the extent to which these results reflect the behaviour of the intact neuromuscular system is not clear. Data from in vivo studies provide inconsistent results regarding metabolites such as [H⁺] and [ADP] (Kent‐Braun et al. 2002; Rico‐Sanz, 2003), but most support a strong association between diprotonated inorganic phosphate ([H₂PO₄ ⁻]) and fatigue (Cooke et al. 1988; Miller et al. 1988; Wilson et al. 1988; Kent‐Braun, 1999, 2002; Lanza et al. 2006, 2007).

Although in vitro experiments provide explicit details about systems in isolation, and in vivo studies can describe the combined function of multiple systems, neither approach provides the opportunity to study intracellular metabolites, neural activation and contractile variables directly and simultaneously. Thus, both in vivo and in vitro approaches have limitations for addressing the mechanisms of fatigue. Computational models, on the contrary, can be used to predict the responses of complicated systems whose interrelated components preclude direct measurement or control. Computational models have been developed that successfully predict the function of multiple biophysical systems, ranging from nervous tissue (Heckman & Binder, 1991) to individual sarcomeres within skeletal muscle (Huxley, 1971). However, few models have been proposed that encompass the full range of physiological processes, from neural activation to intracellular bioenergetics, implicated in neuromuscular fatigue. We present a computational model meant to represent this range of physiological processes. In the present work, we extend a previously validated, integrative model of muscle torque production (Callahan et al. 2013) to predict the return to resting metabolite concentrations following contractions and the relationships that exist between bioenergetic perturbation and limitations on force‐generating capacity (i.e. fatigue).

Evidence in the literature suggests that during isometric or low‐velocity contractions, skeletal muscle fatigue occurs to a lesser extent in the muscles of older adults than young (Narici et al. 1991; Ditor & Hicks, 2000; Bilodeau et al. 2001; Callahan & Kent‐Braun, 2011), an observation first termed the ‘fatigue paradox’ by (Narici et al. 1993). Recent analyses indicate that age‐related fatigue resistance is observed least often during dynamic contractions (Callahan & Kent‐Braun, 2011) and most often during sustained (Hunter et al. 1999; Bazzucchi et al. 2005; Mademli & Arampatzis, 2008 b) or intermittent isometric contractions (Ditor & Hicks, 2000; Kent‐Braun et al. 2002; Chung et al. 2007). These results are supported by meta‐analysis of relevant findings in the literature (Christie et al. 2011). Several mechanisms have been proposed to explain age‐related fatigue resistance during isometric contractions, including alterations in motor neuron (MN) behaviour (Allman et al. 2004; Tevald et al. 2010), greater reliance on oxidative metabolism (Kent‐Braun et al. 2002; Lanza et al. 2007), increased metabolic economy (Hepple et al. 2004; Lanza et al. 2007) and lower net production of fatigue‐inducing metabolites (Coggan et al. 1993; Chilibeck et al. 1998; Kent‐Braun et al. 2002; Lanza et al. 2007) in old compared with young adults. However, conclusive evidence indicating the primacy of any of these potential mechanisms is lacking. This is likely to be the result of the many difficulties associated with performing such relative comparisons and the inability to modify any single aspect of the neuromuscular system independently in vivo.

The goal of the present study, therefore, was to formulate a computational model capable of making accurate predictions of neuromuscular fatigue and the attendant physiological responses observed during repeated voluntary contractions in vivo. We then adapted this model to make predictions regarding the effect of age on fatigue to gain insight into potential physiological mechanisms explaining the phenomenon of age‐related fatigue resistance. To accomplish this goal, various components in the model representing specific aspects of neuromuscular function were adjusted to reflect corresponding processes evaluated experimentally in the ankle dorsiflexors of older men. The overall prediction of fatigue in the age‐adapted model was confirmed by comparison with an independent data set available in the literature. Comparisons between the two versions of the model revealed new insights into the mechanisms of fatigue and suggest that higher glycolytic flux and metabolic cost in younger adults have the greatest impact on age‐related fatigue resistance.

Methods

Computational approach

The modular nature of the present model shares components with our previously published model (Callahan et al. 2013), which was based on in vivo data from the human ankle dorsiflexor muscle group during isometric contractions. To arrive at the simulations presented here, the previous model was extended with new functions representing the following: (i) the bioenergetic cost of activation and torque generation; (ii) the recovery of metabolic homeostasis following activation; and (iii) the influence of these competing processes on torque‐generating capacity. Specifically, the present model contains additional functions describing the efflux of H⁺ resulting from the development of acidosis, synthesis of phosphocreatine (PCr) following each contraction, and a mechanism whereby [H₂PO₄ ⁻] limits force‐generating capacity. The system of equations that dictate neural excitation, muscle activation, contractile kinetics and metabolic perturbations associated with the development of force is identical to our previously published model (Callahan et al. 2013), unless noted otherwise. Experimental, in vivo data have been reported previously (Callahan et al. 2013; Lanza et al. 2007); all experiments from these studies were carried out in compliance with the Institutional Review Board at the University of Massachusetts Amherst and in accordance with guidelines set forth in the Declaration of Helsinki. All simulations were run using Matlab software (MathWorks, Natick, MA, USA).

The model presented here was parameterized using neural, contractile, bioenergetic and musculoskeletal data from a group of healthy young men (21–35 years old, n = 8; Callahan et al. 2013). Briefly, all steps in the forward integration routine in this model began with a single parameter meant to represent voluntary excitation (S; Fig. 1, step 1). This value serves as the input for a modelled pool of 60 MNs (Fig. 1, step 2), which closely follows a model by Fuglevand et al. (1993) and predicts a firing rate (FR) for each simulated neuron. A calcium transient model of activation follows (Fig. 1, step 3), providing input into a standard Hill muscle model (Fig. 1, step 4). Calculations related to the activation‐dependent fluctuation in metabolite concentrations are integrated with the muscle model to allow for prediction of the metabolic cost of contractions and return to homeostasis with rest. At each stage, this cellular bioenergetic model (Fig. 1, step 4a) interacts with the muscle model by affecting activation (Fig. 1, step 3). The linear sum of forces produced by all muscle models is input to a musculoskeletal model of the ankle joint and current joint torque (Tc) at the ankle is predicted (Fig. 1, step 5). Finally, Tc is compared with the ‘target’ torque, as defined a priori, at each point in time (Tt) for the duration of the fatigue protocol. A difference between Tc and Tt causes an increase or decrease of S such that the difference between Tc and Tt is minimized (Fig. 1, step 6). In this model, functions receive no input beyond initial conditions and Tt.

Figure 1. Computational approach and literature sources for model components .

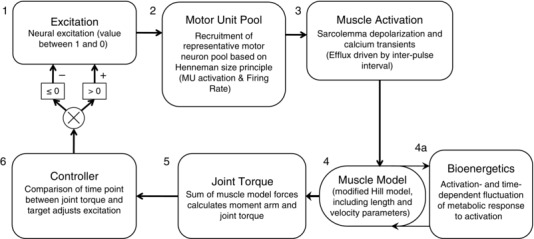
A control function (step 1) dictates excitation to a pool of 60 motor neurons (step 2). Each motor neuron is associated with corresponding fibre‐type‐specific muscle activation kinetics (step 3) and a Hill muscle model (step 4), whose function is modified by predicted concentrations of intracellular metabolites (step 4a). The sum of forces predicted by the Hill muscle models is used in a musculoskeletal model to predict joint torque (step 5), which is compared with a task defined a priori. The result of this comparison is then used to modify excitation (step 6). Abbreviation: MU, motor unit.

Fatigue model parameters

Derivation of the functions describing the control parameter (S), MN activation, force generation in Hill models representing multiple motor units, torque generation and bioenergetic cost have been described previously (Callahan et al. 2013). Additional functions, unique to the present model, were included to reflect the response of the previously published model to repeated activation in young adult males (Y‐Model). In addition, several components of the model were adjusted to reflect age‐related changes in neuromuscular function that have been identified as factors that might mediate the phenomenon of age‐related fatigue resistance; these adjustments to Y‐Model define the age‐adapted model (O‐Model). Differences between O‐Model and Y‐Model are given in Table 1 and described in relevant sections below. Additional differences between O‐Model and Y‐Model relating to neural activation and intracellular metabolism are indicated in Table 2.

Table 1.

Contractile properties and activation kinetics for young and age‐adapted versions of the model

Parameter	Model	MM1	MM60	Weighted average
F max (N)	Y‐Model	0.57	54.51	28.06
	O‐Model	0.53	50.73	26.11
V max (L ceo s−1)	Y‐Model	12.00	18.00	16.43
	O‐Model	12.00	15.75	14.84
τdeact (ms)	Y‐Model	92	64.6	70.2
	O‐Model	120	84.3	91.6
τact (ms)	Y‐Model	60	39	43.4
	O‐Model	60	45	48.2

Contractile element parameters are as follows: maximal force‐generating capacity (F _max); maximal shortening velocity (V _max); deactivation time constant (τ_deact); and activation time constant (τ_act). Data are presented for the young (Y‐Model) and old (O‐Model) parameters of the muscle model (MM). To illustrate the range within each variable across all MMs representing the 60 modelled motor units, values are shown for the first (MM₁) and last (MM₆₀) individual muscle models (step 4 in Fig. 1) within the overall model, along with their average, weighted by MM force‐generating capacity (F _max) in order to provide a relevant comparison with in vivo measures. L _ceo, optimal contractile element length.

Table 2.

Variable and parameter values

	Parameters	Model	MM1	MM60	Weighted Average
Intracellular metabolic variables	PCr (mm)	Y‐Model	38.6	38.6	38.56
		O‐Model	37	37	37.01
	Glycolytic capacity	Y‐Model	0.49	1.92	1.5
		O‐Model	0.24	0.95	0.7443
	pH	Y‐Model	7.01	7.01	7.01
		O‐Model	7.03	7.03	7.03
Intracellular buffering capacity (β)	${\beta }_{\mathrm{C}{\mathrm{O}}_2}$ (Slykes)	Y‐Model	11.8	11.8	11.8
		O‐Model	11.8	11.8	11.8
	βinherent (Slykes)	Y‐Model	5	5	5*
		O‐Model	15	15	15*
	${\beta }_{{\mathrm{P}}_{\mathrm{i}}}$ (Slykes)	Y‐Model	2.99	2.99	2.99
		O‐Model	4.09	4.09	4.09
Motor unit discharge rates	Peak firing rate (Hz)	Y‐Model	55.6	46	n.a.*
		O‐Model	44.6	35
	Minimal firing rate (Hz)	Y‐Model	8	8	n.a.*
		O‐Model	8	8

Values for intracellular metabolic, buffering and motor unit variables and parameters (latter denoted by *) for the range of muscle models (MM_1–60) meant to reflect motor units in young (Y‐Model) and older (O‐Model) neuromuscular systems. Values reflect those used at time = zero in all simulations. By definition, variables varied during the simulation, while parameters remained constant. The weighted average reflects the average of all MMs, scaled by MM force‐generating capacity, thus providing relevant comparison to in vivo measures.

Modelling intracellular bioenergetics, fatigue and recovery

Fatigue was dependent on the predicted accumulation of H₂PO₄ ⁻ through a negative, linear association between [H₂PO₄ ⁻] and activation (step 3; see eqn 3). This is meant to reflect the inverse relationship between [H₂PO₄ ⁻] and Ca²⁺‐mediated force generation observed in vitro (Nosek et al. 1987) and in vivo (Wilson et al. 1988; Kent‐Braun et al. 2002; Lanza et al. 2006). The model predictions for P_i accumulation were activation dependent. This rate was limited by the square root of the percentage of PCr remaining during contraction, as follows:

$${\left(\mathrm{PCr}/\mathrm{PC}{\mathrm{r}}_{\mathrm{rest}}\right)}^{0.5}$$ (1)

A model of glycolysis based on the Michaelis–Menten relationship between [P_i] and glycogen phosphorylase (Chasiotis et al. 1982) was used to predict the rate of proton generation from this metabolic pathway. The K _m of this relationship was assumed to be 18.94 mm (Chasiotis et al. 1982; Ren et al. 1988). Protons were produced from non‐oxidative glycolysis, consumed by the creatine kinase reaction (reflected by the rate of P_i accumulation) and buffered by several intracellular processes as previously described (Callahan et al. 2013).

Following each contraction in which modelled intracellular pH was more acidic than the initial value of 7.05, [H⁺] returned to baseline through a model representing the multiple processes that return postactivation intracellular pH to resting levels (predominately cellular efflux of [H⁺]). The calculation used to predict efflux was based on reported experimental values (van den Broek et al. 2007) and expressed mathematically by the following equation:

$$\mathrm{Efflux}=E_{\mathrm{rate}}\times {}^{-}\mathrm{p}{\mathrm{H}}^2$$ (2)

where E _rate was the linear rate constant for proton efflux (Kemp et al. 1997) and ^–pH was the difference between current pH and baseline pH.

Recovery of [P_i] to baseline following activation was modelled after our own experimental observations. In vivo, phosphorus magnetic resonance spectroscopy was used to monitor the recovery to baseline of [P_i] and [PCr] following contractions at multiple intensities in young and older men (Christie et al. 2014). Recovery rates of [P_i] and [PCr] were fit with a third‐order exponential decay or rise to maximum, for P_i and PCr, respectively. The first derivatives of these equations were used to calculate rates of change for [P_i] in the model.

Experimental observation revealed that the recovery kinetics of [P_i] depended on the extent of [PCr] depletion and was independent of pH at the end of the contraction. These effects were reflected in the model by coefficients that related the rate of recovery to the extent of P_i accumulation. Throughout the simulated contraction protocol, [H₂PO₄ ⁻] was calculated from [P_i] and pH at each time point, according to the following equation:

$${\mathrm{H}}_2\mathrm{P}{{\mathrm{O}}_4}^{-}={\mathrm{P}}_{\mathrm{i}}/\left(1+{10}^{\left(\mathrm{pH}-6.75\right)}\right)$$ (3)

The accumulation of [H₂PO₄ ⁻] limited force in the model and thus simulated fatigue by limiting voluntary excitation (S), and muscle activation (Act) to the motor unit recruitment and muscle models, respectively. These limits (ActLim) were based on literature values (Lanza et al. 2007) and expressed mathematically by the following equation:

$$ActLim=-0.022\times \left({\mathrm{H}}_2\mathrm{P}{{\mathrm{O}}_4}^{-}+1.05\right)$$ (4)

Modelling the motor neuron pool

The modelled pool of MNs was adjusted to reflect changes in discharge properties of α‐MNs of older adults. Peak firing rates for recruited MNs were reduced from 56 Hz in Y‐Model to 45 Hz (Rubinstein & Kamen, 2005). The range of peak firing rates across 60 simulated MNs was also limited from 10 to 8 Hz (Rubinstein & Kamen, 2005). The minimal firing rate was set to 8 Hz; activation thresholds were identical in Y‐Model and O‐Model. A more detailed explanation of the MN model is presented by Callahan et al. (2013).

Modelling activation kinetics

The equations defining activation and deactivation (i.e. Ca²⁺) kinetics were altered slightly from those previously based on He et al. (1991). Evidence for age‐related changes in activation kinetics has been described in rodents (Larsson & Salviati, 1989; Weisleder et al. 2006; Russ et al. 2014) and, to a lesser extent, in humans (Delbono et al. 1997; Lamboley et al. 2015). However, it is likely that the magnitude of age‐related changes in activation kinetics is relatively minor when compared with differences in kinetics between muscle fibres of different myosin heavy chain isoforms. It is likely that muscle fibre‐type‐dependent rates of calcium efflux (Calderon et al. 2009) may lead to an overall slowing of activation in older adults, based on their small shift towards a greater population of type I muscle fibres (Jakobsson et al. 1990). To reflect a fibre‐type‐dependent shift in activation kinetics, the average time constant for activation (60 ms) was not changed in O‐Model, but the 35% range of activation time constants was reduced to 25%. In contrast to the limited evidence for age‐related changes in activation kinetics, ample evidence supports the notion of prolonged deactivation in older muscle. Although the rate of calcium uptake from the cytosol varies by muscle fibre type (Stephenson & Williams, 1981), calcium resequestration within a given fibre type can be as much as 35% slower in older compared with younger human skeletal muscle (Hunter et al. 1999). This slowing of deactivation was described mathematically by Thelen (2003) and has been accomplished here by an increase in the average deactivation time constant from 92 (Y‐Model) to 120 ms (O‐Model). Further revision of the model included a 0.004 s increase of the ‘on’ transient period of the Ca²⁺ signal (from 0.023 to 0.027 s). This was done primarily to ensure that the model was capable of achieving complete activation, despite lower MN firing rates, and is consistent with in vivo data (Chung et al. 2007).

Modelling contractile kinetics

Several variables were altered in the O‐Model to reflect age‐related changes in contractile characteristics (Narici et al. 1991; Ng & Kent‐Braun, 1999), independent of activation (Ca²⁺) kinetics. These alterations are listed in Table 1. Contractile slowing has been observed in vivo (Narici et al. 1991; Allman et al. 2004; Tevald et al. 2010). Reduced rates of force development have been attributed to altered fibre‐type distribution (Larsson et al. 1997) and age‐related contractile slowing that occurs within fibres of the same type (Ochala et al. 2007). In our approach, this contractile slowing was expressed across the population of muscle models (MMs), each of which corresponds to and receives its activation signal from one of 60 MNs. These were co‐ordinated such that the MN recruited first corresponded to the slowest, least forcefully contracting muscle model, MM₁. Although MM₁ had similar maximal shortening velocities (V _max) to MM₁ in Y‐Model, V _max in the muscle model associated with the highest threshold MN (MM₆₀) was reduced by 12.5% compared with MM₆₀ in Y‐Model, based on previous reports (Thelen, 2003) and modified to yield adequate force fusion at relevant physiological firing rates (Fig. 2). Given that the range of force‐generating capacities assigned to these models was not linearly distributed, the overall V _max of all 60 muscle models was not equal to the arithmetic mean V _max of the models; rather, the overall V _max [expressed in terms of optimal contractile element lengths (L _ceo) per second] was weighted according to muscle fibre force‐generating capacity such that the model contributing the greatest force had the greatest influence on V _max. The V _max was 16.43L _ceo s⁻¹ in Y‐Model and 14.84L _ceo s⁻¹ in O‐Model.

Figure 2. Torque–frequency relationships in young and older men .

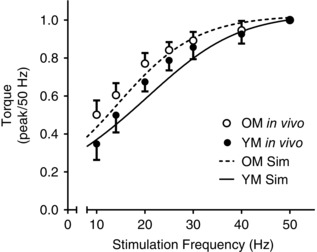
Comparison of experimental torque in response to electrical stimulation of the peroneal nerve with that simulated using the model. Experimental data are indicated by filled (young males, YM) and open circles (older males, OM) representing mean values ± SD at several frequencies. Continuous and dashed lines are five‐parameter sigmoid curves fitted to simulated torque predicted by the Y‐Model and O‐Model, respectively.

In addition to alterations made to the range of V _max across the contractile elements, maximal force‐generating capacity (F _max) was reduced by 4.6% for O‐Model. This alteration was based on a similar reduction in anterior compartment fat‐free muscle cross‐sectional area observed experimentally (Christie et al. 2014).

Simulation procedures and evaluation

The quality of the model excitation and contractile predictions in an aged neuromuscular system were evaluated by simulating a traditional force–frequency analysis in vivo, as described previously (Callahan et al. 2013). Briefly, a train of ‘stimuli’ was simulated by setting S = 1 for the first 0.029 s of the duration between subsequent MN firings (duration = 1/stimulation frequency) to mimic stimulation of the Ca²⁺ transient. This simulation was repeated for frequencies between 1 and 50 Hz in Y‐Model and O‐Model. The resulting force–frequency relationships were fitted by five‐parameter asymmetrical sigmoid functions (Prism; GraphPad Software, La Jolla, CA, USA) and compared with in vivo measures from the literature (Tevald et al. 2010).

To test the ability of the model to predict torque, activation and metabolic changes, a 12 s maximal voluntary contraction (MVC) was simulated using both models. In this case, Tt was set to 110% to ensure the Tc was always <Tt, thus producing maximal activation. A 180 s recovery period was simulated following this contraction to allow for testing of recovery dynamics in the model. The output from these simulations was then compared with in vivo data from older men to test the validity of metabolic predictions using the newly formulated model.

To test the ability of the model to predict fatigue, a simulation of six 12 s contractions was run using both Y‐Model and O‐Model. Each contraction was separated by 12 s of rest. This protocol was designed to match published data from our laboratory, which were used for the comparison of fatigue and intracellular metabolites in healthy young and older male cohorts (Lanza et al. 2007). To investigate further which properties of neuromuscular function had the most profound impact on predicted fatigue, multiple simulations were run in which single components of the model were altered and the results compared between Y‐Model and O‐Model. Specifically, equations describing activation‐dependent PCr depletion rate, PCr recovery following activation, inherent intracellular buffering capacity and activation‐dependent glycolytic flux were each exchanged between Y‐Model and O‐Model. Finally, to predict fatigue in ischaemic conditions, during which oxidative metabolism is negligible, simulations were run in Y‐Model and O‐Model for which the parameters predicting PCr synthesis between activations were excluded. Fatigue predicted by these latter simulations was compared with fatigue reported by Lanza et al. (2007), who used cuff occlusion to eliminate blood flow and thus the oxidative recovery of PCr between contractions. All simulations produced data for 135 s with 0.001 s time resolution.

Results

Y‐Model: fatigue

Metabolic perturbations from the Y‐model simulation and corresponding in vivo measures of a single 12 s MVC are illustrated in Fig. 3 A–C. Simulated depletion and recovery of intracellular metabolites compared well with in vivo measures (Lanza et al. 2006), in both rate and amplitude. Similar results were observed in the prediction of pH through the contraction and recovery cycle. Repeated voluntary contractions were simulated, and the responses of selected metabolites are illustrated in Fig. 4 A–C with corresponding in vivo observations (Fig. 4 D–F) for comparison (Lanza et al. 2007). The simulated fatigue response to repeated contractions showed strong concordance with in vivo results (Fig. 5 A; Lanza et al. 2006).

Figure 3. Simulated metabolic response to a 12 s maximal voluntary contraction .

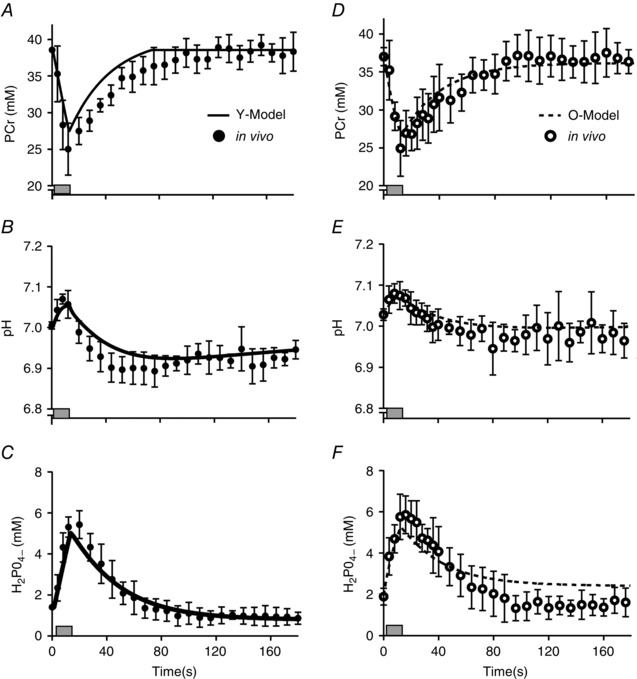
A–C, simulated data from Y‐Model (continuous line) are compared with in vivo observations in young men (filled circles; means ± SD); data are shown for PCr (A), pH⁺ (B) and H₂PO₄ ⁻ (C). D–F, the same data are provided for older men (open circles; means ± SD) and simulated by the O‐Model (dashed line). Shaded rectangles indicate duration of the contraction.

Figure 4. Simulated repeated maximal voluntary contraction protocol .

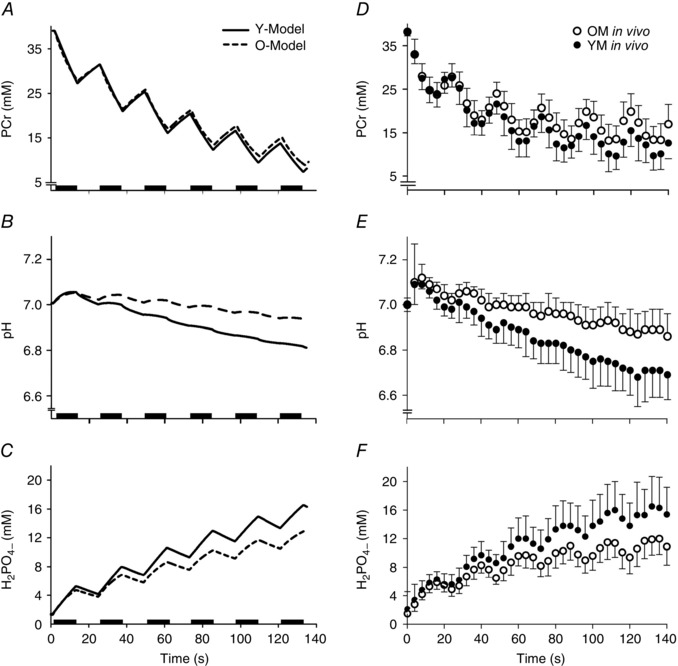
A–C, model output from a simulation of repeated maximal voluntary contractions reveals predicted metabolic responses of intracellular metabolites PCr (A), H⁺ (B) and H₂PO₄ ⁻ (C). Output from Y‐Model (continuous line) is compared with that from O‐Model (dashed line). D–F, experimental data (Lanza et al. 2007) for PCr (D), H⁺ (E) and H₂PO₄ ⁻ (F).

Figure 5. Fatigue predicted from model simulation .

A, fatigue predicted by the Y‐model (continuous line) is compared with previously published (Lanza et al. 2007) in vivo observations in young males (filled circles; means ± SD). B, corresponding data from O‐model (dashed line) are compared with previously published (Lanza et al. 2007) in vivo observations in older males (open circles; means ± SD).

O‐Model: activation and metabolic perturbation

Adjustments made to the model to reflect age‐related changes to activation and contractile characteristics were evaluated for accuracy by comparison with in vivo data (Tevald et al. 2010; Callahan et al. 2013). Comparisons were made by simulating a stimulation pattern meant to emulate neuromuscular stimulation at a range of discrete frequencies. The results from these simulations were compared with in vivo data from the literature for both young and older males (Tevald et al. 2010) and are illustrated in Fig. 2. Torque predicted from O‐Model was, in some instances, below observed torque, but within 1 SD of nearly all measured values. Compared with Y‐Model, simulations from O‐Model demonstrated a leftward shift in the torque–frequency relationship, as is reported in studies of the effects of age on the force–frequency relationship (Narici et al. 1991; Tevald et al. 2010).

A simulation of the metabolic responses to a single 12 s MVC using O‐Model are illustrated in Fig. 3 D–F. As with Y‐Model, bioenergetic perturbation and restitution to baseline values for intracellular metabolites agreed well with previously published in vivo measures (Lanza et al. 2007) and unpublished observations from the same data set. A slight over‐prediction of [H₂PO₄ ⁻] was observed following the contraction (Fig. 3 F), although this may have been an artifact of the spectroscopy measure itself (see Discussion). The simulated bioenergetic response to repeated MVCs predicted by O‐Model are illustrated in Fig. 4 D–F and agree well with in vivo data from the literature (Lanza et al. 2006, 2007; Larsen et al. 2009; Christie et al. 2014), demonstrating reduced acidosis and accumulation of H₂PO₄ ⁻ when compared with Y‐Model and similar PCr depletion (Fig. 4).

O‐Model: age‐related fatigue resistance

The magnitude of fatigue predicted by both models was consistent with in vivo measures (Lanza et al. 2007), as illustrated in Fig. 5 A and B. Comparison of O‐Model with Y‐Model revealed less fatigue in O‐Model (81.1% of initial) than that predicted by Y‐Model (75.2% of initial). This level of fatigue and degree of age‐related resistance agree well with earlier in vivo work using a similar protocol (Lanza et al. 2006, 2007; Chung et al. 2007).

Multiple simulations were run to compare the fatigue response in Y‐Model and O‐Model, with parameters related to glycolytic flux, metabolic cost of contraction and inherent buffering capacity switched between them to investigate the relative impact of each parameter on the fatigue response without altering other age‐related differences. The fatigue predictions for each simulation are presented in Table 3. Although each parameter compared in these analyses affected the fatigue prediction to some extent, switching the parameters that estimated glycolytic flux had the greatest impact on predicted fatigue in Y‐Model and O‐Model. This parameter switch resulted in lesser and greater fatigue predicted from Y‐Model and O‐Model, respectively (Table 3). Switching the rate of P_i recovery between models, such that rate of P_i recovery was reduced in Y‐Model and increased in O‐Model, had the expected result of increasing fatigue in Y‐Model and decreasing fatigue in O‐Model. Changes to inherent buffering capacity and the cost of contraction (rate of PCr depletion) resulted in minimal changes to overall fatigue predicted in both Y‐Model and O‐Model. Finally, eliminating the capacity to resynthesize PCr between activations, thus simulating ischaemia, increased fatigue predicted in both models. These predictions were consistent with in vivo results previously reported by our group (Lanza et al. 2007). In the case of O‐Model, the predictions of fatigue were within 0.1% of the in vivo observation.

Table 3.

Fatigue results from in vivo observations and model simulations

Fatigue (% initial TTI)
	Lanza et al. (2007)		Standard model		Parameter switch
		In vivo		Simulated	Inherent buffering	Activation‐dependent	Pi recovery	Glycolytic
Model	In vivo	(ischaemic)	Simulated	(ischaemic)	capacity	Pi kinetics	kinetics	flux
Y‐Model	75.1	62.8	75.2	67.5	76.1	76.0	73.0	80.0
O‐Model	84.1	76.0	81.1	75.9	80.4	80.4	82.2	77.1

Fatigue data from in vivo observations (Lanza et al. 2007) and multiple simulations performed by Y‐Model and O‐Model. Fatigue is presented as the time tension integral (TTI) of the last contraction, expressed as a percentage of the TTI of the first contraction. In standard simulations, model parameters were assigned as described in the Methods. In simulations indicated by the ‘parameter switch’ column, the model component indicated in the subheading was altered in Y‐Model to match the corresponding component in O‐Model and vice versa. Simulations were run for all models, and fatigue was calculated as described in the Methods. Switching the glycolytic parameters was the only approach to reverse the prediction of age‐related fatigue resistance fully.

Discussion

Simulations generated by our model and presented here suggest that although multiple age‐related changes in neuromuscular function contribute to fatigue, lesser reliance on glycolytic metabolism is the greatest single factor explaining the phenomenon of age‐related fatigue resistance. The simulations presented here are the first to predict the intracellular bioenergetic responses and subsequent fatigue during repeated isometric contractions in vivo, while presenting accurate activation and contractile kinetic components reflective of the neuromuscular systems of young and older adults.

Although previous models have been developed successfully to capture the effects of age on activation and contractile function (Thelen, 2003; Hasson et al. 2009, 2011) and others have predicted fatigue during prolonged or repeated contractions (Rohmert, 1960; Levin & Mizrahi, 1999; Ding et al. 2000; Xia & Frey Law, 2008; Dideriksen et al. 2011), ours is the first model to do both simultaneously. This approach is necessary to interrogate the multiple potential contributors to fatigue resistance and, ultimately, to estimate their relative contribution to the overall neuromuscular behaviour. Simulations produced by O‐Model and Y‐Model predicted age‐related differences in metabolic variables implicated in fatigue resistance. Comparisons with in vivo data confirm the predictions made using these models and support their use as predictive tools to measure the relative impact of specific physiological variables on neuromuscular fatigue. These claims are substantiated by additional simulations that demonstrate the adaptability of the present model; namely, the ability to predict fatigue in ischaemic conditions.

Predictions of voluntary and stimulated force

Predicted voluntary force during a single 12 s contraction agreed with in vivo observation for both Y‐Model (within 0.2% of in vivo observation; Callahan et al. 2013) and O‐Model (within 3.9% of in vivo observation; Christie et al. 2014). The kinetics of force generation and relaxation in Y‐Model and O‐Model were demonstrated via simulation of torque–frequency relationships and compared with in vivo observation (Fig. 2). These comparisons confirmed accurate reproduction of torque output with increasing stimulation frequency, as well as the age‐related leftward shift in the torque–frequency relationship. These relationships are important in the context of fatigue prediction because the limits (ActLim) on stimulation (S) in the model will decrease motor unit discharge rates and thus reduce force production in a manner consistent with in vivo observations (Rubinstein & Kamen, 2005).

Age‐related fatigue resistance

The present models demonstrate both accuracy and flexibility by predicting age‐related fatigue resistance as well as metabolic responses to relatively brief, maximal activation patterns. The declines in peak torque over the entire sequence of contractions were especially well predicted for both Y‐Model and O‐Model (Fig. 5). It is worth noting, however, that fatigue within each simulated contraction was relatively less than that observed in vivo. This within‐contraction discrepancy could not be resolved unless model parameter values were adjusted such that intracellular metabolic predictions were well outside the range of in vivo observation. In addition, these parameter adjustments yielded simulations with less accurate fatigue predictions across the entirety of the contraction protocol. Given the necessary simplification inherent in any computational model, the lesser rate of fatigue within contractions is likely to reflect one or more secondary factors (altered Ca²⁺ sensitivity or membrane excitability) that, while not explicitly represented in the present model, nevertheless contribute to fatigue in vivo. Although there would be trade‐offs associated with adding to the complexity of the model, identifying these factors and their relative contributions could be fruitful targets for future extensions of the model.

An important aspect of this study is the result of simulations in which components of one model were substituted with the other in order to evaluate their impact on age‐related fatigue resistance. As shown in Table 3, our model suggests that a greater reliance on glycolytic ATP production has the greatest impact on differences in fatigue predicted by Y‐Model and O‐Model. This observation is consistent with previous hypotheses related to fatigue resistance in ageing (Kent‐Braun et al. 2002; Lanza et al. 2005, 2007). However, our predictions are in apparent contrast to investigations suggesting that oxidative metabolism and metabolic economy explain the most variation in fatigue (Nakagawa et al. 2005; Sirikul et al. 2007). In our models, substituting the P_i kinetics during activation (an index of metabolic cost of contraction) of O‐Model with those of Y‐Model did little to increase glycolytic flux in O‐Model. Therefore, we performed a simulation inspired by published in vivo work from our laboratory (Lanza et al. 2007), in which PCr recovery was inhibited. It was expected that in O‐Model, increased glycolytic flux would result in greater fatigue during ischaemia. These simulations, in which PCr recovery was inhibited in order to mimic contractions in ischaemic conditions, were consistent with experimental results where fatigue (and glycolytic flux) increased substantially compared with conditions in which PCr was allowed to recover. As with the experimental data, simulated fatigue in O‐Model remained less than the fatigue generated by Y‐Model in the same conditions. Interestingly, fatigue within each simulated contraction in conditions of no PCr recovery (i.e. modelled ‘ischaemic’ conditions) was closer to in vivo observations than predictions for contractions in which PCr recovery was not inhibited (i.e. modelled ‘free‐flow’ conditions; data not shown). This result suggests that blood flow may be one potential source of the modest discrepancy between in vivo and simulated within‐contraction fatigue. Overall, these simulations provide further support for the notion that a greater reliance on glycolysis is the greatest single contributor to the phenomenon of age‐related fatigue resistance.

It is important to note that non‐oxidative glycolytic flux itself does not directly cause fatigue but instead produces H⁺, thus facilitating the formation of H₂PO₄ ⁻ by combination with P_i. Accumulation of H₂PO₄ ⁻ has been suggested to limit force‐generating capacity. The precise mechanisms by which these metabolic byproducts influence fatigue include altered Ca²⁺ sensitivity (Debold et al. 2013), inhibition of excitation–contraction coupling (Lee & Allen, 1991) and reduced force production by actin–myosin cycling (Debold et al. 2008). Our model is not designed to determine which of these mechanisms ultimately causes fatigue, but experimental evidence (Nelson et al. 2014) and models specifically formulated to investigate fatigue at the cross‐bridge level (Shorten et al. 2007) suggest that elevated [H⁺] and [P_i] are likely to have additive effects that both reduce force at the cross‐bridge and inhibit Ca²⁺ sensitivity. Our approach, which uses a Hill‐type model of muscle contraction, was not developed at the scale necessary to investigate fatigue at the level of the sarcomere. Instead, we focused on factors contributing to altered neural activation and intracellular environment and suggest that, among the myriad differences between the neuromuscular systems of young and older adults, a tendency for the young to rely on the glycolytic provision of ATP is the greatest contributor to age‐related differences in acute neuromuscular fatigue.

Methodological considerations

A number of methodological decisions were necessary during the development of this model, and these decisions should be considered when interpreting its results. Values for the parameters incorporated into the model and used to predict metabolic and contractile behaviour fall within the range of in vivo data available from the literature and our own unpublished observations. However, these measures will vary between individuals, and some may depend on factors other than age, such as muscle group or habitual patterns of use (Larsen et al. 2009). In addition, in vivo measures of the intracellular environment depend on multiple factors, not all of which can be quantified precisely. These include, but are not limited to, calcium concentration, buffering capacity and resting metabolic rate. Therefore, our range of inputs were meant to reflect what is currently known about the range of various physiological characteristics and will best reflect group mean responses rather than individual subject characteristics. Likewise, errors in any model can offset one another and lead to reasonable predictions through flawed means. However, the process of developing this phenomenological model included systematic, stepwise comparisons of model output and experimental data at each step (Fig. 1). These comparisons indicated that our inputs produced predictions that were consistent (<2 SD variance in all cases, and <1 SD in the vast majority) with the in vivo functions they were meant to represent. Finally, an advantage of the modular approach taken here is that individual parameters may be revised independently, thus allowing evaluation of the impact of each on force and fatigue.

An explicit prediction of oxidative ATP production is absent from our model. Instead, the contribution of oxidative metabolism to ATP production during contraction and the PCr resynthesis during recovery are implied by predictions of PCr and P_i kinetics, as PCr synthesis following contraction is accomplished primarily via oxidative phosphorylation (Quistorff et al. 1993). At the same time, production of H⁺ by oxidative metabolism during PCr synthesis following contraction is accounted for in our model. In the simulations presented here, our model provided predictions of metabolic changes entirely consistent with in vivo measures (Kent‐Braun et al. 2002; Lanza et al. 2007).

Despite our attempts to incorporate a wide range of physiological components that might influence fatigue, the complexity of the model does not approach that of the human neuromuscular system. As with all computational models, the interest in fully describing complex relationships was balanced with necessary simplification of computational aspects for which precise experimental descriptions are unavailable. For example, variations in age‐related changes to central activation can be found in the literature, with some finding greater failure in older subjects (Bilodeau et al. 2001; Stackhouse et al. 2001) and others reporting minimal or no difference (Chung et al. 2007; Mademli & Arampatzis, 2008 a; Callahan & Kent‐Braun, 2011). The same can be said of inherent buffering capacity (Parkhouse et al. 1985; Lanza et al. 2005), which itself is difficult to measure directly. Future incarnations of the present model might be adapted to include varying degrees of central activation failure, motor unit behaviour, fibre‐type changes, inherent buffering capacity and control of oxidative metabolism. Although the present model was constrained to isometric contractions, it can easily be extended to simulate dynamic contractions in future work.

Finally, the contributions of altered Ca²⁺ sensitivity, excitation–contraction coupling and reduced actin–myosin cycling to fatigue are implicit components in this model but do not have explicit mathematical representations in the model formulation. This limits our ability to interrogate the relative contribution of these sites to fatigue. A multiscale model incorporating both musculoskeletal and sarcomeric representations, which has been a persistent challenge in the field, has recently been addressed (Röhrle et al. 2012; Mordhorst et al. 2015). Although these studies addressed different experimental questions from those we have focused on in the present study, our future efforts may benefit from these examples.

Future directions

The present model has been parameterized to represent the function of healthy, physically active younger men, as well as a group of healthy, relatively sedentary older men. The inputs to the model used to characterize these subject groups can be adapted to represent other populations without significant alterations to the computational approach. Clinical populations characterized by altered neural function (multiple sclerosis), cellular metabolism (McCardle's disease or diabetes) or skeletal muscle atrophy (cancer or human immunodeficience virus) could be investigated with the present version of the model simply by changing the model parameter values. The model could also be applied to questions of sex‐specific differences in fatigue or provide expectations for altered fatigue characteristics following disuse or exercise training.

Conclusion

We have presented a novel computational model that accurately predicts fatigue in response to MVC in humans. This model was used to perform simulations, and the results indicate that a greater reliance on glycolytic phosphorylation in younger men is the greatest single contributor to the phenomenon of age‐related fatigue resistance during isometric contractions. Perhaps most importantly, in establishing the utility of this model, we provide a valuable tool that can be used to guide study design and further our understanding of human neuromuscular function.

Additional information

Competing interests

None declared.

Author contributions

D.M.C. and B.R.U.: conception and design; provision of study materials or patients; collection and assembly of data; data analysis and interpretation; and manuscript writing. J.A.K.: conception and design; financial support; administrative support; provision of study materials or patients; data analysis and interpretation; and manuscript writing. All authors have approved the final version of the manuscript and agree to be accountable for all aspects of the work. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

This work was supported by Office of Extramural Research, National Institutes of Health grants R01 AG21094 (to J.A.K.) and K02 A6023582 (to J.A.K.).