Automated, quantitative measures of grey and white matter lesion burden correlates with motor and cognitive function in children with unilateral cerebral palsy

Abstract

White and grey matter lesions are the most prevalent type of injury observable in the Magnetic Resonance Images (MRIs) of children with cerebral palsy (CP). Previous studies investigating the impact of lesions in children with CP have been qualitative, limited by the lack of automated segmentation approaches in this setting. As a result, the quantitative relationship between lesion burden has yet to be established. In this study, we perform automatic lesion segmentation on a large cohort of data (107 children with unilateral CP and 18 healthy children) with a new, validated method for segmenting both white matter (WM) and grey matter (GM) lesions. The method has better accuracy (94%) than the best current methods (73%), and only requires standard structural MRI sequences. Anatomical lesion burdens most predictive of clinical scores of motor, cognitive, visual and communicative function were identified using the Least Absolute Shrinkage and Selection operator (LASSO). The improved segmentations enabled identification of significant correlations between regional lesion burden and clinical performance, which conform to known structure-function relationships. Model performance was validated in an independent test set, with significant correlations observed for both WM and GM regional lesion burden with motor function (p < 0.008), and between WM and GM lesions alone with cognitive and visual function respectively (p < 0.008). The significant correlation of GM lesions with functional outcome highlights the serious implications GM lesions, in addition to WM lesions, have for prognosis, and the utility of structural MRI alone for quantifying lesion burden and planning therapy interventions.

Graphical abstract

Highlights

• •Presents an automated lesion segmentation approach tailored to cerebral palsy
• •Demonstrates the utility of quantifying lesions from MRI
• •Illustrates the influence that grey matter lesions have on functional impairments

1. Introduction

Cerebral palsy (CP) is an umbrella term that covers a heterogeneous range of brain injury occurring during prenatal or perinatal development, leading to physical disability (Himmelmann and Uvebrant, 2011). Of these injuries, destructive lesions are the most common, with periventricular white matter (WM) lesion observed in around 50% of children with CP and cortical/subcortical grey matter (GM) lesions in approximately 20% (Bax et al., 2006, Krägeloh-Mann and Horber, 2007, Reid et al., 2014) of cases. Magnetic resonance imaging (MRI) is a useful imaging procedure that is commonly used in clinical assessment for identifying and qualitatively characterising brain lesions, as both WM and cortical/deep GM lesions appear as regions of abnormal intensity and/or loss of tissue. Although GM lesions are less common, they may diffusely or more selectively impact critical structures of the brain including the basal ganglia, thalami and cortical GM, and lead to more severe impairments of several functions, in particular motor function (Martinez-Biarge et al., 2010).

Despite the known negative prognostic implications of tissue lesions, the extent of the relationship between regional lesion burden and clinical function has yet to be quantified. This is of particular interest, as these relationships can help provide estimates of function from MRIs early in life, guiding therapeutic strategies for these children. For instance, such information can confirm whether lesion burden in specific brain regions lead to greater impairments to motor function, hence recommending more intensive therapeutic interventions. Hence, this study aims to quantify the correlation between the lesion burden in individual regions and multiples clinical scores which quantify motor, cognitive, communicative and visual function. The study considers both GM and WM lesions solely based on tissue involvement, independent to the timing of the lesion (Krägeloh-Mann and Horber, 2007). Further these WM and GM involvements are considered separately, as it has been previously shown their impact on function differs (Krägeloh-Mann and Horber, 2007, Martinez-Biarge et al., 2010).

For the correlation between structure and function to be calculated, all lesions within large sets of data need to be delineated in three dimensions. Such an approach can be made practical by utilising an automated segmentation algorithm. The field of lesion segmentation is well researched, particularly in the multiple sclerosis (MS) setting. Although multiple reviews have been published discussing various lesion segmentation approaches (García-Lorenzo et al., 2013, Lladó et al., 2012), no studies as yet have performed automated lesion segmentation in the CP setting. This may be due to the comparatively large morphological changes observed in children with CP, which invalidate the anatomical assumptions existing algorithms typically make, resulting in poor segmentation performance.

Hence this study used a modified segmentation method to quantitatively assess the functional impact of brain lesion involvement. As the method incorporates multiple lesion classes in order to automatically segment both WM and GM lesions, this study, to our knowledge, presents the first published quantitative assessment of functional impairment caused by GM lesion involvement in children with CP. In this approach, atlases were used to subdivide the GM regions into individual cortical and subcortical regions, and WM regions into regions with particular WM tracts. Regional WM and GM lesion burdens were computed, and used to predict clinical function using multivariable linear regression. Such approaches could have clinical utility as they can support the radiological assessment of MRIs, and help to tailor treatment strategies for children with CP. A particular advantage of the method is that it only relies on standard structural MRIs and does not resort to more sophisticated sequences that may not be widely available.

2. Materials and methods

2.1. Participants

A total of 125 participants were included in this study: 107 children diagnosed with unilateral CP (57 male, 50 female, mean age: 10.9, age range: 7–16), and 18 children with healthy development (CHD) with (8 male, 10 female, mean age: 11.4, age range: 7–16) were included. Image data was obtained from The University of Queensland Cerebral Palsy and Research Rehabilitation Centre (QCPRRC), Brisbane, and the Stella Maris Foundation, Pisa. Study participants included children who were recruited as part of ongoing studies of children with unilateral CP (Boyd et al., 2013). Diagnoses were made based on clinical assessments by experienced practitioners in the field of CP. Ethics approval was granted for both studies from the appropriate ethics committees. Informed parental consent was obtained for all participants included in these studies.

2.2. MRI data acquisition

All participants underwent T1 Magnetization Prepared Rapid Gradient Echo (MPRAGE) scanning, using two different scanners and three different sets of scanning parameters, including a 3T Siemens' scanner with scanning parameters (TR = 1900 ms, TE = 2.32 ms, flip angle = 9°, slice thickness = 0.9 mm), and a 1.5T GE scanner with two different scanning parameters (TR = 12.36 ms, TE = 5.17 ms, flip angle = 13°, slice thickness = 1 mm) and (TR = 124.29 ms, TE = 4.37 ms, flip angle = 10°, slice thickness = 1 mm). All participants also underwent T2 Turbo Inversion Recovery Magnitude (TIRM) scanning, using a 3T Siemens' scanner (TR = 7000 ms, TE = 79 ms, flip angle = 120°, slice thickness = 4 mm).

2.3. Clinical data

Six clinical scores of function were obtained as part of the data collection study to provide an overview of function. This includes the Assisting Hand Assessment (AHA) score (Krumlinde-Sundholm et al., 2007) quantifying the ability of the impaired hand to assist during bimanual activities. Although not a measure of gross motor function, the Rasch measured AHA score was used for several reasons. Firstly, this score has a has a wide dynamic range (from 0 to 100) making it more suitable for regression analyses compared to the Gross Motor Function Classification System (GMFCS), which only has five levels. Furthermore, most study participants had a GMFCS level of either I or II, making the measure of upper limb manual ability more relevant for this cohort. Finally, this measure has been shown to be a reliable and responsive measure for children with unilateral CP (Krumlinde-Sundholm et al., 2007). Other measures include the Behaviour Rating Inventory of Executive Function (BRIEF) (Gioia et al., 2002) and Strengths and Difficulties Questionnaire (SDQ) (Bourdon et al., 2005) which are both parent reported questionnaires scoring their child's emotional and behavioural function in daily life, the Test of Visual Perception Skills (TVPS) measure (Frostig et al., 1961) for assessing participants' ability to discriminate and memorise visual cues, and the vocabulary (VOC) and word reasoning (WR) subtests of the Wechsler Preschool and Primary Scale of Intelligence (WPPSI-III) (Wechsler, 1967) to assess participants' communicative ability.

2.4. Image pre-processing

Image pre-processing of both the T1-MPRAGE and T2-TIRM images included N4 bias correction (Tustison et al., 2010), image alignment to the Colin 27 Average Brain Atlas using an affine block matching registration algorithm (Rivest-Hénault et al., 2015), and image de-noising using anisotropic diffusion (Perona and Malik, 1990). Skull stripping of the MPRAGE and TIRM images was performed in MATLAB (MathWorks, Natick, MA) using an in-house approach. Tissue probability maps (TPMs) from the Colin 27 Atlas and ICBM DTI-81 Atlas (International Consortium for Brain Mapping, CA) were registered to the T1-weighted MRIs using the fast free-form deformation registration algorithm (Modat et al., 2010).

2.5. Lesion segmentation

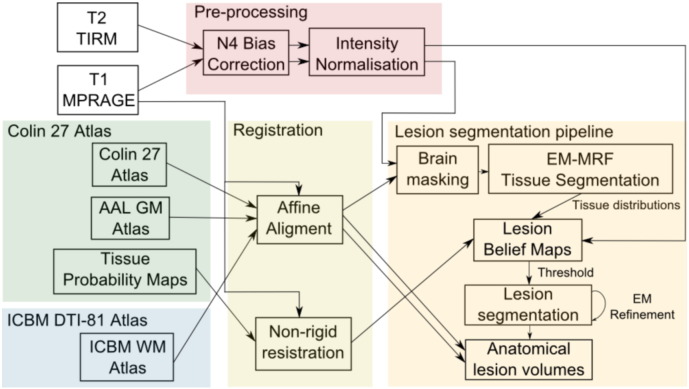
We present an automated lesion segmentation approach tailored specifically for WM and GM lesion involvement in children with CP. Segmentation of the three cerebral tissues (WM, GM and CSF) was initially performed using an Expectation Maximisation (EM) approach interleaved with a modified Markov Random Field (MRF) formulation that penalises discordance between boundaries in the label image and in the MRI (Pagnozzi et al., 2015). This automated pipeline is illustrated in Fig. 1.

Fig. 1.

An illustration of the lesion segmentation pipeline used in this study. Following pre-processing and an affine alignment to the Colin 27 atlas, the T1-MPRAGE undergoes brain masking and tissue segmentation steps. The tissue distributions obtained from this segmentation, along with the pre-processed T2-TIRM and non-rigidly registered Tissue Probability Maps (warped to the T1-MPRAGE), were used to construct lesion belief (probability) maps. Following thresholding, lesion segmentations were refined with the EM algorithm. Using the AAL GM and ICBM WM atlases, which were similarly aligned to the Colin 27 atlas (and by extension, the T1-MPRAGE), anatomical lesion volumes were extracted to use for the statistical analysis.

Initial lesion belief maps for each of the three types of lesions; WM lesions, GM lesions and internal capsule (IC) lesions were generated using the final estimates of tissue distributions obtained from the EM-MRF approach, the aligned T2-TIRM image and the registered WM and GM tissue probabilistic atlases. Denoting the T1-MPRAGE containing n voxels as y = {y_i, i ∈ [1 : n]}, the T2-TIRM as x = {x_i, i ∈ [1 : n]}, the registered TPMs of the WM, GM and CSF, and the parameterised Gaussian mean and standard deviation for each of the three tissue classes as Φ_k = (μ_k, σ_k), where k ∈ {WM, GM, CSF}, the formulae for the three lesion belief maps lb = {lb_i, i ∈ [1 : n]} is given in Eqs. (1), (2), (3).

$$l{b}_{\mathit{WML},i}=\mathit{abs}\left(\frac{y_i-{\mu }_{\mathit{WM}}}{{\sigma }_{\mathit{WM}}}\right)\cdot x_i\cdot \mathit{TP}{M}_{\mathit{WM},i}$$ (1)

$$l{b}_{\mathit{GML},i}=\mathit{abs}\left(\frac{y_i-{\mu }_{\mathit{GM}}}{{\sigma }_{\mathit{GM}}}\right)\cdot x_i\cdot \mathit{TP}{M}_{\mathit{GM},i}$$ (2)

$$l{b}_{\mathit{ICL},i}=\mathit{abs}\left(\frac{y_i-\left({\mu }_{\mathit{WM}}+{\sigma }_{\mathit{WM}}\right)}{{\sigma }_{\mathit{WM}}}\right)\cdot x_i\cdot \mathit{TP}{M}_{\mathit{WM},i}$$ (3)

In each equation, abnormal tissue outliers were identified using an absolute z-score from the mean and standard deviation of the WM and GM distributions established in the EM-MRF segmentation. Note in Eq. (3), IC lesions are segmented separately to WM lesions because the IC typically appears as a higher intensity in structural MRI, and was assumed to be 1 standard deviation above the mean WM intensity. This ensures the detection of IC lesions, which approach healthy WM intensity and hence would not be detected in the lesion belief map for WM shown in Eq. (1). Unlike the T1-MPRAGE, the T2-TIRM was normalised in intensity between 0 and 1, where the most hyperintense regions are characteristic of hemorrhagic injuries.

A threshold, t_thresh, is applied to each of the three lesion belief maps. Using the 75% training set, a Receiver Operator Characteristic (ROC) curve was used to establish which threshold for WM and GM lesions agreed best with the manual classification of lesions. Specifically, the Equal Error Rate (EER), which enforces equal importance to false positives and false negatives, was used to determine the optimal thresholds for the WM and GM lesion belief maps separately, which were found to be t_{thresh , WM} = 0.85 and t_{thresh , GM} = 0.875. These thresholds were used to test the performance of the lesion segmentation algorithm on the independent test set.

Provided more than one voxel exceeds the WM or GM thresholds, the initial lesion segmentation was refined using an EM approach. The mean and standard deviation of the lesion T1 intensity were obtained for the likely lesion voxels, and introduced as an additional lesion classes along with the three healthy tissue classes obtained from the EM-MRF segmentation. Tissue classes were then updated within the EM algorithm, with the lesion intensities modelled as a Gaussian distribution. The probability of the lesion class was weighted by the TIRM intensity, while the probability of the three healthy tissue classes was weighted by the inverse of the TIRM intensity (i.e. 1 − TIRM). The tissue probability maps also weight the posterior probability of each segmented class. The likelihood of each lesion class for the three lesion classes (WM, GM and IC) is given in Eq. (4), e.g. for the WM lesion class:

$$p_{\mathit{WML},i}=\mathit{exp}\left[-{\left(\frac{y_i-{\mu }_{\mathit{WML}}}{{\sigma }_{\mathit{WML}}}\right)}^2\right]\cdot x_i\cdot \mathit{TP}{M}_{\mathit{WM},i}$$ (4)

The likelihood of the healthy tissue classes (WM, GM and CSF) are computed using Eq. (5), e.g. for the WM:

$$p_{\mathit{WM},i}=\mathit{exp}\left[-{\left(\frac{y_i-{\mu }_{\mathit{WM}}}{{\sigma }_{\mathit{WM}}}\right)}^2\right]\cdot \left(1-x_i\right)\cdot \mathit{TP}{M}_{\mathit{WM},i}$$ (5)

This segmentation refinement step is performed separately for WM lesions, GM lesions and IC lesions, yielding separate lesion segmentations in each instance. Hence the classification of GM and WM lesions is obtained automatically from this approach, and allows identification of both lesion types in the same participant. Post-processing of these lesion segmentations consists of a flood fill operation and morphological closing.

2.6. Anatomical lesion volume

Anatomical and regional involvement of the segmented lesions was computed using the Automated Anatomical Labelling (AAL) atlas, which contains cortical and deep GM labels, and the ICBM DTI-81 Atlas which contains WM tract labels. Both atlases were aligned to the same image space as the Colin 27 atlas (Rivest-Hénault et al., 2015). Lesion involvement in each region was then computed as the sum of the lesion segmentation masked by the particular atlas label, multiplied by the known volume (in mL) of each voxel, providing a regional lesion burden in millilitres.

2.7. Statistical analysis

Participants were separated into four cohorts, the CHD children and children with WM (including IC lesions), GM lesions, or combined WM/GM lesions. Children with combined WM/GM lesions were grouped into either WM or GM cohorts for the regression analysis, based on which tissue lesion burden was greater in each participant. Both WM and GM lesion cohorts were randomly separated into 75%/25% training and test sets. In the training set, data-driven variable selection was performed using the Least Absolute Shrinkage and Selection operator (LASSO) method (Tibshirani, 1996) obtained from the ‘glmnet’ package in R statistical software Version 3.2.2, which implicitly performs variable selection with a sparsity term that minimises the sum of non-zero coefficients. LASSO was run with default alpha and lambda parameters, and the upper boundary on the regression coefficients was manually set to zero in order to enforce negative coefficients. Linear regression models were then constructed, using the regional volumes of the WM and GM lesions (in mL) identified from LASSO as independent variables, as well as participant age and gender, and the six clinical scores (AHA, BRIEF, SDQ, TVPS, WR and VOC) as the dependent variable. Multiple comparisons were corrected for using Bonferroni correction. Model residuals were normally distributed for each of the independent outcomes. To assess the generalisability of these models to unseen data, training model performance was validated via correlation between model predictions and the test set outcomes. Additionally, regression models including both WM and GM regional lesion volumes were constructed using the training set, with their performance again validated with the test set. Model comparisons between the WM and GM models, and the WM/GM combined model, were performed using Analysis of Variance (ANOVA), to determine if it is beneficial to consider both lesion types.

3. Results

3.1. Demographics information

The demographics of the four cohorts; the CHD children, those with WM (and/or IC) involvement, GM involvement, and those with combined WM/GM involvement, are presented in Table 1. There was a gender bias observed in both the CHD and WM lesion cohorts. The AHA score, and a measure of global brain injury severity provided from a manual template approach (Fiori et al., 2015), is provided for each cohort, split into those with unilateral and bilateral injury. Only children with WM lesions had observed bilateral injury, which was reflected in the reduced AHA score compared to children with unilateral WM injury. The five children with solely GM lesions had the greatest amount of observed injury from the MRI, with the highest injury severity score of all cohorts. These children, consequently, also had the poorest motor outcomes of all cohorts. Children with unilateral, combined WM/GM injury had similar measures of injury severity and similar AHA motor outcome to those children with bilateral WM lesions.

Table 1.

Demographic characteristics for the CHD children, WM lesion cohort and the GM lesion cohort. For the CHD cohort, information of lesion laterality is not applicable, and their clinical scores were not obtained.

Cohort	CHD cohort	WM lesion	GM lesion	Combined WM/GM
Number of participants	18	80	5	22
Gender
Male	8	40	4	13
Female	10	40	1	9
Age at scan (years)
Mean ± standard deviation	11.42 ± 3.03	11.38 ± 2.92	11.80 ± 1.92	10.54 ± 2.65
Range (minimum–maximum)	7–16	5–17	9–14	6–15
Number with unilateral lesions	NA	55	5	22
Global brain injury severity score (Fiori et al., 2015)
Mean ± standard deviation	0.00 ± 0.00	8.34 ± 5.12	14.00 ± 5.20	9.85 ± 5.64
Range (minimum–maximum)	0–0	2.5–20	9–21	2–20
Assisted Hand Assessment (AHA) Score
Mean ± standard deviation	NA	75.58 ± 20.05	52.60 ± 31.30	64.61 ± 24.78
Range (minimum–maximum)	NA	41–98	26–95	24–98.8
Number with bilateral lesions	NA	25	0	0
Global brain injury severity score (Fiori et al., 2015)
Mean ± standard deviation	0.00 ± 0.00	8.43 ± 4.79	NA	NA
Range (minimum–maximum)	0–0	1–18.5	NA	NA
Assisted Hand Assessment (AHA) Score
Mean ± standard deviation	NA	64.21 ± 19.04	NA	NA
Range (minimum–maximum)	NA	8–97	NA	NA

CHD, children with healthy development; GM, grey matter; NA, not available; WM, white matter.

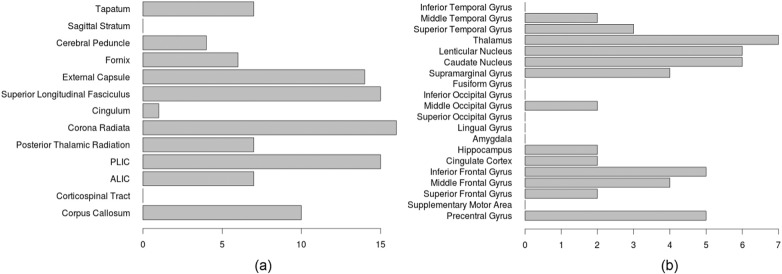
Lesion burden frequency was also investigated across the entire cohort of 107 children with unilateral CP, which are shown in Fig. 2. Most prevalent patterns of WM injury include intraventricular hemorrhage (IVH) and periventricular leukomalacia (PVL), frequently impacting the superior longitudinal fasciculus, corona radiata and posterior limb of the internal capsule (PLIC). Frequent GM patterns of injury include IVH impacting the deep GM, including the lenticular and caudate nuclei and the thalamus. Unilateral malformations were the main pattern of injury impacting cortical GM regions, including the temporal and frontal lobes, and the precentral gyrus.

Fig. 2.

The lesion frequency observed in (a) WM and (b) GM regions among the 107 children with unilateral CP. ALIC, anterior limb of the internal capsule; PLIC, posterior limb of the internal capsule.

3.2. Validation of lesion segmentation algorithm

After training the lesion threshold values t_thresh in the training set, the performance of the lesion segmentation method was validated on the test set against a manual assessment of lesions using the semi-quantitative brain lesion severity scale (Fiori et al., 2015). Table 2 shows the segmentation performance on the WM lesion cohort, the GM lesion cohort, and all cohorts combined.

Table 2.

Lesion segmentation performance compared to the manual ground truth assessment of lesions on the independent test set.

Performance measures	WM lesions	GM lesions	Combined
Sensitivity	0.933	0.818	0.939
Specificity	0.765	0.972	0.929
Accuracy	0.872	0.936	0.936
False positive rate	0.235	0.028	0.071
False negative rate	0.067	0.182	0.061

GM, grey matter; WM, white matter.

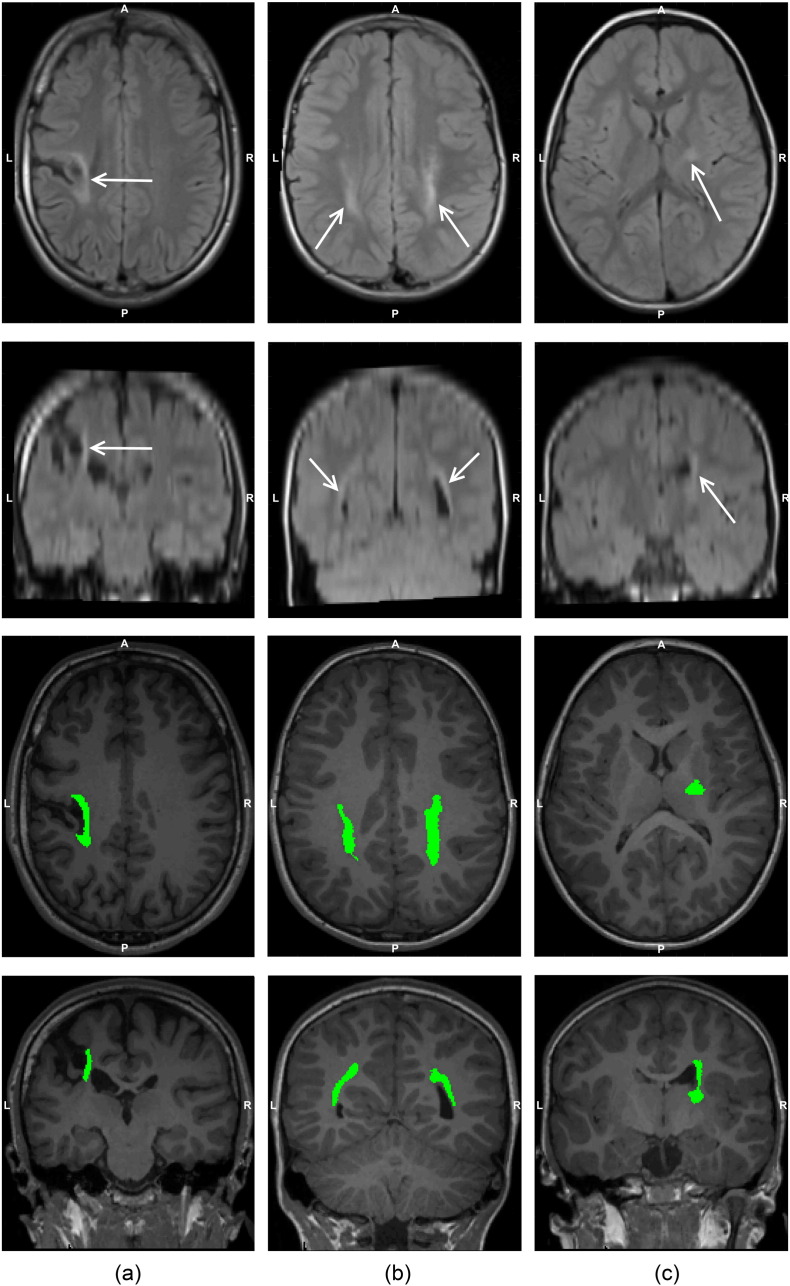
Lesion segmentation performance in the GM had the highest false negative rate, reflecting the difficulty identifying GM lesions due to their more subtle changes in intensity. Conversely, WM lesions had the highest false positive rate, indicating that the false detection of lesions, either from WM intensity changes or moderate intensities in the T2-TIRM, was more common. For the CHD children in the test set, none had lesions identified by the lesion segmentation approach. An illustration of lesion segmentation performance in cases of GM, WM and IC lesions are provided in Fig. 3.

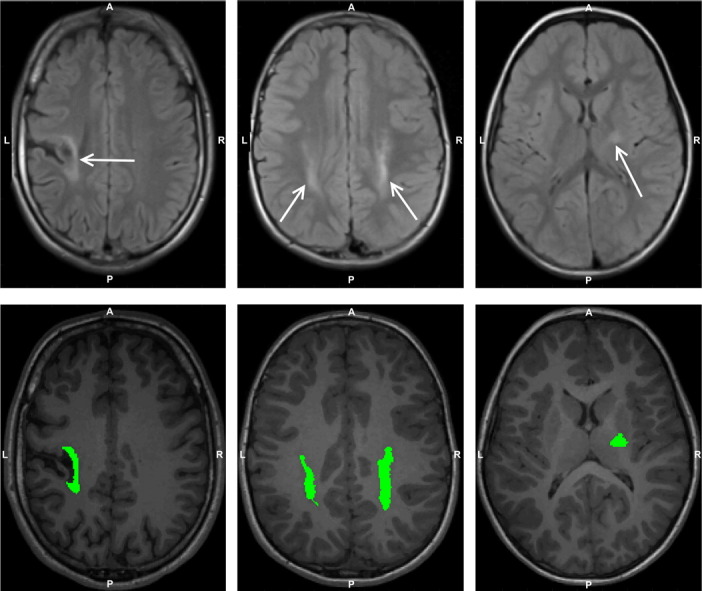
Fig. 3.

Examples of a grey matter (GM) lesion (column (a)), white matter (WM) lesions (column (b)) and internal capsule (IC) lesions (column (c)). The top two rows show the axial and coronal slices of the same T2-TIRM image, where the hyperintense lesions are indicated with white arrows. The segmented lesions, highlighted in green, are presented on the corresponding axial and coronal slices of the T1-MPRAGE image in the bottom two rows. A, anterior; L, left; P, posterior; R, right.

3.3. Comparison to gold standard segmentation approach

To validate the lesion segmentation approach used in this study, we compared its performance to the current state of the art lesion segmentation software, the Lesion Segmentation Toolbox (LST) (Schmidt et al., 2012). The sensitivity, specificity, and several other performance measures of each approached on the independent test set compared to the manual expert classification of lesions is provided in Table 3.

Table 3.

Lesion segmentation performance of the approach used in this paper, and SPM's LST on the 25% independent test set, compared to the manual ground truth assessment of lesions.

Performance measure	Sensitivity	Specificity	Accuracy	False positive rate	False negative rate
Proposed approach	0.939	0.929	0.936	0.071	0.061
SPM's LST	0.893	0.351	0.729	0.649	0.107

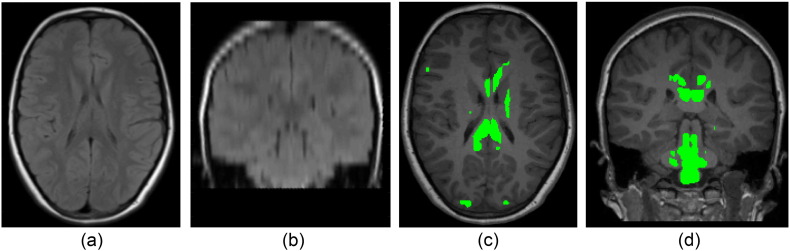
The proposed approach was found to have a greater lesion segmentation accuracy compared to LST on this data (0.936 versus 0.729). The approach used in LST was observed to more frequently produce false positive lesion segmentations, which we hypothesise arises from an inaccurate threshold κ chosen by this method to produce an initial lesion belief map (Schmidt et al., 2012). One example of this false positive segmentation occurring is provided in Fig. 4.

Fig. 4.

An (a) axial and (b) coronal view of the T2 TIRM of a participant with no lesions observed by the manual expert, and the corresponding (c) axial and (d) coronal views of the T1 MPRAGE images with the false lesion segmentations obtained from the LST method shown in green. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.4. Correlation with outcome

The regression models constructed on the training set are detailed in Table 4. In these tables, the regression coefficients can be interpreted as the reduction in the clinical score for every 1 mL of lesion present in that anatomy. The multiple R-squared of the models, which measure strength of the correlation between the outcome and the model predictions, were compared against a Bonferroni corrected alpha value (0.05/6 tests = 0.008), however the p-values of each feature were not corrected, and simply reflects the strength of that feature within the chosen model.

Table 4.

The retained anatomical regions, and corresponding standardised regression coefficients and standard errors, of the GM and WM lesion models, for the six clinical outcome scores, modelled on the 75% training set. For each model, the multiple R-squared is provided. Features that are significant (p < 0.05) in multiple models are bolded.

GM			WM
Variable name	Regression coefficient	Standard error	Variable name	Regression coefficient	Standard error
AHA
Superior frontal gyrus	− 0.265	0.154	Corpus callosum	− 0.018	0.015
Lenticular nucleus	− 0.128⁎⁎⁎	0.036	Corona radiata	− 0.005⁎⁎⁎	0.001
Thalamus	− 0.065⁎⁎⁎	0.015	External capsule	− 0.016⁎⁎⁎	0.004
Middle frontal gyrus	− 0.228⁎⁎	0.083	Cerebral peduncle	− 0.111⁎⁎	0.034
			Cingulum	− 0.266	0.264
Multiple R-squared	0.433⁎⁎⁎		Multiple R-squared	0.514⁎⁎⁎
BRIEF
Caudate nucleus	− 0.2119⁎	0.048	PLIC	− 0.121⁎⁎⁎	0.020
Lenticular	− 0.426⁎⁎⁎	0.119	ALIC	− 0.050	0.050
Superior frontal gyrus	− 0.122⁎	0.058	Cingulum	− 2.012	2.080
Middle frontal gyrus	− 0.549	0.294
Multiple R-squared	0.263⁎⁎⁎		Multiple R-squared	0.386⁎⁎⁎
SDQ
Middle frontal gyrus	− 0.063	0.036	Corpus callosum	− 0.007	0.008
Superior frontal gyrus	− 0.101	0.072	PLIC	− 0.009⁎⁎	0.003
Cingulate cortex	− 0.061	0.047	Corona radiata	− 0.003⁎⁎⁎	0.001
Lenticular nucleus	− 0.034	0.019	External capsule	− 0.002	0.002
Multiple R-squared	0.174⁎		Multiple R-squared	0.529⁎⁎⁎
TVPS
Middle occipital gyrus	− 0.200	0.084	Posterior thalamic radiations	− 0.004	0.130
Middle frontal gyrus	− 0.131	0.236	PLIC	− 0.068⁎⁎⁎	0.017
Superior frontal gyrus	− 0.083	0.396	Fornix	− 0.010	0.130
Inferior frontal gyrus	− 0.119	0.065	Superior longitudinal fasciculus	− 0.029⁎⁎	0.009
Multiple R-squared	0.202⁎⁎		Multiple R-squared	0.507⁎⁎⁎
WR
Middle occipital gyrus	− 0.036⁎	0.018	Fornix	− 0.093⁎⁎	0.033
Superior temporal gyrus	− 0.022	0.024	Superior longitudinal fasciculus	− 0.012⁎	0.002
Supramarginal gyrus	− 0.053⁎	0.021	Posterior thalamic radiations	− 0.003	0.005
Hippocampus	− 0.742	0.703	Corpus callosum	− 0.013	0.009
Multiple R-squared	0.265⁎⁎⁎		Multiple R-squared	0.280⁎⁎⁎
VOC
Precentral gyrus	− 0.037⁎	0.017	External capsule	− 0.015⁎⁎⁎	0.003
Middle temporal gyrus	− 0.041	0.069	Tapatum	− 0.019	0.011
Superior occipital gyrus	− 0.266	0.879	Superior longitudinal fasciculus	− 0.015⁎⁎⁎	0.003
Middle occipital gyrus	− 0.049	0.086	Sagittal Stratum	− 0.057	0.615
Multiple R-squared	0.117⁎		Multiple R-squared	0.491⁎⁎⁎

As WM and GM burdens were used in two models, the individual and combined models respectively, and for the six clinical scores, p-values were compared with the Bonferroni adjusted alpha. AHA, Assisting Hand Assessment; ALIC, anterior limb of the internal capsule; BRIEF, Behaviour Rating Inventory of Executive Function; GM, grey matter; PLIC, posterior limb of the internal capsule; SDQ, Strengths and Difficulties Questionnaire; TVPS, Test of Visual Perception Skills; VOC, vocabulary; WM, white matter; WR, word reasoning.

^⁎p < 0.008, statistically significant model correlations.

^⁎⁎p < 0.0016, statistically significant model correlations.

^⁎⁎⁎p < 0.00016, statistically significant model correlations.

Significant (p < 0.05) regions that were retained by the training models include the superior longitudinal fasciculus and the PLIC (in 3 of the 6 models), and the lenticular nucleus, corona radiata and external capsule (all in 2 of the 6 models). All models were found to be significant (p < 0.0008). The performance of these trained WM and GM models, as well as the WM/GM combined models, on the independent test set are shown in Table 5. Two of the six GM and WM alone models were found to be significant (p < 0.008), while four of the six combined WM/GM models were found to be significant (p < 0. 008). Test set correlations between regional lesion burden computed using the state-of-the-art LST approach and participant outcome were also computed for comparison to the correlations in Table 5. These results are presented in Supplementary Table 1, and show no significant correlations in the independent set (p > 0.008).

Table 5.

The Pearson's R correlation between the predicted outcomes in the test set using the trained linear regression models and the clinical scores of the test set.

	GM models		WM models		WM/GM combined
Pearson's R correlation	95% confidence interval	Pearson's R correlation	95% confidence interval	Pearson's R correlation	95% confidence interval
AHA	0.504⁎	(0.200, 0.719)	0.641⁎⁎	(0.387, 0.805)	0.670⁎⁎⁎	(0.429, 0.822)
BRIEF	− 0.006	(− 0.392, 0.382)	0.263	(− 0.138, 0.590)	0.269	(− 0.132, 0.594)
SDQ	0.182	(− 0.327, 0.610)	0.742⁎⁎	(0.408, 0.901)	0.751⁎⁎	(0.424, 0.905)
TVPS	0.533⁎	(0.184, 0.763)	0.304	(− 0.094, 0.619)	0.614⁎⁎	(0.297, 0.809)
WR	0.435	(0.057, 0.704)	0.063	(− 0.332, 0.440)	0.493⁎	(0.130, 0.739)
VOC	0.077	(− 0.319, 0.452)	− 0.073	(− 0.448, 0.323)	0.085	(− 0.313, 0.457)

Correlations in bold have a statistical significance of p < 0.008. AHA, Assisting Hand Assessment; BRIEF, Behaviour Rating Inventory of Executive Function; GM, grey matter; SDQ, Strengths and Difficulties Questionnaire; TVPS, Test of Visual Perception Skills; VOC, vocabulary; WM, white matter; WR, word reasoning.

^⁎p < 0.008, statistically significant correlations.

^⁎⁎p < 0.0016, statistically significant correlations.

^⁎⁎⁎p < 0.00016, statistically significant correlations.

Results showing the amount of co-dependence between the WM only, GM only, and the combined WM/GM models, using the ANOVA is provided in Table 6. Briefly, the combined WM/GM models for the BRIEF and SDQ measures were not significantly different from the WM alone models, and the WM/GM models for the TVPS and WR measures were not significantly different from the GM alone models for the respective measures (p > 0.05). The differences between the remaining models were significant (p < 0.04), suggesting that although there is limited co-dependence between WM and GM involvement in explaining functional outcomes, there is substantial independence between the impact of WM and GM injuries on five of the six functional outcomes. Hence, there is value in characterising both classes of lesions when assessing functional outcomes.

Table 6.

ANOVA comparisons between the GM and WM only models, and the models combining WM and GM lesion involvement.

	Residual sum of squares	Degrees of freedom	Mean square	F	Significance
AHA
WM/GM combined	81,617	–	–	–	–
WM only	93,130	− 6	− 11,514	2.563	0.023⁎
GM only	110,550	− 8	− 28,933	4.830	< 0.001⁎⁎⁎
BRIEF
WM/GM combined	735,037	–	–	–	–
WM only	825,191	− 7	− 90,154	1.542	0.164
GM only	973,689	− 4	− 238,652	7.143	< 0.001⁎⁎⁎
SDQ
WM/GM combined	6013.7	–	–	–	–
WM only	6386.7	− 7	− 373.07	0.541	0.800
GM only	11,366.0	− 8	− 5352.3	6.787	< 0.001⁎⁎⁎
TVPS
WM/GM combined	439,456	–	–	–	–
WM only	414,153	− 2	− 215,837	21.365	< 0.001⁎⁎⁎
GM only	655,292	− 6	− 40,342	1.331	0.252
WR
WM/GM combined	27,956	–	–	–	–
WM only	29,640	− 4	− 3228.4	2.598	0.041⁎
GM only	31,184	− 4	− 1684.1	1.355	0.256
VOC
WM/GM combined	81,786	–	–	–	–
WM only	148,175	− 4	− 66,390	18.264	< 0.001⁎⁎⁎
GM only	96,119	− 5	− 14,333	3.155	0.011⁎

Asterisked correlations were found to be statistically significant: * p < 0.05; ** p < 0.01, *** p < 0.001. AHA, Assisting Hand Assessment; BRIEF, Behaviour Rating Inventory of Executive Function; GM, grey matter; SDQ, Strengths and Difficulties Questionnaire; TVPS, Test of Visual Perception Skills; VOC, vocabulary; WM, white matter; WR, word reasoning.

4. Discussion

An accurate, validated method for the automatic segmentation of WM and GM lesions has been applied to a cohort of children with unilateral CP. The correlation between regional lesion involvement and functional outcome was examined. Lesion involvements explained between 12–53% of the variance in the clinical score across all training models. We note that including information related to the presumed timing and type of the insults, which cannot be automatically determined using the proposed approach, would further increase the amount of variance explained by these models. The anatomical regions with significant relationships to clinical function (p < 0.05) concurred with previous studies of the roles of individual regions, including the thalamus (Haber and Calzavara, 2009), lenticular (Middleton and Strick, 2000) and caudate nuclei (Grahn et al., 2008), corona radiata (Kraus et al., 2007), cerebral peduncle (Cho et al., 2007), PLIC (Kinnunen et al., 2011), external capsule (Fazio et al., 2009) and superior-longitudinal fasciculus (Bernal and Altman, 2010). Participant age and gender were not observed to be significant predictors of outcome in any trained model. Four of these twelve trained structure-function regression models remained significant after Bonferroni correction in the validation test set, suggesting that these models specifically have identified real, underling relationships in the brain. Overall, these findings demonstrate that these models could help predict functional outcomes arising from lesions in all children with clinically diagnosed unilateral CP.

It was observed that the models consisting of WM lesion involvement had a higher multiple R-squared compared to the corresponding GM models for all six clinical scores, which may be a result of the greater frequency of WM involvement observed in our cohort of data (Table 1). However, two of the six GM models were found to be significantly predictive of outcomes in the independent test set (p < 0.008), the same number as the number of significant WM models. The important impact of GM involvement on outcome observed in this independent test set is consistent with previous findings that children with cortical or deep GM lesions showed noticeable motor and sensory deficits (Martinez-Biarge et al., 2010). Furthermore combining both WM and GM information led to consistently higher correlations with the test set, reaching significance in three of the six combined models (p < 0.008), and highlighting the importance of considering both lesion types. Although GM lesions were found to be predictive of multiple functional impairments, they are comparatively more difficult to segment than WM lesions, as illustrated in the performance measures in Table 2. Despite this, we recommend that future studies into CP as well as other cerebral injuries, including multiple sclerosis and acquired stroke, quantifying the extent of GM injury is critical to provide an assessment of functional impairment.

A technical limitation of the present study is the severe extent of injury present in approximately 25% of children with CP. Although the non-rigid registration techniques used to align the tissue probability maps and atlas labels provide the best possible alignment of the corresponding images, errors were still introduced in severely injured data with significant tissue loss or morphological changes. This could be minimised by instead utilising the GM provided by the EM-MRF segmentation to building the tissue probability map, which has been shown to be robust to morphological injury (Pagnozzi et al., 2015). Additionally, the presence of other injuries such as brain malformations, cases of ventricular enlargement without any associated WM signal abnormalities, or cystic GM loss (which appears black in the TIRM, and potentially mislabelled as CSF in the segmentation) (Krägeloh-Mann and Horber, 2007), have not been identified with the proposed approach. The presence of these injuries introduces additional variance in the clinical motor outcome score not explained solely by the lesion predictor variables, reducing the multiple R-squared of the trained models, necessitating the use of additional algorithms. Another limitation of this study is that the effects of potential plasticity, which may lead to the translocation of specific functions on the cortex. Plasticity has not been accounted for in the regression models and could lead to an unexplained variance in the clinical outcome in these participants. A strength of the present study is that the proposed segmentation approach only requires structural MR images, which are well established sequences and are common in clinical practice. In future, a combination of automated methods for detecting all classes of injury from structural MRIs will be combined to provide a complete assessment of injury and estimation of impairment for children with CP. These estimates can help guide what therapeutic interventions for motor, cognitive, visual or communicative function may be required for individual children, and assisting these interventions to be performed earlier in life, where neuroplasticity may have a greater effect (Cioni et al., 2011). Furthermore, as children with unilateral CP may not respond well to lateralised interventions such as Constraint-Induced Movement Therapy (CIMT), the severity and laterality of brain lesions may guide the potential clinical utility of unimanual CIMT versus bimanual training. Future investigations will also look to apply this approach to children with bilateral CP, when data becomes available.

5. Conclusions

A robust method for performing automated brain lesion segmentation from T1-weighted MRI sequences alone was applied to the segmentation of both white and grey matter lesions from children with unilateral CP, and its performance validated against manual expert classifications of lesions. After computing regional WM and GM lesion burden, LASSO was used to identify regional burdens related to individual clinical functions separately for white and grey matter lesions. The automatically selected regions conformed to established relationships between anatomical regions and function, with significant correlations observed between regional lesion burden and motor and cognitive function. GM lesions led to a significant and generalisable reduction in functional outcomes comparable in magnitude to WM lesions, demonstrating the importance of quantifying GM lesion involvement. When combined with an automated detection of other kinds of developmental injury, a complete assessment of injury and outcome for children with CP can be provided.

Appendix A. Supplementary data

Supplementary material. Provides the correlation between the lesion segmentation's obtained from SPM's LST with multiple clinical outcomes, as well as the accumulation of incorrect lesion classifications with increasing injury severity for both methods.