Abstract
Motivation: Ribosome profiling is a useful technique for studying translational dynamics and quantifying protein synthesis. Applications of this technique have shown that ribosomes are not uniformly distributed along mRNA transcripts. Understanding how each transcript-specific distribution arises is important for unraveling the translation mechanism.
Results: Here, we apply kernel smoothing to construct predictive features and build a sparse model to predict the shape of ribosome footprint profiles from transcript sequences alone. Our results on Saccharomyces cerevisiae data show that the marginal ribosome densities can be predicted with high accuracy. The proposed novel method has a wide range of applications, including inferring isoform-specific ribosome footprints, designing transcripts with fast translation speeds and discovering unknown modulation during translation.
Availability and implementation: A software package called riboShape is freely available at https://sourceforge.net/projects/riboshape
Contact: yss@berkeley.edu
1 Introduction
Gene expression is a fundamental biological process consisting of two parts: transcription of mRNAs from DNAs and translation of proteins from mRNAs. Studying the genome-wide dynamics of both processes is crucial for understanding how cells function and respond to various environmental conditions, thereby giving rise to the impressive complexity of living organisms. Due to technological challenges, translation has not been studied as extensively as transcription, but recent advances in experimental protocol and sequencing technology are providing an unprecedented opportunity to examine the translation process at base-pair resolution.
Ribosome profiling (Ingolia et al., 2009; Ingolia, 2014) applies either translation inhibitors or a flash-freeze protocol to immobilize the ribosomes ‘walking’ along the transcript, and the ribosome-occupied regions (each of length 28–30 nucleotides) can then be extracted and sequenced, providing detailed positional information about ribosomes. Such snapshots of ribosome footprints enable quantitative monitoring and analysis of translational dynamics, making ribosome profiling an important technique for studying protein synthesis. In particular, it has been shown that protein abundance correlates better with ribosome densities than with mRNA abundance (Ingolia et al., 2009).
Various factors may influence the translation mechanism. It has been proposed that the differential usage of synonymous codons, also known as the codon usage bias, is driven by evolutionary forces to facilitate translation speed (Burgess-Brown et al., 2008; Gardin et al., 2014; Maertens et al., 2010; Qian et al., 2012; Tuller et al., 2010b). This hypothesis is supported by the finding that transcripts with wobble base-pairing encounter slower elongation (Stadler and Fire, 2011), and also by the analysis of tRNA-adaptation index (tAI) (Tuller et al., 2010a, 2011). Another hypothesis associates the mRNA secondary structure with translation efficiency, in particular near initiation sites (Kertesz et al., 2010, 2012; Kudla et al., 2009; Gu et al., 2010; Tuller et al., 2010b, 2011; Zur and Tuller, 2012). Studies have found that initiation is the rate-limiting factor of translation and that ribosome densities tend to be higher near initiation sites in Saccharomyces cerevisiae (Ingolia et al., 2009; Shah et al., 2013). Also, positively charged residues on nascent peptides have been found to influence the footprint abundance (Charneski and Hurst, 2013; Lareau et al., 2014; Tuller et al., 2011). We refer the reader to Ingolia (2014) for a review of the major findings from utilizing ribosome profiling.
Although the debate surrounding the main determinant of translational dynamics remains open, the above-mentioned hypotheses have one thing in common; that is, the transcript sequence context plays an important role in governing the efficiency of translation. Hence, investigating how transcript-specific distributions arise and to what extent they depend on the transcript sequence is essential to understanding the translation mechanism. Motivated by this observation and the fact that ribosome footprint profiles are generally not uniformly distributed, we consider here the statistical problem of predicting marginal densities of ribosome footprints from the transcript sequence information alone.
We first apply wavelet analysis to decouple global shapes from local patterns of ribosome marginal densities. Then, by building sparse models to predict the marginal densities projected onto the subspace corresponding to each scale and using asymmetric kernel smoothing, we identify the codon features that best associate with a given scale and estimate the extent to which they influence the ribosome densities. Results on S. cerevisiae ribosome footprints show that the sequence content is highly predictive of the marginal densities at steady state. The ability to predict the marginal densities based solely on transcript sequences has many potential applications. For example, it can be used to guide the design of transcripts with optimal translation speeds in synthetic biology; comparing the steady-state prediction with profiles under various conditions may help to uncover unknown post-transcriptional regulation factors; and the predicted marginal density can serve as a prior in probabilistically mapping reads in the inference of isoform-specific ribosome footprints.
This paper is organized as follows. In Section 2, we describe our proposed method, which consists of the ‘A’ site (decoding site where the aminoacyl tRNA arrives) identification, wavelet decomposition, kernel smoothing and sparse regression model. In Section 3, we test the performance of our method on ribosome profiling data of S. cerevisiae. We then conclude with a discussion of our findings.
2 Methods
2.1 Ribosome footprint alignment and the ‘A’ site identification
The first step of ribosome profiling is immobilizing the ribosomes on transcripts, which can be accomplished by the application of cycloheximide (CHX), proposed by Ingolia et al. (2009). Then, by nuclease digestion, the fragments of the transcript protected by the ribosomes are retained. After converting these footprints into DNA molecules for deep sequencing, one can measure the abundance of footprints at each position along a transcript.
We considered four publicly available datasets of ribosome profiling footprints of S. cerevisiae treated with CHX, available at the NCBI Gene Expression Omnibus under accession GSE13750, GSE52119, GSE34438 and GSE55400, and published in the recent literature (Albert et al., 2014; Ingolia et al., 2009; McManus et al., 2014). We analyzed the ribosome footprints of wild type S. cerevisiae under normal conditions to study the steady-state behavior. The footprint reads were first processed to remove the adapters and trim the poly-A tails, according to published protocols (Albert et al., 2014; Ingolia et al., 2009; McManus et al., 2014). The reads were then mapped to the yeast genome, available at the Saccharomyces Genome Database. Reads with alignment against sequences of RNA genes (rRNAs, tRNAs, snRNAs, snoRNAs and ncRNAs) of S. cerevisiae were filtered out, and the remaining reads were aligned against the ORF genomic sequences or the ORF coding sequences.
There are three active ribosomal sites: the A (arrival), P (polypeptide) and E (exit) sites, where aminoacyl tRNA arrives for decoding, the polypeptide is created and the uncharged tRNA exits, respectively (Fig. 1). We considered reads of length 28, 29 and 30 nucleotides, and focused on the A sites of these ribosome footprints. For a 28-nucleotide footprint read, the A site typically starts at the 16th nucleotide downstream of the 5′ end of the read (Ingolia et al., 2009; Lareau et al., 2014). If that position does not correspond to the first nucleotide of a codon, then, as illustrated in Figure 1, the start position of the A site was adjusted so that it is at either the 15th or the 17th nucleotide, depending on the amount of shift. We applied the same procedure for 29-nucleotide reads. For 30-nucleotide reads, the A site was inferred to start at the 16th, the 17th, or the 18th nucleotide downstream of the 5′ end. Marginal probability density functions of the footprints were obtained by normalizing the histograms of the inferred A site footprint counts along each transcript. Figure 2 shows an example of the marginal density function of CHX-treated ribosome footprints.
Fig. 1.

Inferring the A site of a 28-nucleotide ribosome footprint read. The start position (shown in red) of the A site is inferred to be at the 15th, the 16th or the 17th nucleotide downstream of the 5′ end of the read, depending on the amount of shift
Fig. 2.
Ribosome footprints marginal density on YAL021C decomposed by wavelet analysis with Daubechies-8 basis. Red: the raw ribosome footprints normalized over the transcript. Blue and Green: the raw footprints projected to each subspace. As the scale (index m of Vm) increases, the reconstructed signal includes more details
We also considered the ribosome footprints obtained using the flash-freeze protocol without CHX pre-treatment (Weinberg et al., 2016). These footprints are publicly available at the NCBI Gene Expression Omnibus under accession GSE53313.
2.2 Wavelet decomposition
Wavelet transformation has been widely used for analyzing signals. Its time-frequency localization (Daubechies, 1990) and multiresolution capability (Mallat, 1989) have proved extremely useful for applications of denoising (Donoho, 1995; Donoho and Johnstone, 1998; Donoho et al., 1995; Johnstone and Silverman, 1997), density estimation (Donoho et al., 1996; Kerkyacharian and Picard, 1992), data compression (Chambolle et al., 1998; Chang et al., 2000; Villasenor et al., 1995), and so on. More recently, it has been applied to genetic association analyses in high-throughput sequencing assays (Shim et al., 2015). In ribosome footprint profiles, there may be noise in sequencing and alignment, as well as insufficient sampling due to low sequencing depth. To extract reliable signals for downstream analysis, we adopt wavelet decomposition to build a multiresolution reconstruction of ribosome marginal densities.
Let pt denote the marginal density of ribosomes along a given transcript t, such that represents the probability that the A-site of a randomly sampled ribosome is at position x (in units of codons). We can decompose this function as
| (1) |
where and , with and corresponding to a scaling function and its associated wavelet, respectively (Burrus et al., 1998). The coefficients and are uniquely determined by inner products and , respectively. The spans of and form a multiresolution approximation of as
where and . Figure 2 shows the use of wavelet analysis to build a multiresolution reconstruction, in which global shapes are decoupled from local patterns. In what follows, we use to denote the projection of pt onto subspace S. Table 1 summarizes the reproducibility of ribosome footprint profiles by examining the Pearson correlation coefficients between replicates projected onto different subspaces Vm. These results indicate that wavelet decomposition is important for denoising.
Table 1.
Correlation between the replicates projected onto various subspaces. The Pearson correlation coefficient between the replicates in GSE13750 increases as the scale (index m of Vm) decreases.
| Length | Subspace S | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| (codons) | V0 | V1 | V2 | V3 | V4 | V5 | V6 | V7 | |
| 1–250 | 0.53 | 0.56 | 0.49 | 0.42 | 0.37 | 0.34 | 0.31 | 0.28 | 0.26 |
| 251–500 | 0.59 | 0.55 | 0.46 | 0.38 | 0.30 | 0.26 | 0.22 | 0.19 | 0.17 |
| 501–750 | 0.49 | 0.46 | 0.39 | 0.32 | 0.25 | 0.21 | 0.18 | 0.15 | 0.13 |
| 751–1000 | 0.51 | 0.44 | 0.34 | 0.27 | 0.21 | 0.18 | 0.15 | 0.12 | 0.11 |
| 1001–3745 | 0.53 | 0.45 | 0.36 | 0.27 | 0.21 | 0.17 | 0.14 | 0.12 | 0.10 |
2.3 Kernel smoothing on sequence context
The marginal density at a given position may depend not only on the codon at that position, but also on neighboring codons. Furthermore, the extent of influence may decay as the physical distance from the position increases. We apply kernel smoothing (Silverman, 1986; Wand and Jones, 1994) to capture these effects. First, we represent each transcript as a collection of binary strings, a well-used method for coding categorical variables in regression (Hardy, 1993). Label the 64 codon types by . Given a transcript t with codons, we define a length- binary strings for each , where the character at position x is defined as
Note that, for each position , there is exactly one codon type such that ; all other strings will have a 0 at position x.
Next, we apply kernel smoothing to each string as
| (2) |
where is a suitably chosen kernel. Intuitively, if the ribosome marginal density is affected by sequence context, then a region with a cluster of slow translating codons is likely to become congested with ribosomes. By smoothing with a kernel, we incorporate the distribution of neighboring codons into our model. Figure 3 illustrates the method we propose, in which the black spikes represent the decomposed codon sequences and the red curves are the kernel smoothed estimates with a symmetric Gaussian kernel, , where
Fig. 3.
Illustration of kernel smoothing. The black stems represent the codon sequences of YBR212W, consisting of 0’s and 1’s. The first 350 codon positions of 3 out of 64 sequences are shown in this example. The red curves represent the kernel smoothed codon sequences, with Gaussian kernel. The blue and green curves represent the asymmetric kernel smoothed codon sequences, with and respectively. All the kernel smoothed sequences are scaled such that the maximum is 1 for illustration
Since the flow of ribosomes is directional, a cluster of slow translating codons should have a larger impact on upstream ribosomes than on downstream ribosomes. To take this directionality into account, we therefore employ an asymmetric kernel. An example of asymmetric kernels is the probability density function of the gamma distribution,
where a and b are the shape and scale parameters, respectively, and is the gamma function. It can be shown that the peak of this density function is located at , and the standard deviation is . We define a modified gamma distribution , parameterized by θ and σ, by applying a horizontal shift so that the peak of the function is located at 0 and by reflecting about the y-axis:
where and . The Gamma distribution and the modified gamma distribution are illustrated in Figure 4. We also define a shifted but non-reflected function to take into account the effect of positively charged residues of nascent peptides on the speed of downstream ribosomes (Charneski and Hurst, 2013):
Fig. 4.

Asymmetric kernels. Top: Gamma distribution . Bottom: Modified gamma distribution
In what follows, we set the θ parameter of and to 5, because a ribosome occupies 9–10 codons and there are about 5 codons downstream. Applications of these asymmetric kernels and are depicted as blue and green curves in Figure 3 respectively.
2.4 Sparse regression model
We relate the ribosome marginal density to the transcript sequence context by building a sparse model. In (2), we apply or with B different bandwidths . For each codon type , let denote the codon feature string smoothed using the kernel function with bandwidth σ. If we use Q distinct kernel functions , then for each position x of transcript t, the predictors can be represented as
where
We relate these sequence features to the ribosome marginal density projected onto subspace S, by formulating a sparse regression problem:
| (3) |
where denote regression coefficients. The first part of the objective function represents the residual sum of squares, whereas the second part promotes a sparse solution. The sparsity of the solution depends on the value of the regularization parameter λ. This type of linear estimation, known as LASSO (Tibshirani, 1996; Zhao and Yu, 2006), avoids overfitting the data especially in scenarios where the number of predictors is much larger than the number of observations. It also provides an interpretation of the importance of each predictor, i.e., the variables that correspond to zeros in the solution are not significant to the model. Our goal is to find a significant bandwidth σb. By training the sparse regression model with kernel smoothed codon feature strings with various bandwidths, and selecting the regularization parameter λ with cross validation to minimize mean squared error (MSE), the nonzero terms in the regression coefficients provide insight into the extent to which sequence context affects the ribosome marginal density.
3 Results
After the filtering step described in Section 2.1, we grouped genes according to their length into 5 bins: ≤250 codons, 251–500 codons, 501–750 codons, 751–1000 codons and ≥1000 codons. We then decomposed each ribosome footprint profile using wavelet analysis with Daubechies-8 basis and eight scales, as illustrated in Figure 2. We considered a model with both asymmetric kernels and each with eight bandwidths . For comparison, we also considered a model with the symmetric kernel with the same set of bandwidths, as well as a model with no kernel smoothing. We trained the regression model using 9n/10 randomly chosen genes, where n is the number of genes in the corresponding bin, and chose the regularization parameter in (3) via five-fold cross-validation using the training data. Then the model was tested on the genes that were left out, and the process was repeated until every gene has been tested.
Results of CHX-treated footprints in various spaces are summarized in Table 2. The average performance is presented in terms of the Pearson correlation coefficient between the predicted and the true ribosome marginal densities. Notice that our method using asymmetric kernels achieved high accuracy in subspaces V0 through V4. This suggests that the global shape of transcript-specific ribosome footprint profile is well captured by our proposed kernel-smoothed codon sequences. The performance in the subspace Vk decreases as k increases. This is partly due to noise in the read alignment or the sequencing noise inherent in ribosome profiling. Thus, wavelet analysis is useful for studying the limit of the ribosome profiling technique and focusing on the reliable signals. The results from using non-smoothed codon sequences were the least accurate, supporting that the neighboring codons or interference play an important role in ribosome footprint distributions. Using asymmetric kernel smoothing produced more accurate results than using a symmetric kernel. The same trend also holds for flash-freeze ribosome profiles (Table 2). The performance of our method on CHX-treated ribosome profiles was better than that on the flash-freeze profiles. This may be due to the large amplitude of ramps near the end in CHX-treated profiles (Weinberg et al., 2016). These ramps contribute significantly to global shapes, and can be well captured by asymmetric kernel smoothing.
Table 2.
Accuracy of the prediction of marginal densities for CHX-treated and flash-freeze ribosome footprint data. NS, SK and ASK respectively denote using no kernel smoothing, using symmetric kernel (), and using asymmetric kernels (). The Pearson correlation coefficient between the prediction and the measured ribosome density was averaged over genes. The results are listed for different spaces S and various gene lengths. The prediction achieves high accuracy in the global shape spaces, e.g. V0 and V1. As the scale increases, i.e., as the index m of Vm increases, prediction becomes more difficult.
| Length | Method | CHX: Subspace S | Flash-freeze: Subspace S | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (codons) | V0 | V1 | V2 | V3 | V4 | V5 | V6 | V7 | V0 | V1 | V2 | V3 | V4 | V5 | V6 | V7 | |||
| 1–250 | NS | 0.06 | 0.11 | 0.11 | 0.10 | 0.10 | 0.12 | 0.14 | 0.19 | 0.09 | 0.02 | 0.03 | 0.04 | 0.08 | 0.12 | 0.16 | 0.20 | 0.23 | −0.04 |
| SK | 0.33 | 0.44 | 0.46 | 0.41 | 0.37 | 0.33 | 0.33 | 0.33 | 0.13 | 0.03 | 0.13 | 0.20 | 0.29 | 0.38 | 0.42 | 0.41 | 0.39 | 0.10 | |
| ASK | 0.65 | 0.73 | 0.69 | 0.61 | 0.53 | 0.50 | 0.46 | 0.45 | 0.17 | 0.19 | 0.35 | 0.35 | 0.38 | 0.42 | 0.45 | 0.45 | 0.44 | 0.15 | |
| 251–500 | NS | 0.08 | 0.06 | 0.06 | 0.06 | 0.07 | 0.10 | 0.13 | 0.18 | 0.07 | 0.03 | 0.04 | 0.06 | 0.09 | 0.13 | 0.17 | 0.21 | 0.24 | 0.02 |
| SK | 0.38 | 0.39 | 0.40 | 0.38 | 0.33 | 0.33 | 0.33 | 0.34 | 0.04 | 0.20 | 0.26 | 0.31 | 0.41 | 0.45 | 0.47 | 0.45 | 0.42 | 0.07 | |
| ASK | 0.82 | 0.73 | 0.70 | 0.67 | 0.62 | 0.59 | 0.55 | 0.52 | 0.12 | 0.56 | 0.59 | 0.57 | 0.54 | 0.52 | 0.52 | 0.50 | 0.47 | 0.13 | |
| 501–750 | NS | 0.06 | 0.06 | 0.06 | 0.06 | 0.07 | 0.10 | 0.14 | 0.18 | 0.09 | 0.04 | 0.05 | 0.07 | 0.10 | 0.14 | 0.18 | 0.21 | 0.24 | 0.00 |
| SK | 0.33 | 0.35 | 0.36 | 0.38 | 0.37 | 0.35 | 0.36 | 0.35 | 0.03 | 0.23 | 0.28 | 0.33 | 0.43 | 0.47 | 0.48 | 0.46 | 0.43 | −0.02 | |
| ASK | 0.77 | 0.68 | 0.64 | 0.61 | 0.58 | 0.55 | 0.52 | 0.50 | 0.01 | 0.58 | 0.57 | 0.57 | 0.54 | 0.53 | 0.52 | 0.50 | 0.48 | 0.00 | |
| 751–1000 | NS | 0.06 | 0.05 | 0.05 | 0.05 | 0.07 | 0.10 | 0.14 | 0.19 | 0.13 | 0.05 | 0.06 | 0.07 | 0.09 | 0.13 | 0.18 | 0.22 | 0.24 | 0.14 |
| SK | 0.32 | 0.28 | 0.35 | 0.29 | 0.30 | 0.30 | 0.32 | 0.34 | 0.07 | 0.25 | 0.33 | 0.39 | 0.45 | 0.48 | 0.48 | 0.46 | 0.43 | 0.04 | |
| ASK | 0.66 | 0.58 | 0.55 | 0.52 | 0.49 | 0.47 | 0.45 | 0.46 | 0.07 | 0.55 | 0.59 | 0.55 | 0.54 | 0.52 | 0.52 | 0.50 | 0.48 | 0.03 | |
| 1001–3745 | NS | 0.05 | 0.05 | 0.05 | 0.06 | 0.07 | 0.10 | 0.14 | 0.18 | 0.14 | 0.04 | 0.05 | 0.07 | 0.09 | 0.13 | 0.18 | 0.21 | 0.24 | 0.10 |
| SK | 0.25 | 0.26 | 0.28 | 0.29 | 0.29 | 0.31 | 0.31 | 0.33 | 0.00 | 0.25 | 0.30 | 0.36 | 0.45 | 0.47 | 0.49 | 0.47 | 0.44 | 0.05 | |
| ASK | 0.62 | 0.59 | 0.56 | 0.54 | 0.51 | 0.49 | 0.48 | 0.46 | 0.03 | 0.52 | 0.56 | 0.55 | 0.53 | 0.51 | 0.52 | 0.50 | 0.47 | 0.03 | |
In general, our method with asymmetric kernels was able to predict the global shape of transcript-specific ribosome density with high accuracy. However, for the flash-freeze data, the correlation in the subspace V0 was relatively poor for the genes shorter than 250 codons. This is because the global shape of their profiles in this subspace was rather flat for the flash-freeze data. If the mean squared error is used as the performance measure, the results for shorter genes are not so much worse than that for longer genes. As an example, Figure 5 shows the ribosome density of YBR212W in various subspaces and the corresponding predictions for both CHX-treated and flash-freeze profiles. Figure 6 shows heatmaps of the regression coefficients for transcripts of length ≤250 codons in the space V3. This result shows that CGA (arginine), CCG (proline) and CGG (arginine) have a strong influence on the global shape of ribosome occupancy in flash-freeze data, while CGA and CGG seem to have the dominant effect in CHX-treated data. This may be related to wobble base pairing, which has been found to be associated with slow elongation (Lareau et al., 2014; Stadler and Fire, 2011). In particular, high ribosome occupancy has been observed on wobble-paired proline CCG (G-U base pairing) and arginine CGA (I-A pairing) by Lareau et al. (2014). Furthermore, CGA is one of the codons with the most prolonged elongation rates, consistent with Lareau et al.
Fig. 5.
Ribosome footprint marginal density prediction on YBR212W: (A) CHX-treated data. (B) Flash-freeze data. The marginal density was decomposed by wavelet analysis with Daubechies-8 basis, and shown in black at various scales. The prediction is shown in blue and the Pearson correlation coefficients between the true ribosome marginal density (black) and predicted ribosome marginal density (blue) are indicated on top of each panel
Fig. 6.
Heatmaps of the regression coefficients in the space V3 for transcripts of length ≤250 codons: (A) CHX-treated data. (B) Flash-freeze data. The coefficients are scaled such that the largest absolute value among them is set to 1 for display. These regression coefficients provide insight into the influence of each codon. In particular, they show that codons CGA, CCG and CGG strongly influence the global shape of ribosome occupancy in flash-freeze data, while CGA and CGG seem to have the dominant effect in CHX-treated data
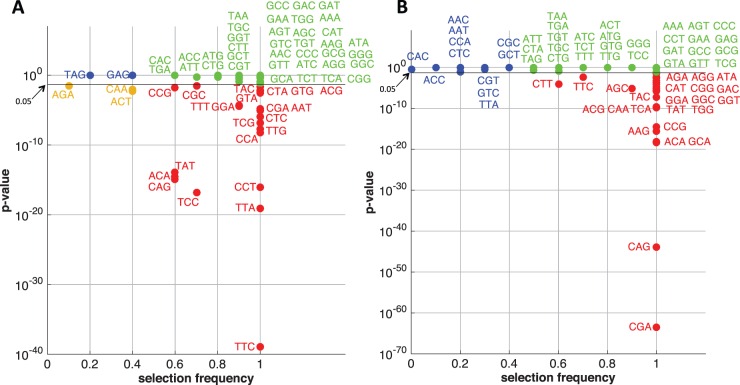
To examine further how the distribution of codons may affect the shape of ribosome footprint profiles, we carried out a sliding-window analysis for each transcript, using a window size of 20 codons. For each transcript, we first identified all windows for which the average ribosome density was larger than twice the transcript-wide average ribosome density, and then considered those windows for codon enrichment analysis. For each selected window, let denote the observed codon distribution, where ωi is the number of codons of type i within the window. We compared this observed codon distribution with the expected distribution , where ηi denotes the expected number of codons of type i within the window, assuming sampling 20 codons without replacement according to the codon distribution in the entire transcript. Note that follows a multivariate hypergeometric distribution. We performed a paired t-test on and over the selected windows and identified the codons enriched in high ribosome-occupancy regions. We then compared the P-values from the enrichment analysis with the frequencies of the regression coefficients being nonzero, as illustrated in Figure 7. The scatter plot for flash-freeze data (Fig. 7B) shows that all of the significantly enriched codons were selected frequently by the regression model. Codons that were selected frequently but not significantly enriched in high density regions might have been selected for prediction in low ribosomal density regions. For example, it has been observed previously (Lareau et al., 2014) that GGG and GTT are some of the codons with the least footprint abundance. For the CHX-treated data, there were a few codons enriched significantly but not selected frequently (Fig. 7A); this could be due to technical biases in the data, discussed in Section 4.
Fig. 7.
Scatter plots of codon enrichment significance versus variable selection frequencies, for transcripts of length ≤250 codons. (A) For the regression coefficients of shown in Figure 6A for the CHX-treated data. (B) For the regression coefficients of shown in Figure 6B for the flash-freeze data. Codons that are significantly enriched and selected frequently in the regression model are shown in red; codons that are neither significantly enriched nor frequently selected are shown in blue; codons that are not significantly enriched but selected frequently are shown in green; codons that are significantly enriched but not selected frequently are shown in khaki. Note that most of the significantly enriched codons were selected frequently by the regression model
4 Discussion
Our results on S. cerevisiae data, especially the CHX-treated footprints, show that the global shape of transcript-specific ribosome density can be predicted with high accuracy. This suggests that the ribosome distribution along a transcript indeed depends on the sequence context. In particular, we find a few codons that dominate the global shape; these codons influence the ribosome density not only at the site where they appear, but also their neighboring positions.
There are several possible reasons why applying kernel smoothing to codon sequences helps in predicting the shape of transcript-specific ribosome occupancy profile. One possible reason is the interference among ribosomes. Another possible explanation is that the physical footprint of each ribosome spans multiple codons (9–10 codons). Lastly, it has been shown (Charneski and Hurst, 2013) that positively charged amino acids on nascent peptides significantly slow down ribosomes downstream from where the residues are encoded. Among all the methods compared, the asymmetric kernel smoothing performed the best. This could be due to the directional movement of ribosomes and the aforementioned effect of positively charged amino acids on downstream elongation speeds. Also, ramps can be better predicted using asymmetric kernels, which partly explains why the prediction accuracy for CHX-treated ribosome profiles was slightly better than that for flash-freeze profiles.
There are other factors not incorporated into our current model that could also help to explain ribosome distributions, e.g. mRNA secondary structure. Notice that in the results for CHX-treated ribosome footprints, we achieved better performance in shorter genes. When applying a sliding window to genes with a prediction correlation coefficient below 0.3 and of length 1001–1500 codons, we observed that the correlation was lower near the 5′ end. Furthermore, when computing differences between the observed ribosome densities and the predicted densities from these poorly predicted genes, we noticed a weak positive correlation (r = 0.0446) between the differences and the likelihood of double stranded conformations, i.e., the PARS (parallel analysis of RNA structure) scores of secondary structure defined by Kertesz et al. (2010) in a genome-wide measurement. Although many potential factors—including mRNA secondary structure, codon usage bias, tRNA-adaption index, etc.—are not explicitly incorporated into our model, most of these factors depend on the sequence context. This may be one of the reasons why considering transcript sequences alone enables reasonably accurate prediction of ribosome footprint profile shapes.
It is possible that some of the features learned by our predictive model are due to technical biases in the data. Library construction is a possible source of bias due to technical artifacts. Artieri and Fraser (2014) found three types of nucleotide biases by comparing mRNA fragments (unprotected by ribosomes) with ribosome footprints to identify shared biases. These include an enrichment of adenine at the 5′ and 3′ ends, and a depletion of cytosine at the fourth nucleotide position in both the mRNA and ribosome footprint reads. However, we note that the flash-freeze ribosome footprint data (Weinberg et al., 2016) we analyzed were generated using a comprehensive set of adapter sequences to avoid the biases discussed in Artieri and Fraser (2014). Furthermore, the flash-freeze protocol avoids the ribosome run-off phenomenon that can occur in CHX pre-treatment.
Different models have been proposed in the literature to estimate elongation rates. Shah et al. (2013) developed a continuous-time, discrete-state Markov model to simulate translational dynamics, in which initiation and elongation rates were inferred using the cell volume, ribosome abundance and tRNA abundance. These elongation rates were codon dependent but not position dependent. The model proposed by Pop et al. (2014) was based on flow conservation, and it assumed that the occurrences of the same codon within an mRNA transcript have the same dwell time, and hence the same elongation rate. Our results suggest that these models should take the codon position into account. In other words, the elongation rate at a particular position along a transcript not only depends on the codon at that position but also the neighboring codons and how the neighboring codons are ordered.
Part of the results presented in this paper is based on combining four publicly available datasets. This overcomes the difficulty of sparse sampling that other work may encounter, e.g. Pop et al. (2014). Although our study is limited to the steady-state distribution of ribosomes, it examines the extent to which the sequence context influences ribosome distributions under normal conditions. One of the important applications of our method is to examine the positions where the steady-state prediction is significantly different from the actual measurements. These positions may lead to important findings of unknown factors that regulate translation. For example, our proposed method can be applied to cells grown under various environmental conditions, or to ribosome profiles obtained by different inhibitors, e.g. harringtonine (Ingolia et al., 2011), anisomycin (Lareau et al., 2014).
Another application is the inference of isoform-specific ribosome footprints. It is known that many human genes have more than one isoform, and these isoforms contribute to the complexity of phenotypes (Johnson et al., 2003; Lander et al., 2001; Wang et al., 2008). Studying the translation of specific isoforms requires correctly assigning ribosome footprints to them. However, since the footprints of ribosomes are short (28–30 nucleotides), identifying the correct isoform becomes challenging. Our method provides a likelihood function for ribosome location, and can facilitate sequence alignment when more than one alignment exists. Synthetic biology is another active research area (Endy, 2005) that can benefit from our work: the ability to predict and compare the ribosome densities along different transcripts under various environmental conditions can facilitate the search for sequences with optimal translational properties and reduce the number of experimental trials necessary to build and test the sequences.
Funding
This research is supported in part by an NSF CAREER Grant DBI-0846015, a Packard Fellowship for Science and Engineering and a Math+X Research Grant from the Simons Foundation.
Conflict of Interest: none declared.
References
- Albert F.W. et al. (2014) Genetic influences on translation in yeast. PLoS Genet., 10, e1004692.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Artieri C.G., Fraser H.B. (2014) Accounting for biases in riboprofiling data indicates a major role for proline in stalling translation. Genome Res., 24, 2011–2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess-Brown N.A. et al. (2008) Codon optimization can improve expression of human genes in escherichia coli: a multi-gene study. Protein Expression Purif., 59, 94–102. [DOI] [PubMed] [Google Scholar]
- Burrus C.S. et al. (1998) Introduction to Wavelets and Wavelet Transforms. Prentice Hall, New Jersey. [Google Scholar]
- Chambolle A. et al. (1998) Nonlinear wavelet image processing: variational problems, compression, and noise removal through wavelet shrinkage. IEEE Trans. Image Process., 7, 319–335. [DOI] [PubMed] [Google Scholar]
- Chang S.G. et al. (2000) Adaptive wavelet thresholding for image denoising and compression. IEEE Trans. Image Process., 9, 1532–1546. [DOI] [PubMed] [Google Scholar]
- Charneski C.A., Hurst L.D. (2013) Positively charged residues are the major determinants of ribosomal velocity. PLoS Biol., 11, e1001508.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daubechies I. (1990) The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory, 36, 961–1005. [Google Scholar]
- Donoho D.L. (1995) De-noising by soft-thresholding. IEEE Trans. Inf. Theory, 41, 613–627. [Google Scholar]
- Donoho D.L., Johnstone I.M. (1998) Minimax estimation via wavelet shrinkage. Ann. Stat., 26, 879–921. [Google Scholar]
- Donoho D.L. et al. (1995) Wavelet shrinkage: asymptopia? J. R. Stat. Soc. Ser. B, 57, 301–369. [Google Scholar]
- Donoho D.L. et al. (1996) Density estimation by wavelet thresholding. Ann. Stat., 24, 508–539. [Google Scholar]
- Endy D. (2005) Foundations for engineering biology. Nature, 438, 449–453. [DOI] [PubMed] [Google Scholar]
- Gardin J. et al. (2014) Measurement of average decoding rates of the 61 sense codons in vivo. Elife, 3, e03735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu W. et al. (2010) A universal trend of reduced mRNA stability near the translation-initiation site in prokaryotes and eukaryotes. PLoS Comput. Biol., 6, e1000664.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardy M.A. (1993) Regression with Dummy Variables. Sage University Paper series on Quantitative Applications in the Social Sciences, series no. 07-093. Newbury Park, CA: Sage. [Google Scholar]
- Ingolia N.T. (2014) Ribosome profiling: new views of translation, from single codons to genome scale. Nat. Rev. Genet., 15, 205–213. [DOI] [PubMed] [Google Scholar]
- Ingolia N.T. et al. (2009) Genome-wide analysis in vivo of translation with nucleotide resolution using ribosome profiling. Science, 324, 218–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ingolia N.T. et al. (2011) Ribosome profiling of mouse embryonic stem cells reveals the complexity and dynamics of mammalian proteomes. Cell, 147, 789–802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson J.M. et al. (2003) Genome-wide survey of human alternative pre-mRNA splicing with exon junction microarrays. Science, 302, 2141–2144. [DOI] [PubMed] [Google Scholar]
- Johnstone I.M., Silverman B.W. (1997) Wavelet threshold estimators for data with correlated noise. J. R. Stat. Soc. Ser. B, 59, 319–351. [Google Scholar]
- Keller T.E. et al. (2012) Reduced mRNA secondary-structure stability near the start codon indicates functional genes in prokaryotes. Genome Biol. Evol., 4, 80–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerkyacharian G., Picard D. (1992) Density estimation in Besov spaces. Stat. Probab. Lett., 13, 15–24. [Google Scholar]
- Kertesz M. et al. (2010) Genome-wide measurement of RNA secondary structure in yeast. Nature, 467, 103–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kudla G. et al. (2009) Coding-sequence determinants of gene expression in Escherichia coli. Science, 324, 255–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lander E.S. et al. (2001) Initial sequencing and analysis of the human genome. Nature, 409, 860–921. [DOI] [PubMed] [Google Scholar]
- Lareau L.F. et al. (2014) Distinct stages of the translation elongation cycle revealed by sequencing ribosome-protected mRNA fragments. Elife, 3, e01257.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maertens B. et al. (2010) Gene optimization mechanisms: A multi-gene study reveals a high success rate of full-length human proteins expressed in Escherichia coli. Protein Sci., 19, 1312–1326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mallat S.G. (1989) A theory for multiresolution signal decomposition: the wavelet representation. IEEE Trans. Pattern Anal. Machine Intell., 11, 674–693. [Google Scholar]
- McManus C.J. et al. (2014) Ribosome profiling reveals post-transcriptional buffering of divergent gene expression in yeast. Genome Res., 24, 422–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pop C. et al. (2014) Causal signals between codon bias, mRNA structure, and the efficiency of translation and elongation. Mol. Syst. Biol., 10, 770.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian W. et al. (2012) Balanced codon usage optimizes eukaryotic translational efficiency. PLoS Genet., 8, e1002603–e1002603.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah P. et al. (2013) Rate-limiting steps in yeast protein translation. Cell, 153, 1589–1601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shim H. et al. (2015) Wavelet-based genetic association analysis of functional phenotypes arising from high-throughput sequencing assays. Ann. Appl. Stat., 9, 665–686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silverman B.W. (1986) Density Estimation for Statistics and Data Analysis. Chapman and Hall, London. [Google Scholar]
- Stadler M., Fire A. (2011) Wobble base-pairing slows in vivo translation elongation in metazoans. RNA, 17, 2063–2073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R. (1996) Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B, 58, 267–288. [Google Scholar]
- Tuller T. et al. (2010a) An evolutionarily conserved mechanism for controlling the efficiency of protein translation. Cell, 141, 344–354. [DOI] [PubMed] [Google Scholar]
- Tuller T. et al. (2010b) Translation efficiency is determined by both codon bias and folding energy. Proc. Natl. Acad. Sci., 107, 3645–3650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuller T. et al. (2011) Composite effects of gene determinants on the translation speed and density of ribosomes. Genome Biol., 12, R110.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villasenor J.D. et al. (1995) Wavelet filter evaluation for image compression. IEEE Trans. Image Process., 4, 1053–1060. [DOI] [PubMed] [Google Scholar]
- Wand M.P, Jones M.C. (1994) Kernel Smoothing. Chapman and Hall, London. [Google Scholar]
- Wang E.T. et al. (2008) Alternative isoform regulation in human tissue transcriptomes. Nature, 456, 470–476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinberg D.E. et al. (2016) Improved ribosome-footprint and mRNA measurements provide insights into dynamics and regulation of yeast translation. Cell Rep., 14, 1787–1799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao P., Yu B. (2006) On model selection consistency of lasso. J. Machine Learn. Res., 7, 2541–2563. [Google Scholar]
- Zur H., Tuller T. (2012) Strong association between mRNA folding strength and protein abundance in S. cerevisiae. EMBO Rep., 13, 272–277. [DOI] [PMC free article] [PubMed] [Google Scholar]