Simultaneous prediction of enzyme orthologs from chemical transformation patterns for de novo metabolic pathway reconstruction

Abstract

Motivation: Metabolic pathways are an important class of molecular networks consisting of compounds, enzymes and their interactions. The understanding of global metabolic pathways is extremely important for various applications in ecology and pharmacology. However, large parts of metabolic pathways remain unknown, and most organism-specific pathways contain many missing enzymes. Results: In this study we propose a novel method to predict the enzyme orthologs that catalyze the putative reactions to facilitate the de novo reconstruction of metabolic pathways from metabolome-scale compound sets. The algorithm detects the chemical transformation patterns of substrate–product pairs using chemical graph alignments, and constructs a set of enzyme-specific classifiers to simultaneously predict all the enzyme orthologs that could catalyze the putative reactions of the substrate–product pairs in the joint learning framework. The originality of the method lies in its ability to make predictions for thousands of enzyme orthologs simultaneously, as well as its extraction of enzyme-specific chemical transformation patterns of substrate–product pairs. We demonstrate the usefulness of the proposed method by applying it to some ten thousands of metabolic compounds, and analyze the extracted chemical transformation patterns that provide insights into the characteristics and specificities of enzymes. The proposed method will open the door to both primary (central) and secondary metabolism in genomics research, increasing research productivity to tackle a wide variety of environmental and public health matters.

Availability and Implementation:

Contact: maskot@bio.titech.ac.jp

1 Introduction

Metabolic pathways are an important class of molecular networks that consist of chemical compounds (or metabolites), enzyme proteins and their interactions. The understanding of global metabolic pathways is extremely important for various applications in ecology (Heidel-Fischer and Vogel, 2015) and pharmacology (Newman and Cragg, 2012). However, large parts of metabolic pathways remain unknown, and most organism-specific pathways contain many missing enzymes. For example, it is estimated that more than one million compounds exist in the plant kingdom (Afendi et al., 2012), although the number of enzymes that are experimentally verified and approved by the International Union of Biochemistry and Molecular Biology (IUBMB) is only approximately 5600 (McDonald and Tipton, 2014). This indicates our lack of knowledge on enzymatic reactions (Fig. 1a) . It is still difficult to experimentally verify enzyme functions in biological processes; thus, there is a strong need for in silico metabolic pathway reconstruction (Karp, 2004).

Fig. 1.

Possible approaches for metabolic pathway reconstruction. Nodes and edges indicate metabolites (chemical compounds) and reactions, respectively. Black nodes indicate compounds for which at least one reaction is known. White nodes indicate compounds for which chemical structures are identified but no reactions are known (referred to as ‘orphan metabolites’). Bold solid lines indicate well-characterized enzymatic reactions for which at least an enzyme is known. Dotted lines indicate putative reactions (previously unknown reactions) for which no enzymes are not known. (a) Known metabolic pathways are surrounded by many orphan metabolites. (b) Enzyme prediction by sequence homology is applicable to reactions with known enzymes. (c) Missing enzyme prediction is performed with gene/protein similarity based on gene co-expression and other omics data. (d) Enzyme prediction by chemical structures, which is the focus of this study, enables the de novo reconstruction of metabolic pathway by finding possible enzymes for putative reactions involving orphan metabolites

A variety of methods have been developed for the in silico reconstruction of metabolic pathways. They can be categorized into three approaches (Fig. 1). The most traditional approach assigns putative enzyme genes to appropriate positions in pre-defined reference pathways based on sequence homology with genes across different organisms (Fig. 1b). This approach is useful for central metabolism (often referred to as primary metabolism), which is common in many organisms, and a number of software packages enabling this approach, such as KAAS (Moriya et al., 2007), MG-RAST (Meyer et al., 2008), Model SEED (Henry et al., 2010), MEGAN (Huson et al., 2011), MAPLE (Takami et al., 2012), BlastKOALA and GhostKOALA (Kanehisa et al., 2016), are available.

However, reference pathways are not available for most of the surrounding metabolism (often referred to as secondary metabolism) that forms a much larger part of the global metabolic pathway (Fig. 1a), because most of the compounds and enzymes are specific to a limited number of organisms and are poorly characterized. This secondary metabolism contains a vast number of ‘orphan metabolites’, the compounds for which no enzymatic reactions or enzyme proteins are yet known. Therefore, one of the challenging issues in systems biology is the de novo reconstruction of global metabolic pathways, i.e. identifying previously unknown reactions and enzymes that are not yet included in the reference pathway maps.

The de novo reconstruction of metabolic pathways has two goals: (i) elucidation of putative reactions (previously unknown reactions) among compounds and (ii) elucidation of the associated enzymes catalyzing the putative reactions. Toward the first goal, several in silico methods have been developed based on the chemical structures of compounds by hypothesizing intermediate compounds necessary between the source and target compounds (Darvas, 1988; Ellis et al., 2008; Faulon and Sault, 2001; Greene et al., 1999; Moriya et al., 2010; Talafous et al., 1994) or by predicting the enzymatic reaction-likeness among many compounds; that is, whether given pairs of compounds can be chemically interconverted by single enzymatic reactions (Hatzimanikatis et al., 2005; Kotera et al., 2008, 2013, 2014a; Nakamura et al., 2012; Yamanishi et al., 2015). All of these previous methods fail to address the second goal, i.e. enzyme prediction for previously unknown reactions.

The use of genomic features and other omics data (gene orders, phylogenetic profiles, gene expression profiles) is a possible approach to enzyme prediction (Enright et al., 1999; Huynen et al., 2000; Kharchenko et al., 2004; Marcotte et al., 1999; Osterman and Overbeek, 2003; Overbeek et al., 1999; Yamanishi et al., 2007). However, this approach is applicable only to missing enzymes that are located near well-characterized enzymes on known metabolic pathways (Fig. 1c), so it cannot handle reactions outside of existing pathway maps.

Enzyme prediction is related to reaction classification. Previous studies have focused on the automated classification of enzymatic reactions from chemical structures (Egelhofer et al., 2010; Hu et al., 2010; Kotera et al., 2004; Latino and Aires-de Sousa, 2009; Matsuta et al., 2013; Nath and Mitchell, 2012; O’Boyle et al., 2007; Rahman et al., 2014; Yamanishi et al., 2009). All these previous methods attempted to predict the Enzyme Commission (EC) numbers or sub-subclasses; that is, grouping enzymes by known reactions. However, because of the principle of EC numbers and sub-subclasses, it is not suitable to use them for predicting enzymes that catalyze previously unknown reactions. Thus, the direct use of enzyme orthologs (grouping enzymes by sequence homology) is required.

In this article, we propose a novel method for the de novo reconstruction of metabolic pathways using metabolome-scale compound sets (Fig. 1d). This approach enables the prediction of putative reaction networks among compounds and the prediction of the associated enzyme orthologs catalyzing the putative reactions in a seamless manner. We have already established an efficient supervised method that enables the prediction of putative reaction networks among compounds (Kotera et al., 2013, 2014a; Yamanishi et al., 2015). In this work, we develop a novel algorithm to predict enzyme orthologs catalyzing the putative reactions. This new algorithm detects the chemical transformation patterns of substrate–product pairs using chemical graph alignments, and constructs a set of joint learning (JL)-based classifiers to simultaneously predict the enzyme orthologs that could catalyze the putative reactions of these substrate–product pairs. In the results section, we demonstrate the usefulness of the proposed method by applying it to some tens of thousands of metabolic compounds, and analyzing the extracted chemical transformation patterns that provide insight into the characteristics and specificities of enzymes. The proposed method will open the door to both primary (central) and secondary metabolism in genomics research, increasing research productivity to tackle a wide variety of environmental and public health matters.

2 Materials

2.1 Enzyme orthologs

Enzymatic reactions and their associated enzyme orthologs were obtained from the KEGG database (Kanehisa et al., 2014). An ortholog is a group of homologous protein-encoding genes that are thought to have the same biological function in different organisms. To retrieve enzyme orthologs, we used KEGG Orthology (KO) database. Each KO entry has an identifier (K number) consisting of the letter ‘K’ and a following five-digit numeral (e.g. K00001 for alcohol dehydrogenase [EC:1.1.1.1]). Starting from 17 553 KO entries, we collected only the orthologs that included complete EC numbers in their definitions (incomplete EC numbers such as EC 1.1.1.‐were not considered); 3584 orthologs were obtained. In this study, we refer to such orthologs as ‘an enzyme ortholog’, or just ‘an enzyme’ for short. We use the word ‘an enzyme protein’ when we mean one of the proteins belonging to the enzyme ortholog.

A sequence similarity matrix of all enzyme orthologs was constructed as follows. First, we regarded at most three enzyme proteins present in eukaryotes and also in prokaryotes as the representative proteins for each enzyme ortholog. Subsequently, we evaluated the similarity among the enzyme orthologs using the maximum value of Smith-Waterman scores (Smith and Waterman, 1981), from the all-to-all comparison of enzyme proteins between enzyme orthologs.

2.2 Chemical structures of metabolic compounds

The chemical structures of metabolites (compounds) were retrieved from the KEGG LIGAND database (Kanehisa et al., 2014), and are converted to the KEGG Chemical Function (KCF) format (Hattori et al., 2003). In the KCF format, atoms and bonds in a chemical structure were represented as vertices and edges, respectively (with the exception of hydrogen atoms). Each vertex is given a label representing different physicochemical properties [e.g. ‘C1a’ for a methyl carbon (CH₃−)]. Hydrogen atoms were implicitly represented in the attached atoms (see http://www.genome.jp/kegg/reaction/KCF.html). Chemically identical compounds with the same structures (duplicates) were removed, so the chemical structures of all compounds were unique. A total of 15 714 metabolic compounds were used in this study. The number of all possible compound–compound pairs (involving 15 714 compounds) is 246 914 082.

2.3 Substrate–product pairs in enzymatic reactions

Substrate–product pairs in enzymatic reactions (also referred to as reactant pairs) were obtained from the KEGG RPAIR database (Kanehisa et al., 2014). A substrate–product pair is defined as the pair of a substrate and a product with a conserved chemical moiety in an enzymatic reaction. For example, an enzymatic reaction ‘ethanol + NAD⁺  = > acetaldehyde + NADH + H⁺’ is decomposed into two substrate–product pairs ‘ethanol - acetaldehyde’ and ‘NAD⁺ - NADH’ based on the flow of atoms other than hydrogen atoms. Of these, frequently used pairs such as the oxidoreduction cofactors ‘NAD⁺ - NADH’ are given the label ‘cofac’, whereas the remaining pairs such as ‘ethanol - acetaldehyde’ are given the label ‘main’. In this study, the substrate–product pairs that have only the ‘main’ label were retrieved, and different reaction directions were dealt with as different pairs (e.g. ‘ethanol–acetaldehyde’ and ‘acetaldehyde–ethanol’) in order to avoid missing the similarity between the forward direction of a reaction and the reverse of another reaction.

In order to explain the value of substrate–product pairs, we clarified the difference between the two vocabularies ‘reaction’ and ‘transformation’. The use of the word ‘reaction’ concerns all molecules in the equation, such as ‘ethanol + NAD⁺ = > acetaldehyde + NADH + H⁺’, whereas the use of ‘transformation’ only concerns a change in the substrate, such as ‘ethanol  = > acetaldehyde’ (Jones and Bunnett, 1989). In other words, a substrate–product pair describes a transformation. In analyzing putative novel reactions that are not yet well characterized, it is more useful to deal with transformations, because transformations are available in many cases even when the reactions are not apparent (Kotera et al., 2014b). We therefore use substrate–product pairs for the de novo reconstruction of metabolic pathways. For the sake of simplicity, we use the word reaction in this paper, considering that a substrate–product pair partially describes the characteristics of a reaction.

We used 7022 substrate–product pairs whose enzymes are known as gold standard data, in which 2514 out of 3584 enzyme orthologs were assigned to at least one substrate–product pair. Known substrate–product pairs were regarded as positive examples for one of the 2514 enzyme orthologs, whereas the remaining substrate–product pairs were regarded as negative examples for the enzyme ortholog. Note that the numbers of positive examples and negative examples differ from enzyme to enzyme.

2.4 Chemical transformation pattern descriptors

The design of chemical transformation patterns of substrate–product pairs is crucial for the task of enzyme prediction. We represented each substrate–product pair by a high-dimensional descriptor based on chemical substructure changes between a substrate and a product using Pairwise Chemical Aligner (PACHA), because it worked the best among existing chemical descriptors for enzymatic reaction-likeness prediction according to previous work (Yamanishi et al., 2015). We applied PACHA to perform a chemical graph alignment in order to detect chemical changes between two chemical compounds, and represented each substrate–product pair as an integer-valued vector (the PACHA feature vector) that describes conserved atoms, as well as generated and eliminated bonds. As the result of this effort, 7022 substrate–product pairs were represented by 3569-dimensional PACHA feature vectors.

We also applied this operation to all possible pairs of compounds in addition to known substrate–product pairs. Note that, in this article, we use the words ‘compound–compound pairs’ when we consider all possible pairs, and the words ‘substrate–product pairs’ when we specifically mention the pairs that occur in known reactions. As the result of this effort, 246 914 082 compound–compound pairs involving 15 714 compounds were represented by 3569-dimensional PACHA feature vectors.

3 Methods

The de novo reconstruction of metabolic pathways consists of (i) prediction of putative reaction networks and (ii) prediction of the associated enzymes catalyzing the putative reactions. Here we present a novel algorithm for the second task.

3.1 Predictive models for enzyme ortholog prediction

We address the problem of enzyme ortholog prediction by focusing on the chemical transformation patterns of compound–compound pairs (e.g. substrate–product pairs). Note that there are thousands of candidates for enzyme orthologs, and different enzyme orthologs may have common characteristics in terms of reaction mechanisms and amino acid sequences. The same reactions are sometimes catalyzed by multiple enzymes. Thus, we propose to formulate the problem in the framework of supervised multiple label prediction.

Suppose that there are M enzyme orthologs, and we are given N compounds as $C_1,C_2,\dots ,C_N$ and all possible compound–compound pairs as $(C_1,C_2),(C_1,C_3),\dots ,(C_{N-1},C_N)$. We consider predicting which enzyme orthologs would catalyze the putative reaction; i.e. the (i, j)-th compound–compound pair (C_i, C_j) $i,j=1,2,\dots ,N$. Each compound–compound pair (C_i, C_j) is represented by a D-dimensional feature vector as $\varphi (C_i,C_j)$. For example, a compound–compound pair is represented by the PACHA feature vector based on the chemical graph alignment between the two compound structures in this study.

We construct a learning set of compound–compound pairs that are substrate–product pairs for which the associated enzyme orthologs are known. There are M candidates for enzyme orthologs, and each compound–compound pair in the learning set is assigned a binary class label representing the m-th enzyme ortholog ($m=1,2,\dots ,M$). Let $y_{m,i,j}\in \{+1,-1\}$ be the class label for the m-th enzyme ortholog assigned to (C_i, C_j), where $y_{m,i,j}=+1$ means that (C_i, C_j) is catalyzed by the m-th enzyme ortholog, and $y_{m,i,j}=-1$ means that (C_i, C_j) is not catalyzed by the m-th enzyme ortholog.

We construct a predictive model to predict whether or not a given compound–compound pair (C_i, C_j) would be catalyzed by the m-th enzyme ortholog ($m=1,2,\dots ,M$). Linear models are a useful tool to analyze extremely high-dimensional data for both prediction and feature extraction tasks. Thus, we adopt a linear function defined as $f_m(C_i,C_j)=w_m{}^{\mathsf{T}}\varphi (C_i,C_j)$, where w_m is a D-dimensional weight vector for the m-th enzyme ortholog. We represent a set of M model weights by a D × M matrix defined as $W:=[w_1,w_2,\dots ,w_M]$, and estimate the weight matrix $W$ by minimizing an objective function based on the learning set.

3.2 Joint learning of multiple models

In order to overcome the scarcity of pre-knowledge concerning relationships between substrate–product pairs and enzyme orthologs, we propose to jointly learn individual predictive models f₁, f₂,…,f_M, sharing information across M enzyme orthologs.

We attempt to jointly estimate all the weight vectors $w_1,w_2$,…,w_M in the models by minimizing the logistic loss as follows:

$$R(W)={\displaystyle {\sum }_{m=1}^M{\displaystyle {\sum }_{i=1}^N\left\{{\displaystyle {\sum }_{j=1}^{i-1}{P}_{m,i,j}}+{\displaystyle {\sum }_{j=i+1}^N{P}_{m,i,j}}\right\}}},$$

where

$$P_{m,i,j}=\log (1+\exp (-y_{m,i,j}{w}_m{}^{\mathsf{T}}\varphi (C_i,C_j))).$$

We introduce a regularization term $\Omega (W)$ to the loss function in order to enhance the generalization properties. Thus, the optimization problem is written as follows:

$$\underset{W}{\min }R(W)+\Omega (W).$$ (1)

Here we introduce two kinds of regularization terms. First, we use a standard ridge regularization term to avoid the over-fitting problem, which is defined as

$${\Omega }_r:=\frac{1}{2}\text{T}r(W{W}^{\mathsf{T}}).$$

Second, we design another regularization term reflecting the amino acid sequence similarities among enzyme orthologs. In this study we evaluated the similarity among enzyme orthologs using the Smith-Waterman score, and construct an M ×  M similarity matrix $S$ for enzyme orthologs in which each element $S_{i,j}$ is a similarity score between the i-th and j-th enzyme orthologs (see the Materials section for more details). Then, we introduce the following regularization term:

$${\Omega }_s(W):=\frac{1}{4}{\displaystyle {\sum }_{l=1}^M{\displaystyle {\sum }_{m=1}^M{S}_{l,m}}}\Vert \frac{w_l}{\sqrt{K_{l,l}}}-\frac{w_m}{\sqrt{K_{m,m}}}\Vert$$

$$=\frac{1}{2}\text{T}r(W{L}_s{W}^{\mathsf{T}}),$$

where $\mathrm{\Vert }·\mathrm{\Vert }$ is the Euclidean norm, $K$ is a diagonal matrix defined as $K_{l,l}:={\sum }_{m=1}^M{S}_{l,m}$, and L_s is a symmetric normalized Laplacian defined as $K^{-1/2}(K-S)K^{-1/2}$. The regularization term ${\Omega }_s(W)$ has the effect of making the weight vectors w_i and w_j close to each other if $S_{l,m}$ is high.

Finally, we introduce the following regularization term in the optimization problem (1):

$$\Omega (W):={\lambda }_s{\Omega }_s(W)+{\lambda }_r{\Omega }_r(W),$$

where ${\lambda }_s\ge 0$ and ${\lambda }_r\ge 0$ are hyper-parameters to control the strength of the regularization terms Ω_s and Ω_r, respectively.

Because Laplacian matrices are positive-semidefinite, the loss function and the regularization terms are convex. Thus, the optimization problem (1) can be solved by using standard gradient-based methods. We apply the Limited memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) algorithm (Liu and Nocedal, 1989) with the following derivatives:

$${\left[\frac{\partial \text{R}(W)}{\partial W}\right]}_{*,m}={\displaystyle {\sum }_{i=1}^N\left\{{\displaystyle {\sum }_{j=1}^{i-1}\frac{\partial P_{m,i,j}}{\partial w_m}}+{\displaystyle {\sum }_{j=i+1}^N\frac{\partial P_{m,i,j}}{\partial w_m}}\right\}},$$

where ${[·]}_{*,m}$ denotes the m-th column vector of a matrix, and the derivatives are calculated as follows:

$$\frac{\partial P_{m,i,j}}{\partial w_m}=-\varphi (C_i,C_j)\frac{y_{m,i,j}\exp (-y_{m,i,j}{w}_m{}^{\mathsf{T}}\varphi (C_i,C_j))}{1+\exp (-y_{m,i,j}{w}_m{}^{\mathsf{T}}\varphi (C_i,C_j))}.$$

The derivatives of the regularization terms can be calculated as follows:

$$\frac{\partial {\Omega }_s(W)}{\partial W}=W{L}_s, \frac{\partial {\Omega }_r(W)}{\partial W}=W.$$

3.3 New enzyme ortholog prediction for any compound–compound pairs

Once we have learned the predictive models, which is estimating $W$, we can apply the predictive model to newly given compound–compound pairs for which the associated enzyme orthologs are unknown. Given a new compound–compound pair $(C_k^{(\text{new})},C_{\ell }^{(\text{new})})$ $(k,l=1,2,\dots .,N_{\text{new}})$, where N_new is the number of new unique compounds, the enzyme ortholog prediction is performed with the learned model $f_m(m=1,2,\dots ,M)$. If the output of $f_m(C_k^{(\text{new})},C_{\ell }^{(\text{new})})$ is a high score, the new compound–compound pair is predicted to be catalyzed by the m-th enzyme ortholog.

3.4 Feature extraction of enzyme-specific chemical transformation patterns

Linear models also have an interpretability of features. Since each element of a feature vector $\varphi (C_i,C_j)$ corresponds to an element of the weight vector w_m, we can extract effective features contributing to the prediction by sorting the feature elements of $\varphi (C_i,C_j)$ according to the corresponding values of the weight vector w_m in the model $f_m(m=1,2,\dots ,M)$. In this study, we extract highly weighted features as the enzyme-specific chemical transformation patterns of the m-th enzyme ortholog.

4 Results

4.1 Performance evaluation of the enzyme ortholog prediction

We tested the ability of the proposed JL method to predict enzyme orthologs from compound–compound pairs (i.e. substrate–product pairs) based on their chemical structure data. We used the PACHA feature vectors to represent the chemical substructure transformation patterns of compound–compound pairs. As a baseline method, we tested the nearest neighbor (NN) method, because the similarity search is the most popular reaction classification approach (Kotera et al., 2004; Rahman et al., 2014; Yamanishi et al., 2009), assuming that the substrate–product pairs associated with the same enzyme are likely to share conserved chemical substructures and their transformation patterns.

As gold standard data, we used 7070 substrate–product pairs associated with at least one of the 2514 enzyme orthologs, where compound–compound pairs associated with an enzyme ortholog were regarded as positive examples and the other compound–compound pairs were regarded as negative examples for the enzyme ortholog. We performed the 5-fold cross-validation as follows. First, we randomly split compound–compound pairs in the gold standard data into five subsets of roughly equal size. Second, we took each subset as a test set and the remaining four subsets as a training set. Note that we used the same training set and the same test set across all enzyme orthologs. Third, we constructed predictive models based on only the training set. Finally, we evaluated the prediction accuracy using the prediction scores of compound–compound pairs in the test set over the five folds. We evaluated the prediction performance using the receiver operating characteristic (ROC) curve, and summarized the performance by the area under the ROC curve (AUC) score.

Figure 2 shows the AUC scores for the 2514 enzyme orthologs resulting from the five-fold cross-validation experiments with the baseline NN method and the proposed JL method. The upper three panels show index-plots of the AUC scores (upper left and middle) and a scatter-plot of the AUC scores (upper right) for the NN and JL methods. In most cases, the JL method outperformed the NN method in terms of higher AUC scores, suggesting that JL is meaningful for the prediction of enzyme orthologs. These results suggest that the proposed JL method can capture the important features of enzyme-specific changes in chemical structure that occur during reactions more effectively than NN method.

Fig. 2.

Evaluation of the ability of the baseline NN method and the proposed JL method to predict 2514 enzyme orthologs. The upper left and upper middle panels show index-plots of the AUC scores of NN and JL, respectively. The upper right panel shows a scatter-plot of the AUC scores between NN and JL. The bottom left and bottom middle panels show scatter-plots of the AUC scores against the degrees (the number of positive examples for each enzyme ortholog) for NN and JL, respectively. The bottom right panel shows a scatter-plot of the average AUC scores calculated on the same degrees between NN and JL

The bottom left and bottom middle panels in Figure 2 show the AUC scores based on the degrees (the number of positive examples for each enzyme ortholog) for the NN method and the JL method, respectively. It can be seen that the AUC scores generally increase with the degrees of enzyme orthologs. This implies that it is difficult to predict enzyme orthologs from compound–compound pairs when the number of known substrate–product pairs in the learning set is small because of the narrow substrate specificity of enzymes. The bottom right panel in Figure 2 shows a comparison of the average AUC scores calculated on the same degrees, obtained using the NN method and the JL method. The JL method worked better than the NN method for any degree, which suggests that the JL method can effectively predict the responsible enzyme orthologs of given compound–compound pairs in practice.

Figure 3 shows several examples of enzyme orthologs and known reactions with various AUC scores obtained while performing the 5-fold cross-validation experiments. In general, the enzyme orthologs with high AUC scores tend to act on a relatively large number of substrates, mediating common types of chemical changes to the characteristic common substructures. A typical example is K05278 (flavonol synthase), which is known to act on four substrates, all mediating the hydroxylation of flavonoid structures. K08710 (N-isopropylammelide isopropylaminohydrolases) are known to catalyze two reactions (RP09384 and RP05147). These reactions are not exactly the same type. RP09384 is the hydrolysis of a primary amine (R-NH2), while RP05147 is the hydrolysis of a secondary amine (R-NH-R′). Nevertheless, they share common characteristics in terms of reactions (hydrolysis of an amine) and a conserved substructure (an ammelide residue), resulting in a relatively high AUC score. If an ortholog is associated with just one known reaction and the reaction has fewer characteristics, it is still difficult to yield high AUC scores (e.g. K00541 and K00933).

Fig. 3.

Examples of enzyme orthologs and known reactions with various AUC scores obtained while performing the five-fold cross-validation experiments

4.2 Extraction of enzyme-specific chemical transformation patterns

The proposed predictive models can extract enzyme ortholog-specific chemical transformation patterns based on highly weighted features in the models. The extracted features correspond to the elements of the PACHA feature vectors, which represent the conserved atoms, the atoms in which the physicochemical properties (or the functional groups) changed, and the chemical bonds generated/eliminated during the reaction.

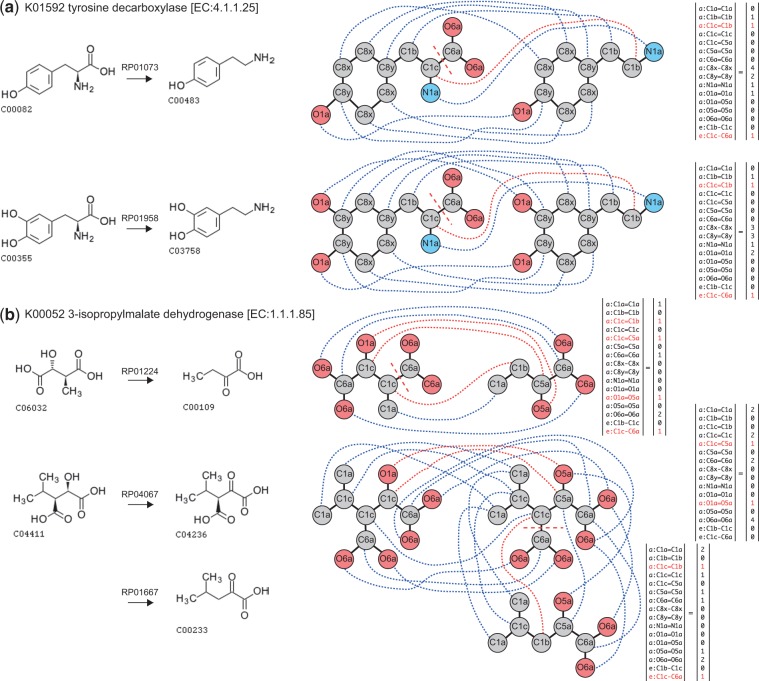
Figure 4 shows several examples of the extracted chemical transformation patterns. The first example is K01592, tyrosine decarboxylase [EC:4.1.1.25]. This enzyme is known to catalyze two reactions, RP01073 and RP01958, which are the same type of reaction, but with different substrates (Fig. 4a, left). The chemical alignment highlighted atoms and chemical bonds that were conserved and changed (Fig. 4a, middle), and they were represented as the PACHA feature vectors (Fig. 4a, right). The two reactions catalyzed by the enzyme ortholog K01592 share many features in common, including ‘e:C1c-C6a’, which represents decarboxylation from a branched sp3 carbon, ‘a:C1c=C1b’, which represents the transformation of a branched sp3 carbon into a methylene carbon, and ‘a:N1a=N1a’, which represents the conserved amino group. These three characteristics can be considered collectively and referred to as ‘decarboxylation from alpha-amino acids’. These common characteristics were represented as the non-zero elements in the PACHA feature vectors, and the corresponding non-zero elements were highly weighted in the models.

Fig. 4.

Examples of extracted features as enzyme-specific chemical transformation patterns. (a) The left panel shows two substrate–product pairs (RP01073 and RP01958) associated with enzyme ortholog K01592, tyrosine decarboxylase. (b) The left panel shows three substrate–product pairs (RP01224, RP04067 and RP01667) associated with enzyme ortholog K00052, 3-isopropylmalate dehydrogenase. In (a) and (b), the chemical graph alignments of the compounds are shown in the middle. Red dashed lines indicate the elimination of chemical bonds, red dotted lines indicate the atoms that change their labels (functional groups), and blue dotted lines indicate the atoms that are preserved during the reaction. The corresponding PACHA feature vectors are shown at the right. Features representing conserved chemical substructures are colored black and the features representing chemical changes are colored red

The second example is K00052, 3-isopropylmalate dehydrogenase [EC:1.1.1.85], which is also known to act on two different substrates (Fig. 4b, left). The reaction converting D-erythro-3-methylmalate (C06032) into 2-oxobutanoate (C00109) involves two chemical changes (RP01224): dehydrogenation of a secondary hydroxy group ‘a:O1a=O5a,” and decarboxylation from a branched sp3 carbon ‘e:C1c-C6a’. The second substrate is 3-isopropylmalate (C04411). It is known in this case that the enzyme catalysis consists of two steps (RP04067 and RP01667). The dehydrogenation of hydroxy group ‘a:O1a = O5a’ occurs in the first step (RP04067), and the spontaneous decarboxylation from a branched sp3 carbon ‘e:C1c-C6a’ (and ‘a:C1c=C1b’) occurs in the second step. Because of this property, these two characteristics are separately represented by two PACHA feature vectors, and the corresponding non-zero elements were highly weighted in the models.

In summary, these two examples have common characteristics (both mediate decarboxylation) and different characteristics (only K00052 mediates dehydrogenation, and the conserved atoms are also different). Our method successfully extracted both the common and different characteristics coded in their PACHA feature vectors.

4.3 Large-scale new predictions for enzyme orthologs

Finally, we performed a large-scale reconstruction of the metabolic pathways connecting 15 714 compounds by predicting the enzymatic reaction-likeness and the associated enzyme orthologs for all possible compound–compound pairs (246 914 082 pairs). First, we performed the enzymatic reaction-likeness prediction using a previously developed method (Yamanishi et al., 2015). This provided 54 919 compound–compound pairs as new substrate–product pairs in reactions. Note that the corresponding enzyme orthologs are not known. Second, we made a comprehensive prediction of the enzyme orthologs for the 54 919 compound–compound pairs using the JL method proposed in this paper. We trained predictive models for 2514 enzyme orthologs using all substrate–product pairs in the gold standard data, and applied the predictive models to the 54 919 compound–compound pairs (potential substrate–product pairs). As the result of this effort, we assigned high scoring enzyme ortholog candidates to each of the compound–compound pairs.

Figure 5 shows examples of newly predicted associations between reactions and enzyme orthologs. Figure 5a and b show the results for the enzyme orthologs K01592 and K00052, respectively. Note that K01592 and K00052 were also analyzed in Figure 4 in the previous subsection. For the enzyme ortholog K01592, the reactions RP01073 and RP01958 have many common PACHA features such as ‘e:C1c-C6a’, ‘a:C1c=C1b.’ and ‘a:N1a=N1a.’, which represent the characteristic ‘decarboxylation of alpha-amimo acids’ (Fig. 4a). The newly predicted reactions for K01592 also have the same characteristics (Fig. 5a), of which the first reaction was verified in the previous study (Pessione et al., 2009).

Fig. 5.

Examples of newly predicted associations between reactions and enzyme orthologs. Four predicted reactions are shown for (a) K01592 and (b) K00052, respectively. Known reactions catalyzed by (c) K01824 and (d) K00213 seem similar, and the predicted reactions for these enzyme orthologs K01824 and K00213 are the same, as shown in (e)

In contrast, for the enzyme ortholog K00052, the reac-tion RP01224 has PACHA features such as ‘a:C1c = C1b’, ‘a:O1a=O5a’, ‘a:C1c=C5a’ and ‘e:C1c-C6a’ (Fig. 4b). The two reactions RP04067 and RP01667 occur consecutively, and the reaction RP04067 has the former two PACHA features (i.e. ‘a:C1c = C1b’ and ‘a:O1a=O5a’), representing the dehydrogenation of a secondary hydroxyl group. The reaction RP01667 has the latter two PACHA features (i.e. ‘a:C1c = C5a’ and ‘e:C1c-C6a’), representing decarboxylation from a branched sp3 carbon. The extracted two PACHA features distinguished these two characteristics. The newly predicted reactions for K00052 have one of these characteristics (Fig. 5b), of which the first reaction was verified in the previous study (Suzuki et al., 1997).

As another example, the enzyme orthologs K01824 (cholesterol delta-isomerase [EC:5.3.3.5]) and K00213 (7-dehydrocholesterol reductase [EC:1.3.1.21]) mediate similar reactions involving similar substrates. K01824 catalyzes the intramolecular translocation of double bonds (Fig. 5c). K00213 catalyzes the dehydrogenation of a carbon–carbon bond to yield a double bond (Fig. 5d). In other words, one of the common characteristics between K01824 and K00213 is the dehydrogenation (intra- or inter-molecular) of a cholesterol-related substrate. Because of these common characteristics, the newly predicted reactions for the two enzyme orthologs were the same (Fig. 5e), and the second reaction was verified to be catalyzed by 7-dehydrocholesterol reductase in the previous study (Shefer et al., 1998). In summary, our proposed method allows us to find possible reactions for certain enzyme orthologs and to find possible enzyme orthologs catalyzing similar reactions.

5 Discussion

In this study, we proposed a novel method for the de novo reconstruction of metabolic pathways from metabolome-scale compound sets. This was made possible by elucidating the putative reaction networks among compounds and by predicting the associated enzyme orthologs catalyzing the putative reactions in a seamless mannar. Particularly, we developed a novel algorithm to predict enzyme orthologs catalyzing the putative reactions in the JL framework. The originality of the method lies in its ability to make predictions for thousands of enzyme orthologs simultaneously, as well as its extraction of enzyme-specific chemical transformation patterns of substrate–product pairs. We demonstrated the usefulness of the proposed method in terms of prediction accuracy, large-scale applicability and interpretability of the predictive models. The proposed method will enable us to analyze both primary (central) and secondary metabolism as well as ‘underground metabolism’, the series of alternative reactions by known enzymes (Notebaart et al., 2014; Colin et al., 2015) which is expected to be useful for various applications.

Here we elaborate on the importance of predicting enzyme orthologs rather than predicting EC numbers. There have been several previous studies to predict EC numbers from chemical structures (Egelhofer et al., 2010; Hu et al., 2010; Kotera et al., 2004; Latino and Aires-de Sousa, 2009; Matsuta et al., 2013; Nath and Mitchell, 2012; O’Boyle et al., 2007; Rahman et al., 2014; Yamanishi et al., 2009). An EC number consists of four numerals connected by dots. The first three numerals (EC sub-subclasses) represent an enzyme classification based on the reactions they catalyze, whereas full EC numbers (including the fourth numeral) are enzyme identifiers, rather than an enzyme classification. When an enzyme is found to catalyze a previously unknown reaction, a new EC number is assigned (McDonald and Tipton, 2014). This makes it reasonable to find existing EC numbers for a known reaction, but it makes no sense to predict existing EC numbers (including the fourth digit) for a previously unknown reaction. In contrast, it still makes sense to predict existing EC sub-subclasses for a previously unknown reaction. However, the number of EC sub-subclasses is much smaller than the number of enzyme orthologs, meaning that an EC sub-subclass generally corresponds to many enzyme orthologs, which makes it ineffective to use EC sub-subclasses for enzyme prediction. For this reason, we attempted to directly link enzyme orthologs to reactions.

An ortholog is a group of highly homologous genes or proteins that are considered to have the same biological function across different organisms. Examples include Clusters of Orthologous Groups (Natale et al., 2000) and KO (Kanehisa et al., 2014). Theoretically, any set of ortholog groups can be used in the analysis, but in this study we used the KO database because of its higher coverage. To date, 17 228 orthologs have been defined in the KO database, of which there are 3584 enzyme orthologs. The number of enzyme orthologs is larger than the number of EC sub-subclasses (281 EC sub-subclasses). More importantly, enzyme orthologs represent groups of enzymes based on the sequence homology, not on the reactions they catalyze. Therefore the enzyme function may change due to amino acid substitutions. A limited number of enzyme proteins within an enzyme ortholog catalyze a verified reaction. Some enzyme proteins may catalyze the same reaction or different reactions, and others may catalyze no reaction at all. It is therefore reasonable to assume that an enzyme ortholog may catalyze a novel reaction that is yet to be identified.

In order to elaborate on our results, we examined the distribution of sequence similarity calculated using the Smith-Waterman score (Smith and Waterman, 1981) within the same enzyme orthologs and between different enzyme orthologs. If the hierarchical classification of enzymes by EC numbers reflected the similarity of enzyme proteins, then enzymes in the same EC sub-subclass whould be more similar than those in different EC sub-subclasses. However, this is not always true. The first, second and third box-plots in Figure 6 show the distributions of sequence similarity scores among enzymes associated with EC 4.1.1.25 and EC 1.1.1.85 (see Figs. 4, 5a and b). The median scores between EC 4.1.1.25 and EC 1.1.1.85 were not significantly different from those within the same EC sub-subclasses. In fact, these two enzymes had common characteristics in their reactions, as shown in Figure 4a for EC 4.1.1.25 and Figure 4b for EC 1.1.1.85.

Fig. 6.

Distributions of the sequence similarity scores within the same, and between the different EC sub-subclasses. The first, second and third box-plots show the distributions of the sequence similarity scores of enzymes belonging to EC 4.1.1.25 and the ‘EC 4.1.1.*’ (enzymes within EC 4.1.1 but not EC 4.1.1.25), enzymes belonging to EC 1.1.1.85 and the ‘EC 1.1.1.*’ (enzymes within EC 1.1.1 but not EC 1.1.1.85), and enzymes belonging to EC 4.1.1.25 and EC 1.1.1.85, respectively. The fourth, fifth and sixth box-plots show the distributions of the sequence similarity scores of enzymes belonging to EC 5.3.3.5 and the ‘EC 5.3.3.*’ (enzymes within EC 5.3.3 but not EC 5.3.3.5), enzymes belonging to EC 1.3.1.21 and the ‘EC 1.3.1.*’ (enzymes within EC 1.3.1 but not EC 1.3.1.21), and enzymes belonging to EC 5.3.3.5 and EC 1.3.1.21, respectively

The fourth, fifth and sixth box-plots in Figure 6 show the distributions of the sequence similarity scores among enzymes associated with EC 5.3.3.5 and EC 1.3.1.21 (see Figures 5c and d). The median scores between EC 5.3.3.5 and EC 1.3.1.21 were larger than those within EC sub-subclass 5.3.3, and also within 1.3.1. This implies that EC 5.3.3.5 and EC 1.3.1.21 are very similar in terms of both enzymatic reactions and enzyme proteins, making it reasonable to predict the same chemical transformations (Fig. 5e). These results demonstrate an advantage of the enzyme ortholog over the EC sub-subclass for the de novo reconstruction of metabolic pathways. The proposed method is expected to reconstruct metabolic pathways consisting of a wide range of new reactions that are not defined within the existing EC numbers.