deBWT: parallel construction of Burrows–Wheeler Transform for large collection of genomes with de Bruijn-branch encoding

Abstract

Motivation: With the development of high-throughput sequencing, the number of assembled genomes continues to rise. It is critical to well organize and index many assembled genomes to promote future genomics studies. Burrows–Wheeler Transform (BWT) is an important data structure of genome indexing, which has many fundamental applications; however, it is still non-trivial to construct BWT for large collection of genomes, especially for highly similar or repetitive genomes. Moreover, the state-of-the-art approaches cannot well support scalable parallel computing owing to their incremental nature, which is a bottleneck to use modern computers to accelerate BWT construction.

Results: We propose de Bruijn branch-based BWT constructor (deBWT), a novel parallel BWT construction approach. DeBWT innovatively represents and organizes the suffixes of input sequence with a novel data structure, de Bruijn branch encoding. This data structure takes the advantage of de Bruijn graph to facilitate the comparison between the suffixes with long common prefix, which breaks the bottleneck of the BWT construction of repetitive genomic sequences. Meanwhile, deBWT also uses the structure of de Bruijn graph for reducing unnecessary comparisons between suffixes. The benchmarking suggests that, deBWT is efficient and scalable to construct BWT for large dataset by parallel computing. It is well-suited to index many genomes, such as a collection of individual human genomes, with multiple-core servers or clusters.

Availability and implementation: deBWT is implemented in C language, the source code is available at https://github.com/hitbc/deBWT or https://github.com/DixianZhu/deBWT

Contact: ydwang@hit.edu.cn

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

With the rapid development and ubiquitous application of high-throughput sequencing, many genomes have been sequenced in cutting-edge genomics studies. For example, 1000 Genomes (The 1000 Genomes Project Consortium, 2015) and UK10K (The UK10K Consortium, 2015) projects have sequenced many thousands of individual human genomes. Moreover, as the cost of sequencing continuously decreases, e.g. the cost of sequencing a human sample has already been lower than 1000 dollars (Watson, 2014), the number of genomes may explosively increase in the future. Under this circumstance, it is fundamental to well organize and index the large amount of genomes to facilitate future genomics studies.

Burrows–Wheeler Transform (BWT; Burrows and Wheeler, 1994; Ferragina and Manzini, 2000) is a self-indexing data structure having many fundamental applications, such as genome indexing (Hon et al., 2004; Karkkainen, 2007), sequence alignment (Lam et al., 2008; Li and Durbin, 2009a; Langmead and Salzberg, 2012), genome compression (Makinen et al., 2010; Cox et al., 2012), genome assembly (Simpson and Durbin, 2012; Li, 2012) and sequencing error correction (Cox et al., 2011). However, the BWT construction of genomic sequence(s) is a non-trivial task. Mainly, the core of BWT construction is to determine the lexicographical order of all the suffixes of the input sequence(s). Because there could be many repetitive sequences within a genome (Treangen and Salzberg, 2012), the cost would be prohibitively high to straightforwardly compare all the suffixes to determine their lexicographical orders. The problem is even more serious for constructing the BWT of many highly similar genomes, such as a large collection of individual human genomes, as there would be many common sequences to make the whole input even more repetitive.

Efforts have been made to BWT construction. As the BWT of input sequence(s) can be directly derived from the corresponding suffix array (SA), many extant SA construction methods (Smyth and Turpin, 2007) are applicable to this task. However, the memory footprint may be not practical for large genomic sequences, e.g. sequence over tens of Giga basepairs (Gbp), as proposed SA construction methods usually need to store the entire SA in memory. Although there are also proposed SA construction methods having smaller memory footprints (Crauser and Ferragina, 2008; Nong et al., 2014), however, they are at the expense of speed, as they need to use external memory.

Most of the state-of-the-art BWT construction methods take the advantage of the incremental construction approach, which is on the basis of the property that the relative lexicographical order of a set of sorted suffixes will not be changed by adding new suffixes. (Hon et al., 2007) proposed the first compressed suffix array (CSA) construction method using this property. Mainly, it logarithmically partitions the input sequence into blocks, and incrementally builds the CSA from shortest to longest suffixes in three steps: (i) construct the SA for a new block of suffixes; (ii) sequentially insert each of the suffixes within the new block into the CSA of the old blocks, based on the property that the relative order of the suffixes within the old blocks do not change, and the CSA values monotonically increase for the suffixes having the same initial character; (iii) merge the new and old blocks to update the CSA. There are other proposed BWT construction methods in this incremental blockwise approach, which have various implementations. (Ferragina et al., 2012) proposed a BWT construction method, bwt-disk, similar to (Hon et al., 2007), which also logarithmically partitions the input sequence. But it sorts each new block with a modified DC3 algorithm, and takes advantage of the last-first mapping (LF-mapping) property of BWT (Ferragina and Manzini, 2005) to merge new and old blocks. (Liu et al., 2014b) also proposed a BWT construction method, ParaBWT, in a similar manner. It uses a longest common prefix table to facilitate the sorting of newly added suffixes, but also merges the new and old blocks based on LF-mapping. The main contribution of this method is that it implements parallelization for the sorting of newly added blocks, which is beneficial for processing large input sequences. Other than constructing BWT for one or more large sequences, this approach is also used for indexing large collections of sequencing reads. Bauer et al. (2013) proposed BCR, an algorithm for constructing the BWT of a large set of reads. It uses a specific partition of SA, i.e. partitioning all the suffixes into blocks by their positions on the corresponding sequencing reads. With this partition, the markers (denoted as specific characters) of the reads can be fully used for improving the efficiency of the sorting and merging of blocks. (Li, 2014) also proposed a similar method, RopeBWT2, with improved ability of handling the sequences in various lengths.

Besides the blockwise incremental approach, there are also other approaches proposed. (Karkkainen, 2007) proposed a method that constructs BWT in a different blockwise manner. It samples a set of suffixes as splitters to bin all the suffixes into various blocks, and for each of the blocks, the proposed method addresses all the suffixes with difference cover sample (DCS). (Liu et al., 2014a) proposed a graphics processing unit (GPU-based) BWT construction method, CX1, for indexing a large set of short reads. The main idea of the method is to bin all the suffixes by their initial k-mers, and address all the bins with GPU-based radix sort. This method is mainly designed for reads with limited length, as the radix sort relies on the auxiliary characters attached to the reads.

The major advantage of the incremental blockwise approach is that, based on the LF-mapping property, it provides an effective way to compare suffixes with long common prefix, which is critical to the BWT construction of large repetitive genomes. However, owing to the incremental nature, this approach is not suitable for parallel computing. Considering the rapid increase of assembled genomes, the input sequence will be much larger than before. In this situation, processing the large sequence with parallel computing is favorable, especially that modern servers and clusters have much more CPU cores and RAM than before. Recent studies have made the efforts to BWT construction with parallel computing. ParaBWT implemented the parallel BWT construction for large sequence; however, the results demonstrated that it is not scalable, i.e. the speedup will saturate when a couple of threads (e.g. eight threads) are used. This is mainly owing to the bottleneck of the incremental blockwise approach. As a non-incremental approach, CX1 is scalable; however, it has limitation on the length of input sequences.

Herein, we propose de Bruijn branch-based BWT constructor (deBWT), a novel scalable parallel BWT construction method, which draws support from de Bruijn graph (dBG). The relationship between dBG and suffix trie was explored in previous studies (Marcus et al., 2014); however, it has still not been fully used in BWT construction. The main contribution of deBWT is to represent and organize the suffixes of input sequence with the property of dBG that all the copies of the same k-mer within the input sequence(s) collapse to the same vertex of the dBG of the sequence(s). The critical point of deBWT is to represent the suffixes with a novel data structure, de Bruijn branch encoding, which is derived from the unipaths of the dBG of the input sequence. This data structure facilitates the comparison between the suffixes with long common prefix. Moreover, deBWT partitions the whole BWT into blocks by their initial k-mers, and uses the property of dBG to avoid unnecessary sorting for some of the blocks, i.e. the BWT characters of some blocks can be derived in constant time based on the topology of the graph.

We benchmarked deBWT with various datasets, and the result suggests that it has fast speed and good scalability to multiple threads. Especially, deBWT is well-suited to the BWT construction of a collection of highly similar genomic sequences, such as multiple human genomes, which may have wide application in the future genomics studies.

2 Methods

2.1 Preliminary

Let a DNA sequence, $G$, be a sequence over the alphabet $\mathrm{\Sigma }=\left\{A,C,G,T\right\}$ having $\left|G\right|$ characters. Further, we assume the sequence to be indexed is $S=G\mathrm{\$}$, where $\mathrm{\$}$ is an auxiliary character, and the lexicographical order of the alphabet of $S$ is $\mathrm{A}\hspace{0.5em}<\hspace{0.5em}C<G\hspace{0.5em}<\hspace{0.5em}T<\$$. Moreover, $S\left[i\right],\mathrm{ }i=0,\dots ,\left|G\right|$ denotes the i-th character of $S$, and $S[i,j]$ denotes the substring of $S$ starting at $S\left[i\right]$ and ending at $S\left[j\right]$.

A suffix of $S$ is a substring $S[i,\left|G\right|]$, $i=0,\dots ,\left|G\right|$, and the SA of $S$ is a function that $SA\left[i\right]=j$, $i=0,\dots ,\left|G\right|$, where $j$ is the starting position of the i-th lexicographically smallest suffix of $S$. The BWT of $S$, $B^S$, is the permutation of the characters of $S$ that, $B^S\left[i\right]=S[SA\left[i\right]-1]$, if $SA\left[i\right]\ne 0$, and $B^S\left[i\right]=\mathrm{\$}$, otherwise.

The dBG of $G$, $D^G$, is a directed graph, where the vertices consist of all the k-mers of $G$. Each of the vertices is denoted as ${KM}_i$, $i=1,\dots ,\left|D^G\right|$, where $\left|D^G\right|$ is the total number of distinct k-mers. For any pair of vertices of $D^G$, $\left({KM}_i,\mathrm{ }{KM}_j\right)$, there is a directed edge ${KM}_i\to {KM}_j$, only if ${KM}_i$ and ${KM}_j$ have a k-1 overlapping, i.e. ${KM}_i\left[1,k-1\right]={KM}_j[0,k-2]$. With this definition, a set of maximal non-branched paths can be derived from $D^G$. Here, a maximal non-branch path indicates a path that meets the following conditions: (i) for the first vertex, the in-degree is 0 or >1, and the out-degree is 1; (ii) for the last vertex, the out-degree is 0 or >1, and the in-degree 1; (iii) for all the other internal vertices, the in- and out-degrees are exactly 1 (Tomescu and Medvedev, 2016). Such paths are usually termed as ‘unipaths’ or ‘unitigs’, which are commonly used in the de novo assembly of genome (Gnerre et al., 2011; Zimin et al., 2013; Tomescu and Medvedev, 2016). We used the term ‘unipath’ in the following sections. For the convenience of discussion, we assign each of the unipaths of $D^G$ an identity, $U_j,\mathrm{ }j=1,\dots ,\left|U^G\right|$, where $\left|U^G\right|$ is the total number of the unipaths.

In the following subsections, we present the unipath-based BWT construction approach at first (Section 2.2), then the overview of deBWT (Section 2.3) and more detailed information about the implementation of the various steps of the method (Section 2.4-2.7).

2.2 Unipath-based BWT construction

2.2.1 The unipath representation of suffix

The DNA sequence $G$ can be represented by a specific walk on the dBG ${\mathrm{D}}^{\mathrm{G}}$, i.e. it equals to the sequence of collapsing a specific ordered list of the vertices of ${\mathrm{D}}^{\mathrm{G}}$, $\left({KM}_0^G,{KM}_1^G,\mathrm{ }\dots ,{KM}_{\left|G\right|-k}^G\right)$, where each ${KM}_i^G,\mathrm{ }i=0,\dots ,\left|G\right|-k$ is the corresponding k-mer starting at position i of $G$, and each of the two neighboring vertices within the list is a specific edge of $D^G$. With this observation, we have the following lemma.

Lemma 1 —

a DNA sequence can be represented by an ordered list of the unipaths of the dBG.

This lemma is easy to justify by collapsing all such edges, ${KM}_i^G\to {KM}_{i+1}^G$, within the ordered list $\left({KM}_0^G,{KM}_1^G,\dots ,{KM}_{\left|G\right|-k}^G\right)$, where ${KM}_i^G$ and ${KM}_{i+1}^G$ are respectively single-out and single-in vertices. Thus, the ordered list can be re-written as $\left(U_1^G,\mathrm{ }{U}_2^G,\dots ,U_{\left|U_G\right|}^G\right)$, where $\left|U_G\right|$ is the total number of the unipaths representing $G$, each $U_i^G,i=1,\dots ,\left|U_G\right|$ represents a unipath. It is also worth noting that, some of the identities within the list may be same to each other, as a unipath could have multiple copies. For each $U_i^G$, we further define its starting position on $G$ as a Unipath Change Point (UCP), ${UCP}_i^G$. An illustration is in Supplementary Figure 1. Furthermore, we have the following corollary.

Corollary 1 —

Each of the suffixes can be represented as an ordered list of unipaths, or a substring of a specific unipath appending an ordered list of unipaths.

Each of the suffixes, $S[i,\left|G\right|]$, can be directly represented by the ordered list $\left({KM}_i^G,{KM}_{i+1}^G,\mathrm{ }\dots ,{KM}_{\left|G\right|-k}^G\right)$, where ${KM}_i^G$ is the corresponding k-mer at position i. If position i is a UCP, the ordered list of k-mers can be re-written as the ordered list of unipaths, $\left(U_j^G,U_{j+1}^G,\dots ,U_{\left|U_G\right|}^G\right)$; otherwise, it can be re-written as $\left(S\left[i,{UCP}_{j+1}^G-1\right],U_{j+1}^G,\dots ,U_{\left|U_G\right|}^G\right)$, where $U_{j+1}^G$ is the UCP closest to position i downstream, and $S\left[i,{UCP}_{j+1}^G-1\right]$ is the substring of the unipath that ${KM}_i^G$ is within (Supplementary Fig. 1). We term this list as the unipath representation of the suffix.

2.2.2 The unipath-based comparison between two suffixes

Given two suffixes of $S$, ${Suf}_i^S=S[i,\left|G\right|]$ and ${Suf}_j^S=S[j,\left|G\right|]$, where $i\ne j$,$\mathrm{ }i<\left|G\right|-k$ and $j<\left|G\right|-k$, the comparison between the two suffixes can be deduced as the following two situations.

First, considering the two ordered lists of k-mers, $\left({KM}_i^G,{KM}_{i+1}^G,\dots ,{KM}_{\left|G\right|-k}^G\right)$ and $\left({KM}_j^G,{KM}_{j+1}^G,\mathrm{ }\dots ,{KM}_{\left|G\right|-k}^G\right)$, if ${KM}_i^G\ne {KM}_j^G$, the lexicographical order of the two suffixes can be easily determined by their initial k-mers.

Secondly, if ${KM}_i^G={KM}_j^G$, the comparison is more complicated. In this situation, the two suffixes are two walks on $D^G$ starting at the same vertex, as all the copies of the same k-mers collapse to the same vertex of the dBG. Thus, $S\left[i,{UCP}_{i+1}^G-1\right]=S\left[j,{UCP}_{j+1}^G-1\right]$, as the two strings are the same substring of the corresponding unipath. An illustration is in Figure 1a.

Fig. 1.

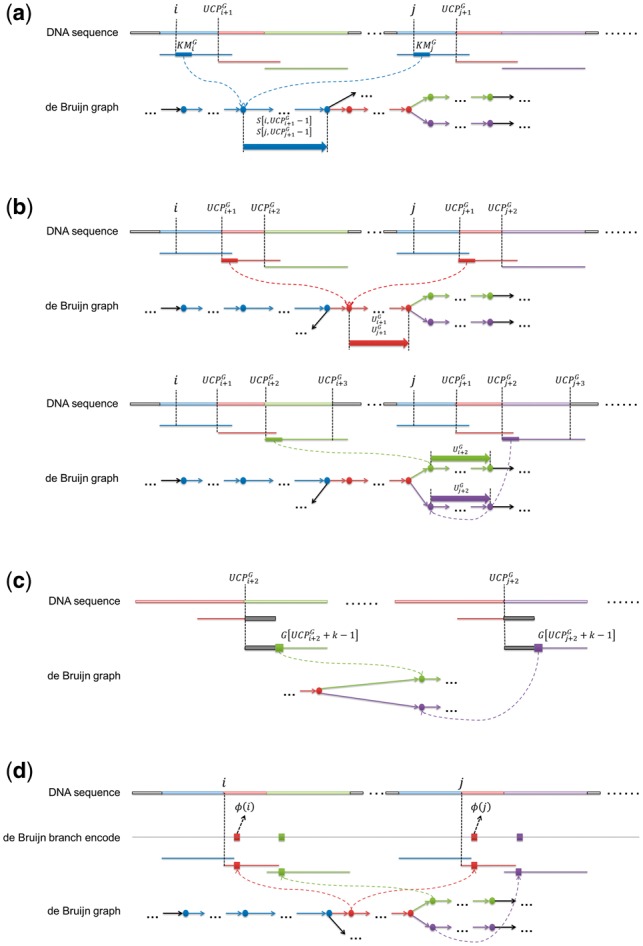
The unipath-based comparison between two suffixes with the same initial k-mer. (a) Because all the copies of the same k-mers collapse to the same vertex of the dBG, two suffixes, ${Suf}_i^G$ and ${Suf}_j^G$ with the same initial k-mer must link to the same offset of the same unipath (the copies of the unipaths on the DNA sequence are marked by segments with various colors). Thus, the lexicographical order of the two suffixes cannot be determined until the comparison reaches the end of the unipath, as all the corresponding characters of the two suffixes are same to each other. (b) When the comparison goes to new unipaths from the finished (same) unipath, the lexicographical order can be determined only if the two suffixes have two different unipaths on the corresponding positions of their unipath representation, otherwise, more unipaths are needed. In this case, both of the two suffixes have the same unipath (the red unipath) successive to the first unipath (the blue unipath), so that the comparison continues to the third unipaths. For the third unipath, the lexicographical order can be determined as the two suffixes goes to two difference branches (green and purple, respectively) at the end of the second unipath. (c) Owing to the property of dBG, two different unipaths must be different to each other at their first k-mers. Furthermore, if two different k-mers have the same precursor, their first (k-1) characters must be same to the last (k-1) characters of their precursor (the gray segments in the figure), i.e. the two branching k-mers are only different at their k-th character (the blocks marked as green and purple in the figure). In this situation, it only needs to compare the k-th characters of two unipaths to determine if they are the same unipath. (d) With this property, the de Bruijn encoding, ${\mathrm{d}\mathrm{E}}^G$, is defined as a string concatenating all such characters, $G\left[x+k\right],x=0,\dots ,\left|G\right|-k-1$, along the DNA sequence, $G$, where the k-mer, ${KM}_x^G$, at the position $x$ of $G$ is a copy of a multiple-out vertex. Each of the $G\left[x+k\right]$s is also termed as a branching character (marked as colored blocks in the figure). And for a position $j$ of $G$, $\varphi \left(j\right)$ is defined as the position of $Br\left(j\right)$ on ${\mathrm{d}\mathrm{E}}^G$, where $Br\left(j\right)$ is the branching character downstream and closest to the position j in $S$.

Then it becomes an iterative comparison between the aligned unipaths, i.e. if the two unipaths, $U_{i+1}^G$ and $U_{j+1}^G$, are different, the lexicographical order can be determined, otherwise we need to compare the following unipaths until we meet two different unipaths (Fig. 1b).

Considering the property of dBG, if the two unipaths, $U_{i+l}^G$ and $U_{j+l}^G$, are identical to each other, the starting vertices of $U_{i+l+1}^G$ and $U_{j+l+1}^G$ must be two vertices with the same precursor; thus, the first k-1 characters of the two vertices must be same, i.e. the comparison can be done by only checking the k-th characters of the two unipaths, i.e. $G\left[{UCP}_{i+l+1}^G+k-1\right]$ and $G\left[{UCP}_{j+l+1}^G+k-1\right]$ (Fig. 1c). Moreover, if the last vertex of $U_{i+l}^G$ ($U_{j+l}^G$) is a single-out vertex, the comparison can be also omitted because the next unipaths must be the same.

With these observations, we designed a novel data structure named as de Bruijn branch encoding (Fig. 1d). The de Bruijn branch encoding of $G$, ${\mathrm{d}\mathrm{E}}^G$, is defined as the concatenation of all such characters $G\left[i+k\right],\mathrm{ }i=0,\dots ,\left|G\right|-k-1$ meeting the condition that ${KM}_i^G$ corresponds to a multiple-out vertex. Each of the characters of ${\mathrm{d}\mathrm{E}}^G$ is also called a branching character. Then, for each of the ${Suf}_j^T$, $j<\left|G\right|-k$, we define its projection suffix on ${\mathrm{d}\mathrm{E}}^G$ as ${\mathrm{d}\mathrm{E}}^G\left[\varphi \left(j\right),\left|{\mathrm{d}\mathrm{E}}^G\right|-1\right]$, where $\varphi \left(j\right)$ is the ${\mathrm{d}\mathrm{E}}^G$ coordinate of the first branching character after the position j in $S$, and $\left|{\mathrm{d}\mathrm{E}}^G\right|$ is the length of ${\mathrm{d}\mathrm{E}}^G$.

Lemma 2: For two suffixes at least k bp long, their lexicographical order can be determined by comparing their projection suffixes defined by the de Bruijn branch encoding of the DNA sequence, if the initial k-mers of the two suffixes are identical.

This lemma is easy to justify with the observations mentioned above, and it provides a cost-effective solution of the comparison between two suffixes with long common prefix.

2.2.3 The k-mer partition of BWT

According to the definition of SA, the suffixes starting with identical k-mers (suppose it as ${KM}_i$) constitute a continuous block in SA, as a suffix with a different initial k-mer (e.g. ${KM}_j$) must be larger or smaller than all the suffixes starting with ${KM}_i$. Thus, given $D^G$, the BWT of $S$ can be partitioned into $\left|D^G\right|+k$ parts. $\left|D^G\right|$ of them correspond to the $\left|D^G\right|$ k-mers of $D^G$, i.e. each of the $\left|D^G\right|$ parts involves all the suffixes with a specific k-mers of $D^G$; and each of the remaining k parts corresponds to a specific suffix whose starting position is less than k bp previous to the end of $S$. This partition (called k-mer partition of BWT) can be constructed in two steps: (i) sort all the k-mers of $D^G$ and the last k suffixes of $S$ by their lexicographical order; (ii) bin all the $>k$ bp long suffixes of $S$ into the corresponding parts by their initial k-mers. After the two steps, the BWT construction becomes $\left|D^G\right|$ sub-problems, i.e. separately determining the lexicographical order of the suffixes within each of the $D^G$, as the lexicographical order of the suffixes with different k-mers have been implicitly determined during the construction of the k-mer partition.

Thus, for each of the $\left|D^G\right|$ parts corresponding to various initial k-mers, the task is the comparison of a series of suffixes with the same initial k-mer, which can be implemented with the help of the de Bruijn branch encoding ${\mathrm{d}\mathrm{E}}^G$. Moreover, the problem can be further reduced with the following lemma.

Lemma 3: If a vertex ${KM}_i$ of $D^G$ ($i=1,\dots ,\left|D^G\right|$) is single-in, the corresponding BWT part consists of $\left|{KM}_i\right|$ same characters, where $\left|{KM}_i\right|$ is the number of the copies of ${KM}_i$ in $G$, only except if the part involves the first suffix.

This lemma is obtained with the observation that if a vertex of the dBG is single-in, all the suffixes with this k-mer must have the same previous character, i.e. the BWT of this part is purely $\left|{KM}_i\right|$ copies of the first character of the precursor of ${KM}_i$. This is except for the parts involving the first suffix, as the BWT character of the first suffix is $. With this lemma, only the parts labeled by multiple-in vertices need to be sorted. Thus, there are at most $\left|U^G\right|$ sub-problems, as such vertices must be the initial k-mers of the unipaths.

2.3 Overview of the deBWT method

As in many cases, the input is not only one, but a set of DNA sequences, such as a set of genomes, chromosomes or assembled contigs, we re-define the sequence to be indexed as $S={\mathrm{G}}_1\hspace{0.17em}\#{\mathrm{G}}_2\hspace{0.17em}\#\dots \#{\mathrm{G}}_{N_D}\mathrm{\$}$, where $N_D$ is the number of input DNA sequences, and each of ${\mathrm{G}}_i,\mathrm{i}\hspace{0.5em}=\hspace{0.5em}1,\dots ,\mathrm{ }{N}_D$ is a specific sequence. $\#$ is another auxiliary character, and the alphabet becomes $\mathrm{A}\hspace{0.5em}<\hspace{0.5em}C<G\hspace{0.5em}<\hspace{0.5em}T<\#<\$$.

DeBWT constructs the BWT of $S$ in the following three major phases.

1. dBG building and analysis: deBWT builds a dBG of all the involved sequences $\left\{{\mathrm{G}}_1,{\mathrm{G}}_2,\dots ,{\mathrm{G}}_{N_D}\right\}$ with a user-defined parameter k, sort the k-mers to build the k-mer partition of the BWT, recognize all the unipaths as well as the multiple-out and multiple-in vertices and solves all the parts corresponding to single-in vertices.

2. de Bruijn branch encoding generation: deBWT computes the de Bruijn branch encoding of $S$ (${\mathrm{d}\mathrm{E}}^S$), bins all the suffixes of $S$ corresponding to the unsolved parts of BWT and computes their projection suffixes.

3. BWT construction with projection suffixes: for each of the unsolved BWT parts, deBWT builds the SA of the involved projection suffixes to determine the BWT characters of the part.

A schematic illustration of the method is in Figure 2.

Fig. 2.

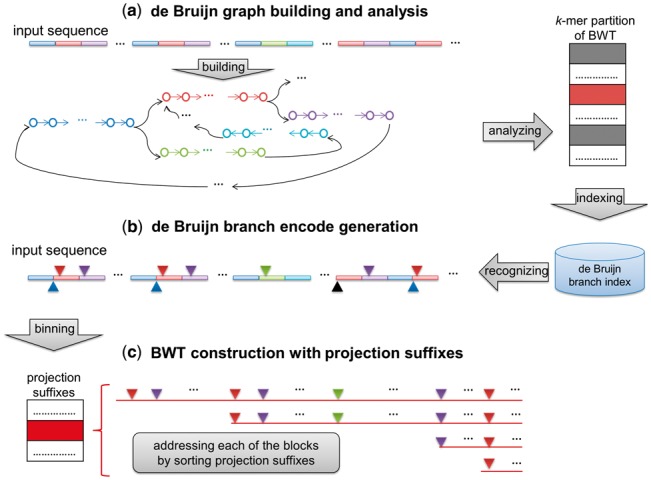
A schematic illustration of the deBWT method. (a) DeBWT initially builds a dBG of the input sequence(s) with a user-defined parameter, k, which determines the size of the vertices. The dBG is then analyzed to build the k-mer partition of the BWT and recognize all the unipaths (the colored bars in the figure indicate the copies of various unipaths of the input sequence). With the unipaths, all the multiple-in and multiple-out vertices are indexed by a hash table-based data structure, de Bruijn branch index. Moreover, all the multiple-in vertices are marked. In this case, the red block indicates the first k-mer of the ‘red’ unipath of the dBG which is a multiple-in vertex, and the grey and the white blocks respectively indicate other multiple-in and -out k-mers. (b) DeBWT scans the input sequence(s) to recognize the branching characters with de Bruijn branch index (marked as colored reverse rectangles above the input sequence) and generate the de Bruijn branch encoding. Meanwhile, the suffixes with initial k-mers corresponding to multiple-in vertices, i.e. the suffixes belonging to the unsolved parts of the BWT, are also recognized with the index (marked as colored rectangles below the input sequence). Furthermore, for each of the suffixes within the unsolved parts, deBWT calculates its $\varphi \left(·\right)$ value to determine the corresponding projection suffix and also recorded it into the de Bruijn branch index. (c) With de Bruijn branch index, deBWT addresses all the unsolved BWT parts by sorting the projection suffixes

2.4 dBG building and analysis

It needs all the k-mers as well as the numbers of their copies in $\left\{{\mathrm{G}}_1,{\mathrm{G}}_2,\dots ,{\mathrm{G}}_{N_D}\right\}$ to build the k-mer partition and solve the single-in parts, i.e. a k-mer counting task. In the current version of deBWT, Jellyfish (Marçais and Kingsford, 2011) is used. As both of the multiple-in and multiple-out vertices are needed in later steps, deBWT counts the edges of the dBG, i.e. the (k + 1)-mers, instead of the k-mers.

To build the k-mer partition of the BWT, deBWT sorts all the (k + 1)-mers by their lexicographic order, and respectively merges all the (k + 1)-mers with identical first k bp prefixes into k-mers to build the partition. For each of the k-mers, its number of copies is calculated by directly summing up the corresponding (k + 1)-mers. Meanwhile, the multiple-out vertices can also be recognized during the merging, and deBWT records all the multiple-out vertices for building the de Bruijn branch encoding in the later step.

The multiple-in vertices is then recognized based on the sorted (k + 1)-mer list. That is, deBWT partitions the sorted (k + 1)-mer list into four ordered lists, each corresponding to a specific initial character, A, C, G or T. Then deBWT recognizes all the multiple-in vertices by a four-way merging on the lists. During the merging, two tasks are done simultaneously, i.e. if a vertex is recognized as single-in, deBWT assigns it the first character of the corresponding (k + 1)-mer and the number of copies to solve the BWT part; otherwise, deBWT records the k-mer in another data structure to generate the $\varphi \left(·\right)$ function in the later step.

It is worth noting that, owing to the existence of the auxiliary character #, deBWT recognizes all the k-mers that have at least one copy previous to and next to # as multiple-out and multiple-in k-mers, respectively.

The parallelization of this step is straightforward. The k-mer counting can be directly parallelized (Marçais and Kingsford, 2011). There are many feasible parallel integer sorting approaches for sorting the (k + 1)-mers and we used a simple approach, i.e. a radix sort is implemented to partition all the (k + 1)-mers into blocks, and each of the blocks is further processed in parallel by integer quick sort. The merging of the k-mer lists is not executed in parallel; however, the cost is linear to the number of (k + 1)-mers and not expensive.

2.5 The generation of de Bruijn branch encoding and projection suffixes

DeBWT builds a hash table-based data structure, de Bruijn branch index, to index all multiple-in and multiple-out k-mers (Supplementary Fig. 2). With this index, the de Bruijn branch encoding and the $\varphi \left(·\right)$ function are simultaneously generated by scanning $S$ one time.

DeBWT initially allocates an empty string as ${\mathrm{d}\mathrm{E}}^S$, a counter ${\mathrm{C}\mathrm{d}\mathrm{E}}^S$ recording the length of ${\mathrm{d}\mathrm{E}}^S$ and a linear table, $\mathrm{P}{\mathrm{d}\mathrm{E}}^S$, which records the positions and the $\varphi \left(·\right)$ values for all the copies of the multiple-in k-mers (Supplementary Fig. 2). Each of the multiple-in k-mers occupies a series of cells of $\mathrm{P}{\mathrm{d}\mathrm{E}}^S$ as a sub-table for their own copies. Each of the sub-table can be accessed with a specific pointer.

DeBWT then scans $S$ from upstream to downstream to check each of the k-mers. For a position $i$ of $S$, if the corresponding k-mer, ${KM}_i^S$, is a multiple-in k-mer, deBWT records the character $S\left[i-1\right]$ and the value $\left({\mathrm{C}\mathrm{d}\mathrm{E}}^S+1\right)$ into the corresponding sub-table of $\mathrm{P}{\mathrm{d}\mathrm{E}}^S$; if ${KM}_i^S$ is a multiple-out k-mer, deBWT appends the branching character $S\left[i+k\right]$ to ${\mathrm{d}\mathrm{E}}^S$ and updates ${\mathrm{C}\mathrm{d}\mathrm{E}}^S$. Here, $S\left[i-1\right]$ is the BWT character of ${KM}_i^S$, and $\left({\mathrm{C}\mathrm{d}\mathrm{E}}^S+1\right)$ is the $\varphi \left(i\right)$ value, as the next branching character must be the first character of the projection suffix of ${KM}_i^S$, and $\left({\mathrm{C}\mathrm{d}\mathrm{E}}^S+1\right)$ is its position on ${\mathrm{d}\mathrm{E}}^S$.

The parallelization of this step is implemented as follows. DeBWT divides $S$ into $P$ segments, and assigns each of the segments to a specific thread to generate local ${\mathrm{d}\mathrm{E}}^S$ and $\varphi \left(·\right)$ values. The value $P$ is equal to the number of threads. It is worth noting that all the threads share the same hash table and $\mathrm{P}{\mathrm{d}\mathrm{E}}^S$ data structures with read-write locks, but have their own ${\mathrm{C}\mathrm{d}\mathrm{E}}^S$ and ${\mathrm{d}\mathrm{E}}^S$. When all the threads accomplish their own tasks, deBWT appends all the local ${\mathrm{d}\mathrm{E}}^S$s and updates the local $\varphi \left(·\right)$ values generated by thread $p\in \left\{1,\mathrm{ }2,\mathrm{ }\dots ,P\right\}$ by the following operation: assume the length of the ${\mathrm{d}\mathrm{E}}^S$ of the j-th segments is $l_j^{dE},j\in \left\{1,\mathrm{ }2,\mathrm{ }\dots ,P\right\}$, for each of multiple-in k-mers, ${KM}_i^S$, within the p-th segments ($p>0$), the corresponding $\varphi \left(·\right)$ value, $\varphi \left(i\right)$, is updated as $\varphi \left(i\right)+{\sum }_{j=0}^{p-1}{l}_j^{dE}$.

2.6 BWT construction with projection suffixes

For each of the BWT parts corresponding to the multiple-in k-mers, deBWT constructs the SA of the projection suffixes with the ${\mathrm{d}\mathrm{E}}^S$ and the $\varphi \left(·\right)$ function. The SA is built by straightforwardly quick-sorting the involved projection suffixes. As all the unsolved parts are independent, it is also easy to accomplish the tasks in parallel.

We did a modification on the recursive process of the original quick-sort method to improve the efficiency. That is, for a specific sub-array of suffixes transferred into the recursive function, deBWT checks whether all the suffixes have the same BWT characters at first. If this is the case, deBWT marks the sub-array as sorted, as the precise lexicographical order of these suffixes is not necessary for the BWT construction; otherwise, deBWT calls the original recursive function to further sort the sub-array. This modification can also be seen as an extension of Lemma 3.

2.7 Additional processing

After all the operations mentioned above, there are still $N_D\times k$ unsolved BWT characters, each corresponding to one of the suffixes, which start less than k positions before # or $. These suffixes are initially set aside, and deBWT builds the SA of such suffixes stand-alone to fill the BWT string. As there are only few such suffixes, this sorting is implemented by directly comparing the original sequences of the suffixes.

3 Results

We benchmarked deBWT with three datasets mimicking various real application scenarios. (i) A dataset consists of 10 in silico human genomes (totally 30.9 Gbp). Each of the genomes is generated by integrating the variants of a specific sample from 1000 Genomes (The 1000 Genomes Project Consortium, 2015) into the human reference genome GRCh37/Hg19. This dataset mimics the indexing of multiple individual human genomes, which has many applications in genomic studies. (ii) A dataset consists of a set of simulated contigs. As long read sequencing technologies, such as Single Molecular Real-Time sequencing, have improved the contig N50 of human genome assembly to >10 million bp (http://www.pacb.com/blog/toward-platinum-genomes-pacbio-releases-a-new-higher-quality-chm1-assembly-to-ncbi/), we randomly extracted 3000 sequences (each is about 10M bp long, totally 30.2 Gbp) from the 10 in silico human genomes with an in-house script, which is revised from Wgsim simulator (Li et al., 2009b; https://github.com/lh3/wgsim). (iii) A dataset consists of eight primate genomes including gibbon, gorilla, orangutan, rhesus, baboon, chimp, bonobo and human (downloaded from: http://hgdownload.soe.ucsc.edu/downloads.html). This dataset assessed the ability of deBWT to index more diverse genomes.

The benchmark was implemented on a server with four Intel Xeon E4820 CPUs (32 cores in total) at 2.00 GHz and 1 Terabytes RAM, running Linux Ubuntu 14.04. DeBWT uses Jellyfish (version 2.1.4; Marçais and Kingsford, 2011) for implementing the k-mer counting of the input sequences (the parameter k is configured as 31). Two recently published methods, RopeBWT2 (Li, 2014) and ParaBWT (version 1.0.8-binary-x86_64) (Liu et al., 2014b), were also performed on the same datasets for comparison.

At first, we tested the performance of deBWT with 32 threads, i.e. running with all the 32 CPU cores of the server. ParaBWT was also run with 32 threads, but RopeBWT2 was run with its default setting, as it does not support parallel computing. The elapsed time (Table 1) indicates that deBWT and ParaBWT have comparable speed, while RopeBWT2 is slower, likely owing to the fact that it does not support parallel computing and the algorithm could not be suited to long sequences. We further investigate the processing of deBWT, and found that the speed of deBWT was largely slowed down by Jellyfish owing to the format of its output file. The default output of Jellyfish is a binary file in an unpublished format. As the details about the format is unknown for us, we used the ‘dump’ command of Jellyfish to convert the output file into text file, and then converted the text file into binary file in our own format as the input of further steps. This file conversion costs a couple of hours for all the three datasets, i.e. about 60–70% of the total running time. The time cost would be much reduced if the output format of jellyfish was available, or if other k-mer counting tools with similar performance and readable output format were used. Deducting the time of file conversion, deBWT is much faster than the other two methods.

Table 1.

Running Time with 32 CPU cores (in minutes)

Methods	Human genomes	Human contigs	Primate genomes
deBWT	134	129	330
deBWT (no conversion)	48	56	100
ParaBWT	241	262	180
RopeBWT2	1694	2247	1546

‘DeBWT’ indicates the elapsed time of deBWT, and ‘deBWT (no conversion)’ deducts the time of the format conversion of Jellyfish output.

We investigated the time cost of the various steps of deBWT (Table 2). Mainly, two issues are observed.

Table 2.

The time of the various steps of deBWT (in minutes)

Steps	Human genomes	Human contigs	Primate genomes
Phase1: dBG building and analysis
k-mer counting	16	16	26
File conversion	87	74	229
k-mer sorting	3	3	8
dBG analysis	8	7	19
Phase2: The generation of de Bruijn branch encoding and projection suffixes
de Bruijn branch encoding and $\varphi \left(·\right)$ values generation	9	12	16
Phase3: BWT construction with projection suffixes
Projection suffixes sorting	4	12	10
Additional processing
Additional processing	7	6	22
Supplement
k-mer counting with KMC2	7	9	12

First, most of the core steps of deBWT, i.e. k-mer counting, k-mer sorting, de Bruijn branch encoding and $\varphi \left(·\right)$ values generation and projection suffixes sorting, are efficient. This is because of a couple of reasons. (i) The de Bruijn branch code greatly reduces the cost of sorting suffixes with long common prefixes. We investigated the lengths of the generated de Bruijn branch code, and found that, for both of the genomes and the contigs datasets, their lengths are respectively one order shorter than those of the original input sequences. Under this circumstance, the comparison between projection suffixes is much less expensive than that of the original suffixes. Furthermore, the k-mer partition of BWT also helps to reduce many unnecessary comparison operations. (ii) The designs of these steps are suitable for parallel computing, which can fully use the multiple CPU cores. It is worth noting that, besides the parallel implementation of the core steps of deBWT, the state-of-the-art k-mer counting tool also has good parallelization. As k-mer counting is still an open problem with wide application, there are a few choices for this step. We also tried a newer published tool, KMC2 (Deorowicz et al., 2015), and obtained even faster speed (Table 2). However, KMC2 also outputs a binary file, which is hard to directly interpret. It would be beneficial if the state-of-the-art k-mer counting tools have an easy-to-interpret output file. (iii) Besides the parallelism, multiple steps, i.e. k-mer counting, the radix sort of k-mers, de Bruijn branch encoding and $\varphi \left(·\right)$ values generation, have quasi linear time complexity.

Second, the I/O operation is the main issue slowing down the method. Other than the file conversion step mentioned above, there are also many I/O operations in the ‘de Bruijn graph analysis’ and the ‘additional processing’ steps. That is, in the dBG analysis step, deBWT needs to merge the files recording the four ordered lists of k-mers to recognize the multiple-in k-mers; and in the additional processing step, deBWT needs to convert the large sequences to be indexed from text (fasta format) into binary format and merge various BWT parts. Although these operations theoretically have low time complexity, they also depend on the performance of the file system of the computer as well as the implementation of the program. It is also an important future work for us to further optimize these operations.

Other than the two issues mentioned above, the time cost of the projection suffixes sorting step is especially critical, as it is the core step to handle the long repetitions within the input sequence(s). The total time cost of this step is ${\sum }_{j=1}^{\left|U^G\right|}t\left(U_j^G\right)$, where $t\left(U_j^G\right)$ is the time for solving the j-th unsolved part of the BWT. As each of the unsolved parts are handled by quicksort, the time cost can be represented as follows (Bentley and Sedgewick, 1997; Karkkainen, 2007): $t\left(U_j^G\right)=O\left(N_{j}log{N}_j+\sum _{i=1}^{N_j}DP\left({PS}_i\right)\right)$, where $N_j$ is the number of the projection suffixes involved in the unsolved part j, and $DP\left({PS}_i\right)$ is the length of the distinguishing prefix of the i-th projection suffix (denoted as ${PS}_i$) of the part. Here, the distinguishing prefix of ${PS}_i$ is the shortest prefix of ${PS}_i$, which is necessary to determine the BWT characters of the corresponding part. For the highly similar input sequences,$\mathrm{ }{\mathrm{G}}_1$, ${\mathrm{G}}_2$, …, ${\mathrm{G}}_{N_D}$, the upper bound of $DP\left({PS}_i\right)$ is $O\left(\left|{\mathrm{d}\mathrm{E}}^{G_M}\right|\right)$ in theory, owing to the existence of long repetitions, where $G_M$ is the input sequence having the longest de Bruijn branch encoding, and $\left|{\mathrm{d}\mathrm{E}}^{G_M}\right|$ is the length of the corresponding de Bruijn branch encoding. For example, two sequences ${\mathrm{G}}_i$ and ${\mathrm{G}}_j$ could be almost the same; thus, the length of distinguishing prefix could be close to the length of the de Bruijn branch encoding of the sequences. As the total number of the branching characters of $G_M$, the value $\left|{\mathrm{d}\mathrm{E}}^{G_M}\right|$ does not only depend on how many unipaths $G_M$ has, but also how many copies of the unipaths there are.

Although the theoretical upper bound is large, however, $DP\left({PS}_i\right)$ also greatly depends on the distributions of genomic variations as well as the repetitiveness of the input sequences, which could make it lower in practice. To more precisely investigate the time cost, we assessed the $\overline{{DP}_j}$ values and the ${DP}_j^M$ values of the most repetitive dataset in the benchmark (i.e. the 10 human genomes dataset), where $\overline{{DP}_j}$ and ${DP}_j^M$ are respectively the mean and maximal length of the distinguishing prefix of the projection suffixes within the j-th unsolved part. A series of quantiles of $\overline{{DP}_j}$ and ${DP}_j^M$ values of the 10 human genomes dataset are shown in Table 3. These quantiles indicate that, for most of the blocks, the distinguishing prefixes are short, e.g. the 0.90 quantile of ${DP}_j^M$ is 11 872, indicating that for 90% of the unsolved BWT parts, the max length of the distinguishing prefixes is shorter than 11 872 characters. This is not expensive to determine their lexicographical orders by a straightforward comparison. Thus, the overall cost of this step is not high, although there is still a small proportion (<0.1%) of BWT parts having long distinguishing prefixes (average value is > 298k).

Table 3.

Quantiles of $\overline{{DP}_j}$ and ${DP}_j^M$ values of the 10 human genomes dataset

Quantiles	0.50	0.90	0.95	0.99	0.999	0.9999
$\overline{{DP}_j}$	107	588	2382	95 019	298 598	515 006
${DP}_j^M$	1760	11 872	238 368	1 925 600	3 232 832	3 387 040

We also run deBWT with 8, 16, 24 threads to investigate its scalability. The results (Table 4) suggest that deBWT can gradually speedup with the increase of threads, i.e. it has good scalability. However, the speed of ParaBWT is nearly the same with the various settings on threads. This is likely owing to the incremental nature of the ParaBWT method, which may limit its performance on modern servers and clusters. The time of the various steps of deBWT with various numbers of threads is in Figure 3. It indicates that the two core steps, de Bruijn branch encoding and $\varphi \left(·\right)$ values generation and projection suffixes sorting (steps 4 and 5 in the figure), are most scalable steps, i.e. they speedup with the increasing number of threads. This property is beneficial for implementing the method with more computational resources.

Table 4.

Running time with various numbers of threads (in minutes)

Methods	8 threads	16 threads	24 threads	32 threads
Human genomes
deBWT	194	153	142	134
deBWT (no conversion)	109	68	56	48
ParaBWT	265	240	240	241
Human contigs
deBWT	183	154	123	129
vdeBWT (no conversion)	116	86	56	56
ParaBWT	294	277	276	262
Primate genomes
deBWT	423	355	332	330
deBWT (no conversion)	193	125	105	100
ParaBWT	196	182	181	180

‘DeBWT’ indicates the elapsed time of deBWT, and ‘deBWT (no conversion)’ deducts the time of the format conversion of Jellyfish output file.

Fig. 3.

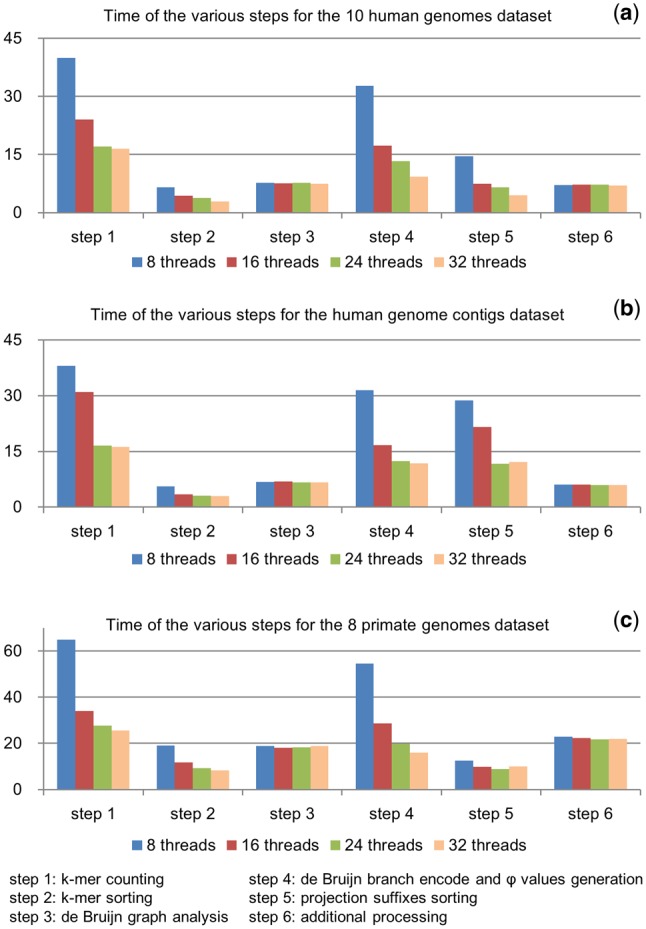
Time consumption of the various steps of deBWT. The bars respectively indicate the elapsed time (in minutes) of the various steps of deBWT for the 10 human genomes dataset (a), the human genome contig dataset (b) and the 8 primate genomes dataset (c). Bars in the same color correspond to a specific number of threads, i.e. blue, red, green and purple bars are respectively for 8, 16, 24 and 32 threads

We further run deBWT on the in silico human genome dataset with various configurations on the k parameter to investigate its effect Table 5. It can be observed from the result that, on a large range of k parameters, i.e. k = 23–31, the total running time is close, but for smaller k parameter, the time consumption is higher. This is likely owing to the fact that the moderate long k-mers (such as 23- to 31-mers) may have similar ability to span short repeats. In this situation, the structure of the dBG does not change much with these k configurations, i.e. there are similar numbers of unipaths as well as their copies in the graph. However, when k is smaller, the unipaths will be shorter and have more copies, which would make the de Bruijn branch encoding longer and more projection suffixes need to be sorted. k > 32 could have better ability to span repeats, which may improve the overall performance; however, it requires much more RAM space, as a k-mer cannot be stored by one 64-bits cell.

Table 5.

Running time of the in silico human genome dataset with various configurations on the k parameter (in minutes)

Methods	k = 19	k = 23	k = 27	k = 31
deBWT	142	124	131	134
deBWT (no conversion)	75	51	47	48

‘DeBWT’ indicates the elapsed time of deBWT, and ‘deBWT (no conversion)’ deducts the time of the format conversion of Jellyfish output file.

The memory footprint of deBWT (Table 6) depends on both of the method itself and the used k-mer counting tool. The memory usage of Jellyfish and KMC2 is highly configurable, and we set them to use relatively large memory to accomplish the k-mer counting step as fast as possible. The major RAM costs of the three phases of deBWT are different. In the first phase, the major cost originates from the data structure of k-mer sorting. Briefly, deBWT uses a linear table like $\mathrm{P}{\mathrm{d}\mathrm{E}}^S$ to bin all the k-mers; however, each cell of the table costs 16 bytes to record the string of the k-mer as well as its number of copies. The cost of the second phase is more complicated. It needs to simultaneously keep the input sequences, the de Bruijn branch index and the generated de Bruijn branch encoding in memory. Thus, the memory usage mainly depends on several issues, i.e. the size of the input sequence(s), the numbers of multiple-out and -in k-mers and the numbers of the copies of the multiple-out and -in k-mers. The last two items respectively determine the length of de Bruijn branch encoding and the number of unsolved suffixes, which need to record in memory. The numbers of the multiple-out and -in k-mers and their copies highly relate to the repetitiveness of the input genomes. We did statistics on the two human datasets (as they are more repetitive), and observed two issues (Table 7).

Table 6.

Memory footprints with 32 CPU cores (in Gigabytes)

Methods	Human genomes	Human contigs	Primate genomes
deBWT	120/78/38	120/63/34	235/203/58
ParaBWT	30	30	29
RopeBWT2	30	24	40
Supplement
KMC2	119	119	119

For the ‘x/y/z’ of deBWT in the memory columns, the x, y and z values respectively indicate the memory footprints of Jellyfish, phase1 of deBWT, and phases2 and phases3 of deBWT.

Table 7.

Statistics on the in silico human genomes and contigs

Statistics	Human genomes	Human contigs
length of input sequences	30955436371	30200003020
distinct k-mers	5073730669	4025285321
multiple-out k-mers	18820763	17238123
multiple-in k-mers	18821805	17237511
copies of multiple-out k-mers	2364004617	2301293218
copies of multiple-in k-mers	2364445711	2300904807

First, for both the datasets, the numbers of multiple-out and -in k-mers are much less than $\left|S\right|$, i.e. the number of characters of the input sequences. Thus, the cost of the hash table is not expensive comparing with the entire input sequences. Moreover, it is also worth noting that for highly similar genomes, the increment of the numbers of multiple-out and -in k-mers would be much smaller comparing with the increment of involved genomes, as there are many common sequences and they would not introduce new branches into the dBG.

Second, the numbers of the copies of multiple-out and -in k-mers are also an order lower than $\left|S\right|$, although human genomes are repetitive. In this situation, the de Bruijn branch encoding can be seen as a DNA sequence an order shorter than $S$, so that the space cost is not large. The major cost originates from the copies of multiple-in k-mers, as it needs to record the $\varphi \left(·\right)$ value and the BWT character with a few bytes for each copy.

The RAM cost of the third step is also similar to that of the second phase. To sort the projection suffixes, it needs to keep the de Bruijn branch encoding and the $\varphi \left(·\right)$ values and the BWT characters of the copies of the multiple-in k-mers in RAM.

4 Discussion

The well organization and indexing of many genomes will be on wide demand in future genomics studies, with the rapid increase of assembled genomes. As an important genome indexing data structure, BWT may have many applications; however, the construction of BWT for a large collection of genomes, especially highly similar re-sequenced genomes (e.g. many human individual genomes), is still a non-trivial task. Moreover, owing to the incremental nature of the state-of-the-art methods, it is hard to construct BWT with scalable parallel computing. This is a bottleneck to fully use the computational resources of modern servers or clusters to handle large amount of data.

We propose deBWT, a novel parallel BWT construction approach, to break the bottleneck. The main contribution of deBWT is its dBG-based representation and organization of suffixes, which facilitates the comparison of suffixes with long common prefixes and avoid unnecessary comparisons. Moreover, owing to its non-incremental design, deBWT has good scalability to various computational resources. These properties make deBWT well-suited to construct BWT for large collections of highly similar or repetitive genomes with modern servers or clusters. In the experiments, deBWT achieves a substantial improvement on the speed of indexing multiple individual human genomes and contigs. For more diverse genomes, e.g. multiple primate genomes, deBWT also shows faster speed and better parallelization; however, the improvement is smaller, likely owing to that the density of the dBG is lower. That is, there are more k-mers and unipaths to handle, but the overall repetitiveness of the input is lower than highly similar genomes.

Comparing with state-of-the-art approaches, deBWT has obviously larger memory footprint. There are potential solutions to reduce the memory footprints of the various phases of deBWT.

For phase 1, it is feasible to bin the k-mers into several subsets and separately sort each of the subsets with limited memory. The results of the multiple subsets can be straightforwardly merged into the ordered list of all the k-mers with small memory space.

For phase 2, it is also possible to reduce the memory footprint by keeping only a proportion of $\varphi \left(·\right)$ values and BWT characters, which can be implemented with the following strategy. Because all the multiple-in k-mers and their numbers of copies are known before the second phase, it can partition the whole set of multiple-in k-mers into several subsets. Each of the subsets has a limited number of k-mer copies. Thus, the second phase can be done with multiple times of scanning on the input sequences, instead of one time. In each time of scanning, only the copies of the multiple-in k-mers within the corresponding subset are recognized, recorded and output to a specific file with limited RAM space. As all the subsets are independent to each other for the third phase, the files of the subsets can be separately processed to generate various parts of BWT. Further, the BWT parts can be directly merged to accomplish the construction. This strategy is feasible to limited workspace, but at the expense of time owing to the fact that it needs multiple executions of phase 2.

For phase 3, it can also keep only a proportion of unsolved of BWT partitions in memory as all such partitions are independent.

There are two possible improvements on deBWT, which are important future works for us.

First, deBWT straightforwardly sorts the projection suffixes by quick-sort. Because the de Bruijn branch encoding can be also seen as a special DNA sequence, it is also possible to use other approaches to further accelerate the projection suffix sorting step. For example, the method proposed by Karkkainen (2007) uses DCS to accelerate the sorting of the binned suffixes of the original input sequence. This method could be also used for sorting the binned projection suffixes without loss of the ability of parallel computing, as it is non-incremental.

Second, for the current version of deBWT, the I/O-intensive steps are still not optimized, which slowed down the speed. We plan to further optimize the I/O-intensive steps to improve the efficiency of deBWT. Meanwhile, as k-mer counting is still an open problem, and advanced k-mer counting tools are developing (Perez et al., 2016), we also plan to replace Jellyfish by other more advanced k-mer counting tools, or remove the file conversion step by directly accessing the default Jellyfish output file, to break the practical bottleneck of the method.

Funding

This work has been partially supported by the National Nature Science Foundation of China (Nos: 61301204 and 31301089), the National High-Tech Research and Development Program (863) of China (Nos: 2015AA020101, 2015AA020108 and 2014AA021505) and the National Science and Technology Major Project (No: 2013ZX03005012).

Conflict of Interest: none declared.