Abstract
Motivation: It remains a challenge to detect associations between genotypes and phenotypes because of insufficient sample sizes and complex underlying mechanisms involved in associations. Fortunately, it is becoming more feasible to obtain gene expression data in addition to genotypes and phenotypes, giving us new opportunities to detect true genotype–phenotype associations while unveiling their association mechanisms.
Results: In this article, we propose a novel method, NETAM, that accurately detects associations between SNPs and phenotypes, as well as gene traits involved in such associations. We take a network-driven approach: NETAM first constructs an association network, where nodes represent SNPs, gene traits or phenotypes, and edges represent the strength of association between two nodes. NETAM assigns a score to each path from an SNP to a phenotype, and then identifies significant paths based on the scores. In our simulation study, we show that NETAM finds significantly more phenotype-associated SNPs than traditional genotype–phenotype association analysis under false positive control, taking advantage of gene expression data. Furthermore, we applied NETAM on late-onset Alzheimer’s disease data and identified 477 significant path associations, among which we analyzed paths related to beta-amyloid, estrogen, and nicotine pathways. We also provide hypothetical biological pathways to explain our findings.
Availability and implementation: Software is available at http://www.sailing.cs.cmu.edu/.
Contact: epxing@cs.cmu.edu
1 Introduction
One of the fundamental problems in genetics is to understand how different genotypes affect phenotypic variations. To find genetic factors of complex diseases such as Alzheimer’s disease (AD) and asthma, researchers have detected single-nucleotide polymorphisms (SNPs) associated with phenotypes (e.g. disease status) (Corder et al., 1993). However, most SNPs associated with complex diseases remain elusive, and the molecular mechanisms of genotype–phenotype associations are largely unknown (Kim and Przytycka, 2012; Manolio et al., 2009). To address the problem, efforts have been made in the past decade to bridge the gap between genotypes and phenotypes by replacing phenotypes with gene expression traits (Gilad et al., 2008), and then conducting association mapping between genotypes and gene expression traits. For example, hypothesis testing (e.g. t-test) or penalized regression methods have been employed to find genotype–gene trait associations (Kendziorski et al., 2006; Lee and Xing, 2012).
Extending the two-way association (i.e. genotypes and gene traits) analysis, three-way association analysis among genotypes, gene traits and phenotypes also has been proposed. Schadt et al. (2005) proposed an integrative genomics approach consisting of a series of statistical tests to identify causal genes to complex phenotypes. Recently, Curtis et al. (2012) developed a visualization-aided approach to detect genome–transcriptome–phenome associations. The previous works showed the great promise of three-way association analysis; however, most of them aim to reveal association relationships for an SNP, a gene trait, and a phenotype. Thus, there is an urgent need to develop an efficient method that can detect three-way associations from a large dataset of genotypes, gene traits, and phenotypes.
In this article, we present a novel method, NETAM (NETwork-driven Association Mapping), to detect ‘path associations’ from SNPs to phenotypes through gene expression traits. Let us first introduce the concept of path associations. Consider a network where nodes represent SNPs, gene traits, or phenotypes and edges represent associations between a pair of nodes, weighted by their strengths. We call it association network. In this network, we define path association by any paths from an SNP to a phenotype. Figure 1 illustrates an example of association network, identified by NETAM in AD dataset (Zhang et al., 2013). NETAM starts with constructing an association network using sparse regression methods such as lasso (Tibshirani, 1996) and group lasso (Yuan and Lin, 2005) under stability selection (Meinshausen and Bühlmann, 2010). Arguably, these techniques perform better than single SNP analysis because they allow us to find weighted edges, considering all SNPs or all gene expression traits simultaneously. Based on the edge weights, we define scores for all path associations, reflecting their significance. Finally, using a K-shortest path algorithm, we identify top K path associations (or all paths with scores greater than a threshold) in the network. To boost the computational efficiency of NETAM for large-scale analysis, we further employ screening techniques (Lee and Xing, 2014; Wang et al., 2013) that can discard a large number of irrelevant edges efficiently.
Fig. 1.
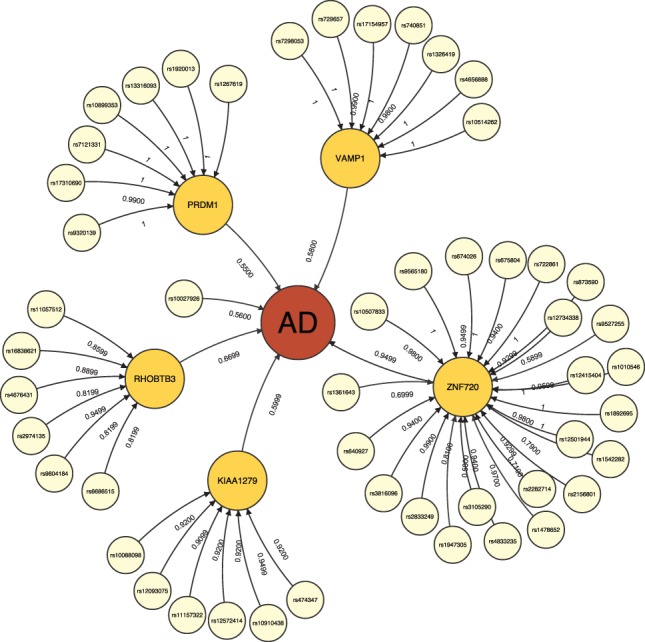
An example of association network for AD identified by NETAM. Nodes represent SNPs (smallest circles), gene traits (mid-sized circles), AD case/control phenotype (the largest circle) and edges represent associations between two nodes. Association strengths are represented by scores attached to edges. We allow both SNP–gene trait–phenotype, and direct SNP–phenotype associations
The proposed approach has advantages over traditional genotype–phenotype association analysis. First, it allows us to better understand the underlying mechanisms of associations (e.g. SNPs affect gene expression traits, and altered expressions influence phenotypes). Furthermore, it can take advantage of gene expression traits to detect phenotype-associated SNPs. When SNPs and phenotypes are weakly associated, gene expression traits can bridge the gap between them, allowing us to find path associations. Finally, it can integrate rapidly growing heterogeneous datasets such as GEO (Gene Expression Omnibus) database (Barrett et al., 2007) and dbGaP (Database of Genotypes and Phenotypes) (Mailman et al., 2007). NETAM requires the same samples only for a pair of datasets (e.g. genotypes and gene expression traits) to create edges, and thus heterogeneous datasets can be integrated through a network.
In our experiments, we first conducted simulation study to verify that NETAM can take advantage of gene expression data to significantly improve the performance to detect phenotype-associated SNPs under false positive control. We then applied NETAM on late-onset AD dataset (Zhang et al., 2013), and identified 477 path associations. Among them, we highlight one path association: rs675804 → ZNF720 → AD status. It turns out that ZNF720 interacts with only the APP gene (Oláh et al., 2011) encoding amyloid beta (A4) precursor protein, a major factor of AD that generates neural waste, called beta-amyloid, in the brain (Bush et al., 1994) (see Section 4 for detailed analysis). We also present biological hypotheses that can explain the path associations identified by NETAM, related to beta-amyloid, estrogen, and nicotine pathways.
Notation: We denote matrices by bold-faced uppercase, vectors by bold-faced lowercase, and scalars by lowercase letters. Given a genotype matrix with N samples and J SNPs, we denote the j-th column by , the i-th row by , and the (i, j) element by . Similarly, we denote the gene expression matrix by , and phenotype matrix by , where K and M are the number of gene traits and phenotypes, respectively.
2 Methods
In this section, we describe NETAM for detecting path associations. We show how to construct an association network, define path scores in the network and introduce screening algorithms that can discard a large number of irrelevant edges efficiently. Based on the path scores, we finally detect top K path associations using a K-shortest path algorithm.
2.1. Constructing an association network
2.1.1. Finding edges in an association network
Given the nodes consisting of SNPs, gene traits, and phenotypes, we show how to make edges between two nodes using sparse regression models (SRMs) such as lasso (Tibshirani, 1996) or group lasso (Yuan and Lin, 2005) under stability selection (Meinshausen and Bühlmann, 2010). SRMs allow us to identify associations between SNPs and gene traits, between SNPs and phenotypes, and between gene traits and phenotypes; stability selection is a technique to control false positives. Advantages of using SRMs over single SNP analysis are as follows: First, SRM is a multivariate regression approach; thereby it can consider all SNPs/traits simultaneously. As a result, when SNPs are weakly or moderately correlated, SRMs can pinpoint true association SNPs (Zhao and Yu, 2006); when highly correlated SNPs are associated with a trait, one of them is selected, which greatly reduces the redundant signals stemming from linkage disequilibrium. Furthermore, SRMs can take advantage of prior biological knowledge such as group structures of SNPs and traits (Lee and Xing, 2012), and graph structures of traits (Kim and Xing, 2009). Finally, coupled with stability selection, SRMs control false positives effectively.
To identify edges in an association network, we use SRMs as follows:
| (1) |
| (2) |
where and are regression coefficient matrices whose non-zeros encode associations. For example, implies association between the k-th gene trait and the m-th phenotype. Also, , and is regularizer that induces sparsity in the coefficient matrix. Using Equation (1), we find edges between genotypes and gene expression traits, where the linear loss is used because gene expression traits are continuous; using Equation (2) we find edges between gene expression traits and phenotypes, where logistic loss is used for binary phenotypes.
Algorithm 1: Sparse Regression Under Stability Selection.
Input: : Input matrix, : Output matrix, where , : selected SNPs for the d-th output by screening, πthr: threshold for stability selection , T: total number of random samples
Output: : selected inputs for the d-th output with scores
1. for
2. Randomly select samples from N samples without replacement
3. Given the subsamples and a SRM (i.e. Equation (1) or (2)), find using cross-validation, denoted by
4. for
5. for t = 1 to T do
6. Randomly select samples from N samples without replacement
7. Given the subsamples, solve a SRM with
8. for all selected terms l for the d-th output
9. for
10. for
To deal with categorical values, one can easily replace it with multi-class logistic loss. Let and be the solutions for Equations (1) and (2). Then, if (or ), we interpret that the edge between the j-th SNP and the k-th gene trait exists (or edge between the k-th gene trait and the m-th phenotype exists). Edges between genotypes and phenotypes can be found using Equation (2) by replacing with .
Popular instances of SRMs include lasso and group lasso: Lasso uses regularizer, i.e. , where λk is the regularization parameter determining the level of sparsity; group lasso uses regularizer, i.e. , where is a set of groups of SNPs or traits and ng is the size of group g. In practice, we determine λk using cross-validation; however, with cross-validation, we often obtain many false positives (i.e. true zero coefficients are non-zero in estimated coefficients). To address this problem, we use SRMs under stability selection, which shall be described in the next section.
Note that different regularizers incorporate different types of prior knowledge into the model. For example, group lasso takes a set of SNP groups, and finds groups of SNPs associated with traits. If we define groups of SNPs based on their genomic locations (e.g. SNPs located within a gene form a group g), group lasso encourages that all SNPs within a gene are selected or discarded jointly.
2.1.2. Stability selection for false positive control
We augment Equations (1) and (2) with stability selection (Meinshausen and Bühlmann, 2010) to make edges in the graph. Stability selection is a bootstrapping-type algorithm that effectively controls false positives. Briefly, stability selection works as follows: Equation (1) or (2) is run on randomly selected subsamples of size for T times, and then stability selection takes SNPs whose coefficients are non-zero for times, where πthr is a user-defined parameter. We summarize sparse regression under stability selection in Algorithm 1.
Let us discuss user-defined parameters T and πthr. We confirmed that is sufficient to achieve false positive control, as reported in Meinshausen and Bühlmann (2010). In practice, πthr is chosen between 0.5 and 1; the larger πthr, the better false positive control at the cost of decreased true positive rate. In theory, under certain conditions, the relationship between the number of false positives and πthr has been established. When finding edges between SNPs and the k-th trait,
| (3) |
where is the expected number of falsely detected SNPs for the k-th trait, and is the number of nonzero coefficients found by a SRM with . Equation (3) shows that the upper bound on the number of false positives is inversely proportional to πthr.
Stability selection provides edges and their weights (called edge scores), reflecting their degrees of significance. For association between the j-th SNP and the k-th trait, edge score is defined by the proportion of the cases where the j-th SNP is selected to the total number of random sampling, as shown in Algorithm 1 (no edge exists if the score is zero). To rank path associations, we further assign scores to paths based on edge scores as follows:
| (4) |
where is the score associated with . The scoring scheme in Equation (4) is motivated by the fact that a path association is significant when all edges involved in the path are significant.
2.1.3. Screening algorithms for efficient computations
Stability selection is computationally expensive because it requires multiple runs of a SRM. This is particularly problematic when finding edges (i.e. associations) between genotypes and gene expression traits at whole-genome scale (e.g. for human genomes, we need to solve J = 500 000 dimensional regression problem on K = 20 000 gene expression traits for T = 100 times); thus, in this section, we focus on solving Equation (1) efficiently. To address the computational challenge, we adopt a screening approach. The key idea of screening is to discard SNPs whose coefficients are zero using simple rules, and then solve a sparse regression problem with the unscreened SNPs. Screening provides a substantial speed-up because we only need to solve Equation (1) with a small number of SNPs that survived after screening.
We note that two types of screening algorithms exist: one is exact, such as dual polytope projections (DPP) rules (Wang et al., 2013), and the other is non-exact, such as sure-screening and strong rules (Fan and Lv, 2008; Tibshirani et al., 2012). Exact screening guarantees that non-zero coefficients in a global optimal solution (i.e. solution obtained by solving Equation (1) without screening) are not discarded. Thus, the solution for Equation (1) obtained with exact screening is the same as the one without screening. In contrast, non-exact screening may mistakenly discard non-zero coefficients in a global optimal solution; at the cost of non-exactness, it can discard more SNPs than exact ones.
Here we briefly introduce DPP rules for lasso and group lasso. For lasso, DPP discards the j-th SNP for the k-th trait if
| (5) |
where . For group lasso, DPP discards the group g for the k-th trait if
| (6) |
where . These rules are applied to each SNP or SNP group for each trait only once, and the screening complexity is O(NJ) for lasso and for group lasso. In practice, for both lasso and group lasso, screening efficiency decreases as the optimal solution gets denser. In our experiments, we achieved ∼1.9× speedup on the AD data using DPP rule for group lasso (Lee and Xing, 2014).
2.2. Finding path associations from an association network using a K-shortest path algorithm
To find significant paths in an association network, we use Yen’s K-shortest path algorithm (Yen, 1971), using the path scores defined in Equation (4) that give larger values for more significant paths. Note, however, that naive use of the K-shortest path algorithm with such scores will give us K-least significant paths. Thus, we transform our edge scores by and path scores by After these transformations, the smaller the path scores, the more significant the paths, and scores are guaranteed to be positive because . We use K-shortest path algorithm with and , resulting in K-significant path associations.
The original algorithm is designed with a single source and a single target; thus, we augment a network with auxiliary source node A and target node T. We also add the scores of 1 into the edges from A to all genotype nodes and from phenotype nodes to T. Briefly, the Yen’s algorithm starts with finding the shortest path in a network. Then it iterates through the steps of generating candidate paths and selecting the best one among the candidates until K-shortest paths are found.
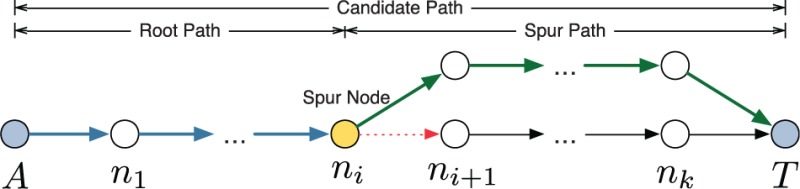
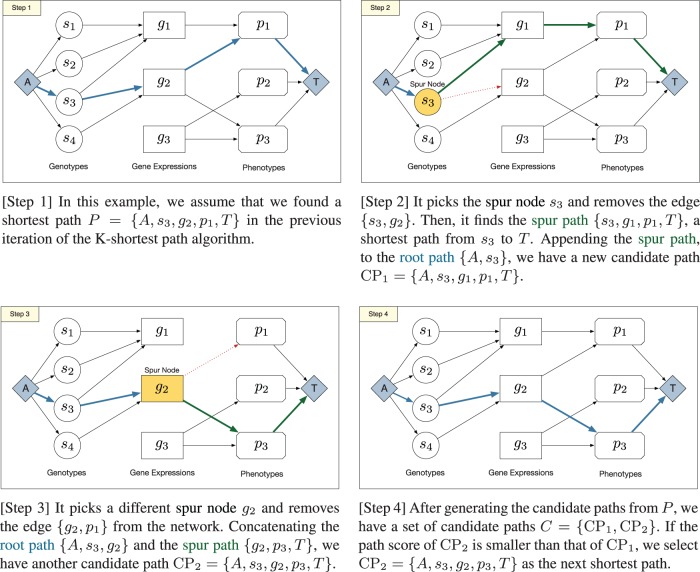
Suppose that we found the k-th shortest path (). To find the -th shortest path, the algorithm produces candidate paths as follows: It picks a spur node from the k-th shortest path (spur node is the node from which the current shortest path is perturbed). For each spur node ni, it removes the outgoing edge from a network and runs a shortest path algorithm to find the spur path, a shortest path from the spur node ni to the target node T in the perturbed network. A candidate path is the result of concatenating root path and spur path, as depicted in the above figure. Removed edges are restored after generating candidate paths. The -th shortest path is found by selecting the shortest path among the candidate paths. Figure 2 illustrates one iteration of Yen’s algorithm with an example of association network.
Fig. 2.
Illustration of one iteration of the K-shortest algorithm with an example of association network
For a network with N nodes and M edges, Yen’s algorithm has a worst case time complexity when it employs Dijkstra’s shortest path algorithm (Dijkstra, 1959) using Fibonacci heap. In our application, the length of any paths from an SNP to a phenotype is either one or two. In such a case, the time complexity of Yen’s algorithm is .
3 Simulation study
To validate the efficacy of NETAM, we evaluate its performance in detecting phenotype-related SNPs. We first explain how simulation data are generated. Then, we compare NETAM with L1-regularized logistic regression with SNPs associated with gene expression traits (eSNPs) (Logistic w/ eSNP), and linear mixed model (LMM) (Zhou and Stephens, 2012) that represents a two-way single SNP analysis. Furthermore, we test NETAM without stability selection (NETAM w/o stability sel.) to verify the benefits of stability selection, where lasso and L1-regularized logistic regression are employed with 10-fold cross-validation. For Logistic w/ eSNP, we choose SNPs only if they are included in the set of eSNPs, assuming that eSNPs hint us causal SNPs to phenotypes (Zhang et al., 2013).
For LMM, we used GEMMA software (Zhou and Stephens, 2012) with default setting and P-value cutoff 0.05 (after Bonferroni correction LMM found no significant associations, and thus we report the results with the lenient P-value cutoff); for Logistic w/ eSNP, we used lasso to detect eSNPs, and 10-fold cross-validation to determine the regularization parameters; for NETAM, we used lasso to create edges, changed πthr from 0.6 to 0.9, set T = 100, and selected up to K = 1000 paths.
For samples, we generate simulation data with 1000 SNPs, 40 gene expressions, and 1 case-control phenotype as follows: We first generated 100 causal SNPs (ground truth to be discovered) and the phenotype with average minor allele frequency 0.2 under Hardy–Weinberg equilibrium, and balanced case-control phenotype (equal number of 0s and 1s). Then, we generated 10 gene expression levels using a three layer neural network (100 nodes SNP layer/10 nodes gene expression layer/1 node phenotype layer), where adjacent layers are fully connected. The neural network was trained until more than 95% phenotypic traits are correctly predicted using a backpropagation algorithm, implemented using TensorFlow (Abadi et al., 2016); after training, we use the values in the middle layer nodes as gene expression levels. To add non-linear relationship between the SNPs and the phenotype, we also applied a sigmoid function to the gene expression layer (, where represents 10 gene expression levels, and represents 100 SNPs for the i-th individual). Finally, for each sample, we added 900 SNPs with minor allele frequency drawn from [0.05, 0.5] uniformly at random, and 30 gene expression levels drawn from N(0, 1) to include SNPs and genes not associated with the phenotype generation mechanism.
In Figure 3, we show receiver operating characteristic (ROC) curves that show true positive and false positive rates of the results produced by NETAM with four different parameter settings , NETAM without stability selection, Logistic w/ eSNP, and LMM. We note that false positives in NETAM’s results were controlled by stability selection. Each panel shows the results on different sample sizes from N = 200 to 1100. Compared to LMM and Logistic w/ eSNP, NETAM showed significantly better performance (larger area under the curve) for N > 200 regardless of the setting for πthr. The results suggest that when phenotype mechanism is complex such that SNPs affect a phenotype via multiple layers, direct SNP-phenotype association analysis can be ineffective to capture causal SNPs. Furthermore, the performance of NETAM w/o stability sel. was unstable; it showed the best performance when N = 800; however, its ROC curve was not comparable to NETAM with stability selection for the other settings, suggesting that stability selection is useful to control false positive edges and produce stable results. It should be noted that even though this simulation scenario is more complex than direct genotype–phenotype association scenarios, real-world biological mechanisms are much more complex because they involve many factors such as gene–gene or protein–protein interactions, pathways, microRNAs, and environmental factors. NETAM opens the opportunities to model such complex association mechanisms between genotypes and phenotypes, and modeling such factors remains as future work.
Fig. 3.
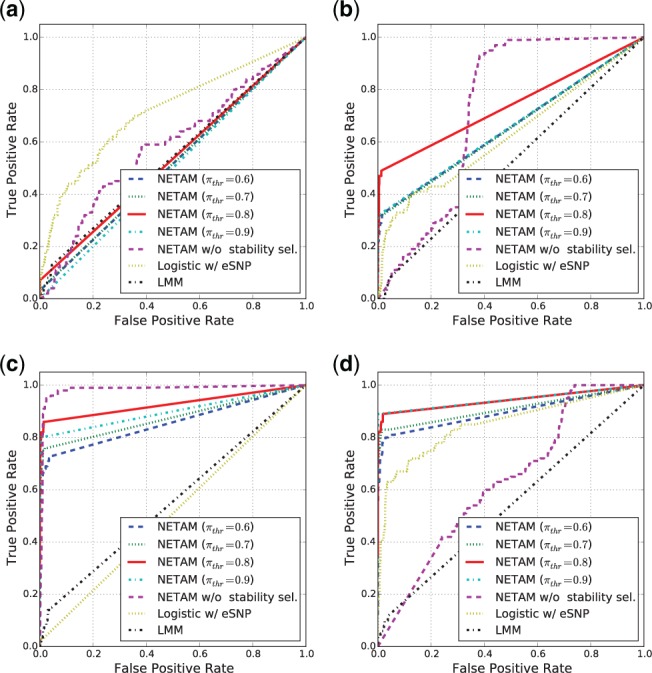
ROC curves to compare the performance of NETAM with association mapping methods such as linear mixed model (LMM) and L1-regularized logistic regression with eSNPs (Logistic w/ eSNP) with different sample sizes: (a) N = 200, (b) N = 500, (c) N = 800, and (d) N = 1100. For NETAM, we show the results with four different settings of πthr from 0.6 to 0.9 under stability selection and without stability selection (lasso is used to create edges between SNPs and gene traits in the association network)
4 Association analysis of AD data
We applied NETAM on late-onset AD data provided by Harvard Brain Tissue Resource Center and Merck Research Laboratories (Zhang et al., 2013). This dataset includes 270 AD cases and 270 controls (non-demented subjects) with 511 997 SNPs (SNPs with minor allele frequency < 0.01 were filtered), and the expression levels of 40 638 DNA probes from the same samples including known and predicted genes, miRNAs, and non-coding RNAs in the cerebellum in the brain. For phenotype, we used binary AD case/control status. To account for different variances/scales in the SNPs and the expression traits, we standardized them. Because of the large numbers of SNPs and traits, it is particularly expensive to find edges between genotypes and expression traits. Therefore, we adopted DPP group lasso screening (Wang et al., 2013), which can also be safely applied to the case where groups overlap (Lee and Xing, 2014). In the screening with group lasso, each SNP group was defined by the SNPs within the transcribed region of a gene. With the survived SNPs, we ran Algorithm 1 with lasso, 10-fold cross-validation, , and T = 100. For πthr, we chose the lowest valid value to include all potentially interesting paths.
In total, we found 477 path associations in the AD data. Of these, two paths directly connect an SNP to the AD status phenotype, and 475 paths involve an SNP, an expression trait, and the phenotype. To the best of our knowledge, AD-related path associations have not been reported in previous literature. Among all the path associations, SNPs in only three paths (out of 477 paths) were also identified by single SNP analysis, with false discovery rate control at significance level 0.05. Compared to the results by Zhang et al. (2013) (with Bonferroni corrected P-value cutoff 0.05), we found one overlap: rs2532501 → VAMP1 → AD. Small number of overlaps was expected because NETAM detected six gene traits associated with AD.
Here, we focus on analyzing top 36 paths involving ZNF720, RHOBTB3 or VAMP1 because these genes are related to beta-amyloid, estrogen, and nicotine pathways, crucially involved in AD (Bush et al., 1994; Paganini-Hill and Henderson, 1994; Van Duijn and Hofman, 1991). The 36 path associations are summarized in Table 1. Below, we investigate the biological underpinnings of path associations based on path directions and our extensive literature survey. Note that we present hypotheses for path associations, and further biological studies are required to confirm them.
Table 1.
Top 36 path associations found by NETAM in the AD data (Zhang et al., 2013) related to VAMP1, RHOBTB3, and ZNF720 genes
| SNP | SNP location | Genes nearby SNP within 1 Mbp | Gene | Gene Location | Path Score | Related Biology | SNP-pheno P-val |
|---|---|---|---|---|---|---|---|
| rs1892695 | chr21:31366451 | GRIK1 | ZNF720 | chr16:31724565-31766243 | 0.95 | Beta-amyloid | 0.01 |
| rs9565180 | chr13:75129470 | LINC00347 | ZNF720 | chr16:31724565-31766243 | 0.95 | Beta-amyloid | 0.01 |
| rs12415404 | chr10:61035110 | PHYHIPL,FAM13C | ZNF720 | chr16:31724565-31766243 | 0.95 | Beta-amyloid | 0.11 |
| rs873590 | chr11:122175599 | ZNF720 | chr16:31724565-31766243 | 0.95 | Beta-amyloid | 0.01 | |
| rs1542282 | chr2:52915337 | ZNF720 | chr16:31724565-31766243 | 0.95 | Beta-amyloid | 0.84 | |
| rs675804 | chr6:150761402 | IYD | ZNF720 | chr16:31724565-31766243 | 0.95 | Beta-amyloid | 4.9e-3 |
| rs3816096 | chr2:11670369 | MIR4429,GREB1,E2F6 | ZNF720 | chr16:31724565-31766243 | 0.94 | Beta-amyloid | 0.67 |
| rs10507833 | chr13:75124139 | LINC00347 | ZNF720 | chr16:31724565-31766243 | 0.93 | Beta-amyloid | 0.01 |
| rs12501944 | chr4:112716904 | ZNF720 | chr16:31724565-31766243 | 0.93 | Beta-amyloid | 0.07 | |
| rs4833235 | chr4:122914585 | TRPC3 | ZNF720 | chr16:31724565-31766243 | 0.92 | Beta-amyloid | 2.1e-3 |
| rs1010546 | chr17:62115026 | ICAM2,DQ572107,ERN1,SCN4A,C17orf72 | ZNF720 | chr16:31724565-31766243 | 0.91 | Beta-amyloid | 0.28 |
| rs674026 | chr6:150743619 | IYD | ZNF720 | chr16:31724565-31766243 | 0.90 | Beta-amyloid | 0.67 |
| rs722861 | chr22:44046385 | EFCAB6 | ZNF720 | chr16:31724565-31766243 | 0.89 | Beta-amyloid | 0.35 |
| rs3105290 | chr4:112593771 | ZNF720 | chr16:31724565-31766243 | 0.89 | Beta-amyloid | 0.05 | |
| rs640927 | chr11:75022553 | SNORD15B,SNORD15A,ARRB1,TPBGL,RPS3,MIR326 | ZNF720 | chr16:31724565-31766243 | 0.89 | Beta-amyloid | 0.04 |
| rs12734338 | chr1:200736345 | DDX59,CAMSAP2 | ZNF720 | chr16:31724565-31766243 | 0.88 | Beta-amyloid | 7.7e-5 |
| rs2282714 | chr1:21460435 | ECE1 | ZNF720 | chr16:31724565-31766243 | 0.88 | Beta-amyloid | 0.69 |
| rs2833249 | chr21:31358680 | GRIK1 | ZNF720 | chr16:31724565-31766243 | 0.77 | Beta-amyloid | 4.6e-3 |
| rs2156801 | chr11:122159265 | ZNF720 | chr16:31724565-31766243 | 0.75 | Beta-amyloid | 0.11 | |
| rs1478652 | chr13:54155871 | ZNF720 | chr16:31724565-31766243 | 0.67 | Beta-amyloid | 0.2 | |
| rs1361643 | chr11:29594339 | ZNF720 | chr16:31724565-31766243 | 0.67 | Beta-amyloid | 2.1e-3 | |
| rs9527255 | chr13:54150358 | ZNF720 | chr16:31724565-31766243 | 0.56 | Beta-amyloid | 0.25 | |
| rs1947305 | chr11:29567353 | ZNF720 | chr16:31724565-31766243 | 0.55 | Beta-amyloid | 3.4e-3 | |
| rs2974135 | chr2:80028801 | CTNNA2 | RHOBTB3 | chr5:95053336-95091797 | 0.64 | Estrogen | 0.03 |
| rs16838621 | chr2:207275786 | ADAM23,ZDBF2 | RHOBTB3 | chr5:95053336-95091797 | 0.60 | Estrogen | 0.02 |
| rs11057512 | chr12:123254323 | HCAR3,HCAR1,VPS37B,DENR,CCDC62,HCAR2,HIP1R | RHOBTB3 | chr5:95053336-95091797 | 0.58 | Estrogen | 0.26 |
| rs4676431 | chr2:241105073 | MYEOV2,OTOS | RHOBTB3 | chr5:95053336-95091797 | 0.55 | Estrogen | 0.17 |
| rs6686515 | chr1:198326330 | NEK7 | RHOBTB3 | chr5:95053336-95091797 | 0.55 | Estrogen | 0.02 |
| rs9804184 | chr10:63908170 | ARID5B,RTKN2 | RHOBTB3 | chr5:95053336-95091797 | 0.55 | Estrogen | 0.91 |
| rs10514262 | chr5:83062888 | HAPLN1 | VAMP1 | chr12:6571403-6579843 | 0.58 | Nicotine | 1 |
| rs4656888 | chr1:158395294 | AK057554,OR10R2,CD1E,OR10T2,CD1B,OR10K2,OR10K1 | VAMP1 | chr12:6571403-6579843 | 0.58 | Nicotine | 0.67 |
| rs729657 | chr7:21750561 | DNAH11 | VAMP1 | chr12:6571403-6579843 | 0.58 | Nicotine | 0.34 |
| rs7298053 | chr12:6489314 | CD27,SCNN1A,TAPBPL,CD27-AS1,LTBR,VAMP1,PLEKHG6,TNFRSF1A | VAMP1 | chr12:6571403-6579843 | 0.58 | Nicotine | 0.06 |
| rs740851 | chr12:6508610 | CD27,SCNN1A,TAPBPL,CD27-AS1,LTBR,VAMP1 | VAMP1 | chr12:6571403-6579843 | 0.58 | Nicotine | 0.04 |
| MRPL51,PLEKHG6,TNFRSF1A,NCAPD2 | |||||||
| rs17154957 | chr7:80705911 | VAMP1 | chr12:6571403-6579843 | 0.57 | Nicotine | 0.19 | |
| rs1326419 | chr13:88080652 | MIR4500HG | VAMP1 | chr12:6571403-6579843 | 0.57 | Nicotine | 3.9e-3 |
Note: In this table, we omit the AD case/control phenotype because it is identical for all paths. For reference, in the column of ‘SNP-pheno P-val’, we show P-value for the association between SNP and the phenotype, computed by PLINK software (Purcell et al., 2007).
In the other 441 paths not discussed in the article, three other gene traits were involved including KIAA1279, RPS15A, and PRDM1. We found no reported associations between these genes and AD. However, these genes are related to brain-related disorders (Courts et al., 2008; Hamosh et al., 2005; Uechi et al., 2006), and investigation of their relationship with AD is left for future work.
4.1. Direction of path associations
In a path association, the edge between a gene trait and the phenotype can be interpreted in two ways: the gene trait affects the phenotype, or the phenotype affects the gene trait. In the 36 path associations involving ZNF720, RHOBTB3, and VAMP1, our analysis supports the former case.
To investigate the directions of the 36 path associations, we computed P-values for associations between the SNPs and the phenotype in those paths, using single SNP analysis by PLINK software (Purcell et al., 2007). Note that, if the gene traits affect the phenotype, it is likely that there are some degrees of associations (even though they are not statistically significant) between the SNPs and the phenotype because the SNPs may affect the phenotype through the gene traits. In contrast, if the phenotype affects the gene traits and not vice versa, we expect no associations between the SNPs and the phenotype. Figure 4 shows Q–Q plot of observed negative log P-values, versus the expected negative log P-values under the null hypothesis of no associations; the plot significantly deviates from the 95% confidence interval, showing that the observed P-value distribution does not follow the expected null distribution (see the last column of Table 1 for the SNP-phenotype P-values). Therefore, it supports the hypothesis that the gene expression traits may influence the phenotype in the path associations.
Fig. 4.
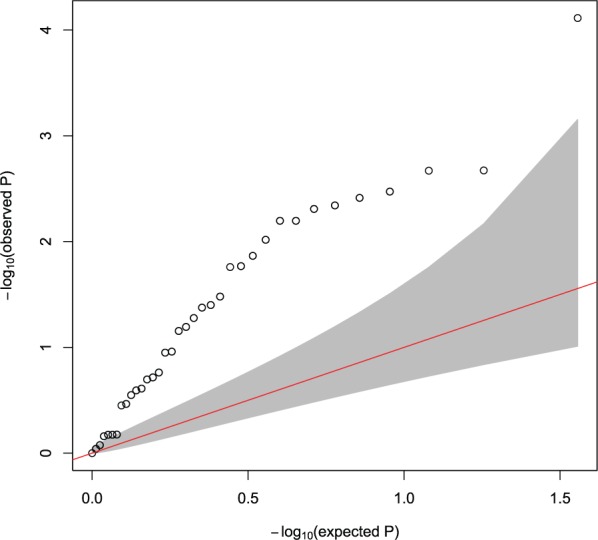
Q–Q plot of for associations between SNPs and the AD status phenotype in the paths that involve ZNF720, RHOBTB3 or VAMP1 identified by NETAM (see Table 1 for the list of the paths) versus a uniform distribution, where the 95% confidence interval is shaded in gray
4.2. Beta-amyloid-related path associations
We identified 23 (out of 36) path associations that involve ZNF720 (zinc finger protein 720). According to the human protein–protein interaction database (Oláh et al., 2011; Orii and Ganapathiraju, 2012), ZNF720 interacts with only APP (amyloid beta (A4) precursor protein). Notably, APP protein generates beta-amyloid, i.e. a major component of amyloid plaques that deteriorate nerve cells in the brains of AD patients (Bush et al., 1994). Next, we attempt to investigate biological mechanisms underlying associations between the SNPs and APP in 4 out of 23 path associations with ZNF720.
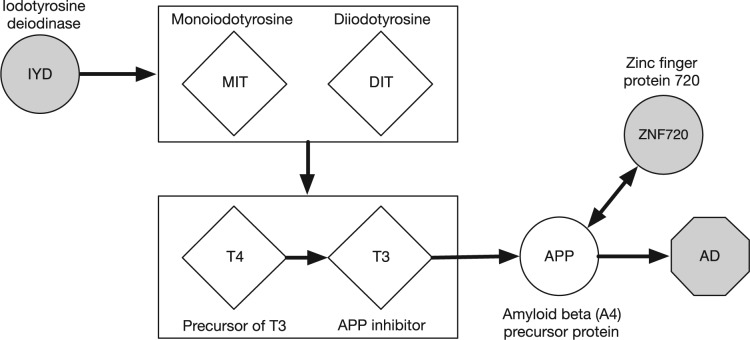
4.2.1. Path: rs675804 (IYD) → ZNF720 (APP) → AD
In this path association, rs675804 is located 35 637 bp downstream of iodotyrosine deiodinase (IYD), a gene encoding an enzyme that catalyzes the deiodination of monoiodotyrosine (MIT) and diiodotyrosine (DIT); MIT and DIT are precursors of thyroid hormones such as triiodothyronine (T3) and tetraiodothyronine (T4). It has been reported that defects in IYD resulted in high levels of MIT and DIT and low levels of T3 and T4 (Rokita et al., 2010). Another link between IYD and T3 and T4 is that IYD is associated with hypothyroidism (Moreno et al., 2008), caused by insufficient production of thyroid hormones, suggesting that IYD affects the synthesis of T3 and T4. Furthermore, it is known that T3 negatively regulates APP (Van Osch et al., 2004).
Combining the evidence mentioned above, we hypothesize the mechanism of the path association as follows: The SNP rs675804 (or possibly nearby ungenotyped SNPs in linkage disequilibrium (LD)) causes defects in IYD, which drives high levels of MIT and DIT, and low levels of T4 and T3; then low levels of T3 result in high levels of APP. Finally, high APP levels positively regulate the beta-amyloid synthesis, which increases the risk of AD. Figure 5 illustrates our hypothesis for the path association.
Fig. 5.
Hypothetical pathway for the path association involving rs675804 (close to IYD), ZNF720, and AD. Nodes involved in the path association found by NETAM are shaded in gray
We observed that P-value for association between rs675804 and the AD status is 0.0049 computed by single SNP analysis. This small P-value also suggests that rs675804 is associated with AD through IYD.
4.2.2. Path: rs2833249 (GRIK1) → ZNF720 (APP) → AD
This is an interesting path association with cis-effect. Notably, the SNP rs2833249 (chr21:31358680), GRIK1 (chr21:30909253-31312282), and APP (chr21:27252860-27342862) are located nearby in the genome. GRIK1 (glutamate receptor, ionotropic, kainate 1) is a gene encoding a member of glutamate receptors, i.e. predominant excitatory neurotransmitter receptors (Maglott et al., 2005), and GRIK1’s association with AD was reported in Tan et al. (2010). Furthermore, we observed a small P-value 0.0046 for association between rs2833249 and the AD status phenotype, supporting the direction of this path from the SNP to the phenotype. Combining these presents two possible scenarios. One is that rs2833249 affects GRIK1 levels, which then change APP levels; the other is that rs2833249 affects the expression levels of the nearby genes including GRIK1 and APP independently.
4.2.3. Path: rs4833235 (TRPC3) → ZNF720 (APP) → AD
TRPC3 (transient receptor potential cation channel, subfamily C, member 3) is a gene located 90369bp upstream of rs4833235. It has been reported that TRPC3 protects neurons by deregulating tau protein (Yamamoto et al., 2007), another major factor associated with AD. We also found that misfolded beta-amyloid induces misfolded tau protein (Nussbaum et al., 2013). Based on these, we consider two hypotheses. First, rs4833235 changes TRPC3 levels, and the perturbed TRPC3 levels affect beta-amyloid levels, which in turn affect tau protein levels. Second, rs4833235 affects TRPC3, which then affects both APP and tau protein independently, leading to the change of AD risk.
4.2.4. Path: rs722861 (EFCAB6) → ZNF720 (APP) → AD
EFCAB6 (EF-hand calcium binding domain 6) is located 121762bp upstream of rs722861, and it interacts with androgen receptor and PARK7 (Parkinson protein 7) (Niki et al., 2003; Szklarczyk et al., 2011), a gene related to Parkinson’s disease. It has been shown that reduced androgen levels increase the levels of beta-amyloid and hyperphosphorylated tau protein (Drummond et al., 2009). Therefore, we hypothesize that EFCAB6 regulates beta-amyloid levels through androgen receptors, and EFCAB6 may be involved in multiple neurological diseases such as Parkinson's disease and AD.
4.3. Estrogen-related path associations
We identified six path associations that involve RHOBTB3 (rho-related BTB domain containing 3), which is a putative anti-estrogen resistance gene for breast cancer patients (Van Agthoven et al., 2009). In the early stage of breast cancer, the growth of tumors requires estrogens, which can be inhibited by anti-estrogens. However, as the tumor progresses, it becomes anti-estrogens resistant, and genes involved in such a process are called anti-estrogen resistance genes. In our literature survey, we also found that estrogen protects neurons against beta-amyloid (Yao et al., 2007), and estrogen has been extensively studied for AD therapy (Henderson, 2014; Kawas et al., 1997;). Combining these, we suggest that RHOBTB3 is related to AD though an estrogen receptor. As examples, we investigate possible association mechanisms for the following two paths.
4.3.1. Path: rs2974135 (CTNNA2) → RHOBTB3 → AD
In this path, rs2974135 is located within a gene encoding CTNNA2 (catenin, alpha 2), which is neuronal-specific catenin. CTNNA2 is reportedly associated with late-onset AD in the Amish populations (Cummings et al., 2012). We also found a small p-value in our data for the SNP-phenotype association (p-value = 0.033). Previous studies and our results support that associations exist between CTNNA2 and the AD status, and between RHOBTB3 and the AD status. It would be interesting to conduct biological experiments to investigate if CTNNA2 interacts with RHOBTB3 to confirm this path association.
4.3.2. Path: rs11057512 (CCDC62) → RHOBTB3 → AD
The SNP rs11057512 is located 4732 bp upstream of CCDC62 (coiled-coil domain containing 62), a nuclear receptor co-activator that can enhance transactivation of ESR1 (estrogen receptor 1) and ESR2 (estrogen receptor 2) (Chen et al., 2009). It seems that CCDC62 is associated with RHOBTB3 through estrogen pathways. Furthermore, it has been reported that CCDC62 is associated with Parkinson’s disease risk in a Han Chinese population (Liu et al., 2013). It would be interesting to exam CCDC62’s pleiotropic effects on neurological disorders including Parkinson’s disease and AD.
4.4. Nicotine-related path associations
We also found seven path associations that involve vesicle-associated membrane protein 1 (VAMP1). VAMP1 is a gene encoding SNARE complex that controls neurotransmitter release via vesicle-mediated synaptic transmission (Fernandez-Castillo et al., 2012); further, it is involved in nicotine pathway through SNARE complex. Interestingly, nicotine’s involvement in AD has been extensively studied, and nicotinic receptors have been suggested as drug targets for AD (Maelicke et al., 2001; Newhouse et al., 1997). Furthermore, Zou et al. (2010) reported that eSNPs within VAMP1 are associated with late-onset AD. Below, we explore two path associations with VAMP1.
4.4.1. Path: rs10514262 (HAPLN1) → VAMP1 → AD
The SNP rs10514262 is located 93 475 bp downstream of hyaluronan and proteoglycan link protein 1 (HAPLN1). It has been reported that HAPLN1 is one of the major components forming a ‘perineuronal net’ that protects AD cortical and subcortical neurons against iron-induced oxidative stress (Suttkus et al., 2014). This has been experimentally validated via knockout experiments, where mice lacking HAPLN1 failed to develop a normally shaped perineuronal net. This suggests that HAPLN1 is potentially associated with AD. To confirm this path association, it would be interesting to examine the status of VAMP1 when HAPLN1 is knocked out, and the effects of VAMP1 levels on the formation of perineuronal net.
4.4.2. Path: rs4656888 (CD1E) → VAMP1 → AD
The SNP rs4656888 is located 68804bp downstream of CD1E (cluster of differentiation 1E), a member of the CD1 family. CD1 is structurally related to major histocompatibility complex (MHC) proteins (Wilson and Bjorkman, 1998); further, the relationships between MHC proteins and nicotinic attenuation of central nervous system has been reported (Shi et al., 2009). Therefore, it seems that CD1E is associated with VAMP1 through its involvements in the nicotine pathway; for future work, it would be interesting to study the interactions between CD1E and VAMP1 in the nicotine pathway.
5 Conclusions
We proposed a new paradigm of path associations to detect associations among genotypes, gene expression traits, and phenotypes. Furthermore, we developed a network-driven method, NETAM, using state-of-the-art machine learning techniques. Specifically, we employed SRMs to find edges in an association network considering all SNPs or all expression traits simultaneously, and stability selection and screening for false positive control and large-scale analysis. In the analysis of the late-onset AD data, NETAM found 477 significant path associations, among which, we investigated the paths that include ZNF720, RHOBTB3, and VAMP1 genes. These findings suggest various association mechanisms through beta-amyloid, estrogen, and nicotine pathways, which seemed to be crucially related to AD.
One promising future research direction would be to extend association networks to capture complex association mechanisms by introducing additional edges between different SNPs, between different gene traits or between different phenotypes. Further, when adding edges in the networks, we can take advantage of the structures in the genome (e.g. linkage disequilibrium) or gene–gene interaction networks. It would also be interesting to develop a theory to estimate false discovery rate for path associations in NETAM, and to conduct biological experiments to validate our proposed hypotheses for AD-related path associations.
Acknowledgements
This work was done under a support from NIH 1 R01 GM087694-01; NIH 1RC2HL101487-01 (ARRA); NSF IIS-0713379; and P30 DA035778A1.
References
- Abadi M. et al. (2016) TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv:1603.04467 [cs.DC]. [Google Scholar]
- Barrett T. et al. (2007) NCBI GEO: mining tens of millions of expression profilesdatabase and tools update. Nucleic Acids Res., 35 (Suppl 1), D760–D765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bush A.I. et al. (1994) Rapid induction of Alzheimer A beta amyloid formation by zinc. Science, 265, 1464–1467. [DOI] [PubMed] [Google Scholar]
- Chen M. et al. (2009) CCDC62/ERAP75 functions as a coactivator to enhance estrogen receptor beta-mediated transactivation and target gene expression in prostate cancer cells. Carcinogenesis, 30, 841–850. [DOI] [PubMed] [Google Scholar]
- Corder E. et al. (1993) Gene dose of apolipoprotein E type 4 allele and the risk of Alzheimers disease in late onset families. Science, 261, 921–923. [DOI] [PubMed] [Google Scholar]
- Courts C. et al. (2008) Recurrent inactivation of the PRDM1 gene in primary central nervous system lymphoma. J. Neuropathol. Exp. Neurol., 67, 720–727. [DOI] [PubMed] [Google Scholar]
- Cummings A. et al. (2012) Sequence analysis of CTNNA2 and LRRTM1 for late-onset Alzheimers disease in the Amish. Alzheimer’s Dement, 8, P664. [Google Scholar]
- Curtis R. et al. (2012). Finding genome-transcriptome-phenome association with structured association mapping and visualization in genamap. In Pacific Symposium on Biocomputing, Hawaii, USA, 327–338. [PubMed] [Google Scholar]
- Dijkstra E.W. (1959) A note on two problems in connexion with graphs. Numerische Mathematik, 1, 269–271. [Google Scholar]
- Drummond E.S. et al. (2009) Androgens and Alzheimer’s disease. Curr. Opin. Endocrinol. Diabetes Obes., 16, 254–259. [DOI] [PubMed] [Google Scholar]
- Fan J., Lv J. (2008) Sure independence screening for ultrahigh dimensional feature space. J. R. Stat. Soc. Series B Stat. Methodol., 70, 849–911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernandez-Castillo N. et al. (2012) Candidate pathway association study in cocaine dependence: the control of neurotransmitter release. World J. Biol. Psychiatry, 13, 126–134. [DOI] [PubMed] [Google Scholar]
- Gilad Y. et al. (2008) Revealing the architecture of gene regulation: the promise of eQTL studies. Trends Genet., 24, 408–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamosh A. et al. (2005) Online mendelian inheritance in man (OMIM), a knowledgebase of human genes and genetic disorders. Nucleic Acids Res., 33 (Suppl 1), D514–D517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henderson V.W. (2014) Alzheimer’s disease: review of hormone therapy trials and implications for treatment and prevention after menopause. J. Steroid Biochem. Mol. Biol., 142, 99–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawas C. et al. (1997) A prospective study of estrogen replacement therapy and the risk of developing Alzheimer’s disease: the Baltimore Longitudinal Study of Aging. Neurology, 48, 1517–1521. [DOI] [PubMed] [Google Scholar]
- Kendziorski C. et al. (2006) Statistical methods for expression quantitative trait loci (eQTL) mapping. Biometrics, 62, 19–27. [DOI] [PubMed] [Google Scholar]
- Kim S., Xing E. (2009) Statistical estimation of correlated genome associations to a quantitative trait network. PLoS Genet., 5, e1000587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim Y.A., Przytycka T.M. (2012) Bridging the gap between genotype and phenotype via network approaches. Front. Genet., 3 http://dx.doi.org/10.3389/fgene.2012.00227 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S., Xing E. (2012) Leveraging input and output structures for joint mapping of epistatic and marginal eqtls. Bioinformatics, 28, i137–i146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S, Xing E.P. (2014). Screening rules for overlapping group lasso. arXiv:1410.6880 [stat.ML].
- Liu R.R. et al. (2013) CCDC62 variant rs12817488 is associated with the risk of Parkinson’s disease in a Han Chinese population. Eur. Neurol., 71, 77–83. [DOI] [PubMed] [Google Scholar]
- Maelicke A. et al. (2001) Allosteric sensitization of nicotinic receptors by galantamine, a new treatment strategy for Alzheimers disease. Biol. Psychiatry, 49, 279–288. [DOI] [PubMed] [Google Scholar]
- Maglott D. et al. (2005) Entrez gene: gene-centered information at ncbi. Nucleic Acids Res., 33, D54–D58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mailman M.D. et al. (2007) The NCBI dbGaP database of genotypes and phenotypes. Nature Genet., 39, 1181–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manolio T. et al. (2009) Finding the missing heritability of complex diseases. Nature, 461, 747–753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meinshausen N., Bühlmann P. (2010) Stability selection. J. R. Stat. Soc. Series B Stat. Methodol., 72, 417–473. [Google Scholar]
- Moreno J.C. et al. (2008) Mutations in the iodotyrosine deiodinase gene and hypothyroidism. N. Engl. J. Med., 358, 1811–1818. [DOI] [PubMed] [Google Scholar]
- Newhouse P.A. et al. (1997) Nicotinic system involvement in Alzheimers and Parkinsons diseases. implications for therapeutics. Drug. Aging, 11, 206–228. [DOI] [PubMed] [Google Scholar]
- Niki T., et al. (2003). DJBP: A novel DJ-1-binding protein, negatively regulates the androgen receptor by recruiting histone deacetylase complex, and DJ-1 antagonizes this inhibition by abrogation of this complex. Mol. Cancer Res., 1(4), 247–261. [PubMed] [Google Scholar]
- Nussbaum J.M. et al. (2013) Alzheimer disease: a tale of two prions. Prion, 7, 14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oláh J. et al. (2011) Interactions of pathological hallmark proteins tubulin polymerization promoting protein/p25, β-amyloid, and α-synuclein. J. Biol. Chem., 286, 34088–34100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orii N., Ganapathiraju M.K. (2012) Wiki-pi: a web-server of annotated human protein-protein interactions to aid in discovery of protein function. PloS One, 7, e49029.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paganini-Hill A., Henderson V.W. (1994) Estrogen deficiency and risk of Alzheimer’s disease in women. Am. J. Epidemiol., 140, 256–261. [DOI] [PubMed] [Google Scholar]
- Purcell S. et al. (2007) PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet., 81, 559–575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rokita S.E., Jr, et al. (2010) Efficient use and recycling of the micronutrient iodide in mammals. Biochimie, 92, 1227–1235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schadt E.E. et al. (2005) An integrative genomics approach to infer causal associations between gene expression and disease. Nat. Genet., 37, 710–717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi F.D. et al. (2009) Nicotinic attenuation of central nervous system inflammation and autoimmunity. J. Immunol., 182, 1730–1739. [DOI] [PubMed] [Google Scholar]
- Suttkus A. et al. (2014) Aggrecan, link protein and tenascin-r are essential components of the perineuronal net to protect neurons against iron-induced oxidative stress. Cell Death Dis., 5, e1119.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szklarczyk D. et al. (2011) The STRING database in 2011: functional interaction networks of proteins, globally integrated and scored. Nucleic Acids Res., 39 (Suppl 1), D561–D568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan M.G. et al. (2010) Genome wide profiling of altered gene expression in the neocortex of Alzheimer’s disease. J. Neurosci. Res., 88, 1157–1169. [DOI] [PubMed] [Google Scholar]
- Tibshirani R. (1996) Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol., 58, 267–288. [Google Scholar]
- Tibshirani R. et al. (2012) Strong rules for discarding predictors in lasso-type problems. J. R. Stat. Soc. Series B Stat. Methodol., 74, 245–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uechi T. et al. (2006) Ribosomal protein gene knockdown causes developmental defects in zebrafish. PLoS One, 1. doi:10.1371/journal.pone.0000037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Agthoven T. et al. (2009) Functional identification of genes causing estrogen independence of human breast cancer cells. Breast Cancer Res. Treat., 114, 23–30. [DOI] [PubMed] [Google Scholar]
- Van Duijn C.M., Hofman A. (1991) Relation between nicotine intake and Alzheimer’s disease. British Med. J., 302, 1491.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Osch L.A. et al. (2004) Low thyroid-stimulating hormone as an independent risk factor for Alzheimer disease. Neurology, 62, 1967–1971. [DOI] [PubMed] [Google Scholar]
- Wang J. et al. (2013) Lasso screening rules via dual polytope projection. Adv. Neural. Inf. Process. Syst., 1070–1078. arXiv:1211.3966. [Google Scholar]
- Wilson I.A., Bjorkman P.J. (1998) Unusual MHC-like molecules; CD1, fc receptor, the hemochromatosis gene product, and viral homologs. Curr. Opin. Immunol., 10, 67–73. [DOI] [PubMed] [Google Scholar]
- Yamamoto S. et al. (2007) Transient receptor potential channels in Alzheimer’s disease. Biochimica Et Biophysica Acta (BBA)-Molecular Basis of Disease, 1772, 958–967. [DOI] [PubMed] [Google Scholar]
- Yao M. et al. (2007) Estrogen regulates bcl-w and bim expression: role in protection against β-amyloid peptide-induced neuronal death. J. Neurosci., 27, 1422–1433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yen J.Y. (1971) Finding the k shortest loopless paths in a network. Manag. Sci., 17, 712–716. [Google Scholar]
- Yuan M., Lin Y. (2005) Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Series B Stat. Methodol., 68, 49–67. [Google Scholar]
- Zhang B. et al. (2013) Integrated systems approach identifies genetic nodes and networks in late-onset Alzheimers disease. Cell, 153, 707–720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao P., Yu B. (2006) On model selection consistency of lasso. J. Mach. Learn. Res., 7, 2541–2563. [Google Scholar]
- Zhou X., Stephens M. (2012) Genome-wide efficient mixed-model analysis for association studies. Nat. Genet., 44, 821–824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou F. et al. (2010) eSNPs within VAMP1 show genetic association with late onset Alzheimer’s disease. Alzheimer’s Dement., 6, S114. [Google Scholar]