Abstract
Motivation: Mechanistic models based on ordinary differential equations provide powerful and accurate means to describe the dynamics of molecular machinery which orchestrates gene regulation. When combined with appropriate statistical techniques, mechanistic models can be calibrated using experimental data and, in many cases, also the model structure can be inferred from time–course measurements. However, existing mechanistic models are limited in the sense that they rely on the assumption of static network structure and cannot be applied when transient phenomena affect, or rewire, the network structure. In the context of gene regulatory network inference, network rewiring results from the net impact of possible unobserved transient phenomena such as changes in signaling pathway activities or epigenome, which are generally difficult, but important, to account for.
Results: We introduce a novel method that can be used to infer dynamically evolving regulatory networks from time–course data. Our method is based on the notion that all mechanistic ordinary differential equation models can be coupled with a latent process that approximates the network structure rewiring process. We illustrate the performance of the method using simulated data and, further, we apply the method to study the regulatory interactions during T helper 17 (Th17) cell differentiation using time–course RNA sequencing data. The computational experiments with the real data show that our method is capable of capturing the experimentally verified rewiring effects of the core Th17 regulatory network. We predict Th17 lineage specific subnetworks that are activated sequentially and control the differentiation process in an overlapping manner.
Availability and Implementation: An implementation of the method is available at http://research.ics.aalto.fi/csb/software/lem/.
Contacts: jukka.intosalmi@aalto.fi or harri.lahdesmaki@aalto.fi
1 Introduction
During the past years, several computational approaches have been proposed to infer the structure and dynamics of gene regulatory networks from either steady-state or time–course measurements (Marbach et al., 2012). The approaches range from statistical and information theoretic methods to mechanistic models. Mechanistic models are capable of describing the actual molecular dynamics originating from reaction kinetics and the underlying network structure can also be accurately estimated by combining these models with appropriate statistical techniques (see e.g. Intosalmi et al., 2015; Schulz et al., 2009; Xu et al., 2010). Typically, a mechanistic model consists of a set of interacting molecular components and a formal description for the possible mechanisms affecting the time-evolution of the components. While the mechanistically motivated network inference works well for static network topologies, the standard approach cannot be applied if the molecular mechanisms depend on transient cellular processes, and in particular, if the network structure is dynamically rewired. A good example of such transient processes are epigenetic modifications that typically are not observed in detail but can have a major effect on regulatory interactions, for instance, during cellular differentiation. In the presence of such transient processes, the structure of network becomes time-dependent and, consequently, the network inference becomes notably more challenging.
The importance of dynamically evolving regulatory mechanisms has been recognized in many recent experimental studies and also computational techniques have been developed to analyze and understand measurements that are possibly affected by transient mechanisms (see e.g. Yosef et al., 2013). The existing computational approaches that address this problem primarily focus on state-space models, such as non-stationary dynamic Bayesian networks (Dondelinger et al., 2013; Grzegorczyk and Husmeier, 2011; Robinson and Hartemink, 2010) and probabilistic Boolean networks and their variants (Shmulevich et al., 2002). To our best knowledge, general approaches that would complement mechanistic models so that they could be used to study and detect dynamically evolving regulatory networks do not exist. The inevitable strength of mechanistic models is that they are capable of describing the underlying molecular mechanisms in detail, and when combined with statistical modeling, they can take the analysis of time–course data well beyond the state-space models. In other words, by means of mechanistic models it is possible to describe and analyze the actual processes behind the data and not only find patterns, correlations, or other dependencies in time-series. Given these strengths of mechanistic modeling, it is obvious that a high practical value can be obtained by extending this model class to account also for dynamically evolving molecular networks.
In this study, we develop a novel mechanistic analysis method that can be used to detect and analyze latent processes which affect the molecular mechanisms by rewiring the underlying network structure. The method that we introduce is called the latent effect mechanistic (LEM) model and it is based on the notion that all mechanistic ordinary differential equation (ODE) models can be coupled with a latent process that approximates the net impact of transient mechanisms affecting the structure of molecular network. We embed the LEM model into a well-defined statistical framework that allows us to infer possible latent effects simultaneously with the model structure and rate parameters. In addition to the theoretical derivation of the LEM model, we also outline numerical techniques that are required to carry out the analysis. We exemplify the performance of our method using simulated data and conclude that we can rigorously recover the underlying model using our inference algorithms. Further, we apply our method to study the regulatory interactions during T helper 17 (Th17) cell differentiation using time–course RNA sequencing (RNA-seq) data and conclude that our analysis results are in agreement with the previously observed results regarding the time-dependency of the regulatory network that steers Th17 lineage specification.
2 Approach
To illustrate our modeling idea, let us consider a gene and some transcription factor A that activates the gene. Let us also assume that, prior to stimulation, the gene’s locus is covered with epigenetic marks that prevent the transcription factor A binding the promoter (Fig. 1, left panel) and the gene remains inactive. Upon stimulation, epigenetic marks are removed by unknown enzymatic signals (Fig. 1, middle panel) and eventually the promoter region becomes clear from the repressive marks and the transcription factor can bind the promoter (Fig. 1, right panel). As a result of binding, the gene is activated and a gene product B is produced (Fig. 1, right panel). In mathematical terms this unobserved activation process corresponds to moving from the ‘no interaction’ network structure (Fig. 1, left panel) to ‘interaction activated’ network structure (Fig. 1, right panel). Because molecular reactions steering the epigenetic signaling are stochastic in nature, the change from the initial state to the active state does not occur synchronously in a cell culture. In other words, the fraction of cells in the active state increases gradually after stimulation while the fraction of cells in the inactive state decreases. Even though we may neither know nor be able to measure the molecular events that participate in the removal of the repressive epigenetic marks, we can construct an ODE model that describes the net impact of these events at the population level. In this toy example, the model can be, for instance, the ODE system
| (1) |
| (2) |
where x1 and x2 denote the relative fractions of cells in the inactive and active states, u(t) is an input signal representing stimulus, and θx is a free conversion rate parameter. In this study, we call the solution of this model a latent process. Figure 2(a) illustrates the possible dynamics of the above latent process with different conversion rates and Figure 2(b) shows an example of a latent process that consists of three sequential states (latent processes with multiple sequential phases will be discussed more in Section 3.5).
Fig. 1.
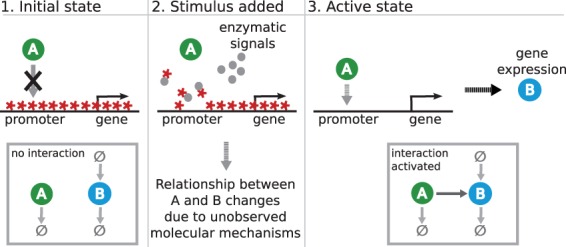
Illustration of a dynamically evolving silencing mechanism that controls the relationship between the transcription factor A and the gene product B
Fig. 2.
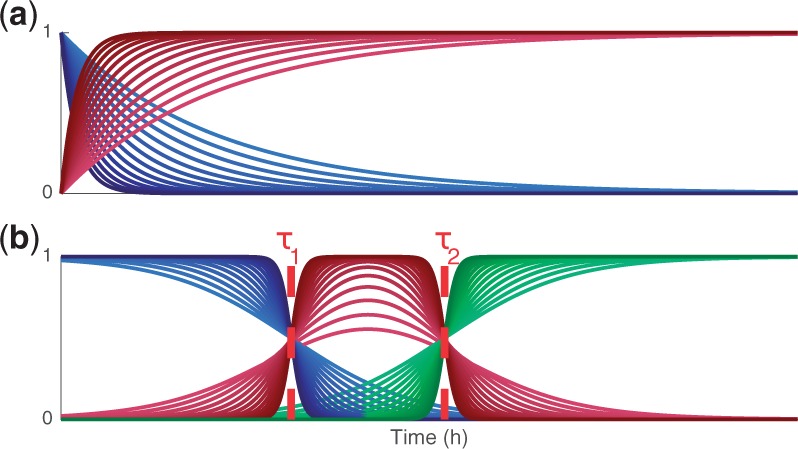
Examples of latent processes. (a) A latent process consisting of two states. The conversion from the first state to the second state can occur rapidly or slowly depending on the parameterization of the latent process. (b) A latent process consisting of three sequential states. The conversion from one state to another can occur smoothly or rapidly depending on the parameterization and, further, the parameters τ1 and τ2 determine the time instants for switching
In general, if we have some understanding about the mechanisms that influence the production and degradation of the transcription factor A and the gene product B, we can build a mechanistic model that would rigorously describe their dynamics. For instance, we can construct a model in the form of an ODE system
| (3) |
| (4) |
where we have assumed that A and B degrade at rates δ1 and δ2, respectively, B is produced at the basal rate k0, and A activates B at the rate k1. This simple model corresponds to the mechanisms illustrated in the right panel in Figure 1. If the assumptions of the mechanisms incorporated into the model are reasonably realistic, the parameters of the model can be inferred from time–course population average data on A and B by means of statistical techniques. However, if the interaction between A and B is affected (i.e. rewired) by transient silencing of the gene, parameter and model inference results may become seriously biased or wrong.
The LEM model for the above example system can be constructed by considering the standard ODE model (Eqs 3 and 4) and coupling it with the two-state latent process described by Eqs 1 and 2. In this example, the latent state x1 represents the early state with inactive gene (silencing on) and the state x2 the late state in which the repressive marks are removed. The LEM model is constructed by coupling the ODE system with the latent process. This results in the time–variant ODE system
| (5) |
| (6) |
where . The binary parameters z1, z2 parameterize the network structure and indicate whether the interaction between A and B is active in the latent states x1 and x2 or not. Effectively this results in four alternative models that are listed in the Table 1. By means of quantitative model comparison, we can select the most likely configuration for z1 and z2 and detect if transient mechanisms are present. Further, the model selection and parameter inference provide information about the possible dynamics of latent processes which, in the context of our example, means that we can infer the rate at which the cells leave the inactive state and enter active state. Naturally, if model selection indicates that most likely and , it is obvious that the LEM model reduces to the standard ODE model.
Table 1.
Alternative models for the example system
| Parameters for weighting | Interaction A → B | # of parameters |
|---|---|---|
| no interaction | 3 + 0 | |
| early interaction | 4 + 1 | |
| late interaction | 4 + 1 | |
| sustained interaction | 4 + 0 |
Here, the number of parameters is a sum over the number of parameters in the actual model and the latent process, respectively.
In the above example, the latent process can naturally be coupled with all mechanisms included into the model, that is, the basal induction, degradation, and interaction between A and B. In this case, the model selection should be carried out by considering alternative model structures compared to 24 model structures in the standard ODE model. For example, stimulus dependent degradation could be detected along with transient interaction between A and B.
3 Methods
3.1 Formal definition of the LEM model
As illustrated above, the first component of our model is a standard mechanistic ODE model. The standard model can be constructed using the law of mass action, Michaelis–Menten or Hill kinetics, or any other similar approach. Without any loss of generality, we assume that the resulting model can be expressed in the form
| (7) |
where , Ji is the number of functions fij affecting the component yi (and we denote ), and . In addition, we need to design a latent process which represents M possible underlying latent states. The latent process can be constructed by means of heuristically motivated ODE modeling, as presented for the toy model above, or by defining a well-motivated parametric form for the process (as we do in Section 3.5). Regardless how the latent process is constructed, it is important that its functional form is flexible enough so that it is possible to infer latent dynamics from the data.
Given a standard ODE model and a latent process, the LEM model is constructed by coupling them. Formally, we can write
| (8) |
where
| (9) |
is a weight function depending on the latent state and . The binary parameters zjk determine if fij is effective in the latent state xk or not (the values 1 and 0, respectively). It is convenient to store these binary parameters into a J × M matrix Z so that . Note that in the standard ODE approach the network structure is defined by a vector. The LEM modeling approach allows the network structure to be rewired and the consecutive rewiring steps (and thus the dynamically evolving network structure) is defined by a binary J × M matrix Z. Now
| (10) |
is the solution of the ODE system that is coupled with the latent process and we define the model output to be
| (11) |
which can consist of some subset of the state variables y.
In this study, we aim to infer the parameters θy and θx as well as the most likely configuration of the matrix Z from time–course data. In order to do this in a rigorous manner, we need to formulate the problem in statistical terms.
3.2 Statistical framework to infer the model parameters and the network structure Z
It is important to combine mathematical modeling with time–course data using well-motivated, data type specific statistical models. Statistical modeling makes it possible to weight the data in an objective way and propagate the uncertainty in the measurements through the models in a proper manner. In the following, we present a general statistical framework for the LEM model. By means of this framework it is possible to combine the LEM model with any data type or combination data types including, for instance, read count sequencing data and qPCR measurements. The only requirement is that we are capable of making some assumptions about the distribution of the chosen data type(s).
Let Dkl be a measurement of the kth component of the output at time tl and let us denote . A statistical model can be constructed by assuming that the observation Dkl is distributed according to some distribution g which depends on the model output and the parameters of the distribution θd. In other words,
| (12) |
In the context of our ODE model, is fully determined by the parameters θy, θx and Z, and consequently, we can write . Further, by introducing the notation , the distribution can be expressed in the form . Now, if we have time–course data on the state variables and we can assume that the measurements are independent given , we can define the likelihood function
| (13) |
where .
A Bayesian statistical model can be obtained by combining the likelihood function with a prior distribution on the parameters, (for details about Bayesian methodology, see e.g. Robert, 2007). In our model formulation, the different configurations of the binary matrix Z define a discrete set of network structures and it is convenient to write the prior distribution in the form , where is the prior distribution over network structures. By applying Bayes’ theorem, we obtain the parameter posterior distribution
| (14) |
where
| (15) |
is the marginal likelihood of the model specified by Z. When the marginal likelihoods of different configurations for matrix Z are available, model ranking can easily be done by means of the posterior distribution
| (16) |
or equivalently,
| (17) |
where C is a constant.
3.3 Estimating logarithmic posterior probabilities for alternative models
Several different techniques exist to estimate the marginal likelihood (for a review, see e.g. Friel and Wyse, 2012). In this study, we approximate the marginal likelihood by means of Laplace method and some further simplifications that are discussed in detail, for instance, by Ripley (1996) (pages 63-64). This approximation allows us to write the estimator for the logarithmic posterior probabilities of the alternative models (Eq. 17) in the form
| (18) |
where is the maximum likelihood, is the number of parameters, and n is the number of observations. For model ranking purposes, we can simply neglect the constant C and compare unnormalized logarithmic posterior probabilities. Further, if the prior distribution over alternative configurations of binary matrix Z is uniform, Eq. 18 reduces to a form that corresponds to the Bayesian information criterion (Schwarz, 1978).
3.4 Forward-backward-stepwise selection to speed up model ranking
If we consider a LEM model that consists of J mechanisms and M latent states, we have altogether alternative models (i.e. the number of different configurations of binary matrix Z). Typically, the numbers of mechanisms and latent states are such that the estimation of marginal likelihood for all alternative configurations is out of reach. Therefore, we suggest to speed up the model ranking task by means of forward-backward-stepwise selection. This leads essentially to an algorithm that can be implemented through the following four steps:
Set free elements in Z to zero and estimate for this model.
- Generate J × M matrices by flipping elements in Z, that is,
and estimate for the corresponding models. Update Z to correspond the model that produces the highest posterior probability, that is, the highest .
Stop if the best ranked model does not indicate improvement in the model fit compared to the previous values.
Otherwise go back to Step 2.
3.5 LEM model for the core regulatory network driving Th17 cell specification
T helper 17 (Th17) cells play a crucial role in the adaptive immune system (Korn et al., 2009) and they have been noted to have important functions in various autoimmune diseases (Weaver et al., 2013). Recent experimental and computational studies have shed light to the regulatory mechanisms that steer the differentiation from a naive CD4+ helper T cell to a specialized Th17 cell (see e.g. Ciofani et al., 2012; Intosalmi et al., 2015; Yosef et al., 2013). Yosef et al. (2013) also report notable rewiring of the Th17 cell specific regulatory network during early phase of the lineage specification and, consequently, this provides us with a good application to test how LEM model analysis performs in practice.
Figure 4(a) illustrates the core Th17 regulatory network that was experimentally derived by Ciofani et al. (2012). The core network consists of five transcription factors, the retinoic acid receptor-related orphan receptor gamma t (RORC), signal transducer and activator of transcription 3 (STAT3), basic leucine zipper transcription factor (BATF), transcription factor Maf (MAF) and interferon regulatory factor 4 (IRF4), and contains only links that have been experimentally validated. For instance, RORC knock-out experiments show that RORC does not participate in any of the feedback mechanisms regulating STAT3 and, consequently such interactions are excluded from the network.
Fig. 4.
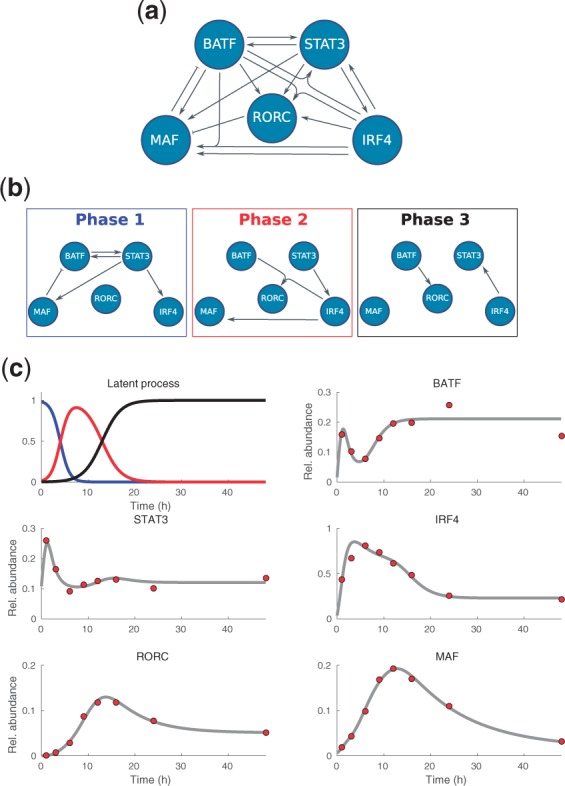
Experimentally validated core regulatory network steering Th17 lineage specification, inferred sequential subnetworks, and the predicted dynamics of the latent process and mRNA levels. (a) Full network which consists of all mechanistically possible interactions. (b) Predicted subnetworks that are active in three sequential phases. (c) Inferred dynamics (gray lines) plotted against experimental data (red circles). The color coding of the latent process corresponds to the three sequentially activated subnetworks shown above
To convert the network structure into a quantitative dynamic model, we denote the time-dependent expression levels of the genes by (here, N = 5) and assume that the genes can have activating and inhibiting interactions, and, in addition, we allow basal activation and degradation. Each of these mechanisms can be associated with a corresponding rate equation and, as a result, we obtain an ODE system specified by
| (19) |
where and are unknown basal activation, independent activation, synergistic activation, inhibition and degradation rate constants, respectively. The rate constants are defined to be strictly positive and setting a specific rate constant to zero removes that mechanisms (and parameter) from the model. We use the experimentally validated network (Fig. 4(a)) as a basis for our inference and include all experimentally validated interactions to the mechanistic model. To construct the LEM model, the system in Eq. 19 is combined with an appropriate latent process.
The latent process for Th17 LEM model is constructed based on the findings reported by Yosef et al. (2013). They suggest that there are three sequential wiring states during the early phase of Th17 cell differentiation. From the mechanistic modeling perspective it is obvious that transitions between the states must occur gradually and two different wiring states can affect the observations simultaneously during the transitions. To describe a continuum of realistic transitions occurring between the sequential rewiring states, we define the latent process
| (20) |
| (21) |
| (22) |
where λ1, λ2, τ1 and τ2 are the parameters of the process. Because the rewiring occurs in sequential states, we also introduce the restriction . Figure 2(b) illustrates dynamics of this latent process.
To analyze the core Th17 regulatory network using the LEM model, we make use of the time–course RNA-seq data provided by Ciofani et al. (2012). To obtain these data, Ciofani et al. (2012) purified naive CD4+ cells from lymph nodes and spleen of wild-type mice, cultured the cells in Th17 conditions, and harvested a proportion of cells at the time-points 0, 1, 3, 6, 9, 12, 16, 24 and 48 h for RNA-seq processing (see the original article for details). We use the fragments per kilobase of transcript per million mapped reads (FPKM) values of each gene to inform the LEM model and by assuming independent normally distributed noise, we can write the likelihood function (confer Eq. 13) in the form
| (23) |
where we use same notation as in Section 3.2, is the normal probability density function with mean μ and variance , and α and β parameterize the likelihood function. To construct this statistical model, we have assumed that the noise in the data depends on the signal strength according to the parameter β and, in addition, there is some basal level of variance that is determined by α. The original data consists of one measurement at each time point except at time 6 h there are three replicates. We treat the measurements at 6 h as a single measurement which is taken to be the mean of three replicates. The initial state for each model is fixed according to the measurement at time t = 0 h.
The prior distribution over the alternative configurations of the matrix Z can be constructed in numerous ways and, in this study, we use the truncated geometric distribution. More specifically, we define h(Z) to denote the number of nonzero elements in the matrix Z and set
| (24) |
where , and p = 0.3. Intuitively, we set the prior over the number of nonzero elements in the matrix Z and, with the chosen parameterization, the impact of this prior distribution is rather weak. However, the prior distribution is introduced to prevent the forward-backward-stepwise selection algorithm proceeding in the cases in which the parametric dimension of the model remains the same and the model fit is improved in negligibly small fractions due to overly complex network structure.
3.6 Computational implementation
The LEM model, the estimation of unnormalized logarithmic posterior model probabilities, and the forward-backward-stepwise selection algorithm are implemented in Matlab (The MathWorks Inc., Natick, MA, USA). The ODE systems are solved numerically using the CVODES solver from the SUNDIALS package (Hindmarsh et al., 2005). Maximum likelihood estimates for parameters are obtained using multi-start local optimization strategy in a similar manner as outlined by Raue et al. (2013, 2015). In brief, we solve sensitivity equations in parallel with the ODE system, compute the gradient of the likelihood function accordingly, and use this information to carry out efficient local optimization. For each model, we sample random initial parameter values using Latin hypercube sampling and carry out the local optimization using lsqnonlin optimization routine in Matlab. If the optimization routine happens to operate in a parameter range that results in ODE responses that cannot be solved by using the default settings of the CVODES solver, the likelihood values at such points are mapped to a very small value.
4 Results
4.1 Testing the method using simulated data
Before applying the LEM model to real data, we test the method and the related numerical procedures using simulated data. To simulate data, we construct a four gene network that is assumed to contain all mechanistically possible interactions (Fig. 3(a)). Further, we assume that the interactions are affected by sequentially occurring latent states in a similar manner as in our Th17 cell differentiation application. The three different wirings of the network are shown in Figure 3(b) and these wirings affect the observed dynamics in an overlapping manner (see the latent process in Figure 3(c)). In other words, we assume that the whole cell population does not switch the wiring synchronously but the cells move gradually form one wiring state to another. To construct a quantitative model based on the interactions shown in Figure 3(a), we assume the same structure for rate equations as in Section 3.5 for the Th17 cell specific core network and build the full ODE model according to the Eq. 19. Here, we assume that two genes (i.e. the genes A and B in Fig. 3(a)) have basal transcription mechanisms and the mRNA levels of all genes are allowed to degrade at independent rates. Further, these mechanisms are assumed to be present in all wiring states, that is, the corresponding rows in the matrix Z are fixed to contain only ones (see Table 2). To construct the LEM model for this system, we couple the full ODE model with the latent process defined by Eqs. 20–22. The parameters that we use to simulate data are given in parentheses after the inferred values in Table 2 and the resulting response consisting of the latent process and the solution of the ODE model is shown in Figure 3(c) (dashed lines). Figure 3(c) also shows the actual data points that are simulated by adding normal fluctuations to the deterministic response according to the statistical model (Eq. 23). In this example inference, the rate parameters are assumed to lay in the range and we use 100 random initial parameter values in the multi-start local optimization. Otherwise the inference for the simulated data is implemented using the same specifications that are used for the real data.
Fig. 3.
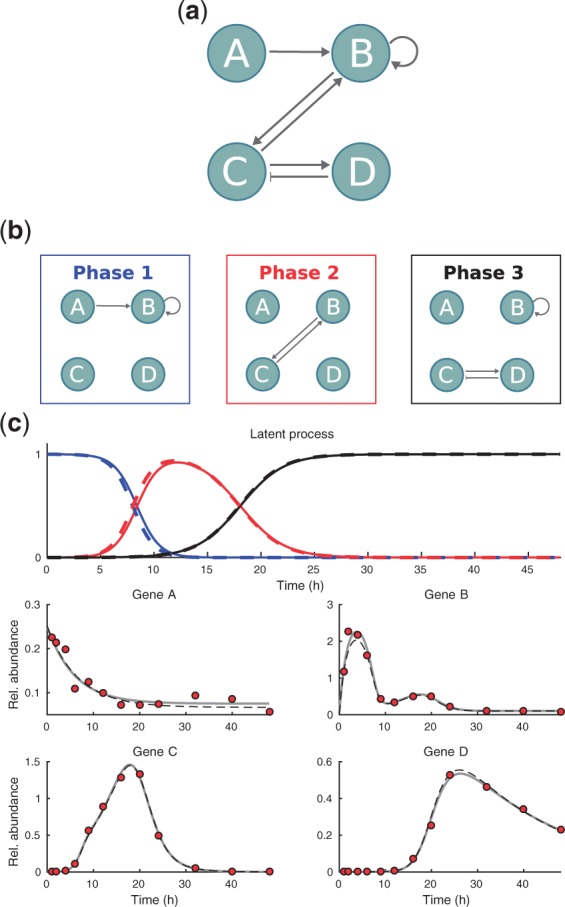
Artificial dynamically evolving network and inference results with simulated data. (a) Full network which consists of all mechanistically possible interactions. (b) Subnetworks that are active in three sequential phases. (c) Inferred dynamics plotted against simulated data (red circles). The color coding of the latent process corresponds to the three sequentially activated subnetworks shown above. Dashed lines represent the response that is used to simulate the data with fixed parameters and the solid lines represent the inferred dynamics
Table 2.
Inferred parameters for simulated data (the correct parameter values are shown within parentheses)
| Mechanistic ODE model and matrix Z | |||||
|---|---|---|---|---|---|
| j | Mechanism | Rate param. | |||
| 1 | Basal activ. of A | 1 | 1 | 1 | 0.012 (0.01) |
| 2 | Basal activ. of B | 1 | 1 | 1 | 0.047 (0.05) |
| 3 | A activates B | 1 | 0 | 0 | 6.410 (6) |
| 4 | B activates B | 1 | 0 | 1 | 2.864 (2) |
| 5 | B activates C | 0 | 1 | 0 | 0.633 (0.5) |
| 6 | C activates B | 0 | 1 | 0 | 1.343 (1) |
| 7 | C activates D | 0 | 0 | 1 | 0.096 (0.1) |
| 8 | D inhibits C | 0 | 0 | 1 | 0.423 (0.5) |
| 9 | Degrad. of A | 1 | 1 | 1 | 0.169 (0.15) |
| 10 | Degrad. of B | 1 | 1 | 1 | 3.321 (2.5) |
| 11 | Degrad. of C | 1 | 1 | 1 | 0.096 (0.05) |
| 12 | Degrad. of D | 1 | 1 | 1 | 0.047 (0.05) |
| Latent process | ||
|---|---|---|
| Parameter | Value | Allowed range |
| λ1 | 0.950 (1) | [0.25, 3] |
| τ1 | 8.387 (8) | [2, 10] |
| λ2 | 0.491 (0.5) | [0.25, 3] |
| τ2 | 18.057 (18) | [12.5, 30] |
In the statistical model, the parameters α and β have the values, 0.0001 and 0.1, respectively.
The inference results for the simulated data are summarized in Figure 3 and Table 2. We conclude that the forward-backward-stepwise selection algorithm converges successfully to the correct configuration of matrix Z and the inferred parameter values are very close to the values that are used to simulate the data (see Table 2). Note that our approximative marginal likelihood computation together with prior for network structure imply appropriate Occam’s razor and prevent inferring too complex models. Further, the model response, that is solved using the inferred parameters of the best model, is in a good agreement with the response that was used to generate the data (confer the solid versus dashed lines in Fig. 3(c)). All in all, the inference and model selection perform well in this test case and we can proceed to analyze real data.
4.2 LEM model captures rewiring effects of regulatory interactions during early Th17 lineage specification
We initiate the analysis of real data by visually inspecting the time–course FPKM values. Our first observation is that the initial expression level of RORC is very low and, as a consequence, we deduce that the basal expression of the RORC gene is on a rather weak level. To incorporate this prior information into the LEM model analysis, we remove the basal RORC expression from the mechanistic model but allow basal transcription for other genes. The initial expression levels for the ODE models are taken directly from the experimental data. Further, we allow the mRNA levels of all genes to degrade during the experiment.
We run the LEM model inference for the Th17 RNA-seq data using the specifications given in Sections 3.5 and 3.6. In our analysis, the rate parameters are constrained to the range and we use 300 random initial parameter values in the multi-start local optimization (the analysis is also repeated using 600 random initial parameter values to assure ourselves that the forward-backward-stepwise selection algorithm is not affected by suboptimal optimization performance). The inference results for the Th17 RNA-seq data are summarized in Figure 4 and Table 3. Intriguingly, the LEM model inference supports many interactions that were experimentally validated using combinations of different measurement techniques and experimental conditions in Ciofani et al. (2012) (for instance, knock-out experiments). The inferred LEM model structure is illustrated in Figure 4(b) and parameter values are given in Table 3.
Table 3.
Inferred parameters for the Th17 core network LEM model and dynamically rewired network structure matrix Z
| Mechanistic ODE model and matrix Z | |||||
|---|---|---|---|---|---|
| j | Mechanism | Rate param. | |||
| 1 | Basal activ. of BATF | 1 | 1 | 1 | 0.115 |
| 2 | Basal activ. of STAT3 | 1 | 1 | 1 | 9.620 |
| 3 | Basal activ. of IRF4 | 1 | 1 | 1 | 0.097 |
| 4 | Basal activ. of MAF | 1 | 1 | 1 | 0.001 |
| 5 | BATF activates STAT3 | 1 | 0 | 0 | 88.177 |
| 6 | STAT3 activates BATF | 1 | 0 | 0 | 1.021 |
| 7 | STAT3 activates IRF4 | 1 | 1 | 0 | 1.900 |
| 8 | IRF4 activates STAT3 | 0 | 0 | 1 | 9.249 |
| 9 | IRF4 activates RORC | 0 | 0 | 0 | – |
| 10 | IRF4 activates MAF | 0 | 1 | 0 | 0.043 |
| 11 | STAT3 activates RORC | 0 | 0 | 0 | – |
| 12 | BATF activates RORC | 0 | 0 | 1 | 0.035 |
| 13 | STAT3 activates MAF | 1 | 0 | 0 | 0.055 |
| 14 | BATF activates MAF | 0 | 0 | 0 | – |
| 15 | BATF and IRF activate STAT3 | 0 | 0 | 0 | – |
| 16 | BATF and IRF activate RORC | 0 | 1 | 0 | 0.309 |
| 17 | BATF and IRF activate MAF | 0 | 0 | 0 | – |
| 18 | MAF inhibits BATF | 1 | 0 | 0 | 72.134 |
| 19 | RORC inhibits MAF | 0 | 0 | 0 | – |
| 20 | Degrad. of BATF | 1 | 1 | 1 | 0.546 |
| 21 | Degrad. of STAT3 | 1 | 1 | 1 | 97.332 |
| 22 | Degrad. of IRF4 | 1 | 1 | 1 | 0.422 |
| 23 | Degrad. of RORC | 1 | 1 | 1 | 0.145 |
| 24 | Degrad. of MAF | 1 | 1 | 1 | 0.078 |
| Latent process | ||
|---|---|---|
| Parameter | Value | Allowed range |
| λ1 | 1.016 | [0.5, 3] |
| τ1 | 4.018 | [1, 8] |
| λ2 | 0.500 | [0.5, 3] |
| τ2 | 12.976 | [12.5, 30] |
In the statistical model, the parameters α and β have the values, 0.0001 and 0.035, respectively.
Our LEM model inference does not only provide important information about the regulatory interactions between the genes but can also be used to generate predictions on the sequentially activated subnetworks (Fig. 4(b)) as well as the time evolution of the latent states that determine the impact of the subnetworks (Fig. 4(c)). The predicted latent process in Figure 4(c) shows that the first phase of differentiation seems to be rather fast, the second state occurs approximately within the time window form 4 to 13 h, and, eventually, after 20 h, the gene expression levels settle to the stable pattern in a long-lasting third state. This temporal behavior is in line with three transcriptional phases reported by Yosef et al. (2013), that is, early induction (up to 4 h), intermediate onset of phenotype and amplification (4–20 h), and late stabilization (20–72 h). The predicted latent process (Fig. 4(c)) suggests that these three phases occur in an overlapping manner which seems very natural from the biological point of view. Further, the maximum likelihood fit of the selected model is in a good agreement with the time–course data (Fig. 4(c)).
The regulatory mechanisms that we predict to occur in three waves (Fig. 4(b), (c) and Table 3) have also clear interpretations. In the first phase, T cell activation and cytokine driven mechanisms are induced and they prepare cells for lineage commitment (Phase 1 in Fig. 4(b) and (c)). In the second phase, RORC is induced and the differentiation signals are amplified, for instance, through MAF and IRF4 activation (Phase 2 in Fig. 4(b) and (c)). In the third phase, the lineage commitment is maintained through RORC activation by BATF and STAT3 activation by IRF4 (Phase 3 in Fig. 4(b) and (c)).
A significant feature in the sequentially occurring subnetworks is that STAT3 has a clear regulatory role during the first two phases. Given the central role of STATs in T helper cell lineage commitment in general (see e.g. Vahedi et al., 2012), we find this behavior natural. As a matter of fact, STAT3 is directly activated by the inducing cytokines that initiate the Th17 cell differentiation process (Korn et al., 2009) and, besides this important role as an early activator, STAT3 also plays an important role in mechanisms that amplify and stabilize the differentiation response (see e.g. Zhou et al., 2007).
To assess the uncertainty in the estimated parameter values of the inferred model, we carry out parameter identifiability analysis by using the profile likelihood method. The parameter profile likelihood for jth parameter can be defined by writing
| (25) |
which essentially is the maximized log-likelihood that is evaluated as a function of a fixed value p for the jth parameter (Kreutz et al., 2013). The profile likelihood can be used to determine confidence intervals for estimated parameter values given a fixed confidence level (for details, see Kreutz et al., 2013; Meeker and Escobar, 1995). A flat parameter profile likelihood results in an infinite confidence interval and, thus, indicates structural non-identifiability (Kreutz et al., 2013). On the other hand, a confidence interval that is constrained at one end and extends infinitely to another direction indicates practical non-identifiability (Kreutz et al., 2013). Figure 5 shows the parameter profile likelihoods for the parameters of the inferred Th17 LEM model. Most of the parameters are identifiable but the basal transcription and degradation of STAT3 as well as two STAT3 activating interactions (independent activation mechanisms by BATF and IRF4) turn out to be practically non-identifiable. However, this non-identifiability can presumably be avoided through a simple reparameterization, for instance, with respect to the degradation rate of STAT3 (for details about reparameterization, see e.g. Raue et al., 2013).
Fig. 5.
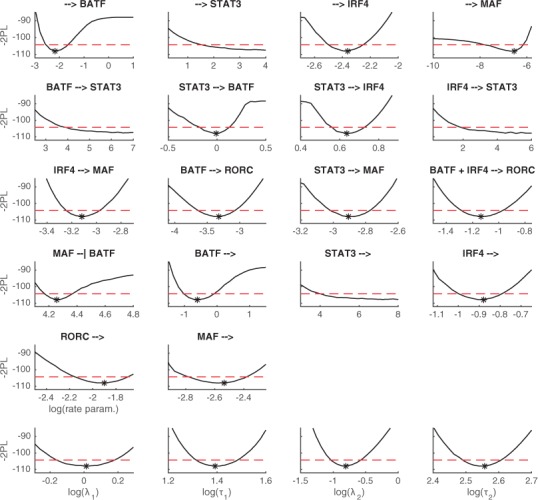
Parameter profile likelihood for the parameters of the inferred Th17 core network LEM model. The first five rows show the estimated profile likelihoods for the rate parameters and the bottom row shows the estimated profile likelihoods for the parameters of the latent process. The dashed red line shows the 95% confidence threshold and the asterisk shows the maximum likelihood estimate of the parameter when an unique value is available
All in all, running the LEM model inference for the Th17 RNA-seq data confirms that the developed methodology provides a very powerful formalism to analyze regulatory interactions in the presence of unknown latent processes that effectively correspond to dynamical rewiring of the regulatory network structure. The strengths of our approach are further emphasized when the above results are compared with the results that are obtained by running the forward-backward-stepwise selection algorithm for the static Th17 network (Fig. 6 and Table 4). The analysis with the static network supports only three experimentally validated interactions and, further, the model fitting against the time–course data is poor (Fig. 6).
Fig. 6.
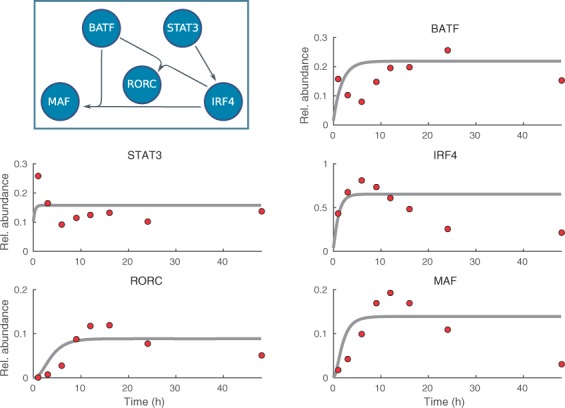
The predicted network structure and the dynamics of the mRNA levels obtained by running the forward-backward-stepwise selection algorithm for the static network without rewiring (i.e. the matrix Z is reduced to a vector which defines the static network structure). The inference algorithm is run by using the same premises as in the above LEM model analysis for the same Th17 RNA-seq data. The inset shows the predicted static interactions. The predicted dynamics (gray lines) are plotted against the time–course data (red circles)
Table 4.
Inferred parameters for the Th17 core network using static network structure
| j | Mechanism | Rate parameter |
|---|---|---|
| 1 | Basal activation of BATF | 0.122 |
| 2 | Basal activation of STAT3 | 0.473 |
| 3 | Basal activation of IRF4 | 0.011 |
| 4 | Basal activation of MAF | 0.001 |
| 7 | STAT3 activates IRF4 | 4.069 |
| 16 | BATF and IRF activate RORC | 0.310 |
| 17 | BATF and IRF activate MAF | 12.214 |
| 20 | Degradation of BATF | 0.557 |
| 21 | Degradation of STAT3 | 2.995 |
| 22 | Degradation of IRF4 | 1.000 |
| 23 | Degradation of RORC | 0.501 |
| 24 | Degradation of MAF | 12.560 |
In the statistical model, the parameters α and β have the values, 0.0001 and 0.035, respectively.
5 Discussion and conclusions
In this study, we introduce a general methodology that enables us to analyze and predict dynamically evolving regulatory networks using mechanistic modeling. In the past years, statistical and computational approaches have been developed to infer dynamically evolving regulatory networks (see e.g. Dondelinger et al., 2013; Wang et al., 2014) and, in the context of mechanistic models, methods to infer input signals simultaneously with system parameters have been developed (see e.g. Schelker et al., 2012). To our best knowledge, general mechanistic modeling approaches to infer dynamically evolving networks do not exist and, consequently, the methodology that we present in this study is novel.
A central strength of the LEM model inference is that it can easily be applied to any dataset that is accompanied with some knowledge about the mechanistic interactions between the molecular components. In this sense, the methodology, that we present in this study, provides us with an out-of-the-box method that can be used to obtain quantitative predictions about dynamically evolving regulatory mechanisms. Further, when applied as a first step analysis method, the LEM model inference also serves as an excellent starting point for further model refinement and, for instance, for the construction of detailed mathematical or biophysical models. The LEM model inference is beneficial especially if the molecular system of interest contains several components and the exhaustive construction of detailed alternative models for mechanisms driving the dynamically evolving network structure is out of reach.
The construction of the LEM model is transparent and the LEM extension can be applied to virtually any standard (stationary) ODE model. Even though the modeling approach is fully general, an obvious challenge in its practical application is the related model ranking problem over a large set of alternative models (i.e. over different network structures for each latent state). In general, for the case of standard stationary ODE models, the total number of network structures is . In the case of the LEM model, the total number of network structures increases to . An exhaustive search over all possible model configurations can be carried out only for simple toy systems but this limitation holds both the standard and the LEM models. In this study, we explore the model space using the forward-backward-stepwise selection. In practice, the forward-backward-stepwise selection results in a heuristic search algorithm which performs well in most cases but, on the other hand, there is no theoretical guarantee that the global optimum is always found. The possible sub-optimality of the search algorithm may be hard to detect, especially if large networks are considered, and this naturally limits the practical scalability of the LEM model inference and, as a matter of fact, constrains also the scalability of the search over standard ODE model structures. However, the practical scalability can be improved, for instance, by means of probabilistic search algorithms that explore the model space more efficiently. Thus, there is still room for further development of the search algorithms that can be used to calibrate the LEM model but these extensions are out of scope of this study and we leave them for future studies.
The analysis that we carry out for T helper 17 cell differentiation combines two major experimental studies that provide information about the regulatory interactions steering the Th17 lineage commitment. More precisely, we use the experimentally validated static core network provided by Ciofani et al. (2012) and combine it with the dynamic view on the regulatory interactions (Yosef et al., 2013) using our novel methodology. We are the first ones to study the dynamically evolving Th17 regulatory network by means of mechanistic modeling and our results are in line with the current understanding about the detailed biochemical mechanisms. While our methodology is here tested using the five-gene core Th17 network, the proposed model can also easily be extended and used to predict novel core genes or regulatory interactions for further experimental validation.
In summary, the latent effect mechanistic (LEM) model, which we introduce in this study, provides us with a flexible yet rigorous means to detect and analyze transient phenomena that affect the wiring of molecular networks. In addition to introducing this novel model class, we present a general statistical framework that can be used to infer the model structure as well as the model parameters.
Acknowledgements
The authors acknowledge the computational resources provided by the Aalto Science-IT project and thank Henrik Mannerstöm for helpful discussions.
Funding
This work has been supported by the Academy of Finland [Centre of Excellence in Molecular Systems Immunology and Physiology Research (2012–2017) as well as the projects 275537 and 292832], EU FP7 grant [EC-FP7-SYBILLA-201106] and EU ERASysBio ERA-NET.
Conflict of Interest: none declared.
References
- Ciofani M. et al. (2012) A validated regulatory network for Th17 cell specification. Cell, 151, 289–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dondelinger F. et al. (2013) Non-homogeneous dynamic Bayesian networks with Bayesian regularization for inferring gene regulatory networks with gradually time-varying structure. Mach. Learn., 90, 191–230. [Google Scholar]
- Friel N., Wyse J. (2012) Estimating the evidence: a review. Stat. Neerl., 66, 288–308. [Google Scholar]
- Grzegorczyk M., Husmeier D. (2011) Non-homogeneous dynamic Bayesian networks for continuous data. Mach. Learn., 83, 355–419. [Google Scholar]
- Hindmarsh A.C. et al. (2005) SUNDIALS: suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw., 31, 363–396. [Google Scholar]
- Intosalmi J. et al. (2015) Analyzing Th17 cell differentiation dynamics using a novel integrative modeling framework for time-course RNA sequencing data. BMC Syst. Biol., 9, 81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korn T. et al. (2009) IL-17 and Th17 Cells. Annu Rev Immunol, 27, 485–517. [DOI] [PubMed] [Google Scholar]
- Kreutz C. et al. (2013) Profile likelihood in systems biology. FEBS J., 280, 2564–2571. [DOI] [PubMed] [Google Scholar]
- Marbach D. et al. (2012) Wisdom of crowds for robust gene network inference. Nat. Methods, 9, 796–804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meeker W.Q., Escobar L.A. (1995) Teaching about approximate confidence regions based on maximum likelihood estimation. Am. Stat., 49, 48–53. [Google Scholar]
- Raue A. et al. (2013) Lessons learned from quantitative dynamical modeling in systems biology. PLoS ONE, 8, e74335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raue A. et al. (2015) Data2dynamics: a modeling environment tailored to parameter estimation in dynamical systems. Bioinformatics, 31, 3558–3560. [DOI] [PubMed] [Google Scholar]
- Ripley B.D. (1996) Pattern Recognition and Neural Networks, 1st ed. Cambridge University Press, Cambridge. [Google Scholar]
- Robert C.P. (2007) The Bayesian Choice: From Decision-Theoretic Foundations to Computational Implementation, 2nd ed. Springer, New York. [Google Scholar]
- Robinson J.W., Hartemink A.J. (2010) Learning non-stationary dynamic Bayesian networks. J. Mach. Learn. Res., 11, 3647–3680. [Google Scholar]
- Schelker M. et al. (2012) Comprehensive estimation of input signals and dynamics in biochemical reaction networks. Bioinformatics, 28, i529–i534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schulz E.G. et al. (2009) Sequential polarization and imprinting of type 1 T helper lymphocytes by interferon-gamma and interleukin-12. Immunity, 30, 673–683. [DOI] [PubMed] [Google Scholar]
- Schwarz G. (1978) Estimating the dimension of a model. Ann. Stat., 6, 461–464. [Google Scholar]
- Shmulevich I. et al. (2002) Probabilistic boolean networks: a rule-based uncertainty model for gene regulatory networks. Bioinformatics, 18, 261–274. [DOI] [PubMed] [Google Scholar]
- Vahedi G. et al. (2012) STATs shape the active enhancer landscape of T cell populations. Cell, 151, 981–993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X. et al. (2014) Reconstructing evolving signalling networks by hidden Markov nested effects models. Ann. Appl. Stat., 8, 448–480. [Google Scholar]
- Weaver C.T. et al. (2013) The Th17 pathway and inflammatory diseases of the intestines, lungs, and skin. Annu. Rev. Pathol. Mech., 8, 477–512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu T.R.R. et al. (2010) Inferring signaling pathway topologies from multiple perturbation measurements of specific biochemical species. Sci. Sig., 3, 134. [PubMed] [Google Scholar]
- Yosef N. et al. (2013) Dynamic regulatory network controlling TH17 cell differentiation. Nature, 496, 461–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou L. et al. (2007) IL-6 programs TH-17 cell differentiation by promoting sequential engagement of the IL-21 and IL-23 pathways. Nat. Immunol., 8, 967–974. [DOI] [PubMed] [Google Scholar]


