Influence maximization in time bounded network identifies transcription factors regulating perturbed pathways

Abstract

Motivation: To understand the dynamic nature of the biological process, it is crucial to identify perturbed pathways in an altered environment and also to infer regulators that trigger the response. Current time-series analysis methods, however, are not powerful enough to identify perturbed pathways and regulators simultaneously. Widely used methods include methods to determine gene sets such as differentially expressed genes or gene clusters and these genes sets need to be further interpreted in terms of biological pathways using other tools. Most pathway analysis methods are not designed for time series data and they do not consider gene-gene influence on the time dimension.

Results: In this article, we propose a novel time-series analysis method TimeTP for determining transcription factors (TFs) regulating pathway perturbation, which narrows the focus to perturbed sub-pathways and utilizes the gene regulatory network and protein–protein interaction network to locate TFs triggering the perturbation. TimeTP first identifies perturbed sub-pathways that propagate the expression changes along the time. Starting points of the perturbed sub-pathways are mapped into the network and the most influential TFs are determined by influence maximization technique. The analysis result is visually summarized in TF-Pathway map in time clock. TimeTP was applied to PIK3CA knock-in dataset and found significant sub-pathways and their regulators relevant to the PIP3 signaling pathway.

Availability and Implementation: TimeTP is implemented in Python and available at http://biohealth.snu.ac.kr/software/TimeTP/.

Supplementary information: Supplementary data are available at Bioinformatics online.

Contact: sunkim.bioinfo@snu.ac.kr

1 Introduction

Our goal in this article is to develop a computational method to perform analysis of time series transcriptome data in terms of biological pathways and also to determine regulators for differentially expressed gene (DEG) sets or perturbed pathways. Analyzing transcriptome data can be done in many different ways for different purposes. Thus there are numerous computational methods and we begin by surveying the literature in the categories such as (i) methods for determining perturbed pathways, (ii) methods for analyzing time series transcriptome data, (iii) methods for the pathway based analysis of time series data and (iv) methods for identifying regulators while analyzing time series data.

1.1 Methods for determining perturbed pathways

Pathway perturbation has been one of the primary research subjects in systems biology because the identification of perturbed pathways can reveal the dysregulated biological mechanism that originates from stimuli or in disease conditions (Khatri et al., 2012; Kristensen et al., 2014; Ramanan et al., 2012). The early methods of pathway analysis include the gene set enrichment analysis (GSEA) by Subramanian et al. (2005) and improved versions of GSEA (Medina et al., 2009; Nam et al., 2010) that use gene-level statistics calculated from the test of differential expression. Later, graph-based algorithms for pathway analysis were developed to utilize interaction information between genes or proteins in terms of curated pathway databases such as KEGG (Kanehisa and Goto, 2000). The graph-based pathway analysis has been developing with a seminal work called the signaling pathway impact analysis (SPIA) by Tarca et al. (2009) and the current trend is to focus on locating perturbed sub-pathways, rather than entire pathways. Tools to determine perturbed pathways include DEGraph (Jacob et al., 2010), DEAP (Haynes et al., 2013) and Clipper (Martini et al., 2013).

1.2 Methods for analyzing time series transcriptome data

Considering the time dimension, identifying perturbed (sub-)pathways in the time-series transcriptome data is much more challenging. Due to the computational challenges, many computational methods for the time series analysis do not utilize pathway information directly. The widely used time-series analysis methods employ a strategy of finding DEGs by fitting the gene expression data to a model with distributional assumption such as Gaussian or negative binomial distribution. By utilizing statistical methods such as ANOVA (Park et al., 2003), several tools and algorithms (Bar-Joseph et al., 2003; Conesa et al., 2006; Storey et al., 2005) have been developed for detecting DEG from time-series microarray data. With the emergence of next-generation sequencing data, DEG detection algorithms utilized Gaussian process (Äijö et al., 2014) or hidden Markov models (Leng et al., 2015) to identify DEGs from time series RNA-seq data. Instead of identifying DEGs, clustering approaches have been developed to determine a set of genes with a similar pattern of gene expression profile. Clustering expression data in the gene-time dimension is performed by considering correlation (Wen et al., 1998) or by model-based clustering methods (Ramoni et al., 2002; Schliep et al., 2003). Recent methods such as (Zhao and Zaki, 2005) are further developed to handle data with higher dimensions such as gene-sample-time. The main limitation of DEG or clustering approaches is that a list of DEGs or genes in clusters requires further analysis in terms of curated knowledge such as KEGG pathways and the selection of significant pathways is usually determined by simple statistical methods such as Fisher's exact test. In this way, analysis process does not consider curated knowledge such as relationships among genes, e.g. those in KEGG pathways, to determine how genes interact over time. More advanced methods consider relationship between genes or between time points (e.g. dynamic Bayesian network) to infer the gene regulatory network (GRN) (Honkela et al., 2010) or protein–protein interaction network (PIN) (Kim et al., 2014b). These methods, although powerful, are limited to the analysis of small size gene sets (Kim et al., 2014a).

1.3 Methods for the pathway based analysis of time series data

To incorporate pathway information for the time series data analysis, pathways are modeled as graphs. Two recent graph-based pathway analysis algorithms for time-series data are TRAP (Jo et al., 2014) and TimeClip (Martini et al., 2014). TRAP (Jo et al., 2014) leverages the technique similar to SPIA (Tarca et al., 2009) to detect pathways with a significant expression propagation along the pathway graph in the time order. TimeClip (Martini et al., 2014) employs a junction tree algorithm to form sub-pathways using the same method used in Clipper (Martini et al., 2013) to determine significant sub-pathways in terms of the first principal component from the gene expression data. Although these algorithms produce a list of biological processes with significant changes over time, few attempts have been made to locate the regulator that initiates the pathway perturbation.

1.4 Methods for identifying regulators while analyzing time series data

DREM (Ernst et al., 2007) is an example of incorporating regulators in clustering analysis. It estimates transcription factors (TFs) regulating a cluster by Input–Output Hidden Markov Model, but it is hard to discover biological implication from the result due to the clusters with multiple or overlapping biological functions. Master regulator analysis (MRA) (Carro et al., 2010) introduces a method to rank TFs in the GRN, but not considering dynamic expression profiles of genes.

1.5 Motivation

Analysis of time-series omics data is very difficult and there are only a few tools available (Spies and Ciaudo, 2015). In addition, it is desirable to identify regulators such as TF that are likely to induce changes in transcriptome over time. However, on top of the complexity of analyzing time series data, considering regulators such as TF makes the complexity of the time series data analysis task dramatically high. In this study, we propose a novel bioinformatics method for analyzing time series omics data to identify both perturbed pathways and regulating TFs. Two main ideas are:

1. We start the analysis by identifying perturbed pathways in comparison of control vs. treatment group and then focusing on TFs that are relevant to the perturbed pathways. In this way, much smaller number of TFs and pathways are considered, thus the complexity of the analysis task is significantly reduced.

2. To systematically analyze the effect of TFs over time, we adopt and further develop the influence maximization technique in the bounded time.

With these two main ideas, we designed and implemented a time-series analysis method of finding TFs regulating perturbed sub-pathways (TimeTP). The key properties of TimeTP are as follows. (i) TimeTP identifies perturbed sub-pathways that propagate their expression levels along time and also identifies TFs triggering that pathway perturbation by our four-step approach. (ii) TimeTP adopts two well-established computational methods, cross-correlation (Ianniello, 1982) and influence maximization (Kempe et al., 2003), from the fields of signal processing and social network. (iii) The novel framework of TimeTP produces the TF-Pathway map in time clock to trace the pathway perturbation triggered from TF to pathway. As well as the effective visualization of TF-Pathway map, TimeTP provides user-friendly interface by handling a diverse range of input data in terms of type of dataset (RNA-seq or microarray) and type of condition (single time-series or control-treatment).

The rest of the article is organized as follows. The process of perturbed sub-pathway mining in TimeTP will be described in Sections 2.1–2.3. Sections 2.4 and 2.5 explain the time bounded network construction and the influence maximization algorithm for finding TFs. TimeTP is tested by using the biological dataset and the result is compared with other pathway/sub-pathway mining tools and regulator analysis algorithms in Section 3.

2 Methods

The overview of the proposed method is depicted in Figure 1. To model pathways over time, we created an augmented pathway graph where a node is a gene augmented with a differential expression vector as an attribute of a node. By measuring cross-correlation, we determine a set of perturbed sub-pathways containing only genes that are connected to propagate expression changes over time. The next major task is to determine TFs regulating the perturbed pathways. In general, TFs are not included in pathways, thus we used GRN to establish orthogonal relationship between regulators and pathways. Identification of regulating TFs requires to estimate the system-wide effect of a TF. To estimate the system-wide influence of a TF, we first augment GRN with PIN. As a result, we have a network of GRN and PIN combined and the network is big enough to have connections from TF to genes in the pathways. To evaluate of the influence of TF on the perturbed pathways, we used a labeled influence maximization algorithm.

Fig. 1.

Overview of TimeTP analysis workflow. TimeTP uses an integrated network of GRN and PIN. Each biological pathway is analyzed by TimeTP and the perturbed sub-pathways are identified with the time-delay-bounded propagation of gene expression. The starting point or a gene of each perturbed sub-pathway is mapped to the integrated network and then regulators of the perturbed sub-pathways are identified by the labeled influence maximization algorithm

2.1 Differential expression vector

Each pathway in the curated pathway database such as KEGG can be represented as a directed graph $G=(N,E)$. Genes and their interactions correspond to nodes and edges in the pathway graph, respectively. TimeTP assigns a time vector $\vec{v}$ for each node, representing the differentially expressed time points as 1(overexpressed) or −1(underexpressed) and otherwise as 0. For example, if data has T number of measured time points and has control and treatment conditions to compare, either −1, 1 or 0, will be assigned for each time point in a differential expression vector $\vec{v}$ of length T. If the data are generated in a single condition, the differential expression can be tested between two time points (e.g. relative to the first time point or adjacent) resulting in a vector of length T − 1. Whether two groups of samples are differentially expressed is determined by Limma (Smyth, 2005) for microarray or by DESeq2 (Love et al., 2014) for RNA-seq data.

2.2 Perturbed sub-pathway with delay-bounded expression propagation

For each pathway, TimeTP searches for the perturbed sub-pathway by choosing valid edges from the edges in the original pathway information. The validity of edges is determined by looking at the relationship between differential expression vectors of two nodes. We propose two criteria for edges in the perturbed sub-pathway. First, every edge of the perturbed sub-pathway is required to propagate the differential expression pattern along the given direction. Assume that an edge $N_1\to N_2$ from a node N₁ to a node N₂ has differential expression vectors $\overrightarrow{v_1}$ and $\overrightarrow{v_2}$, respectively. The direction of propagation and the number of delayed time points for a pair of expression vectors can be approximated by cross-correlation, which is a measure of similarity of two time-series in signal processing. Cross-correlation of two vectors $\overrightarrow{v_1}$ and $\overrightarrow{v_2}$ is defined as

$$(\overrightarrow{v_1}\mathrm{\star }\overrightarrow{v_2})(n)={\displaystyle {\sum }_{t=-\infty }^{\infty }\overrightarrow{v_1}}(t)\overrightarrow{v_2}(t+n)$$ (1)

where $\vec{v}(t)=0$ for $t\le 0$ or t > T (This happens at the preceding or trailing entries of two vectors). When the two vectors overlap most with n delay, cross-correlation is maximized with a parameter n. Therefore, TimeTP finds the shortest possible delay between two differential expression vectors $d(\overrightarrow{v_1},\overrightarrow{v_2})$ where cross-correlation between two vectors is maximized.

$$d(\overrightarrow{v_1},\overrightarrow{v_2})=\underset{n}{\arg \max }(\overrightarrow{v_1}\mathrm{\star }\overrightarrow{v_2})(n)$$ (2)

When $d(\overrightarrow{v_1},\overrightarrow{v_2})$ of a directed edge (N₁, N₂) is negative, it implies that the direction of the expression propagation is opposite to the given direction. In this case, the edge is considered as invalid and excluded from the perturbed sub-pathway. Next, a threshold for delay is used to filter out edges with a long positive delay, i.e. bigger than a user defined threshold value, so that the expression propagation in the sub-pathway is bounded within a time period that the user allows. Figure 2 shows the examples of delay analysis, where the edge in Figure 2a has a one time point of delay with maximum cross-correlation 2. Figure 2b is an example of an invalid edge due to the negative delay. Perturbed sub-pathway with one edge is disregarded. Since TimeTP determines the best delay between two genes, different delays can be assigned to different gene pairs, which can reflect the different speed of signaling steps in the biological pathways.

Fig. 2.

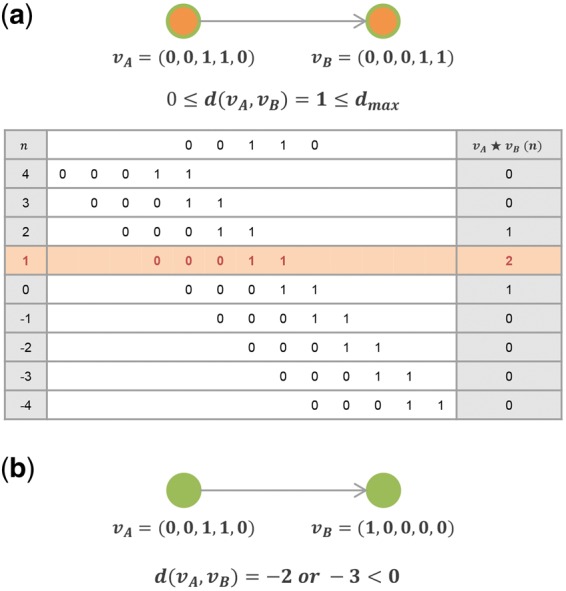
Cross-correlation examples. (a) Cross-correlation of two vectors $\overrightarrow{v_{\text{A}}}$ and $\overrightarrow{v_{\text{B}}}$ is maximized with the delay 1. The directed edge is valid and remains in the graph, because the estimated delay is non-negative. (b) Cross-correlation of two vectors $\overrightarrow{v_{\text{A}}}$ and $\overrightarrow{v_{\text{B}}}$ is maximized with the delay −2 or −3 which indicates the optimal direction of the edge is opposite. The edge is invalid and removed from the graph

Once perturbed sub-pathways with bounded propagation is determined from each pathway, source nodes with no incoming edge in the sub-pathways are labeled as targets in the time bounded network. Node weights of labeled source nodes are set as the number of nodes in the sub-pathway and for the other nodes not labeled, zero or negative numbers are assigned so that no profit can be earned from non-labeled nodes. This profit assignment scheme is used to define and rank regulators.

Algorithm 1. Greedy Labeled IM (G, k)

1: Initialize $S=\varphi ,SeedInfSet=\varphi ,T=t|t\in TFSet$ and Round = 1000

2: for $n\leftarrow 1,k$ do

3:   Set $Inf[t]$ = 0, for all $t\in T$.

4:   for $i\leftarrow 1,Round$ do

5:     Derive $G\prime$ by removing each edge from G according to the edge probability $1-p$.

6:     for each node $t\in T\mathrm{\setminus }SeedInfSet$ do

7:      $Inf[t]\leftarrow$

      $Inf[t]+{\displaystyle \sum _{v\in InfSet(t,G\prime )}Profit(v)}/len(InfSet(t,G\prime ))$

8:     end for

9:   end for

10:  $newSeed\leftarrow t\in T$ with maximum $Inf[t]/Round$

11:  $S\leftarrow S\cup \left\{newSeed\right\}$

12:  $SeedInfSet\leftarrow SeedInfSet\cup InfSet(newSeed)$

13:  $T\leftarrow T\mathrm{\setminus }\left\{newSeed\right\}$

14:  end for

2.3 P-value for perturbed sub-pathway

P-value of the perturbed sub-pathway is estimated by the permutation test. The null hypothesis is that perturbed sub-pathways determined by TimeTP are randomly generated, without considering the order of genes and their expression patterns in the pathway. To test the hypothesis, differential expression vector for each gene is randomly re-assigned from the vector set of the whole genes and sub-pathways are sampled according to the same procedure described in Section 2.2. Given that the ratio of DEGs is not aberrantly high, sampled sub-pathways determined from the randomly assigned expression vectors are most likely to have a short path length. Cross-correlation of each edge is likely to be small as well due to the short overlap of two expression vectors. Therefore, a sum of the cross-correlation of every node pair in the sampled sub-pathway is chosen to be a pathway-level statistic and the p-value for a perturbed sub-pathway is derived as the probability of having higher statistics in the sample distribution.

2.4 Time bounded network construction

To search for upstream regulators of perturbed sub-pathways, an integrated network of GRN and PIN is constructed. Interaction information between TF and target genes (TGs) in GRN is derived from HTRIdb (Bovolenta et al., 2012) that provides experimentally verified or computationally predicted TF-DNA-binding sites from six public databases and literature (Ernst et al., 2010). Protein–protein interaction for PIN is from STRING (Szklarczyk et al., 2014) database. Integrated network of GRN and PIN is used to determine TFs that have the most overall effect on perturbed sub-pathways and to connect the TFs and perturbed sub-pathways. Two expression vectors that do not preserve the time order are filtered out so that expression propagation along the connecting path is always valid in terms of time clock, as described in Section 2.2. This process produces a time bounded network. As for undirected edges of PIN, delay of Equation 2 is calculated for both directions and directed edge with nonnegative delay remains.

2.5 Labeled influence maximization for TF detection

The main goal of influence maximization is to locate a set of seed nodes in the network that could maximize the spread of influence (Kempe et al., 2003) and the technique has been successfully used to select marketing targets in the social network. A modified version called the labeled influence maximization developed by Li et al. (2011) exploits profit values of nodes to prefer seed nodes that have an influence on a specific node set. TimeTP utilizes a greedy version of the labeled influence maximization algorithm to the time bounded network with a few modifications (see below) so that influence of a gene on the perturbed sub-pathways are properly modeled.

Labeled influence maximization algorithm (Algorithm 1) used in TimeTP is intended to determine the most influential k regulators in the time bounded network G, especially TFs targeting the starting nodes of the perturbed sub-pathways. It first initializes a set of seed nodes S and a set of nodes that can be influenced by seed nodes SeedInfSet as an empty set. For every TF t not selected as a seed node and not influenced by the current seed nodes, its influence $Inf[t]$ is quantified by the average profit values of nodes that the TF can reach. The same procedure is repeated for Round times creating a subgraph $G\prime$ from G according to the edge weight between 0 and 1 regarded as a probability of an edge (line 4–9). Probability of edges is derived from the confidence score of STRING and 1 for GRN edges. After the iteration, a TF with the maximum influence is included in the seed set and SeedInfSet is updated as well.

3 Results

TimeTP is tested with a genome-wide RNA-seq dataset of non-transformed human breast epithelial cells MCF10a starved overnight and stimulated with 10 ng/ml EGF for 15, 40, 90, 180 and 300 min (Kiselev et al., 2015), in WT and PIK3CA knock-in samples. To test the power of influence maximization, we need to choose datasets with many time points and also with sequencing data to accurately model influence of TFs. Note that many datasets with only two time points are not meaningful for this analysis. In addition, to test the performance of the proposed approach, data should have replicates to determine differential expression accurately and the interval between time points should be short to model signaling effects. The MCF10a data were the only one to meet the criteria.

PIK3CA knock-in samples (referred to as ‘PIK3CA H1047R’) contains a mutated gene that encodes the p110α catalytic subunit (PIK3CA). PIK3CA is a component gene of Class IA phosphoinositide-3-kinases (PI3Ks) and the mutated form of PIK3CA is expected to exhibit chronic activation of phosphatidylinositol (3,4,5)-trisphosphate (PIP3) signaling. PI3K/PIP3 signaling pathway plays a key role in cell growth and migration. In addition, several driver mutations in PI3K/PIP3 pathway have been found in multiple types of cancer. Especially, oncogenic mutations of PIK3CA gene are discovered in up to 45% of human breast cancer samples (Network et al., 2012). Thus, this experiment is designed to trigger long-term activation of PIP3 signaling by the modification of PIK3CA and track its downstream effect. Analysis result of TimeTP is composed of the TF-Pathway map in time clock and the whole list of perturbed pathways as shown in Figure 3 and Table 1. Javascript library of Cytoscape is used for TF-Pathway map visualization (Shannon et al., 2003).

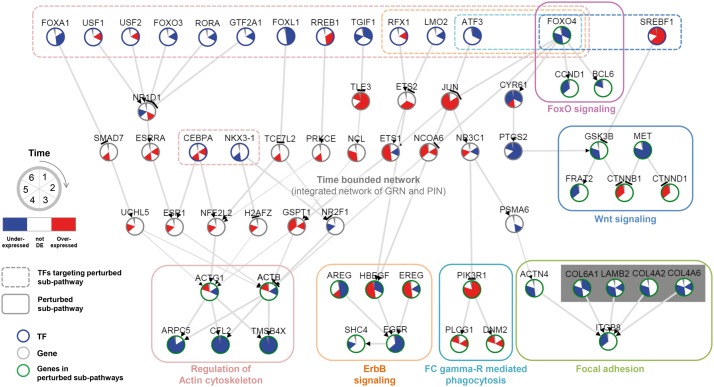
Fig. 3.

TF-Pathway map in time clock. Expression propagation paths (gray-bordered nodes) from TFs (blue-bordered nodes in box with dashed border) to perturbed sub-pathway genes (green-bordered nodes in box with solid border) in the integrated network of GRN and PIN are specified. For each node, time-series differential expressions of six time points are colored as red (overexpressed), blue (underexpressed) and white (otherwise) in a clockwise direction. Although ATF3 and FOXO4 are marked with one color, two TFs regulates both FC gamma-R mediated phagocytosis and Focal adhesion pathway

Table 1.

Significantly perturbed pathways in PIK3CA H1047R samples found by TimeTP and comparison with other representative pathway tools (+: found, −: not found)

Pathway	Pathway name	DEG P-value	Path	Path P-value	Combined P-value	Sub-pathway		Pathway		References
						non-TS	TS	non-TS	TS
						DEAP	TimeClip	SPIA	TRAP
hsa04012	ErbB signaling pathway	0.000	Path1	0.000	0.000	−	−	−	−	Hynes and Lane (2005)
hsa04810	Regulation of actin cytoskelet…	0.000	Path1	0.001	0.000	−	−	−	−	Jiménez et al. (2000)
			Path2	0.005	0.000
hsa04520	Adherens junction	0.000	Path1	0.020	0.000	−	−	−	−	Berglund et al. (2013)
hsa04310	Wnt signaling pathway	0.001	Path1	0.021	0.000	−	+	−	−	Essers et al. (2005), Perry et al. (2011), Vadlakonda et al. (2013)
hsa04510	Focal adhesion	0.000	Path1	0.024	0.000	−	+	+	+
hsa04068	FoxO signaling pathway	0.004	Path1	0.027	0.000	−	−	−	−	Zhang et al. (2011)
hsa04666	Fc gamma R-mediated phagocytos…	0.003	Path1	0.019	0.001	−	−	−	−	Zhang et al. (2010)
hsa04151	PI3K-Akt signaling pathway	0.032	Path1	0.005	0.001	−	+	−	+	Kiselev et al. (2015)
hsa04114	Oocyte meiosis	0.032	Path1	0.020	0.005	−	−	−	−	Coticchia et al. (2009)
hsa04921	Oxytocin signaling pathway	0.032	Path1	0.023	0.006	−	−	−	+	Coticchia et al. (2009)
TS: time-series.

Pathways with DEG P-value and sub-path P-value below 0.05 are shown.

3.1 TF-Pathway map in time clock

Figure 3 is the map of influence path from the TFs selected by the influence maximization algorithm to perturbed sub-pathways. Pathways perturbed but not affected by TFs are excluded in the TF-Pathway map. For example, TimeTP detected perturbation of the PI3K-Akt signaling pathway (Table 1) but it was not included the TF-Pathway map in time clock (Fig. 3) because PI3K-Akt signaling pathway is directly activated by the modification of PIK3CA in the experiment.

As in Figure 3, FOXO4 is on the top of the TF-Pathway map and propagates its effect to all of the downstream pathways and FoxO signaling pathway itself. The forkhead box O (FoxO) TFs are known as targets of the serine/threonine protein kinases (PKB)/Akt (Zhang et al., 2011) that is directly affected by PIP3 generation (Kiselev et al., 2015). Specifically, Akt inhibits FoxOs and causes consequent inactivation of FoxO signaling pathway, which can be clearly shown in the TF-Pathway map of PIK3CA H1047R samples. Wnt signaling pathway is one of the activated pathways in PIK3CA H1047R samples. TimeTP estimated that differential expression of the TF FOXO4 and SREBF1 in the early time points (1–3) is propagated through the path and activated Wnt signaling. Although the first gene GSK3B of the perturbed sub-pathway is down-regulated, consequently it made CTNNB1 that encodes β-catenin activated to further transduce the signal to other cytoplasmic regions or into the nucleus. Interaction of FoxOs with β-catenin has an inhibitory effect on β-catenin activity (Essers et al., 2005), while TimeTP inferred a devious route that has the same consequence. As for the cooperation between PI3K-Akt signaling and Wnt signaling, several studies provide the logical underpinnings (Perry et al., 2011; Vadlakonda et al., 2013).

The activation process of ErbB signaling pathway and Regulation of actin cytoskeleton is more complicated. Albeit both perturbed sub-pathways themselves are seemingly down-regulated first, the path from TF to the first genes of the sub-pathway (ACTB, ACTG1, HBEGF) is activated and finally three genes are activated in the last time point, forecasting the late activation of two pathways beyond the observed time points. As in the previous studies (Hynes and Lane, 2005), ErbB signaling pathway encompasses the PI3K-Akt signaling pathway. The perturbed sub-pathway that TimeTP detected in the ErbB signaling pathway includes the cell surface receptor EGFR, which is the upstream part of PI3K-Akt pathway. Taken together, the effect of Akt signaling activation attributes the delayed activation of the ErbB signaling, which can be the positive feedback loop of the Akt signaling pathway. Detection of a transcriptional feedback loop of PIP3 signaling is the major contribution of the original article of the dataset (Kiselev et al., 2015) and the analysis result of TimeTP can be a parallel contribution of the study. Moreover, TF-Pathway path to the Regulation of actin cytoskeleton pathway found in TimeTP result suggests for further research in addition to the previously suggested path (Jiménez et al., 2000).

Fc gamma-R mediated phagocytosis is one of the activated pathways in PIK3CA knock-in samples. Mammary epithelial cells can act as phagocytes (Monks et al., 2005). During phagocytosis, ligated Fc gamma-R on plasma membranes induces recruitment of PI3K and increased synthesis of PIP3 (Zhang et al., 2010). TimeTP found the perturbation of phagocytosis pathway starting from PI3K receptor and its downstream genes. One of the TFs expected to trigger the perturbation is ATF3 (Fig. 3) down-regulated in the early time points, which is a key regulator that inhibits the immune response of macrophage (Gilchrist et al., 2006). Our analysis correctly suggested that ATF3 would function similarly in MCF10a cells. TimeTP detected the same sub-pathway in Oocyte meiosis and Oxytoxin signaling. In both pathways, Calcium/calmodulin (CALM) signaling pathway is included and its sub-pathway was found as perturbed. Previous studies of mammary carcinoma cells report that calmodulin mediates Akt activity (Coticchia et al., 2009; Deb et al., 2004), suggesting that the increased PIP3 not only recruited Akt by itself but also induced calmodulin-dependent activation of Akt signaling pathway.

3.2 Comparison with existing pathway/regulator analysis tools

Most of the pathway analysis tools assume that the expression value for each gene follows the Gaussian distribution, which is not appropriate next generation sequencing data. Therefore, we selected four representative tools without the Gaussian assumption in each class of pathway analysis tools: DEAP(sub-pathway analysis), timeClip(sub-pathway analysis, time-series), SPIA(pathway analysis), TRAP(pathway analysis, time-series). Samples of different time points are treated as replicates in DEAP and SPIA that do not perform time-series analysis, and WT samples are not used for TimeClip that does not support control vs. treatment group analysis. Table 1 shows a list of sub-pathways with significant expression propagation from TimeTP analysis. DEAP and SPIA failed to choose most of the pathways including PI3K-Akt signaling pathway that is expected to be activated in PIK3CA H1047R samples, presumably due to the disregard of time factor. timeClip and TRAP selected out more significant (sub-)pathways, yet disregarded FoxO signaling pathway and ErbB signaling pathway presumably pertaining to PIP3 signaling as described in Section 3.1. Pathways that were not detected by TimeTP but by other (sub-)pathway analysis tools are summarized in Supplementary Table 1. Relevance to PI3K was evaluated using a state of the art context-aware literature search tool, BEST (http://best.korea.ac.kr/). Running times of the methods are compared in Supplementary Table 3. Even though TimeTP performs an additional step, that is, influence maximization, compared with competing pathway analysis tools, overall running time of TimeTP is similar to those of other pathway analysis tools. As for the sub-pathway detection process of TimeTP, running time of TimeTP (408.862 s) is smaller than the average running time of other four tools (849.077 s) and the overall process including the regulator search by influence maximization takes similar time (906.767 s) in average.

Two regulator analysis methods are compared with TimeTP. MRA is a method for selecting and ranking TFs in GRN and DREM is a tool for time-series clustering. WT samples are not used for DREM that does not support control versus treatment analysis. Table 2 is the list of master TFs selected from TimeTP, MRA and DREM. TFs from TimeTP are regulators of the perturbed sub-pathways chosen and ranked by the labeled influence maximization algorithm. Among 16 TFs from the TimeTP result, USF1, TGIF1 and RREB1 are TFs expected to bind to strongly genes regulated in the PI3K signaling-activated samples based on the motif activity analysis in the original paper of the dataset, corroborating the credibility of TimeTP. MRA performs Fisher's exact test to first confirm the ratio of signature genes among its TGs and ranks TFs that passed the test by the number of signature genes. To apply the same standard with TimeTP, TF-gene interaction information is extracted from the same GRN and 18 genes that start the perturbation in each sub-pathway are used as signature genes for MRA. However, only one TF, SREBF1 that directly targets Wnt signaling pathway satisfied the criteria of MRA. Distinct from the one-to-one mapping of a MRA, the influence maximization algorithm rescued 15 TFs with indirect influence on targeted pathways in the network structure in addition to SREBF1. Furthermore, TFs that target multiple pathways are prioritized higher than TFs with a single target. LMO2, ATF3, FOXO4 and RFX1 in the Figure 3 are such examples. TFs that do not target multiple pathways but are highly ranked have the small number of downstream genes, thus the ratio of genes in the perturbed pathway is relatively high among its downstream genes. DREM performed time-series clustering and found three TFs different from TimeTP or MRA, regulating one of the clusters (Supplementary Figure S1). The three TFs target the same cluster with 71 genes, but the cluster is not enriched with any KEGG pathway by Fisher's exact test (Supplementary Table S2).

Table 2.

TFs found by TimeTP and other tools. TFs in boldface are the intersection with TFs selected as significant in the original article

TimeTP		MRA		DREM
Rank	TF	Rank	TF	TF
1	NKX3-1	1	SREBF1	FOXF2, NF1, SRF
2	LMO2
3	ATF3
4	FOXA1
5	CEBPA
6	FOXO4
7	FOXL1
8	RFX1
9	TGIF1
10	SREBF1
11	FOXO3
12	USF2
13	USF1
14	GTF2A1
15	RORA
16	RREB1

TFs from DREM do not have ranks.

4 Conclusion

We presented TimeTP, a four-step approach to locate perturbed sub-pathways and their regulators from time-series transcriptome data. TimeTP has two novel contributions: estimation of delay between two expression vectors that leads to the construction of a time bounded sub-graph, and introduction of the influence maximization technique into the analysis of times series data in search of TFs that are involved in perturbed pathways. TimeTP is the first sub-pathway mining tool for time-series data that analyzes and visualizes the explicit expression pattern, providing a holistic picture of the pathway perturbation dynamics. In particular, TF-Pathway map in time clock enables user to navigate the perturbation propagation route along time.

Analysis of the PIK3CA knock-in dataset shows that TimeTP can capture the perturbation in PI3K-Akt signaling, confirming the main objective of the biological experiment and re-producing consequent changes in the downstream pathways. Especially, FOXO4 is expected to be the master regulator of the perturbation of five pathways in TF-Pathway map, which is in an agreement with the fact that FoxO TFs are the known targets of Akt. As well as the perturbation in FoxO and Wnt signaling pathway directly affected by FoxOs, TimeTP suggests the late activation of ErbB pathway that highlights the same assumption of previous study, a positive feedback loop of the Akt signaling. In addition, TFs predicted and ranked by TimeTP include three important TFs from the original article of the dataset while MRA or DREM failed to discover any TF in the list.

TimeTP supports various types of dataset with flexible parameters that can be adjusted for the search of regulators. We believe that TimeTP will be a very valuable tool to identify both perturbed pathways and their regulators, especially in analysis of time series sequencing data.

Funding

This research was supported by Next-Generation Information Computing Development Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT and Future Planning (NRF-2012M3C4A7033341), Collaborative Genome Program for Fostering New Post-Genome industry through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT and Future Planning (NRF-2014M3C9A3063541) and a grant of the Korea Health Technology R&D Project through the Korea Health Industry Development Institute (KHIDI), funded by the Ministry of Health & Welfare, Republic of Korea [grant number: HI15C3224].

Conflict of Interest: none declared.