Finite element modeling of finite deformable, biphasic biological tissues with transversely isotropic statistically distributed fibers: toward a practical solution

Abstract

The distribution of collagen fibers across articular cartilage layers is statistical in nature. Based on the concepts proposed in previous models, we developed a methodology to include the statistically distributed fibers across the cartilage thickness in the commercial FE software COMSOL which avoids extensive routine programming. The model includes many properties that are observed in real cartilage: finite hyperelastic deformation, depth-dependent collagen fiber concentration, depth- and deformation-dependent permeability, and statistically distributed collagen fiber orientation distribution across the cartilage thickness. Numerical tests were performed using confined and unconfined compressions. The model predictions on the depth-dependent strain distributions across the cartilage layer are consistent with the experimental data in the literature.

1. Introduction

The mechanical behavior of articular cartilage is complex and is characterized by being time dependent, anisotropic, structurally heterogeneous, asymmetric in tension–compression, and nonlinear in the stress–strain response [1,2]. Many of these aspects are attributed to the distributed collagen fibers, which form a three-dimensional network that is adapted to the mechanical loading of the joint [3,4]. Based on the cellular density, cellular morphology, and collagen fiber arrangement, articular cartilage can be divided into three distinct morphological zones. In the superficial zone (10–20 % of the total thickness), collagen fibers are oriented parallel to the articular surface; in the middle zone (40–60 % of the total thickness), there is no preferred orientation for the collagen fibers; and in the deep zone (30 % of the total thickness), the collagen fibers are approximately perpendicular to the articular surface. The volumetric concentration of collagen fibers varies from 16–31 % in the superficial zone to 14–42 % in the deep zone [5,6]. Collagen fibers are substantially stiffer than the surrounding cartilage matrix, and they have a Young's modulus of 2–40 MPa [7]. The complexity of the mechanical behavior of cartilage is largely due to the effects of the distributed collagen fibers, thus many studies have focused on the development of microscale-based cartilage models including collagen fibers.

One representative group of these microscale cartilage models is fibril-reinforced models. In these models, the solid phase is considered to be an isotropic matrix reinforced by fibrils. The total stress in the solid is the sum of the matrix and fibril stresses. There are two kinds of fibril-reinforced models: discrete spring-based models [8,9] and continuum models [10,11]. In the spring-based models, fibrils are considered as nonlinearly elastic and they can carry tensile load only. The limitation of spring-based models is that the direction of the fibril alignment has to be consistent with that of the elements, thus restricting their use for general practical problems. In continuum fibril-reinforced models, the fibril orientation is independent of the mesh, thus these models can be applied to represent geometrically realistic collagen networks. In both spring-based and continuum fibril-reinforced models, the fibrils can be nonlinear and viscoelastic.

Another representative group of microscale cartilage models is based on homogenization methods. In these models, the heterogeneous material properties of the articular cartilage are considered to be the statistically averaged effects of the local tissue variations. Homogenization theories have been developed originally for composite materials [12–14] and were proposed for cartilage [15,16] and later generalized [17–20]. Taylor et al. [21] developed a linear viscoelastic homogenization approach to describe the time-dependent mechanical behaviors, and they applied their model to a practical problem [22]. Constitutive models of soft tissues including distributed fibers for finite deformation have been formulated for several tissues [14,17,23–26]. Federico et al. formulated cartilage models [17–20] that include collagen fibers in arbitrary directions and statistically distributed across the cartilage layer. Recently, Seifzadeh et al. [27] proposed a nonlinear biphasic viscoelastic FE model that considers two families of distributed collagen fibers.

The distribution of collagen fibers across the cartilage layer is statistical in nature. Therefore, distributed fiber models [18,19] would appear to be a reasonable approach for solving practical problems. After the proof-of-concept numerical implementation of these statistically distributed fiber models by Federico and Gasser [19], simulations of articular cartilage behavior including realistic depth-dependent fiber distribution [28] have been performed in the commercially available package ABAQUS [29] and in the open-source package FEBio [30]. In the latter case, the effect of the presence of the statistically oriented fibers on the tissue's permeability [20,31,32] has been included as well. Another model including the effect of fiber distribution on both elasticity and permeability, with variation of the collagen orientation across cartilage depth, has been developed by Pierce et al. [33] and implemented in FEAP. However, all of these implementations require extensive programming of user subroutines and thus require engineers to have programming skills. In addition, a consistent approach to discretize the continually distributed fibers for practical problems has not been established.

The goal of this study was to develop a methodology for engineers to solve practical problems without the need for extensive routine programming, and with the sole use of the native features of a commercially available FE package. Specifically, we developed a methodology to include the statistically distributed fibers across the cartilage thickness in the commercially available FE software COMSOL based on the concepts proposed by Federico and Herzog [18] and Federico and Gasser [19]. Furthermore, we included the interstitial fluid and considered the effects of the deformation- and depth-dependent hydraulic permeability in the modeling, without, however, including the effect of the fibers on the permeability. In addition, we developed a practical and consistent approach to model the randomly distributed fibers for realistic cartilage samples using a discrete sets of statically distributed fibers. We applied the proposed methodology to analyze cartilage samples with distributed fiber orientations, as observed in clinical studies, and performed numerical tests using confined and unconfined compression tests.

2. Methods

2.1. Biphasic model for finite deformation

In a solid–fluid biphasic system, the solid phase (subscript s) and the fluid phase (subscript f) are assumed to coexist at every point. The motion of the solid phase is described by the configuration map χ, mapping points X = (X₁, X₂, X₃) in the reference configuration ${\mathcal{B}}_R$ into points x = (x₁, x₂, x₃) in the physical space $\mathcal{S}$. The deformation gradient F is defined as the tensor with components F_iJ = χ_i,J ≡ ∂χ_i/∂X_J. The determinant J = det F is the volume ratio, and C = F^T.F is the right Cauchy-Green deformation tensor.

In the current configuration, the volumetric fractions of solid and fluid are denoted ϕ_s and ϕ_f, respectively, and are constrained to the saturation condition

$${\varphi }_s+{\varphi }_f=1,$$ (1)

everywhere in the tissue. The solid volumetric fraction in the reference configuration (which is constant, in the absence of sources/sinks and fluxes of mass) is obtained by means of the Piola transformation

$${\varphi }_{sR}=J{\varphi }_s,$$ (2)

from which, considering the referential saturation condition ϕ_sR+ϕ_fR = 1, the referential fluid volumetric fraction ϕ_fR is obtained as

$${\varphi }_{fR}=1-J{\varphi }_s.$$ (3)

Equations (2) and (3) state that the current fractions ϕ_s and ϕ_f depend on the volume ratio J. It is important to recall that, although the solid and the fluid phases are both intrinsically incompressible, the biphasic mixture is overall compressible. This is true both locally, as fluid can escape from or enter into a certain point X, and globally, as fluid and escape or enter through the boundaries of the system [20].

The equation of conservation of mass for a biphasic mixture, comprised of an incompressible fluid and an incompressible solid, reads [34]

$$\mathrm{div}({\varphi }_f{\mathit{v}}_f+{\varphi }_s{\mathit{v}}_s)=0,$$ (4)

where v_s and v_f are the velocities of solid and fluid, respectively. The total Cauchy stress (σ_t) in the biphasic mixture is the sum of the stresses in the solid phase (σ_s) and in the interstitial fluid (σ_f),

$${\sigma }_t={\sigma }_s+{\sigma }_f,$$ (5)

where

$$\begin{array}{cc}\hfill {\sigma }_s=& -{\varphi }_{s}p\mathit{i}+{\sigma }_e,\hfill \\ \hfill {\sigma }_f=& -{\varphi }_{f}p\mathit{i},\hfill \end{array}$$ (6)

where i is the unit tensor, p is the fluid pressure, and σ_e is the elastic stress in the solid phase. The fluid pressure, p, is governed by Darcy's law,

$$\mathit{w}={\varphi }_f({\mathit{v}}_f-{\mathit{v}}_s)=-k\mathrm{grad}\left(p\right),$$ (7)

where w is the effective fluid flux and k is the isotropic hydraulic permeability, which may be location and deformation-dependent.

Assuming hyperelastic behavior, for a finite deformation problem, the elastic Cauchy stress is defined by

$${\sigma }_e=J^{-1}\mathit{F}{\mathit{S}}_e{\mathit{F}}^T,{\mathit{S}}_e=2\frac{\partial W}{\partial \mathit{C}}\left(\mathit{C}\right),$$ (8)

where S_e is the elastic second Piola-Kirchhoff stress and W is the elastic potential (or elastic strain energy).

2.2. Nonlinear elasticity of a medium including statistically distributed fibers

The effect of distributed fibers on the mechanical properties of cartilage is included in the elastic potential, W. The solid phase of cartilage is considered to be a composite comprised of a nearly incompressible, homogeneous matrix (subscript 0), and nearly incompressible, distributed fibers (subscript 1). The matrix and fiber fractions with respect to the solid are defined, in the current and reference configurations, as

$${\tilde{\varphi }}_0=\frac{{\varphi }_0}{{\varphi }_s},{\tilde{\varphi }}_1=\frac{{\varphi }_1}{{\varphi }_s},{\tilde{\varphi }}_{0R}=\frac{{\varphi }_{0R}}{{\varphi }_{sR}},{\tilde{\varphi }}_{1R}=\frac{{\varphi }_{1R}}{{\varphi }_{sR}},$$ (9)

where ϕ₀ and ϕ₁ are the current fractions with respect to the whole mixture, and ϕ_0R and ϕ_1R are the referential fractions with respect to the whole mixture. The matrix and fiber fractions relative to the solid are such that

$${\tilde{\varphi }}_0+{\tilde{\varphi }}_1=1,{\tilde{\varphi }}_{0R}+{\tilde{\varphi }}_{1R}=1.$$ (10)

The fiber orientation is assumed to be statistical at every point, and varying across cartilage depth, and the volumetric concentration of the fibers is assumed to be depth-dependent. The formulations of statistical fiber distribution by Federico et al. [18–20] were adopted in the current study. In the reference configuration, the probability to find a fiber oriented in direction $\mathit{M}\in {\mathbb{S}}^2{\mathcal{B}}_R$ (where ${\mathbb{S}}^2{\mathcal{B}}_R$ is the referential unit sphere) is given by ψ(M). The probability ψ is normalized over the unit sphere, i.e.,

$${\int }_{{\mathbb{S}}^2{\mathcal{B}}_R}\psi \left(M\right)\mathrm{d}S=1.$$ (11)

The matrix is assumed to be isotropic with elastic potential W₀, and the fibers are assumed to be anisotropic, with elastic potential W₁ given by

$$W_1(\mathit{C},\mathit{A})=W_{1i}\left(\mathit{C}\right)+\mathcal{H}(I_4(\mathit{C},\mathit{A})-1)W_{1a}(\mathit{C},\mathit{A}),$$ (12)

where W_1i is an isotropic contribution, W_1a is an anisotropic contribution, function of the structure tensor $\mathit{A}=\mathit{M}\otimes \mathit{M}$, function $\mathcal{H}$ is the Heaviside step, with argument I₄(C, A) – 1. The invariant

$$I_4(\mathit{C},\mathit{A})=\mathit{C}:\mathit{A}=C_{IJ}{A}_{IJ}=C_{IJ}{M}_I{M}_J$$ (13)

is usually called the fourth invariant of C and equals the square of the stretch in the fiber direction. Therefore, when I₄(C, A) – 1 > 0, the fiber is in extension and the anisotropic term W_1a(C, A) is active since $\mathcal{H}(I_4(\mathit{C},\mathit{A})-1)=1$. In contrast, when I₄(C, A) – 1 < 0, the fiber is in contraction and the anisotropic term W_1a(C, A) is “killed” since $\mathcal{H}(I_4(\mathit{C},\mathit{A})-1)=0$.

The overall elastic potential articular cartilage, seen as a composite with a continuous infinity of fiber families, is obtained via rule of mixture, i.e.,

$$W\left(\mathit{C}\right)={\tilde{\varphi }}_{0R}{W}_0\left(\mathit{C}\right)+{\tilde{\varphi }}_{1R}{\int }_{{\mathbb{S}}^2{\mathcal{B}}_R}\psi \left(\mathit{M}\right)\left[W_{1i}\left(\mathit{C}\right)+\mathcal{H}(I_4(\mathit{C},\mathit{A})-1)W_{1a}(\mathit{C},\mathit{A})\right]\mathrm{d}S,$$ (14)

which, considering that W_1i(C) does not depend on direction and that the probability ψ is normalized to 1 (Eq. (11)), reduces to

$$W\left(\mathit{C}\right)={\tilde{\varphi }}_{0R}{W}_0\left(\mathit{C}\right)+{\tilde{\varphi }}_{1R}\left[W_{1i}\left(\mathit{C}\right)+{\int }_{{\mathbb{S}}^2{\mathcal{B}}_R}\psi \left(\mathit{M}\right)\mathcal{H}(I_4(\mathit{C},\mathit{A})-1)W_{1a}(\mathit{C},\mathit{A})\mathrm{d}S\right]$$ (15)

We remark again that, although the matrix and fibers are incompressible, the presence of the pores makes the mixture overall compressible. Therefore, the potential must be assumed compressible [20]. Note also that, in [20], the potential was defined using the referential fractions ϕ_0R and ϕ_1R with respect to the whole mixture. Using the fractions referential fractions ${\tilde{\varphi }}_{0R}$ and ${\tilde{\varphi }}_{1R}$ with respect to the solid, as we do here, is equivalent, and practically amounts to rescaling the potentials W₀ and W₁ of a factor ϕ_sR.

For practical problems, it is convenient to consider a set of N fiber directions M_α (each with structure tensor ${\mathit{A}}_{\alpha }={\mathit{M}}_{\alpha }\otimes {\mathit{M}}_{\alpha }$), such that the probability takes the N discrete values ψ_α = ψ(M_α), which must obey, at each point X in the reference configuration, the normalization condition

$$\sum _{\alpha =1}^N{\psi }_{\alpha }=1,$$ (16)

which is the discretized version of Eq. (11). The overall elastic potential (15) takes the discretized form

$$W\left(\mathit{C}\right)={\tilde{\varphi }}_{0R}{W}_0\left(\mathit{C}\right)+{\tilde{\varphi }}_{1R}\left[W_{1i}\left(\mathit{C}\right)+\sum _{\alpha =1}^N\mathcal{H}(I_4(\mathit{C},{\mathit{A}}_{\alpha })-1){\psi }_{\alpha }{W}_{1a}(\mathit{C},{\mathit{A}}_{\alpha })\right].$$ (17)

2.3. Finite Element implementation

For the Finite Element implementation, we consider a compressible Mooney-Rivlin model for the isotropic matrix term W₀ (the Mooney-Rivlin coefficients, usually indicated by C₁₀ and C₀₁, are here denoted A₀ and B₀, in order to avoid confusion with the superscripts 0 and 1 used for matrix and fibers), a compressible neo-Hookean model for the isotropic fiber term W_1i, and an anisotropic neo-Hookean-like term for the anisotropic fiber term, i.e.,

$$\begin{array}{cc}\hfill W_0\left(\mathit{C}\right)=& A_0({\stackrel{‒}{I}}_1\left(\mathit{C}\right)-3)+B_0({\stackrel{‒}{I}}_2\left(\mathit{C}\right)-3)+\frac{1}{2}\kappa {(J-1)}^2,\hfill \\ \hfill W_{1i}\left(\mathit{C}\right)=& \frac{1}{2}{C}_{1i}(I_1\left(\mathit{C}\right)-3)-C_{1i}\ln J+\frac{1}{2}\lambda {\left(\ln J\right)}^2,\hfill \\ \hfill W_{1a}(\mathit{C},\mathit{A})=& \frac{1}{2}{C}_{1a}{(I_4(\mathit{C},\mathit{A})-1)}^2,\hfill \end{array}$$ (18)

where A₀, B₀, and κ are the material parameters for the matrix, C_1i, λ, and C_1a are the material parameters for collagen fibers, and the invariants other than the already defined I₄ (Eq. (13)) are

$$\begin{array}{cc}\hfill & I_1\left(\mathit{C}\right)=\mathrm{tr}\left(\mathit{C}\right),\hfill \\ \hfill & I_2\left(\mathit{C}\right)=\frac{1}{2}[{\left(\mathrm{tr}\mathit{C}\right)}^2-\mathrm{tr}\left({\mathit{C}}^2\right)],\hfill \\ \hfill & {\stackrel{‒}{I}}_1=J^{-2∕3}{I}_1,{\stackrel{‒}{I}}_2=J^{-4∕3}{I}_2.\hfill \end{array}$$ (19)

Note that COMSOL uses the distortional invariants Ī₁ and Ī₂ for the definition of the Mooney-Rivlin model, resulting in a decoupled elastic potential, i.e., the sum of a function of the distortional deformation C̄ and a function of the volume ratio J. A decoupled potential would be suitable only for a quasi-incompressible material [35]. However, in this case, the coupling is provided by the isotropic and anisotropic fiber potentials W_1i and W_1a, which are functions of the whole right Cauchy-Green deformation tensor C. Therefore, the overall potential is suitable for a material like cartilage, which has an apparent compressibility due to the fact that the fluid can escape from the boundaries of the system [20].

If the probability distribution of orientation ψ is transversely isotropic, the fiber direction vector is conveniently expressed in polar coordinates, as

$${\left\{\mathit{M}(\theta ,\phi )\right\}}^T=\left[\sin \theta \cos \phi \sin \theta \sin \phi \cos \theta \right]$$ (20)

where θ and φ represent the colatitude and the longitude angle, respectively. The colatitude angle varies in the range from 0° to 90°, which represents the fiber direction in the transverse and normal planes relative to the cartilage surface, respectively. The fibers are considered to be randomly distributed in the range from 0° to 360° along the longitudinal direction, φ.

If direction three is selected to be the cartilage depth, cartilage is assumed to be transversely isotropic in this direction, and the deformation is axisymmetric in the same direction. Then, the right Cauchy-Green deformation tensor takes the matrix representation

$$\left[\mathit{C}\right]=\left[\begin{array}{ccc}\hfill C_{11}\hfill & \hfill 0\hfill & \hfill C_{13}\hfill \\ \hfill 0\hfill & \hfill C_{22}\hfill & \hfill 0\hfill \\ \hfill C_{31}\hfill & \hfill 0\hfill & \hfill C_{33}\hfill \end{array}\right],$$ (21)

and the invariants are expressed explicitly as

$$\begin{array}{cc}\hfill I_1\left(\mathit{C}\right)=& C_{11}+C_{22}+C_{33},\hfill \\ \hfill I_2\left(\mathit{C}\right)=& \frac{1}{2}({\left(I_1\left(\mathit{C}\right)\right)}^2-C_{11}^2-C_{22}^2-C_{33}^2-2C_{13}{C}_{31}),\hfill \\ \hfill I_4(\mathit{C},\mathit{M})=& M_1(C_{11}{M}_1+C_{13}{M}_3)+M_2{C}_{22}{M}_2+M_3(C_{31}{M}_1+C_{33}{M}_3),\hfill \end{array}$$ (22)

where M_I(θ, φ) (I = 1, 2, 3) have been defined in Eq. (20).

2.4. Case study

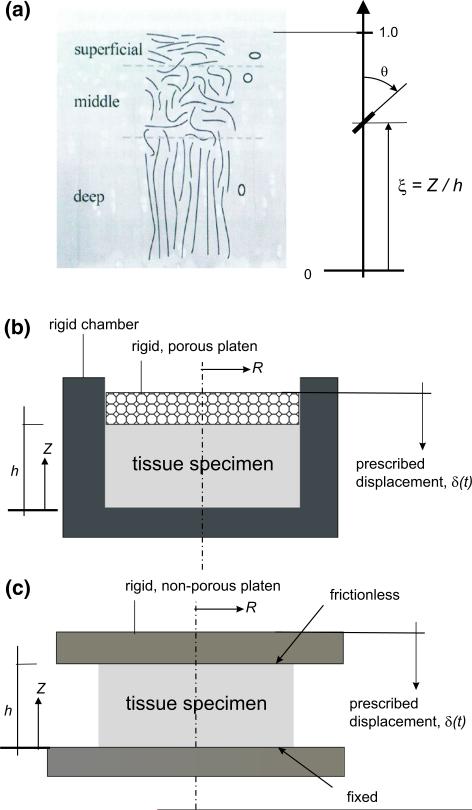
A representative cartilage sample, as illustrated in Fig. 1a, is considered to test our approach. The location of the fiber is defined by the normalized depth, ξ = Z/h with Z and h being the coordinate in direction 3 (direction of the depth of the tissue) in the reference configuration and the referential cartilage thickness, respectively. The fiber orientation is defined by the colatitude angle, θ. Typically, the fiber orientation is close to 90° and 0° near the articular surface (ξ → 1) and the bone–cartilage interface (ξ → 0), respectively.

Fig. 1.

Cartilage model. a Definition of the cartilage depth and fiber orientation. b Confined compression test. c Unconfined compression test. The cartilage depth is defined by the normalized depth, ξ = Z/h with Z and h being the vertical coordinate and cartilage thickness, respectively. The fiber orientation is defined by the colatitude angle, θ

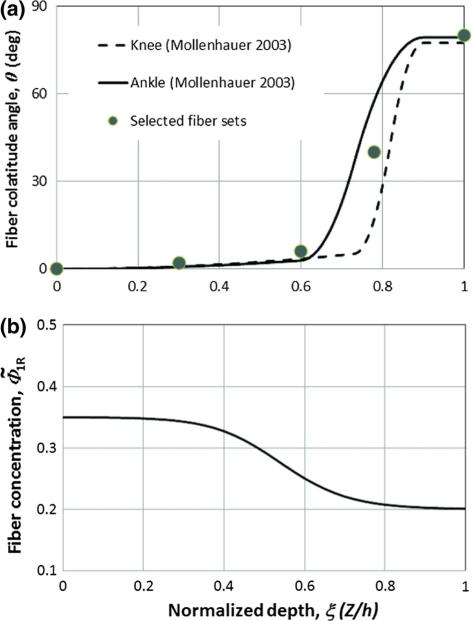
The fiber orientation distributions across the cartilage thickness have been determined experimentally in a previous study [28], and typical results for cartilage layers at the knee and ankle are shown in Fig. 2a. For numerical testing, we selected five representative fiber sets (N = 5) from five different cartilage depths (ξ_α equal to 0.0, 0.3, 0.6, 0.75, 1.0, θ_α equal to 0°, 2°, 6°, 40°, 80°, with α ∈ {1, 2,. . . ,5}. For a transversely isotropic problem, the fibers are assumed to be equally distributed on the transverse plane, i.e., for a fixed colatitude θ, all longitudes φ have the same probability. Each of the fiber sets (α ∈ {1, . . . ,5}) is evenly distributed in the range from 0° to 360° in the longitudinal direction (φ); and they are represented by five evenly distributed orientations, i.e., φ_β = (β · 72)°, with β ∈ {1, . . . , 5}, i.e., at 0°, 72°, 144°, 216°, 288°.

Fig. 2.

The fiber orientation and volumetric concentration as a function of cartilage depth. a The fiber orientation for representative human ankle and knee cartilage layers [28]. From the deep zone (ξ =0) to the superficial zone (ξ = 1.0), the fiber orientation varies from nearly vertical to the contact surface (approximately 0°) to nearly parallel to the contact surface (approximately 80°). A set of five fiber orientations (symbols) are selected to represent the test data. b Fiber volumetric fraction with respect to the solid, ${\tilde{\varphi }}_{1R}\left(\xi \right)$, as a function of cartilage depth (constructed based on experimental data [5,36])

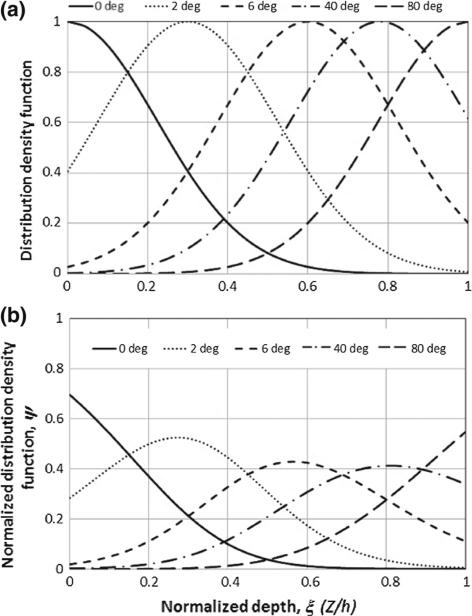
We further assume that the distribution density of the α-th fiber set follows a normal distribution:

$$f_{\alpha }\left(\xi \right)=\exp \left[-b{(\xi -{\xi }_{\alpha })}^2\right]$$ (23)

where b is a parameter determining the distribution concentration. Assuming that the fiber concentration parameter is b = 10 for all five fiber sets, the fiber density distribution, f_α(ξ), is defined and plotted in Fig. 3a. The α-th fiber set (α ∈ {1, . . . ,5}) has the maximal density at ξ_α and that density decreases rapidly with increasing distance from ξ_α. The distribution density function is constructed by normalizing the normal distribution density (23):

$${\psi }_{\alpha }\left(\xi \right)=\frac{\exp \left[-b{(\xi -{\xi }_{\alpha })}^2\right]}{{\sum }_{\alpha =1}^5\exp \left[-b{(\xi -{\xi }_{\alpha })}^2\right]}.$$ (24)

It is clear that the distribution density function (24) satisfies ${\sum }_{\alpha =1}^5{\psi }_{\alpha }\left(\xi \right)=1$ everywhere. The distribution density function set used in our simulations is shown in Fig. 3b. Since the distribution of each fiber set in the longitudinal direction is discretized in five evenly distributed orientations (β ∈ {1, 2, . . . ,5}), there is a total of 25 fiber families and the normal distribution function for each of families is ${\stackrel{‒}{\psi }}_{\alpha ,\beta }=\frac{1}{5}{\psi }_{\alpha }$, consequently, ${\sum }_{\alpha =1}^5{\sum }_{\beta =1}^5{\stackrel{‒}{\psi }}_{\alpha ,\beta }=1$ is satisfied everywhere.

Fig. 3.

The distribution density functions of the five selected fibers (0°, 2°, 6°, 40°, and 80°). a Distribution density functions. b Normalized distribution density functions

The elastic potential associated with the effect of the fibers [Eq. (17)] is expressed explicitly as

$$\begin{array}{cc}\hfill W_1=& {\tilde{\varphi }}_{0R}\left[A_0({\stackrel{‒}{I}}_1-3)+B_0({\stackrel{‒}{I}}_2-3)+\frac{1}{2}\kappa {(J-1)}^2\right]\hfill \\ \hfill & +{\tilde{\varphi }}_{1R}[\frac{1}{2}{C}_{1i}(I_1-3)-C_{1i}\ln J+\frac{1}{2}\lambda {\left(\ln J\right)}^2+\phantom{]}\hfill \\ \hfill & \phantom{[}+\frac{1}{2}{C}_{1a}\sum _{\alpha =1}^5\frac{{\psi }_{\alpha }}{5}\sum _{\beta =1}^5\mathcal{H}(I_4({\theta }_{\alpha },{\phi }_{\beta })-1){(I_4({\theta }_{\alpha },{\phi }_{\beta })-1)}^2],\hfill \end{array}$$ (25)

where I₄(θ_α, φ_β) is a short notation for I₄(C, A_α), at each value of C.

The referential fiber volumetric concentration is considered to be depth-dependent, i.e., expressed as a function ${\tilde{\varphi }}_{1R}\left(\xi \right)$, and is shown in Fig. 2b. The volumetric concentration of the matrix is ${\tilde{\varphi }}_{0R}\left(\xi \right)=1-{\tilde{\varphi }}_{1R}\left(\xi \right)$. The model parameters (A₀ = B₀ = C₀ = 0.1 MPa, κ = 20 C₀, C_1i = 0.1 MPa, and C_1a = 5 MPa) were adopted from previous studies [19]. Assuming ν = 0.3, the parameter λ is estimated to be λ = 2C_1iν/(1 – 2ν) = 0.15 MPa. The matrix and fibers were assumed to be stress-free in the reference configuration, at t = 0.

2.5. Numerical tests

Simulations were performed for confined (Fig. 1b) and unconfined compression (Fig. 1c) configurations. For the case of confined compression, the tissue specimens were compressed in a confining chamber with a rigid, porous platen connected to a load cell. For the case of unconfined compression, the tissue specimens were compressed between two rigid, non-porous platens; the boundary at the bottom was fixed, simulating the cartilage–bone bound, and the fluid pressure was assumed to be zero at the lateral surface of the specimen. An axisymmetric FE model is used for all four numerical tests. The sample has a referential thickness h = 2 mm and diameter of 4 mm. A displacement of 0.1 mm was applied on the surface via an exponential ramp function

$$\delta \left(t\right)={\delta }_0\left[1-\exp \left(-\frac{t}{{\tau }_0}\right)\right],$$ (26)

where δ₀ = 0.1 mm and τ₀ = 250 s are constants.

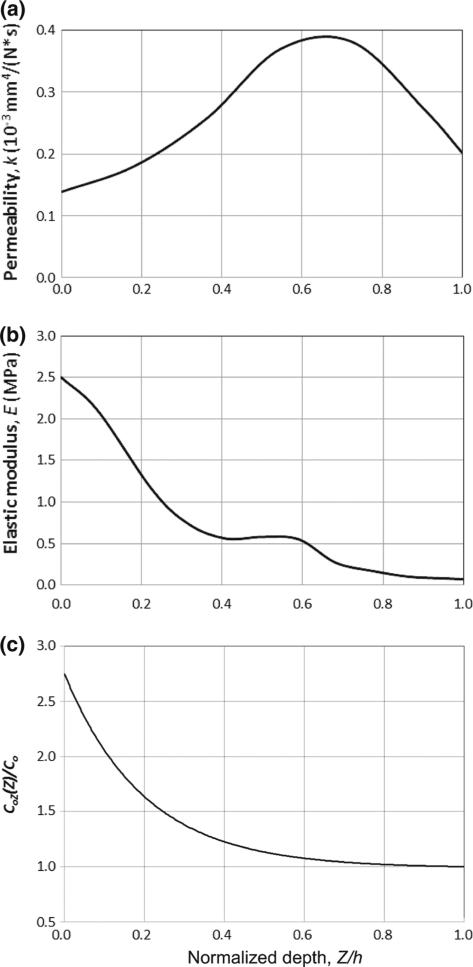
Four numerical tests (A, B, C, and D) were performed in the current study. Tests A and B were designed to reproduce the results by [37] and to validate the biphasic modeling in the current study. The cartilage samples for tests A and B were isotropic and did not include distributed fibers; the tests were performed in confined compression. For test A, the solid phase was assumed to be linearly elastic and homogenous (Poisson's ratio 0.10; Young's modulus 0.55 MPa; hydraulic permeability 0.250×10⁻³ mm⁴ N⁻¹ s⁻¹). For test B, cartilage was isotropic and inhomogeneous, with depth-dependent hydraulic permeability [38] and Young's modulus [39] as shown in Fig. 4a, b, respectively.

Fig. 4.

Depth-dependent hydraulic permeability (a), elastic modulus (b), and normalized cartilage matrix stiffness (C_0inh/C₀) (c) used in the numerical simulations. The data are based on published experimental studies on inhomogeneous permeability [38] and stiffness [39]. Note that, for Tests C and D, which assume a deformation-dependent permeability, the graph is intended to refer to the undeformed permeability k₀

Tests C and D are the primary focus of the current study. The cartilage samples for tests C and D included distributed fibers, and the tests were performed in unconfined compression. Cartilage was assumed to embed distributed fibers, with a fiber across the tissue depth as described in the previous section. Fibers and matrix were assumed to be hyperelastic, and the material properties from [19] were used. The hydraulic permeability was assumed to be depth- and deformation-dependent and was used as defined by [40],

$$k\left(\xi \right)=k_0\left(\xi \right){\left(\frac{J-{\varphi }_{sR}}{1-{\varphi }_{sR}}\right)}^2\exp \left[\frac{M_0}{2}(J^2-1)\right],$$ (27)

where k₀(ξ) is the depth-dependent permeability for the undeformed state, as plotted in Fig. 4a. M₀ (=1.3) is a non-dimensional material parameter. Test D was designed to fit experimental data. The model structure, material parameters, and loading conditions in Test D were the same as those in Test C, except that the stiffness of the matrix was depth-dependent and was adjusted to fit to the experimental data. In Test D, the stiffness parameters of the matrix, A₀, B₀, and κ, were considered to be A₀ = B₀ = C_0inh and κ = 20 C_0inh, where the inhomogeneous stiffness C_0inh is a function of tissue depth (Fig. 4c), given by

$$C_{0inh}\left(\xi \right)=C_0\left(1+a_{C_0}\frac{1-\exp \left(b_{C_0}(1-\xi )\right)}{1-\exp \left(b_{C_0}\right)}\right),$$ (28)

where a_C0 and b_C0 are positive, dimensionless parameters that determine the magnitude and tendency, respectively, of the variations of C_0inh(ξ). It is easy to see that C_0inh(ξ) increases from C_0inh(1) = C₀ at the articular surface (ξ = Z/h = 1) to C_0inh(0) = (1 + a_C0)C₀ at the cartilage/bone interface (ξ = Z/h = 0). The matrix stiffness variation function (28) (a_C0 = 1.75 and b_C0 = 5.0) is constructed based on the experimental data [39,41–43] and is plotted in Fig. 4c.

The FE formulations have been implemented into the commercial FE software COMSOL (version 3.5a). We applied Standard and Structural Modules in the FE software package. Darcy's equation (7) was solved by an analog to the diffusion process. The biphasic modeling was simulated by coupling diffusion with dynamic solid mechanics. The descriptions of the test models and all material parameters used in the FE modeling are listed in Table 1.

TABLE 1.

The material parameters of the soft tissue matrix and collagen fibers used in the FE modeling

Test A	Permeability	k	2.50	10–3 mm4 N–1 s–1
Linearly elastic, isotropic, homogeneous	Young's modulus	E	0.55	MPa
	Poisson's ratio	ν	0.1	–
Test B	Permeability	k(ξ)	Fig. 4a	10–3 mm4 N–1 s–1
Linearly elastic, isotropic, inhomogeneous	Young's modulus	E(ξ)	Fig. 4b	MPa
	Poisson's ratio	ν	0.1	–
Test C	Undeformed permeability	k0(ξ)	Fig.4a	10–3 mm4 N–1 s–1
Hyperelastic, finite deformation, with collagen fibers, homogeneous matrix	Permeability parameter	M 0	1.3	–
	Matrix material parameter	A 0	C 0	MPa
	Matrix material parameter	B 0	C 0	MPa
	Matrix material parameter	κ	20 C0	MPa
	Matrix material parameter	C 0	0.1	MPa
	Fiber material parameter	C 1i	0.1	MPa
	Fiber material parameter	λ	0.15	MPa
	Fiber material parameter	C 1a	5.0	MPa
	Matrix-to-solid fraction	${\tilde{\varphi }}_{0R}$	$1-{\tilde{\varphi }}_{1R}$	–
	Fiber-to-solid fraction	${\tilde{\varphi }}_{1R}$	Fig. 2b	–
Test D	Undeformed permeability	k0(ξ)	Fig.4a	10–3 mm4 N–1 s–1
Hyperelastic, finite deformation, with collagen fibers, inhomogeneous matrix	Permeability parameter	M 0	1.3	–
	Matrix material parameter	A 0	C0inh(ξ)	MPa
	Matrix material parameter	B 0	C0inh(ξ)	MPa
	Matrix material parameter	κ	20 C0inh(ξ)	MPa
	Matrix material parameter	C0inh(ξ)	Fig.4c	MPa
	Matrix material parameter	a C0	1.75	–
	Matrix material parameter	b C0	5.0	–
	Fiber material parameter	C 1i	0.1	MPa
	Fiber material parameter	λ	0.15	MPa
	Fiber material parameter	C 1a	5.0	MPa
	Ref. matrix-to-solid fraction	${\tilde{\varphi }}_{0R}$	$1-{\tilde{\varphi }}_{1R}$	–
	Ref. fiber-to-solid fraction	${\tilde{\varphi }}_{1R}$	Fig. 2b	–
All Tests	Referential solid fraction	ϕ s R	0.2	–
	Referential fluid fraction	ϕ f R	0.8	–

3. Results

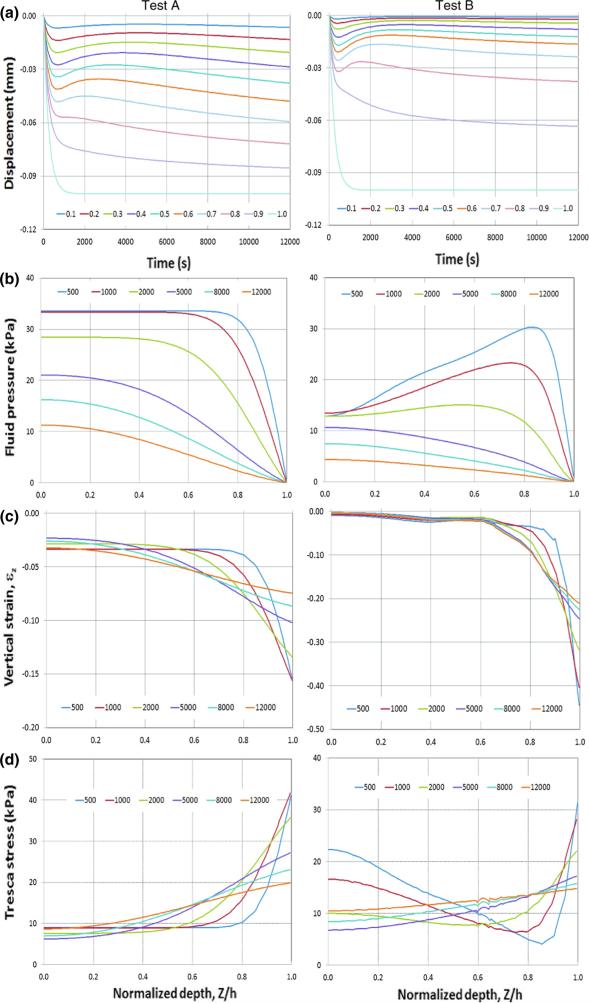
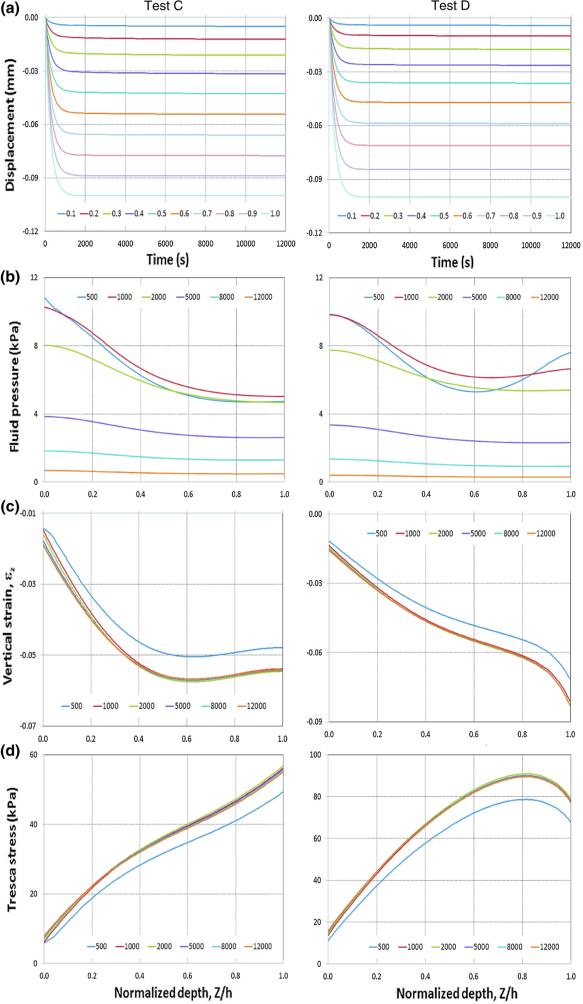
The simulated displacement as a function of depth and time is shown in Fig. 5a left and right, for Tests A and B, and in Fig. 6a left and right, for Tests C and D, respectively. The results of the benchmark Tests A (with homogeneous, isotropic elastic properties) and B (with inhomogeneous, isotropic elastic properties) were compared with those obtained using the analytical modeling [37] and they agree well (results not shown). Comparison of the isotropic Tests A and B with fiber-reinforced, anisotropic Tests B and C shows that the distributed fibers have a substantial effect on cartilage deformation. The surface displacements for all four tests are the same (they are prescribed), whereas the displacements within the cartilage layer are quite different: the cartilage with distributed fibers (Tests C and D, Fig. 6a) has more uniformly distributed displacements across the cartilage thickness compared to those obtained using the isotropic models (Tests A and B, Fig. 5a). In addition, the displacements across the cartilage depth for the distributed fiber model (Fig. 6a) reach steady state faster than those of the isotropic cartilage models (Fig. 5a).

Fig. 5.

The predicted vertical displacements, fluid pressure, vertical nominal strain, and Tresca stress as a function of cartilage depth and time for Tests A and B (isotropic models). All parameters were taken at R = 0, where R is the referential radial coordinate. a vertical displacement. b Fluid pressure. c Vertical nominal strain. d Tresca stress. Left column Test A. Right column Test B. The time histories of the vertical displacement at ten different depths (ξ = Z/h equal to 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0) are plotted. ξ is the normalized depth with ξ = 0 and 1.0 referring to the bone–cartilage interface and contact surface, respectively. The fluid pressure, vertical nominal strain, and Tresca stress for six time points (t equal to 500, 1000, 2000, 5000, 8000, and 12000 s) across the cartilage layer are plotted

Fig. 6.

The predicted vertical displacements, fluid pressure, vertical nominal strain, and Tresca stress as a function of cartilage depth and time for Tests C and D (distributed fiber models). All parameters were taken at R = 0, where R is the referential radial coordinate. a Vertical displacement. b Fluid pressure. c Vertical nominal strain. d Tresca stress. Left column Test C. Right column Test D. The time histories of the vertical displacement at ten different depths (ξ = Z/h equal to 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0) are plotted. ξ is the normalized depth with ξ = 0 and 1.0 referring to the bone–cartilage interface and contact surface, respectively. The fluid pressure, vertical nominal strain, and Tresca stress for six time points (t equal to 500, 1000, 2000, 5000, 8000, and 12000 s) across the cartilage layer are plotted

The predicted fluid pressures as a function of cartilage depth (ξ = Z/h) at six time points (500, 1000, 2000, 5000, 8000, 12000 s) are shown in Fig. 5b left and right, for Tests A and B, and in Fig. 6b left and right, for Tests C and D, respectively. The results for all test models show that the fluid pressure decreases with time during the entire loading process (as expected), but does not reach steady state even at 12000 s. The difference of the predicted fluid pressure of test A (Fig. 5b left) from that of test B (Fig. 5b right) reflects the effects of the non-uniformity of the cartilage matrix. The fluid pressure tends to vary more dramatically across the cartilage thickness for t < 1000 s and the fluid pressure at the cartilage–bone interface (Z/h = 0) reduces by approximately 50 % for extended time (t > 5000 s), when the cartilage elasticity and permeability are changed from constant to being depth dependent (Table 1). In contrast, the effects of the change of the properties of the matrix from homogeneous to inhomogeneous are less dramatic for the samples with distributed fibers (Fig. 6b). The change of the cartilage elasticity from constant to being depth dependent caused only slight variations in the fluid pressure distributions across the depth for t < 1000 s and little effects on the fluid pressure distribution for extended time (t > 5000 s).

The predicted vertical nominal strains (ε_Z) as a function of cartilage depth (ξ = Z/h) at six time points (500, 1000, 2000, 5000, 8000, 12000 s) are shown in Fig. 5c left and right, for Tests A and B, and in Fig. 6c left and right, for Tests C and D, respectively. For the isotropic models (Tests A and B), the vertical nominal strain (ε_Z) increases with ξ and reaches a maximum at the contact surface (ξ = 1.0) (Fig. 5c). The inhomogeneous model (Test B) produces the most dramatic variations in the strain distributions across the cartilage layer (Fig. 5c right). In contrast, for the distributed fiber models (Tests C and D), the vertical nominal strain (ε_Z) also increases with ξ and reaches maximum around superficial layer (Fig. 6c); however, the magnitude of the maximal strain is substantially smaller and varies less dramatically with time. The predicted strain of the distributed fiber models (Tests C and D) reached steady state after 1000 s (Fig. 6c), whereas it did not reach steady state even after 12000 s for the isotropic models (Fig. 5c). The change of the cartilage elasticity of the distributed fiber models from homogeneous (Test C) to being depth dependent (Test D) causes an increase in the strain magnitude in the proximity of the articular surface (Fig. 6c left vs. right).

The predicted Tresca stress as a function of cartilage depth (ξ = Z/h) at six time points (500, 1000, 2000, 5000, 8000, 12000 s) are shown in Fig. 5d left and right, for Tests A and B, and in Fig. 6d left and right, for Tests C and D, respectively. The general trends of the stress distributions across the cartilage thickness are consistent with those of the strains, in that the stress of the distributed fiber models (Tests C and D) reached steady states after 1000 s (Fig. 6d), whereas it did not reach steady state even after 12000s for the isotropic models (Fig. 5d). The maximal stress occurs at the superficial zone at all times, for all four tests. The change of the cartilage elasticity of the distributed fiber models from homogeneous (Test C) to being depth dependent (Test D) causes a decrease in the stress magnitude near the superficial layer (Fig. 6d left vs. right).

4. Discussion and conclusion

Variability in mechanical properties within a biological specimen is often high. Collagen fibril orientation and density in a single study may vary by 10–40 %. Therefore, models including probability distributions of the collagen fibers, such as those proposed by [18–20], are promising for tackling practical problems. These models have been implemented numerically [19,29,30], based on extensive programming of user subroutines. In the current study, we developed a discretization methodology to implement the probability distribution models [18,19] into a commercially available FE software package (COMSOL), without using any routine programming, and with the sole use of native functions of the FE package. The implementation includes the representation of the elastic properties as well as the presence of the fluid phase, and has been applied to a practical problem.

The fibers in articular cartilage have a complex arrangement that can be captured well by the use of a probability distribution parameterized by the depth coordinate. For example, Federico and Herzog [18] analytically predicted the anisotropy of the permeability and reproduced experimental results on the depth dependence of cartilage permeability by using a probability distribution obtained from the experimental data [28], which we report in Fig. 2. According to the experimental data [28], in the deep zone (ξ = 0), about 70 % of all fibers have an orientation of 0°, 28 % have 2°, 2 % have 6°, and the fraction of fibers with an orientation greater than 6° is negligible. In the superficial zone (ξ = 1.0), about 55 % of the fibers have an orientation of 80°, 34 % have 40°, 11 % have 6°, and a negligible proportion of fibers has an orientation of less than 6°. However, the fiber orientation is typically assumed to be 100 % at a 0° and 90° orientation for the deep and superficial zones of the cartilage [11], respectively.

The collagen fibers cause the anisotropy and inhomogeneity of the properties of cartilage and one way to indirectly take this into account is to assume inhomogeneous elastic properties and permeability across the tissue depth. However, this can only be used for uni-dimensional problems such as confined compression [37], where anisotropy does not come into play, and an inhomogeneous but otherwise isotropic model suffices, at least for certain aspects. Indeed, our results confirm that the effects of distributed fiber orientation cannot be simulated by simply using depth-dependent permeability and elastic modulus in otherwise isotropic models. This lack of agreement may be due to the neglected effects of interactions between fibers and matrix, variations in the fiber orientations in the deformed state, and compression–tension asymmetry induced by the fibers.

The predicted tissue strain distribution across the cartilage layer (Fig. 6c right) agrees well with the experimental data by [39], which show that the strain increases about six times from the deep to the superficial zone. The current prediction is also consistent in trend with the experimental data by [41–43], which indicate that the strain increases slowly from the deep zone within approximately 70 % of the cartilage thickness, increases more dramatically in the middle-superficial zone within the remaining 30 % of the cartilage thickness, and reaches its maximum at the contact surface. The measured tissue strain data show especially large variations near the contact surface. These substantial strain variations were attributed to the differences in anatomic structure among specimens, as evidenced in the historical analysis [43].

It is interesting to observe that, for Test C, the strain varies little in approximately 40 % of the cartilage thickness, corresponding roughly to the superficial zone (Fig. 6c left), whereas the corresponding Tresca stress increases by approximately 45 % (Fig. 6d left). For Test D and within the same cartilage zone, the strain increases by approximately 50 % (Fig. 6c right), whereas the corresponding Tresca stress varies little (Fig. 6d right). This is likely because the cartilage in superficial zone is stressed in the stiffening region for Test C, whereas it is stressed in the plateau region for Test D. A stress-strain curve of fiber-rich tissues (e.g., composite scaffolds) typically shows three regions in compressions [44]: an initial region, where the stress increases nearly linearly with increasing strain, a plateau region, where the stress increases little with increasing strain, and a stiffening region, where the stress increases dramatically with increasing strain. Our results seem to indicate that passing from matrix with elastic properties uniform through the tissue depth (Test C) to matrix with depth-dependent elastic properties (Test D) causes, in an interval of depths, the overall stress–strain relation (as reported in [44]) to change in such a way that the strain stiffening region is shifted to higher strain levels.

It is known that compressive load on cartilage is shared by the fluid and solid phase. From our parametric study (Figs. 5 and 6), it is seen that the fluid pressures calculated using the distributed fiber models are smaller than that using isotropic models, meaning that the solid matrix will carry more load. This explains why the cartilage stress calculated using the distributed fiber model are more than those obtained with the isotropic models.

The depth-dependent elastic modulus used in the numerical test B (Fig. 4b) was taken from published experimental data [45]. The data show that the elastic modulus at the superficial zone is only about 4 % of that observed in the deep zone, which makes sense physiologically. Indeed, in the literature, the elastic modulus of the matrix of articular cartilage is usually obtained through compressive tests, by applying loading normal to the contact surface. The proteoglycans have a higher volumetric fraction in the deep zone compared to the superficial zone, and consequently the compressive stiffness of the tissue is higher in the deep zone than that in the superficial zone. One would therefore expect that the trend of the depth-dependent elastic modulus in the direction parallel to the surface should be the opposite: the elastic modulus in the superficial zone should be much greater than that expected in the deep zone, because the collagen fibers are oriented in the transverse plane. Articular cartilage maintains mechanical stability under physiological conditions because it carries mainly tensile stress in the direction parallel to the surface in the superficial zone. These phenomena have been included in the fiber distribution model (Tests C and D), whereas they were not considered in the isotropic model (Test B). This is one of the reasons why the isotropic models cannot correctly describe the mechanical behavior of articular cartilage under physiological conditions.

In the current study, we demonstrated how one can represent an experimentally observed fiber distribution using discrete fiber families. More precise results may be obtained by using a greater number of fiber sets. However, we have not yet performed numerical tests to verify this speculation.

The distributed fibers affect not only the mechanical characteristics, but also the permeability of the cartilage; consequently, the cartilage permeability is anisotropic. The deformation-dependent anisotropy of cartilage permeability has been studied in previous works [30–33,46,47], but has not been included in this work, which focuses on the elasticity of the tissue. Therefore, in the current study, the cartilage permeability is considered as being deformation dependent, but isotropic.

The depth-dependent mechanical characteristics of the cartilage are also associated with the fixed charge density of the proteoglycans, which are distributed unevenly across the depth [11]. The current model is focused on the effects of the distributed collagen fibers and does not include the fixed charge density; therefore, the swelling characteristics cannot be simulated using the current model. Another limitation of the proposed approach is that the distribution density function (23) was not based directly on experimental observation. Consequently, solutions may be different if different density distribution functions (23) are applied. More experimental data are needed to determine the distribution density function (23); otherwise, one could assume a range of b-values in Eq. (23) to predict the solution range for practical problems. It is in our future plans to explore the development of models of articular cartilage, and of fiber-reinforced soft tissues in general, considered within the broader context of mixture theory (e.g., [48,49]), micromorphic materials (e.g., [50,51]), for which finite element implementations are available (e.g., [52–54]), and higher-gradient materials (e.g., [55–57]). Moreover, it would be interesting to adapt the practical solution method presented in this work to the cases of remodeling and growth [58,59]. This should be done to investigate the influence of these phenomena on the material response of biological tissues (cf., e.g., [60], where the response was studied in the isotropic case, with the aid of the computational algorithm outlined in [61]).